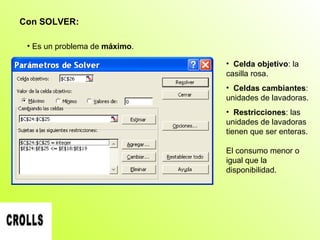
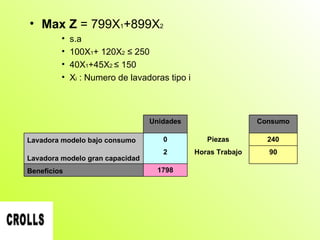
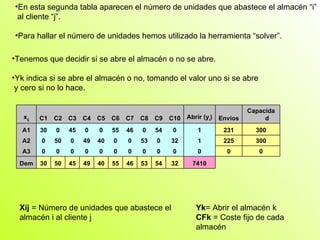
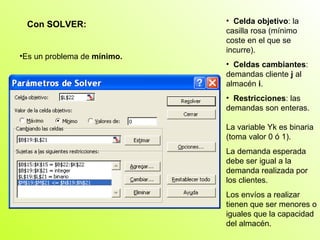
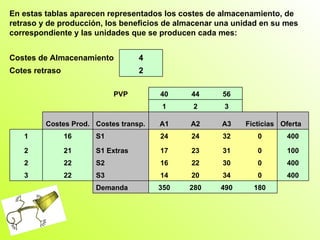
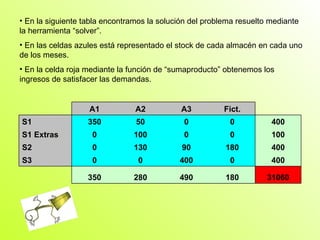
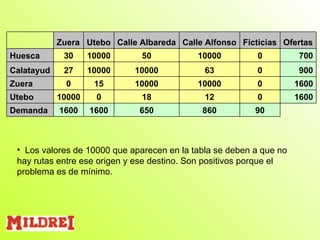
Este documento presenta la resolución de cuatro problemas de investigación operativa utilizando herramientas como WinQSB y Solver. Los problemas incluyen un problema de programación entera sobre la producción de lavadoras, un problema de programación binaria sobre la ubicación de bodegas, un problema de asignación sobre la producción de lámparas, y un problema de transporte sobre la distribución de pasteles. Los problemas se resuelven mediante la formulación de modelos matemáticos y la optimización de funciones objetivo sujetas a restricciones.

1. Juan José Isla Gallinat Vanessa Jaime Álvarez Samuel Lainez Fernández Alberto Lanas Lara Arturo Lorenzo Melendo Rubén Marco Navasa Investigación operativa

2. INDICE INTRODUCCIÓN PROGRAMACIÓN ENTERA PROGRAMACIÓN BINARIA PROBLEMA DE ASIGNACIÓN PROBLEMA DE TRANSPORTE CONCLUSIONES BIBLIOGRAFÍA

3. INTRODUCCIÓN La investigación operativa permite la resolución de problemas que se plantean en el mundo real utilizando herramientas matemáticas, estadísticas y algoritmos de diversos tipos. Estudia complejos sistemas reales con la finalidad de mejorar u optimizar el funcionamiento de los mismos. Algunos historiadores consideran el comienzo de la investigación operativa como una doctrina orientada hacia la resolución de problemas militares, lo cierto es que el desarrollo posterior de este área de conocimiento ha permitido que la investigación operativa se plantee como una de las claves para el análisis de los procesos de toma de decisiones. En este nuevo contexto, hemos realizado nuestro trabajo, en el cual hemos ido resolviendo una serie de problemas de decisión de diversas empresas.

4. INTRODUCCIÓN Hemos planteado cuatro problemas, los dos últimos en relación con el tema 5, uno de ellos sobre transporte y el otro sobre asignación; y los dos primeros sobre la temática vista en el tema 6, el primero es un problema de programación entera y el segundo es acerca de programación binaria. Hemos elegido estos problemas por que nos han parecido interesantes para desarrollar lo visto en clase y porque nos ha parecido que están acorde con lo que se pedía para el trabajo. El primero de ellos lo hemos resuelto tanto con WinQsB como con solver y el resto únicamente con solver. Los problemas están contextualizados dentro del marco de la forma de operar de varias empresas reales. Debido a las dificultades a la hora de encontrar algunos datos y parámetros necesarios para la realización del trabajo, hemos tenido que hacer algunas adaptaciones. Además hemos modificado los nombres originales de las empresas .

5. Programación entera: Crolls La empresa CROLLS S.A se dedica a la producción de lavadoras. Durante los últimos meses han ido observando que sus ventas han descendido considerablemente debido a una mala planificación de la producción y por tanto nos han solicitado obtener la cantidad de lavadoras que deberían producirse para maximizar el beneficio de esta empresa. La empresa produce varios tipos de lavadoras, pero concretamente nos han pedido que calculemos el número de lavadoras de dos tipos, el modelo de bajo consumo y el modelo de gran capacidad.

6. LAVADORA BAJO CONSUMO : LAVADORA GRAN CAPACIDAD : Los beneficios unitarios son 799 y 899 u.m respectivamente.

7. Las restricciones debidas a la mano de obra y a la materia prima vienen dadas por la siguiente tabla: M.B.C M.G.C Disp. Piezas 100 120 250 Horas de trabajo 40 45 150 Beneficio 799 899

8. Con SOLVER: Celda objetivo : la casilla rosa. Celdas cambiantes : unidades de lavadoras. Restricciones : las unidades de lavadoras tienen que ser enteras. El consumo menor o igual que la disponibilidad. Es un problema de máximo .

9. Max Z = 799X 1 +899X 2 s.a 100X 1 + 120X 2 ≤ 250 40X 1 +45X 2 ≤ 150 X i : Numero de lavadoras tipo i Unidades Consumo Lavadora modelo bajo consumo 0 Piezas 240 Lavadora modelo gran capacidad 2 Horas Trabajo 90 Beneficios 1798

10. Con WinQSB: Se trata de un problema de Máximo, escribimos las variables X1 y X2 así como las constantes. Debemos indicar que las variables son enteras.

11. A continuación, hacemos click en “Solve the problem” y resolvemos el problema. La solución que nos queda es la siguiente: La solución es X1= 0 y X2= 2, es decir, para maximizar el beneficio se deben fabricar 2 lavadoras de gran capacidad y ninguna de bajo consumo.

12. Programación binaria : Bodegas Boyardo S.A. La empresa riojana BOYARDO S.A., quiere construir varias bodegas que se utilizarán para abastecer a 10 clientes, cuyas demandas mensuales son: 30, 50, 45, 49, 40, 55, 46, 53, 54 y 32. Se pueden construir en 3 posibles ubicaciones, siendo conocidos los costes unitarios de transporte entre estos lugares y los clientes. Los costes fijos mensuales son: 200, 300 y 300. La capacidad del almacén es de 300 unidades. ¿Cuántos almacenes hay que abrir? ¿En donde?

13. C ij = Coste unitario de abastecer del almacén i al cliente j. MIN Z=Σ Cij * Xij +ΣCfi * Yi` En primer lugar planteamos el problema de mínimo: La tabla siguiente muestra los costes unitarios de la empresa boyardo s.a.: C ij C1 C2 C3 C4 C5 C6 C7 C8 C9 C10 Cap C. fijos A1 20 22 15 21 20 16 20 18 15 26 300 200 A2 24 10 15 12 16 19 22 13 18 19 300 300 A3 19 15 16 18 20 16 19 25 26 24 300 300 Dem 30 50 45 49 40 55 46 53 54 32

14. Xij = Número de unidades que abastece el almacén i al cliente j En esta segunda tabla aparecen el número de unidades que abastece el almacén “i” al cliente “j”. Para hallar el número de unidades hemos utilizado la herramienta “solver”. Tenemos que decidir si se abre el almacén o no se abre. Yk indica si se abre el almacén o no, tomando el valor uno si se abre y cero si no lo hace. Yk = Abrir el almacén k CFk = Coste fijo de cada almacén x ij C1 C2 C3 C4 C5 C6 C7 C8 C9 C10 Abrir (y i ) Envios Capacidad A1 30 0 45 0 0 55 46 0 54 0 1 231 300 A2 0 50 0 49 40 0 0 53 0 32 1 225 300 A3 0 0 0 0 0 0 0 0 0 0 0 0 0 Dem 30 50 45 49 40 55 46 53 54 32 7410

15. Con SOLVER: Es un problema de mínimo. Celda objetivo : la casilla rosa (mínimo coste en el que se incurre). Celdas cambiantes : demandas cliente j al almacén i . Restricciones : las demandas son enteras. La variable Yk es binaria (toma valor 0 ó 1). La demanda esperada debe ser igual a la demanda realizada por los clientes. Los envíos a realizar tienen que ser menores o iguales que la capacidad del almacén.

16. Asignación : Lámparas Aparicio La fábrica de lámparas Aparicio, está planificando la producción para los próximos 3 meses. Las demandas mensuales durante este período serán 350, 280 y 490 unidades. La demanda de cada mes puede satisfacerse la producción de ese mes, debido al suministro que se realiza al final del mismo. Se ha estimado que los precios de venta durante cada mes serán 40, 44 y 56 u.m respectivamente. El coste de producción de cada unidad de producto es 16 u.m. para el primer mes y 22 u.m. para los dos restantes. El exceso de producción puede almacenarse con un costo, de 5 u.m. por mes. La compañía puede producir un máximo de 400 unidades cada mes. Además, durante el primer mes podrá contratar horas extraordinarias, lo que hará que pueda incrementar su producción mensual en 100 unidades, con un incremento en los costos de producción de 6 u.m., por unidad de producto.

17. En estas tablas aparecen representados los costes de almacenamiento, de retraso y de producción, los beneficios de almacenar una unidad en su mes correspondiente y las unidades que se producen cada mes: Costes de Almacenamiento 4 Cotes retraso 2 PVP 40 44 56 1 2 3 Costes Prod. Costes transp. A1 A2 A3 Ficticias Oferta 1 16 S1 24 24 32 0 400 2 21 S1 Extras 17 23 31 0 100 2 22 S2 16 22 30 0 400 3 22 S3 14 20 34 0 400 Demanda 350 280 490 180

18. En la siguiente tabla encontramos la solución del problema resuelto mediante la herramienta “solver”. En las celdas azules está representado el stock de cada almacén en cada uno de los meses. En la celda roja mediante la función de “sumaproducto” obtenemos los ingresos de satisfacer las demandas. A1 A2 A3 Fict. S1 350 50 0 0 400 S1 Extras 0 100 0 0 100 S2 0 130 90 180 400 S3 0 0 400 0 400 350 280 490 180 31060

19. Celda objetivo : la casilla roja (máximo ingreso que obtiene la empresa). Celdas cambiantes : las celdas azules (Cantidad de stock que pueden guardar los almacén cada mes). Restricciones : la fila verde debe ser igual a las demandas y la columna verde deber ser igual a las ofertas.

20. Transporte: Mildrei La empresa pastelera Mildrei posee 2 naves situadas en Huesca y Calatayud que disponen de 700 y 900 unidades de pasteles respectivamente. Las pastelerías a las que envía los pasteles se encuentran situadas en la calle Albareda y la calle Alfonso, demandan 650 y 860 unidades respectivamente. Hay rutas directas desde Huesca hasta la calle Albareda y desde Calatayud hasta Calle Alfonso, pero las entregas de Huesca a calle Alfonso y de Calatayud a la calle Albareda deben hacerse vía Zuera y luego a Utebo.

21. Los costes de transporte a lo largo de estas rutas son: De Huesca a calle Albareda: 50 u.m. De Huesca a Zuera : 30 u.m. De Calatayud a Calle Alfonso : 63 u.m. De Zuera a Utebo : 15 u.m. De Calatayud a Zuera: 27 u.m. De Utebo a Calle Albareda: 18 u.m. De Utebo a Calle Alfonso: 12 u.m.

22. Vías de transporte: HU ZUERA UTEBO AX CA AL 50 30 15 18 27 63 12

23. Los valores de 10000 que aparecen en la tabla se deben a que no hay rutas entre ese origen y ese destino. Son positivos porque el problema es de mínimo. Zuera Utebo Calle Albareda Calle Alfonso Ficticias Ofertas Huesca 30 10000 50 10000 0 700 Calatayud 27 10000 10000 63 0 900 Zuera 0 15 10000 10000 0 1600 Utebo 10000 0 18 12 0 1600 Demanda 1600 1600 650 860 90

24. Por tanto, la ruta más económica es la de Huesca – Calle Albareda, cuyo coste es 50 u.m Zuera Utebo Calle Albareda Calle Alfonso Ficticias Ofertas Huesca 0 0 650 0 50 700 Calatayud 860 0 0 0 40 900 Zuera 740 860 0 0 0 1600 Utebo 0 740 0 860 0 1600 Demandas 1600 1600 650 860 90 78940

25. Celda objetivo : la casilla roja (mínimo coste en el que se incurre). Celdas cambiantes : demandas cliente j al almacén i . (celdas azules) Restricciones : tanto las demandas como las ofertas esperadas tienen que ser iguales a las demandas y ofertas reales.

26. CONCLUSIONES Poner en práctica lo aprendido en clase. Saber resolver problemas de programación lineal (entera y binaria), de asignación y transporte con las herramientas WinQSB y Solver. Poder trabajar en grupo y poner en común los conocimientos adquiridos. Conocer como las empresas calculan los costes o maximizan sus beneficios aplicando un modelo matemático.

27. BIBLIOGRAFÍA www.empresasdelmundo.com www.dosomontano.com www.tuvinoencasa.com www.Zona - Hogar.com www.wikipedia.org www.google.es / imagenes www.lamparasaparicio.com

28. FIN