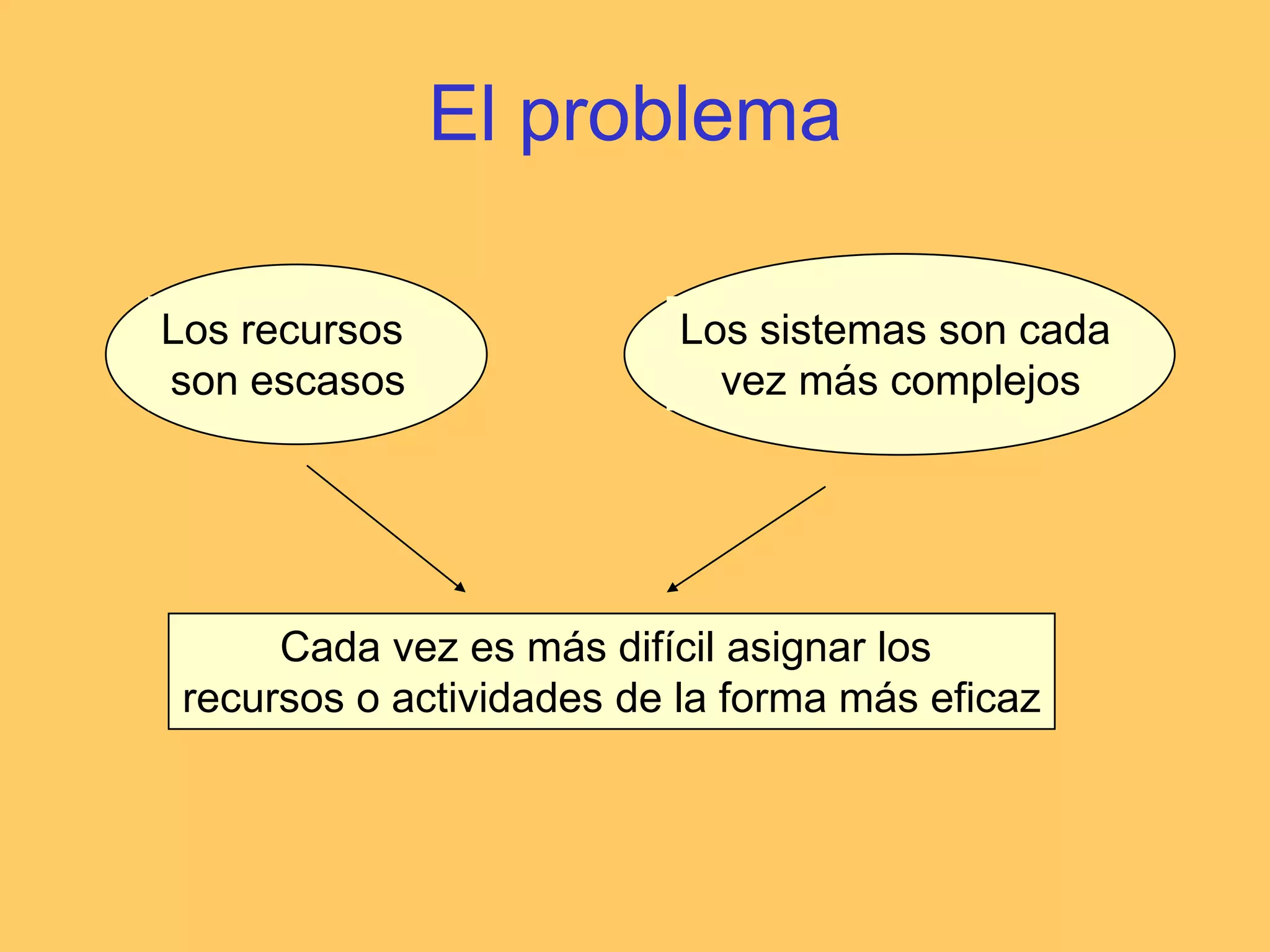
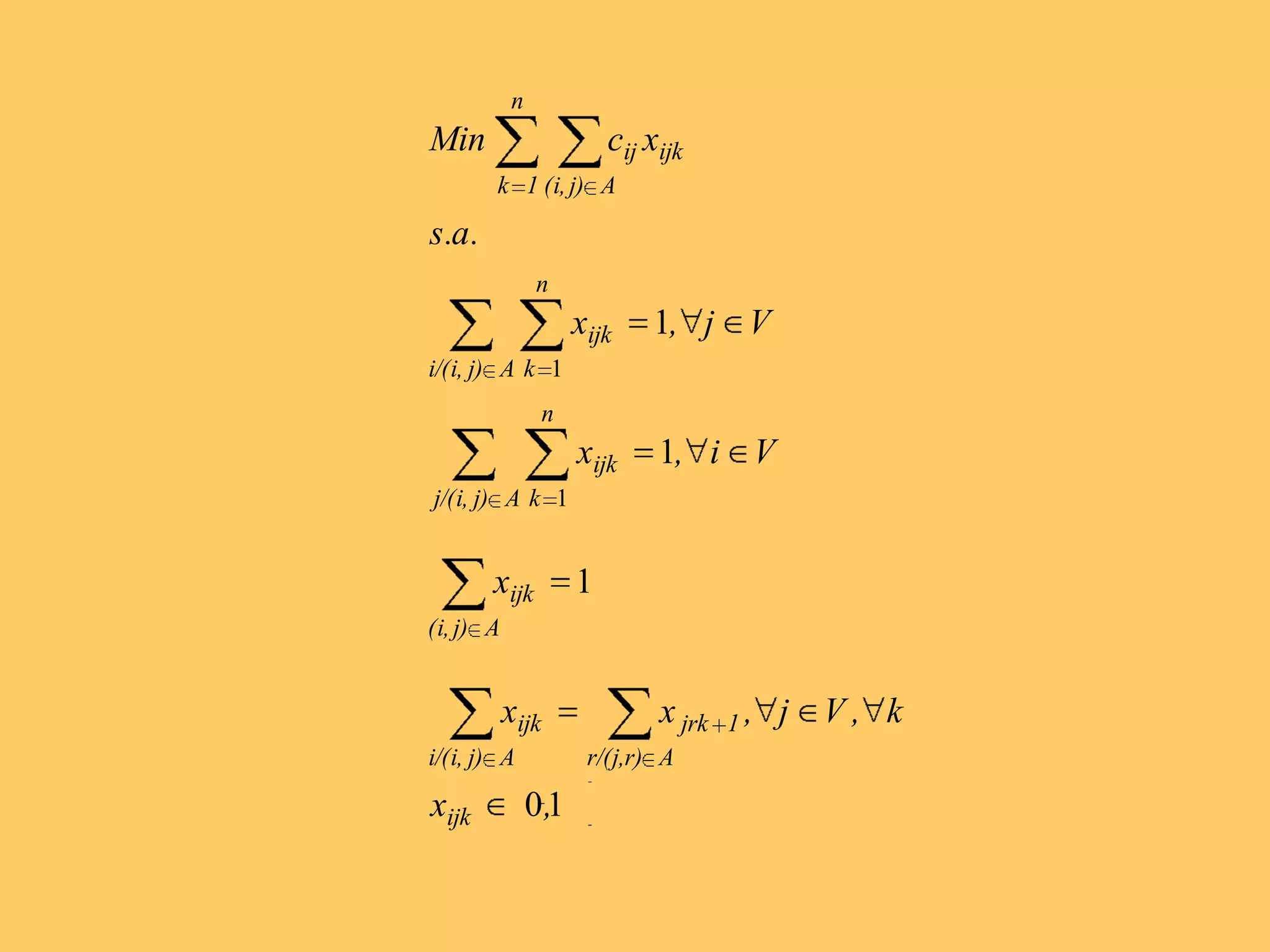Este documento describe los conceptos fundamentales de la investigación operativa, incluyendo su definición, historia, métodos y aplicaciones. La investigación operativa se aplica para asignar recursos de forma eficaz mediante el desarrollo de modelos matemáticos. Algunos de los modelos más comunes son la programación lineal, entera y no lineal, los cuales se usan para resolver problemas como el transporte, flujo en redes y asignación.

1. Investigación Operativa DESARROLLO DE MODELOS

2. El problema Los recursos son escasos Los sistemas son cada vez más complejos Cada vez es más difícil asignar los recursos o actividades de la forma más eficaz

3. Investigación operativa (I.O.) Es la aplicación del método científico para asignar los recursos o actividades de forma eficaz, en la gestión y organización de sistemas complejos Su objetivo es ayudar a la toma de decisiones Requiere un enfoque interdisciplinario

4. Historia de la I.O. Se aplica por primera vez en 1780 Antecedentes: Matemáticas: modelos lineales (Farkas, Minkowski) (s.XIX) Estadística: fenómenos de espera (Erlang, Markov) (años 20) Economía: Quesnay (x.XVIII), Walras (s.XIX), Von Neumann (años 20) El origen de la I.O. moderna se sitúa en la 2ª Guerra Mundial

5. Historia de la I.O. Al terminar la guerra, sigue el desarrollo en la industria, debido a: competitividad industrial progreso teórico RAND (Dantzig) Princeton (Gomory, Kuhn, Tucker) Carnegie Institute of Technology (Charnes, Cooper) gran desarrollo de los ordenadores

6. Actualidad de la I.O. Sigue habiendo un gran desarrollo, en muchos sectores, con grandes avances sobre todo en el campo de la Inteligencia Artificial Más información: Sociedad Española de Estadística e Inv. Op. (SEIO) www.cica.es/aliens/seio Association of European O.R. Societies (EURO) www.ulb.ac.be/euro/euro_welcome.html Institute for O.R. and the Management Sci. (INFORMS) www.informs.org International Federation of O.R. Societies (IFORS) www.ifors.org

7. El método de la I.O. Definición del problema Formulación del problema y construcción del modelo Resolución Verificación, validación, refinamiento Interpretación y análisis de resultados Implantación y uso extensivo A lo largo de todo el proceso debe haber una interacción constante entre el analista y el cliente

8. El modelado Es una ciencia análisis de relaciones aplicación de algoritmos de solución Y a la vez un arte visión de la realidad estilo, elegancia, simplicidad uso creativo de las herramientas experiencia

9. Definición del problema Consiste en identificar los elementos de decisión objetivos (uno o varios, optimizar o satisfacer) alternativas limitaciones del sistema Hay que recoger información relevante (los datos pueden ser un grave problema) Es la etapa fundamental para que las decisiones sean útiles

10. Formulación del problema Modelo: representación simplificada de la realidad, que facilita su comprensión y el estudio de su comportamiento Debe mantener un equilibrio entre sencillez y capacidad de representación Modelo matemático: modelo expresado en términos matemáticos hace más claras la estructura y relaciones facilita el uso de técnicas matemáticas y ordenadores a veces no es aplicable

11. Construcción del modelo Traducción del problema a términos matemáticos objetivos: función objetivo alternativas: variables de decisión limitaciones del sistema: restricciones Pero a veces las relaciones matemáticas son demasiado complejas heurísticos simulación

13. Programación estocástica

14. Gestión de inventarios

15. Fenómenos de espera (colas)

16. Teoría de juegos

18. Verificación y validación Eliminación de errores Comprobación de que el modelo se adapta a la realidad

19. Interpretación y análisis Robustez de la solución óptima obtenida: Análisis de sensibilidad Detección de soluciones cuasi-óptimas atractivas

20. Implantación Sistema de ayuda y mantenimiento Documentación Formación de usuarios

21. Ejemplo nº1 En una fábrica de cerveza se producen dos tipos: rubia y negra. Su precio de venta es de 50 ptas/l y 30 ptas/l, respectivamente. Sus necesidades de mano de obra son de 3 y 5 empleados, y de 5.000 y 2.000 ptas de materias primas por cada 1000 l. La empresa dispone semanalmente de 15 empleados y 10.000 ptas para materias primas, y desea maximizar su beneficio. ¿Cuántos litros debe producir?

22. Formulación

23. El modelo de P.L.

24. El modelo de P.L. z: función objetivo CT (c1,...,cn): vector de coeficientes de la f.o. XT (x1,...,xn): vector de variables de decisión A (...,aij,...): matriz de coeficientes técnicos b (b1,...,bm): vector de demandas Matricialmente, Opt CTX s.a. AX b x  0 Forma canónica

25. Propiedades del modelo lineal Proporcionalidad La contribución al coste y a las restricciones es directamente proporcional al valor de cada variable Aditividad El coste y las restricciones son la suma directa de las variables Divisibilidad Las variables pueden dividirse en cualquier tipo de fracción

26. Modelos de prog. entera El modelo matemático es el modelo de P.L., pero con algunas variables enteras Programación entera mixta (MIP) x  R+, y  Z+ Programación entera pura (IP) x  Z+ Programación binaria ó 0-1 (0-1 MIP, 0-1 IP, BIP) x  {0,1}: variables de asignación, lógicas Son problemas más complicados de resolver que los de P.L. El primer algoritmo de resolución se planteó en el año 1958 (Gomory)

27. Problemas típicos Problema del transporte Problema de flujo con coste mínimo en red Problema de asignación Problema de la mochila (knapsack) Problema del emparejamiento (matching) Problema del recubrimiento (set-covering) Problema del empaquetado (set-packing) Problema de partición (set-partitioning) Problema del coste fijo (fixed-charge) Problema del viajante (TSP) Problema de rutas óptimas

28. Problema del transporte Minimizar el coste total de transporte entre los centros de origen y los de destino, satisfaciendo la demanda, y sin superar la oferta xij: unidades a enviar de origen i a destino j cij: coste unitario de transporte de i a j ai: unidades de oferta en el punto origen i bj: unidades de demanda en el punto destino j Se supone oferta total igual a demanda total

29. Flujo con coste mínimo en red Embarcar los recursos disponibles a través de la red para satisfacer la demanda a coste mínimo xij: unidades enviadas de i a j (flujo) cij: coste unitario de transporte de i a j bi:recursos disponibles en un nodo i oferta: bi>0 demanda: bi<0 transbordo: bi=0 Se supone oferta total igual a demanda total

30. Problema de asignación Minimizar el coste total de operación de modo que: - cada tarea se asigne a una y sólo una máquina - cada máquina realice una y sólo una tarea xij: 1 si la tarea i se hace con la máquina j cij: coste de realizar la tarea i con máquina j n tareas m máquinas Si hay más máquinas que tareas se formula con desigualdades, y se resuelve con tareas ficticias

31. Problema de la mochila Escoger un grupo de productos que maximice el valor total sin exceder el espacio disponible n objetos aj: espacio que ocupa el objeto j cj: valor del objeto j b: volumen de la mochila xj: 1 si se escoge el objeto j

32. Problema de emparejamiento Distribuir un conjunto por parejas de tal forma que el valor sea máximo. Si hay elementos sin pareja: emparejamiento imperfecto. Si están en dos conjuntos, emparejamiento bipartito. xij=1 si los elementos i y j son pareja cij: valor de la pareja i-j i<j

33. Problema de recubrimiento Minimizar el coste de las actividades que en su conjunto cubren todas las características al menos una vez m características n actividades xj=1 si la actividad j se realiza cj: coste unitario de la actividad j aij=1 si la característica i está en la actividad j A: matriz de incidencia

34. Problema de empaquetado Maximizar el beneficio total de forma que hay que elegir conjuntos completos de actividades, y que no se realice una actividad dos veces m actividades n conjuntos de actividades xj=1 si se elige el subconjunto j cj: beneficio por realizar el conjunto j aij=1 si el conjunto j incluye la actividad i A: matriz de incidencia

35. Problema de partición Si en el problema de recubrimiento o en el de empaquetado las desigualdades se cambian por igualdades m actividades n conjuntos de actividades xj=1 si se elige el subconjunto j cj: beneficio por realizar el conjunto j aij=1 si el conjunto j incluye la actividad i A: matriz de incidencia

36. Problema del coste fijo Decidir la cantidad de cada producto de modo que se minimicen los costes de producción y se satisfaga la demanda xij: unidades del producto j cj: coste unitario de producción de j yk=1 si se usa la instalación k fk: coste de arranque de la instalación k akj=1 si el producto j usa la instalación k bj: demanda del producto j M: número lo suficientemente grande

37. Problema del viajante Encontrar un circuito que visite exactamente una vez cada ciudad empezando en la primera y que tenga longitud mínima xij=1 si de i va directamente a j cij: distancia entre i y j A: conjunto de arcos V: conjunto de nodos

39. Problema de rutas Minimizar el coste total, visitando todos los clientes N: clientes M: vehículos xijk=1 si el vehículo k visita j después de i cij: coste unitario de transporte de i a j dij: distancia de i a j tij: tiempo de i a j qi: demanda si: tiempo de descarga i: prioridad Qk: capacidad rok, dok: período tiempo disponible ck: coste fijo por uso

40. Formulación con var. binarias Restricciones disyuntivas K de N alternativas deben darse Restricciones condicionales equiv. a Decisiones contingentes x  y y  x