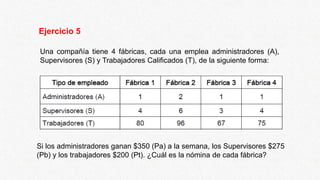
Este documento presenta información sobre el uso de matrices en ingeniería. Explica que las matrices tienen múltiples aplicaciones en áreas como el cálculo estructural, la ingeniería de tránsito, la topografía, el dibujo asistido por computadora, la estática y la hidráulica. También incluye ejemplos de cómo representar datos como cantidades de materias primas y salarios de empleados usando matrices.

1. APLICACIÓN DE MATRICES
Julio César Tovar Cardozo
Ingeniero en Electrónica y Telecomunicaciones
Especialista en Alta Gerencia
Especialista en Gestión de la Informática Educativa
Magister en Tecnología de la Informática Educativa
julio.tovar@hotmail.com
julio.tovarc@gmail.com

2. Las matrices, aunque parezcan al principio objetos extraños, son una
herramienta muy importante para expresar y discutir problemas que
surgen en la vida real. En los negocios a menudo es necesario
calcular y combinar ciertos costes y cantidades de productos.
Las tablas son una forma de representar estos datos. Sin embargo,
agrupar los datos en un rectángulo nos muestra una representación
más clara y fácil de los datos. Tal representación de los datos se
denomina matriz. En lugar de presentar los datos del consumo de
materias primas de una empresa en una tabla. Estos se representan
en un grupo de matrices.
Matrices

3. Matrices en Ingeniería
La Ingeniería es una especialidad que en el proceso de sus acciones
también hace uso de las matemáticas ya que se utiliza para el
diseño de sistemas estructurales en las diversas áreas que ocupa
la Ingeniería.
Las matrices tienen múltiples aplicaciones en el área de ingeniería
dando lugar a al óptimo manejo de recursos humanos y de
materiales controlados desde un sistema. Podemos denotar además
que las matrices tienen su importancia en el manejo de sistemas de
información fundamentales.

4. Las matrices tienen diversas aplicaciones en la ingeniería, por ejemplo:
• En el cálculo estructural para analizar la capacidad de carga y el diseño
de elementos.
• En ingeniería de tránsito para generar matrices de información en la
planificación de transporte y aforos vehiculares.
• En topografía para realizar resúmenes de datos y cuadricular terrenos
para curvas de nivel.
• En dibujo asistido por computadora en el software Autocad.
• En estática para resolver problemas de equilibrio en el espacio en 3D
con operaciones vectoriales.
• En hidráulica para hacer referencias del estudio de la pérdida de
energía por accesorios (circuito cerrado) y en el análisis, diseño y
distribución de caudales para la población.
• En análisis numérico para resolver sistemas de ecuaciones lineales.
Matrices en Ingeniería

5. Aplicación de Matrices
Las matrices, aunque parezcan al principio objetos extraños, son una
herramienta muy importante para expresar y discutir problemas que
surgen en la vida real. En los negocios a menudo es necesario calcular y
combinar ciertos costes y cantidades de productos.
Las tablas son una forma de representar estos datos. Sin embargo,
agrupar los datos en un rectángulo nos muestra una representación más
clara y fácil de los datos. Tal representación de los datos se denomina
matriz. En lugar de presentar los datos del consumo de materias primas
de una empresa en una tabla (en nuestro ejemplo de una empresa que
produce cerveza).

6. Aplicaciones de matrices
En 4 semanas, las dos compañías productoras de cerveza, Alfa y Beta, necesitan las siguientes
cantidades de materia prima de levadura, malta y agua (unidades de cantidad: T = Toneladas):
1ª semana: 2ª semana:
Alfa: 8 T levadura, 4 T malta, 12 T agua Alfa: 10 T levadura, 6 T malta, 5 T agua
Beta: 6 T levadura, 3 T malta, 12 T agua. Beta: 9 T levadura, 5 T malta, 4 T agua
3ª semana: 4ª semana:
Alfa: 7 T levadura, 8 T malta, 5 T agua Alfa: 11 T levadura, 7 T malta, 9 T agua
Beta: 7 T levadura, 0 T malta, 5 T agua. Beta: 11 T levadura, 6 T malta, 5 T agua.
Los datos se representan en forma sencilla:
Para la Empresa Alfa Para la Empresa Beta

7. Ejercicios
Ejercicio 1
Escribe en forma de tabla el siguiente enunciado: “ Una familia gasta
en enero $400 en comida y $150 en vestir; en febrero, $500 en comida
y $100 en vestir; y en marzo, $300 en comida y $200 en vestir ”.

8. Ejercicio 2

9. Ejercicio 3
Cinco estudiantes reciben las siguientes subvenciones (subvenciones para
niños) por cada mes:
a) Calcula la cantidad de subvenciones para niños y
la cantidad de becas, que recibe cada estudiante por
año.
b) ¿Cuál es el estudiante que recibe la subvención
más alta?
Subvención Beca
Juan
José
Camila
Alejo
Raúl
Subvención Beca
Juan
José
Camila
Alejo
Raúl

10. Para el cálculo de los costos por 15 y 30 días se realiza una multiplicación algebraica
EJERCICIO 4:
Si por mano de obra para construir el techo de una casa nos cobran 25 por peón, 30 por
operario y 40 por el maestro de obra (precio por día) y necesitamos 10 peones, 5
operarios y 1 maestro. ¿Cuánto nos costará contratarlos por 15 días y cuánto por un mes?
Primero organizamos en un cuadro para notar la diferencia en trabajar con cuadros y
matrices:
Ahora para calcular el precio total
por trabajador realizaremos la
multiplicación de matrices:
A = 1 5 10
40
B= 30
25
1x3
3x1
40
A x B = 1 5 10 30 = 40+150+250 = 440
25
*

11. Ejercicio 5
Una compañía tiene 4 fábricas, cada una emplea administradores (A),
Supervisores (S) y Trabajadores Calificados (T), de la siguiente forma:
Si los administradores ganan $350 (Pa) a la semana, los Supervisores $275
(Pb) y los trabajadores $200 (Pt). ¿Cuál es la nómina de cada fábrica?

12. TIPO DE TRABAJADOR
F1  Administrador (A)
F2  Supervisor (B)
F3  Trabajador (T)
FABRICA
C1 C2 C3 C4
Fab1 Fab2 Fab3 Fab4
TRABAJADOR
F1  Administrador (A)
F2  Supervisor (B)
F3  Trabajador (T)
*
SALARIO
Solución: Lo que se pide es el monto pagado por cada fábrica el cual es igual al
número de cada empleado por su respectivo ingreso salarial. En general, será: Ii =
PA AI + PS SI + PT TI, donde Ii es el monto de la fábrica i. Por ejemplo el moto de la
fábrica 1 será I1 = PA A1 + PS S1 + PT T1 = 350 *1 * 4 * 275 + 80 * 200 = 17450
Con este sencillo cálculo puede obtener fácilmente los 3 montos restantes. Sin
embargo, si hubiera más tipos de empleado o un mayor numero de fábricas el
cálculo se complicaría. Existe otra forma para calcular directamente los montos de
todas las fábricas. El cuadro anterior equivale a cantidades de especialistas de
cada fábrica . Entonces si estas cantidades son multiplicada por su salario
respectivo debería obtenerse la nómina de cada fábrica. Llevando esto a matrices:
A3x4 * B3x1

13. [Tipo Trabajador x _Fábrica ] X [ Tipo Trabajador x salario ]
No es posible realizar la multiplicación de estas dos matrices,
pues el número de columnas de la primera matriz es diferente
al número de columnas de la segunda matriz
TIPO DE TRABAJADOR
F1  Administrador (A)
F2  Supervisor (B)
F3  Trabajador (T)
FABRICA
C1 C2 C3 C4
Fab1 Fab2 Fab3 Fab4
TRABAJADOR
F1  Administrador (A)
F2  Supervisor (B)
F3  Trabajador (T)
*
A3x4 * B3x1
SALARIO

14. FABRICA
F1  Fábrica 1
F2  Fábrica 2
F3  Fábrica 3
F4  Fábrica 4
TRABAJADOR
C1 C2 C3
Adm Sup Trab
*
A4x3 * B3x1
TRABAJADOR
F1  Administrador (A)
F2  Supervisor (B)
F3  Trabajador (T)
SALARIO
=

15. FABRICA
F1  Fábrica 1
F2  Fábrica 2
F3  Fábrica 3
F4  Fábrica 4
TRABAJADOR
C1 C2 C3
Adm Sup Trab
*
A4x3 * B3x1
TRABAJADOR
F1  Administrador (A)
F2  Supervisor (B)
F3  Trabajador (T)
SALARIO
=
[Fabrica x _Tipo Trabajador] X [Tipo Trabajador x salario] = [ Fabrica x salario ]
SI es posible realizar la multiplicación de estas dos matrices.
El resultado obtenido es una matriz de tamaño 4x1 que
contiene la información de los salarios de los trabajadores
para cada una de las fábricas.

16. Para poder calcular el costo total de una obra, primero necesitaremos "cuantificar“ que
no es otra cosa más que calcular el volumen total de "conceptos " o trabajos que se van a
realizar en dicha obra.
Dependiendo de la complejidad de la obra, vamos a tener mayor cantidad de conceptos,
todos estos los vaciaremos en un listado de los conceptos donde se mostrará el volumen
a ejecutar y el precio unitario por cada uno de ellos.
Es importante que tengamos en cuenta:
• MATERIAL: Que se va a utilizar en obra (ladrillo, cemento, fierro, etc.)
• CUANTIFICAR: Se refiere a cuanto necesitaremos de cada uno de los conceptos que
vas a manejar.
• PRECIO UNITARIO: Es el precio por unidad de medida (m2, m3, lote, pieza, etc.)
• MANO DE OBRA: Es la cantidad de personas, cuadrillas, y cuanto les vas apagar para
la ejecución de la obra.
• HERRAMIENTA: Es la herramienta que esas personas van a utilizar para el trabajo.
• INDIRECTOS: Son los costos indirectos que te genera la ejecución de la
obra(transporte de materiales, alquiler de maquinas, etc.)

17. Ejercicio 6
Tres personas, A, B, C, quieren comprar las siguientes cantidades de fruta:
• A: 2 kg de peras, 1 kg de manzanas y 6 kg de naranjas.
• B: 2 kg de peras, 2 kg de manzanas y 4 kg de naranjas.
• C: 1 kg de peras, 2 kg de manzanas y 3 kg de naranjas.
En el pueblo en que viven hay dos fruterías F1 y F2.
En F1, las peras cuestan 1,5 pesos/Kg, las manzanas 1 pesos/Kg y las naranjas 2 pesos/Kg.
En F2, las peras cuestan 1,8 pesos/Kg, las manzanas 0,8 pesos/Kg y las naranjas 2 pesos/Kg.
1. Expresa matricialmente la cantidad de fruta (peras, manzanas y naranjas) que quiere
comprar cada persona (A, B, C).
2. Escribe una matriz con los precios de cada tipo de fruta en cada una de las dos fruterías.
3. Obtén una matriz, a partir de las dos anteriores, en la que quede reflejado lo que se gastaría
cada persona haciendo su compra en cada una de las dos fruterías.

18. Frutas x personas: En las filas va la información de frutas y en las columnas la información de Personas, así:
Observe que la segunda matriz es la transpuesta de la primera matriz (las columnas se convierten en filas)
1. Expresa matricialmente la cantidad de fruta (peras, manzanas y naranjas) que quiere comprar cada
persona (A, B, C).
A: 2 kg de peras, 1 kg de manzanas y 6 kg de naranjas.
B: 2 kg de peras, 2 kg de manzanas y 4 kg de naranjas.
C: 1 kg de peras, 2 kg de manzanas y 3 kg de naranjas.
Hay dos formas de expresar la matriz:
Personas x Frutas: En las filas va la información de personas y en las columnas la información de Frutas; así:
PERSONAS Pera Manana Naranja
A 2 1 6
B 2 2 4
C 1 2 3
FRUTAS
FRUTAS A B C
Pera 2 2 1
Manzana 1 2 2
Naranaja 6 4 3
PERSONAS
Recuerde que la información
que contiene la matriz es la
cantidad de frutas por persona
(En Kilogramos)

19. Frutas x Frutería: En las filas va la información de frutas y en las columnas la información de Frutería (la
información que contiene es precio), así:
Observe que la segunda matriz es la transpuesta de la primera matriz (las columnas se convierten en filas).
2. Escribe una matriz con los precios de cada tipo de fruta en cada una de las dos fruterías.
En el pueblo en que viven hay dos fruterías F1 y F2.
• En F1, las peras cuestan 1,5 pesos/Kg, las manzanas 1 pesos/Kg y las naranjas 2 pesos/Kg.
• En F2, las peras cuestan 1,8 pesos/Kg, las manzanas 0,8 pesos(Kg y las naranjas 2 pesos/Kg.
Igual que en el caso anterior, hay dos formas de expresar la matriz:
Frutería x Frutas: En las filas va la información de Frutería y en las columnas la información de Frutas (la
información que contiene es precio), así :
FRUTAS F1 F2
Pera 1,5 1,8
Manzana 1 0,8
Naranja 2 2
FRUTERÍA
FRUTERÍA Pera Manzana Naranja
F1 1,5 1 2
F2 1,8 0,8 2
FRUTAS
Recuerde que la información
que contiene la matriz es el
costo de Kilogramo de fruta
por frutería ($)

20. 3. Obtén una matriz, a partir de las dos anteriores, en la que quede reflejado lo que se
gastaría cada persona haciendo su compra en cada una de las dos fruterías.
Tenemos dos alternativas para obtener los resultados:
La primera es una matriz de Personas x Frutería y la segunda es una matriz de Frutería x
Personas. En cada una de estas dos matrices el dato contenido es el valor gastado.
Para el primer caso Persona x Frutería, tenemos:
La pregunta es: ¿Qué matrices de las ya conocidas debemos multiplicar para llegar a una
matriz de 3x2 que contenga la información Personas x Fruterías?
Personas FruteríaFrutas Frutas
PERSONAS Pera Manana Naranja
A 2 1 6
B 2 2 4
C 1 2 3
FRUTAS
PERSONAS F1 F2
A
B
C 3x2
FRUTERÍA
FRUTAS F1 F2
Pera 1,5 1,8
Manzana 1 0,8
Naranja 2 2
FRUTERÍA
PERSONAS F1 F2
A 16 16,4
B 13 13,2
C 9,5 9,4
FRUTERÍA
Persona x Frutería

21. Para el segundo caso Frutería x Personas, tenemos:
La pregunta es: ¿Qué matrices de las ya conocidas debemos multiplicar para llegar a una matriz
de 2x3 que contenga la información Frutería x Personas.
PersonasFrutería Frutas
FRUTERÍA A B C
F1
F2
PERSONAS
Frutas
FRUTERÍA Pera Manzana Naranja
F1 1,5 1 2
F2 1,8 0,8 2
FRUTAS
FRUTAS A B C
Pera 2 2 1
Manzana 1 2 2
Naranaja 6 4 3
PERSONAS
FRUTERÍA A B C
F1 16 13 9,5
F2 16,4 13,2 9,4
PERSONAS

22. Hemos obtenido la solución al problema de las siguientes formas:
PERSONAS Pera Manana Naranja
A 2 1 6
B 2 2 4
C 1 2 3
FRUTAS
FRUTAS F1 F2
Pera 1,5 1,8
Manzana 1 0,8
Naranja 2 2
FRUTERÍA
PERSONAS F1 F2
A 16 16,4
B 13 13,2
C 9,5 9,4
FRUTERÍA
FRUTERÍA Pera Manzana Naranja
F1 1,5 1 2
F2 1,8 0,8 2
FRUTAS
FRUTAS A B C
Pera 2 2 1
Manzana 1 2 2
Naranaja 6 4 3
PERSONAS
FRUTERÍA A B C
F1 16 13 9,5
F2 16,4 13,2 9,4
PERSONAS
Observe que las matrices Persona x Frutería y Frutería por Personas son
transpuestas (se intercambian filas por columnas).
Igualmente, las matrices Personas x Frutas y Frutas x Personas son
transpuestas; y las matrices Frutas x Frutería y Frutería x Frutas.
Si definimos:
A = Personas x Frutas
B = Frutas x Frutería
C = Personas x Frutería
Tendríamos: C = A x B
Ct = Bt x At

23. EJERCICIO 7
Tres familias F1, F2 y F3 tienen los siguientes consumos de pan, carne y
mantequilla
• F1 consume 160 kgr de pan, 200 Kgr de carne y 1,5 Kgr de mantequilla
• F2 consume 200 Kgr de pan, 230 Kgr de carne y 2 Kgr de mantequilla
• F3 consume 90 Kgr de pan, 150 Kgr de carne y 1,75 Kgr de mantequilla.
Los precios, en pesos, del pan, de la carne y de la mantequilla en los años
2009,2010, 2011 y 2012 fueron:
• 2009: el pan costaba $1,45, la carne $13 y la mantequilla $15
• 2010: el pan costaba $1,56, la carne $13 y la mantequilla $16,3
• 2011: el pan costaba $1,71, la carne $13,5 y la mantequilla $16
• 2012: el pan costaba $1,80, la carne $14 y la mantequilla $18
Utiliza matrices para calcular el gasto anual de cada familia en el total de los
cuatro productos.

24. El problema nos solicita presentar los gastos
anuales de cada familia.
Así, tenemos dos alternativas para la presentación
de los resultados:
La primera alternativa es una matriz de Familia x
Año con un tamaño de 3 x 4, en la que las Familias
están en las filas y los años en las columnas.
FAMILIA 2009 2010 2011 2012
F1
F2
F3
AÑOS
AÑOS F1 F2 F3
2009
2010
2011
2012
FAMILIA
La segunda alternativa es una matriz de Año por
Familia un tamaño de 4 x 3, en la que los
Productos están en las filas y los años en las
columnas.
Vamos a desarrollar el ejercicio para la primera alternativa Familia x Año.
Los datos que contendrá la Matriz será Pesos y corresponderá al gasto en Pesos de las familias
para cada uno de los años.

25. MATRIZ BMATRIZ A
Familia x año = [Familia x __________ ] X [ __________ x Año ]
R3x4 = A3x___ x B___x4
FAMILIA 2009 2010 2011 2012
F1
F2
F3
AÑOS
Familia x año = [Familia x producto ] X [ producto x Año ]
R3x4 = A3x3 x B3x4
El resultado que busco es una matriz de Familia x año, tal como esta:

26. Familia x año = [Familia x producto ] X [ producto x Año ]
A3x3 x B3x4 = R3x4
Solución:
Vamos a definir dos matrices: la matriz A para los consumos y la matriz B para los precios
de los productos en los diferentes años. A partir de ellas calcularemos el gasto anual.
donde cada fila representa el consumo de cada
familia de pan, carne y mantequilla. La matriz A
tiene 3 filas ( una por cada familia) y tres
columnas (una por cada producto)
donde cada fila representa
uno de los productos y cada
columna uno de los años.
Producto
Pan Carne Mantenquilla
Fam 1
Fam 2
Fam 3
2009 2010 2011 2012
Pan
Carne
Mantenquilla

27. Ahora vamos a calcular el gasto anual:
Como el gasto es el resultado de multiplicar el consumo (en kg) por el precio del kilogramo
debemos calcular A × B . Este producto es posible porque A es una matriz de dimensión 3 x
3 y la dimensión de B es 3 x 4. Por tanto la matriz producto tendrá dimensión 3 x 4.
Donde cada elemento de la matriz nos indica el gasto total de cada familia
en el año correspondiente. Por ejemplo, el elemento a23 nos indica el gasto
total en pan, carne y mantequilla de la familia F2 durante el año 2010.
[Familia x Producto] X [Producto x Año] = [Familia x Año]
A3x3 x B3x4 = R3x4
Fam 1
Fam 2
Fam 3
2009 2010 2011 2012

28. EJERCICIO 8
La empresa Construir Ltda. quiere producir acero. Serán necesarias, entre otras materias
primas, mineral hierro y carbón duro. La siguiente tabla nos muestra las demandas (en
toneladas) de mineral hierro y carbón duro en un periodo de 3 semanas:
Existen tres proveedores diferentes que
ofrecen estas materias primas. ¿Cuál es el
proveedor que ofrece mayor beneficio?
En la siguiente tabla se muestran los costes
por tonelada de materia prima para cada
proveedor:
Las sumas son:
Esto significa que la compañía Ruhr AG es el
proveedor más económico y por lo tanto más rentable.
S
e
m
a
n
a
M
i
n
e
r
a
l
Mineral
Proveedor Proveedor
S
e
m
a
n
a
18780 20390 18960

29. EJERCICIO 9
En 4 semanas, las dos compañías constructoras, Alfa y
Beta, necesitan las siguientes cantidades de materia prima
de Cemento, Hierro y agua (unidades de cantidad: T =
Toneladas):
1ª semana:
Alfa: 8 T Cemento, 4 T Hierro, 12 T agua
Beta: 6 T Cemento, 3 T Hierro, 12 T agua.
2ª semana:
Alfa: 10 T Cemento, 6 T Hierro, 5 T agua
Beta: 9 T Cemento, 5 T Hierro, 4 T agua
3ª semana:
Alfa: 7 T Cemento, 8 T Hierro, 5 T agua
Beta: 7 T Cemento, 0 T Hierro, 5 T agua.
4ª semana:
Alfa: 11 T Cemento, 7 T Hierro, 9 T agua
Beta: 11 T Cemento, 6 T Hierro, 5 T agua.

30. Los datos se representan de manera sencilla.
Para la Empresa Alfa:
Y para la Empresa Beta:
Ahora los elementos pueden ser comparados directamente y fácilmente. Para conseguir más
información acerca de las dos compañías o compararlas, se requiere la suma y resta de matrices.
Cemento Hierro Agua
1 Semana 8 4 12
2 Semana 10 6 5
3 Semana 7 8 5
4 Semana 11 7 9
Cemento Hierro Agua
1 Semana 6 3 12
2 Semana 9 5 4
3 Semana 7 0 5
4 Semana 11 6 5
Cemento Hierro Agua
SEM
1
2
3
4
Cemento Hierro Agua
SEM
1
2
3
4

31. Suma de Matrices
¿Qué cantidad de materia prima se necesita para ambas compañías en cada semana?
En la primera semana la compañía Alfa necesita 8 T y la compañía Beta 6 T de la materia
prima Cemento, lo que significa: 8+6 =14 Toneladas de Cemento, lo mismo ocurre para el
Hierro: 4+3=7 T Hierro, y para el agua: 12+12=24 T agua.
Cuando las tablas están escritas en forma de arreglos rectangulares de números, resulta
más claro y rápido sumarlas. Para sumar dos matrices del mismo tipo, por ejemplo las
matrices de Alfa y Beta, simplemente se suman los elementos correspondientes.
Cemento Hierro Agua
SEM
1
2
3
4

32. Resta de matrices
¿Cuál es la diferencia de consumo de ambas compañías en cada semana?
En la primera semana la compañía Alfar necesita 8 T y la compañía Beta 6 T de la materia
prima Cemento, lo cual significa que la diferencia es de 2 T: 8-6 =2 T Cemento,
Lo mismo ocurre para el Hierro: 4-3=1 T Hierro, y para el agua: 12-12=0 T agua.
Cuando las tablas están escritas en forma de arreglo rectangular de números, resulta más
claro y rápido restarlas.
Para restar dos matrices del mismo tipo, por ejemplo las matrices de Alfa y Beta,
simplemente se restan los elementos correspondientes.
El resultado nos muestra que la compañía Alfa necesita más materia prima que la compañía Beta.
La demanda de materia prima para ambas compañías es la misma para cuatro periodos. Por lo
tanto el valor de la diferencia es 0. Podría también darse el caso de obtener resultados negativos.
Esto significaría que la compañía Beta necesita más materia prima que la compañía Alfa.
A – B =
Cemento Hierro Agua
SEM
1
2
3
4
Compañía A Compañía B

33. Producto escalar:
¿Cuánto es el consumo de materia prima por semana para
5 compañías como Alfa, suponiendo que necesitan la
misma cantidad de materia prima que la compañía Alfa?
Para multiplicar una matriz por un número real es necesario
multiplicar cada elemento por este número.
5 x A =
Cemento Hierro Agua
SEM
1
2
3
4

34. Producto de dos matrices:
Consideremos que la compañía Alfa recibe materia prima de dos proveedores (Hop
AG y Malt y co) a los costos unitarios por tonelada indicados el cuadro de abajo.
Esta tabla corresponde a la matriz de costes P, porque los elementos representan los
costes de las tres materias primas para ambos proveedores.
Hop AG Malt y Co
Cemento 50 55
Hierro 136 127
Agua 80 79
Cemento
Hierro
Agua
Hop AG Malt y Co
Ahora la pregunta sería cuál de los dos proveedores es el de menor costo, teniendo en
cuenta que los proveedores sólo pueden cambiar de una semana a otra.

35. Para la compañía Alfa tenemos:
Costes de la compañía en Hop AG:
1ª semana: 8*50+4*136+12*80 =1.904
2ª semana: 10*50+6*136+5*80 =1.716
3ª semana: 7*50+8*136+5*80 =1.838
4ª semana: 11*50+7*136+9*80 =2.222
Costes de la compañía en Malt y co.:
1ª semana: 8*55+4*127+12*79 =1.896
2ª semana 10*55+6*127+5*79 =1.707
3ª semana: 7*55+8*127+5*79 =1.542
4ª semana: 11*55+7*127+9*79 =2.205
Cemento Hierro Agua
1 Semana 8 4 12
2 Semana 10 6 5
3 Semana 7 8 5
4 Semana 11 7 9
Materia Prima
Cemento Hierro Agua
Semana
1
2
3
4
Hop AG Malt y Co
Cemento 50 55
Hierro 136 127
Agua 80 79
Materia
Cemento
Hierro
Agua
PROVEEDOR
Hop AG Malt y Co

36. Sumando, la tabla de
costes resulta:
Lógicamente la matriz con los elementos de coste de los proveedores se
denomina matriz de coste K.
La matriz de costes K resulta de la multiplicación de la matriz (matriz de
Alfa) y la matriz P (matriz de costes):
PROVEEDOR
Hop AG Malt y Co
SEM
1
2
3
4

37. Recordemos que:
Este tipo de multiplicación, puede efectuarse sólo si el número de
columnas de la primera matriz (en nuestro ejemplo 3) y el número de
filas de la segunda matriz (en nuestro ejemplo también 3) es el mismo.
La matriz resultante tendrá las siguientes dimensiones:
Iguales
[Semana x Materia Prima] X [Materia Prima x Proveedor] = [Semana x Proveedor]

38. EJERCICIO 10
Una empresa Tolimense tiene una delegación en Espinal, otra en Mariquita y otra
en Honda. En el momento actual, en la delegación de Espinal hay 30 CD, 20 DVD,
42 televisiones y 15 vídeos, en la de Mariquita, 18 CD, 10 DVD, 12 televisiones y 15
vídeos y en la de Honda hay 25 CD, 34 DVD, 60 televisiones y 30 vídeos.
a. Consideramos una matriz de orden 3×4, de manera que en cada fila se considera
una de las tres ciudades: Espinal, Mariquita y Honda y en cada columna uno de los
cuatro productos: CD, DVD, televisiones y vídeos. Así, la matriz E1 representa el
nivel de existencia de cada producto en cada delegación de la Empresa.
C
i
u
d
a
d
CD DVD TV VIDEOS

39. b. Calcular el nuevo nivel de existencias de la empresa si se realiza el siguiente reparto: en
Espinal, 4 CD, 12 DVD, 8 televisiones y 10 vídeos, en Mariquita, 3 CD, 7 DVD, 8 televisiones y
12 vídeos y en Honda, 7 CD, 10 DVD, 25 televisiones y 15 vídeos.
Si se representa el reparto hecho por la matriz R, entonces el nuevo nivel de existencia es E2 = E1 + R.
c. Calcular el nuevo nivel de existencias de la empresa si se realizan las siguientes
ventas: en Espinal, 7 CD, 8 DVD, 10 televisiones y 6 vídeos, en Mariquita, 3 CD, 5 DVD,
12 televisiones y 7 vídeos y en Honda, 25 CD, 14 DVD, 43 televisiones y 15 vídeos.
Si se representan las ventas hechas por la matriz V, entonces el nuevo nivel de
existencia es E3 = E2 – V.

40. Por lo tanto, las existencias de la delegación de Espinal tienen un valor de $77.580, la de
Mariquita de $33.120 y la de Honda de $75.120.
d. Tras un estudio de mercado la empresa tiene expectativas de aumentar sus ventas y decide
doblar el nivel de existencias en cada delegación, ¿cuál será el nuevo nivel de existencias?.
El nuevo nivel de existencia es E4 = 2 x E3
e. Si el precio de venta de un CD es de 300 euros, el de un DVD de 360 euros, el de una televisión,
480 euros y el de un vídeo 150 euros, ¿cuál es el valor de las existencias en cada delegación?.
Escribiendo los precios de cada producto en una matriz columna
se tiene la matriz
Haciendo el producto de la matriz de existencia E4 por esta matriz de precios se obtiene el valor
de las existencias en cada delegación.

41. Así, en la delegación de Espinal se han de vender 31 CD, 26 DVD, 80 televisores y 31
videos; en la de Mariquita 36 CD, 9 DVD, 8 televisores y 13 videos y en la de Honda se ha
de vender 10 CD, 28 DVD, 40 televisores y 15 videos.
f. ¿Cuánto se ha de vender si la empresa quiere que le queden las siguientes existencias: en
Espinal, 23 CD, 22 DVD, ninguna televisión y 7 vídeos, en Mariquita, ningún CD,
televisiones y 27 vídeos y en Honda, 4 CD, 32 DVD, 44 televisiones y 45 vídeos?.
Llamamos X a la matriz que recoge la información de las ventas que se han de realizar.
Por lo tanto, ha de ocurrir que E4 – X =
De donde

42. EJERCICIO 11
En un edificio hay tres tipos de viviendas: L1, L2 y L3. Las
viviendas L1 tienen 4 ventanas pequeñas y 3 grandes; las
L2 tienen 5 ventanas pequeñas y 4 grandes, y las L3, 6
pequeñas y 5 grandes.
Cada ventana pequeña tiene 2 cristales y 4 bisagras, y las
grandes, 4 cristales y 6 bisagras.
a) Escribe una matriz que describa el número y el tamaño de
las ventanas de cada vivienda y otra que exprese el
número de cristales y bisagras de cada tipo de ventana.
b) Calcula la matriz que expresa el número de cristales y de
bisagras de cada tipo de vivienda.

43. Observe que la segunda matriz es la transpuesta de la primera en la
que se han cambiado las filas por columnas (o las columnas por filas).
Para el número y tamaño de las ventanas se tienen dos alternativas para mostrar el número y
tamaño de las ventanas de cada vivienda. La primera es a través de una matriz de Viviendas
x Ventanas de tamaño 3x2.
Representación
mediante Tablas
Representación
mediante Matrices
La segunda alternativa es a través de una matriz de Ventanas x Vivienda de tamaño 2x3.
VIDIENDAS Pequeñas Grandes VIVIENDAS Pequeñas Grandes
L1 4 3 L1 4 3
L2 5 4 L2 5 4
L3 6 5 L3 6 5 3x2
VENTANAS VENTANAS
VENTANAS L1 L2 L3 VENTANAS L1 L2 L3
Pequeñas 4 5 6 Pequeñas 4 5 6
Grandes 3 4 5 Grandes 3 4 5 2x3
VIVIENDAS VIVIENDAS
a) Escribe una matriz que describa el número y el tamaño de las ventanas de cada
vivienda y otra que exprese el número de cristales y bisagras de cada tipo de ventana.

44. Para el número de cristales y bisagras (llamados materiales) por cada
tipo de ventana, tenemos igualmente dos alternativas. La primera es a
través de una matriz de Ventanas x materiales de tamaño 2x2.
VENTANAS Cristales Bisagras VENTANAS Cristales Bisagras
Pequeñas 2 4 Pequeñas 2 4
Grandes 4 6 Grandes 4 6 2x2
MATERIALES MATERIALES
Representación
mediante Tablas
Representación
mediante Matrices
La segunda alternativa es a través de una matriz de Materiales x Ventanas de tamaño 2x2.
MATERIAES Pequeñas Grandes MATERIAES Pequeñas Grandes
Cristales 2 4 Cristales 2 4
Bisagras 4 6 Bisagras 4 6 2x2
VENTANAS VENTANAS
Observe que la segunda matriz es la transpuesta de la primera en la
que se han cambiado las filas por columnas (o las columnas por filas).

45. Para calcular el número de cristales y de bisagras (materiales) para
cada tipo de vivienda, tenemos:
Materiales x Vivienda = [ Materiales x Ventana ] X [ Ventanas x Vivienda ]
R2x3 = A2x2 x B2x3
MATERIALES L1 L2 L3 MATERIALES Pequeñas Grandes VENTANAS L1 L2 L3
Cristales 20 26 32 = Cristales 2 4 X Pequeñas 4 5 6
Bisagras 34 44 54 2x3 Bisagras 4 6 2x2 Grandes 3 4 5 2x3
VIVIENDASVIVIENDAS VENTANAS