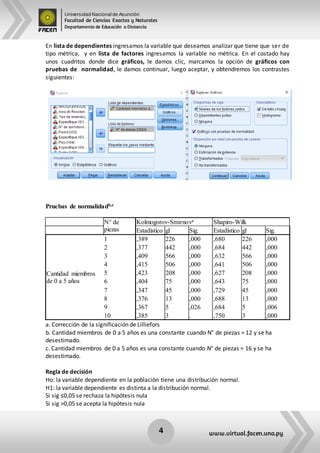
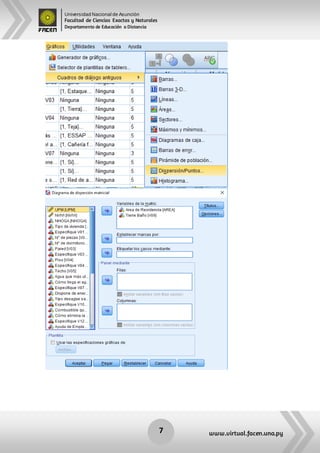
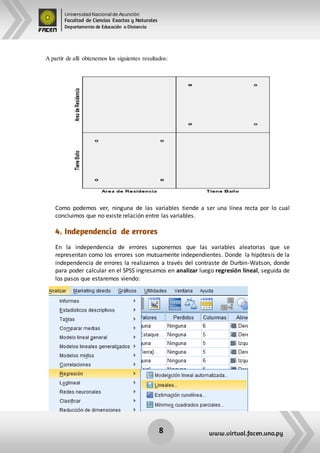
Este documento resume los principales supuestos de los modelos de regresión, incluyendo la normalidad univariada y multivariada, homocedasticidad, linealidad y independencia de errores. Explica cómo evaluar cada supuesto estadísticamente en el software SPSS, como utilizando histogramas, gráficos P-P y pruebas como Kolmogorov-Smirnov, Shapiro-Wilk y Levene.