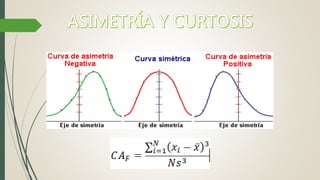
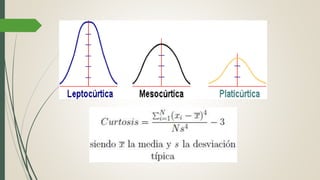
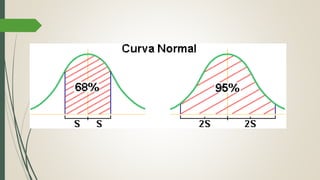
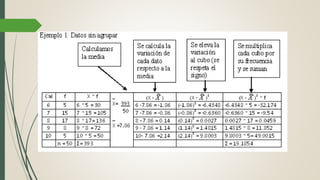
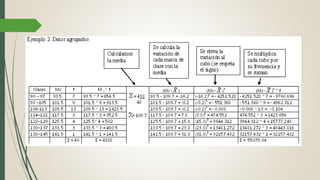
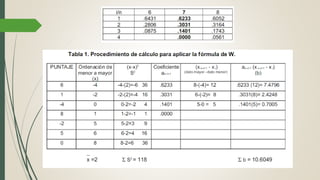
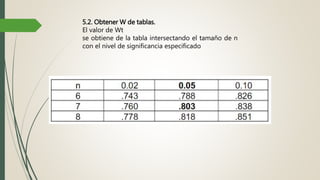
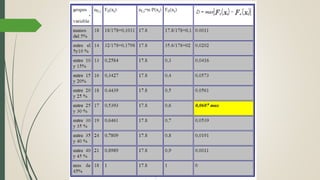
Este documento describe cómo realizar una prueba de Shapiro-Wilk para determinar si los datos de una muestra siguen una distribución normal. Explica los pasos para establecer las hipótesis, seleccionar la prueba estadística apropiada, especificar el nivel de significación, obtener el estadístico de prueba y tomar una decisión estadística sobre si rechazar o no la hipótesis nula de normalidad. Finalmente, aplica este procedimiento a un ejemplo de datos reales y concluye que la distribución de

8. OBJETIVO
Determinar si una muestra aleatoria presenta distribución
normal. La lógica de la prueba se basa en las desviaciones
que presentan las estadísticas de orden de la muestra
respecto a los valores esperados de los estadísticos de
orden de la normal estándar.

9. SUPUESTOS
1. Una muestra
2. Observaciones independientes
3. Muestreo aleatorio
4. Variables en escala de intervalo o razón
TIPO DE HIPÓTESIS A PROBAR
Ho: La muestra aleatoria tiene una distribución
normal.
Hipótesis alterna sin dirección
Hi: La muestra aleatoria no tiene una distribución
normal.

10. DISTRIBUCIÓN MUESTRAL
Cuantiles de W.
TIPO DE DATOS
Puntajes individuales
REGLA DE DECISIÓN
Si Wo≤Wt, α∴Rechazamos Ho
(Tabla cuantiles de W)

11. EJEMPLO
En un centro de investigación sobre trastornos de la
alimentación se llevó cabo un estudio para probar
una nueva terapia en mujeres anoréxicas. Los
efectos benéficos de la intervención se observarían
en el peso ganado (en kg.) por las mujeres al
término de tres meses. El estudio se realizó con una
muestra aleatoria de siete mujeres y los datos
obtenidos son los siguientes.
6
1
-4
8
-2
5
0
Antes de proceder a analizar los datos con pruebas
de inferencia estadística se desea corroborar si se
distribuyen de manera normal. Probar la hipótesis
nula de que la distribución de la muestra es normal.

12. SOLUCIÓN
Variable en escala de razón:
peso ganado
Paso 1.
Establecer las hipótesis a probar
Ho: La distribución de la muestra es normal.
Hi: La distribución de la muestra no es normal.
Paso 2.
Elegir la prueba estadística
Dado que interesa probar que la muestra presenta
distribución normal y se cuenta con puntajes
individuales y en escala de razón, y la muestra fue
tomada de forma aleatoria, se aplicará la prueba de
Shapiro-Wilk.
Paso 3. Especificar alfa
Se empleará un
α= 0.05

13. Paso 4. Región de Rechazo
Todos los valores menores o iguales a Wt con un alfa de
0.05
Paso 5. Decisión
Para obtener el valor observado de W y tomar la decisión
estadística se aplica el procedimiento con la fórmula de W.
5.1. Obtener el estadístico
Calcular los datos necesarios para aplicar la fórmula
de W como se muestra en la siguiente tabla.

16. 5.2. Obtener W de tablas.
El valor de Wt
se obtiene de la tabla intersectando el tamaño de n
con el nivel de significancia especificado

17. 5.3 Comparar el valor observado y el valor esperado aplicando la regla de
decisión
Si Wo≤Wt,α∴Rechazamos Ho
.9530 > .803
Dado que Wo > Wt ,α 0.05; podemos aceptar Ho
Decisión estadística:
Dado que aceptamos Ho podemos decir que la distribución de la muestra
es normal.
Conclusión:
Existe suficiente evidencia estadística para decir que
los datos de la muestra redistribuyen de manera
normal, por lo tanto, se puede asumir que se
cumple el
supuesto de normalidad y se puede proceder a anali
zar los datos con estadística paramétrica.

18. Este procedimiento es un test no paramétrico que permite establecer si dos
muestras se ajustan al mismo modelo probabilístico (Varas y Bois, 1998).
Es un test válido para distribuciones continuas y sirve tanto para muestras
grandes como para muestras pequeñas (Pizarro et al, 1986)
Así mismo Pizarro (1988), hace referencia a que, como parte de la aplicación de
este test, es necesario determinar la frecuencia observada acumulada y la
frecuencia teórica acumulada; una vez determinadas ambas frecuencias, se
obtiene el máximo de las diferencias entre ambas.

19. Se trata , por tanto , de comprobar si la muestra se
ajusta o proviene de una población con una
determinada distribución de probabilidad. Como se
planteó en el esquema el test de K-S es más
adecuado cuando la muestra viene planteada
en escala ordinal.

20. El procedimiento consiste en establecer las frecuencias relativas
acumuladas referentes a la información muestral. Fo(xi).. Establecer ,
también, en base a la distribución de probabilidad hipotética las
frecuencias relativas acumuladas Ft(xi).
Compararemos ambas frecuencias creando el estadístico es decir, el
valor máximo de entre todas las diferencias entre frecuencias relativas
acumuladas teóricas y observadas para los mismos valores o
intervalos de la variable.
Dicho estadístico D se comparará con el correspondiente de la tabla
del test de K-S en base al nivel de significación establecido y el
tamaño muestral ; de manera que si
D<D(tabla, n,a) no rechazaremos la hipótesis de que la muestra
procede de la hipotética población con distribución establecida ,
mientras que si D>D(tabla, n,a) rechazaremos dicha hipótesis.

21. Se ha realizado una muestra a 178 municipios al respecto del porcentaje de población
activa dedicada a la venta de ordenadores resultando los siguientes valores :
Queremos contrastar que el
porcentaje de municipios para cada
grupo establecido se distribuye
uniformemente con un nivel de
significación del 5%.
Bajo la hipótesis nula cada grupo
debiera de estar compuesto por el
10% de la población dado que existen
diez grupos . Así podemos establecer
la tabla

23. siendo la máxima diferencia =0,0607 y
por tanto el estadístico de K-S que compararemos
con el establecido en la tabla que será para un nivel
de significación de 5% y una muestra de
178 dado que el estadístico es menor
(0,0607) que el valor de la tabla (0,1019) no
rechazamos la hipótesis de comportamiento
uniforme de los grupos establecidos al respecto de la
población activa dedicada a la venta de ordenadores.