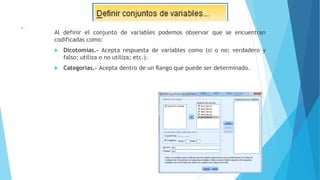
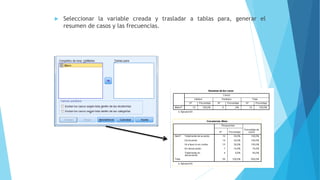
Este documento describe la función Analizar en SPSS, la cual permite realizar diversos cálculos estadísticos con una base de datos. Entre los análisis descritos se encuentran el modelo lineal general, regresión, pruebas paramétricas y no paramétricas como chi-cuadrado y Wilcoxon. El documento también explica conceptos como variables dependientes, independientes, y cómo formular hipótesis nulas y alternativas.

1. UNIVERSIDAD CENTRAL DEL ECUADOR
Facultad de Ciencias Económicas
Carrera de Economía
Tema: SPSS- Función Analizar.
Integrantes:
- Moreta Sofia
- Naranjo Jenny
- Lara Pablo

2. FUNCIÓN ANALIZAR
• Es una de las funciones
disponibles dentro del programa
SPSS que permite realizar
diversos cálculos estadísticos con
respecto a una base de datos
ingresada.

3. • Modelo Lineal General
Estima un modelo lineal general en donde una variable de interés es interpretada por
una o más variables explicativas.
• Univariante: análisis de varianza para una variable dependiente mediante uno o más
variables.
• Multivariante: análisis de varianza para variables dependientes múltiples mediante
una o más variables.
Variable Dependiente  Variable Cuantitativa (Escala)  Análisis
V. Independiente  V. Cuantitativa o Cualitativa (Escala, Nominal)  Relación
Ejemplo: Analizar la relación entre el Precio de Venta y el Tipo de Inmueble
SPSS  ANALIZAR  MODELO LÓGICO LINEAL  UNIVARIANTE

4. • Regresión
La Regresión Lineal o Ajuste Lineal es un método matemático que modela la
relación entre una variable dependiente (Y) y una independiente (X). SPSS
provee de datos para armar la función del modelo analizado y así estimar
valores de la variable dependiente.
Variable Dependiente
Variable Independiente
Ejemplo: Establecer una función que estime el Precio de Venta de un
Inmueble tomando en cuenta la superficie del mismo.
SPSS  ANALIZAR  REGRESIÓN  LINEAL
Variables Cuantitativas
(Escala)

5. Las pruebas no paramétricas no asumen
acerca de los parámetros de
distribución ni se preocupa por el tipo
de distribución, sino trabajan con
simple ordenación y recuento
(asignando rankings) a los valores de la
variable sin importar la distribución.
FORMULACIÓN DE HIPÓTESIS
NULA (H0): Es aquella en la que se asegura
que los dos parámetros analizados son
independientes uno del otro.
ALTERNATIVA (H1): Es aquella en la que se
asegura que los dos parámetros analizados sí
son dependientes

6. Chi-Cuadrado
•Es el nombre de una prueba de hipótesis que determina si dos variables están relacionadas o no.
Binomial
•Permite averiguar si una variable dicotómica sigue o no un determinado modelo de probabilidad.
•En cada prueba del experimento sólo son posibles dos resultados: éxito y fracaso.
Rachas
•Para determinar si una muestra de observaciones es o no aleatoria, es decir, para determinar si las observaciones de
una determinada secuencia son independientes entre sí.
•Es una secuencia de observaciones similares.
Kolmogorov-
smirnov
•Es una prueba de bondad de ajuste: sirve para contrastar la hipótesis nula de que la distribución de una variable se
ajuste a una determinada distribución teórica de probabilidad.

7. McNemar
•Sirve para contrastar hipótesis sobre igualdad de proporciones.
Signos
Wilcoxon
•Puede ser usada para saber si una variable tiende a ser mayor que otra.
•Permite contrastar la hipótesis de igualdad entre dos medianas poblacionales.
Cochran
•Esta prueba es idéntica a la prueba de Friedman, pero se aplica cuando todas las respuestas son binarias.
Friedman
Kendall
•La prueba examina los rangos de los datos generados en cada periodo de tiempo para determinar si las variables
comparten la misma distribución continua de su origen.
•Nos sirve para conocer la concordancia entre rangos, más que para probar que existe una diferencia entre las
medianas.

8. Rachas de
Wald-
Wolfowitz
•Contrasta si dos muestras con datos independientes proceden de poblaciones con la misma distribución.
U de Mann-
Whitney
•Es la alternativa no paramétrica a la comparación de dos promedios independientes.
Moses
Kolmogorov
- Smirnov
•Sirve para estudiar si existe diferencia en el grado de dispersión o variabilidad de dos distribuciones.
•Sirve para contrastar la hipótesis de que dos muestras proceden de la misma población.
- Mediana
- Kruskal-
Wallis
- Jonckeere-
Terpsta
•Contrasta diferencias entre dos o más grupos en relación con su mediana, Es similar a la prueba Chi-cuadrado.
•Comparar grupos independientes y variables cuantitativas que no tienen distribución normal o que sean ordinales.
•Cuando existe una ordenación a priori (ascendente o descendente) de las K poblaciones de las que se extraen las
muestras.

9. Respuesta Múltiple
Son variables que se crean a partir de variables individuales en la data.

10. . Al definir el conjunto de variables podemos observar que se encuentran
codificadas como:
 Dicotomías.- Acepta respuesta de variables como (si o no; verdadero y
falso; utiliza o no utiliza; etc.).
 Categorías.- Acepta dentro de un Rango que puede ser determinado.

11.  Seleccionar la variable creada y trasladar a tablas para, generar el
resumen de casos y las frecuencias.