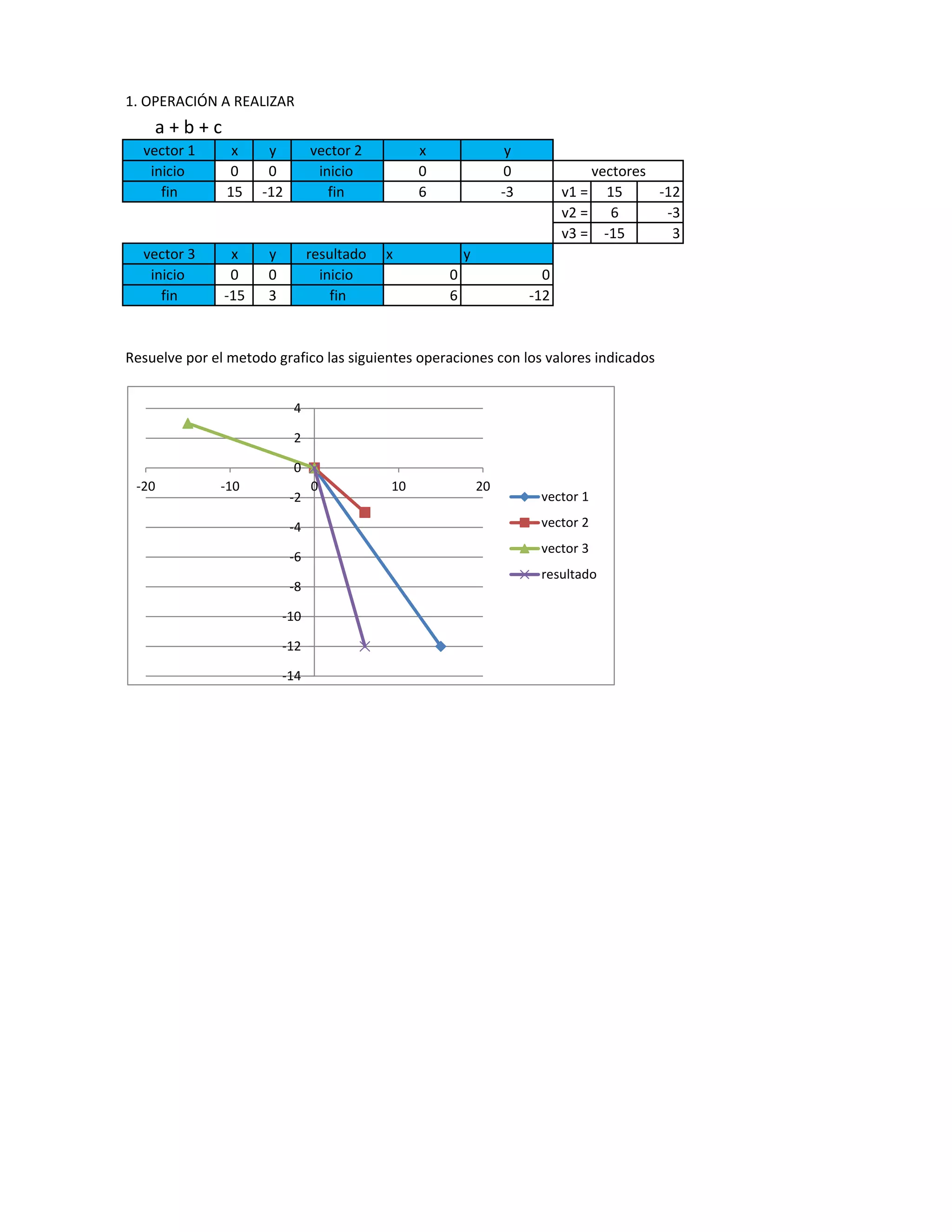
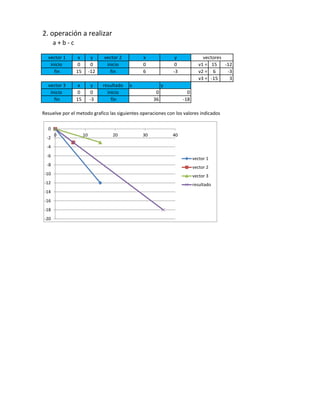
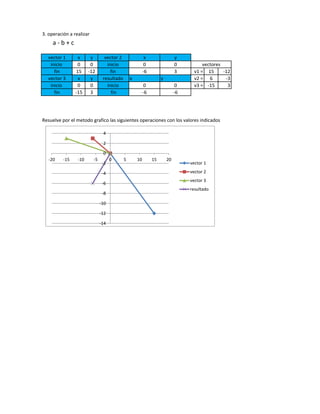
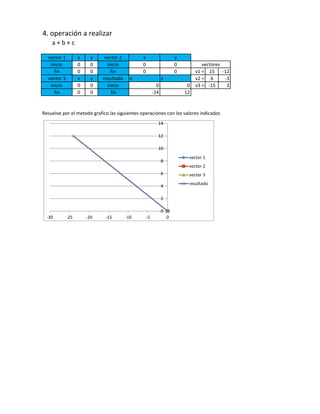
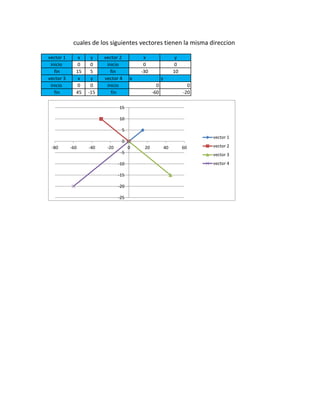
El documento presenta varios ejemplos de operaciones entre vectores resueltas gráficamente. Explica cómo realizar sumas, restas, productos punto y productos vectoriales de vectores dados sus componentes. También determina la dirección y magnitud de vectores resultantes de dichas operaciones.

1. 1. OPERACIÓN A REALIZAR
vector 1 x y vector 2 x y
inicio 0 0 inicio 0 0
fin 15 -12 fin 6 -3 v1 = 15 -12
v2 = 6 -3
v3 = -15 3
vector 3 x y resultado x y
inicio 0 0 inicio 0 0
fin -15 3 fin 6 -12
Resuelve por el metodo grafico las siguientes operaciones con los valores indicados
a + b + c
vectores
-14
-12
-10
-8
-6
-4
-2
0
2
4
-20 -10 0 10 20
vector 1
vector 2
vector 3
resultado

2. 2. operación a realizar
vector 1 x y vector 2 x y
inicio 0 0 inicio 0 0 v1 = 15 -12
fin 15 -12 fin 6 -3 v2 = 6 -3
v3 = -15 3
vector 3 x y resultado x y
inicio 0 0 inicio 0 0
fin 15 -3 fin 36 -18
Resuelve por el metodo grafico las siguientes operaciones con los valores indicados
a + b - c
vectores
-20
-18
-16
-14
-12
-10
-8
-6
-4
-2
0
0 10 20 30 40
vector 1
vector 2
vector 3
resultado

3. 3. operación a realizar
vector 1 x y vector 2 x y
inicio 0 0 inicio 0 0
fin 15 -12 fin -6 3 v1 = 15 -12
vector 3 x y resultado x y v2 = 6 -3
inicio 0 0 inicio 0 0 v3 = -15 3
fin -15 3 fin -6 -6
Resuelve por el metodo grafico las siguientes operaciones con los valores indicados
a - b + c
vectores
-14
-12
-10
-8
-6
-4
-2
0
2
4
-20 -15 -10 -5 0 5 10 15 20
vector 1
vector 2
vector 3
resultado

4. 4. operación a realizar
vector 1 x y vector 2 x y
inicio 0 0 inicio 0 0
fin 0 0 fin 0 0 v1 = 15 -12
vector 3 x y resultado x y v2 = 6 -3
inicio 0 0 inicio 0 0 v3 = -15 3
fin 0 0 fin -24 12
Resuelve por el metodo grafico las siguientes operaciones con los valores indicados
a + b + c
vectores
0
2
4
6
8
10
12
14
-30 -25 -20 -15 -10 -5 0
vector 1
vector 2
vector 3
resultado

5. cuales de los siguientes vectores tienen la misma direccion
vector 1 x y vector 2 x y
inicio 0 0 inicio 0 0
fin 15 5 fin -30 10
vector 3 x y vector 4 x y
inicio 0 0 inicio 0 0
fin 45 -15 fin -60 -20
-25
-20
-15
-10
-5
0
5
10
15
-80 -60 -40 -20 0 20 40 60
vector 1
vector 2
vector 3
vector 4

6. v1 = 15 5
v2 = -30 10
v3 = 45 -15
v4 = -60 -20
vectores

7. OPERACIÓN 1 A + B + C
I J K
A 5 15 3
B -15 6 -3
C 3 -15 -7
= -7 6 -7
OPERACIÓN 2 A-B
I J K
A 5 15 3
B -15 6 -3
= 20 9 6
AXB
I J K
A 5 15 3
B -15 6 -3
resultado-63 -30 255
AXC
I J K
A 5 15 3
C 3 -15 -7
resultado-60 44 -120
A· B
I J K
A 5 15 3
B -15 6 -3
resultado6
el modulo del vector A es igual a 35, determiner el valor de "x"
si el vector a es "x,-NL" representalo graficamente
35^2= 1225 38.0788655
15^2= 225
1450
VECTORES
VECTORES
√1450=
PRODUCTO PUNTO
PRODUCTO CRUZ
PRODUCTO CRUZ
VECTORES
VECTORES
VECTORES
cada vector se ordena con su
respectiva literal y se realiza la
operacion correspondiente
ejemplo para i
i=5+(-15)+3 y sale a -7
al igual que en lo anterior cada literal
con su literal pero esta vez se restan
ejemplo para i
i=5-(-15) y sale a 20
se multiplican de forma cruzada los vectores y para
poderlo determinar se realiza una matriz con los
vectores requeridos
ejemplo para i
se multiplican los vectores que se te piden segun su
literal se suman y restan segun lo que te pida y solo
queda un valor
ejemplo
=5(-15)+15(6)+3(-3)= -75+90+(-9)=6