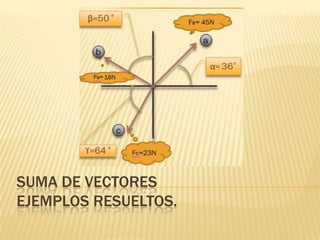
Este documento proporciona instrucciones para resumir vectores utilizando fórmulas. Explica cómo descomponer cada vector en componentes ortogonales usando senos y cosenos, sumar los componentes para obtener valores de fuerza total y ángulo de inclinación, y luego aplicar el teorema de Pitágoras para determinar la magnitud de la resultante. También incluye un ejemplo numérico para ilustrar el proceso paso a paso.

1. Suma de vectoresejemplos resueltos.

2. FORMULAScomponentesFy= F SEN αFx= F SEN αSuma de los componentes Fx y FyΣFy= Fyₐ + Fyb +Fyc . . .FynΣFx = Fxa + Fxb +Fxc . . .FxnresultanteR= (ΣFy)² + =(ΣFy)² Angulo o direccionα= tan¯ˡΣFyΣFxβ=50 ˚ Fa= 45Nabα= 36˚Fb= 16NcFc=23Nϒ=64 ˚

3. los componentes de cada vector.Una manera sencilla para trabajar ordenadamente utilizando las formulas de descomposición de vectores y la sumatoria de los mismos es:En pocas palabras se unas las formulas para sacar los componentes y suma de componentes a la vezEjemplo:ΣFyFya = Fa sen = 45N sen (36) = 26.45NFyb= Fa sen = 16N sen(50) = 12.25N Fyc= Fa sen = 23N sen(64) = -20.67NΣFy 18.03N ΣFxFya = Fa cos= 45N cos(36) = 36.40NFya = Fa cos = 16N cos(50) = -10.28NFya= Fa cos = 23N cos(64) = -10.08NΣFx = 16.04N

4. ΣFy = 18.03NΣFx = 16.04NAhora se obtiene la resultante utilizando el teorema de Pitágoras ejemplo:R= (ΣFy)² + =(ΣFy)² R= (18.03N) ² + (16.04N) ²R= 325.08 + 257.28R= 582.36R= 24.13 N

5. Ahora pasaremos a calcular el ángulo que forma la resultante , usando la función tangente, ejemplo.α=tan⁻ˡΣFy = ΣFxα= tan⁻ˡ= 18.03N = 16.04Nα= tan⁻ˡ 1.12 =Para meter la tan⁻ˡ en la calculadora se presiona shift y después tangente, o 2nd y después tan, esto depende de la calculadora.α = 48.3428002 α=48 ̊20 ̒34.04”