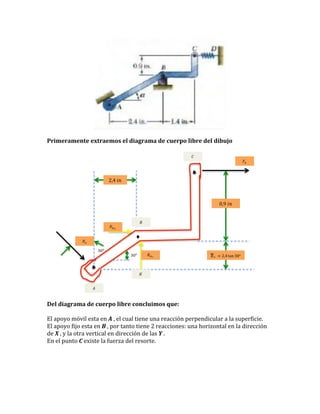
(1) Se extrae el diagrama de cuerpo libre de un dibujo que muestra un resorte y apoyos fijos y móviles; (2) Del diagrama se concluye que hay reacciones en los apoyos y una fuerza del resorte; (3) Aplicando ecuaciones de equilibrio se determinan las reacciones y la constante del resorte.

1.
Primeramente
extraemos
el
diagrama
de
cuerpo
libre
del
dibujo
!!
!! !
2,4!!"!
0,9!!"!
!!
!! ! !
!! !
30! !
!! ! !
30! !
!! ´ = 2,4 tan 30°!
!´ !
!!
Del
diagrama
de
cuerpo
libre
concluimos
que:
El
apoyo
móvil
esta
en
A
,
el
cual
tiene
una
reacción
perpendicular
a
la
superficie.
El
apoyo
fijo
esta
en
B
,
por
tanto
tiene
2
reacciones:
una
horizontal
en
la
dirección
de
X
,
y
la
otra
vertical
en
dirección
de
las
Y
.
En
el
punto
C
existe
la
fuerza
del
resorte.

2. e-Body Diagram:
ee-Body Diagram:
(a) From free-body diagram of lever BCD
(a) From free-body diagram of lever
ΣM C = 0: TAB ((50 mm ) − 200 N ( 75 mm ) = 0
ΣM C = 0: TAB 50 mm
∴ TAB = 300
∴ TAB = 300
Aplicando
las
ecuaciones
de
equilibrio
tendremos:
(b) From free-body diagram of lever BCD
(b) From free-body diagram of lever
e Solutions Manual Organization System
on 19.
m:
ΣFxx = 0: 0: 𝑅 xsin0.6 ( 300 N ) = 0 𝐹 = 0 (𝒂)
ΣF 𝐹 0: 200 N + C x + 30 + 𝑅! + !
= = 200 N + !
!
!
∴ C xx = −380 N
or
C x = 380 N
∴ C = −380 N
or
C x = 380 N
ΣFyy = 0: C yy + 0.8 ( 300 N ) = 0
ΣF = 0: C + 0.8 300 N = 0
𝐹! = 0: − 𝑅! cos 30 + 𝑅!! = 0 (𝒃)
∴ C = −240 N
(a)
From free-body diagram of lever∴ Cyy = −240 N
BCD
C y = 240 N
C y = 240 N
or
or
2
ΣMThen0: TAB (C =mm )22−+200 N ( 75380 )2 + (0240 )2 = 449.44 N
50 C
mm ) =
C = C xx + C yy = ( 380 2 + 240 2 = 449.44 N
C =
C2 =
Then
𝑀! = 0: 𝑅! sin 30 2,4 tan 30 + 𝑅! cos 30 2,4 − 𝐹! 0,9 = 0 (𝒄)
∴T
= 300
AB
⎛ Cy ⎞
⎛ − 240 ⎞
⎛C ⎞
⎞
⎛
and
θ = tan −−1 ⎜ y ⎟ = tan −11⎜ − 240 ⎟ = 32.276°
⎜ ⎟
and diagramθ = lever1⎜
tan BCD⎟ = tan − ⎜
⎟ = 32.276°
(b)
From free-body
of
⎜C ⎟
⎝ − 380 ⎠
⎝ C xx ⎠
⎝ − 380 ⎠
⎠
⎝
𝐷𝑒𝑙 𝑒𝑛𝑢𝑛𝑐𝑖𝑎𝑑𝑜 𝑡𝑒𝑛𝑒𝑚𝑜𝑠 𝑞𝑢𝑒: 𝑹 𝑨449 N 32.3° ▹
ΣFx = 0: 200 N + Cx + 0.6 ( 300 N ) = 0
or C = 449 N
32.3
or C = = 𝟑 𝒍𝒃
° ▹
∴ C x = −380 N
or
C x = 380 N
De
la
ecuación
(c)
tenemos
que:
ΣFy = 0: C y + 0.8 ( 300 N ) = 0
3 sin 30 2,4 or 30 C+= 240 N 30 2,4 = 𝐹! 0,9
tan
3 cos
∴ C y = −240 N
y
2
2
C = C x + C y3 = sin 30 + ( 240 ) 30 449.44 N cos 30 2,4 = 𝟗, 𝟐𝟒 𝒍𝒃
Then
( 380 )2 2,4 tan2 = + 3
𝑭𝑹 =
0,9
⎛ Cy ⎞
−1
−1 ⎛ − 240 ⎞
and
θ = tan ⎜ ⎟ = tan ⎜
⎟ = 32.276°
⎜C ⎟
Determinaremos
la
constante
K
mediante
la
fuerza
en
el
resorte
⎝ − 380 ⎠
⎝ x⎠
or C = 449 N
32.3° ▹
𝑭 𝑹 = 𝝌𝜿
𝐹!
9,24
𝜿=
=
= 𝟕, 𝟕 𝒍𝒃 𝒊𝒏
𝜒
1,2
Bien
ahora
para
la
reacción
en
B
tendremos
que:
De
la
ecuación
(a)
:
𝑹 𝑩 𝒙 = −𝑅! sin 30 − 𝐹! = −3 sin 30 − 9,24 = 𝟏𝟎, 𝟕𝟒 𝒍𝒃 ó 𝑹 𝑩 𝒙 = 𝟏𝟎, 𝟕𝟒 𝒍𝒃 ←
De
la
ecuación
(b)
:
Mechanics for Engineers: Statics and Dynamics, 8/e, Ferdinand P. Beer, E. Russell Johnston, = 𝟐, 𝟔𝟎 𝒍𝒃 ó 𝑹 𝑩 = 𝟐, 𝟔𝟎 𝒍𝒃 ↑
𝑹 𝑩 = 𝑅! cos Beer, = 3 cos 30 Jr.,
r Mechanics for Engineers: Statics and Dynamics, 𝒚8/e, Ferdinand P.30 E. Russell Johnston, Jr.,
𝒚
. Eisenberg, William E. Clausen, David Mazurek, Phillip J. Cornwell
R. Eisenberg, William E. Clausen, David Mazurek, Phillip J. Cornwell
The McGraw-Hill Companies.
07 The McGraw-Hill Companies.
∴ 𝑹 𝑩 =
𝑅!! ! + 𝑅!! ! =
eers: Statics and Dynamics, 8/e, Ferdinand P. Beer, E. Russell Johnston, Jr.,
10,74
!
+ 2,60
!
= 𝟏𝟏, 𝟎𝟓 𝒍𝒃