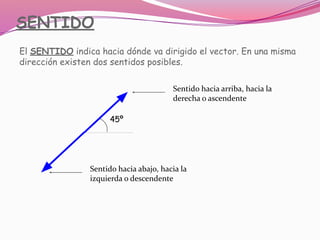
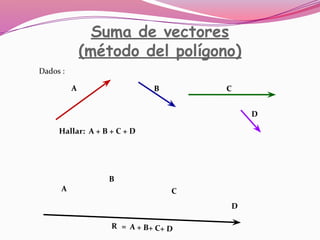
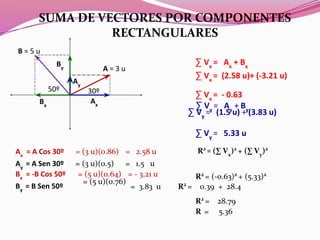
Este documento describe los conceptos básicos de los vectores, incluyendo su representación, características, suma, resta y descomposición. Un vector se representa como un segmento dirigido con un punto de origen y un punto terminal. Tiene cuatro características: módulo, dirección, sentido y punto de aplicación. Existen métodos para sumar y restar vectores como el triángulo, paralelogramo y polígono. También se puede realizar operaciones con las componentes rectangulares de los vectores.

1. Prof. Eudy José Piña
VECTORES

2. Un vector V, se representa como un segmento dirigido con origen o punto de
aplicación en A y extremo o punto terminal en B. Se representa por AB, siendo
los extremos A y B
Los puntos en los que empieza y termina un vector se llaman origen y extremo,
respectivamente.
Dada una dirección, el sentido del vector es el indicado por la flecha en la que
termina
A
(origen)
B
(extremo)
B
(origen)
A
(extremo)
AB
BA

3. CARACTERÍSTICAS DE UN VECTOR
Las características de un vector son cuatro:
▪ MÓDULO
▪ DIRECCIÓN
▪ SENTIDO
▪ PUNTO DE APLICACIÓN

4. MÓDULO
El MÓDULO viene dado por la longitud de la flecha. El módulo está
determinado por un vector unidad u.
3 cm

5. DIRECCIÓN
La DIRECCIÓN es la recta que lo contiene. Viene expresada por el
ángulo que forma la recta con la horizontal: 0º (horizontal), 30º, 47º,
90º (vertical), 130º, 249º, etc.
45º
- 100º = 260º
120º
- 30º = 330º

6. SENTIDO
El SENTIDO indica hacia dónde va dirigido el vector. En una misma
dirección existen dos sentidos posibles.
45º
Sentido hacia arriba, hacia la
derecha o ascendente
Sentido hacia abajo, hacia la
izquierda o descendente

7. Suma de vectores
(método del triángulo)
A B
A
R R = A+ B
B

8. Suma de vectores
(método del paralelogramo)
A B
A
B
A
B
R R = A+ B

9. Suma de Vectores:
Paralelogramo. Si deseamos sumar dos vectores, una vez dibujados coincidiendo con el
origen, por el extremo de cada vector trazamos una paralela al otro. Ambas paralelas se
cortan en un punto. El vector cuyo punto de aplicación coincide con el de los vectores
sumandos y cuyo extremo es el que termina en el punto de corte de las paralelas es el vector
suma
B
A

10. Suma de vectores
(método del polígono)
A B C
Hallar: A + B + C + D
A B C
R
Dados :
D
A
B
C
D
= A + B+ C+ D

11. Suma de Vectores:
Polígono. Se emplea, sobre todo, cuando se desean sumar varios vectores a la vez. En el
extremo del primer vector se sitúa el punto de aplicación del segundo, sobre el extremo del
segundo vector se coloca el punto de aplicación del tercero y así hasta terminar de dibujar
todos los vectores. El vector resultante es el que se obtiene al unir el punto de aplicación del
primero con el extremo del último

12. Suma de Vectores:
Analíticamente, se suman las componentes.
A = (0, 5)
B = (5, 4)
A + B = (0,5) + (5,4) = (0 + 5, 5 + 4) = (5, 9)

13. Resta de Vectores:
La resta se realiza en forma análoga a la suma

14. Resta de Vectores:
Aritméticamente restamos las componentes verticales y horizontales entre sí.
A = (7, 2)
B = (5, 4)
A - B = (7, 2) - (5, 4) = (7 - 5, 2 - 4) = (2, - 2)

15. Conmutativa
a + b = b + a
Asociativa
(a + b) + c = a + (b + c)
Elemento neutro o vector 0
a + 0 = 0 + a = a
Elemento simétrico u opuesto
a'
a + a' = a' + a = 0
a' = -a
Propiedades de la suma de Vectores:

16. Producto de Vectores:
El producto escalar de dos vectores no es otro vector sino un número. Se
determina multiplicando las coordenadas de ambos vectores, componente a
componente y sumando los resultados. Por ejemplo:
(-3,2) x (5,1) = ((-3) x5) +(2x1) = -15+2 = -13
Propiedades de la suma de Vectores:
Conmutativa
A * b = b * a
Asociativa
(a + b) * c = a * (b + c)

17. COMPONENTES RECTANGULARES
DE UN VECTOR
ө
A
Ax
Ay
Sen ө =
Ay
A
Cos ө =
Ax
A
Ay

18. B = 5 u
A = 3 u
30º
50º
Ax
Ay
Bx
By
Ax
= A Cos 30º
Ay
= A Sen 30º
Bx
= -B Cos 50º
By
= B Sen 50º
= (3 u)(0.86) = 2.58 u
= (3 u)(0.5) = 1.5 u
= (5 u)(0.64) = - 3.21 u
= (5 u)(0.76)
= 3.83 u
∑ Vx
= Ax
+ Bx
∑ Vy
= Ay
+ By
∑ Vx
= (2.58 u)+ (-3.21 u)
∑ Vy
= (1.5 u) + (3.83 u)
R2
= (∑ Vx
)2
+ (∑ Vy
)2
R2
= (-0.63)2
+ (5.33)2
∑ Vx
= - 0.63
∑ Vy
= 5.33 u
R2
= 0.39 + 28.4
R = 5.36
R2
= 28.79
SUMA DE VECTORES POR COMPONENTES
RECTANGULARES

19. 45º 40º
30º
7u
6u
5u

20. DESCOMPOSICIÓN DE FUERZAS
En Matemáticas podemos también identificar vectores, componerlos y descomponerlos
usando coordenadas cartesianas:
y
x
1 2 3 4 5 6
5
4
3
2
1
y
x
1 2 3 4 5 6
5
4
3
2
1
Para componer dos vectores a partir de sus cordenadas cartesianas: