clase semana 1 .pdf

Sistemas de ecuaciones lineales
Ing. César Gutiérrez Cuba
Dr. César Gutiérrez - Métodos Numéricos

Matriz triangular superior
Matriz triangular Inferior

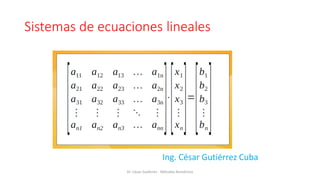
Sistema de ecuaciones Lineales
• Los sistemas de ecuaciones lineales surgen en el modelado de
muchos problemas físicos y de ingeniería.
• El sistema lineal de ecuaciones con m ecuaciones en n variables x1, x2,
…….,xn tiene la siguiente forma:

• El sistema de ecuaciones lineales, en forma matricial puede
expresarse de la forma:
- La matriz A es una matriz de coeficientes, y el vector X es un vector solución.
- Si cada elemento del vector B es cero, entonces el sistema se llama sistema
homogéneo. De lo contrario, es un sistema no homogéneo. Para cualquier
sistema homogéneo, la solución cero siempre es una solución, y también se
conoce como solución trivial.

Métodos de solución
• Existen muchos métodos directos e iterativos para las soluciones de
sistemas de ecuaciones lineales.
• Ambos tipos de métodos tienen algunas ventajas y desventajas.
Depende del tamaño y la estructura de los coeficientes de la matriz A,
recursos informáticos disponibles y estrategias de solución
adoptadas.

Métodos Directos:
1. Método de eliminación de Gauss
2. Métodos de descomposición LU
3. Método de Thomas para sistemas tridiagonales.
Métodos Indirectos:
1. Método de Jacobi
2. Método de Gauss-Seidel

E1
E2
E3
E4

Operaciones que se puede realizar sobre un
sistema de ecuaciones:
1. Multiplicar la ecuación Ei por cualquier constante no nula k y se
puede utilizar la ecuación que resulta en lugar de Ei. Esta operación se
denota por:
𝑘𝐸𝑖 → 𝐸𝑖
2( 1 1 0 0)→ 2 2 0 0
2𝐸1 → 𝐸1

2. Las ecuaciones Ei y Ej pueden intercambiarse de orden. Se denota
esta operación por:
𝐸𝑖 ↔ 𝐸𝑗
𝐸1 ↔ 𝐸2
E1
E2

3. Se puede multiplicar la ecuación Ej por cualquier constante k y sumar
a la ecuación Ei, y utilizar el resultado en vez de Ei. Esta operación se
denota por:
𝐸𝑖 + 𝑘𝐸𝑗 → 𝐸𝑖
𝐸2 + (−
1
3
)𝐸1 → 𝐸2
0
1
3
−
1
3
0
1 −
1
3
∗ 3=0 1 −
1
3
∗2=
1
3
0 −
1
3
∗ 1=-
1
3
0 −
1
3
∗0=0

Método de eliminación de Gauss
• El método de eliminación de Gauss es uno de los procedimientos
algorítmicos más simples en todos los métodos directos conocidos
con un número mínimo de operaciones aritméticas y, por lo tanto, el
método directo más utilizado.

Reescribamos el sistema:
en la forma de matriz aumentada [A: B] de la siguiente manera:

En el método de eliminación de Gauss, la solución del sistema de
ecuaciones, se obtiene en dos fases:
1. Primera fase, el sistema de ecuaciones lineales se convierte en un
sistema triangular superior equivalente con la ayuda de operaciones de
fila elementales.

(1)
1ra Etapa:
2da Etapa:
Multiplicadores

En forma algebraica, la última matriz se puede escribir de la siguiente
manera:

2. Segunda fase: La solución se obtiene mediante sustituciones hacia
atrás.
Calculamos la solución del sistema triangular superior (1) de la
siguiente manera: a partir de la última ecuación del sistema (1), se
puede calcular la variable xn de la siguiente manera:
Al usar el valor de xn en la segunda última ecuación, tenemos:
De la última ecuación
De la penúltima
ecuación

Del mismo modo, las ecuaciones restantes del sistema (1) producen:
En general:

Multiplicadores:
1ra Etapa: 𝑚21 =
𝑎21
𝑎11
, 𝑚31 =
𝑎31
𝑎11
, … . . , 𝑚𝑛1 =
𝑎𝑛1
𝑎11
2da Etapa: 𝑚32 =
𝑎32
𝑎22
, 𝑚42 =
𝑎42
𝑎22
, … . . , 𝑚𝑛2 =
𝑎𝑛2
𝑎22
3ra Etapa: 𝑚43 =
𝑎43
𝑎33
, 𝑚53 =
𝑎53
𝑎33
, … . . , 𝑚𝑛3 =
𝑎𝑛3
𝑎33

Multiplicadores:
E1
E2
E3
E4
Intercambio de filas
1ra Etapa:
Ejemplo:

(-6/12)
E2
-m21 E1
E2
E3
-m31 E1
E3
(-3/12)
Operaciones:

-(-6/12)
E4
-m41 E1
E4

¿Como resolver?
• Se puede hacer por etapas a mano y con calculadora
• Se puede usar una hoja electrónica como el Excel
• Se puede usar software como Maple
• Se puede usar un código de programa por ejemplo en Matlab o
Phyton.

Ejercicio:
Resolver el sistema de ecuaciones:
Empleando el método de eliminación de Gauss.

La matriz aumentada junto con los multiplicadores de fila mi1 son:
o
pivot
multiplicadores
Primera Fase:

multiplicadores
o
pivot

multiplicador
o
pivot

El proceso del algoritmo de sustitución hacia atrás aplicado al sistema triangular
produce la solución:
Segunda Fase:

La siguiente
función de
MATLAB
ngaussel.m
encuentra la
solución de
un sistema
lineal.
Las
ENTRADAS
son una
matriz A de
nxn y un
vector de
coeficientes
b de n x 1.

Ejercicio:
• Resolver el sistema de ecuaciones con el método de eliminación
Gaussiana empleando Excel:
Una solución en Matlab es:

Método de Descomposición LU
• En este método, la matriz de coeficientes A se factoriza en el producto
de dos matrices triangulares, una matriz L triangular inferior y otra
matriz U triangular superior:

(2)

Si:
Entonces el sistema anterior se reduce a:
El sistema LY = B es el sistema triangular inferior. Por lo
tanto, el vector Y se puede determinar fácilmente
mediante el uso de sustitución directa.
Método de Crout
Luego el vector X se puede calcular fácilmente mediante el uso
de sustitución inversa del siguiente sistema triangular superior:

Ejercicio:
• Use el método de Crout para calcular la solución del siguiente sistema
de ecuaciones lineales:

1ra
Columna
1ra Fila
2da columna
2da Fila
3ra columna

• Primera etapa:
Primera Columna:
Segunda etapa:
Primera Fila:
y

Tercera etapa:
Segunda Columna:
y
Cuarta etapa:
Segunda Fila:

Tercera Columna:
Quinta etapa:

• Entonces, se puede escribir la matriz de coeficientes A en términos de
las matrices L y U de la siguiente manera

• El sistema LY = B viene dado por:
Este sistema de ecuaciones
se puede reescribir de la
siguiente manera:
Resolviendo se obtiene:

• Usando los valores de y, se procede a resolver:
Se obtiene:

Ejercicio:
Resolver el sistema de ecuaciones con el método de Crout empleando
Excel:

Sistemas tridiagonales
- En algunas aplicaciones aparecen a menudo sistemas de ecuaciones en los que la matriz
de coeficientes tiene una estructura especial. Por regla general, es preferible resolver estos
sistemas utilizando un algoritmo hecho a la medida que tome ventaja de dicha estructura
particular, por ejemplo los sistemas tridiagonales.
- Un sistema tridiagonal es de la forma:
(1)
Ing. César Gutiérrez Cuba - Métodos Numéricos

Método de Thomas:
• Este sistema de ecuaciones (1), se puede escribir de la siguiente manera:
Donde:
Se aplicará el algoritmo de Thomas para la solución del sistema (1).
El algoritmo de Thomas es una forma simplificada del método de eliminación de
Gauss para sistemas tridiagonales.
(2)

• A partir de (1), la variable xi se puede expresar en términos de xi +1 de
la siguiente manera:
y
(3)
(4)
Al sustituir la ecuación (4) en (2), obtenemos:
(5)

• Comparando (3) y (5):
(6)
Estas relaciones de recurrencia se pueden usar para calcular los valores de
las constantes P y Q. Para iniciar la relación de recurrencia, requerimos
valores iniciales P0 y Q0. Estos valores se pueden calcular a partir de la
ecuación (2) para i = 1:
(7)

• Al comparar (7) con (5) para i = 1, tenemos:
(8)
Podemos calcular todas las constantes P y Q usando las ecuaciones (8) y (6).
El sistema (3) implica un sistema triangular superior de ecuaciones.
Luego se calcula los valores de las variables xi utilizando sustituciones hacia atrás.
Usando la constante cn = 0 en la ecuación (6), obtenemos Pn = 0.
Usando la ecuación (3), tenemos:
(9)
Ahora, se puede usar la ecuación (3) para calcular:

Ejercicio:
• Use el algoritmo de Thomas para calcular la solución del siguiente
sistema de ecuaciones lineales:

• La forma de matriz asociada para el sistema tridiagonal es:

• Dónde:
a1=0,
, c4=0

Con:
Las relaciones de recurrencia dan los resultados:

De la ecuación (9):
De la ecuación (3):
La solución del sistema tridiagonal es:

Ejercicio:
• Realizando un balance de calor de una varilla, se obtuvieron las
siguientes ecuaciones en 4 puntos nodales:
• Determinar la distribución de temperatura empleando el método de
Thomas (a mano).
• También resolver el problema empleando Excel.
−50 + 2.2𝑇1 − 𝑇2 = 4
−𝑇1 + 2.2𝑇2 − 𝑇3 = 4
−𝑇2 + 2.2𝑇3 − 𝑇4 = 4
−𝑇3 + 2.2𝑇4 − 300 = 4
𝑇1 𝑇2 𝑇3 𝑇4

Métodos Iterativos:
• Ciertos problemas científicos producen muchas ecuaciones y están
involucrados grandes cantidades de cálculos aritméticos. Los métodos
directos son fáciles de implementar, pero el error de redondeo es
significativo en el caso de sistemas grandes.
• Los procedimientos iterativos pueden usarse para la solución de tales
sistemas. Los métodos iterativos pueden requerir un gran número de
iteraciones para producir el resultado con mayor precisión.
• Pero, una vez que se implementan los algoritmos para estos métodos,
estas iteraciones se pueden calcular fácilmente con la ayuda de
computadoras.
• Los procedimientos iterativos no siempre convergen a las soluciones y
la tasa de convergencia es el segundo criterio importante en las
aplicaciones de estos métodos.

Métodos Iterativos de solución:
1. Método Jacobi (o) Método de desplazamiento simultáneo
2. Método Gauss-Seidel (o) Método Liebmann (o) Método de
desplazamiento sucesivo

Método de Jacobi:
• El sistema lineal de ecuaciones se puede reescribir de la siguiente
manera:
Sistema lineal
de ecuaciones:

• Se requiere alguna aproximación inicial para calcular el vector:
y si esa aproximación es:
Si usamos estos valores en las expresiones anteriores para obtener la
próxima aproximación:
Se tiene:

• En general, el proceso se repite hasta obtener la precisión deseada.
• La iteración (k + 1) puede obtenerse a partir de la iteración k
mediante la siguiente fórmula de iteración de Jacobi:

Método de Gauss Seidel:
• En un patrón similar al método de Jacobi, para el sistema de
ecuaciones lineales se tiene:

• En el método de Gauss-Seidel, se utilizan los últimos valores disponibles de las
variables al momento; mientras que en el método de Jacobi, los valores en la
última aproximación se utilizan para obtener una nueva aproximación. De esta
forma, la próxima aproximación de la iteración de Gauss-Seidel es:

• En general, la iteración (k + 1) del método Gauss-Seidel se puede
obtener de la iteración k mediante la siguiente fórmula:

Ejercicio:
• Resolver el siguiente sistema de ecuaciones lineales que corrige hasta
tres decimales utilizando el procedimiento iterativo de Gauss-Seidel.
Tome el vector cero como el vector de solución inicial.

• Para resolver el sistema, reescribimos el sistema de la siguiente manera:

Valores de Inicio:
Primera Iteración:

• Para la segunda aproximación:

Tercera Iteración:
Cuarta Iteración:
Quinta Iteración:
Sexta Iteración:
Séptima Iteración:

Ejercicio:
• Resolver el sistema de ecuaciones lineales empleando el método de
Jacobi y Gauss-Seidel:
Ing. César Gutiérrez - Métodos Numéricos
a) Resolver a mano
b) Resolver empleando Excel

clase semana 1 .pdf

Recomendados

Recomendados

Más contenido relacionado

Similar a clase semana 1 .pdf

Similar a clase semana 1 .pdf (20)

Último

Último (20)

clase semana 1 .pdf