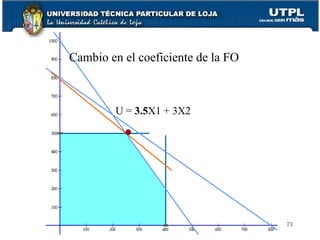
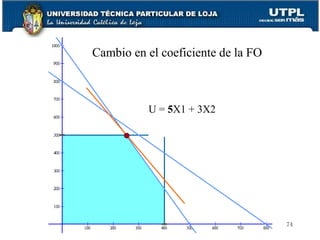
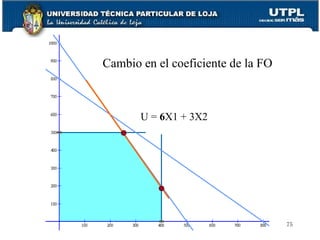
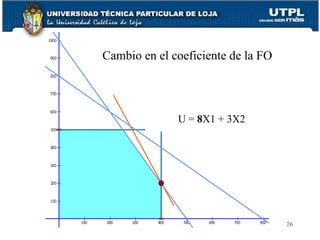
Este documento presenta una introducción a la investigación de operaciones (IO) y la programación lineal. Explica los pasos básicos de la IO, incluida la identificación del problema, la determinación de alternativas y criterios de evaluación, y la elección e implementación de una solución. Luego describe conceptos clave de la programación lineal como funciones objetivo, variables, restricciones y métodos de resolución como el método gráfico y el método simplex. Finalmente, cubre el análisis de sensibilidad para evaluar cómo cambios en los

1. ESCUELAS : CONTABILIDAD Y AUDITORIA ADMINISTRACIÓN DE EMPRESAS BANCA Y FINANZAS PROFESOR: Ing. ANGEL VICENTE TENE TENE INVESTIGACIÓN OPERATIVA PERÍODO: OCTUBRE/2008 – FEBRERO/2009

2. Contenido Introducción Toma de decisiones Programación Lineal Preguntas del Trabajo a Distancia

4. Segunda Guerra mundial Problemas logísticos, estratégicos y tácticos propios de la guerra. Objetivo.- Causar el mayor daño con el menor esfuerzo y gasto de recursos.

5. La IO, CA o MC, es una disciplina que ayuda a la toma de decisiones mediante la aplicación de un enfoque científico a problemas administrativos que involucran factores cuantitativos.

6. El análisis cuantitativo se basa en datos cuanti-tativos asociados al problema y desarrolla expresiones matemáticas que describen el objetivo, las restricciones y las relaciones existentes en el problema, que se conoce como Modelo .

7. Identificar el problema Determinar el conjunto de soluciones Determinar el criterio o criterios que se usarán para evaluar las alternativas Evaluar las alternativas Elegir una alternativa

8. Implementar la alternativa seleccionada Evaluar los resultados

9. Costo Total = Costo fijo + Costo Variable Costo fijo: No varía con la producción Costo variable: Varía con la producción

10. Ingreso = aX a = precio de venta de una unidad de producto X = Número de unidades vendidas

11. Utilidad total = Ingreso total – Costo total UT = aX – (Costo fijo + Costo variable) UT = aX-Costo fijo – Costo variable

12. Ejemplo: Costo total = Costo fijo + Costo variable Costo total = 50 + 4X Ingreso Total = aX Ingreso Total = 9X

13. Utilidad total = Ingreso - Costo UT = 9X – (50 + 4X) Si X = 10 UT = 9(10) – (50 + 4(10)) UT = 90 – 50 – 40 UT = 0

14. Utilidad total = Ingreso - Costo UT = 10X – (50 + 4X) Si X = 20 UT = 10(20) – (50 + 4(20)) UT = 200 – 50 – 80 UT = 70

15. PE, cuando la producción no genera ni pérdidas ni ganancias. La utilidad es cero Ejemplo: Utilidad total = Ingreso - Costo UT = 9X – (50 + 4X) 0 = 9X – 50 – 4X 5X = 50 X = 10(producción en el PE)

18. Formulación del problema Alternativas de decisión Estados de la naturaleza Resultado

20. Alternativas de decisión (Tamaño del Complejo) Estados de la naturaleza (Demanda) S1 (fuerte) S2 (débil) D1 (pequeño) 8 7 D2 (mediano) 14 5 D3 (grande) 20 -9

22. Se tiene poca confianza en la evaluación de las probabilidades Un análisis simple del mejor y del peor caso Enfoques Enfoque optimista Enfoque conservador

23. Evalúa cada alternativa de decisión en función del mejor resultado que pueda ocurrir La alternativa de decisión que se recomienda es la que da el mejor resultado posible Resultados posibles: Maximax: máximizar utilidades Minimin: Minimizar costos

24. ¿Cuál es el mejor resultado para cada alternativa de decisión? Seleccionamos la alternativa de decisión que proporcione el máximo resultado Alternativas de decisión Estados de la naturaleza S1 (fuerte) S2 (débil) D1 (pequeño) 8 7 D2 (mediano) 14 5 D3 (grande) 20 -9

25. Alternativas de decisión Estados de la naturaleza S1 (fuerte) S2 (débil) D1 (pequeño) 8 7 D2 (mediano) 14 5 D3 (grande) Decisión recomendada 20 Resultado máximo -9

26. Evalúa cada alternativa de decisión desde el punto de vista del peor resultado que pueda ocurrir La alternativa de decisión recomendada es la que proporciona el mejor de los peores resultados posibles Resultado: maximizar la ganancia mínima o minimizar el resultado máximo.

27. Alternativas de decisión Estados de la naturaleza S1 (fuerte) S2 (débil) D1 (pequeño) 8 7 D2 (mediano) 14 5 D3 (grande) 20 -9

28. Consecuencia de una mala decisión ¿Cuánto se dejo de ganar?

29. Alternativas de decisión Estados de la naturaleza S1 (fuerte) S2 (débil) D1 (pequeño) 8 (12) 7 (0) D2 (mediano) 14 (6) 5 (2) D3 (grande) 20 (0) -9 (16)

30. Se dispone de las probabilidades de los estados de la naturaleza La mejor alternativa de decisión se identifica a través del Valor Esperado (VE) El VE de una alternativa de decisión es la suma de los resultados ponderados para la alternativa de decisión.

31. Estado de la naturaleza Prob. Alternativas de decisión Complejo pequeño, d1 Complejo mediano, d2 Complejo grande, d3 Demanda fuerte, s1 0.8 8 14 20 Demanda débil, s2 0.2 7 5 -9

32. Valor Esperado (VE) Estados de la naturaleza P Alternativas de decisión Complejo pequeño, d1 Complejo mediano, d2 Complejo grande, d3 s1 0.8 8x0.8 = 6.4 14x0.8 = 11.2 20x0.8 = 16.0 s2 0.2 7x0.2 = 1.4 5x0.2 = 1.0 -9x0.2 = -1.8 (VE) 7.8 12.2 14.2

34. ¿Cuál sería la decisión y el resultado si se supiera con seguridad que la demanda será fuerte (S1)? ¿Cuál sería la decisión y el resultado si se supiera con seguridad que la demanda será débil (S2)?

35. VALOR ESPERADO CON INFORMACIÓN PERFECTA (VEcIP) VEcIP = 20 x 0.8 + 7 x 0.2 = 17.4 Estado de la naturaleza Prob. Alternativas de decisión Complejo pequeño, d1 Complejo mediano, d2 Complejo grande, d3 Demanda fuerte, s1 0.8 8 14 20 Demanda débil, s2 0.2 7 5 -9

36. VEIP = VEcIP – VEsIP VEIP = 17.4 – 14.2 = 3.2 millones 3.2 millones representa el valor esperado adicional que podría obtenerse si se dispusiera de información perfecta acerca de los estados de la naturaleza.

38. Modelos Matemáticos Modelos de Programación Lineal (PL) Resolución de Modelos de PL Análisis de sensibilidad (AS)

39. Y = aX I = Cit U = PV – C Ct = Cf + Cv Ut = U1 + U2 Y = a X

40. Ut = U1 + U2 2X + 3Y = 24 2X1 + X2 ≤ 16 2X + 3X2 ≥ 24

41. 3X + 2Y = 6

42. Función Objetivo Restricciones Variables de decisión y parámetros

43. Maximización Max U = 5X1 + 5X2 + 9X3 Minimizar Min C = 12X1 + 15X2 + 20X3

44. Menor o igual 5X1 + 3X2 + 4X3 ≤ 200 Mayor o igual 2X1 + 3X2 + 5X3 ≥ 60 Igual X1 + X2 + X3 = 100

45. Max U = 5 X1 + 5 X2 + 9 X3 5 X1 + 3 X2 + 4 X3 ≤ 200 2 X1 + 3 X2 + 5 X3 ≥ 60 X1 + X2 + X3 = 100 X1 , X2 , X3 ≥ 0

46. Max U = 5 X1 + 5 X2 + 9 X3 5 X1 + 3 X2 + 4 X3 ≤ 60 2 X1 + 3 X2 + 5 X3 ≥ 60 X1 + X2 = 100 X1, X2, X3 ≥ 0

47. F. Objetivo: Max = 3X1 + 5X2 Restricciones X1 ≤ 4 tiempo planta 1 2X2 ≤ 12 tiempo planta 2 3X1 + 2X2 ≤ 18 tiempo planta 3 X1 ≥ 0 no negatividad X2 ≥ 0 no negatividad

48. F. Objetivo: Min = 2X1 + 3X2 Restricciones X1 + X2 ≥ 350 Prod. (A+B) X1 ≥ 125 Demanda de A 2X1 + X2 ≤ 600 Tipo disponible X1, X2 ≥ 0 No negatividad

49. Max = 40X1 + 24X2 + 36X3 + 23X4 2X1 + 1X2 + 2.5X3 + 5X4 ≤ 120 1X1 + 3X2 + 2.5X3 ≤ 160 10X1 + 5X2 + 2X3 + 12X4 ≤ 1000 X1 ≤ 20 X3 ≤ 16 X4 ≥ 10 X1, X2, X3, X4 ≥ 0

50. 3 RESOLUCI Ó DE MODELOS DE PROGRAMACIÓN LINEAL

51. Objetivo Método Gráfico Método Simplex Análisis de Sensibilidad Solución por computadora

52. Valores de las variables de decisión X1, X2, . . . . Xn Xi ≥ 0 Optimizar la Función Objetivo Maximizar Minimizar Sujeto a restricciones

53. Formular el modelo de PL Graficar las restricciones Determinar la región factible Graficar la función objetivo Encontrar el punto solución Resolver las ecuaciones Encontrar el valor de las variables y el de la FO.

54. Maximizar U = 6X1 + 7X2 Sujeto a: 2X1 + 3X2 ≤ 24 2X1 + X2 ≤ 16 X1, X2 ≥ 0

56. 2X1 + 3X2 ≤ 24

57. 2X1 + 1X2 ≤ 16

58. 2X1 + 3X2 ≤ 24 2X1 + 1X2 ≤ 16 Región Factible

59. 2X1 + 3X2 ≤ 24 2X1 + 1X2 ≤ 16 Región Factible 6X1 + 7X2 = 42 Max = 6X + 7X2

60. 2X1 + 3X2 ≤ 24 2X1 + 1X2 ≤ 16 Región Factible Solución: X1 = 6, X2 = 4 U = 64

61. Maximizar U = 3.5X1 + 3X2 Sujeto a: 2X1 + 1X2 ≤ 1000 X1 + X2 ≤ 800 X1 ≤ 400 X2 ≤ 500 X1, X2 ≥ 0

62. 2X1 + X2 ≤ 1000

63. 2X1 + X2 ≤ 1000 X1 + X2 ≤ 800

64. 2X1 + X2 ≤ 1000 X1 + X2 ≤ 800 X1 ≤ 400

65. X1 + X2 ≤ 800 2X1 + X2 ≤ 1000 X1 ≤ 400 X2 ≤ 500 Región Factible

66. Max U = 3.5X1 + 3X2 3.5X1 + 3X2 = 1050 X1 = 250, X2 = 500 U = 2.375

67. Para las restricciones ≤ 2X1 + 1X2 + h1 = 1000 h1 = 0 X1 + X2 + h2 = 800 h2 = 50 X1 + h3 = 400 h3 = 150 X2 + h4 = 500 h4 = 0

68. X1 = 250, X2 = 500 U = 2.375 Cambios en los lados derechos de las restricciones

69. X1 ≤ 400

70. X1 ≤ 300

71. Otros cambios

72. Cambio en el sentido de una restricción

73. Cambio en el coeficiente de la FO U = 3.5 X1 + 3X2

74. Cambio en el coeficiente de la FO U = 5 X1 + 3X2

75. Cambio en el coeficiente de la FO U = 6 X1 + 3X2

76. Cambio en el coeficiente de la FO U = 8 X1 + 3X2

77. F. Objetivo: Min = 2X1 + 3X2 Restricciones X1 + X2 ≥ 350 Producci ó n (A+B) X1 ≥ 125 Demanda de A 2X1 + X2 ≤ 600 Tiempo disponible X1, X2 ≥ 0 No negatividad Minimización Guía p41-45 (Texto 247)

78. X1 + X2 ≥ 350

79. X1 + X2 ≥ 350 X1 ≥ 125

80. X1 ≥ 125 X1 + X2 ≥ 350 2X1 + X2 ≤ 600

81. Min C = 2X1 + 3X2 2X1 + 3X2 = 600 X1 = 250 X2 = 100 C = 800

82. Para las restricciones ≥ X1 + X2 - e1 = 350 e1 = 0 X1 - e2 = 125 e2 = 125 2X1 + X2 + h3 = 600 h3 = 0

83. X1 ≥ 225 X1 = 250 X2 = 100 C = 800

84. Min C = 2X1 + 3X2

85. Min C = 3X1 + 3X2 X1 = 250 X2 = 100 C = 1050 X1 = 125 X2 = 225 C = 1050

86. Min C = 4X1 + 3X2 X1 = 125 X2 = 225 C = 1175

87. Ing. Ángel Vicente Tene T. [email_address] 2588730 (Ext, 2518) Ing. Beatriz Hurtado R [email_address] 2588730 (Ext, 2705)