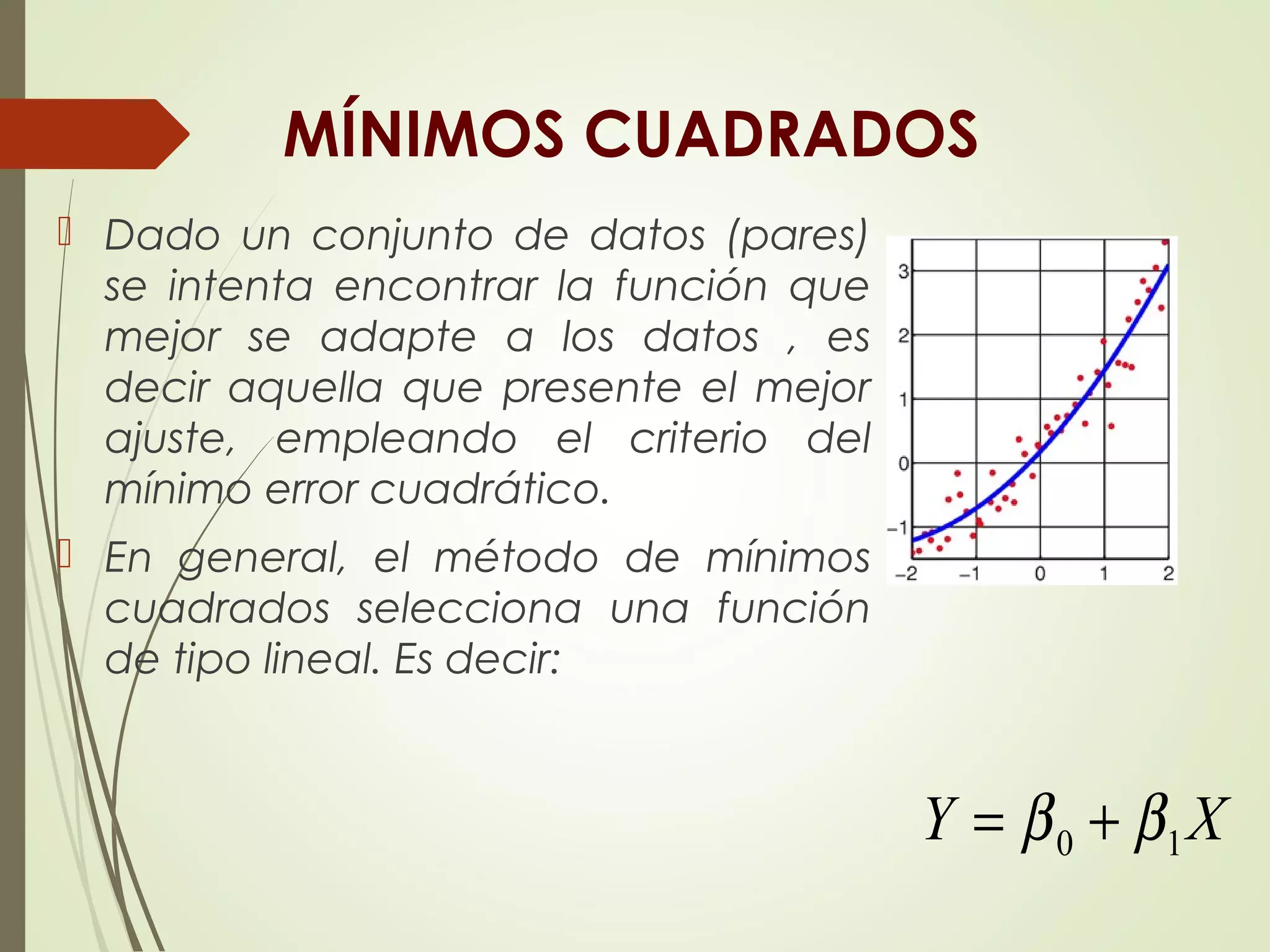
Este documento presenta diferentes métodos de proyección como mínimos cuadrados, subjetivos y causales. Explica que los mínimos cuadrados intentan encontrar la función que mejor se ajusta a los datos históricos minimizando el error cuadrático. También describe la forma general de la ecuación de regresión lineal y cómo calcular la pendiente y el punto de intersección con el eje Y usando estos métodos.

1. PONTIFICA UNIVERSIDAD CATÓLICA
DEL ECUADOR SEDE AMBATO
ESTADÍSTICA
MÉTODOS DE PROYECCIÓN
MÍNIMOS CUADRADOS
Integrantes:
Ausay Carmen
Cruz Mónica
Mera Lorena
Salinas Cecilia
Jines David
Quevedo William

2. INTRODUCCIÓN
Para realizar una proyección se requiere
conocer el comportamiento de los
componentes del estudio de mercado en el
pasado, en el presente y en el futuro.
Los modelos y técnicas de proyección
ayudan a determinar éste comportamiento
futuro.
Los resultados de la proyección está relacionada
con la calidad de los datos de entrada.

3. ¿Qué es una proyección?
Son métodos de predicción en los que,
partiendo de determinadas series de
datos, se formula una “proyección” a
futuro con el objetivo de evaluar la
ocurrencia probable de cualquier
acontecimiento. Una estimación del
comportamiento de una variable en el
futuro.

4. Porque son necesarias?
Toda organización debe planear como enfrentar las
condiciones futuras.
Los proyectos se ejecutan buscando rentabilidad
financiera, luego es necesario saber cómo
evolucionará el mercado en el tiempo.
Estimar cómo evolucionaran las variables
independientes asociadas con la demanda, oferta y
precios.
Cómo afectará la política económica cada una de
las variables en estudio.

5. La efectividad del método elegido
se evaluará en función de:
Precisión: Cualquier error en su pronóstico tendrá
asociado un costo. No es posible exigir una certeza total,
pero si, la reducción al mínimo del costo del error en su
proyección.
Sensibilidad: En un medio cambiante, debe ser lo
suficientemente estable para enfrentar una situación de
cambios lentos como dinámica para enfrentar cambios
agudos.
Objetividad: La información que se tome como base de la
proyección debe garantizar su validez y oportunidad en
una situación histórica.

6. Dificultades para pronosticar
Dificultades para pronosticar
Eventos que no hayan
ocurrido en el pasado
Desarrollo de
nuevas
tecnologías
Incorporación de
competidores con
sistemas
comerciales no
tradicionales
Variaciones en las
políticas económicas
gubernamentales
Etc.
Antecedentes históricos = variables referenciales

7. Tipos de Métodos de Proyección
 Cualitativos
 Cuantitativos
 Mínimo Cuadrado
 Método subjetivo
 Método causales
 Coeficiente de correlación
 Métodos promedios móviles
 Métodos de tendencias
 Método incremental
 Combinación de factores

8. MÉTODOS DE PROYECCIÓN MAS
COMUNES
Métodos subjetivos
Su importancia resalta cuando los métodos cuantitativos basados en
información histórica no pueden explicar por sí solos el comportamiento futuro
esperado de alguna de sus variables o cuando no existen suficientes datos
históricos. Se basa en la opinión de expertos
Se usa cuando:
El tiempo de elaboración es escaso, no se dispone de todos los antecedentes
o datos, los datos no son confiables para predecir, no se puede explicar
alguna variable.
Ejm: Método Delphi

9. MÉTODOS DE PROYECCIÓN MAS COMUNES
MÉTODOS CAUSALES
Proyectan el mercado sobre la base de antecedentes cuantitativos
históricos.
Suponen que los factores condicionantes del comportamiento
histórico de alguna o todas las variables del mercado permanecerán
estables.
Una variable depende de muchas causas o factores que explican su
comportamiento.
Estos son :
Modelo de regresión
Modelo econométrico
Método de encuestas de intenciones de compra
Modelo de insumo producto

10. MÍNIMOS CUADRADOS
 Dado un conjunto de datos (pares)
se intenta encontrar la función que
mejor se adapte a los datos , es
decir aquella que presente el mejor
ajuste, empleando el criterio del
mínimo error cuadrático.
 En general, el método de mínimos
cuadrados selecciona una función
de tipo lineal. Es decir:
XY 10 ββ +=

11. PRINCIPIO DE MÍNIMOS
CUADRADOS
Recta de “mejor ajuste”
 Técnica empleada para obtener la
ecuación de regresión, minimizando la
suma de los cuadrados de las distancias
verticales entre los valores verdaderos
de Y y los valores pronosticados de Y.

12. FORMA GENERAL DE LA
ECUACIÓN DE REGRESIÓN
LINEAL
Y´= a + bX
Donde:
“Y´”se lee Y prima, es el valor pronosticado de la variable Y
para un valor seleccionado de X.
“a” es la ordenada de la intersección con el eje Y, es decir, el
valor estimado de Y cuando X = 0. Dicho de otra forma,
corresponde al valor estimado de Y, donde la recta de
regresión cruza el eje Y, cuando X = 0.
“b” es la pendiente de la recta, o el cambio promedio en Y´
por unidad de cambio (incremento o decremento) en la
variable independiente X.
“X” es cualquier valor seleccionado de la variable
independiente.

13. PENDIENTE DE LA LÍNEA DE
REGRESIÓN
Donde:
“X” es un valor de la variable independiente.
“Y” es un valor de la variable dependiente.
“n” es el número de elementos en la muestra.

14. PUNTO DONDE SE
INTERCEPTA CON EL EJE Y
Donde:
“X” es un valor de la variable independiente.
“Y” es un valor de la variable dependiente.
“n” es el número de elementos en la muestra.

15. ANÁLISIS DE REGRESIÓN
 En lo expuesto anteriormente se desarrollan medidas para
expresar la intensidad y la dirección de la relación
existente entre dos variables.
 Mediante el análisis de regresión se quiere determinar una
ecuación para expresar la relación lineal (en línea recta)
entre dos variables, llamada también ecuación de
regresión.
 Se desea estimar el valor de la variable dependiente Y,
con base en un valor de la variable independiente X. A la
técnica empleada para desarrollar la ecuación y dar las
estimaciones se conoce como análisis de regresión.

16. ECUACIÓN DE REGRESIÓN
 Es una ecuación que define la relación lineal entre dos
variables.