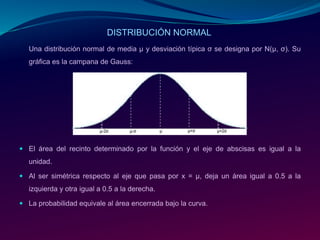
Este documento resume las características principales de tres distribuciones de probabilidad: 1) La distribución normal, descrita por Gauss, que tiene forma de campana y depende de los parámetros media y desviación estándar. 2) La distribución binomial, que modela experimentos con dos resultados posibles y probabilidad constante. 3) La distribución de Poisson, que describe eventos aleatorios en el tiempo o espacio con probabilidad proporcional al intervalo.

1. Equipo 1
Jessenia Ramos 25.602.547
Javier Medina 26.821.610
Freddy Valencia 18133362
Estadística II

2. DISTRIBUCIÓN NORMAL
Fue reconocida por primera vez por el francés Abraham de Moivre (1667-1754).
Posteriormente, Carl Friedrich Gauss (1777-1855) elaboró desarrollos más profundos
y formuló la ecuación de la curva; de ahí que también se le conozca, más
comúnmente, como “La Campana de Gauss“.
Se dice que la v.a continua X es una v.a. normal con parámetros µ y σ² si su función
de densidad es:
Se denota X~ N (µ,σ²) y se dice X se distribuye normal con parámetros µ

3. Una distribución normal de media μ y desviación típica σ se designa por N(μ, σ). Su
gráfica es la campana de Gauss:
 El área del recinto determinado por la función y el eje de abscisas es igual a la
unidad.
 Al ser simétrica respecto al eje que pasa por x = µ, deja un área igual a 0.5 a la
izquierda y otra igual a 0.5 a la derecha.
 La probabilidad equivale al área encerrada bajo la curva.
DISTRIBUCIÓN NORMAL

4. Propiedades de la Distribución Normal
 Tiene una única moda, que coincide con su media y su mediana (aproximadamente).
 La curva normal es asintótica al eje de las abscisas. Por ello, cualquier valor entre
menos infinito e infinito es teóricamente posible. El área bajo la curva normal es igual
a la unidad.
 La curva normal es asintótica al eje de abscisas. Por ello, cualquier valor entre -∞ y
+∞ es teóricamente posible. El área total bajo la curva es, por tanto, igual a 1.
 El área bajo la curva comprendida entre los valores situados aproximadamente a dos
desviaciones estándar de la media es igual a 0.95. En concreto, existe un 95% de
posibilidades de observar un valor comprendido en el intervalo.

5.  La forma de la campana de Gauss depende de los parámetros µ y desviación
estándar
 La media indica la posición de la campana, de modo que para diferentes valores
de µ la gráfica es desplazada a lo largo del eje horizontal.
 La desviación estándar determina el grado de apuntamiento de la curva. Cuanto
mayor sea el valor de la desviación estándar, más se dispersarán los datos en torno a
la media y la curva será más plana. Un valor pequeño de este parámetro indica, por
tanto, una gran probabilidad de obtener datos cercanos al valor medio de la
distribución.
Propiedades de la Distribución Normal

6. Distribución Normal Estándar
También conocida como tipificada o reducida, es aquella que tiene por media el
valor cero, μ =0, y por desviación típica la unidad, σ =1.
La probabilidad de la variable X dependerá del área del recinto sombreado en la
figura. Y para calcularla se utiliza una tabla, para su uso se tiene que transformar la
variable X que sigue una distribución N(μ, σ) en otra variable Z que siga una
distribución N(0,1).

7. Cálculo de Probabilidades en Distribución Normal
La tabla nos da las probabilidades de P(z ≤ k), siendo z la variable tipificada. Estas
probabilidades nos dan la función de distribución Φ(k):
Φ(k) = P(z ≤ k)
Búsqueda en la tabla de valor de k:
 Unidades y décimas en la columna de la izquierda.
 Centésimas en la fila de arriba.
 P(Z ≤ a):

8. Cálculo de Probabilidades en Distribución Normal
 P(Z > a) = 1 - P(Z ≤ a)
 P(Z ≤ −a) = 1 − P(Z ≤ a)
 P(Z > −a) = P(Z ≤ a)
 P(a < Z ≤ b ) = P(Z ≤ b) − P(Z ≤ a)
 P(−b < Z ≤ −a ) = P(a < Z ≤ b )
El caso inverso, se conoce el valor de
la probabilidad y halla el valor de la
abscisa. Ahora tenemos que buscar en
la tabla el valor que más se aproxime a
K.

9.  P(−b < Z ≤ −a ) = P(a < Z ≤ b )
El caso inverso, se conoce el valor de
la probabilidad y halla el valor de la
abscisa. Ahora tenemos que buscar en
la tabla el valor que más se aproxime a
K.
 P(−a < Z ≤ b ) = P(Z ≤ b) − [ 1 − P(Z ≤ a)]
Cálculo de Probabilidades en Distribución Normal

10. 1. Supongamos que Z es una variable alectorias que se distribuye según una distribución
N(0,1) calcular:
a. P(Z1.47) b. P(Z>1.47) c. P(Z -1.47) d. P(Z<1.47) e. P(0.45< Z 1.47)
f. P(-1.47<Z -.045) g. P(-1.47<Z 0.45) h. P=0.75
SOLUCIÓN:
La solución se realiza por tabla, para cada propiedad.
a)
b)
c)
d)
e)

11. f)
g)
h)

12. Es un caso particular de probabilidad de variable aleatoria discreta, y por sus
aplicaciones, es posiblemente la más importante. Esta distribución corresponde a la
realización de un experimento aleatorio que cumple con las siguientes condiciones:
 Al realizar el experimento sólo son posible dos resultados: el suceso A, llamado éxito, y
el suceso B, llamado fracaso.
 Al repetir el experimento, el resultado obtenido es independiente de los resultados
obtenidos anteriormente.
 La probabilidad del suceso A es constante, es decir, no varía de una prueba del
experimento a otra.
 En cada experimento se realizan n pruebas idénticas.
DISTRIBUCIÓN BINOMIAL

13.  Su formula es
Experimento binomial
Existen muchas situaciones en las que se presenta una experiencia binomial. Cada
uno de los experimentos es independiente de los restantes (la probabilidad del
resultado de un experimento no depende del resultado del resto). El resultado de
cada experimento ha de admitir sólo dos categorías (a las que se denomina éxito y
fracaso). Las probabilidades de ambas posibilidades han de ser constantes en todos
los experimentos (se denotan como p y q o p y 1-p).
 Se designa por X a la variable que mide el número de éxitos que se han producido en
los n experimentos.
 Cuando se dan estas circunstancias, se dice que la variable X sigue una distribución
de probabilidad binomial, y se denota B(n,p).

14. EJERCICIO: La última novela de un autor ha tenido un gran éxito, hasta el punto de que
el 80% de los lectores ya la han leído. Un grupo de 4 amigos son aficionados a la
lectura:
a. ¿Cuál es la probabilidad de que en el grupo hayan leído la novela 2 personas?
b. ¿Y cómo máximo 2?
SOLUCIÓN: a)
b)

15. Es una de las más importantes distribuciones de variable discreta. Sus principales
aplicaciones hacen referencia a la modelización de situaciones en las que nos interesa
determinar el número de hechos de cierto tipo que se pueden producir en un intervalo de
tiempo o de espacio, bajo presupuestos de aleatoriedad y ciertas circunstancias
restrictivas. Otro de sus usos frecuentes es la consideración límite de procesos
dicotómicos reiterados un gran número de veces si la probabilidad de obtener un éxito es
muy pequeña.
Su formula es:
DISTRIBUCIÓN POISSON

16. Proceso experimental del que se puede hacer derivar esta distribución se puede
hacer derivar de un proceso experimental de observación en el que tengamos las
siguientes características:
 Se observa la realización de hechos de cierto tipo durante un cierto periodo de
tiempo o a lo largo de un espacio de observación.
 Los hechos a observar tienen naturaleza aleatoria; pueden producirse o no de una
manera no determinada.
 •La probabilidad de que se produzcan un número x de éxitos en un intervalo de
amplitud t no depende del origen del intervalo (Aunque, sí de su amplitud).
 La probabilidad de que ocurra un hecho en un intervalo infinitésimo es prácticamente
proporcional a la amplitud del intervalo.
 La probabilidad de que se produzcan 2 o más hechos en un intervalo infinitésimo es
un infinitésimo de orden superior a dos. En consecuencia, en un intervalo infinitésimo
podrán producirse O ó 1 hecho pero nunca más de uno.
 Si en estas circunstancias aleatoriamente de forma que la variable aleatoria X
signifique o designe el "número de hechos que se producen en un intervalo de tiempo
o de espacio", la variable X se distribuye con una distribución de parámetro .

17. EJERCICIO: Suponga que 220 errores de impresión están distribuidos aleatoriamente a lo
largo de un libro de 2000 páginas. Encuentre la probabilidad de que una página contenga:
a. Ningún error de impresión.
b. 1 error de impresión.
c. 2 errores de impresión
d. 2 o más errores de impresión
SOLUCIÓN:
errores
220 errores 2000 paginas
1

18. Continuación:
a)
b)
c)
d)