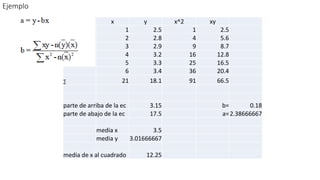
El documento describe los métodos causales para realizar pronósticos. Estos métodos incluyen el análisis de regresión, modelos econométricos, modelos de insumos/productos e indicadores líderes. El análisis de regresión lineal establece una relación entre una variable dependiente y una o más variables independientes para pronosticar valores futuros.