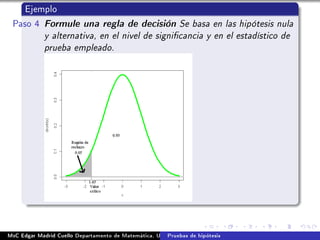
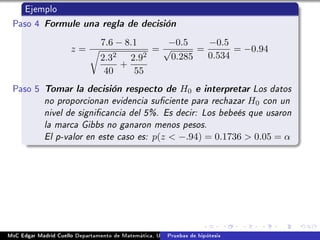
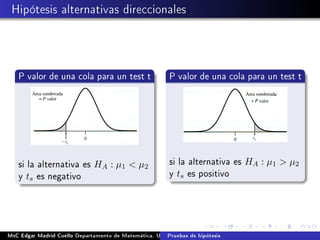
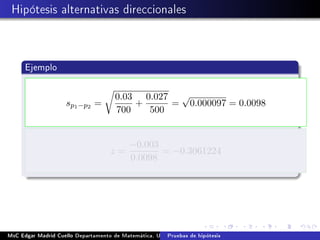
Este documento describe los procedimientos para realizar pruebas de hipótesis para comparar dos medias con muestras independientes. Explica cómo formular las hipótesis nula y alternativa, calcular el estadístico de prueba, establecer una regla de decisión y tomar una decisión sobre la hipótesis nula. También cubre el uso de pruebas unilaterales cuando la hipótesis alternativa es direccional. Finalmente, presenta un ejemplo completo de cómo aplicar estos conceptos para comparar las proporciones de defectos en