Este documento presenta las autoras del Texto del Estudiante y Guía Didáctica del Profesor de Matemática 3o Básico. Incluye los nombres de las autoras del texto y guía, así como de quienes participaron en la edición, diseño, ilustraciones y producción del material. Además, presenta un índice de contenidos de la guía didáctica.








![9Introducción
PÁGINAS DE DESARROLLO
• Objetivos de Aprendizaje: se especifican los Objetivos de Aprendizaje que se
trabajan en las actividades propuestas, extraídos de las Bases Curriculares 2012.
• Actividad inicial: se plantean orientaciones que permitan extraer los conocimien-
tos de entrada de sus alumnos, relacionados con los contenidos que se trabajarán.
Además, se proponen actividades para motivar el estudio de dichos temas.
• Habilidades que se desarrollan en las actividades del texto: se especifican las
habilidades que se trabajan en cada actividad.
• Orientaciones para el desarrollo de las actividades: se dan indicaciones
respecto de procedimientos que se desarrollarán en las distintas actividades, el uso
de recursos y estrategias pedagógicas, entre otros, para potenciar de mejor manera
el desarrollo de las habilidades en los estudiantes.
• Indicaciones respecto del contenido: en esta sección, se plantean sugerencias o
aclaraciones específicas del contenido que se trabaja, tales como: definiciones,
propiedades, formalizaciones, etc.
• Actividades complementarias: se presentan actividades que permitan reforzar o
ampliar el contenido y las habilidades que se están trabajando.
• Evaluación formativa: se entrega orientación para la evaluación del logro de los
aprendizajes sobre los contenidos específicos trabajados hasta el momento, a partir
de la sección ¿Cómo voy? del Texto del Estudiante. Se presenta un cuadro con
las habilidades que se evalúan, actividades remediales y una rúbrica,
cuando es pertinente.
PÁGINAS DE CIERRE
• Taller de ejercitación: se plantean orientaciones para las actividades propuestas,
que incluyen todos los contenidos trabajados durante la unidad.
• Síntesis: se entregan orientaciones para organizar y sintetizar lo aprendido,
mediante las actividades presentadas en la sección Organizo lo aprendido, del
Texto del Estudiante.
• Evaluación sumativa: se orienta la evaluación de las actividades presentadas en
la sección ¿Qué aprendí?, para medir los logros alcanzados por sus alumnos en la
unidad. Se sugieren actividades remediales, para los casos en que se observe algu-
na dificultad específica.
• Evaluación fotocopiable: se incluye una evaluación sumativa para cada uni-
dad anexada al final de la Guía, complementaria a la presentada en el Texto del
Estudiante. Además, se sugiere una rúbrica que incorpora los criterios e indicado-
res para cada ítem.
38 Guía Didáctica Matemática 3º Básico
UNIDAD 1
OBJETIVOS DE APRENDIZAJE
Generar, describir y registrar patrones
numéricos, usando una variedad de
estrategias en tablas del 100, […]
ACTIVIDAD INICIAL
Antes de comenzar a completar el
tablero de números del 1 al 100, el o la
docente puede preguntarle a los y las
estudiantes: ¿cómo lo harían?, o ¿qué
estrategia utilizarían? El objetivo es
que ellos y ellas se den cuenta de que
existe más de un procedimiento para
realizar esta actividad; lo importante es
lograr que en el tablero los números
queden escritos en secuencias de 1
en 1.
Actividad
Habilidades que
se desarrollan
1, 2
Resolver problemas,
representar.
3
Resolver problemas,
argumentar y comunicar.
4 Resolver problemas
5, 6, 7
Resolver problemas,
argumentar y comunicar.
6 Resolver problema.
1
12 Números hasta el 100
Números hasta el 100
Para recordar los números, los niños y niñas del curso completan un tablero del
1 al 100. Primero ubican el 1 y el 100. Luego escriben los números de 10 en 10.
Observa el tablero y completa con el número que corresponda.
a) El número que está inmediatamente antes.
58
30
49
b) El número que está inmediatamente después.
59
35
60
c) El número que está entre los dos indicados.
58 60
47 49
72 74
2
Escribe los números según se indica y luego responde.
a) Elige una columna del tablero y copia los números de la secuencia.
• ¿Qué observas?
b) Elige una fila del tablero y copia los números de la secuencia.
• ¿Qué observas?
3
Completa el tablero y comenta cómo lo hiciste.
1
10
20
100
1
Fila
Columna
ORIENTACIONES PARA EL DESARROLLO DE LAS ACTIVIDADES
• Las actividades presentadas tienen como propósito que los alumnos y alumnas
ejerciten la secuencia (patrones numéricos), lectura y formación de números
del 0 al 100. Además de la aplicación y descubrimiento de reglas aditivas en
distintas secuencias.
• En la actividad 1, antes de comenzar se puede pedir a los y las estudiantes que
digan a coro la secuencia de los múltiplos de 10 (10, 20, 30) de forma ascen-
dente y descendente y las secuencias entre estos múltiplos (11, 12, 13, ...; 21,
22, 23,... ). Esto permitirá completar el tablero con mayor facilidad. Es impor-
tante que el o la docente recuerde a los niños y niñas cómo se debe completar
la tabla, distinguiendo entre filas y columnas. Una vez concluida la completa-
ción de la tabla, puede orientarlos hacia la observación de regularidades.
56 Guía Didáctica Matemática 3º Básico
UNIDAD 1
30 Evaluación de la unidad 1
¿Qué aprendí?
Completa las siguientes afirmaciones sobre un calendario.
a) Un año tiene meses.
b) El mes de marzo tiene días.
c) Cada estación dura meses.
d) El 27 de julio es el día .
e) El mes de julio tiene domingos.
Ubica en la línea de tiempo las fechas en que comienzan las estaciones. Guíate
por el ejemplo.
enero
fe
bre
ro
m
arz
o
abril
m
ayo
ju
nio
ju
lio
agostose
ptiem
bre
oct
ubrenoviem
bre
diciem
bre
Inicia el invierno
21 de junio
• Explica con tus palabras para qué sirve una línea de tiempo.
Dibuja los globos que faltan para llegar a 20 y completa.
a) b) c) d)
= + = + = + = +
Resuelve las siguientes adiciones y sustracciones, usando alguna estrategia de
cálculo mental aprendida en la unidad.
a) 27 + 33 = d) 45 – 20 = g) 84 – 45 =
b) 26 – 18 = e) 58 + 34 = h) 77 + 26 =
c) 42 + 12 = f) 56 + 14 = i) 100 – 76 =
1
3
4
2
EVALUACIÓN SUMATIVA
Esta evaluación sumativa permite evaluar los logros alcanzados por sus alumnos y
alumnas en la unidad. Los criterios de evaluación por ítem son:
Ítem 1: completar la información sobre calendarios.
Ítem 2: representar en la línea de tiempo las fechas de las estaciones del año.
Ítem 3: representar pictóricamente y numéricamente números desconocidos en
una adición.
Ítem 4: resolver mentalmente adiciones y sustracciones, siguiendo alguna estrategia.
En el ítem de selección múltiple, se tienen los siguientes criterios: agrupar en decenas
y unidades (pregunta 1), modelar respuesta a un problema (pregunta 2), relacionar
adiciones y sustracciones (preguntas 3) y resolver problema (pregunta 4).
¿QUÉ APRENDÍ?
Ítem
Habilidades que
se evalúan
1, 2, 3 Representar.
4 Resolver problemas.
Preguntas de selección múltiple
1 a 4
Resolver problema,
modelar.
39
Guía Didáctica Matemática 3º Básico
ACTIVIDADES COMPLEMENTARIAS• Completan tablas de númerosincompletas.
(Habilidades: resolver problema).• Dicen en forma oral, y sin apoyo dela tabla, tramos de la secuencia del0 al 100, que incluyan cambios delos múltiplos de 10.
(Habilidad: resolver problema).• Trabajan los conceptos de ante-cesor, sucesor e intermedio a par-tir de una cinta numerada dondese refuerce la visualización de estasrelaciones.
(Habilidad: representación).• Crean secuencias ascendentes odescendentes, determinando elnúmero de inicio y la regla aditi-va a aplicar. Luego, comparten lassecuencias con sus compañeros ycompañeras y determinan la reglaque se ha aplicado.
(Habilidades: resolver problemas,argumentar y comunicar).• Completan y comparan una secuen-cia de números pares (del 2 al 30) yuna secuencia de números impares(del 1 al 29).
(Habilidad: resolver problema).• Representan un número con monedasu otro material y luego representansu sucesor y antecesor, comparanlas representaciones.(Habilidades: representar).
INDICACIONES RESPECTO AL CONTENIDO
• Para desarrollar la actividad 2 es necesario que los niños y niñas comprendan
el concepto de “estar inmediatamente antes”, “inmediatamente después” e
“intermedio”. Esto se puede apoyar en la observación de la tabla. También el
o la docente puede utilizar las operaciones de sustracción (sustraer 1) o adición
(adicionar 1) para determinar el antecesor y el sucesor, respectivamente. Para
trabajar el concepto de “estar entre” se sugiere ejemplificar en contextos
distintos al numérico, como formar una fila con algunos alumnos y alumnas y
preguntar quién está entre dos compañeros o compañeras.
• Para la actividad 3, el o la docente deberá corroborar que los y las estudiantes
hayan completado el tablero de forma adecuada y que comprendan la forma
en que se sigue la lectura de la tabla cuando se llega a un múltiplo de 10. Una
vez realizada esta actividad se sugiere que el profesor o la profesora se detenga
en las preguntas abiertas, realizando una puesta en común de las respuestas y
oriente la observación de regularidades.
13
Unidad 1
Números, operaciones y mediciónCompleta las siguientes secuencias, según la regla.
a) Regla: de 1 en 1.
b) Regla: de 10 en 10.
4
32
Descubre la regla utilizada en la siguiente secuencia.
La regla utilizada es _____________________________
5
30 33 36 39 42 45 48 51 54
Observa las tablas y realiza los ejercicios.
2 4 6 8
3 5 7 9
22 24 26 28
33 35 37 39
42 44 46 48
53 55 57 59
62 64 66 68
73 75 77 79
82 84 86 88
93 95 97 99
a) Pinta de color verde los siguientes números.
Veintiséis
Seis
Sesenta y dos
Ochenta y ocho.
b) Pinta de color amarillo los siguientes números.
Tres
Cincuenta y tres
Setenta y cinco
Noventa y nueve
c) ¿En qué se parecen los números que pintaste con verde?, ¿y los que pintaste
con amarillo?
6
13
Marca con una 8 la opción correcta.a) ¿Qué número está inmediatamente después de 72?
A. 70
B. 71
C. 73
D. 74
b) ¿Con cuál de los siguientes grupos de monedas se tienen $ 70?
A. 1 moneda de $ 50 y 4 de $ 5.
C. 6 monedas de $ 5 y 3 de $ 10.
B. 7 monedas de $ 1 y 7 de $ 10.
D. 5 monedas de $ 10 y 2 de $ 5.
7
Texto para el Estudiante 12 y 13
57
Guía Didáctica Matemática 3º Básico
31
Marca con una la opción correcta.
Unidad 1
¿Qué logré?
Leo e interpreto líneas de tiempo y calendarios.
Cuento números hasta el 100. Agrupo elementos en decenas. Describo y aplico estrategias de cálculo mental.
Comprendo la relación entre la adición y sustracción.
Encuentro números desconocidos en adiciones y sustracciones.
Sé hacerlo fácilmente.
Sé hacerlo, pero con dificultad.No sé hacerlo todavía.
Evalúa tu desempeño en la unidad, de acuerdo con la siguiente pauta.
Pinta 1, 2 ó 3 recuadros, según la pauta anterior.
• ¿Qué te gustó más de esta unidad?, ¿por qué?
• ¿Qué conocimientos que ya tenías facilitaron tu aprendizaje?
Unidad 1
1. Al agrupar 75 bolitas de cristal endecenas y unidades se obtiene:A. 8 decenas y 5 unidades.B. 7 decenas y 5 unidades.C. 6 decenas y 5 unidades.D. 5 decenas y 7 unidades.
4. A Juan se le quebró en dospartes su regla de 30 cm. Si unaparte mide 18 cm, ¿cuánto mideel otro pedazo?
A. 11 cm
B. 12 cm
C. 13 cm
D. 14 cm
2. Ana vendió 57 huevos el lunes y eldía martes, 18 huevos más. ¿Cuántoshuevos se recolectaron ese día? Pararesolver este problema puedes usar:A. 57 + 18
B. 57 – 18
C. 75 +18
D. 75 –18
3. Si 13 + 27 = 40, las sustraccionesasociadas son:
A. 40 – 17 = 13 y 40 – 23 = 27B. 27 – 13 = 40 y 40 – 27 = 13C. 40 – 27 = 13 y 40 – 13 = 27C. 40 + 27 = 13 y 40 + 13 = 27
Texto para el Estudiante 30 y 31
ACTIVIDADES REMEDIALES• Preguntan las fechas de cumplea-ños a 5 compañeros y las marcanen el calendario. Luego, usan lalínea de tiempo de la actividad2 y ubican estas fechas en elorden correspondiente.• Realizan la actividad 3, perocompletan solo 10 globos.• Inventan problemas en que puedanusar algunas adiciones y sustraccio-nes de la actividad 4. Luego, escribela solución y la comprobación,usando la relación entre la adicióny la sustracción.
EVALUACIÓN FOTOCOPIABLEEn las páginas 218 y 219 de esta guía,se presenta una evaluación que puede
fotocopiar y utilizar cómo evaluaciónsumativa. El tiempo estimado para surealización es de 40 minutos, el cualpuede ser modificado según las carac-
terísticas de sus estudiantes. Para eva-luar el desempeño de sus estudiantes,
utilice la rúbrica de la página 214.
A continuación, se presenta una rúbrica que le permitirá conocer el nivel de logro
de cada estudiante.
Ítem
Logrado
Medianamente logrado
Por lograr
1 Completa correctamente cada afirma-
ción sobre calendarios. Completa por lo menos 3 afirmaciones
correctamente. Completa a lo más una afirmacióncorrectamente.
2 Ubica correctamente en la línea detiempo las cuatro estaciones del año.
Ubica correctamente en la línea detiempo, por lo menos, dos estacionesdel año. Ubica correctamente en la línea detiempo, a lo más, una estación del año.
3
Dibuja la cantidad correcta de globos
que se necesitan y escribe la adiciónasociada correctamente.
Dibuja la cantidad correcta de globos
que se necesitan, pero la adiciónasociada es incorrecta.
No dibuja la cantidad correcta deglobos, ni escribe la adicióncorrespondiente.
4 Resuelve correctamente la adición,mentalmente. Resuelve correctamente la adición,pero en forma escrita. No resuelve la adición correctamente.](https://image.slidesharecdn.com/123112-150514161041-lva1-app6891/85/Didactica-del-profesor-Matematica-9-320.jpg)






















![36 Guía Didáctica Matemática 3º Básico
UNIDAD 1
OBJETIVOS DE APRENDIZAJE
Generar, describir y registrar patrones
numéricos, usando una variedad de
estrategias en tablas del 100 […].
ACTIVIDAD INICIAL
Antes de comenzar a completar el
tablero de números del 1 al 100, el
docente puede preguntar a los estu-
diantes: ¿cómo lo harían?, o ¿qué
estrategia utilizarían? El objetivo es
que se den cuenta de que existe más
de un procedimiento para realizar
esta actividad; lo importante es lograr
que en el tablero los números queden
escritos en secuencias de 1 en 1.
Actividad
Habilidades que
se desarrollan
1 y 2
Resolver problemas,
representar.
3
Resolver problemas,
argumentar y comunicar.
4 Resolver problemas.
5, 6 y 7
Resolver problemas,
argumentar y comunicar.
6 Resolver problemas.
1
12 Números hasta el 100
Números hasta el 100
Para recordar los números, los niños y niñas del curso completan un tablero del
1 al 100. Primero ubican el 1 y el 100. Luego escriben los números de 10 en 10.
Observa el tablero y completa con el número que corresponda.
a) El número que está inmediatamente antes.
58 30 49
b) El número que está inmediatamente después.
59 35 60
c) El número que está entre los dos indicados.
58 60 47 49 72 74
2
Escribe los números según se indica y luego responde.
a) Elige una columna del tablero y copia los números de la secuencia.
• ¿Qué observas?
b) Elige una fila del tablero y copia los números de la secuencia.
• ¿Qué observas?
3
Completa el tablero y comenta cómo lo hiciste.
1 10
20
100
1
Fila
Columna
ORIENTACIONES PARA EL DESARROLLO DE LAS ACTIVIDADES
• En la actividad 1, antes de comenzar se puede pedir a los estudiantes que digan
a coro la secuencia de los múltiplos de 10 (10, 20, 30) en forma ascendente y
descendente, y las secuencias entre estos múltiplos (11, 12, 13,... ; 21, 22, 23,...).
Esto permitirá completar el tablero con mayor facilidad. Es importante que el
docente recuerde a los estudiantes cómo se debe completar la tabla, distinguien-
do entre filas y columnas. Una vez concluida la completación de la tabla, puede
orientarlos hacia la observación de regularidades.
• Para desarrollar la actividad 2 es necesario que los estudiantes comprendan el
concepto de “estar inmediatamente antes”, “estar inmediatamente después” y
“estar entre”. Para trabajar el concepto “estar entre” se sugiere ejemplificar en
contextos distintos al numérico, como formar una fila con algunos alumnos y
alumnas y preguntar quién está entre otros.](https://image.slidesharecdn.com/123112-150514161041-lva1-app6891/85/Didactica-del-profesor-Matematica-36-320.jpg)

![38 Guía Didáctica Matemática 3º Básico
UNIDAD 1
1
14 Agrupaciones en decenas
Agrupaciones en decenas
La mamá de José trabaja en una feria y le pasó a su hijo una bolsa llena de
porotos para que practique el conteo.
a) ¿Cómo agrupó José los porotos?
____________________________________
b) ¿Cuántos porotos hay en la mesa?,
¿a cuántas decenas equivalen?
____________________________________
1
Para no olvidar
Llamamos decena (D) a la agrupación de 10 elementos.
1. Reúnanse en parejas o tríos y formen los siguientes
grupos:
a) 7 grupos de 10 hojas de papel.
b) 12 grupos de 10 palos de fósforo.
c) 20 grupos de 10 lentejas.
2. Cuenten la cantidad reunida en cada grupo de objetos.
3. Escriban a cuántos grupos de 10 corresponden:
a) 90 porotos:
b) 150 fichas:
c) 220 cartas:
Materiales:
• Palos de fósforo.
• Lentejas o semillas.
• Hojas de papel.
En equipo
• ¿Qué estrategia se ocupó para contar las lentejas, papeles y fósforos?
• ¿Qué otras agrupaciones puedes realizar?
Comento
OBJETIVOS DE APRENDIZAJE
Identificar y describir las unidades,
decenas, […] en números naturales […],
representando las cantidades de acuer-
do a su valor posicional, con material
concreto, pictórico y simbólico.
ACTIVIDAD INICIAL
Las actividades presentadas en estas
páginas tienen como propósito que los
estudiantes realicen conteos de objetos
agrupándolos en decenas y determinen
cuántos grupos de 10 unidades (dece-
nas) hay en una cantidad dada.
Para que entiendan las ventajas de
contar agrupando, antes del trabajo de
la sección En equipo hágalos contar
cantidades grandes sin una indicación
previa y luego pídales que compartan
las dificultades de contar, por ejemplo,
de 1 en 1. Seguramente comprenderán
que al contar cantidades mayores es
muy fácil perder la cuenta.
Actividad
Habilidades que
se desarrollan
En equipo
Resolver problemas,
representar.
Comento Argumentar y comunicar.
1 y 2 Resolver problemas.
3, 4 y 5 Representar.
6 Resolver problemas.
ORIENTACIONES PARA EL DESARROLLO DE LAS ACTIVIDADES
• El trabajo En equipo permitirá a los alumnos y las alumnas trabajar con material
concreto el conteo mediante agrupaciones de 10. Es importante que recalque a
sus estudiantes que si se cuenta agrupando se debe procurar que cada grupo
tenga, efectivamente, la cantidad que se desea agrupar, ya que de no ser así
el conteo final será erróneo.
• Con la actividad 1 se busca que los estudiantes reconozcan la estrategia de
conteo formando grupos de 10 elementos, que se representa pictóricamente en
la imagen. Para complementar el problema, puede preguntar ¿cuántos porotos
habría en la mesa si se agregan dos grupos más con la misma cantidad?](https://image.slidesharecdn.com/123112-150514161041-lva1-app6891/85/Didactica-del-profesor-Matematica-38-320.jpg)

![40 Guía Didáctica Matemática 3º Básico
UNIDAD 1
1
16 Cálculo mental de adiciones y sustracciones hasta el 100
Cálculo mental de adiciones y sustracciones hasta el 100
Paula tiene 15 láminas de sobre animales y Bruno tiene 12. Ellos quieren saber
cuántas láminas tienen entre los dos. Observa cómo lo resolvió cada uno y
luego comenta con tus compañeros y compañeras.
Calcula mentalmente las siguientes adiciones, usando una estrategia de
descomposición.
a) 10 + 34 = c) 25 + 25 = e) 38 + 22 =
b) 16 + 27 = d) 24 + 14 = f) 45 + 42 =
1
Calcula las siguientes adiciones de dobles.
a) 2 + 2 = c) 4 + 4 = e) 6 + 6 = g) 8 + 8 =
b) 3 + 3 = d) 5 + 5 = f) 7 + 7 = h) 9 + 9 =
2
• ¿Cómo explicarías las estrategias de Paula y Bruno? Comparte un
ejemplo con tus compañeros.
• ¿Cuál de los dos procedimientos te parece más sencillo?, ¿por qué?
• ¿Cómo lo harías tú? Explica.
Comento
15 + 12
• Descompuse los sumandos. 10 + 5 + 10 + 2
• Agrupé las decenas y las unidades. 10 + 10 + 5 + 2
• Sumé las decenas y las unidades. 20 + 7
• Obtuve la suma final. 27
15 + 12
• Descompuse solo uno de los sumandos. 15 + 10 + 2
• Al primer sumando le sumé la decena. 25 + 2
• Sumé las unidades y obtuve la suma final. 27
A estas estrategias las llamaremos estrategias de descomposición.
ORIENTACIONES PARA EL DESARROLLO DE LAS ACTIVIDADES
• En las actividades 1, 3 y 5, se recomienda que el docente oriente el análisis,
paso a paso, de los procedimientos para cálculo mental presentados. Para ello,
es conveniente copiar estos procedimientos en la pizarra y fomentar que los
alumnos y alumnas vayan explicando con sus palabras cada uno de los pasos.
Si es necesario, se pueden utilizar las monedas de la bolsa de matemática para
apoyar los cálculos.
• Es importante que el docente siempre establezca relaciones entre lo que los
niños y las niñas conocen y los nuevos contenidos. En este sentido, es recomen-
dable que relacionen los ejercicios de descomposición canónica conocidos con
los procedimientos de cálculo mental que están aprendiendo.
• Para la estrategia de cálculo mental presentada en la actividad 3, se requieren
conocimientos previos sobre la suma de dobles, por lo que se recomienda que,
OBJETIVOS DE APRENDIZAJE
Describir y aplicar estrategias de cálculo
mental para las adiciones […] hasta 100.
• por descomposición
• completar la decena más cercana
• usar dobles […]
ACTIVIDAD INICIAL
Como actividad previa se sugiere rea-
lizar un mapa de ideas sobre lo que
saben de adición y sustracción y las
situaciones asociadas a cada una de
estas operaciones (adición: agregar,
juntar y avanzar; sustracción: quitar,
separar y retroceder). Puede indagar,
además, en las estrategias que ellos
conocen de los cursos anteriores y
relacionarlas con las que realizaran
a continuación.
Al realizar actividades de cálculo men-
tal es importante considerar que, en un
primer momento, los y las estudiantes
pueden necesitar el apoyo de registros
escritos y utilicen una estrategia propia
para llegar a los resultados.
Actividad
Habilidades que
se desarrollan
Comento Argumentar y comunicar.
1 y 2 Resolver problemas.
3 Argumentar y comunicar.
4 Resolver problemas.
5 Argumentar y comunicar.
6 Resolver problemas.](https://image.slidesharecdn.com/123112-150514161041-lva1-app6891/85/Didactica-del-profesor-Matematica-40-320.jpg)

![42 Guía Didáctica Matemática 3º Básico
1
18 Cálculo mental de adiciones y sustracciones hasta el 100
Resuelve mentalmente las siguientes sustracciones, usando una descomposición.
a) 25 – 15 = d) 48 – 23 =
b) 27 – 13 = e) 54 – 31 =
c) 34 – 12 = f) 78 – 44 =
8
Calcula mentalmente las siguientes sustracciones, usando la estrategia anterior.
a) 11 – 9 = d) 15 – 6 =
b) 11 – 5 = e) 17 – 9 =
c) 11 – 8 = f) 18 – 9 =
10
Tomás tiene 20 lápices de colores en su estuche y presta 12 lápices a sus
compañeros. Tomás quiere saber cuántos lápices le quedan sin tener que
contarlos. Observa cómo lo resolvió Tomás y luego, responde.
• Descompuse el sustraendo 12 en 10 y 2.
• Resté las decenas.
• Resté las unidades y obtuve la resta final.
• El resultado sería 8.
a) ¿En qué otras situaciones has necesitado resolver sustracciones?
b) ¿Qué otra forma de descomponer se te ocurre?
c) Describe con tus palabras la estrategia de Tomás. Comparte un ejemplo con
tus compañeros.
7
20 – 12
20 – 10 – 2
10 – 2
8
Una profesora pregunta a su curso cómo calculan la resta de: 11 – 3. Observa
cómo explica Pamela lo que hizo en su mente y completa.
9
• Descompuse el sustraendo 3 en 1 y 2
para lograr obtener como minuendo 10.
• Resté 11 – 1 para obtener 10.
• Luego a 10 le resté 2 y obtuve el
resultado final.
11 – 3
11 – 1 –
– 2
ORIENTACIONES PARA EL DESARROLLO DE LAS ACTIVIDADES
• Antes de realizar la actividad 7, es probable que los estudiantes no describan
correctamente la manera en que descompuso Tomás. Se sugiere hacer notar el
tipo de descomposición que se realiza al número 12, que es la descomposición
en unidades y decenas.
• Al realizar los ejercicios propuestos, es posible que algunos estudiantes necesiten
apoyo gráfico y no logren realizar los cálculos de forma mental por completo. En
estos casos, es importante no prohibir este apoyo, ya que representa un pri-
mer paso en el desarrollo de esta habilidad.
• Las actividades 9 y 11 están muy relacionadas. La actividad 9 es un primer
paso, donde se realizan sustracciones, restando hasta 10, mientras que en la
actividad 11 se resta hasta la decena más cercana. Es importante que realice
esta comparación cuando trate las actividades 10 y 12, de modo que sus
estudiantes relacionen las estrategias.
OBJETIVOS DE APRENDIZAJE
Describir y aplicar estrategias de cálculo
mental para […] sustracciones hasta
100:
• por descomposición;
• completar la decena más cercana;
• usar dobles […].
Actividad
Habilidades que
se desarrollan
7
Argumentar y comunicar,
resolver problemas.
8 Resolver problemas.
9
Argumentar y comunicar,
resolver problemas.
10 a 13 Resolver problemas.
UNIDAD 3](https://image.slidesharecdn.com/123112-150514161041-lva1-app6891/85/Didactica-del-profesor-Matematica-42-320.jpg)

![44 Guía Didáctica Matemática 3º Básico
UNIDAD 1
ORIENTACIONES PARA EL DESARROLLO DE LAS ACTIVIDADES
• En las actividades 1 y 2, se sugiere realizar una puesta en común donde puedan
exponer y representar en la pizarra los diferentes procedimientos seguidos,
para verificar la comprensión de esta nueva situación. Es importante que el
docente permita que sus estudiantes expliquen con sus propias palabras cada
uno de los procedimientos y los expresen como una adición o sustracción según
corresponda, y enfatice la posibilidad de llegar a una misma respuesta a través
de distintos caminos.
• Para la actividad 4, la resolución de problemas está orientada a la aplicación de
la estrategia de sumar en vez de restar. Considerando esto, puede leer junto
con sus alumnos los problemas y determinar por qué se debe ocupar la
sustracción para solucionarlos.
OBJETIVOS DE APRENDIZAJE
Describir y aplicar estrategias de cálculo
mental para las adiciones y sustracciones
hasta 100 […]:
• sumar en vez de restar […].
ACTIVIDAD INICIAL
Previo a enfrentar las preguntas de la
sección Comento, invite a sus alumnos
y alumnas a resolver la sustracción del
problema inicial con alguna estrategia
aprendida anteriormente, para luego
presentar el procedimiento apoyado en
la recta numérica. Es importante que
comprendan la situación aditiva presen-
tada y la identifiquen como una com-
paración de cantidades donde se debe
determinar la diferencia entre ellas, y
que reconozcan que la misma situación
se puede representar como una adición
donde se desconoce uno de los suman-
dos o como una sustracción donde
el resultado o resta corresponde a
la diferencia.
Actividad
Habilidades que
se desarrollan
Comento Argumentar y comunicar.
1, 2, 3 y 4
Representar, resolver
problemas.
5
Representar, argumentar
y comunicar, resolver
problemas.
1
20 Más estrategias de cálculo mental
Más estrategias de cálculo mental
Calcula las siguientes sustracciones utilizando la estrategia anterior. Explica paso
a paso cómo lo hiciste.
a) 56 – 13, comienza en el 13, avanza de 10 en 10 hasta llegar al 53 y luego avanza de
1 en 1 hasta el 56. ¿Cuánto es 56 – 13?
b) 69 – 28, comienza en el 28, avanza de 10 en 10 hasta llegar al 68 y luego avanza de
1 en 1 hasta el 69. ¿Cuánto es 68 – 28?
c) 80 – 20, comienza en el 20, avanza de 20 en 20 hasta llegar al 80. ¿Cuánto es 80 – 20?
1
Calcula las siguientes sustracciones utilizando la estrategia anterior. Explica paso
a paso cómo lo hiciste.
a) 77 – 11 = b) 96 – 15 =
2
Resuelve mentalmente las siguientes sustracciones, utilizando la estrategia
utilizada por Daniela.
a) 23 – 12 = e) 54 – 32 =
b) 25 – 16 = f) 56 – 44 =
c) 34 – 13 = g) 68 – 33 =
d) 45 – 24 = h) 85 – 56 =
3
• ¿Qué estrategia crees que es más fácil para resolver la sustracción
mentalmente?, ¿por qué?
• ¿Se te ocurre otra manera para contar mentalmente desde 23 hasta
48? Inventa un ejemplo y compártelo con tus compañeros.
Comento
Observa cómo Daniela y Gabriel resuelven 48 – 23.
Desde el número menor,
que es 23, cuento hacia
delante hasta llegar a 48.
Yo comienzo en el
48, retrocedo 23 y llego al
25, que es el resultado.
23 43 48
520
25 48
23](https://image.slidesharecdn.com/123112-150514161041-lva1-app6891/85/Didactica-del-profesor-Matematica-44-320.jpg)

![46 Guía Didáctica Matemática 3º Básico
UNIDAD 1
1
22 Más estrategias de cálculo mental
Andrés y Paola quieren comprar las siguientes estampillas. Observa cómo
calcularon el precio total y comenta con tu curso.
Andrés calculó así: 21 + 13 = 34
34 + 10 = 44
Camila calculó así: 13 + 10 = 23
23 + 21 = 44
a) ¿Quién crees que realizó el cálculo correctamente?, ¿por qué?
b) Si agrupas de otra manera, ¿obtendrías el mismo resultado? Verifica tu respuesta con
dos ejemplos.
6
Resuelve las siguientes adiciones, agrupando de dos maneras distintas, para
verificar que se cumple la propiedad asociativa de la adición. Guíate por el
ejemplo.
32 + 10 + 4 = (32 + 10) + 4 32 + 10 + 4 = 32 + (10 + 4)
= 42 + 4 = = 32 + 14
= 46 = 46
a) 10 + 12 + 5 = e) 32 + 8 + 12 =
b) 16 + 4 + 10 = f) 45 + 15 + 5 =
c) 13 + 5 + 15 = g) 48 + 2 + 10 =
d) 24 + 16 + 6 = h) 55 + 25 + 20 =
7
Resuelve mentalmente las siguientes adiciones, agrupando de manera
conveniente para facilitar tus cálculos.
a) 12 + 12 + 8 = d) 30 + 10 + 8 =
b) 13 + 7 + 20 = e) 20 + 15 + 45 =
c) 25 + 15 + 15 = f) 45 + 45 + 10 =
8
Para no olvidar
En adiciones con más de dos sumandos, aunque se agrupen de otra manera los
sumandos, el resultado sigue siendo el mismo. Esta es la propiedad asociativa de
la adición.
ORIENTACIONES PARA EL DESARROLLO DE LAS ACTIVIDADES
• En la actividad 6, se espera que los alumnos y las alumnas concluyan la propie-
dad asociativa de la adición (sin especificar su nombre). Para esto es importante
orientar la observación de las formas de cálculo de ambos niños, de modo que
comprendan que se diferencian en la manera de agrupar los sumandos para
resolver las adiciones. Puede apoyar esta visualización planteando las adiciones
de la siguiente manera:
21 + 13 + 10 21 + 13 + 10
34 + 10 21 + 23
44 44
• En los problemas de la actividad 10, es recomendable pedirles que parafraseen
cada problema y expliquen el procedimiento de cálculo efectuado, explicitando
los pasos.
OBJETIVOS DE APRENDIZAJE
Describir y aplicar estrategias de cálculo
mental para las adiciones y sustraccio-
nes hasta 100 […]:
• aplicar la asociatividad.
Actividad
Habilidades que
se desarrollan
6
Argumentar y comunicar,
resolver problemas.
7 a 10 Resolver problemas.](https://image.slidesharecdn.com/123112-150514161041-lva1-app6891/85/Didactica-del-profesor-Matematica-46-320.jpg)















![62 Guía Didáctica Matemática 3º Básico
UNIDAD 2
2
34 Conteo de números hasta 1 000: de 5 en 5, de 10 en 10 y de 100 en 100
Para pagar un helado de $ 120 don Pedro entrega a Tomás solo monedas de
$ 5. Cuenta de 5 en 5 y completa la tabla para saber cuántas monedas debe
recibir Tomás.
Cantidad de Suma Total Cantidad de Suma Total
1 5 5 17 80 + 5 85
2 5 + 5 10 18 85 + 5 90
3 10 + 5 15
4 15 + 5 20
115
120
a) ¿Cuántas monedas de $ 5 debe recibir Tomás?
b) Observa los totales y escribe con tus palabras cómo va cambiando el dígito de la unidad.
Conteo de números hasta 1 000: de 5 en 5, de 10 en 10
y de 100 en 100
• ¿De qué otra manera le pueden pagar a Tomás por el helado?
• Si una persona le paga solo con monedas de $ 5, ¿cuántas monedas
necesita?
• ¿De qué otra manera le podrían pagar con monedas a Tomás?
Comento
Tomás anota en una libreta los precios de los productos del quiosco de su
padre para saber cuánto le tienen que pagar por ellos.
1
¿Con cuántas
monedas de $ 10 me deben pagar
exactamente un helado de $ 120?
OBJETIVOS DE APRENDIZAJE
Contar números naturales del 0 al
1 000 de 5 en 5, de 10 en 10 y de
100 en 100:
• empezando por cualquier número
natural menor que 1 000 […].
ACTIVIDAD INICIAL
Antes de responder las preguntas de la
sección Comento, recuerde a sus estu-
diantes las distintas maneras de contar
que conocen, de 1 en 1 y de 2 en 2,
entre otras.
Las preguntas de la sección Comento
están orientadas a que hagan combina-
ciones con monedas de $ 1, $ 5, $ 10
y $ 100; sin embargo, las respuestas
que incluyan monedas de $ 50 no las
considere incorrectas y compleméntelas
preguntando cuántas monedas de $10
(de $ 5 o $ 1) se necesitan para com-
pletar $ 50.
Cuando los alumnos y las alumnas
cuenten las monedas, incentívelos a
que las sumen una a una, de modo
que comiencen a familiarizarse con
el conteo de 5 en 5 y de 10 en 10.
Actividad
Habilidades que
se desarrollan
Comento
Resolver problemas,
argumentar y comunicar.
1 Modelar.
2 Argumentar y comunicar.
3 Resolver problemas.
4 Argumentar y comunicar.
5 Resolver problemas.
ORIENTACIONES PARA EL DESARROLLO DE LAS ACTIVIDADES
• En la actividad 1, aclare a sus estudiantes cómo se debe completar la tabla, que
la suma es sucesiva, que siempre se va sumando el total anterior con 5. Puede
complementar con la pregunta: ¿cómo va cambiando el dígito de la decena en
los totales?
• En la actividad 2, pídales a sus estudiantes que verifiquen que su cuenta es
correcta, usando lo aprendido en la actividad 1, referido al cambio de las
unidades y decenas.
• La actividades 3 y 4 tratan el conteo de 10 en 10. Guíe a sus alumnos y alum-
nas a que concluyan que el conteo de 10 en 10 es similar al conteo de 1 en 1,
pero agregando ceros en la unidad.](https://image.slidesharecdn.com/123112-150514161041-lva1-app6891/85/Didactica-del-profesor-Matematica-62-320.jpg)

![64 Guía Didáctica Matemática 3º Básico
UNIDAD 2
ORIENTACIONES PARA EL DESARROLLO DE LAS ACTIVIDADES
• En las actividades 1 y 2, proponga a sus estudiantes que en el momento
de contar, con lápiz grafito vayan encerrando la cantidad de elementos
correspondientes en cada actividad, para que no pierdan la cuenta.
• Las actividades 3 y 4 están orientadas a que reconozcan cómo es una secuencia
de 3 en 3 y de 4 en 4. Para hacer más claro el ciclo que cumple el dígito de
la unidad, puede realizar un listado solo con estos dígitos, de manera que
los estudiantes identifiquen cada cuánto se van repitiendo los términos en
cada caso.
OBJETIVOS DE APRENDIZAJE
Contar números naturales del 0 al
1 000 […].
• de 3 en 3, de 4 en 4,… empezando
por cualquier múltiplo del número
correspondiente.
ACTIVIDAD INICIAL
Antes analizar la imagen inicial y
responder las preguntas de la sección
Comento, recuerde a sus estudiantes
que hay distintas maneras de contar
una cantidad, y así hacer una cuenta
de manera más rápida y eficaz.
Las preguntas de la sección Comento
buscan que sus estudiantes sientan la
necesidad de contar realizando otras
agrupaciones. Contar de 3 en 3 y de
4 en 4 es más complicado que contar
de 5 en 5 y de 10 en 10, dado que
reconocer una secuencia y encontrar
un patrón en ella requiere de
mayor tiempo.
Actividad
Habilidades que
se desarrollan
Comento
Resolver problemas,
argumentar y comunicar.
1 y 2 Resolver problemas.
3 y 4 Argumentar y comunicar.
5
Resolver problemas,
argumentar y comunicar.
2
36 Conteo de números hasta 1 000: de 3 en 3 y de 4 en 4
Cuenta de 3 en 3 los vegetales de la chacra. ¿Cuántos hay?1
Cuenta de 4 en 4 las manzanas de los árboles. ¿Cuántas hay?2
Conteo de números hasta 1 000: de 3 en 3 y de 4 en 4
• Si una bolsa de globos trae solo 3 unidades y el papá de Tomás compró
8 bolsas, ¿cuántos globos tiene para vender?, ¿cómo lo calculaste?
• Tomás quiso contar los huevos que estaban en una caja: hizo 4 grupos
de 5 y le sobraron 4 huevos, pasó lo mismo cuando hizo grupos de 10.
¿De qué manera Tomás podría agrupar los huevos para que no sobre
ninguno? Compara tu respuesta con la de tus compañeros.
Comento
Tomás ayuda a su papá a contar la mercadería que compra para el quiosco.](https://image.slidesharecdn.com/123112-150514161041-lva1-app6891/85/Didactica-del-profesor-Matematica-64-320.jpg)







![72 Guía Didáctica Matemática 3º Básico
UNIDAD 2
ORIENTACIONES PARA EL DESARROLLO DE LAS ACTIVIDADES
• Al desarrollar las actividades 1 y 2 se espera que logren contar una cantidad de
elementos en grupos de 100, grupos de 10 y unidades, procedimiento que se
debe formalizar mediante el cuadro Para no olvidar, en el cual se presentan
las relaciones entre unidades, decenas y centenas.
• En la actividad 3, los alumnos y las alumnas deberán representar numéricamen-
te las cantidades contadas mediante agrupaciones. Es importante que refuerce,
a través de esta actividad y de la actividad 4, la relación entre los grupos de
100 elementos y las centenas, los grupos de 10 elementos y las decenas, y los
elementos sin agrupar con las unidades, reforzando, además, la posición en que
se ubican en el número cada una de estas.
OBJETIVOS DE APRENDIZAJE
Identificar y describir las unidades,
decenas y centenas en números natu-
rales del 0 al 1 000, representando las
cantidades de acuerdo con su valor
posicional, con material concreto,
pictórico […].
ACTIVIDAD INICIAL
Puede realizar con sus estudiantes
actividades de conteo en grupos,
trabajando con material concreto,
como palos de helado sueltos y atados
con elástico, o papel cuadriculado
(1 cuadradito equivale a una unidad,
una fila de 10 cuadraditos equivale a
una decena y un cuadrado de 10 · 10
cuadraditos equivale a una centena).
A partir de estas actividades puede
realizar preguntas como: ¿cómo se
llaman los grupos de 10?, ¿y los grupos
de 100?, ¿cuántas unidades hay en
una decena?, ¿y en una centena?
Es importante que antes de realizar la
primera actividad, los alumnos y las
alumnas comenten la ilustración inicial
y planteen sus hipótesis respecto de la
estrategia que está utilizando Martín
para realizar el conteo y propongan
estrategias propias, argumentando en
torno a la conveniencia de eligir una
u otra.
Actividad
Habilidades que
se desarrollan
Comento Resolver problemas.
1, 2, 3 y 4 Representar.
En equipo Resolver problemas.
2
44 Agrupaciones en decenas y centenas
• ¿Qué estrategia está usando Martín para contar sus tapas?, ¿de qué
otra forma podría hacerlo?
Comento
Para no olvidar
Una decena equivale a 10 unidades. Una centena equivale a 100 unidades.
Martín decidió guardar sus tapas de botella en bolsas de 100 tapas cada una.
Observa, responde y completa.
a) Cuántas sueltas hay?
b) ¿Cuántas torres de 10 hay?
c) ¿Cuántas
hay?
d) Completa: Martín tiene tapas de botellas.
1
¿Cuántas unidades, decenas y centenas de tiene Martín?, ¿cómo lo sabes?2
Agrupaciones en decenas y centenas
Martín cuenta las tapas de botella que tiene en su colección.](https://image.slidesharecdn.com/123112-150514161041-lva1-app6891/85/Didactica-del-profesor-Matematica-72-320.jpg)

![74 Guía Didáctica Matemática 3º Básico
UNIDAD 2
2
46 Composición y descomposición de números hasta el 1 000
Completa con la cantidad de argollas que se deben encajar en cada tronco para
obtener el puntaje indicado, usando la menor cantidad de argollas posible.
Guíate por el ejemplo de Javiera.
Puntaje obtenido
1
231 2 3 1
257
442
654
853
977
• ¿En qué te fijaste para saber cuántas argollas se deben encajar en cada tronco para
obtener el puntaje señalado?
1
100 10
Composición y descomposición de números hasta el 1 000
• ¿Cuántas argollas logró encajar Javiera en el tronco verde?, ¿y en el
tronco rojo?, ¿y en el tronco azul?, ¿cuántos puntos obtuvo por las
argollas que encajó en cada tronco?, ¿cómo lo calculaste?
• ¿Cuántos puntos en total obtuvo Javiera?, ¿cómo lo calculaste?
Comento
Durante sus vacaciones, Javiera fue a una feria de entretenciones. Allí jugó a
tirar la argolla.
100 puntos
10 puntos
1 punto
ORIENTACIONES PARA EL DESARROLLO DE LAS ACTIVIDADES
• Antes de realizar la actividad 1, asegúrese de que sus estudiantes comprenden
la actividad, dando algunos ejemplos en la pizarra. Puede comenzar realizando
descomposiciones con el menor número de monedas de $ 100, $ 10 y de $ 1,
y asociar de esta manera la actividad con los conocimientos previos.
• En principio, a sus estudiantes les puede resultar complejo descomponer y
componer números en las actividades 2 y 3; por lo tanto, relaciónelas con la
sección Para no olvidar y oriente a sus estudiantes en el uso del cuadro de
C, D, U.
OBJETIVOS DE APRENDIZAJE
Identificar y describir las unidades,
decenas y centenas en números
naturales del 0 al 1 000, representando
las cantidades de acuerdo a su valor
posicional […].
ACTIVIDAD INICIAL
Verifique que sus alumnos y alumnas
manejan el procedimiento de descom-
posición canónica de números de hasta
2 cifras, trabajado en cursos anteriores.
Para ello, puede pedirles que descom-
pongan cantidades de dinero, usando
la menor cantidad de monedas de
$ 10 y $ 1, y escriban la frase aditiva
correspondiente.
A partir de la situación inicial y de las
preguntas de la sección Comento,
escriben en la pizarra la adición que
realizaron para determinar el puntaje
que obtuvo en total Javiera. Guíelos
para que relacionen esta adición con
la descomposición aditiva canónica
del número. Es importante, además,
mencionarles que este tipo de descom-
posición aditiva se realiza considerando
el valor de los dígitos de acuerdo con
su posición, transfiriendo lo que saben
respecto de la descomposición canónica
con números de hasta dos cifras al
nuevo ámbito numérico.
Actividad
Habilidades que
se desarrollan
Comento
Resolver problemas,
argumentar y comunicar.
1 Representar.
2 y 3 Resolver problemas.
4 y 5
Resolver problemas,
argumentar y comunicar.](https://image.slidesharecdn.com/123112-150514161041-lva1-app6891/85/Didactica-del-profesor-Matematica-74-320.jpg)

![76 Guía Didáctica Matemática 3º Básico
UNIDAD 2
2
48 Cálculo de adiciones y sustracciones hasta 1 000, sin reserva
Tu helado
costó $ 150 y el mío,
$ 120. ¿Cuánto pagamos
en total?
Cálculo de adiciones y sustracciones hasta 1 000, sin reserva
• ¿Qué estrategia de adición que conoces usarías para calcular cuánto
deben pagar Paula y Bruno por sus helados?
• Comparte con tus compañeros las estrategias y comenten cuál es la
más sencilla y la más difícil.
• ¿Cuánto dinero deben pagar en total Paula y Bruno?
Comento
Paula y Bruno compraron helados en el quiosco del papá de Tomás.
Usa las monedas del material recortable para calcular las siguientes adiciones.
Guíate por el ejemplo.
Para resolver la adición 150 + 120 realizo los siguientes pasos:
Represento 150 con monedas
Represento 120 con monedas
Junto todas las monedas y las cuento
En total la suma es igual a 270.
a) 130 + 140 = d) 512 + 281 =
b) 250 + 310 = e) 632 + 157 =
c) 423 + 245 = f) 777 + 222 =
1
ORIENTACIONES PARA EL DESARROLLO DE LAS ACTIVIDADES
• Antes de realizar la actividad 1, y si es necesario, recuerde a sus estudiantes las
representaciones de números con monedas que se realizaron en páginas anteriores
y recuérdeles que un número puede ser representado de varias maneras, pero
priorice la representación con la menor cantidad de monedas de $ 100, de
$ 10 y de $ 1.
• En la actividad 2, pueden destacar las centenas, decenas y unidades de distinto
color, para poder visualizar claramente los valores posicionales. Asegúrese de
que comprenden los procesos mostrados, pidiéndoles que den ejemplos de
adiciones. Oriéntelos a transferir el procedimiento aplicado a adiciones de más
de dos sumandos.
• En las actividades 3 y 4, pida a sus estudiantes que expliquen las estrategias
que usaron para resolver las adiciones.
OBJETIVOS DE APRENDIZAJE
Demostrar que comprenden la adición
y la sustracción de números naturales
hasta 1 000:
• usando estrategias personales con y
sin el uso de material concreto […];
• aplicando algoritmos […] sin reserva,
[…] en la adición de hasta cuatro
sumandos y en la sustracción de
hasta un sustraendo.
ACTIVIDAD INICIAL
En la unidad 1 se trató el cálculo men-
tal de adiciones y sustracciones hasta
el 100, ya que en años anteriores se
había trabajado el cálculo escrito en
este ámbito numérico. En esta unidad
se aumenta el ámbito numérico y se
trata el cálculo escrito en el ámbito de
los números hasta el 1 000. En princi-
pio, es importante que los estudiantes
trabajen con material concreto como
monedas, para que se familiaricen con
las adiciones y sustracciones de números
hasta el 1 000.
En la sección Comento se hacen
preguntas sobre estrategias de cálculo.
Seguramente los estudiantes recorda-
rán las estrategias de cálculo mental de
la unidad anterior; sino, haga una activi-
dad inicial que les permita recordarlas.
Actividad
Habilidades que
se desarrollan
Comento Argumentar y comunicar.
1 Representar.
2 Argumentar y comunicar.
3 y 4 Resolver problemas.](https://image.slidesharecdn.com/123112-150514161041-lva1-app6891/85/Didactica-del-profesor-Matematica-76-320.jpg)

![78 Guía Didáctica Matemática 3º Básico
UNIDAD 2
2
50 Cálculo de adiciones y sustracciones hasta 1 000, sin reserva
En el correo, están calculando el total de cartas que han entregado los últimos
tres meses. Explica la estrategia que utilizaron y resuelve las siguientes adiciones,
aplicando la estrategia que se muestra.
299 = 300 – 1
298 = 300 – 2
+ 297 = 300 – 3
= 900 – 6 La suma es 894.
a) 195 + 199 + 198 = c) 393 + 291 + 195 =
b) 185 + 189 + 186 = d) 485 + 290 + 295 =
5
Jaime juntó dinero para comprar un cuaderno nuevo. Observa y completa los
pasos para saber cuánto dinero le sobrará a Jaime.
a) Representa con monedas de $ 100 y $ 10 el dinero que juntó Jaime.
Cantidad Representación con monedas
$ 750
b) Tacha las monedas que representan los $ 520 que vale el cuaderno.
c) Cuenta el dinero que queda sin tachar: ¿cuánto es?, ¿qué representa?
d) Completa: A Jaime le sobrarán
6
Resuelve las siguientes sustracciones, usando la estrategia anterior con las
monedas del material recortable.
a) 420 – 310 =
b) 545 – 312 =
c) 647 – 235 =
7
Durante
la semana junté
$ 750 y el cuaderno
cuesta $ 520. ¿Cuánto
dinero me sobrará?
ORIENTACIONES PARA EL DESARROLLO DE LAS ACTIVIDADES
• En la actividad 5, oriéntelos para que reconozcan que se ha aproximado cada
número a la centena siguiente.
• Para las actividades 6 y 7 puede sugerir a sus estudiantes que usen los recortables
del texto o monedas reales, de modo de trabajar con material concreto e intro-
ducir las sustracciones con números de tres cifras.
• En la actividad 8, pida a sus estudiantes que expliquen qué entienden por restar.
Escriba en el pizarrón las respuestas y saquen una conclusión en común. Para esto,
puede sugerirles que busquen en un diccionario o texto de matemática, o que lo
infieran de las experiencias que han tenido y lo que ya han aprendido. Además,
puede plantear situaciones similares a la inicial, pero en un ámbito numérico infe-
rior, como: Juan tiene una colección de 40 láminas. De ellas, 10 las ganó jugando
con sus amigos y el resto las compró. ¿Cuántas láminas compró Juan?
OBJETIVOS DE APRENDIZAJE
Demostrar que comprenden la adición
y la sustracción de números naturales
hasta 1 000:
• usando estrategias personales con y
sin el uso de material concreto […];
• aplicando algoritmos […] sin reserva,
[…] en la adición de hasta cuatro
sumandos y en la sustracción de
hasta un sustraendo.
Actividad
Habilidades que
se desarrollan
Comento Argumentar y comunicar.
1 y 2 Argumentar y comunicar.
3 Representar.](https://image.slidesharecdn.com/123112-150514161041-lva1-app6891/85/Didactica-del-profesor-Matematica-78-320.jpg)

![80 Guía Didáctica Matemática 3º Básico
UNIDAD 2
2
52 Cálculo de adiciones y sustracciones hasta 1 000, con reserva
Cálculo de adiciones y sustracciones hasta 1 000, con reserva
• ¿Qué estrategia de adición que conoces usarías para calcular cuánto
deben pagar Paula y Bruno por sus helados?
• Comparte con tus compañeros las estrategias y comenten cuál es la
más sencilla y la más difícil.
• ¿Cuánto dinero deben pagar en total Paula y Bruno?
Comento
Carlos calculó el total de inscritos en el país para participar en una Olimpiada
deportiva escolar. Observa cómo lo hizo y comenta con tus compañeros.
• Primero sumo los dígitos de las unidades,
9 + 3 = 12.
• Luego, sumo los dígitos de las decenas,
1 + 6 = 7.
• Finalmente, sumo los dígitos de las centenas,
5 + 2 = 7.
• Como 9 + 3 = 12, y el número 12 está
formado por una decena y 2 unidades,
sumo esta decena a las 7 decenas que
tenía y obtengo 782.
Otra estrategia es la siguiente:
• Comienzo sumando las unidades. Como
9 más 3 es 12, escribo el 2 en las unidades
y los 10 los sumo a las decenas.
• Luego, sumo las decenas, las centenas y las
unidades de mil, anotando los valores
obtenidos en las posiciones correspondientes.
C D U
5 1 9
+ 2 6 3
7 7 12
7 8 2
1
1
519
+ 263
782
Resuelve las adiciones, usando la estrategia de la tabla con valor posicional.
a)
C D U C D U C D U
1 3 9 4 4 5 5 3 8
+ 2 6 4 + 3 8 6 + 2 2 2
1
b) c)
ORIENTACIONES PARA EL DESARROLLO DE LAS ACTIVIDADES
• Es importante que comprendan el algoritmo de la adición usando los valores
posicionales antes de realizar la actividad 1, para lo cual puede presentar
adiciones en un ámbito menor al estudiado.
• Antes de realizar la actividad 2, cerciórese de que los estudiantes haya com-
prendido el algoritmo de la adición convencional. En el caso de que aún no
quede claro el algoritmo, repase la adición por descomposición usando la
tabla de C, D, U.
• En la actividad 3, se plantean dos estrategias para realizar una adición con
más de dos sumandos. Pida a sus estudiantes que resuelvan alguna de las
adiciones de la actividad, usando otra estrategia y, al terminar la actividad,
haga una puesta en común de las estrategias que ocuparon sus estudiantes.
OBJETIVOS DE APRENDIZAJE
Demostrar que comprenden la adición
y la sustracción de números naturales
hasta 1 000:
• usando estrategias personales con y
sin el uso de material concreto […];
• aplicando algoritmos con […]
reserva, […] en la adición de hasta
cuatro sumandos y en la sustracción
de hasta un sustraendo.
ACTIVIDAD INICIAL
En la actividad inicial, se introduce
el algoritmo convencional de la adi-
ción con reserva. Oriéntelos para que
concluyan que el 1 sobre las decenas
representa diez unidades, es decir,
una decena.
De ser necesario, realice la adición
usando las descomposiciones de los
números, sumando centenas con cen-
tenas, decenas con decenas y unidades
con unidades, y luego explíqueles que
para realizar la composición se debe
transformar las 12 unidades en una
decena más dos unidades.
Actividad
Habilidades que
se desarrollan
Comento
Argumentar y comunicar,
resolver problemas.
1, 2 y 3 Resolver problemas.
4
Resolver problemas,
argumentar y comunicar.](https://image.slidesharecdn.com/123112-150514161041-lva1-app6891/85/Didactica-del-profesor-Matematica-80-320.jpg)

![82 Guía Didáctica Matemática 3º Básico
UNIDAD 2
2
54 Cálculo de adiciones y sustracciones hasta 1 000, con reserva
El encargado de un Parque Nacional visitó a los alumnos y alumnas de un
3º Básico para darles información sobre el parque. Observa y responde.
a) ¿Qué nueva información se puede obtener a partir de lo que señala el encargado del
Parque Nacional?
b) Si el encargado del Parque Nacional realiza la sustracción 324 – 185, ¿qué crees que
quiere averiguar?
5
Observa dos métodos distintos para resolver la sustracción 324 – 185.
• Método por descomposición
• Método reducido: primero hago los canjes necesarios para poder restar en cada
posición, comenzando por las unidades.
1 14 2 11 14 2 11 14
324 3 2 4 3 2 4 3 2 4
– 185 – 1 8 5 – 1 8 5 – 1 8 5
1 3 9
a) Describe las diferencias y semejanzas de los dos métodos.
b) ¿Cuál te resulta más sencillo? Explícalo con tus palabras.
6
324
– 185
324
– 185
139
300 + 20 + 4
– (100 + 80 + 5)
200 + 120 + 4
– (100 + 80 + 5)
200 + 110 + 14
– (100 + 80 + 5)
100 + 30 + 9
Se descompone
aditivamente el
minuendo y el
sustraendo.
Se canjea 1 centena
por 10 decenas para
restar las decenas.
Se canjea 1 decena por
10 unidades para restar
las unidades.
Este fin de
semana, 185 personas visitaron
el parque, y el anterior, 324.
ORIENTACIONES PARA EL DESARROLLO DE LAS ACTIVIDADES
• Aproveche la actividad 5 para explorar los conocimientos alcanzados por sus
estudiantes en relación con el cálculo escrito de adiciones y sustracciones,
realizando preguntas, tales como: ¿cómo resolverían la sustracción 324 – 185?,
¿qué información les entrega la adición 324 + 185, en la situación planteada?,
¿cómo resolverían esa adición? Pídales que expliquen algunas estrategias de
cálculo escrito de adiciones y sustracciones aprendidas.
• En la actividad 6, puede ocurrir que les resulte difícil entender la razón del
cambio de descomposición 324 = 300 + 20 + 4 a la descomposición
324 = 200 + 120 + 4. Guíelos para que comprendan que el método reducido
se basa en el canje de unidades. Antes de pasar a la actividad 7, asegúrese de
que sus estudiantes comprendan los dos métodos presentados.
OBJETIVOS DE APRENDIZAJE
Demostrar que comprenden la adición
y la sustracción de números naturales
hasta 1 000:
• usando estrategias personales con y
sin el uso de material concreto […];
• aplicando algoritmos con […] reserva,
[…] en la adición de hasta cuatro
sumandos y en la sustracción de
hasta un sustraendo.
Actividad
Habilidades que
se desarrollan
5 y 6 Argumentar y comunicar.
7 y 8 Resolver problemas.
9
Resolver problemas,
argumentar y comunicar.](https://image.slidesharecdn.com/123112-150514161041-lva1-app6891/85/Didactica-del-profesor-Matematica-82-320.jpg)

![84 Guía Didáctica Matemática 3º Básico
UNIDAD 2
ORIENTACIONES PARA EL DESARROLLO DE LAS ACTIVIDADES
• En la actividad 1 se muestra una estrategia gráfica de resolución de problemas
que puede aplicarse a la situación de la sección Comento. A modo de síntesis,
escriba las ideas principales de esta estrategia en la pizarra.
• Es importante que en la actividad 2 los estudiantes resuelvan los problemas,
usando distintas estrategias. Por lo tanto, pídales que verifiquen sus respuestas
resolviendo el problema mediante a aplicación de otra estrategia.
• En la actividad 3 es necesario trabajar con los datos de la imagen de la activi-
dad inicial. A modo de ejemplo, invente un problema y escríbalo en la pizarra.
OBJETIVOS DE APRENDIZAJE
Demostrar que comprenden la adición
y la sustracción de números naturales
hasta 1 000 […]:
• creando y resolviendo problemas de
adición y sustracción que involucren
operaciones combinadas, en forma
concreta, pictórica y simbólica;
también se puede usar software
educativo. […]
ACTIVIDAD INICIAL
Previo al desarrollo de la sección
Comento, recuerde en conjunto con
sus alumnos y alumnas las estrategias
de adición y sustracción que han estu-
diado.
Después de que los estudiantes hayan
resuelto el problema con una estrategia
propia, realice una puesta en común de
las distintas formas de resolver el pro-
blema planteado.
Actividad
Habilidades que
se desarrollan
Comento
Resolver problemas,
argumentar y comunicar.
1
Resolver problemas,
representar.
2 Resolver problemas.
3 Representar.
2
56 Problemas de adición y sustracción
Problemas de adición y sustracción
• Si Andrés envía una carta certificada a Valdivia y otra a Paraguay, y
paga con $ 1 000, ¿cuánto recibirá de vuelto?, ¿cómo lo calculaste?
Comento
Observa cómo calculó Andrés el vuelto que recibió por las cartas que envió.
450 + 350 = 800
En total gasté $ 800.
Como pagué con $ 1 000, calculo:
1 000 – 800 = 200
Recibí $ 200 de vuelto.
• ¿Cómo explicarías la estrategia que utilizó Andrés?
1
Tarifas cartas
Nacional
Normal: $ 280
Certificada: $ 450
Internacional
América del Sur: $ 350
Resto de América: $ 370
Resto del mundo: $ 410
El 3º A está de visita en el correo. Cada uno enviará cartas a niños o niñas de
otro lugar.
Cantidad de dinero con que pagué
Costo de la
carta certificada
a Valdivia
$ 1 000
$ 450 $ 350 ?
Costo de
la carta a
Paraguay
Vuelto
que
recibí](https://image.slidesharecdn.com/123112-150514161041-lva1-app6891/85/Didactica-del-profesor-Matematica-84-320.jpg)



![88 Guía Didáctica Matemática 3º Básico
UNIDAD 2
ORIENTACIONES PARA EL DESARROLLO DE LAS ACTIVIDADES
• Previo a la actividad 1, recuerde con sus alumnos y alumnas la manera de
comparar dos números naturales. También es importante que identifiquen
qué operación deben realizar para responder las preguntas planteadas.
• Es posible que en la actividad 1, los alumnos y las alumnas inventen preguntas
cuya respuesta se extraiga directamente desde la observación de la tabla. Guíe
a sus estudiantes para que puedan realizar preguntas cuya respuesta requiera
realizar una operación matemática, adición o sustracción, o por lo menos una
comparación entre los datos de la tabla.
OBJETIVOS DE APRENDIZAJE
[…] clasificar y organizar los datos obte-
nidos en tablas.
ACTIVIDAD INICIAL
Antes de responder las preguntas de la
sección Comento, pregunte a sus estu-
diantes por qué es importante realizar
encuestas y sobre qué temas realizarían
encuestas.
Oriente a sus estudiantes para que
concluyan que organizar los datos en
tablas facilita su análisis; en cambio, el
análisis se dificulta si los datos escritos
están en prosa.
Actividad
Habilidades que
se desarrollan
Comento Argumentar y comunicar.
1 Argumentar y comunicar.
2 y 3 Representar.
2
60 Lectura e interpretación de datos en tablas
Lectura e interpretación de datos en tablas
• ¿Por qué crees que Sebastián organizó los resultados de su encuesta en
una tabla?
• ¿Qué información entrega la tabla que hizo Sebastián?
Comento
Observa la tabla anterior y responde en tu cuaderno.
a) ¿Qué tipo de programa es el de mayor preferencia?, ¿y el de menor preferencia?
b) ¿Cuántas personas más prefieren ver películas que programas deportivos?, ¿cómo
lo calculaste?
c) Inventa dos preguntas que se pueden responder a partir de los datos de la tabla
anterior y, luego, respóndelas.
Pinta de color rojo las preguntas que no puedes responder con la información de
la tabla anterior.
1
2
Sebastián consultó a su familia y amigos por sus programas favoritos de
televisión y anotó los resultados en una tabla.
Programa Número de preferencias
Dibujos animados 18
Noticiarios 6
Películas 14
Deportivos 9
Culturales 12
¿Cuántas personas prefieren ver dibujos
animados más que programas culturales?
¿Cuántas personas
fueron encuestadas?
¿A cuántas personas les gustan
los documentales de animales?
¿Cuántas personas no ven televisión?](https://image.slidesharecdn.com/123112-150514161041-lva1-app6891/85/Didactica-del-profesor-Matematica-88-320.jpg)















![104 Guía Didáctica Matemática 3º Básico
UNIDAD 3
3
72 Cuerpos poliedros y cuerpos redondos
Cuerpos poliedros y cuerpos redondos
• ¿En qué se parecen los objetos que ordena Pedro y los que ordena
Laura?, ¿y en qué se diferencian?
• ¿Qué objetos pueden rodar: los que ordena Pedro o los que ordena
Laura?, ¿por qué?
Comento
En los siguientes objetos, pinta de color rojo las superficies planas y de color azul
las superficies curvas que observes. Luego, responde en tu cuaderno.
1
El tarro de jurel tiene una superficie curva, por lo cual puede rodar.
En cambio, la caja de detergente y la vela tienen solo superficies
planas, por lo cual no pueden rodar.
Laura y Pedro ayudan a ordenar algunas cajas en el almacén. Laura ordena
la repisa inferior y Pedro, la superior.
a) ¿Cuáles de los objetos anteriores tienen solo superficies planas?,
¿y cuál tiene superficies planas y curvas?, ¿cómo lo supiste?
b) ¿Qué otros objetos con superficies curvas conoces?
OBJETIVOS DE APRENDIZAJE
Describir cubos, paralelepípedos, esferas,
conos, cilindros y pirámides […]
ACTIVIDAD INICIAL
Basándose en la ilustración inicial y en
las preguntas planteadas en la sección
Comento, establezca un diálogo con
sus estudiantes orientado a que reco-
nozcan semejanzas y diferencias entre
cuerpos poliedros y cuerpos redondos.
Invítelos a buscar, explorar y manipular
objetos como los de la imagen que
tengan forma parecida a los cuerpos
poliedros y redondos, verifiquen cuáles
de ellos pueden rodar e infieran qué
característica de estos objetos permite
que lo hagan.
Actividad
Habilidades que
se desarrollan
Comento Argumentar y comunicar.
1 y 2 Argumentar y comunicar.
3 Representar.
ORIENTACIONES PARA EL DESARROLLO DE LAS ACTIVIDADES
• La actividad 1 tiene como propósito que los y las estudiantes distingan los
cuerpos que pueden rodar de los que no, a partir de la observación de sus
superficies, determinando si son solo planas o planas y curvas. Es conveniente
que los alumnos y las alumnas manipulen cuerpos geométricos correspondientes
a cada objeto propuesto en la actividad, para facilitar su desarrollo.
• En la actividad 2, deberán aplicar el contenido formalizado en la sección Para
no olvidar. Se sugiere que los estudiantes realicen conjeturas acerca de la posi-
bilidad que tiene cada cuerpo de rodar en diferentes posiciones y, luego, las
verifiquen manipulando estos cuerpos. Pídales, además, que justifiquen la clasi-
ficación que realizaron de cada cuerpo describiendo sus superficies: solo planas,
planas y curvas o solo curvas.](https://image.slidesharecdn.com/123112-150514161041-lva1-app6891/85/Didactica-del-profesor-Matematica-104-320.jpg)

![106 Guía Didáctica Matemática 3º Básico
UNIDAD 3
ORIENTACIONES PARA EL DESARROLLO DE LAS ACTIVIDADES
• Al finalizar la actividad 1, puede pedir a sus alumnos y alumnas que cuenten las
aristas de los prismas y traten de encontrar una relación entre el número total de
aristas y el número de lados de las caras basales de los primas, aprovechando
así esta instancia para desarrollar la habilidad de modelar.
• El trabajo en equipo servirá para introducir la noción de redes de cuerpos
geométricos. Procure revisar que los niños y las niñas no copien más caras de
las que existen en el cuerpo. Dé ejemplos de posibles resultados, dibujándolos
en la pizarra.
OBJETIVOS DE APRENDIZAJE
Demostrar que comprende la rela-
ción que existe entre las figuras de
tres dimensiones y las figuras de dos
dimensiones: […] desplegando una
figura de tres dimensiones.
ACTIVIDAD INICIAL
Después de discutir las preguntas de
la sección Comento, pregunte a sus
alumnos y alumnas qué otras figuras
podrían aparecer en el juego encaje y
qué cuerpos se podrían calzar por
esas figuras.
Actividad
Habilidades que
se desarrollan
Comento Resolver problemas.
1
Argumentar y
comunicar.
En equipo
Resolver problemas,
argumentar y comunicar.
3
74 Relación entre figuras y cuerpos geométricos
Relación entre figuras y cuerpos geométricos
• ¿Qué figuras geométricas reconoces en el juego?
• ¿Qué cuerpos geométricos identificas?
• ¿Podrías ayudar a Javier a encajar las piezas correctamente?, ¿cómo lo
harías? Explica.
Comento
Marca de color rojo los vértices y de color azul las aristas de los siguientes cuerpos.
Luego, cuenta y completa el número total de caras que tiene cada uno.
caras caras caras
1
A Javier, en su primer cumpleaños le regalaron el
siguiente juego de encaje, en el cual cada pieza
solo calza en un espacio del cubo.
Los elementos de un cuerpo geométrico son las caras, los vértices y las aristas.
Cada superficie plana es una cara.
Cada segmento donde se unen dos caras es una arista.
Cada punto donde se encuentran tres o más aristas es un vértice.
Para no olvidar
vérticearista cara](https://image.slidesharecdn.com/123112-150514161041-lva1-app6891/85/Didactica-del-profesor-Matematica-106-320.jpg)

![108 Guía Didáctica Matemática 3º Básico
UNIDAD 3
3
76 Prismas y pirámides
Prismas y pirámides
Pedro volvió a su casa con las cosas que le habían encargado comprar
en el almacén del barrio.
• ¿En qué se parece la forma de la caja de té a la de la vela?,
¿y en qué se diferencia?
• ¿Cuáles de los objetos que compró Pedro tienen forma de prisma?, ¿cómo
lo sabes?
• ¿Cuál de los objetos que compró Pedro tiene forma diferente
a la de un prisma?, ¿cómo lo sabes?
Comento
a) ¿Qué tienen en común todas las cajas con forma de prisma?
b) ¿Qué tienen en común las cajas que no encerraste?
Los cuerpos geométricos que no encerraste se llaman pirámides.
Observa la forma de los siguientes cuerpos geométricos. Encierra todos
los que tengan forma de prisma y, luego, responde.
1
ORIENTACIONES PARA EL DESARROLLO DE LAS ACTIVIDADES
• En 1º básico, los estudiantes trabajaron con prismas rectos de base triangular y
rectangular, por lo que se espera que puedan mencionar algunas de sus carac-
terísticas al realizar la actividad 1. Sin embargo, es importante que les recuerde
que sus caras laterales son paralelogramos y tienen dos caras basales, paralelas
e iguales. Además, pregúnteles si los prismas son cuerpos redondos o poliedros,
y pídales que justifiquen sus respuestas, en función de las superficies que los
delimitan.
• Es conveniente anticipar la posible dificultad que pueden presentar los alumnos
y alumnas frente al prisma de base triangular. Oriente su observación hacia las
caras triangulares y paralelas que representan las caras basales de este prisma.
OBJETIVOS DE APRENDIZAJE
Describir cubos, paralelepípedos, […] y
pirámides de acuerdo a la forma de sus
caras, el número de aristas y la canti-
dad de vértices.
ACTIVIDAD INICIAL
Comente con los estudiantes respecto
de los cuerpos geométricos que cono-
cen. Pídales que señalen en qué se
diferencia un cuerpo geométrico de
una figura geométrica, y qué tipos de
cuerpos geométricos conocen. A partir
de esta conversación podrá explorar
sus conocimientos sobre las
formas de tres dimensiones.
Invítelos a manipular, en equipos, un
conjunto de objetos como cajas o ador-
nos y pídales que señalen a qué cuerpo
geométrico se parecen. Luego, pídales
que los clasifiquen según algún criterio
propuesto por ellos y que expongan
sus clasificaciones al curso. Finalmente
comenten a partir de la ilustración
inicial y las preguntas de la sección
Comento.
Actividad
Habilidades que
se desarrollan
Comento Argumentar y comunicar.
1 y 2 Argumentar y comunicar.
3
Argumentar y comunicar,
resolver problemas.](https://image.slidesharecdn.com/123112-150514161041-lva1-app6891/85/Didactica-del-profesor-Matematica-108-320.jpg)



![112 Guía Didáctica Matemática 3º Básico
Pedro juega a adivinar el objeto escondido. Observa y responde en tu cuaderno.2
• ¿Cuál de los siguientes objetos
puede estar tocando Pedro?, ¿por qué?
• ¿Qué objetos de la imagen tienen forma parecida a la de un cuerpo
geométrico redondo?, ¿cómo lo sabes?
Comento
Observa los siguientes objetos y escribe el nombre del cuerpo redondo al que se
parecen. Luego, comenta con tu curso.
1
• ¿En qué te fijaste para determinar a qué cuerpo redondo se parece cada objeto?
En el barrio donde viven Pedro y Laura, todos los años se organizan actividades
recreativas en las que participan hombres, mujeres, niños, niñas y personas de
la tercera edad.
80
Cilindros, conos y esferas3
Cilindros, conos y esferas
El objeto que estoy
tocando tiene una superficie curva
y dos caras basales.
ORIENTACIONES PARA EL DESARROLLO DE LAS ACTIVIDADES
• Una vez realizada la actividad 1, haga una puesta en común con las respuestas
de los y las estudiantes, en la cual distingan entre cilindros y conos, a partir de
la cantidad de caras basales que poseen. Se sugiere formular, en conjunto, una
descripción de cada cuerpo, en función de las superficies que lo delimitan (pla-
nas o curvas), la forma y cantidad de caras basales y la presencia de cúspide.
• En la actividad 2, los alumnos y las alumnas deben relacionar cada objeto con
un cilindro o un cono. Pídales que justifiquen sus respuestas y promueva que
usen un lenguaje geométrico básico al hacerlo.
OBJETIVOS DE APRENDIZAJE
Describir […] esferas, conos, cilindros
[…] de acuerdo a la forma de sus
caras […]
ACTIVIDAD INICIAL
A partir de la ilustración inicial y de
las preguntas planteadas en la sección
Comento, motive un diálogo con sus
estudiantes orientado a que mencionen
lo que saben respecto de los cuerpos
redondos, realizando preguntas como:
¿qué características debe tener un
cuerpo para ser redondo?, ¿qué objetos
de la sala de clases corresponden a
cuerpos redondos? Puede solicitarles
encerrar en una cuerda las formas de
la ilustración que se asemejan a cuer-
pos geométricos redondos y pedirles
que determinen qué tienen en común
todos ellos.
Actividad
Habilidades que
se desarrollan
Comento Argumentar y comunicar.
1 Argumentar y comunicar.
2 Resolver problemas.
3 y 4 Argumentar y comunicar.
Me
conecto
Resolver problemas.
UNIDAD 3](https://image.slidesharecdn.com/123112-150514161041-lva1-app6891/85/Didactica-del-profesor-Matematica-112-320.jpg)









![122 Guía Didáctica Matemática 3º Básico
UNIDAD 3
3
90 Traslación, reflexión y rotación de figuras
Traslación, reflexión y rotación de figuras
Un camión de circo debe desplazarse desde Chillán hasta Temuco. Observa
las imágenes.
• ¿Qué cambia y qué se mantiene en ambas imágenes?
• Si el camión del circo se trasladó, ¿cómo explicarías qué es una traslación?
Comento
Una traslación es el movimiento que se hace al deslizar o mover una figura en línea
recta. Puedes trasladar las figuras hacia abajo o arriba, hacia la derecha o la izquierda
y también en diagonal. En general, en cualquier dirección.
Para no olvidar
Calca la figura y trasládala tres veces para crear un diseño. Luego, inventa otra
figura y crea un diseño con ella.
2
Calca, en cada caso, la figura A y verifica si se puede obtener la figura B aplicándole
una traslación.
a) b) c)
1
fig. A fig. B fig. A fig. B fig. A fig. B
ORIENTACIONES PARA EL DESARROLLO DE LAS ACTIVIDADES
• En la actividad 1 y 2, propicie el desarrollo de la habilidad de argumentar y
comunicar en cada una de las preguntas, pidiendo a sus alumnas y alumnos
que digan cómo fue la traslación realizada o qué es necesario hacer cuando no
es suficiente realizar una traslación.
• Para complementar la actividad 3, pida a los niños que den ejemplos de figuras
similares, donde haya situaciones con reflejos.
• Para hacer más llamativa la actividad 4, pueden realizar guirnaldas con dise-
ños simétricos. Fomente la originalidad en los diseños. Para motivarlos puede
comenzar con la típica guirnalda de niños tomados de las manos.
OBJETIVOS DE APRENDIZAJE
Reconocer en el entorno figuras de dos
dimensiones que están trasladadas,
reflejadas […]
ACTIVIDAD INICIAL
Indague sobre los conocimientos pre-
vios de los estudiantes respecto de los
conceptos de traslación, simetría y rota-
ción, realizando una lluvia de ideas en
la cual lo relacionen con términos como
“correspondencia” o “semejanza”.
Actividad
Habilidades que
se desarrollan
Comento Argumentar y comunicar.
1 Argumentar y comunicar.
2 Representar.
3 Argumentar y comunicar.
4 Representar.
5 Argumentar y comunicar.
6 Representar.](https://image.slidesharecdn.com/123112-150514161041-lva1-app6891/85/Didactica-del-profesor-Matematica-122-320.jpg)








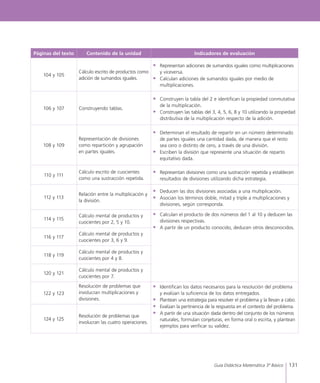




![136 Guía Didáctica Matemática 3º Básico
UNIDAD 4
4
100 Representación de multiplicaciones
• ¿Cuántos tarros de atún aportaron Luisa, Pedro y Camilo, en total?,
¿cómo lo calculaste?
Comento
Representación de multiplicaciones
Observa cómo se puede calcular el total de tarros de atún que aportaron los tres niños
y completa.
Resuelve, agrupando, como en el ejemplo anterior.
a)
1
b)
Luisa, Pedro y Camilo compraron tarros de atún en la feria para aportar en
una campaña solidaria de su escuela. Cada uno aportó con dos tarros de atún.
3 veces 2 es igual a 6.
3 por 2 es igual a .
3 · 2 es igual a .
4 veces 4 veceses igual a es igual a
por es igual a por es igual a
•
es igual a es igual a•
OBJETIVOS DE APRENDIZAJE
Demostrar que comprenden las tablas
de multiplicar hasta 10 […]:
• usando representaciones concretas
y pictóricas […].
ACTIVIDAD INICIAL
Pida que representen gráficamente
o con material concreto situaciones
relacionadas con aportes equitativos
que se puedan resolver por medio de
multiplicaciones. Por ejemplo, propon-
ga a sus estudiantes que representen
5 sobres con 4 láminas en cada uno
y calculen, agrupando los elementos,
cuántas láminas hay en total. Luego,
pídales que representen la situación ini-
cial de la página 100 con algún material
concreto y promueva que determinen la
relación que existe entre los niños y los
tarros de atún (1 niño, 2 tarros de atún;
2 niños, 4 tarros de atún;...). Pregunte
cuántos tarros de atún habría si cada
uno de los niños hubiese aportado 3,
4 y 5 tarros, y promueva que expliquen
sus procedimientos.
Actividad
Habilidades que
se desarrollan
Comento
Resolver problemas,
argumentar y comunicar.
1 y 3 Representar.
2 Modelar y representar.
ORIENTACIONES PARA EL DESARROLLO DE LAS ACTIVIDADES
• Una vez que hayan contestado las preguntas de la sección Comento, guíelos
para que relacionen la expresión “veces” con la expresión “por” (o “multiplicado
por”), facilitando la posterior comprensión del signo.
• En la actividad 2, verifique que los dibujos sean representativos de cada situación
y destaque que la información que se debe encontrar es la cantidad total de
elementos. En la frase multiplicativa, pídales que expliquen qué indica cada
factor y producto, en cada contexto en particular (por ejemplo, en el ejercicio a,
el factor 3 indica la cantidad de bolsas).
• Antes de realizar la actividad 3, recuerde cómo sumar o restar usando la recta
numérica y pídales que expliquen el procedimiento empleado para resolver una
multiplicación utilizando la recta.](https://image.slidesharecdn.com/123112-150514161041-lva1-app6891/85/Didactica-del-profesor-Matematica-136-320.jpg)

![138 Guía Didáctica Matemática 3º Básico
UNIDAD 4
ORIENTACIONES PARA EL DESARROLLO DE LAS ACTIVIDADES
• La imagen de la actividad 4 describe un arreglo rectangular que representa,
de una manera alternativa a la realizada en las páginas anteriores, una multipli-
cación. Utilice el procedimiento usado en las actividades de la página 100 para
que sus estudiantes formulen la multiplicación relacionada con la situación. Al
final de la actividad puede proponer que establezcan la relación entre el número
de elementos en cada fila y columna, y la multiplicación que se obtiene, y aplicar
dicha relación en situaciones similares.
• Una vez que hayan contestado las preguntas de la actividad 5, guíelos para que
concluyan que, en una situación donde los elementos están ordenados en filas y
columnas, es posible calcular la cantidad de objetos utilizando una multiplicación,
y que apliquen esta conclusión en la actividad 6.
OBJETIVOS DE APRENDIZAJE
Demostrar que comprenden las tablas
de multiplicar hasta 10 […]:
• usando representaciones concretas
y pictóricas […].
ACTIVIDAD INICIAL
Después de discutir las preguntas de
la sección Comento, pregunte a sus
alumnos y alumnas qué otras figuras
podrían aparecer en el juego de encaje
y qué cuerpos se podrían calzar por
esas figuras.
Actividad
Habilidades que
se desarrollan
4 y 8
Resolver problemas,
argumentar y comunicar.
5 Argumentar y comunicar.
6
Argumentar y comunicar,
y representar.
7
Modelar, argumentar
y comunicar.
4
102
a) ¿Cómo explicarías a un compañero o compañera el procedimiento de don Luis?
b) ¿En qué situaciones has ordenado objetos en filas y columnas?
Tengo 6 filas con 5 lechugas en cada una.
6 • 5 = 30
Entonces, tengo 30 lechugas en mi huerto.
En su huerto, don Luis plantó 5 filas con 6 zanahorias cada una. Representa esta
situación con un dibujo y calcula el total de zanahorias que plantó don Luis,
usando una multiplicación.
6
• =
Representación de multiplicaciones
Don Luis es vendedor de la feria. Él cultiva sus productos en un huerto. Observa la
imagen y responde en tu cuaderno.
4
Observa cómo calculó don Luis cuántas lechugas tiene en su huerto y comenta.5
a) ¿Cuántas lechugas hay en cada fila?
b) ¿Cómo expresarías la cantidad de lechugas que tienen don Luis en el huerto, utilizando una
adición de sumandos iguales?, ¿con qué otra operación podrías expresar esta cantidad?](https://image.slidesharecdn.com/123112-150514161041-lva1-app6891/85/Didactica-del-profesor-Matematica-138-320.jpg)

![140 Guía Didáctica Matemática 3º Básico
UNIDAD 4
104 Cálculo escrito de productos como adición de sumandos iguales
4 Cálculo escrito de productos como adición
de sumandos iguales
Catalina es la encargada de comprar los globos para una celebración.
Mmmm… en
cada bolsa vienen
6 globos… llevaré 3 bolsas.
• ¿Cuántos globos llevará Catalina en total?
• Y si Catalina prefiere llevar 6 bolsas con 3 globos en cada una, ¿cuántos
globos llevará?, ¿cómo lo calculaste?
• Catalina dice que si lleva 4 bolsas con 6 globos en cada una, puede
calcular el total de globos resolviendo 6 + 6 + 6 + 6. ¿Estás de acuerdo
con lo que afirma Catalina?, ¿por qué?
Comento
a) Si hay 3 aves, ¿cuántas patas hay?
2 + 2 + 2 = ___
___ veces ____ es igual a ____
___ • ___ = ____
Hay ___ patas en total.
b) Si hay 4 insectos, ¿cuántas patas hay?
___ + ____ + ____ + ____ = ____
___ veces ____ es igual a ____
___ • ___ = ____
Hay ___ patas en total.
c) Si hay 4 arácnidos, ¿cuántas patas hay?
___ + ___ + ___ + ___ = ____
___ veces ____ es igual a ____
___ • ___ = ____
Hay ___ patas en total.
d) Si hay 5 arácnidos, ¿cuántas patas hay?
___ + ___ + ___ + ___ + ___ = ____
___ veces ____ es igual a ____
___ • ___ = ____
Hay ___ patas en total.
Los insectos tienen 6 patas y los arácnidos tienen 8 patas. Completa y responde.1
ORIENTACIONES PARA EL DESARROLLO DE LAS ACTIVIDADES
• En la actividad 1, enfatice la relación entre la expresión “veces” y la expresión
“por” (o “multiplicado por”), y utilícela para proponer a sus alumnos y alumnas
que traduzcan expresiones escritas en lenguaje natural mediante multiplicaciones,
y que las resuelvan utilizando adiciones de sumandos iguales. Por ejemplo: “Si en
la casa de Luis un balón de gas se cambia tres veces al mes”, ¿cuántos balones de
gas se consumirán al cabo de 6 meses?
• En la actividad 2 puede proponer, en forma adicional, que expresen el total
como otra adición de sumandos iguales. De esta manera puede orientarlos a
concluir que un mismo número puede ser producto de dos multiplicaciones
diferentes.
OBJETIVOS DE APRENDIZAJE
Demostrar que comprenden las tablas
de multiplicar hasta 10 […]:
• expresando una multiplicación
como una adición de sumandos
iguales […].
ACTIVIDAD INICIAL
Relacione la adición de sumandos
iguales con la representación gráfica
de multiplicaciones descritas en las
páginas anteriores. Si lo estima nece-
sario, vuelva a las páginas 100 y 101
del texto y solicite a sus alumnos y
alumnas representar aquellas situacio-
nes que involucran aporte equitativo
como una suma de términos iguales y,
luego, como una multiplicación. Pídales
que identifiquen el significado de los
sumandos y de la suma, de acuerdo al
contexto de cada problema, y oriénte-
los para que relacionen las adiciones
construidas con las multiplicaciones
correspondientes. Promueva la utilidad
de la multiplicación en la simplificación
de las operaciones que involucran adi-
ción de sumandos iguales, como por
ejemplo, escribir la adición: 9 + 9 + 9 +
9 + 9 + 9 + 9 + 9 versus 9 · 9.
Actividad
Habilidades que
se desarrollan
Comento
Resolver problemas,
argumentar y comunicar.
1, 2 y 4 Representar.
3
Representar, argumentar
y comunicar.](https://image.slidesharecdn.com/123112-150514161041-lva1-app6891/85/Didactica-del-profesor-Matematica-140-320.jpg)

![142 Guía Didáctica Matemática 3º Básico
UNIDAD 4
106 Construyendo tablas
4 Construyendo tablas
Felipe hizo un cartel con la tabla del 2. Observa.
Multiplicación Representación Producto
2 • 1 2
2 • 2 4
2 • 3 6
2 • 4 8
2 • 5 10
2 • 6 12
2 • 7 14
2 • 8 16
2 • 9 18
2 • 10 20
• ¿Cuántas cerezas más que la fila anterior agregó en cada caso?
• ¿Es lo mismo multiplicar 4 • 2 que 2 • 4?, ¿y 6 • 2 que 2 • 6?, ¿por qué?
• Felipe dice que puede saber cuánto es 4 • 3, calculando 2 • 3 + 2 • 3.
¿Crees que es correcta su afirmación?, ¿por qué?
Comento
Pinta con color rojo los productos de la tabla del 2 en el cuadro multiplicativo.1
1 2 3 4 5 6 7 8 9 10
2 4 6 8 10 12 14 16 18 20
3 6 9 12 15 18 21 24 27 30
4 8 12 16 20 24 28 32 36 40
5 10 15 20 25 30 35 40 45 50
6 12 18 24 30 36 42 48 54 60
7 14 21 28 35 42 49 56 63 70
8 16 24 32 40 48 56 64 72 80
9 18 27 36 45 54 63 72 81 90
10 20 30 40 50 60 70 80 90 100
¿Cómo son los productos de 2 • 5 y de 5 • 2?, ¿y los de 2 • 10 y 10 • 2?, ¿ocurrirá siempre
lo mismo?, ¿por qué?
ORIENTACIONES PARA EL DESARROLLO DE LAS ACTIVIDADES
• En la actividad 1, oriente a sus estudiantes a descubrir que los múltiplos de 2
son los números pares; para esto, haga preguntas acerca de las regularidades
que observan en torno a los números que están pintados. Si lo prefiere, puede
sugerirles que subrayen el dígito de las unidades de los números para que
la regularidad se aprecie más claramente.
• Utilice las preguntas finales de la actividad 1 para consolidar la propiedad
conmutativa de la multiplicación. Discuta con ellos las ventajas que conlleva
esta propiedad, en particular, aquella que facilita y diversifica las estrategias
de cálculo mental; por ejemplo, para determinar el producto de 7 · 3, a algunos
les es más sencillo invertir los factores y calcular el producto de 3 · 7.
OBJETIVOS DE APRENDIZAJE
Demostrar que comprenden las tablas
de multiplicar hasta 10 […]:
• usando la propiedad distributiva
como estrategia para construir las
tablas hasta el 10.
ACTIVIDAD INICIAL
Utilice material concreto para represen-
tar las multiplicaciones propuestas en las
preguntas 2 y 3 de la sección Comento.
En la segunda pregunta, oriente a sus
estudiantes para que logren reconocer
la propiedad conmutativa de la multipli-
cación. Si tiene alumnos que no logran
hacerlo, utilice la tabla multiplicativa
para resolver otras multiplicaciones
orientadas a visualizar la conmutatividad
en la multiplicación. Luego, utilice la
tercera pregunta para introducir la pro-
piedad distributiva de la multiplicación
respecto de la adición. Es importante
que los estudiantes comprendan a
cabalidad esta propiedad, pues la
utilizarán para la construcción de las
tablas hasta el 10.
Actividad
Habilidades que
se desarrollan
1, 2 y 3
Representar, argumentar
y comunicar.
4
Representar y resolver
problemas.](https://image.slidesharecdn.com/123112-150514161041-lva1-app6891/85/Didactica-del-profesor-Matematica-142-320.jpg)

![144 Guía Didáctica Matemática 3º Básico
4
108 Representación de divisiones como repartición y agrupación en partes iguales
Representación de divisiones como repartición
y agrupación en partes iguales
• ¿Cuántos choclos dibujaste en cada plato?
• ¿Qué estrategia utilizaste para repartir en cantidades iguales los 8 choclos?
Comento
Observa y completa con los datos de la situación anterior.
8 : 4 =
número de platos en que se debe hacer la repartición
cantidad de choclos
por repartir
cantidad de
choclos por plato
cantidad de elementos para repartir cantidad de elementos por parte
Para no olvidar
Para repartir una cantidad de elementos en partes iguales, usamos la división.
El signo que utilizaremos para representar una división es: “:”.
24 : 6 = 4
Divisor
número de partes iguales en que se debe hacer la repartición
Dividendo Cuociente
Don Jaime y doña Marcela reparten en cantidades iguales los 8 choclos que
compraron en la feria entre sus 4 hijos. Dibuja la repartición.
ORIENTACIONES PARA EL DESARROLLO DE LAS ACTIVIDADES
• En las actividades donde se plantea la situación de reparto equitativo, oriente a
sus estudiantes para que asocien esta repartición en partes iguales con la división.
Puede pedirles que expresen, a través de una división, las actividades concretas
de reparto equitativo que realizaron en la actividad previa, distinguiendo el
significado de cada uno de sus términos.
• En la actividad 1, se presenta una situación de reparto equitativo para que sus
estudiantes la resuelvan de manera gráfica. En esta actividad puede insinuar el
carácter inverso que tiene la división respecto de la multiplicación formulando,
por ejemplo, la pregunta: Si en cada bolsa hay 4 limones, ¿cuántos limones
hay en 6 bolsas?
OBJETIVOS DE APRENDIZAJE
Demostrar que comprenden la división
[…]:
• representando y explicando la divi-
sión como repartición y agrupación
en partes iguales, con material
concreto y pictórico;
• creando y resolviendo problemas en
contextos que incluyan la repartición
y la agrupación […].
ACTIVIDAD INICIAL
Realice actividades de reparto equitati-
vo con material concreto como láminas,
tapas de bebida o palos de helado.
Pídales, por ejemplo, que repartan en
cantidades iguales 12 láminas entre
4 estudiantes y determinen cuántas
láminas recibió cada uno, registrando
las acciones realizadas y reflexionando
en torno al concepto de reparto equita-
tivo y su relación con la división. Puede
que algún estudiante concluya que es
la operación inversa de la multiplicación;
si es así, aproveche para introducir
esta idea.
Actividad
Habilidades que
se desarrollan
Comento Argumentar y comunicar.
1 y 2
Representar y resolver
problemas.
3
Resolver problemas,
argumentar y comunicar.
UNIDAD 4](https://image.slidesharecdn.com/123112-150514161041-lva1-app6891/85/Didactica-del-profesor-Matematica-144-320.jpg)

![146 Guía Didáctica Matemática 3º Básico
UNIDAD 4
ORIENTACIONES PARA EL DESARROLLO DE LAS ACTIVIDADES
• Recorra los puestos de sus alumnos y alumnas para verificar que las representa-
ciones gráficas que realizaron en las actividades 1 y 2 sean las adecuadas.
• En cada uno de los problemas presentados en la actividad 3, si observa que
sus estudiantes tienen dificultades en plantear la división o en reconocer los
términos de esta, pídales que primero realicen una representación gráfica de
la situación y luego formulen la sustracción iterada correspondiente. No olvide
recordarles que no basta solo con escribir el resultado, sino que ínstelos a res-
ponder la pregunta que se está pidiendo, usando una redacción adecuada.
OBJETIVOS DE APRENDIZAJE
Demostrar que comprenden la división
[…]:
• expresando la división como una
sustracción repetida […].
ACTIVIDAD INICIAL
Utilice material concreto para repre-
sentar la situación planteada en la
sección Comento. En vez de huevos
puede utilizar lápices o palitos de helado.
Pídales a sus alumnos que, de un grupo
con doce elementos, vayan quitando
paulatinamente tres elementos y formen
conjuntos con ellos. De esta manera,
se forman cuatro conjuntos de tres
elementos y no sobra ninguno. En este
caso recalque que el cuociente de la
división corresponde al número de
conjuntos de tres elementos que se
pueden obtener, es decir, cuatro.
Luego, para responder la tercera pre-
gunta de la sección Comento, inste a
sus estudiantes a repetir la misma estra-
tegia usada anteriormente para calcular
la cantidad de huevos que iría en cada
canasto. Verifique que sus alumnos
reconozcan adecuadamente los térmi-
nos de la división en la situación.
Finalmente formule otras divisiones
para que sus alumnos y alumnas pue-
dan representarlas con el material que
tienen y calculen su valor utilizando la
estrategia dada. Pídales que verifiquen
sus respuestas dividiendo mediante
agrupación.
Actividad
Habilidades que
se desarrollan
Comento
Resolver problemas,
argumentar y comunicar.
1, 2 y 4 Representar.
3 Resolver problemas.
110
4
Cálculo escrito de cuocientes como una sustracción repetida
Cálculo escrito de cuocientes como una sustracción repetida
Doña María y don Alonso atienden en el almacén del barrio. Observa lo que
pide la señora Ana.
Quiero 12 huevos,
repartidos en partes iguales
en 3 canastos.
12 – 3 = 9, 9 – 3 = 6,
6 – 3 = 3 y 3 – 3 = 0
Hay que poner 4 huevos
en cada canasto.
12 : 3 = 4
Son 4 huevos en
cada canasto.
Para no olvidar
Es posible calcular el resultado de una división restando el divisor al dividendo hasta
obtener 0. Por ejemplo:
15 : 5 = ___ 15 – 5 = 10 10 – 5 = 5 5 – 5 = 0
Como resté 3 veces el divisor, 15 – 5 – 5 – 5 = 0, el cuociente 3, es decir, 15 : 5 = 3
La tía Mónica compró 45 pastelitos y colocó 9 en cada una de las bandejas que tenía.
¿Cuántas bandejas utilizó? Encierra en grupos de 9 los 45 pastelitos y luego completa.
45 : 9 = ___ 45 – 9 = ___ ___ – ___ = ___ _____________________________
Como resté ___ veces el divisor, 45 – _____________ = ___, 45 : 9 = ____
1
• ¿Quién realizó los cálculos correctamente?, ¿cómo lo sabes?
• ¿Cómo habrías calculado tú la cantidad de huevos que se deben poner
en cada canasto?, ¿por qué?
• Si la señora Ana hubiese pedido 20 huevos repartidos en partes iguales
en 4 canastos, ¿cómo calcularías la cantidad de huevos que iría en cada
canasto utilizando el procedimiento de doña María?
Comento](https://image.slidesharecdn.com/123112-150514161041-lva1-app6891/85/Didactica-del-profesor-Matematica-146-320.jpg)

![148 Guía Didáctica Matemática 3º Básico
UNIDAD 4
112
Completa y, luego, responde.
a) Si quiere hacer 5 guirnaldas y ocupa 7 tiras de papel en cada una, ¿cuántas tiras
necesita en total?
____ • ____ = ____ Necesita ____ tiras en total.
b) Si tiene 35 tiras de papel y ocupa 7 tiras en cada guirnalda, ¿cuál es la mayor cantidad
de guirnaldas que puede hacer?
____ : ____ = ____ Puede hacer a lo más ____ guirnaldas.
c) Si tiene 35 tiras de papel y quiere hacer 5 guirnaldas, ¿cuántas tiras ocupará en cada
guirnalda?
____ : ____ = ____ Ocupará ____ tiras en cada guirnalda.
d) Si 5 • 7 = 35, 35 : 7 = 5 y 35 : 5 = 7. ¿Qué puedes concluir?
1
Relación entre la multiplicación y la división
4 Relación entre la multiplicación y la división
Camila decidió hacer guirnaldas para adornar la sala en la celebración del curso.
• Si Camila quiere hacer 3 guirnaldas y en cada una ocupa 5 tiras de papel,
¿cuántas tiras necesitará?
• Si tiene 15 tiras de papel y ocupa 5 tiras en cada guirnalda, ¿cuál es la
mayor cantidad de guirnaldas que puede hacer?
Comento
Para no olvidar
Una multiplicación entre dos factores distintos se puede relacionar con dos
divisiones. Por ejemplo:
8 • 9 = 72
72 : 8 = 9 72 : 9 = 8
ORIENTACIONES PARA EL DESARROLLO DE LAS ACTIVIDADES
• Para cada uno de los problemas de la actividad 1, puede sugerir a sus estudiantes
que formulen un problema que se pueda resolver aplicando la operación inver-
sa. Por ejemplo, en la actividad a, se puede formular: “si en una sala de clases
hay 5 guirnaldas con igual cantidad de tiras en cada una y en total hay 35 tiras,
¿cuántas tiras hay en cada guirnalda?”
• En la actividad 2, recuerde a sus estudiantes que, en todas las divisiones que
deben formar, el dividendo debe ser mayor que el divisor. Establezca, también,
la relación entre los elementos de la multiplicación y los de sus divisiones asocia-
das: el producto de la multiplicación corresponde al dividendo de las divisiones y
los factores de la multiplicación son el divisor y el cuociente de las divisiones.
OBJETIVOS DE APRENDIZAJE
Demostrar que comprenden la división
[…]:
• describiendo y aplicando la relación
inversa entre la división y la multipli-
cación […].
ACTIVIDAD INICIAL
Plantee situaciones similares a la de
la sección Comento en las que se
presenten dos problemas relativos a
un mismo tema, usando los mismos
datos y que uno se resuelva usando
una multiplicación y el otro, mediante
una división. Pídales que relacionen
los elementos de ambas operaciones
(factores, producto, dividendo, divisor y
cuociente) y oriéntelos a que descubran
regularidades, como por ejemplo, que
el producto de la multiplicación siempre
corresponde al dividendo de la división.
Actividad
Habilidades que
se desarrollan
1
Resolver problemas,
argumentar y comunicar.
2 y 3 Representar.
4 Resolver problemas.](https://image.slidesharecdn.com/123112-150514161041-lva1-app6891/85/Didactica-del-profesor-Matematica-148-320.jpg)

![150 Guía Didáctica Matemática 3º Básico
UNIDAD 4
• ¿Cuántas frutas hay en 2 cajas?
• ¿Cuántas frutas hay en total? Escribe la multiplicación que te
permite saberlo.
Comento
4
114 Cálculo mental de productos y cuocientes por 2, 5 y 10
Cálculo mental de productos y cuocientes por 2, 5 y 10
En un puesto de la feria, decidieron ordenar los tipos de fruta que vendían en
cajas de 10 unidades. Observa.
Completa los siguientes cuadros, siguiendo el orden de las flechas.2
a) ¿Cómo completaste los cuadros, multiplicando o dividiendo?, ¿por qué?
b) ¿Qué ocurre si el 4 lo multiplicas por 10 y, luego, lo divides por 10?, ¿ocurrirá lo
mismo con cualquier otro número? Verifica tu respuesta, formulando tres ejemplos.
1 2 3 4 5 6 7 8 9 10
5 20
1 2 3 4 5 6 7 8 9 10
40
: 5
: 10
• 5
• 10
Usa la recta numérica para completar las siguientes multiplicaciones. Guíate por el
ejemplo. Luego, responde en tu cuaderno.
1
0 1 2 3 4 5 6 7 ... 18 19 20
2 + 2 + 2 = 6 3 • 2 = 6
a) 1 • 2 = c) 3 • 2 = e) 5 • 2 = g) 7 • 2 = i) 9 • 2 =
b) 2 • 2 = d) 4 • 2 = f) 6 • 2 = h) 8 • 2 = j) 10 • 2 =
• ¿Qué relación encuentras entre el producto y el primer factor?
Ejemplo:
ORIENTACIONES PARA EL DESARROLLO DE LAS ACTIVIDADES
• La actividad 1 permite introducir la tabla del 2, utilizando la recta numérica.
Pídales que digan la secuencia de dos en dos, desde el 2 al 20, que la relacionen
con esta tabla y que comenten las características de los números que resultan
al multiplicar por 2.
• En la actividad 2, promueva que concluyan que los productos por 5 siempre
terminan en 5 y 0, y por 10, siempre terminan en 0. Puede pedirles que pinten
el dígito de las unidades, para que observen estas regularidades fácilmente.
• En la actividad 3, se espera que logren comprender que la multiplicación y la
división son operaciones inversas, y que apliquen esta relación. Si presentan
dificultades, promueva el uso de algún material concreto, como palos de
helado, para visualizar esta relación con más claridad.
OBJETIVOS DE APRENDIZAJE
Demostrar que comprenden las tablas
de multiplicar hasta 10 de manera
progresiva […]:
• aplicando los resultados de las
tablas de multiplicación hasta
10x10, sin realizar cálculos […].
Demostrar que comprenden la división
en el contexto de las tablas de hasta
10x10 […]:
• describiendo y aplicando la
relación inversa entre la división
y la multiplicación;
• aplicando los resultados de las
tablas de multiplicación hasta
10x10, sin realizar cálculos.
ACTIVIDAD INICIAL
En la situación inicial, es posible que los
estudiantes respondan las preguntas
planteadas contando la cantidad de
frutas de la ilustración. Guíelos para que
escriban la multiplicación correspondien-
te a través de preguntas tales como:
¿cuántas frutas hay en cada caja?,
¿cuántas cajas hay en total?, ¿cuántas
veces hay 10 frutas? Luego, pídales que
formulen situaciones similares en que
deban multiplicar por 10 y que las
representen gráficamente, explicando
las regularidades que observan.
Actividad
Habilidades que
se desarrollan
Comento
Resolver problemas
y modelar.
1 Representar.
2 y 3
Representar, argumentar
y comunicar.](https://image.slidesharecdn.com/123112-150514161041-lva1-app6891/85/Didactica-del-profesor-Matematica-150-320.jpg)

![152 Guía Didáctica Matemática 3º Básico
UNIDAD 4
116 Cálculo mental de productos y cuocientes por 3, 6 y 9
4 Cálculo mental de productos y cuocientes por 3, 6 y 9
Observa la estrategia de Pedro para calcular la tabla del 6 y, luego, responde.2
Completa la siguiente tabla y explica, en tu cuaderno, cómo lo hiciste.1
Tabla del
3
1 2 3 4 5 6 7 8 9 10
3 15 30
• 3
Si sabes la tabla del 3, podrás calcular fácilmente la tabla del 6. Por ejemplo,
si sabes que 3 • 4 es igual a 12, entonces 6 • 4 es igual al doble de 12, es decir,
es igual a 24. Esto ocurre porque 6 es el doble de 3.
a) Algo similar ocurre con la tabla del 9. Si sabes que 3 • 2 es igual a 6, entonces puedes
calcular fácilmente que 9 • 2 es igual a 18. Explica, en tu cuaderno, por qué.
b) Completa las tablas del 6 y del 9, aplicando las estrategias anteriores.
Tabla del
6
1 2 3 4 5 6 7 8 9 10
• 6
Tabla del
9
1 2 3 4 5 6 7 8 9 10
• 9
Pedro compra lápices para hacer los carteles de la exposición.
Comento • ¿Cuántos lápices llevará Pedro, en total?, ¿cómo lo calculaste?
• Si Pedro lleva 2 estuches con 6 lápices cada uno, ¿cuántos lápices llevará?,
¿y si lleva 2 estuches con 9 lápices cada uno?, ¿cómo lo calculaste?
En este estuche
vienen 3 lápices... llevaré
2 de estos estuches.
ORIENTACIONES PARA EL DESARROLLO DE LAS ACTIVIDADES
• Antes de trabajar la actividad 1, pida a sus alumnos y alumnas que digan la
secuencia numérica de 3 en 3, y antes de comenzar la actividad 2, que hagan
lo mismo con la secuencia de 6 en 6 y de 9 en 9.
• Para lograr un óptimo desarrollo y comprensión de las actividades 1 y 2, es
conveniente que permita a sus estudiantes que se apoyen en material concreto
o bien en representaciones gráficas.
• En la actividad 2, es conveniente que trabaje en conjunto con los estudiantes para
que quede clara la relación referente a que el doble de 3 es 6 y que 9 es su tri-
ple. Utilice material concreto si observa dificultades en su comprensión. Incluya el
uso de calculadora y pídales que tripliquen y luego dupliquen un número dado,
y anoten el resultado; que luego multipliquen el número dado por 6 y comparen
este resultado con el obtenido anteriormente; finalmente, pídales que
OBJETIVOS DE APRENDIZAJE
Demostrar que comprenden las tablas
de multiplicar hasta 10 de manera
progresiva […]:
• aplicando los resultados de las
tablas de multiplicación hasta
10x10, sin realizar cálculos […].
Demostrar que comprenden la división
en el contexto de las tablas de hasta
10x10 […]:
• describiendo y aplicando la
relación inversa entre la división
y la multiplicación;
• aplicando los resultados de las
tablas de multiplicación hasta
10x10, sin realizar cálculos.
ACTIVIDAD INICIAL
Observan la situación inicial y responden
a partir de las preguntas de la sección
Comento. Promueva que expliquen
cómo calcularon la cantidad de lápices
que llevará Pedro en total, en las tres
situaciones propuestas, y que deter-
minen la multiplicación cuyo resultado
permite obtener la respuesta. Pídales,
además, que expresen la multiplicación
como una adición de sumandos igua-
les y que propongan y calculen otras
multiplicaciones en las que uno de los
factores sea 3 y el otro, un dígito entre
1 y 10.
Actividad
Habilidades que
se desarrollan
Comento
Resolver problemas,
argumentar y comunicar.
1, 2, 4 y 5 Representar.
3
Representar, argumentar
y comunicar.](https://image.slidesharecdn.com/123112-150514161041-lva1-app6891/85/Didactica-del-profesor-Matematica-152-320.jpg)

![154 Guía Didáctica Matemática 3º Básico
UNIDAD 4
4
118 Cálculo mental de productos y cuocientes por 4 y 8
Javiera y su profesora ordenan las sillas para los estudiantes que asistirán
a la exposición sobre los derechos del niño.
Comento • ¿Cuántas sillas hay en el grupo de sillas que cuenta Javiera?,
¿cómo lo supiste?
• Si 4 • 3 = 12, ¿cómo se puede calcular el producto de 8 • 3?
Completa la siguiente recta numérica con los números en los que caerías si
avanzaras de 4 en 4. Luego, completa la tabla.
1
• Escribe una regla que te facilite el cálculo de productos al multiplicar por 8 y verifícala,
formulando tres ejemplos.
Tabla del
4
1 2 3 4 5 6 7 8 9 10
4 20 40
• 4
0 4 8 20 40
Observa el ejemplo y completa. Luego, responde en tu cuaderno.2
Si sabes la tabla del 4, podrás
calcular fácilmente la tabla
del 8.
a) 4 • 3 = , entonces 8 • 3 =
b) 4 • 4 = , entonces 8 • 4 =
c) 4 • 5 = , entonces 8 • 5 =
d) 4 • 6 = , entonces 8 • 6 =
e) 4 • 7 = , entonces 8 • 7 =
f) 4 • 8 = , entonces 8 • 8 =
g) 4 • 9 = , entonces 8 • 9 =
12 24
Cálculo mental de productos y cuocientes por 4 y 8
Aquí hay 12 sillas.
¿Cuántas hay allá?
ORIENTACIONES PARA EL DESARROLLO DE LAS ACTIVIDADES
• Antes de realizar la actividad 1, recuérdeles cómo se ubican los números en
la recta numérica y cuál es su utilidad. Si es necesario, realice una pequeña
introducción en la cual recuerden los contenidos relacionados con el tema.
• En la actividad 2, guíelos para que concluyan que al cuadruplicar y luego
duplicar un número, el resultado es equivalente a multiplicar por 8. O bien
que el doble del doble del doble de un número equivale a 8 veces el número.
Solicíteles que verifiquen ambos procedimientos utilizando la calculadora.
Si detecta dificultad en la comprensión, invítelos a utilizar material concreto.
OBJETIVOS DE APRENDIZAJE
Demostrar que comprenden las tablas
de multiplicar hasta 10 de manera
progresiva […]:
• aplicando los resultados de las
tablas de multiplicación hasta
10x10, sin realizar cálculos […].
Demostrar que comprenden la división
en el contexto de las tablas de hasta
10x10 […]:
• describiendo y aplicando la relación
inversa entre la división y la
multiplicación;
• aplicando los resultados de las
tablas de multiplicación hasta
10x10, sin realizar cálculos.
ACTIVIDAD INICIAL
Observan la situación inicial y la comen-
tan, cuentan la cantidad de sillas que
hay en cada grupo y conversan sobre
las preguntas de la sección Comento.
Motívelos para que formulen diversas
hipótesis sobre la relación existente entre
la tabla del 4 y del 8, aplicando lo apren-
dido sobre las tablas del 3, 6 y 9.
Actividad
Habilidades que
se desarrollan
Comento
Resolver problemas,
argumentar y comunicar.
1, 3, 4 y 5 Representar.
2 Modelar.](https://image.slidesharecdn.com/123112-150514161041-lva1-app6891/85/Didactica-del-profesor-Matematica-154-320.jpg)

![156 Guía Didáctica Matemática 3º Básico
UNIDAD 4
120
4
En equipo
En esta actividad ejercitarán, a través de un juego, el
cálculo mental de productos y cuocientes por 7. Formen
grupos de tres integrantes y sigan las instrucciones.
1. Recorten 20 tarjetas de cartulina de igual tamaño y escriban
en ellas las siguientes multiplicaciones y divisiones.
2. Resuelvan las multiplicaciones y divisiones anteriores, usando la calculadora. Luego,
escriban los productos y cuocientes obtenidos, en una nueva tarjeta. Aunque se repita
un resultado, deben volver a escribirlo.
3. Mezclen las tarjetas y póngalas boca abajo sobre la mesa. Por turnos, saquen dos
tarjetas. Cada vez que alguno de ustedes logre juntar una multiplicación con su
producto o una división con su cuociente, debe guardar esta pareja de tarjetas. Gana
quien logre juntar más parejas de tarjetas.
7 • 1 7 • 2 7 • 3 7 • 4 7 • 5
7 • 6 7 • 7 7 • 8 7 • 9 7 • 10
7 : 7 14 : 7 21 : 7 28 : 7 35 : 7
42 : 7 49 : 7 56 : 7 63 : 7 70 : 7
Materiales:
• Cartulina.
• Tijeras.
• Lápices.
• Calculadora.
Javiera está jugando con las siguientes tarjetas. Ella tomó una tarjeta roja,
que utilizó como dividendo y una tarjeta amarilla, que utilizó como divisor.
Si obtuvo como cuociente el número 7, ¿qué par de tarjetas utilizó?, ¿cómo
lo supiste?
1
49 35
10 7
28 70
Comento • Si en una semana hay 7 días, ¿cuántos días hay en 4 semanas?,
¿y en 8?, ¿y en 9?, ¿cómo lo calculaste?
Cálculo mental de productos y cuocientes por 7
Cálculo mental de productos y cuocientes por 7
ORIENTACIONES PARA EL DESARROLLO DE LAS ACTIVIDADES
• Antes de desarrollar la actividad 1, repase con sus alumnos y alumnas los ele-
mentos que forman parte de la división. Si es necesario, realice una introducción
respecto del tema, pues si no manejan bien este contenido, el trabajo de la
actividad 1 se verá dificultado. En esta actividad, se espera que los estudiantes
realicen una de las combinaciones trabajadas de forma correcta y sean capaces
de relacionar de forma adecuada dividendo, divisor y cuociente. Si presentan
dificultades para encontrar las tarjetas adecuadas, pídales que realicen cada una
de las divisiones posibles y de esa forma descubran la correcta.
• Antes de realizar la actividad 2, escriba en la pizarra un número del 1 al 10 y pida
a sus estudiantes que calculen su doble; luego, que multipliquen por 4 y por 8. Si
presentan dificultades en la actividad, permítales usar material concreto. Finalice
el trabajo con una puesta en común y la corrección de los errores detectados.
OBJETIVOS DE APRENDIZAJE
Demostrar que comprenden las tablas
de multiplicar hasta 10 de manera
progresiva […]:
• aplicando los resultados de las
tablas de multiplicación hasta
10x10, sin realizar cálculos […].
Demostrar que comprenden la división
en el contexto de las tablas de hasta
10x10 […]:
• describiendo y aplicando la relación
inversa entre la división y la
multiplicación;
• aplicando los resultados de las
tablas de multiplicación hasta
10x10, sin realizar cálculos.
ACTIVIDAD INICIAL
Antes de comenzar la actividad En
equipo, comparta con sus estudiantes
la finalidad u objetivo de la misma.
Continúe leyendo con el curso la acti-
vidad, antes de formar los equipos de
trabajo, y verifique que los pasos hayan
sido comprendidos por la totalidad
de sus alumnos y alumnas. Una vez
que las tarjetas estén listas, monitoree
que cada grupo esté llevando a cabo
la actividad de forma adecuada. Al
finalizar, realice una puesta en común
en la que apliquen la relación inversa
entre la multiplicación y la división; por
ejemplo: ¿qué divisiones se desprenden
de la multiplicación 7 · 5? Conversan
respecto de la pregunta planteada en
la sección Comento.
Actividad
Habilidades que
se desarrollan
Comento
y 1
Resolver problemas,
argumentar y comunicar.
2 Resolver problemas.](https://image.slidesharecdn.com/123112-150514161041-lva1-app6891/85/Didactica-del-profesor-Matematica-156-320.jpg)

![158 Guía Didáctica Matemática 3º Básico
UNIDAD 4
4
122 Resolución de problemas que involucran multiplicaciones y divisiones
Resolución de problemas que involucran multiplicaciones
y divisiones
La señora Berta fue a la feria y compró manzanas.
5 leches
6 leches
9 leches
La cantidad de asientos de cada bus. La cantidad de abuelitos que iban de paseo.
2 leches
• ¿Cuánto dinero, en total, debió pagar la señora Berta por las manzanas?,
¿cómo lo calculaste?
• ¿Qué información te faltaría conocer para calcular cuánto cuesta cada
manzana?, ¿por qué?
Comento
Lee los siguientes problemas y pinta la respuesta correcta.
a) En un supermercado, hay una oferta de leches que dice “lleve 3 y pague 2”.
Si Carolina ha sacado 9 leches, ¿cuántas leches deberá pagar?
• ¿Qué operación utilizaste para resolver el problema anterior? .
b) Un grupo de abuelitos se fue de paseo a la playa. Se distribuyeron en 3 buses, con
igual cantidad de personas en cada bus. ¿Qué información se necesita para saber
cuántas personas iban en cada bus?
1
Tengo bolsas
de manzanas
a $ 500.
Quiero 3 bolsas,
por favor.
ORIENTACIONES PARA EL DESARROLLO DE LAS ACTIVIDADES
• En la actividad 1, puede ser útil que los estudiantes representen gráficamente
cada situación. Promueva el diálogo entre pares en torno a los datos que consi-
deraron en cada problema, la relación entre estos y la pregunta por responder,
y las condiciones necesarias que se deben cumplir para obtener algunas infor-
maciones. Esto les permitirá reforzar sus maneras de proceder o hacerlas cada
vez más efectivas y eficientes.
• A partir de la actividad 2, pida a sus estudiantes que planteen nuevas pregun-
tas y desafíen a sus compañeros y compañeras a responderlas. Cada estudiante
puede confeccionar tarjetas con diferentes números y crear situaciones similares
a la de esta actividad.
OBJETIVOS DE APRENDIZAJE
Demostrar que comprenden las tablas
de multiplicar hasta 10 de manera
progresiva […]:
• aplicando los resultados de las
tablas de multiplicación hasta
10x10, sin realizar cálculos;
• resolviendo problemas que
involucren las tablas aprendidas
hasta el 10.
Demostrar que comprenden la división
en el contexto de las tablas de hasta
10x10 […]:
• aplicando los resultados de las
tablas de multiplicación hasta
10x10, sin realizar cálculos.
ACTIVIDAD INICIAL
A partir de la situación inicial, plantee
preguntas similares a las que aparecen
en la sección Comento, tales como:
¿cuántas manzanas se llevó don Jaime
si compró 8 bolsas? Si la señora Julia
se llevó 36 manzanas, ¿cuántas bolsas
compró? En cada pregunta, pida a sus
estudiantes que justifiquen su respues-
ta, indicando si realizaron una división
o una multiplicación.
Actividad
Habilidades que
se desarrollan
Comento
y 2
Resolver problemas,
argumentar y comunicar.
1 y 3 Argumentar y comunicar.](https://image.slidesharecdn.com/123112-150514161041-lva1-app6891/85/Didactica-del-profesor-Matematica-158-320.jpg)













![172 Guía Didáctica Matemática 3º Básico
UNIDAD 5
5
132 Fracciones en la vida cotidiana
Fracciones en la vida cotidiana
• ¿De qué otra manera podrías haber dividido el cuadrado en 4 partes iguales?Comento
Realiza las siguientes actividades con papel lustre.
a) Divide de dos formas distintas un cuadrado de papel lustre en dos partes iguales.
b) Los siguentes cuadrados representan las hojas de papel lustre que dividiste en dos
partes iguales. Marca en cada una las líneas que muestran estas divisiones.
c) Divide un cuadrado de papel lustre en tres partes iguales.
d) El siguente cuadrado representa la hoja de papel lustre que dividiste en tres partes
iguales. Marca las líneas que muestran esta división.
1
Si se divide en partes iguales una hoja y se reparte equitativamente entre
2 personas, ¿qué parte de la hoja le toca a cada una?, ¿y si se reparte entre
4 personas?, ¿y entre 3 personas?
2
Observa dos formas de repartir en partes iguales un cuadrado de papel
lustre entre 4 personas.
Si se reparte un cuadrado de papel lustre entre
4 personas, cada una recibe la cuarta parte
del cuadrado de papel lustre. La fracción
que representa cada cuarto del cuadrado es 1
4
.
1
4
1
4
La fracción que representa
cada parte en que se dividió
cada cuadrado es 1
2
y se lee
un medio.
La fracción que representa
cada parte en que se dividió el
cuadrado es 1
3
y se lee un tercio.
OBJETIVOS DE APRENDIZAJE
Demostrar que comprende las fracciones
de uso común […]:
• describiendo situaciones, en las cuales
se puede usar fracciones […].
ACTIVIDAD INICIAL
En la actividad inicial los alumnos y
las alumnas realizarán actividades de
reparto equitativo utilizando papel
lustre. Enfatice el hecho de que un
reparto equitativo implica que el papel
debe quedar dividido en partes iguales.
Lean en conjunto el desafío planteado
en la sección Comento y otórgueles
el tiempo necesario para que lleven la
actividad a cabo. Una vez terminada,
invite a uno o más estudiantes para
que pasen adelante y muestren a sus
compañeros y compañeras las respues-
tas a las que llegaron y expliquen cómo
las obtuvieron. Determinen entre todos
si efectivamente el reparto realizado
por cada uno fue equitativo o no.
Actividad
Habilidades que
se desarrollan
Comento
Representar, argumentar
y comunicar.
1 Representar.
2 Resolver problemas.
3 Argumentar y comunicar.
ORIENTACIONES PARA EL DESARROLLO DE LAS ACTIVIDADES
• En la actividad 1, si sus estudiantes presentan dificultades para dividir el papel lustre
en tres partes iguales, propóngales que utilicen una regla, o bien, que lo doblen
como si fuera un tríptico, procurando que el ancho de cada parte sea el mismo.
• Antes de trabajar en las actividades de la página 133 es conveniente realizar
otras actividades de reparto equitativo en las que un entero se divida en partes
iguales. Puede utilizar distintos tipos de material concreto para que sus estudian-
tes comiencen a entender de manera intuitiva el concepto de entero y de parte.
La idea es que surja en ellos y ellas la necesidad de incorporar las fracciones.
• Con el desarrollo de la actividad 3, los estudiantes conocerán el nombre de
cada una de las partes de un objeto repartido en 2, 3 y 4 partes iguales. Luego
de realizar la actividad, puede doblar hojas de papel lustre de diferentes colores
en 2, 3 y 4 partes iguales, de distintas maneras, pedir a sus estudiantes que las](https://image.slidesharecdn.com/123112-150514161041-lva1-app6891/85/Didactica-del-profesor-Matematica-172-320.jpg)

![174 Guía Didáctica Matemática 3º Básico
UNIDAD 5
ORIENTACIONES PARA EL DESARROLLO DE LAS ACTIVIDADES
• Las actividades de estas páginas están orientadas a que los estudiantes se fami-
liaricen con el concepto y uso de las fracciones, reconozcan sus características
más relevantes, puedan escribirlas y comprender el significado del numerador y
del denominador.
• Para introducir los conceptos de entero y partes de un entero, se sugiere
comenzar realizando acciones concretas de fraccionamiento. Para esto, puede
repartir a cada alumno y alumna una hoja blanca y decirles que la doblen, de
modo que queden cuatro partes de igual tamaño. Pídales que marquen con
un lápiz las líneas determinadas por los dobleces y que pinten de distinto color
cada una de las partes resultantes. Luego, realice preguntas como por ejemplo:
¿en cuántas partes se dividió la figura?, ¿cuántas partes se pintaron?, ¿a qué
fracción del entero corresponde la parte pintada?, entre otras. De esta manera,
irán descubriendo los conceptos de entero y partes de un entero.
OBJETIVOS DE APRENDIZAJE
Demostrar que comprende las fracciones
de uso común […]:
• describiendo situaciones, en las
cuales se puede usar fracciones;
• explicando que una fracción
representa la parte de un todo […].
ACTIVIDAD INICIAL
En la actividad planteada en la sección
En Equipo ayude a los alumnos y las
alumnas a organizar su trabajo, asig-
nando los papeles que cada uno deberá
realizar: encargado de materiales, encar-
gado de registrar información, etc.
Lea con sus estudiantes las instrucciones
para realizar el trabajo, a fin de ir
solucionando las posibles dudas que
se puedan presentar.
Le sugerimos pedirles que peguen el
trozo de lana sin cortar y, los que ya
han cortado, los peguen en una hoja
de bloc o cartulina, para que no lo
extravíen y puedan trabajar de manera
más ordenada al responder las pregun-
tas que se plantean.
Una vez que sus estudiantes hayan
respondido las preguntas de la sección
Comento, ínstelos a encontrar regula-
ridades entre la cantidad de partes que
se toman del entero y la fracción repre-
sentada en cada caso. Existe la posibili-
dad de que algún estudiante relacione
la fracción obtenida con la cantidad de
lanas que se toma respecto de la can-
tidad total. Si eso sucede, puede intro-
ducir los significados de numerador y
denominador de una fracción.
Actividad
Habilidades que
se desarrollan
Comento Argumentar y comunicar.
1 Resolver problemas.
5
134 Representación de fracciones como parte de un entero
Representación de fracciones como parte de un entero
• ¿Con cuántos trozos de la lana que se cortó en 3 partes iguales se
pueden representar 2
3
?
• ¿Con cuántos trozos de la lana que se cortó en 4 partes iguales se
pueden representar
3
4
?
Comento
En esta actividad deberán dividir en partes iguales
un trozo de lana de 30 cm. Formen grupos de cuatro
integrantes y sigan las instrucciones.
1. Repartan un trozo de lana para cada uno y el que sobra
estírenlo en el centro de la mesa.
2. Uno de los integrantes corta su trozo de lana en 2 partes iguales.
3. Observen los trozos que obtuvo, comenten y respondan:
a) ¿En cuántas partes quedó cortado el trozo de lana?
b) ¿Qué fracción del trozo de 30 cm representa cada
trozo obtenido?
4. Comparen cada trozo obtenido con el que dejaron
en el centro de la mesa y estimen su medida.
Verifiquen su estimación, midiendo con la huincha.
5. Por turno, repitan la actividad con los trozos de lana que tiene cada uno,
pero dividiéndolos ahora en 3 y en 4 partes iguales.
Materiales:
• Cinco trozos de lana
de 30 cm cada uno.
• Tijeras.
• Huincha de medir.
En equipo
Cada parte
representa 1
2
.
Cada parte
representa 1
4
.
Cada parte
representa 1
3
.](https://image.slidesharecdn.com/123112-150514161041-lva1-app6891/85/Didactica-del-profesor-Matematica-174-320.jpg)

![176 Guía Didáctica Matemática 3º Básico
UNIDAD 5
5
136 Representación de fracciones como parte de un entero
En las actividades anteriores, cada diagrama estaba
dividido en partes iguales y solo se habían pintado
algunas de ellas.
Observa el diagrama. Fíjate en cuántas partes está
dividido y cuántas de ellas se pintaron.
Para no olvidar
2
3
Une cada diagrama con la fracción que representa la parte pintada.4
3
4
1
2
1
3
2
3
Resuelve los siguientes problemas.
a) Cuatro amigos repartirán esta pizza en partes iguales
para compartirla. ¿En cuántas partes deben dividirla?
Deben dividirla en partes iguales.
b) Tres niños quieren repartir un pastel en 3 partes
iguales para compartirlo. ¿Qué parte del pastel
le corresponde a cada niño?
A cada niño le corresponde del pastel.
c) Si cuatro niños quisieran repartir un pastel igual
al anterior en 4 partes iguales para compartirlo.
¿Qué parte del pastel le correspondería a cada niño?
A cada niño le correspondería del pastel.
3
ORIENTACIONES PARA EL DESARROLLO DE LAS ACTIVIDADES
• Si observa que sus estudiantes presentan dificultades para responder las pre-
guntas de la actividad 3, puede desarrollarla con el apoyo de material concreto,
para facilitar su comprensión.
• En la actividad 4, es importante que observen con atención los diagramas y
reconozcan que se han dividido en partes iguales. Puede, además, mostrarles
diagramas que no estén divididos en partes iguales, a modo de contraejemplos.
• En los problemas a y b de la actividad 5, puede apoyarse con una representa-
ción gráfica de las fracciones, pintando todas las partes en las que se dividió el
entero, para que sus estudiantes reconozcan que, si el numerador y el denomi-
nador de una fracción son iguales, entonces la fracción es igual a la unidad.
OBJETIVOS DE APRENDIZAJE
Demostrar que comprende las fracciones
de uso común […]:
• describiendo situaciones, en las
cuales se puede usar fracciones;
• explicando que una fracción
representa la parte de un todo […].
Actividad
Habilidades que
se desarrollan
2, 3 y 4 Representar.
5 Resolver problemas.](https://image.slidesharecdn.com/123112-150514161041-lva1-app6891/85/Didactica-del-profesor-Matematica-176-320.jpg)

![178 Guía Didáctica Matemática 3º Básico
UNIDAD 5
5
138 Comparación de fracciones de igual denominador
Comparación de fracciones de igual denominador
• Al comparar fracciones de igual denominador, ¿cómo puedes saber cuál
es mayor?, ¿por qué?
Comento
Observa cada pareja de diagramas y compara las fracciones que representan
las partes pintadas, usando los signos <, > o =, según corresponda.
a) b)
1
En esta actividad aprenderán a comparar fracciones
de igual denominador. Formen grupos de cuatro
integrantes y sigan las instrucciones.
1. Cada integrante divide un cuadrado de papel lustre en
4 cuadrados iguales, haciendo dobleces como se muestra
en la figura.
2. Uno de los integrantes representa en su cuadrado la fracción , otro , otro
y otro , pintando 1, 2, 3 o 4 partes, según corresponda.
3. Comparen sus representaciones y respondan en sus cuadernos:
a) Si comparan la representación de con la de , ¿cuál representa una mayor
parte del cuadrado?, ¿cómo lo saben?
b) Y al comparar 1
4
con
3
4
, ¿cuál es mayor?, ¿cómo lo saben?
4. Ahora busquen una forma para representar las fracciones
1
3
,
2
3
y
3
3
en nuevos
cuadrados de papel lustre y ordénenlas, desde la menor hasta la mayor. Compartan
sus resultados con el curso y guarden sus representaciones para una próxima actividad.
Materiales:
• 12 cuadrados de
papel lustre.
• Lápices de colores.
En equipo
1
4
2
4
3
44
4
1
4
2
4
3
4
2
4
1
3
2
3
ORIENTACIONES PARA EL DESARROLLO DE LAS ACTIVIDADES
• En la actividad 1, es fundamental que los estudiantes se den cuenta de que las
parejas de diagramas tienen la misma forma y tamaño, y están divididas en par-
tes iguales; por eso se puede realizar la comparación según el numerador.
• En la actividad 2, se espera que logren aplicar las conclusiones y conocimientos
obtenidos respecto del procedimiento para comparar fracciones de igual
denominador. Si observa dificultades para el desarrollo de la tarea, sugiérales
que dibujen diagramas para representar las fracciones, procurando que estén
divididas en partes iguales y que tengan la misma forma y tamaño.
• La actividad 3 tiene como finalidad que los alumnos y las alumnas apliquen los
conocimientos adquiridos en la comparación de fracciones de igual denomi-
nador. Entregue a sus estudiantes un tiempo para que analicen el problema y
busquen la solución; luego, pídales que compartan con el curso las respuestas
y estrategias usadas.
OBJETIVOS DE APRENDIZAJE
Demostrar que comprende las fracciones
de uso común […]:
• describiendo situaciones, en las
cuales se puede usar fracciones;
• comparando fracciones de un
mismo todo, de igual denominador.
ACTIVIDAD INICIAL
Escriba dos fracciones simples de igual
denominador en el pizarrón y pida a
los estudiantes que piensen distintas
estrategias para compararlas y determi-
nar cuál es mayor o menor. Anote las
ideas entregadas por los alumnos y las
alumnas y pruebe algunas de las estra-
tegias propuestas, evaluando en con-
junto su efectividad. Luego, proponga
realizar las actividades de la sección
En equipo.
Una vez concluida la actividad, realice
con sus estudiantes un análisis de los
resultados obtenidos y oriéntelos para
que concluyan por sí mismos que,
al comparar fracciones de igual
denominador, es mayor aquella
con mayor numerador.
Actividad
Habilidades que
se desarrollan
Comento Argumentar y comunicar.
1 y 2 Representar.
3
Resolver problemas,
argumentar y comunicar.](https://image.slidesharecdn.com/123112-150514161041-lva1-app6891/85/Didactica-del-profesor-Matematica-178-320.jpg)



![182 Guía Didáctica Matemática 3º Básico
UNIDAD 5
ORIENTACIONES PARA EL DESARROLLO DE LAS ACTIVIDADES
• Antes de desarrollar la actividad 1, explique a sus alumnos y alumnas cómo se
comparan las masas de dos cuerpos, utilizando una balanza: si la balanza está
equilibrada, es decir, con los dos platos a la misma altura, significa que los objetos
puestos en los platos tienen igual masa; por otra parte, si los platos de la balanza
no quedan a la misma altura, el cuerpo que está en el plato que queda más
abajo tiene mayor masa que el que está en el plato que queda más arriba.
• En la actividad 2, recuerde a sus estudiantes que las divisiones deben ser equita-
tivas, es decir, en dos partes iguales. Si no se cuenta con una balanza es muy
difícil que la división sea exacta, por lo que deberá orientar a sus estudiantes y
corregirlos en caso de que su división haya sido muy desequilibrada. Promueva
el orden y la limpieza en el interior de la sala de clases.
OBJETIVOS DE APRENDIZAJE
Demostrar que comprende la medición
del peso (g y kg):
• comparando y ordenando dos o
más objetos a partir de su peso de
manera informal […].
ACTIVIDAD INICIAL
Comparta con sus estudiantes situa-
ciones de la vida cotidiana en la que
tienen que “pesar” objetos utilizando
una balanza. Posteriormente, presente
pares de objetos y pregúnteles cuál
de ellos es “más pesado”, tal como se
realiza en la sección Comento. Luego,
pídales que corroboren su respuesta
tomando ambos objetos, uno en cada
mano, y que estimen cuál tiene mayor
y cuál menor peso.
También puede establecer la diferencia
entre la masa y el tamaño de un cuerpo,
concluyendo que no necesariamente
un cuerpo más grande que otro tiene
mayor masa. Por ejemplo, al comparar
un globo inflado con una piedra, el
volumen del globo es mucho mayor
que el de la piedra; sin embargo, su
masa es menor. Puede usar ese mismo
ejemplo para desafiar a sus estudian-
tes con la pregunta: ¿qué tiene mayor
masa: un kilogramo de piedras o un
kilogramo de globos?
Actividad
Habilidades que
se desarrollan
Comento
Resolver problemas,
argumentar y comunicar.
1 Representar.
2 y 3
Resolver problemas
y representar.
142 Orden y comparación a partir del “peso”
Orden y comparación a partir del “peso”
Don Juan tienen en su mesón una malla de papas y una espinaca, como muestra
la lámina. Observa.
5
• ¿Qué tiene mayor masa: la malla de papas o la espinaca?, ¿por qué?Comento
Observa las balanzas y completa con las palabras más, menos o igual.
a) c)
b) d)
1
Estas papas “pesan”
que estas guindas.
Estas paltas “pesan”
que estos limones.
Los “pesos” de estas sandías son
.
Esta sandía “pesa”
que estas frutillas.](https://image.slidesharecdn.com/123112-150514161041-lva1-app6891/85/Didactica-del-profesor-Matematica-182-320.jpg)

![184 Guía Didáctica Matemática 3º Básico
UNIDAD 5
144 Relación entre gramos y kilogramos
5 Relación entre gramos y kilogramos
Don Luis fue a la feria a comprar manzanas. Observa.
• ¿A cuántos gramos equivale 1 kilogramo?
• ¿A cuántos gramos equivale medio kilogramo?, ¿cómo lo supiste?
• ¿A cuántos gramos equivale un cuarto de kilogramo?
Comento
El kilogramo (kg) es la unidad en que expresamos la masa de los objetos.
Generalmente, para expresar las masas menores a 1 kg usamos el gramo (g).
1 kg = 1 000 g 1
2
kg = 500 g 1
4
kg = 250 g
Para no olvidar
Escribe el nombre de cuatro productos que se vendan por kilogramos y cuatro que
se vendan en gramos.
1
Javier dice que su masa es 43 kg y Cecilia dice que es 43 g.
¿Quién tiene la razón?, ¿por qué?
2
En kilogramos En gramos
Quiero
1 kilogramo,
por favor.
La balanza marca
1 000 gramos, o sea,
1 kilogramo.
ORIENTACIONES PARA EL DESARROLLO DE LAS ACTIVIDADES
• A partir de lo que se pide en la actividad 1, tendrá la oportunidad de generar
un debate con sus estudiantes en torno a la utilización de distintas unidades que
permiten medir la misma característica física de un cuerpo (en este caso, la masa).
Puede formular preguntas como: ¿por qué en la vida diaria la masa de algunos
cuerpos se expresa en kilogramos y la de otros, en gramos?, ¿en qué situaciones
es preferible representar la masa de una cantidad en kilogramos?, ¿cuándo es
preferible hacerlo en gramos?, ¿qué otras unidades de masa conocen?, etcétera.
• Promueva el análisis de la pertinencia de las soluciones obtenidas en diferentes
casos relacionados con masas de distintos elementos de uso cotidiano, realizan-
do preguntas similares a la planteada en la actividad 2. Por ejemplo, puede pre-
guntar si la masa de un gato adulto es 5 kg o 5 g. Estimule a sus estudiantes a
elegir la alternativa correcta a partir de la imposibilidad de que un gato adulto
mase 5 g.
OBJETIVOS DE APRENDIZAJE
Demostrar que comprende la medición
del peso (g y kg):
• usando modelos para explicar la
relación que existe entre gramos
y kilogramos […].
ACTIVIDAD INICIAL
Es importante que sus estudiantes
puedan transformar correctamente
una cantidad medida en kilogramos a
gramos o al revés, ya que la conversión
de unidades de medida es un procedi-
miento que ocuparán durante todo el
proceso de enseñanza y también en su
vida cotidiana. Pídales que mencionen
situaciones en las que sea útil saber
cómo transformar una cantidad medida
en gramos a kilogramos, y viceversa.
Por ejemplo, al comprar el pan, una
persona que pide medio kilogramo de
pan debe saber que la balanza digital
con la que el pan se “pesa” registrará
un valor cercano a 500 g.
Actividad
Habilidades que
se desarrollan
Comento
Resolver problemas,
argumentar y comunicar.
1 y 2 Argumentar y comunicar.
3 Representar.
4 Resolver problemas.](https://image.slidesharecdn.com/123112-150514161041-lva1-app6891/85/Didactica-del-profesor-Matematica-184-320.jpg)

![186 Guía Didáctica Matemática 3º Básico
UNIDAD 5
146 Estimación del “peso”
5 Estimación del “peso”
Javier investigó el “peso” de algunos animales en peligro de extinción. Observa.
• Si un puma “pesa” 80 kilogramos, ¿cuánto estimas que puede “pesar”
un gato?, ¿por qué?
• Si un pudú “pesa” 10 kilogramos, ¿cuánto estimas que puede “pesar”
una vaca?, ¿por qué?
Comento
Estima cuál es el “peso” de cada producto y completa la tabla marcando una X
donde corresponda.
Menos de 1 kg
Aproximadamente
1 kg
Más de 1 kg
2
10
30
1
1
Entre 50 y 80 kilogramos.
10 kilogramos
aproximadamente.
ORIENTACIONES PARA EL DESARROLLO DE LAS ACTIVIDADES
• A partir de los resultados obtenidos en la actividad 1, puede proponer a sus
alumnos y alumnas estimar la masa de bolsas con distintos tipos de frutas,
mediante la formulación de problemas. Por ejemplo, realice la siguiente pregunta:
¿cuál es la masa aproximada de una bolsa con 30 naranjas, 20 manzanas
y 30 tomates?
• Pida a sus estudiantes que elaboren una tabla como la de la actividad 1 y que
clasifiquen en ella objetos presentes en la sala de clases. El referente no necesa-
riamente debe ser 1 kg, sino que también se puede utilizar
1
2
kg o
1
4
kg.
• Como actividad complementaria, pida a sus alumnos y alumnas que nombren
productos cuya masa sea aproximadamente 1 kg,
1
2
kg y
1
4
kg.
OBJETIVOS DE APRENDIZAJE
Demostrar que comprende la medición
del peso (g y kg):
• estimando el peso de objetos de uso
cotidiano, usando referentes […].
ACTIVIDAD INICIAL
Utilice material concreto para que sus
alumnos y alumnas puedan estimar
masas de diferentes objetos a partir de
un referente dado. Ponga especial cui-
dado en que dicho referente tenga una
masa conocida, como por ejemplo, una
bolsa de sal de un kilogramo. Ínstelos
a tomar con una mano el cuerpo de
masa conocida y, con la otra, el cuerpo
de masa desconocida y que puedan
determinar si el cuerpo en cuestión
“pesa” más o menos que 1 kg.
Actividad
Habilidades que
se desarrollan
Comento
Resolver problemas,
argumentar y comunicar.
1 Representar.
2 Argumentar y comunicar.
3 Resolver problemas.](https://image.slidesharecdn.com/123112-150514161041-lva1-app6891/85/Didactica-del-profesor-Matematica-186-320.jpg)













![200 Guía Didáctica Matemática 3º Básico
UNIDAD 6
6
156 Concepto de perímetro
Concepto de perímetro
El equipo de Julia ganó la competencia de fútbol. El papá de Julia va a poner
una cinta roja al borde la fotografía que se tomaron, como si fuera el marco.
Observa cómo calculó Julia el largo de cinta que necesita para bordear
completamente la fotografía. Luego, comenta con tu curso.
• ¿Cómo explicarías el procedimiento que usó Julia para determinar el largo de cinta que
necesita para bordear la fotografía?, ¿de qué otra forma podría haberlo hecho?, ¿por qué?
Necesito 50 cm
de cinta roja para
bordear por completo
mi fotografía.
• ¿Cómo calcularías el largo de cinta que se necesita para bordear
completamente la fotografía?
• ¿Qué información te podría ser útil para realizar este cálculo?, ¿por qué?
Comento
OBJETIVOS DE APRENDIZAJE
Demostrar que comprenden el perímetro
[…]:
• midiendo y registrando el perímetro
de figuras del entorno, en el contex-
to de la resolución de problemas;
• determinando el perímetro de un
cuadrado y de un rectángulo.
ACTIVIDAD INICIAL
A partir de la ilustración inicial y de
las preguntas planteadas en la sección
Comento, establezca un diálogo con
sus estudiantes en el cual compartan
los diferentes procedimientos que
utilizarían para calcular la longitud de
la cinta que se necesita para bordear
completamente la fotografía, promo-
viendo que los evalúen y determinen
cuál les parece más sencillo y adecuado.
Luego, pregúnteles cuál debería ser
la longitud de la cinta, si la fotografía
tiene forma rectangular y la medida
de sus lados es de 10 cm de ancho
y 25 cm de largo, y pídales que
expliquen cómo lo supieron.
Actividad
Habilidades que
se desarrollan
Comento
Resolver problemas,
argumentar y comunicar.
1 y 2
Resolver problemas,
argumentar y comunicar.
ORIENTACIONES PARA EL DESARROLLO DE LAS ACTIVIDADES
• Una vez que hayan respondido las preguntas de la actividad inicial, pídale a
los alumnos y las alumnas que observen la secuencia de imágenes que mues-
tra el procedimiento para determinar la longitud de la cinta. Solicite a algunos
estudiantes que describan los pasos seguidos por la niña y oriéntelos para que
relacionen la longitud de la cinta con la medida del contorno de la fotografía.
Luego, guíelos para que concluyan que puede determinarse la longitud de la
cinta que se necesita para bordear por completo la fotografía midiendo cada
lado de ella y sumando las medidas obtenidas.
• Una vez que hayan desarrollado la actividad 1, haga una puesta en común en
la cual compartan sus respuestas y los procedimientos empleados. Guíelos para
que concluyan que una fotografía cuadrada y otra rectangular pueden tener la
misma medida total de contorno, aunque las medidas de sus lados no coincidan.](https://image.slidesharecdn.com/123112-150514161041-lva1-app6891/85/Didactica-del-profesor-Matematica-200-320.jpg)

![202 Guía Didáctica Matemática 3º Básico
UNIDAD 6
ORIENTACIONES PARA EL DESARROLLO DE LAS ACTIVIDADES
• Es importante promover que los estudiantes propongan otras estrategias para
calcular el perímetro de la cancha diferente a la demostrada. Es posible que
lleguen a la estrategia de multiplicar la medida del ancho y del largo por 2 y
sumar ambos productos, que se trabaja en la página 160. Si es así, es impor-
tante que les pida que verifiquen la estrategia propuesta calculando el perí-
metro de rectángulos con medidas diferentes a las de la cancha. Esta es una
buena oportunidad para desarrollar la habilidad de modelar.
• Formalice el procedimiento para calcular el perímetro de polígonos a partir de
la información de la sección Para no olvidar, y pida a sus alumnos y alumnas
que dibujen en sus cuadernos otros polígonos y, utilizando regla, calculen sus
perímetros y los compartan con sus compañeros y compañeras.
OBJETIVOS DE APRENDIZAJE
Demostrar que comprenden el perímetro
de una figura regular y de una irregular
[…] en el contexto de la resolución de
problemas.
ACTIVIDAD INICIAL
A partir de la ilustración inicial y de
las preguntas planteadas en la sección
Comento, oriente a los alumnos y las
alumnas para que reconozcan que la
forma de la cancha es rectangular y
que argumenten, aludiendo a la canti-
dad de lados, la longitud de sus lados
y ángulos. Guíelos para que relacionen
la cantidad de metros que se recorren
al dar una vuelta a la cancha con la
medida de su perímetro y pídales que
calculen la cantidad de metros que
se recorren al dar dos y tres vueltas.
Además, puede dibujar en la pizarra
canchas con diferentes medidas y
desafiarlos a determinar en cuál de
las canchas se recorren más metros
al dar una vuelta alrededor de ella.
Actividad
Habilidades que
se desarrollan
Comento
Resolver problemas,
argumentar y comunicar.
1 Resolver problemas.
2
Resolver problemas,
argumentar y comunicar.
6
158 Perímetros de polígonos
• ¿Qué forma tiene la cancha que dibujaron Andrés y Julia?, ¿en qué te
fijaste para saberlo?
• Si Julia da una vuelta completa alrededor de la cancha, ¿cuántos metros
recorrerá?, ¿cómo lo calculaste?
Comento
Perímetros de polígonos
Andrés y Julia participan en una competencia. Esta consiste en dar una vuelta
trotando alrededor de la cancha en el menor tiempo posible.
Para saber los metros que deberán recorrer, hicieron un dibujo de la cancha.
Observa cómo calculó Julia los metros que debía recorrer trotando, al dar una vuelta
completa alrededor de la cancha y, luego, comenta con tu curso.
• ¿Qué otra estrategia podría haber utilizado Julia para calcular el perímetro de la cancha?
Verifica tu respuesta, aplicando tu estrategia para calcular el perímetro de la cancha
y comparando tu resultado con el que obtuvo Julia.
Para determinar cuántos metros recorreré al dar la vuelta alrededor
de la cancha, debo calcular el perímetro de la cancha. Para ello,
sumo la medida de sus lados. Así:
Lado 1 + Lado 2 + Lado 3 + Lado 4
38 m + 65 m + 38 m + 65 m
P = 206 metros
Recorreré 206 metros al dar una vuelta alrededor de la cancha.
65 m
65 m
38 m 38 m](https://image.slidesharecdn.com/123112-150514161041-lva1-app6891/85/Didactica-del-profesor-Matematica-202-320.jpg)

![204 Guía Didáctica Matemática 3º Básico
UNIDAD 6
160 Perímetro de un cuadrado y de un rectángulo
6
• ¿Es posible calcular el perímetro de un rectángulo conociendo solo la
medida de uno de sus lados?, ¿por qué?
• ¿Qué medidas necesitas conocer para calcular el perímetro de un
rectángulo?, ¿por qué?
• En conjunto, formulen una estrategia para calcular el perímetro de un
cuadrado, conociendo la medida de uno de sus lados, y el perímetro
de un rectángulo, conociendo la medida de su largo y ancho. Luego,
verifíquenla con dos ejemplos para cada caso.
Comento
En esta actividad calcularán el perímetro de cuadrados
y rectángulos. Reúnanse en grupos de tres integrantes
y sigan las instrucciones.
1. Cada integrante dibuja un cuadrado en una hoja de cuaderno, utilizando una regla.
Luego, mide cada lado del cuadrado, expresando esta medida en milímetros y calcula
su perímetro.
2. Con la información registrada por cada integrante, completen la siguiente tabla y
respondan las preguntas en sus cuadernos.
a) ¿Es posible calcular el perímetro de un cuadrado conociendo solo la medida
de uno de sus lados?, ¿por qué?
b) Si la medida del lado de un cuadrado se duplica, ¿qué ocurre con su perímetro?
3. Ahora, cada integrante dibuja un rectángulo en otra hoja de cuaderno y repite el
procedimiento anterior. Luego, completan la siguiente tabla.
Materiales:
• Ocho hojas
cuadriculadas.
• Reglas.
• Lápices.
En equipo
Polígono Medida de cada lado Perímetro
Cuadrado 1
Cuadrado 2
Cuadrado 3
Polígono Medida del largo Medida del ancho Perímetro
Rectángulo 1
Rectángulo 2
Rectángulo 3
Perímetro de un cuadrado y de un rectángulo
ORIENTACIONES PARA EL DESARROLLO DE LAS ACTIVIDADES
• La actividad En equipo tiene por finalidad que los alumnos y las alumnas logren
establecer un procedimiento abreviado que permita calcular el perímetro de
cuadrados conociendo la medida de uno de sus lados, y el perímetro de un rec-
tángulo conociendo las medidas de su largo y ancho. Es importante promover
que verifiquen sus conclusiones con ejemplos de estos polígonos, considerando
diferentes medidas para sus lados.
• En la actividad 1, es importante que los estudiantes escriban, paso a paso, el
método que utilizan para solucionar el problema: cálculo de medidas ausentes,
en algunos casos el cálculo directo de los perímetros de cada figura y finalmente
el cálculo que permitirá responder la pregunta al problema. Es importante que los
estudiantes escriban la repuesta al problema y no solo los números asociados sin
un contexto.
OBJETIVOS DE APRENDIZAJE
Demostrar que comprenden el períme-
tro […] determinando el perímetro de
un cuadrado y de un rectángulo.
ACTIVIDAD INICIAL
En 2º básico, los alumnos y las alumnas
estudiaron cuadrados, rectángulos y
triángulos caracterizándolos en función
del número y longitud de sus lados.
Es conveniente que, como actividad
previa, retome estas caracterizaciones,
recordándoles que los cuadrados tienen
todos sus lados de igual medida, que
los rectángulos tienen dos pares de
lados de igual medida y que los trián-
gulos pueden tener sus tres lados de
igual medida, solo dos lados de igual
medida, o bien todos sus lados de
distintas medidas.
Actividad
Habilidades que
se desarrollan
En equipo
Resolver problemas,
argumentar y comunicar.
Comento
Argumentar y comunicar,
modelar.
1 Resolver problemas.
2
Representar y resolver
problemas.
Me
conecto
Resolver problemas.](https://image.slidesharecdn.com/123112-150514161041-lva1-app6891/85/Didactica-del-profesor-Matematica-204-320.jpg)

![206 Guía Didáctica Matemática 3º Básico
UNIDAD 6
6 Perímetros en la vida cotidiana
• ¿Cómo describirías la forma de cada uno de los huertos?
• ¿En qué se parece y en qué se diferencia la forma del huerto del 3º A
a la del 3º B?
• ¿Qué huerto crees que tiene un mayor perímetro?, ¿cómo lo sabes?
Comento
Observa cómo se puede calcular el perímetro de la siguiente figura. Luego, comenta
con tu curso.
• Al sumar el perímetro del cuadrado más el perímetro del rectángulo, ¿obtendremos
el perímetro total de la figura anterior?, ¿por qué? Verifica tu respuesta realizando
los cálculos correspondientes.
162 Perímetros en la vida cotidiana
Los terceros básicos A y B de una escuela del Cajón del Maipo hicieron un
huerto para su proyecto de Ciencias. Cada curso necesita calcular cuántos
metros de reja debe comprar para cercar su huerto. Observa.
Para calcular el perímetro de la siguiente figura,
podemos descomponerla en un cuadrado y un
rectángulo y, así, determinar las medidas de los
lados que faltan. Luego, sumamos la medida de
sus lados.
4 + 2 + 2 + 2 + 2 + 4 = 16
P = 16 m
2 cm
2 cm
2 cm
2 cm
4 cm
4 cm
3º A 3º B
ORIENTACIONES PARA EL DESARROLLO DE LAS ACTIVIDADES
• Pida a los estudiantes que observen la figura compuesta de la página 162 y
pregúnteles a qué huerto de la ilustración se asemeja. Luego, guíelos para que
expliquen cómo se dedujeron las medidas que no estaban explícitas en el dibujo,
para lo cual deben considerar que la figura ha sido descompuesta en un cua-
drado y un rectángulo, y apoyarse en la cuadrícula. Es importante promover
que los estudiantes concluyan que el perímetro de una figura compuesta por
un cuadrado y un rectángulo no es igual a la suma de los perímetros de cada
polígono, pues es frecuente que cometan el error de agregar al perímetro la
medida de los segmentos interiores con los que descompusieron la figura.
• Para apoyar el desarrollo de la actividad 1, es conveniente dibujar el plano en la
pizarra y responder las preguntas en conjunto con el curso. Una vez desarrollada
la actividad, recuérdeles que el perímetro de la casa corresponde a la medida de
su contorno, sin considerar divisiones internas.
OBJETIVOS DE APRENDIZAJE
Demostrar que comprenden el períme-
tro […] en el contexto de resolución de
problemas.
ACTIVIDAD INICIAL
A partir de la ilustración inicial y de
las preguntas de la sección Comento,
promueva que los alumnos y las alum-
nas describan la forma de cada uno de
los huertos y estimen cuál de ellos tiene
mayor perímetro. Pídales que justifiquen
sus respuestas y que busquen una estra-
tegia para verificar su estimación. Una
forma en que pueden verificar cuál de
los huertos tiene mayor perímetro es
bordeando cada uno con un trozo de
lana, cortar la longitud exacta de lana
que logra bordear por completo cada
huerto y, luego, comparar la longitud
de los trozos.
Actividad
Habilidades que
se desarrollan
Comento,
1, 2
Resolver problemas,
argumentar y comunicar.](https://image.slidesharecdn.com/123112-150514161041-lva1-app6891/85/Didactica-del-profesor-Matematica-206-320.jpg)

































