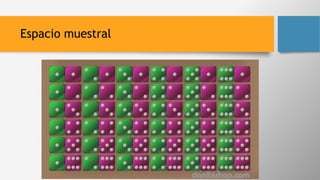
El documento introduce conceptos clave de probabilidad, incluyendo eventos aleatorios, espacio muestral y tasas de probabilidad. Se analizan operaciones con sucesos como la unión e intersección, así como distintos tipos de sucesos y probabilidades condicionadas. También se presenta el famoso 'problema del cumpleaños', que demuestra que es probable que al menos dos personas compartan un cumpleaños en grupos de tamaño relativamente pequeño.

1. INTRODUCCIÓN A LA PROBABILIDAD
2º DE BACHILLERATO CIENCIAS SOCIALES

2. Contenido
- ¿Qué es la probabilidad?
- Conceptos rápidos
- Cálculo de probabilidades
- Unión e intersección de sucesos
- Tipos de sucesos
- Probabilidad condicionada
- Probabilidad compuesta
- El problema final

3. Algunos ejemplos
Si entrásemos en una habitación con 30 personas, ¿apostarías a que
al menos dos personas cumplen años el mismo día? ¿ Con cuantas
personas crees que tendrías a favor la apuesta?
Tiramos un dado, si sale 2,3 o 5 ganas 1 € si sale 4 ganas
2€ y si sale 1 o 6 pierdes 3€ ¿Jugarías a ese juego?

4. ¿QUÉ ES LA PROBABILIDAD?
• La probabilidad es el estudio de la aleatoriedad y la
incertidumbre.
• La probabilidad estudia lo que denominamos sucesos aleatorios.
• Un suceso aleatorio es toda experiencia que dependa del azar
Ejemplos:
Tirar un dado o moneda.
Una partida de póker.
Loteria de Navidad.

5. Conceptos rápidos
• Espacio muestral: Es el conjunto de todos los posibles resultados
de una experiencia aleatoria, lo representaremos por Ω.
• Suceso: Cada uno de los resultados posibles de nuestro
experimento o experiencia aleatoria.
• Suceso elemental: Cada uno de los elementos que forman parte
del espacio muestral.
• Suceso compuesto: Suceso compuesto es cualquier subconjunto
del espacio muestral.

6. Un ejemplo para entender estos conceptos
• Tirada de dos dados

7. Espacio muestral

8. ¿Cómo calculamos probabilidades?
Definición de Laplace (clásica)
La probabilidad de cualquier suceso A ocurra es igual al cociente entre el
número de resultados favorables para que se dé A y el número total de
elementos del espacio muestral Ω. Los sucesos deben ser equiprobables.
𝑃 𝐴 =
𝐶𝑎𝑠𝑜𝑠 𝑓𝑎𝑣𝑜𝑟𝑎𝑏𝑙𝑒𝑠
𝐶𝑎𝑠𝑜𝑠 𝑝𝑜𝑠𝑖𝑏𝑙𝑒𝑠
La probabilidad es un número entre 0 y 1.

9. Ejemplos
• Con un dado calcular la probabilidad de que salga:
Un 6.
Un número par.
Un número mayor que 7.
Un número menor que 7.

10. Ejemplos
• Con dos dados calcula la probabilidad de que salga:
Un doble 5.
Un 6 en al menos un dado.
Un número mayor que 9 entre los dos dados.

11. Espacio muestral

12. Unión de sucesos
Sean A y B dos sucesos:
- La unión de A y B es el suceso formado por los elementos de A y
los de B y se escribe AUB.
- Se lee P(AUB): Probabilidad de que ocurra A o B.

13. Intersección de sucesos
Sean A y B dos sucesos:
- La intersección de A y B es el suceso formado por lo elementos que
comparten A y B y se escribe A⋂B.
- Se lee P(A ⋂ B): Probabilidad de que ocurra A y B.

14. Diagramas de Venn
Una manera de ver visualmente estos conceptos es con los
denominados diagramas de Venn
Https://www.geogebra.org/m/611127
Fórmula que relaciona la probabilidad de AUB y A⋂B
P(AUB) = P(A) + P(B) – P(A⋂B )

15. Ejemplo
Sean : A = Probabilidad de sacar un número par en un dado
B = Probabilidad de sacar un 1 o 2 en un dado
A = {2,4,6}
B = {1,2}
AUB = {1,2,4,6}
A⋂B = {2}

16. Tipos de sucesos I
• Suceso seguro: Un suceso A se dice que es seguro si está formado
por todo el espacio muestral
P (A) = 1
• Suceso imposible: Un suceso A se dice que es imposible si no
contiene ningún elemento del espacio muestral.
P(A) = 0
• Suceso contrario: Sea A un suceso, se denomina suceso contrario a
A y se denota con Ā al suceso que engloba todos los elementos del
espacio muestral menos los que tiene A.
P(Ā) = 1- P(A)

17. Tipos de sucesos II
• Sucesos compatible: Se dice que dos sucesos A y B son compatibles
si tienen algún elemento en común.
• Suceso incompatible: Se dice que dos sucesos A y B son
incompatbles si no tienen ningún elemento en común
• Suceso dependiente: Dos sucesos, A y B, son dependientes cuando
la probabilidad de que suceda A se ve afectada porque haya
sucedido o no B.
• Suceso independiente: Dos sucesos, A y B, son independientes
cuando la probabilidad de que suceda A no se ve afectada porque
haya sucedido B.

18. Ejemplos sucesos
• A = {1,2,3}, B = {3,5,6}
• A = {1,2,3}, B = {5,6}
• A = {Salga un 6 en la primera tirada de un dado}
B = {Salga un 6 en una segunda tirada de un dado}
• A = {Sacar un as de una baraja de póker}
B = {Sacar un as despúes de haber hecho A}

19. Probabilidad condicionada
• Sean A y B dos sucesos.
• Se llama probabilidad del suceso A condicionado a B y se
representa por P(A/B) a la probabilidad del suceso A una vez ha
ocurrido el B.
P(A/B) =
𝑃 𝐴⋂𝐵
𝑃(𝐵)
• Dos sucesos A y B son independientes si P(A/B) = P(A)

20. Ejemplos
• Probabilidad de sacar un 6 en un dado sabiendo que ha salido un 6
en la tirada anterior.
• Probabilidad de haber sacado un 6 en una tirada de dado sabiendo
que ha salido par.

21. Probabilidad compuesta
• Sean A y B dos sucesos sobre el mismo espacio muestral. La
probabilidad de que ocurran los dos es:
• Sucesos independientes:
𝑃 𝐴⋂𝐵 = 𝑃 𝐴 · 𝑃(𝐵)
• Sucesos dependientes:
𝑃 𝐴⋂𝐵 = 𝑃 𝐴 · 𝑃(𝐵/𝐴)

22. Veamoslo con algún ejemplo
• Se tiene una baraja de 40 cartas, se saca una y se vuelve a meter.
¿Cuál es la probabilidad de extraer dos ases?
• Se tiene una baraja de 40 cartas, se extraen dos cartas. ¿Cuál es la
probabilidad de extraer dos ases?

23. Problema del cumpleaños I
• Si entrásemos en una habitación con 30 personas, ¿apostarías a
que al menos dos personas cumplen años el mismo día? ¿ Con
cuantas personas crees que tendrías a favor la apuesta?

24. Problema del cumpleaños II
Conceptos que vamos a usar y que hemos estudiado.
- Regla de Laplace
- Probabilidad de que ocurra lo contrario a un suceso A es 1 – P(A)
- Probabilidad compuesta

25. Problema del cumpleaños III
IDEA
Hallar la probabilidad de que ninguna coincida y luego hacer el
complementario.

26. Problema del cumpleaños IV
• Empezamos con la probabilidad de que el cumpleaños de dos
personas no coincida
𝑃 2 𝑝𝑒𝑟𝑠𝑜𝑛𝑎𝑠 𝑛𝑜 𝑐𝑜𝑖𝑛𝑐𝑖𝑑𝑎𝑛 =
365
365
·
364
365
= 0,9972
Si queremos ver la probabilidad de que coincida el cumpleaños de
dos personas es 1 – 0,9972 = 0,0028. Que ni por asomo se acerca a
nuestro 50%

27. Problema del cumpleaños V
• Ahora vamos a ver la probabilidad de que el cumpleaños de tres
personas no coincida.
𝑃 3 𝑝𝑒𝑟𝑠𝑜𝑛𝑎𝑠 𝑛𝑜 𝑐𝑜𝑖𝑛𝑐𝑖𝑑𝑎𝑛 =
365
365
·
364
365
·
363
365
= 0,9917
La probabilidad de que coincida el cumpleaños de alguna de las 3
personas es 1 – 0,9917 = 0,0083. Todavía no nos vale.

28. Problema del cumpleaños VI
• Función que representa el problema.
Y si la representamos podemos ver cual es la curiosa solución.

29. Problema del cumpleaños VII

30. Problema del cumpleaños VII
• Con n = 23 ya hay un 50,7 % de probabilidad de que dos personas
cumplan años.
• Con n = 60 la probabilidad de que haya dos personas que coincidan
en el día de su cumpleaños ya es de un 99,51%