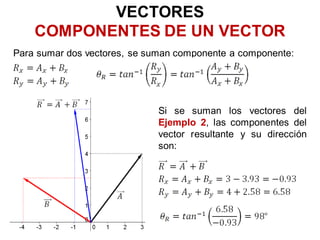
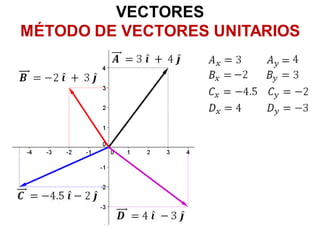
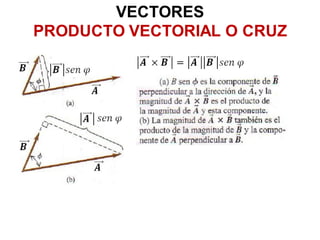
Este documento introduce conceptos básicos sobre vectores, incluyendo métodos para representar y sumar vectores utilizando sus componentes y vectores unitarios, así como definiciones y ejemplos del producto escalar y producto vectorial (o producto cruz) de vectores.