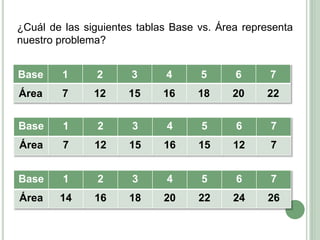
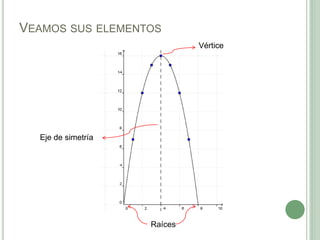
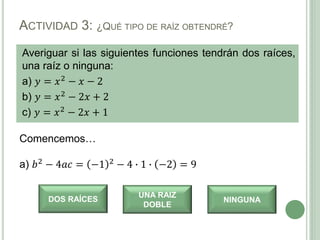
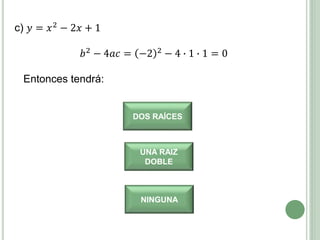
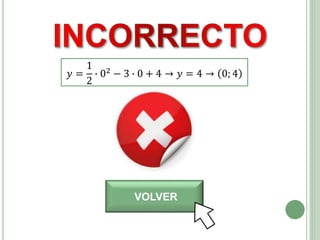
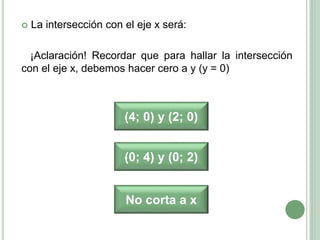
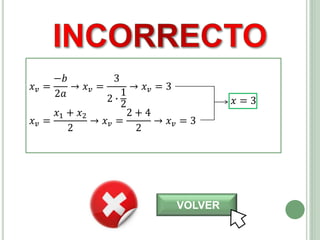
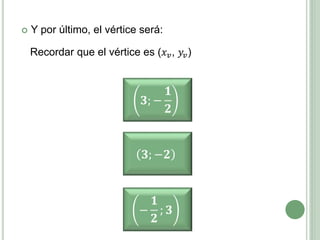
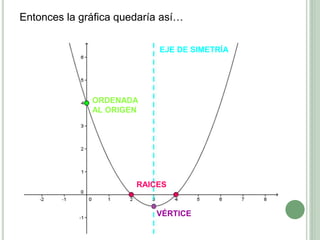
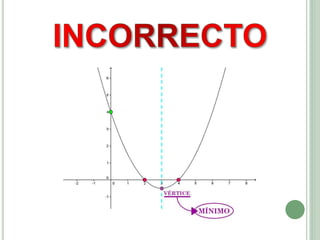
El documento presenta los objetivos, contenidos y actividades de una clase sobre funciones cuadráticas. Los objetivos incluyen reconocer y representar funciones cuadráticas gráfica y analíticamente. Los contenidos cubren la representación gráfica y analítica de funciones cuadráticas, incluyendo elementos como vértice, raíces y eje de simetría. Las actividades guían a los estudiantes en el análisis de estas características a través de ejemplos numéricos y gráficos.