El documento abarca una amplia variedad de temas de álgebra, organizados en capítulos que incluyen exponentes, polinomios, ecuaciones, funciones, logaritmos y matrices. Cada capítulo presenta conceptos teóricos junto con ejercicios prácticos para reforzar el aprendizaje. Los contenidos están dirigidos a estudiantes de cuarto año de secundaria, con un enfoque en el desarrollo de habilidades matemáticas fundamentales.










![Capítulo
14
Colegios
TRILCE Central: 6198-100
Aprende más
1. Relacionar correctamente:
P(x)=2x4+5x2+3x A
Polinomios
idénticos
P(x)=x2+x3+x+5 B
Polinomio
ordenado
P(x;y)=2x2y5+3x3y4 C
Polinomio
completo
P(x;y) ≡ Q(x;y) D
Polinomio
homogéneo
2. Indicar Verdadero (V) o Falso(F) respecto al
polinomio: P(x;y)=xmyn+xm+1yn–1+xm–1yn+2
A. Si: GR(x)=10 → m =9.............................( )
B. Si: GR(y)=12 → n =12............................( )
C. Si: GA=15 → m+n =14.........................( )
D. Si: m=3, n=5 → GA =9.........................( )
3. Completar:
A.
El polinomio: P(x;y)=2x4y5+5x6y3+3x2y7
es un polinomio.....................
B. El polinomio: P(x;y)=x100+2x50+3x10+4
es un polinomio.....................
C. El polinomio: P(x;y)=2x4+5x3+4x2+5x+2
es un polinomio.....................
D. Si los polinomios: ax2+bx+c y mx2+ nx+p
son identicos → a=.....; b=.....; c=.....
4. Dado el polinomio:
P(x;y) = xm+2yn–1 + xm+6yn – xm+4yn+4
Si el G.R.(x) = 20 y el grado absoluto es igual a
40, calcular el G.R.(y).
a) 22 b) 20 c) 18
d) 24 e) 28
5. Indique el grado de "R", sabiendo que:
R(x) = x
n – 1
2 +3x
11 – n
3 + 219 es un polinomio.
a) 1 b) 2 c) 3
d) 4 e) 5
6. En el polinomio:
P(x;y)=4xm+n–2ym–3+8xm+n+5ym–4+7xm+n–6ym+2
Se verifica que la relación entre los grados
relativos de "x" e "y" es 2; y además el menor
exponente de ‘‘y’’ es 3. Hallar su grado absoluto.
a) 15 b) 16 c) 17
d) 18 e) 21
7. El polinomio:
P(x;y;z)=xm–nyp–mzn+6+xm–2nyp+3nzn+4+xm+3nyp–2mzn+2
contiene término independiente para cada una
de sus variables.
Halle: G.A.(P) + G.R.(x) + G.R.(y) + G.R.(z)
a) 38 b) 36 c) 40
d) 24 e) 28
8. Dados los polinomios "P" y "Q" de los que se
conoce:
G.A. PQ
` j
4 = 3
G.A. (P3 ÷ Q) = 4
¿Cuál es el grado de "Q"?
a) 2 b) 4 c) 6
d) 8 e) 10
9. Dado el polinomio homogéneo:
P(x;y)=5x3a+2by4 – x2ayb+7+xa–1ya–3b
Calcular: G.A.(P) + ab
a) 1 b) 2 c) 3
d) 4 e) 5
10. Si el siguiente polinomio de 14 términos es
completo y ordenado:
P(x) = xn+4+...+xa – 1+xa–2+xa–3
Calcular: a + n
a) 3 b) 9 c) -4
d) 16 e) 12
11. Calcular "A + B + C", si:
(x+1)[A(x+2)+B(x–2)–3x]+15x≡(x–2)[3x+C(x+2)]
Se verifica para todo "x".
a) 20 b) 21 c) 22
d) 23 e) 24
12. Si "P(x)" es idénticamente nulo, hallar "a - b" en:
P(x–a) = b(x+2)+a(x+3)+2
2](https://image.slidesharecdn.com/lgebra4-240617025348-2ba3a9a6/85/Algebra_4-pdf-TEMAS-SELECTOS-DE-PREPARACION-14-320.jpg)

![Capítulo
16
Colegios
TRILCE Central: 6198-100
Tú puedes
2
1. Si la expresión: E(a;b)=
x–25
12
y+3
48
a . b es de cuarto grado con respecto a "a" y de sexto grado absoluto, el
valor de (x – y) es:
a) 28 b) 29 c) 31 d) 32 e) 35
2. Dado el polinomio: P(x;y) = 2xa(b–4)
– 3ya2(b – 4)
– (xy)a(b – 4)
+4y4+a(b – 4)
, donde "a" y "b" son números
naturales. Si la suma de los grados absolutos de los términos del polinomio es (a2 + 2)2, el valor de "b"
será:
a) 2 b) 4 c) 6 d) 8 e) 10
3. Si el polinomio: P(x) = (x2+x+3)(a – b)+(x2+x+4) (b – c)+(x2+x+5) (c – a) es idénticamente nulo,
el valor de: [(b + c) ÷ a] es:
a) 1 b) -1 c) 2 d) -2 e) 3
4. Si el polinomio: P(x;y)= 3 xm–2yn–1(x7+y2n–3) es un polinomio homogéneo cuyo grado de homoge-
neidad es 16, hallar "mn".
a) 30 b) 20 c) 35 d) 41 e) 45
5. Un polinomio "P(x)" de tercer grado, cumple con la siguiente condición: P(x) – P(x – 1) ≡ 2x(3x + 2).
Hallar el coeficiente de "x" en el polinomio "P(x)".
a) 1 b) 2 c) 3 d) 4 e) 5
11. Hallar "a + b + p" en:
(aaa
– 2)x5+(bb – 3)x3+(p – 7)≡14x5+24x3+10
12. Se tiene: (a – 4)xy2 – (20 – b)x2y+ax2y ≡ 0
Determinar: ab .
13. Si el polinomio:
P(x) = mxp – 8+nxm–4+pxn+5+qxq – 2
es completo y ordenado en forma descendente,
calcular la suma de coeficientes.
14. Las aulas del colegio TRILCE tienen losetas
de colores: "P", "Q" y "R" de forma cuadrada
(de dimensiones: "a" , "b" y "c" respectiva-
mente); y de colores: "M" y "N" de forma rec-
tangular (de dimensiones: "x", "m" y "c" , "n"
respectivamente) que conforman un área de:
5P+3Q+2R+M+N . ¿Cuál es el área total?
15. El sueldo "S1" y "S2" de dos profesionales
depende del número de semanas "x" que
laboran y está dado por:
S1: (n+1)x5 + 10x2 + (p+1)
S2: 8x5 + (m –2)x2 + 11
Si ambos profesionales trabajan tres semanas y
perciben la misma cantidad, hallar "m+n+p"
y cuál será su sueldo.](https://image.slidesharecdn.com/lgebra4-240617025348-2ba3a9a6/85/Algebra_4-pdf-TEMAS-SELECTOS-DE-PREPARACION-16-320.jpg)


![Capítulo
20
Colegios
TRILCE Central: 6198-100
Aprende más
1. Relacionar correctamente:
2(x2+y2) A (x+y)2+(x – y)2
4xy B x3+y3+z3=3xyz
xy=6 C (x+y)2 – (x – y)2
x+y+z=0 D (x – 2)2+(y – 3)2=0
2. Indicar Verdadero (V) o Falso (F) respecto a los
productos notables:
A. (x – y)3 = x3 – y3 – 3 x y (x – y).............( )
B. (x – y )(x+ y )=x – y ........................( )
C. (x – 2)4 (x + 2)3 = (x2 – 4)7 ...................( )
D. x2 + y2+ z2=2(xy+xz+yz)...................( )
3. Completar:
A. (x + y)2 +2(x + y) + 1= ..........................
B. ( x + y )( x – y ) =.............................
C. Si: x+y+z=0 → x3+y3+z3 ......................
D. (x + y)3 = .................................................
4. Reducir:
P = ( ) ( – )
7 3 7 3
2 2
+ +
a) 2 b) 10 c) 20
d) 40 e) 16
5. Si: a + b = 4 ∧ ab = 1
hallar: S = a3 + b3
a) 52 b) 51 c) 50
d) 49 e) 60
6. Si:
y
x
x
y
+ = 2; calcular:
x y
x y xy
2
8 3
5 5
4 4
+
+
a)
11
3 b)
3
11 c) 1
d) 2 e)
11
1
7. Hallar el valor numérico de:
P(x) = (x + 1)(x – 1)(x4 + x2 + 1)
Para: x = –
4 15 4 15
+ +
a) 666 b) 444 c) 111
d) 999 e) 333
8. Hallar “n”:
( )( )( )( )
13 85 7 6 7 6 6
4 4 8 8 16
+ + +
8
= 7n–3
a) 4 b) 6 c) 7
d) 8 e) 5
9. Hallar el valor numérico de:
(x+1)(x2 – x+1)(x6 – x3+1)(x9 – 1) – x18+1
para: x = 2012
a) 0 b) 2012 c) 201218
d) 1 e) 2012!
10. Si: a + b + c = 0, calcular:
M =
( )( )( )
( ) ( ) ( )
a b b c c a
a b b c c a
3 3 3
+ + +
+ + + + +
a) 3 b) –3 c) 4
d) –2 e) 16
11. Hallar el valor numérico de:
E = (a2 – b2) [(a2 + b2)2 – a2b2]
Para: a3 = 2 +1 ∧ b3 = 2 – 1
a) 9 b) 2 c) 4 2
d) 6 e) 1
12. Si: x2 – 5 x + 1 = 0; calcular:
M = x4 + x2 +
x
1
2
+
x
1
4
a) 10 b) 11 c) 12
d) 13 e) 14
13. Si: x = 8
4
∧ y = 2
4
Calcular:
( ) – ( – )
x y
x y x y
2 2
4 4
+
+
= G
1
2
a) 2 b) 4 c) 3
d) 3 2 e) 2 2
3](https://image.slidesharecdn.com/lgebra4-240617025348-2ba3a9a6/85/Algebra_4-pdf-TEMAS-SELECTOS-DE-PREPARACION-20-320.jpg)



![Álgebra
25
www.trilce.edu.pe Cuarto año de secundaria
Aplica lo comprendido
Saberes previos
1. Efectuar:
a)
x
x
9
45
5
25
=......... b)
x
x
4
12
2
6
=.........
c) .
x
x x
7
56
12
13 6
=......... d) .
x
x x
9
72
8
3 6
=.........
2. Si: P(x) = 5x2 +3x + 1, calcular:
• P(2) = ________ • P(–1) = _________
• P(0) = ________ • P(1) = _________
3. Si: P(x) = 3x3 + 6x4 + 4x2 + 3x + 2, completar:
• Variable: ................................
• Grado del polinomio: ................................
• Coeficientes: ................................
• Coeficiente principal: ................................
• Término independiente: ............................
4. Si: P(x) = –5x +2x4 + 3x2 + 1, entonces:
• Completar el polinomio: .............................
• Ordenar crecientemente:.............................
• Ordenar decrecientemente:.........................
• Término independiente: .............................
• Suma de coeficientes:..................................
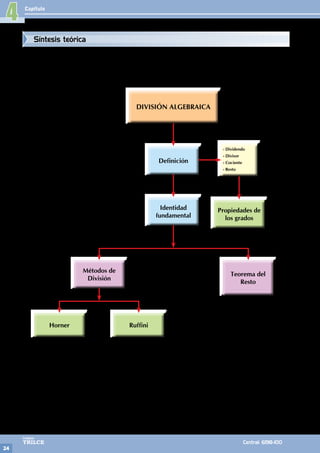
5. Identificar en la siguiente división:
4x2+8x+9 x+1
3x+8 4x+1
• Dividendo: .................
• Divisor:......................
• Cociente:................
• Residuo: ................
1. Relacionar correctamente:
D(x)=d(x)q(x)+R(x) A R(x)=0
Grado[D] – Grado[d] B
Identidad
fundamental
de la división
División exacta C Grado[R]máx
Grado[d] – 1 D Grado[q]
2. Indicar Verdadero (V) o Falso(F) respecto a la
división:
–
x x
x x x x
5 1
12 11 3 6
2
4 3 5
+
+ + + +
A. El grado del polinomio dividendo es 5.....( )
B. El grado del polinomio divisor es 2
.............................................................( )
C. El grado del polinomio cociente es 2.....( )
D. El grado máximo del polinomio residuo es
1 ..........................................................( )
3. De la división, completar:
–
–
x x
x x x x
2 3 5
2 3 9 15
2
4 3 2
+
+ + +
Cociente: q(x) =
Residuo: R(x) =
4. De la división, hallar el resto:
–
–
x
x x x
1
4 6 2 1
8 4 2
+ +
5. De la división, hallar el resto:
–
–
x
x x
1
2 1
50
100 50 +](https://image.slidesharecdn.com/lgebra4-240617025348-2ba3a9a6/85/Algebra_4-pdf-TEMAS-SELECTOS-DE-PREPARACION-25-320.jpg)



































![Álgebra
69
www.trilce.edu.pe Cuarto año de secundaria
Aprende más
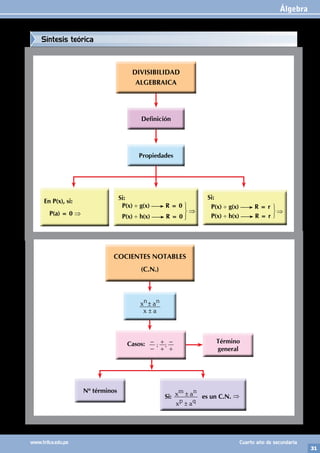
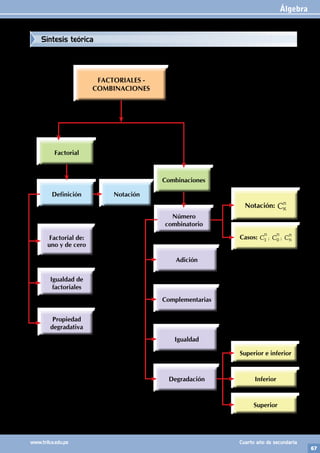
1. Relacionar correctamente:
C
7
3 A 41
C
n
k +C
n
k+1 B !( – )!
!
k n k
n
C
7
3 +C
4
2 C C
n+1
k+1
C
n
k D
3
7 C
6
2
2. Indicar Verdadero (V) o Falso (F) respecto al
factorial y número combinatorio:
A. Si: M=
!
!
29
31 → M=930 .........................( )
B. C
10
1 + C
10
2 = C
11
2 ................................... ( )
C. C
4
0 + C
4
1 + C
5
2 = C
6
4 .........................( )
D. Si: E=
! !
!
49 50
51
+
→ E=50! .................... ( )
3. Completar:
A. Si: (5x – 2)! =120 → x =
B. Si: (n – 9)! =1→ n =........ ; ........
C. Si: C
x
3 = C
x
4 → x=........
D. Si: M=C
24
0 +C
24
1 +C
25
2 → M=
4. Si:
A =
! !
! ! !
6 7
6 7 8
+
+ +
B =
! !
!
69 70
71
+
Calcular "A.B"
a) 56 b) 560 c) 65
d) 650 e) 1
5. Calcule el valor de "x", si:
( )! ( )!
( )!( )!
x x
x x
6 5 5
5 11
+ + +
+ +
= 20!
a) 8 b) 9 c) 10
d) 11 e) 12
6. Indique la suma de los valores de "x" que
verifican la ecuación:
C
35
x2 = C
35
2x
a) 4 b) 5 c) 6
d) 7 e) 8
7. Sabiendo que: 3C
77
7k = 11C
76
7k–1 ; k ∈ +,
Calcular:
!
( !)!
k
k
a) 1 b) 20 c) 120
d) 160 e) 180
8. Reducir: A =
!
!– !
!
!– !
!
!– !
9
11 10
8
10 9
7
9 8
+ + +...
a) 380 b) 385 c) 386
d) 387 e) 400
9. Si: A =
! ( – )!
( !)–( – )( – )!
n n
n n n
1
2 1 1
+
, n ∈ +.
Entonces podemos afirmar que:
a) A < 0 b) A > 2 c) A=1
d) A ∉ e) A<1
10. Calcular el valor de "n" en:
1 + 2.2! + 3.3! + ... + n.n! = 719
a) 5 b) 6 c) 7
d) 8 e) 9
11. Hallar la suma de todas las soluciones de:
[C
x
2]
[C
x
3]
= 36x – 2
a) 1 b) 3 c) 4
d) 6 e) 7
12. Hallar "x" en:
1024.(x – 1)![1.3.5.7....(2x – 3)] = (2x – 2)!
a) 8 b) 9 c) 10
d) 11 e) 12
13. Hallar "a+b" si:
C
a+3
10 + C
a+1
7 + 2C
a+1
8 + C
a+1
9 = C
b+2
b–3
a) 20 b) 22 c) 24
d) 26 e) 28](https://image.slidesharecdn.com/lgebra4-240617025348-2ba3a9a6/85/Algebra_4-pdf-TEMAS-SELECTOS-DE-PREPARACION-69-320.jpg)
!
9. Resolver:
! ( )!
! .( – )! !–
y y
y y
y
y
1
2 1 23
+ +
+
=
10. Resolver:
1.1! + 2.2! + 3.3! + ... + x.x! = 40 319
11. Determinar: x+y, si:
C C C
x
x
x
x
x
y
5
1
5
3
+ =
+
+
+
+
12. Simplificar:
( ! !)( ! !)( ! !)..." "
( ! ! !)( ! ! !)( ! ! !)..." "
n factores
n factores
1 2 2 3 3 4
1 2 3 2 3 4 3 4 5
+ + +
+ + + + + +
13. Hallar "x":
C
x
0 + C
x
1 + C
x
2 + C
x
3 = –
x x
6
6 3
3
+ ; x ∈ +
11](https://image.slidesharecdn.com/lgebra4-240617025348-2ba3a9a6/85/Algebra_4-pdf-TEMAS-SELECTOS-DE-PREPARACION-70-320.jpg)









![Álgebra
83
www.trilce.edu.pe Cuarto año de secundaria
Tú puedes
1. Sea "z" un número complejo que satisface:
–
z
z
1
1
+ = 1 ; entonces:
a) Re(z)>0 b) Re(z) ≤ 0 c) Im(z) ≥ 0
d) "z" es un número real. e) "z" es un número imaginario puro.
2. Si: a bi
+
3
=m+ni ; {a; b; m; n} ⊂ R, i2 = –1. Calcular: –
m
a
n
b
1 1
3 3
+
c c
m m
a) 3i b) 1 c) –1 d) –3i e) 3
3. Sean: z1, z2 ∈ C; reducir: ( . ) ( . )
– –
Re Re
z z z z
z z z z
1 2 1 2
1 2 1 2
+
+
2 2
a) 1 b)
2
1 c) 2 d) 3 e)
3
1
4. Efectuar: ( ) ( ) ( ) ( )
m nw n mw m nw n mw mn
2
2 2 2 2 2 2
+ + + + + + + +
Si: n > m; w = 1
3
a) m + n b) m – n c) n – m d) 2n – m e) 2m – n
5. Sabiendo que "z1" y "z2" representan un número real puro e imaginario puro respectivamente, hallar
el valor de: R = a – b; ab ≠ 0
Donde: z1 =
– –
a b i
a b i
3
2
+ + ; z2 =
–
( )
a bi
a b i
8
+ +
; a ∧ b ∈
a) 30 b) –3 c) –60 d) 10 e) 24
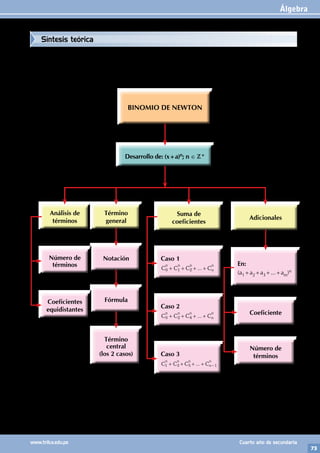
13. Indique la parte imaginaria del complejo
definido por:
Z=(1+2i)2+(1+3i)2+(1+4i)2+...+[1+(n+1)i]2
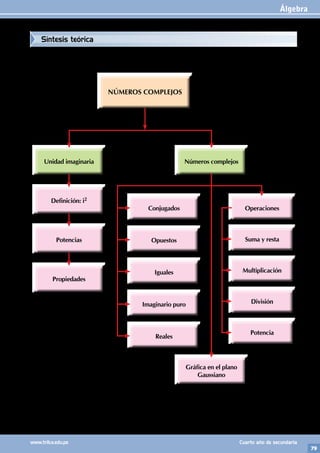
14. Calcular la suma de los 40 primeros términos
de una sucesión, donde el término general está
definido por: Tn=nin ; n ∈ *,siendo: i = –1 .
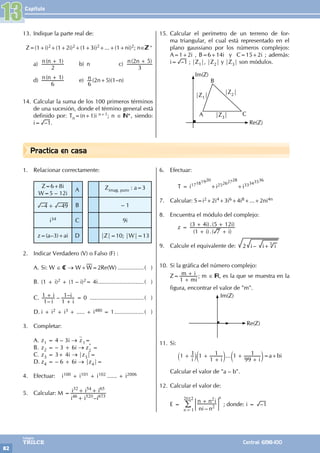
15. Calcular el perímetro de un terreno de forma
triangular, el cual está representado en el plano
gaussiano por los números complejos : A=2+i,
B=10+7i y C=18+i; además : i = –1 ;
|Z1| , |Z2| y |Z3| son módulos.
z1 z2
z3
A
B
C
1m(z)
RE(z)](https://image.slidesharecdn.com/lgebra4-240617025348-2ba3a9a6/85/Algebra_4-pdf-TEMAS-SELECTOS-DE-PREPARACION-83-320.jpg)


![Álgebra
87
www.trilce.edu.pe Cuarto año de secundaria
Aprende más
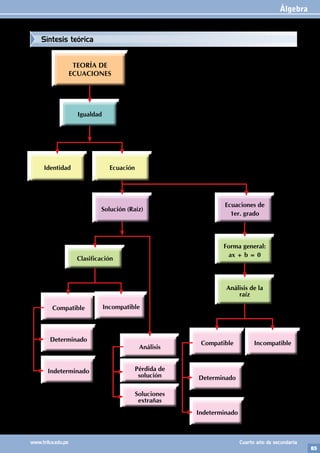
1. Relacionar correctamente, a partir de la ecua-
ción lineal: ax+b=0
t
a≠0∧b∈ ⇒x=–
a
b A
Compatible
indeterminada
a=0;b≠0⇒0x=–b B
Si: n=2; a≠0
⇒Ecuación lineal
x+axn–1=n C
Compatible
determinada
a=0;b=0⇒0x=0 D Incompatible
2. Indicar Verdadero (V) o Falso (F):
A. Al resolver: 2x + 3x – 30 = 3x + 30; el
valor de "x" es 30.....................................( )
B. Al resolver: 2-[2–x–(–x)]=x+2; el valor de
"x" es 2 ...................................................( )
C. Al resolver: 5(x - 3)=4( 3 – x ); el valor de
"x" es 3 ...................................................( )
D. Al resolver: x+ x x
2 3
+ =44 ; el valor de "x"
es 24 .......................................................( )
3. Completar las siguientes proposiciones:
A. La igualdad: 4x+1=x+7 es una acuación
compatible ............
B. La igualdad: 9x+5=5+9x es una ecuación
compatible ................
C. Al resolver:
– –
x x
3
1 1
3
1
+ = + x – 2; la
ecuación es.............................
D. Si la raíz de la ecuación;
ax+3= x
7
2 31
+ es: x = 2; el valor de "a" es
.......
4. Resuelva: – – –
x x x
2
5 2
3
3 4
4
7 5
+ = – 1
a)
2
1 b)
3
1 c) –
3
1
d) 3 e) – 2
5. Resolver: x x x
3
2
5
1
2
+ + + = +2
a) 34 b) 17 c) 33
d) 18 e) – 17
6. Calcule el valor de "x" en:
– – – – –
x x x x x
2
5
5
7
2
4 5 4
5
8 5
2
11 3
+ = +
a) 0 b) – 1 c) 1
d) 2 e)
2
1
7. Resuelva: x – – 3– –
x x
5
3 2
3
2 5
=
a) 0 b) 1 c) 2
d) 4 e) 16
8. Resuelva en "x".
(x + a2) (x + b2) = (x + ab)2 ; a ≠ b
a) {0} b) {1} c) {6}
d) {a} e) {ab}
9. Resuelva en "x": – –
b
x a
a
x b
+ =2
a) {a+b} b) {b–a} c) {a–b}
d) {a} e) {b}
10. Calcule "x" en: x x x x
3 35 15 63
+ + + =6
a)
2
27 b)
2
17 c)
2
37
d)
2
7 e) 1
11. Resuelva: –
x x x
32
17
56
7
51
2
+ + + + =3
a) {49} b) {32} c) {51}
d) {
9
7 } e) {45}
12. Resolver en "x": – –
b
a
x
a
a
b
x
b
1 1 1
+ =
` c
j m
a) a+b b) ab c) a – b
d) 1 e) a2+ab+1
13. Indicar el valor de "x" en:
– – –
bc
x a
ca
x b
ab
x c
a b c
2 1 1 1
+ + = + +
c m
a)
a b c
1 1 1
+ + b) a+b+c c) abc
d) a2+b2+c2 e) a+b – c](https://image.slidesharecdn.com/lgebra4-240617025348-2ba3a9a6/85/Algebra_4-pdf-TEMAS-SELECTOS-DE-PREPARACION-87-320.jpg)
![Capítulo
88
Colegios
TRILCE Central: 6198-100
Practica en casa
1. Relacionar correctamente, a partir de la
ecuación lineal: mx+n=0
m≠0; n∈ ; n
x=–
m
n A Incompatible
m=0; n ≠ 0
⇒0x=–n
B
Si: n=2; m ≠ 0
⇒Ecuación lineal
x+mxn–1=n C
Compatible
indeterminada
m=0 ; n=0
⇒ 0x=0
D
Compatible
determinada
2. Indicar Verdadero (V) o Falso (F):
A. Al resolver: 2x+3x – 30=3x+30; el valor
de "x" es 30.............................................( )
B. Al resolver: 6–[6–x–(–x)]=x+6; el valor de
"x" es 2...................................................( )
C. Al resolver:5(x – 9)=4( 9 – x ); el valor de
"x" es 9 ..................................................( )
D. Al resolver: x+ x x
4 5
+ =58; el valor de "x"
es 40.......................................................( )
3. Completar las siguientes proposiciones:
A. La ecuación de primer grado se llama
también .............................
B. La igualdad: 7x+4=4+7x es una ecuación
compatible .........................
C. Al resolver:
– –
x x
5
1 5
5
1
+ = +x ; la ecuación
es .....................
D. Si la raíz de la ecuación; ax+3 = x
25
2 33
+
es: x = 1; el valor de "a" es .............
4. Resolver: – –
x x
4
2
2
4
+ =2
5. Resolver: – –
x x
7
3 1
3
2 1
+ =x
6. Resolver: –
x x
3
2
5
1
4
3
3
6
+ =
c c
m m
7. Resolver: x – (5x – 1) – – x
10
7 5 =1
8. Resolver: – – – –
x x x
4
1
5
7
3
1
4
7
2
1
3
7
+
c ` c
m j m=0
9. Resolver: – –
b
x a
a
x b
+ =2 ; a ≠ b
10. Dar el C.S. de la ecuación:
.
...
.
x x x x
5 45 9 13 21 25
+ + + + =6
11. Resolver:
– – –
x x x
15
32
4
51
13
34
+ + =1
14. Mathías decide repartir 100 soles entre tres
personas, de manera que la primera reciba 5
soles más que la segunda, y que esta reciba
10 soles más que la tercera. ¿Cuánto recibe la
tercera persona?
15. En cierto lugar del país, la temperatura en
inviernodesciendemedianteelcomportamiento
lineal: TF = T0 – t
2
3
Donde: Tf : Temperatura final (°C)
T0 : Temperatura inicial (°C)
Dt : Variación del tiempo en horas
Si a las nueve de la noche la temperatura era
de 8°C, ¿a qué hora la temperatura habrá
descendido 2°C?
14](https://image.slidesharecdn.com/lgebra4-240617025348-2ba3a9a6/85/Algebra_4-pdf-TEMAS-SELECTOS-DE-PREPARACION-88-320.jpg)














![Capítulo
106
Colegios
TRILCE Central: 6198-100
Practica en casa
16. Siendo "x1" y "x2" raíces de la ecuación:
x2 – 8x – 12 = 0
calcular: (x1 + 1)–1 + (x2 + 1)–1
a)
5
8 b)
21
10 c) –
3
10
d)
15
2 e) – 5
17. Hallar el valor de “k” para el cual la ecuación:
x2 + 2(k + 2)x + 9k = 0 tiene raíces iguales.
Indique el mayor valor.
a) 4 b) 2 c) – 4
d) – 1 e) 3
18. Dada la ecuación: 5x2+7x+3=0, determinar
la ecuación de segundo grado que tiene por
raíces las inversas de las raíces de la ecuación
dada.
a) x2+7x+5=0 b) x2+2x – 3=0
c) 2x2 – 7x+3=0 d) x2+5x+7=0
e) 3x2+7x+5=0
19. Si "x1", "x2" y "x3" son raíces de:
x3 – 6x2+11x – 6=0
Calcular: (x1x2x3) ÷ (x1 + x2 + x3)
a)
2
1 b) – 1 c) 1
d)
5
6 e)
3
11
20. Simplificar:
–
( )
i i
i i
2 8
9 4
3 6
+
= G
2
; i 1
= -
a) 8 b) – 8 c) 4
d) – 4 e) 2
17
1. El término central en la expansión de:
P(x)=(x4+xn)14 ; es de grado 49; hallar "n".
2. Hallar "x" en la ecuación:
( – )!
( – )!–
x
x
4 2
3 4 2
+
= 2
3. De la ecuación:
C
a+1
a +C
a+2
a+1+C
a+3
a+2+...+C
2a
2a–1 =126
Obtener el valor de: M= a
5 4
+
4. Calcular la posición del término en el desarro-
llo de: ax
x
y
2
3
2
+
c m
4
, x ≠ 0, que adopta la forma:
24xnyn.
5. Efectuar:
– – – –
16 2 63 12 2 35 8 2 15 4 12
+ + +
6. Efectuar:
–
5 2 6
1
7 2 10
3
8 2 15
2
+ +
+
+
7. Resolver:
16x–[3x – (6–9x)] = 30x+[–(3x+2) – (x+3)]
8. Formar la ecuación de segundo grado, si sus
raíces son:
x1 = 3+ 5
x2 = 3 – 5
9. Simplificar: –
i i i
i i i
2 4 4
5 4 7
3 13 28
15 6 25
+
+
+
10. Hallar "m", si las raíces de la ecuación son
iguales: x2 – 2 (1+3m)x+7(3+2m)=0; (m>0)](https://image.slidesharecdn.com/lgebra4-240617025348-2ba3a9a6/85/Algebra_4-pdf-TEMAS-SELECTOS-DE-PREPARACION-106-320.jpg)


![Álgebra
109
www.trilce.edu.pe Cuarto año de secundaria
Adición
Multiplicación por un
escalar
Multiplicación de
matrices
A = [aij]m×n
B = [bij]m×n
A = [aij]m×n
"k" es un número real
A = [aij]m×n
B = [bij]n×p
A + B = [aij +bij]m×n kA = [kaij]m×n
MATRICES
Arreglo rectangular de números
ordenados en filas y columnas
A × B = C
A m × n . B n × p = C m × p
Síntesis teórica](https://image.slidesharecdn.com/lgebra4-240617025348-2ba3a9a6/85/Algebra_4-pdf-TEMAS-SELECTOS-DE-PREPARACION-109-320.jpg)
![Capítulo
110
Colegios
TRILCE Central: 6198-100
Aplica lo comprendido
Saberes previos
1. Relacionar correctamente dada la siguiente
matriz:
A =
4
8
3
7
e o
a11+a12 A 11
Traz(A) B 10
a11+a21 C 7
a12+a22 D 12
2. Indicar verdadero (V) o falso (F) respecto a la
siguiente matriz:
B =
2
9
1
5
e o
• Su traza es 10........................................( )
• La traza de su transpuesta es 7...............( )
• Es de orden 4........................................( )
• a11 + a22 = 8 .......................................( )
3. Completar correctamente a partir de la matriz:
C =
4
0
1
3
e o
• Ct =
• 2C =
• C2 =
4. Calcular "abcd" si:
–
–
–
–
a
b
c
d
3
1
2
0
5
4
1
1
=
e e e
o o o
5. Calcular "x+y+z+w", si:
–
–
2
–
–
x
y
z
w
1
2
1
3
0
1
2
1
=
e e e
o o o
1. Resolver:
• –
x
2
3 1= x + 5 → x = ___________
• x x
3 2 6
5
+ = → x = ___________
• (x+1)(x+3)=x2 → x = ___________
2. Siendo: A =
4
3
8
1
5
6
e o
Completar:
• Elementos de la fila 1: __________________
• Elementos de la fila 2: __________________
• Elementos de la columna 1: _____________
• Elementos de la columna 2: _____________
• Elementos de la columna 3: _____________
3. Resolver:
• x+2[x+2(x+2)] = 6 → x =
• 3 – {x – (1 – x)} = x → x =
4. Si:
a
b
c
d
a c
b d
+ =
+
+
e e e
o o o
Calcular "mn", en:
m
n
1
2
3
4
+ =
e e e
o o o
5. Si: (a b) – (c d) = (a – c b – d)
Calcular "x+y", en: (7 4) – (1 3) = (x y)
18](https://image.slidesharecdn.com/lgebra4-240617025348-2ba3a9a6/85/Algebra_4-pdf-TEMAS-SELECTOS-DE-PREPARACION-110-320.jpg)


![Álgebra
113
www.trilce.edu.pe Cuarto año de secundaria
Practica en casa
1. Relacionar correctamente las tablas respecto a
la matriz.
A =
6
2
4
5
e o
Traz(A) A 6
a21+a12 B –22
Traz(–At) C 11
a21a12 – a11a22 D –11
2. Indicar verdadero (V) o falso (F) según
corresponda, dada la matriz:
B =
3
7
5
4
e o
• b11b22 = b21+b12 ...................................( )
• La traza de "B" equivale a 12...................( )
• El orden de la matriz es 2×2....................( )
3. Dada la siguiente matriz:
A =
3
0
0
4
2
0
5
3
1
f p
Completar:
• "A" se denomina matriz triangular _________
• El valor de su traza es: __________________
• La suma de sus elementos es: ____________
4. Sean las matrices:
A =
–
–
x y x
x y
2
3
= G ; B =
y
2
3
4
4
+
= G
Hallar "xy", si: A = B.
5. Luego de escribir explícitamente la matriz,
hallar "Traz(B)", si: B = [bij]3x3 / bij = 2i – j
6. Sean las matrices:
A =
–
x y x
y
3
1
e o ; B =
–
–
y
x
2
1
6
6
e o ; C =
– –
4
2
8
3
e o
Si: A = B, hallar: 3A + 2C.
7. Sean las matrices:
A =
2
1
3
2
e o ; B =
–
1
4
2
1
3
2
e o
Hallar "AB".
8. Hallar "x" al resolver el sistema de matrices x,y
x y A
x y B
2
2 3
- =
+ =
)
Donde: x ; y ∈ k2x2
A =
–
6
7
3
4
e o ; B =
–
12
7
8
8
e o
9. Dados:
A =
–
2
1
1
2
e o ; B =
–
5
0
1
1
e o
Si: P(x; y) = x+y+2, hallar: P(A; B)
10. Dada la matriz:
A =
–
– –
x y
y x
x y
x y
x
x y
2
3
9
3
8
2
2
7
+
+
> H
Donde se cumple:
Traz(A) = 16 ; a21+a31=a22+1
Calcular "xy".
11. Calcular "xy", si las matrices:
A =
12
1
3
4
e o ; B =
–
x
y
21
16
48
1
e o
verifican: A2 = B
12. Hallar la matriz "x" que resuelve:
x
1
2
3
1
11
7
4
3
=
e e
o o
Indicar como respuesta la suma de sus
elementos.
13. Sea: B = [bij]3x3 ; si: bij = 2i – (–2)j
Indique la traza de "B".](https://image.slidesharecdn.com/lgebra4-240617025348-2ba3a9a6/85/Algebra_4-pdf-TEMAS-SELECTOS-DE-PREPARACION-113-320.jpg)


![Capítulo
116
Colegios
TRILCE Central: 6198-100
19
Orden 1 Orden 2
Propiedades
• |A| = |At| • |AB| = |A||B| • B
A
B
A
= ; B ≠ 0
• |kA| =kn |A|
k : Es un escalar ; A : una matriz de orden "n"
Orden 3
A = [a11] A =
a11 a12
a21 a22
A =
a11 a12 a13
a21 a22 a23
a31 a32 a33
|A| = a11 |A| = a11 a22 –a21 a12
|A| = (a11a22 a33 +a12 a23a31+a21a32a13)
– (a31a22a13+a21a12a33+a32a23a11)
DETERMINANTES
|A| o Det (A)
"A" una matriz cuadrada
Síntesis teórica](https://image.slidesharecdn.com/lgebra4-240617025348-2ba3a9a6/85/Algebra_4-pdf-TEMAS-SELECTOS-DE-PREPARACION-116-320.jpg)





![Álgebra
123
www.trilce.edu.pe Cuarto año de secundaria
Aplica lo comprendido
Saberes previos
1. Resolver:
• –
x x
3
4
2
5
+ = → x =
• – –
x x
2
2 1
3
3 1
+ = x → x =
2. Resolver:
• –
x 4 = 5 → x =
• –
x 1
3
= 2 → x =
3. Resolver:
•
x x
1
1
1
6
5
+
+
= → CS =
• –
x x
2
1
3
1
6
1
+ +
= → CS =
4. Resolver:
• 4x2 – 49 = 0 → C.S. = { ; }
• 9x2 – 1 = 0 → C.S. = { ; }
5. Resolver:
• x2 – x = 20 → C.S. = { ; }
• x2 + x = 30→ C.S. = { ; }
1. Resolver:
–
x y
x y
9
1
+ =
=
) A xy=15
–
x y
x y
2 11
2 1
+ =
=
) B x+y=5
x y
x y
2 11
2 4
+ =
+ =
) C xy=20
x y
x y
3 3
3 13
+ =
+ =
) D x+y=4
2. Indicar verdadero (V) o falso (F) dado el sistema:
x y
x y
4 5 2
5 6 1
+ =
+ =
)
• Es compatible indeterminado................( )
• No tiene solución..................................( )
• Es compatible determinado...................( )
• Se cumple que: x+y=–1......................( )
3. Completar respecto al sistema:
mx y
x my
1
1
+ =
+ =
)
• Si: m=1, el sistema es .............................
• Si: m=–1, el sistema es ...........................
• Si: m=2, el sistema es .............................
4. Indicar el valor de "x+y" del sistema:
x y
x y
7 4 3
5 3 1
+ =
+ =
)
5. Calcular "x" al resolver el sistema:
x y
x y
4 3 3
2 6 3
+ =
+ =
Z
[
]
]
]](https://image.slidesharecdn.com/lgebra4-240617025348-2ba3a9a6/85/Algebra_4-pdf-TEMAS-SELECTOS-DE-PREPARACION-123-320.jpg)
![Capítulo
124
Colegios
TRILCE Central: 6198-100
Aprende más
1. Relacionar al sistema: ax by c
mx ny p
+ =
+ =
)
Sistema incompati-
ble
A
m
a
n
b
p
c
= =
Sistema compatible
determinado
B
m
a
n
b
!
Sistema compatible
indeterminado
C
m
a
n
b
p
c
!
=
2. Indicar verdadero (V) o falso (F) según
corresponda:
• El sistema incompatible tiene infinitas
soluciones............................................. ( )
• El sistema indeterminado no tiene solución
............................................................. ( )
• Todo sistema inconsistente es incompati-
ble ................................................ ( )
• Todo sistema indeterminado es inconsis-
tente ................................................ ( )
3. Completar:
• Un sistema lineal es de ............... grado.
• Se usa los determinantes para resolver un
sistema lineal usando la regla de .................
• Las ecuaciones de un sistema lineal,
gráficamente representan .......... en el
plano cartesiano.
4. Calcular "xy" al resolver:
x y
x y
2 3 8
4 5 14
+ =
+ =
)
a) 1 b) 2 c) 3
d) 4 e) 5
5. Resolver:
–
x y
x y
7 3
2
4
+ =
=
*
Indicando el valor de "x+y"
a) 3 b) 7 c) 10
d) 12 e) 15
6. Calcular "x – y" al resolver:
1 2
6
7
2 1
3
4
x y
x y
+ =
+ =
Z
[
]
]
]
a) 2 b) 3 c) 1
d) –1 e) –2
7. Calcular "x" al resolver:
( ) ( )
( ) ( )
x y
x y
2 3 3 2 18
3 4 4 3 36
+ + + =
+ + + =
)
a) –12 b) –6 c) 0
d) 6 e) 12
8. Calcular "a" en el sistema incompatible:
( )
( )
a x ay
x a y
2 2 7
5 3 8
+ + =
+ + =
)
a) 2 b) 4 c) 6
d) 8 e) 10
9. Indicar el valor de "m" en el sistema
indeterminado:
–
–
mx y
x my
1
1
+ =
=
)
a) 1 b) – 1 c) ±1
d) 2 e) – 2
10. Calcular "m" para que el siguiente sistema sea
inconsistente:
( – )
( – )
m x y
x m y
3 3 5
2 2 7
+ =
+ =
)
a) 1 b) 3 c) 5
d) 7 e) 9
11. Calcular "m" para que el siguiente sistema tenga
solución única:
x y
x y
x my
2 3 13
4 5 23
6 18
+ =
+ =
+ =
Z
[
]
]
]
a) 2 b) 4 c) 6
d) 7 e) 8
20](https://image.slidesharecdn.com/lgebra4-240617025348-2ba3a9a6/85/Algebra_4-pdf-TEMAS-SELECTOS-DE-PREPARACION-124-320.jpg)
![Álgebra
125
www.trilce.edu.pe Cuarto año de secundaria
Practica en casa
12. Calcular "a" para que el sistema siguiente sea
compatible determinado:
– –
–
–
x y
x y
x ay
3 1
5 7 11
9 35
=
=
=
Z
[
]
]
]
a) 3 b) 5 c) 7
d) 9 e) 11
13. Calcular "6x" del sistema:
–
–
–
x y x y
x y x y
3
2
3
4 3
3
2
3
4 1
+
+ =
+
=
Z
[
]
]
]
a) 1 b) 3 c) 5
d) 7 e) 9
14. Edú, Mathías y Carla pueden soldar 37 metros
lineales por hora cuando trabajan juntos. Edú
y Mathías juntos pueden soldar 22 metros
lineales por hora, mientras que Edú y Carla
juntos pueden soldar 25 metros lineales por
hora. ¿Cuántos metros lineales por hora pueden
soldar cada uno de ellos por separado?
15. Un ciclista tiene un promedio a distintas
velocidades cuesta arriba, en terreno llano y
cuesta abajo. Él estima el siguiente kilometraje
para sus tres últimos recorridos:
km cuesta
arriba
km terreno
llano
km cuesta
abajo
Tiempo
total (horas)
2 15 5 1,5
6 9 1 1,4
8 3 8 1,6
¿Cuáles son las velocidades promedio cuesta
arriba, en terreno llano y cuesta abajo?
1. Relacionar correctamente:
x y
x y
2 3 4
4 6 8
+ =
+ =
) A
Compatible
determinado
x y
x y
10 15 30
2 3 5
+ =
+ =
) B
Comtapible
Indeterminado
x y
x y
2 3 5
3 2 5
+ =
+ =
) C Incompatible
2. Indicar verdadero (V) o falso (F) según corres-
ponda:
• Todo sistema incompatible es inconsistente
...............................................................( )
• Todo sistema inconsistente es indetermina-
do ..........................................................( )
• Un sistema compatible puede tener dos
soluciones............................................... ( )
• El sistema incompatible no tiene solución.... ( )
3. Dado el sistema:
ax by c
bx ay d
+ =
+ =
)
Completar:
• El sistema es inconsistente si ..............
• El sistema es indeterminado si .....................
• El sistema es .......... si: a=b y c ≠ d
4. Calcular: (x + y)y – x , al resolver:
– –
x y
x y
2 5 26
3 4 7
+ =
=
)
5. Calcular "xy" al resolver:
x y
x y
2 3 6
4 2 8
3 2
2 4
+ =
+ =
)
6. Indicar el valor de "7y" luego de resolver:
( ) ( )
( ) ( )
x y
x y
3 5 5 3 36
4 2 2 4 18
+ + + =
+ + + =
)
7. Indicar "x" que verifica el sistema:
4 3 4
2 – 6 –3
x y
x y
+ =
=
Z
[
]
]
]](https://image.slidesharecdn.com/lgebra4-240617025348-2ba3a9a6/85/Algebra_4-pdf-TEMAS-SELECTOS-DE-PREPARACION-125-320.jpg)
![Capítulo
126
Colegios
TRILCE Central: 6198-100
Tú puedes
8. Resolver e indicar el valor de "y":
3 – 4 5
2
1
5
2
x
y
x
y
=
+
=
Z
[
]
]
]
]
9. Para qué valor de "m" el siguiente sistema:
( – )
( )
m x y
x m y
2 3 4
6 2 1 12
+ =
+ + =
)
tiene infinitas soluciones.
10. Hallar "m" para que el sistema sea incompatible:
( )
( )
m x y
m x y
1 2 5 7
2 4 8
+ + =
+ + =
)
11. Calcular "a2 + b2" en el siguiente sistema com-
patible indeterminado.
( – ) – ( – )
–
x y
x y
3 5 10
4 3 5
α β =
=
)
12. Calcular " x y
+ " al resolver:
–
x y
x y
9 4 108
3 2 18
=
+ =
)
13. Luego de resolver el sistema:
x y x y
x y x y
3 2 2 3 7 10
2 2 3 2 3 7 14
– – –
– –
+ + =
+ + + =
)
Indicar el valor de "3x – 2y".
14. La edad de Edú es la suma de las edades de
Fatima y Mathías. La edad de Fatima es 2 años
más que la suma de las edades de Mathías y
Marco. La edad de Mathías es cuatro veces la
edad de Marco. La suma de las cuatro edades
es 42. ¿Qué edad tiene Edú?
15. En una feria campestre los boletos para los
adultos se venden en $ 5,50; para los jóvenes
en $ 4,00 y para los niños $ 1,50. El día de la
apertura, el número de boletos para jóvenes y
niños que se vendieron fue 30 más que la mitad
de los boletos de adultos vendidos. El número
de boletos para jóvenes vendidos tiene cinco
más que cuatro veces el número de boletos
para niños. ¿Cuántos boletos de cada tipo se
vendieron, si la venta total de boletos ascendió
a $ 14 970?
20
1. Calcular "y" al resolver:
–
x y xy
x y
2 8 9
2 1
+ + =
=
)
a) 4 b) 6 c) 8
d) 16 e) 32
2. Hallar "xy" del sistema:
–
–
–
–
x y
x y
x y
x y
4
3
2 7
2 5
3
2
+
+
=
+
+
=
a) 2 b) 3 c) 4
d) 5 e) 6
3. Calcular "xyz" al resolver:
1 1 – 1 6
1 – 1 1 4
1 1 1
x y z
x y z
y z x
+ =
+ =
+ =
Z
[
]
]
]
]
]
]
a)
2
1 b)
90
1 c)
60
1
d)
30
1 e) 1
4. Indicar "xy" luego de resolver el sistema:
– –
–
–
–
–
x a
a
y b
b a b
x a
a
y b
b a b
+ = +
=
Z
[
]
]
]
]
a) a b) b c) a – b
d) a+b e)1+ a b ab
+ +
5. Indicar "x – y" al resolver:
( – )
–
ax by a b
bx ay a b
2 2 2
2 2
+ =
+ =
)
a) a+b b) a – b c) a
d) b e) 1](https://image.slidesharecdn.com/lgebra4-240617025348-2ba3a9a6/85/Algebra_4-pdf-TEMAS-SELECTOS-DE-PREPARACION-126-320.jpg)


![Capítulo
130
Colegios
TRILCE Central: 6198-100
Aprende más
1. Relacionar correctamente:
a ≥ b A ab+a3 ≤ 0
b ≤ a ≤ 0 B a2 ≥ b2
0 ≤ b ≤ a C a3 ≥ b3
a ≤ 0 ≤ b D a2 ≤ b2
2. Indicar verdadero (V) o falso (F) según corres-
ponda:
• x ≥ 1 → x2 ≥ 1.......................................( )
• –1 < x ≤ 2 → 0 ≤ x2 ≤ 4.......................( )
• –4 < x ≤ – 2 → 4 ≤ x2 ≤ 16..................( )
• x ≤ – 2 → x2 ≤ 4...................................( )
3. Completar adecuadamente:
• Representado gráficamente como un
segmento de recta, al conjunto de infinitos
puntos reales se le denomina .....................
• Ningún número real elevado al cuadrado
puede ser ...............
• El único número real que no tiene inversa es
el ...............
4. Si: –2 < x ≤ 3, calcular el intervalo de: x2 – 1
a) ]– 1 ; 8] b) [3 ; 9] c) ]3 ; 8]
d) [– 1 ; 8] e) ]– 1 ; 8[
5. Si: x ∈ 〈– 2 ; 5], hallar el intervalo de variación
de: M =
–
x
x
6
2 1
+
a) ;
8
3 11
; E b) – ;
8
3 11
; E c) – ;
8
3 3
; E
d) – ;
11
8
3
; e) ;
8
3 11@
6. Si: x, y ∈ +, calcular el máximo valor que
puede tomar "xy", si: x+y=14
a) 50 b) 49 c) 48
d) 7 e) 0
7. Si: x ∈ +, indicar el mínimo valor que toma:
x
x
6
150
+
a) 5 2 b) 5 c) 10
d) 10 e) 25 10
8. ¿Cuántos valores enteros negativos verifican?
– –
x x x
3 6 2 4
1
<
a) 2 b) 1 c) 3
d) 5 e) Ninguno
9. Indicar la suma de los valores enteros que
verifican: 1 – 2x < 10 + x < 15 – 4x
a) – 2 b) – 6 c) – 4
d) – 3 e) – 5
10. Indicar el menor valor que puede tomar "x" en:
–
x x
3
2 1
4
3 1
+ + ≥ x + 3
a) 5 b) 8 c) 4
d) –3 e) 7
11. Indicar la raíz cuadrada del mayor número
entero que verifica la inecuación:
x x x
6
1
2
1
2
1
5 3
1
10
2 3
<
+ + + +
` ` `
j j j
a) 5 b) 3 c) 4
d) 2 e) 6
12. Indicar cuántos valores enteros de "x" verifican
el sistema:
9
2 –3
5
–1 2
3
2
5
3 –2 4
x x
x x
<
>
+
+ +
Z
[
]
]
]
a) 5 b) 3 c) 4
d) 2 e) 1
13. Para: a<b<0, calcular el máximo valor que
podría tomar "x" en la desigualdad:
( ) –
a
b x
b
a
a
b
b
a
1 4
2
2
#
+ + c m
a)
( )
b a b
a
4
2
+
b)
( )
a a b
b
4
2
+
c)
a b
ab
4
+
d)
b
a
4
2
e)
a
b
4
2
21](https://image.slidesharecdn.com/lgebra4-240617025348-2ba3a9a6/85/Algebra_4-pdf-TEMAS-SELECTOS-DE-PREPARACION-130-320.jpg)



![Álgebra
135
www.trilce.edu.pe Cuarto año de secundaria
Saberes previos
1. Resolver:
• – –
x x
3
1
5
2 1
>
• x x
6 3
1
$
+
2. Si: x ∈ 〈1; 7] , indicar a qué intervalo pertenece:
• (8 – x) ∈ ..........
• (2x – 1) ∈ ..........
3. Si: x ∈ [2; 5〉, indicar el intervalo de variación
de:
•
x 1
3 !
+
c m ..........
4. Si: x∈〈–2; 6〉, indicar los intervalos de variación
de:
• (x2 – 4) → x ∈
• (x – 4)2 → x ∈
5. Si: x ∈ [1; 5], indicar el intervalo de variación
de:
•
x
x
1
2
+
+
c m ∈ ..........
1. Relacionar correctamente:
x2+1 ≥ 0 A x ∈ φ
x2+1<0 B x ∈ {1}
x2 – 1≤ 0 C x ∈
(x – 1)2 ≤ 0 D x ∈ [–1 ; 1]
2. Indicar verdadero (V) o falso (F):
• Si: x2 – x+1<0 → x ∈ φ ........................( )
• Si: x2 – x+1>0 → x ∈ .......................( )
• Si: x2 – x>0 → x ∈ 〈0 ; 1〉 .....................( )
• Si: x2+x<0 → x ∈ φ ..............................( )
3. Completar:
• Si: (x – 5)2<0 → x ∈ ...........
• Si: (x – 5)2 ≤ 0 → x ∈ ...........
• Si: (x – 5)2 ≥ 0 → x ∈ ...........
• Si: (x – 5)2 >0 → x ∈ ...........
4. Resolver:
(x – 2)(x – 4) (x – 6) < 0
5. Resolver:
(x2+4)(x2 – 4) ≥ 0
Aplica lo comprendido](https://image.slidesharecdn.com/lgebra4-240617025348-2ba3a9a6/85/Algebra_4-pdf-TEMAS-SELECTOS-DE-PREPARACION-135-320.jpg)
![Capítulo
136
Colegios
TRILCE Central: 6198-100
Aprende más
1. Relacionar correctamente:
(x – n)2 ≥ 0 A x ∈ { }
(x – n)2 ≤ 0 B x ∈ – {n}
(x – n)2 < 0 C x ∈ {n}
(x – n)2 > 0 D x ∈
2. Indicar verdadero (V) o falso (F) según corresponda:
• Si: –3<x<4 → 9<x2<16....................( )
• Si: –5<x<–2 → 0<x2<25..................( )
• Si: – 6<x<5 → 0 ≤ x2<36..................( )
• Si: x>–1 → x3>–1...............................( )
3. Completar:
• En una inecuación fraccionaria, los puntos
críticos que provienen del .................
siempre son abiertos.
• Si el discriminante de un polinomio de
segundo grado es positivo, se aplica el
método de los puntos .............
• Un polinomio de segundo grado será no
negativo, si el coeficiente principal es
positivo y el ............ negativo o cero.
4. Resuelva: 15x2 – 2x – 8 ≤ 0; calcula el producto
del mínimo y el máximo valor de su conjunto
solución.
a)
15
4 b) –
5
2 c) –
15
1
d) –
15
8 e)
15
8
5. Si: 〈–∞ ; b] ∪ [1; +∞〉, es el conjunto solución
de la inecuación: 2x2+ax+1≥ 0; calcular: b – a
a) 7 b)
2
7 c) –
2
3
d)
2
1 e)
4
1
6. Resuelva la inecuación cuadrática:
x2+14x+49 ≥ 0
a) 〈
3
5 ; +∞〉 b) 〈–∞; –2] ∪ 〈3;+∞〉
c) + d) φ
e)
7. Calcular el valor de (a – 2) si la inecuación en
"x": x2 + 2(1 – 2 )x+ a ≤ 0, se verifica para un
solo valor de "x".
a) 2 b) 1+2 2 c) 2 2 – 1
d) 2 2 e) 1 – 2 2
8. Resuelva la inecuación polinomial:
(x+2)(4x – 1)(–x + 3) > 0
e indica cuántos enteros no negativos la verifican.
a) 4 b) 3 c) 2
d) 1 e) 0
9. Hallar el máximo valor entero de "M" de modo
que se cumpla lo siguiente:
x2 – 5x+4 – M ≥ 0 ; ∀ x ∈
a) – 3 b) – 5 c) – 4
d) 0 e) –2
10. Luego de resolver la inecuación:
(x – 4)5 (x2 – x+2)2 (2x – 1)3 (x4 – 16)<0
se obtiene: C.S. = 〈– a ;
a
1〉 ∪ 〈a ; b〉
Calcular el valor de "ab".
a) 2 b) 4 c) 6
d) 8 e) 12
11. Luego de resolver la inecuación:
(x2 – x)2 (x3 – 1)(2x2 – 3x+1) (2x – 1)4<0
se obtiene: C.S. = 〈– ∞ ; m〉 – {n}
Calcular el valor de: mn.
a) 9 b) 8 c) 4
d) 1 e) 0
12. Resuelva las siguientes inecuaciones:
>
– 0
–
– 0
x
x
x
x x
4
2 1
1
2
2
/
G
+
+
e indica el intervalo solución común.
a) 〈–4 ;
2
1〉 b) 〈– 2 ;
2
1] c) 〈–2; +∞〉
d) 〈– 4 ;
2
1] e) 〈–2 ; 2〉
13. Luego de resolver la inecuación fraccionaria:
–
–
x
x
x
2 1
2 1
+ <0, se obtiene: C.S.= 〈a;0〉 ∪ 〈b;–a〉
Calcular el valor de (2b + a).
22](https://image.slidesharecdn.com/lgebra4-240617025348-2ba3a9a6/85/Algebra_4-pdf-TEMAS-SELECTOS-DE-PREPARACION-136-320.jpg)
![Álgebra
137
www.trilce.edu.pe Cuarto año de secundaria
Practica en casa
a) 0 b)
2
1 c) 1
d) 2 e) 4
14. Un rebaño de venados se introduce en una isla
pequeña. Al principio el rebaño aumenta con
rapidez; pero finalmente, el alimento disminuye
y la población también. Suponga que el
número "N(t)" de venados, a los "t" años, es:
N(t) = - t4 + 21t2 + 100, donde: t > 0
Determine los valores de "t" para los cuales:
N(t) > 0.
15. Un fabricante de cierto artículo ha estimado
que su ganancia en miles de dólares está dada
por la expresión: - 6x4+30x2 - 10, donde "x"
(miles) es el número de unidades producidas.
¿Qué nivel de producción le permitirá obtener
una ganancia de al menos $ 14 000?
1. Relacionar correctamente:
x2 ≤ 9 A x ∈ φ
(x2+3)(x–3) ≤ 0 B x ∈
x2 ≤ –9 C x ∈ [–3 ; 3]
x2 ≥ –9 D x ∈ 〈–∞ ; 3]
2. Indicar verdadero (V) o falso (F) según corres-
ponda:
• Si: x2 ≤ 0, entonces: x ∈ φ ....................( )
• Si: x2 ≥ 0, entonces: x∈ ....................( )
• Si: x3 ≤ 0, entonces: x ∈ –...................( )
• Si: x3 ≥ 0, entonces: x ∈ +..................( )
3. Completar al resolver las inecuaciones:
• Si:
–
–
x b
x a < 0 ; a<b → x ∈ ..............
• Si: (x – a)(x – b) ≥ 0 ; a>b → x ∈ ..............
• Si: (x – a)2(x – b) ≤ 0 ; a<b → x ∈ ..............
4. Resolver: 3x2 – x –10 > 0
5. Resolver la siguiente inecuación cuadrática:
4x2 – 4x + 6 ≤ 0
6. Luego de resolver la inecuación: ax2+bx+c ≤ 0,
por el criterio de los puntos críticos, se obtiene:
C.S.=[
2
1; 2] . Calcular el valor de: –
a
b c
7. Hallar el mínimo valor entero de "a", que
verifique la inecuación: 1+8x–3x2<a; ∀x∈ .
8. Resolver: x3 > x
9. Dadas las inecuaciones:
• –
x
x
2
2 1
+
< 1 → C.S.=A
• –
x
x
1
1
+
> 0 → C.S. = B
Hallar "A – B".
10. Indique el conjunto solución de: x3+x2 ≤ 42x
11. Resolver:
(x+6)4 (x+2)6 (x – 4)8 (x – 3)11 > 0
12. Indica la suma de valores enteros que verifican:
( )(– – )
(– )( – )
x x
x x x
9 4
8 2 8
2
2
+
+ +
≤ 0
13. Resuelva la inecuación polinomial:
(x – 2)(x – 4)(x – 6) ... (x – 44)<0
indicar la suma de soluciones enteras.](https://image.slidesharecdn.com/lgebra4-240617025348-2ba3a9a6/85/Algebra_4-pdf-TEMAS-SELECTOS-DE-PREPARACION-137-320.jpg)
![Capítulo
138
Colegios
TRILCE Central: 6198-100
22
14. El precio de venta de un artículo está dado por:
p = (200 - 3q) dólares, en donde "q" es el número
de artículos vendidos. El costo de producir estos
"q" artículos es: C=(650+5q) dólares. ¿Cuántas
unidades de este artículo se deben producir y
vender de manera que la utilidad no sea menor
que 2500 dólares?
15. Un rebaño de venados se introduce en una isla
pequeña. Al principio el rebaño aumenta con
rapidez, pero finalmente, el alimento disminuye
y la población también. Suponga que el número
"N(t)" de venados, a los "t" años, es:
N(t) = - t4 + 32t + 144 ; donde: t > 0
Determine los valores de "t" para los cuales:
N(t)>0.
1. El C.S. de la inecuación:
( – ) –
( – )( ) –
–
a b x
a b x
x a b
x
1
1 1<
+
+
es: 〈– ∞ ; – 1〉; entonces:
a) a – b = 2 b) b – a = 1 c) b + 2a = 1 d) 3b + 2 = a e) b – 2a = 1
2. Resolver: (x – 2)3 . . .( – 4) . –
x x x x
1 3 64
5 7 6 2
4
+ + ≥ 0
a) [–3; –1] ∪ [2 ;+∞> b) [–3; –1] ∪ [2; 8] c) [–3; –1] ∪ [2; 8] ∪ {–8}
d) e) +
3. Resuelva: x(2x + 1) (x – 2) (2x – 3) > 63
Indique el producto de valores enteros negativos mayores que –5.
a) 6 b) –6 c) 24 d) –24 e) 12
4. Determinar el conjunto "A", si: A = /
( – )
( – ) –
( – )
( – ) –
x
x
x
x
x
19 1
19 2
19 2
19 4
<
+ +
!
' 1
3 3
2 2
a) x<17 b) 7<x<19 c) 0<x<17 d) x>19 e) 0<x<19
5. Indique las soluciones negativas de la inecuación:
– –
( – – )( )( – )
x x x
x x x x
2 2
2 35 2 1
5 3 2
2 3
+
+
≥ 0
a) – b) 〈–1; 0〉 c) 〈–7; 0〉 d) [–5; –2] e) [–5; –1]
Tú puedes](https://image.slidesharecdn.com/lgebra4-240617025348-2ba3a9a6/85/Algebra_4-pdf-TEMAS-SELECTOS-DE-PREPARACION-138-320.jpg)


![Capítulo
142
Colegios
TRILCE Central: 6198-100
Practica en casa
1. Relacionar correctamente:
x +1 ≤ 0 A x ∈ [0 ; +∞〉
x – 1 ≥ 0 B x ∈ [1; +∞〉
x – 1 ≤ 0 C x ∈ φ
x +1 ≥ 0 D x ∈ [0; 1]
23
4. Resolver: –
x 4 <3
a) [0; 1[ b) ]–3; 2] c) [4; 13[
d) ]–2; 2] e) ]1; 3]
5. Resolver: –
x 2 ≥ 3
a) 〈–∞; 3] b) 〈–∞; 11〉 c) 〈2; 9〉
d) 〈11; +∞〉 e) [11; +∞〉
6. Resolver: – x
3 +1>0
a) 〈–∞ ; 3] b) 〈–∞ ; –3] c) 〈–3; 3〉
d) 〈3; +∞〉 e) [3 ; +∞〉
7. Resolver: – x
2 <x
a) [0; 1[ b) ]0; 2] c) [4; 6[
d) ]–2; 2] e) ]1; 2]
8. Resolver: –
x 5 +3<0
a) [0; 5[ b) ]0; 5] c) [0; 3[
d) ]–3; 5] e) φ
9. Resolver: –
x 4 ≤ –
x 1
a) 〈–∞ ; 4] b) 〈–∞ ; 4〉 c) 〈1; 4〉
d) 〈1 ; +∞〉 e) [4; +∞〉
10. Resolver: – –
x x
3 6
+ ≥ 0
a) 〈–∞ ; 3] b) 〈–∞ ; 6] c) 〈3; 6〉
d) [3; 6] e) [3; +∞〉
11. Resolver: –
x 11
3
≤ – 2
a) 〈–∞ ; 3] b) 〈–∞ ; 11] c) 〈2; 11]
d) 〈11 ; +∞〉 e) [11 ; +∞〉
12. Resolver la inecuación:
( ) ( )
( – ) . –
x x
x x x
1 2 5
4 2 25 2 8
2 9
8 2 3 5
+ +
+ <0
a) 〈1; 2〉 b) 〈2; 3〉 c) 〈3; 4〉
d) 〈4; 5〉 e) 〈5; 6〉
13. Resuelve: –
x x 2
2
+ <5 – x
a) 〈– ∞ ; –1] ∪ [1;
11
25 〉 b) 〈– ∞ ; –2] ∪ [1;
11
27 〉
c) 〈– ∞ ; –4] ∪ [2;
11
23 〉 d) x ∈ {0}
e) x ∈
14. Para que un medicamento tenga efectos
benéficos, su concentración en la sangre debe
ser mayor que un determinado valor, llamado
concentración terapéutica mínima. Supóngase
que la concentración "C", en mg/L, de
determinado medicamento a las "t" horas después
de haberla ingerido oralmente, es: C(t) =
t
t
4
20
2
+
.
Si la concentración terapéutica mínima es 4 mg/L,
determinar cuándo se rebaja esta.
15. Para el tratamiento de la arritmia. Se aplica
un medicamente mediante una inyección
intravenosa. Supóngase que la concentración "C"
del fármaco, después de "t" horas, está dado por:
C(t) =
,
t
t
1
3 5
+
mg/L. Si la concentración terapéutica
mínima es 1,5 mg/L, determine cuándo se rebasa
esa concentración.
2. Indicar verdadero (V) o falso (F) según
corresponda:
• Si: x
3
<–1 , entonces: x ∈ φ.................... ( )
• Si: x >–1 , entonces: x ∈ .................. ( )
• Si: x
3
≤ 0 , entonces: x ∈ {0}.................( )
• Si: x 2
3 3
$ , entonces: x ∈ [2;+∞〉.........( )](https://image.slidesharecdn.com/lgebra4-240617025348-2ba3a9a6/85/Algebra_4-pdf-TEMAS-SELECTOS-DE-PREPARACION-142-320.jpg)
![Álgebra
143
www.trilce.edu.pe Cuarto año de secundaria
1. Indica un intervalo solución de la siguiente
inecuación: – – – – –
x x x x
1 1 3 3 3
> +
a) [–1; 3〉 b) <0;
3
1]
c) 〈–1;3] ∪ 〈4;+∞〉 d) [–3; 0〉
e) 〈–3; 1] ∪ [3; +∞〉
2. Resolver:
– –
– –
x
x x
5 16
3 4
2
2
≥ x2 – 2x – 29
a) [–4; –1] ∪ {4} b) [–3; –1] ∪ {4}
c) [–2; –1] ∪ {4} d) [–2; 1] ∪ {4}
e) x ∈ {0}
3. Sea "S" el conjunto solución de:
–
–
x x x
x x
5 5
4
2
2 2
≠
+ +
+ ≥ (x – 3) x 2
+ ; entonces:
10. Resolver:
(x – 2)3. 1 . 3
x x
5 7
+ +
^ ^
h h(x – 4)6. 64–x2
4
^ h ≥0
11. Si: A = 〈– ∞ ; a] ∪ [b ; c〉 , es el conjunto solu-
ción de: –
x x
5 4
2
+ <7 – x; calcular el valor
de "a+b+c".
12. Resolver:
–
–
x
x
4
2 < 2
13. Resolver: –
x
6 2 >x+1
14. Después de "t" minutos de introducir un
bactericida experimental en cierto cultivo,
el número de bacterias está dado por:
t 1
10 000
2
+
+ 2000. Determine el momento en
que el número de bacterias esté por debajo de
4000.
15. Para que un medicamento tenga efectos
benéficos, su concentración en la sangre
debe ser mayor que un determinado valor,
llamado concentración terapéutica mínima.
Supóngase que la concentración "C", en mg/L,
de determinado medicamento a las "t" horas
después de haberla ingerido oralmente, es:
C(t) =
t
t
3
12
2
+
. Si la concentración terapéutica
mínima es 3 mg/L, determinar cuándo se rebaja
esta.
3. Completar:
• En las inecuaciones irracionales de radicales
de índice ........ no se hace restricciones
previas.
• En los radicales de índice par se hace la
restricción: ........ mayor o igual a cero.
• El radicando puede ser ......... o ........... en
radicales de índice impar.
4. Resolver: – –
x x
5 2 10
>
5. Resolver:
x 1
1
+
> x – 1
6. Resolver la desigualdad: x+2 ≤ x 8
3
3
+
7. Resolver: –
x 9
2
≤ 4
8. Al resolver:
–
–
x
x
9
4
2
2
+5>0
Se obtiene: x ∈ 〈a ; b] ∪ [c ; d〉
Hallar el valor de: E = a + b + c + d
9. Resolver:
–
– – .( – )
x
x x x x
1
6 8 5
2 2
+
≥ 0
a) S = 〈–2; 3〉 b) S ⊂ [–2; 2]
c) S ⊂ [1; +∞〉 d) S = [0; 1〉
e) S ⊂ 〈– ∞ ; 0]
4. Resuelva: – –
x x x
2 1 2
>
+
a) [
2
2 5
+ ; +∞〉 b) [
2
1 7
+ ; +∞〉
c) [
2
3 10
+ ; +∞〉 d) 〈
2
1 7
+ ; +∞〉
e) 〈
2
3 10
+ ; +∞〉
5. Resolver:
– –
– –
–
–
x x
x x
x x
x x
1 1
1 1
1 1
1 1
8 8
4 4
8 2
16
8 8
#
+
+
+ +
+ +
a) x ∈ {1; 2} b) x ∈ {9; 12}
c) x ∈ 〈0; 1] d) x ∈ {1}
e) x ∈ {2}
Tú puedes](https://image.slidesharecdn.com/lgebra4-240617025348-2ba3a9a6/85/Algebra_4-pdf-TEMAS-SELECTOS-DE-PREPARACION-143-320.jpg)


![Álgebra
147
www.trilce.edu.pe Cuarto año de secundaria
Aprende más
1. Relacionar correctamente, a partir de los
siguientes conjuntos:
A = {x ∈ / x ∈ 〈0 ; 4] }
B = {x ∈ / x ∈ [2 ; 4}
n(A×B) A 16
n(B2) B 144
n(A2) C 12
n(A2×B2) D 9
2. Indicar verdadero (V) o falso (F), dados los
conjuntos:
A = {1; 2; 3} ; B = {1; 3; 5}
• El par (2; 5) ∈ A×B ................................ ( )
• El par (3; 3) ∈ A2 ................................... ( )
• El par (5; 1) ∈ B×A ................................ ( )
• El conjunto: R = {(2; 3), (3; 3), (1; 1)} es una
relación de A×B .................................... ( )
3. Completar a partir de los conjuntos:
A = {3; 4; 5} ; B = {4; 5}
• Si: R={(x; y) ∈ A×B / x=y}
entonces: R = { _______________ }
• Si: R = {(x; y) ∈ A×B / x ≥ y}
entonces: R = { _______________ }
• Si: R = {(x; y) ∈ A×B / x<y}
entonces: R = { _______________}
4. Calcular "ab" en la igualdad:
(a+b; 8) = (10; a+1)
a) 12 b) 21 c) 18
d) 9 e) 24
5. Calcular el número de elementos del producto
cartesiano: A2×B2, si: A={1;2;3;4} y B={5;6;7}
a) 150 b) 144 c) 81
d) 160 e) 80
6. Si: A={x ∈ / 1<x ≤ 6} y B={x∈ / 3 ≤ x<9};
indicar el número de elementos de: A×B
a) 21 b) 32 c) 48
d) 49 e) 30
7. Calcular la suma de elementos del dominio de:
R1 = {(x; y) ∈ A×B / x<y}
Si: A = {7; 19; 21; 24} y B = {4; 5; 16; 20}
a) 33 b) 47 c) 28
d) 26 e) 76
8. Si: A={9; 10;15} y B={5; 7}, indicar el número
de elementos de: R2={(x; y)∈A×B/x+y≥17}
a) 1 b) 2 c) 4
d) 3 e) 0
9. Si: A={x ∈ + / –3 ≤ x ≤ 3}
B={x ∈ – / –2 ≤ x ≤ 2}
Indicar el número de elementos de: A2×B2
a) 36 b) 4 c) 25
d) 9 e) 16
10. Calcular "
y
x " en la siguiente igualdad:
(x+y; 4) = (12; x – y)
a) –1 b) 4 c) 3
d) 2 e) 1
11. Si: A={–6; –8; 3; 4} y B={–4; –2; –1; 2},
indicar el número de elementos de:
R4={(x; y) ∈ A×B / xy>0}
a) 8 b) 12 c) 4
d) 9 e) 10
12. Dado el conjunto: A={0; 1; 2; 3; 4; 5; 6; 7; 8; 9}
se define:
R = {(x; y) ∈ A×A / 2x+y=10}
Indicar la suma de elementos del dominio de
"R".
a) 18 b) 15 c) 14
d) 19 e) 10
13. Del conjunto:
A = {x ∈ / (x – 2)5 (x+3)7(x – 5)6<0}
se define: R={(a; b) ∈ A×A / a+b ≥ 0}. Indicar
el número de elementos de "R".
a) 2 b) 5 c) 4
d) 6 e) 7](https://image.slidesharecdn.com/lgebra4-240617025348-2ba3a9a6/85/Algebra_4-pdf-TEMAS-SELECTOS-DE-PREPARACION-147-320.jpg)
![Capítulo
148
Colegios
TRILCE Central: 6198-100
Practica en casa
1. Relacionar correctamente a partir de los
conjuntos:
A = {x ∈ /x ∈ 〈1; 5〉} ; B = {x ∈ /x ∈ [0;3]}
n(B×A) A 16
n(B2) B 9
n(A2) C 12
n(A2×B2) D 144
2. Indicar verdadero (V) o falso (F), dados los
conjuntos:
A = {2; 4; 6} y B = {0; 2; 4}
• (2; 4) ∈ A2 .............................................. ( )
• (2; 0) ∈ B×A ........................................... ( )
• (A×B) ∩(B×A) tienen dos pares ordenados
en su intersección .................................. ( )
• R={(2; 2), (4; 4), (6; 6)} es una relación de
"A" en "B" .. ............................................ ( )
3. Completar correctamente, dados los conjuntos:
A = {1; 2; 3; 4} y B = {4; 6; 8; 10}
• Si: R1={(x ; y) ∈ A × B / x < y}, entonces:
n(R1)= _______________________
• Si: R2={(x ; y) ∈ B × A / x = 2y}, entonces:
n(R2)= _______________________
• Si: R3={(x ; y) ∈ A × B / x = y}, entonces:
n(R3)= _______________________
4. Calcular "ab" en la igualdad:
(a + b ; 5) = (12 ; a – 4)
5. Calcular el número de elementos del producto
cartesiano "A×B", si: A={8; 9; 0} y B={5; 6; 2; 7}
6. Si: A={x ∈ / 3 ≤ x ≤ 5} y B={x ∈ /2<x<6},
indicar el número de elementos de: A×B.
7. Calcular la suma de elementos del dominio de:
R = {(x ; y) ∈ A×B / x=2y}
Si: A={8; 9; 10} y B={4; 5; 16; 20}
8. Si: A={6; 8} y B={5; 9}, indicar el número de
elementos de: R={(x;y) ∈ A×B / x+y<15}
9. Calcular la suma de elementos del dominio de:
R = {(x; y) ∈ B×A / x<y}
Si: A={8; 9; 10} y B={1; 2; 12; 18}
10. Si: A={–6; –8} y B={–5; –3; 1; 2}, indicar la
suma de elementos del rango de:
R={(x; y) ∈ A×B / xy<0}
11. Si: A={–1; 0; 1} y R={(x; y) ∈ A2 / x2=y2},
indicar el número de elementos de "R".
24
14. Un ciclista corre en línea recta 200 m hacia el
este. Luego 200 m hacia el norte, 300 m al nor
este y 100 m hacia el este; 100 m al norte y 150
m al nor este. ¿A qué distancia del punto de
origen está?
15. En un negocio de comidas se observa los
siguientes carteles:
A
Entradas Segundo
Sopa Arroz con pollo
Ensalada mixta Escabeche
Papa a la huancaina Cau Cau
Papa rellena Tallarín rojo
Salpicón de pollo Ají de gallina
Lomo saltado
B
Entradas Segundo
Sopa Arroz con pato
Choclo con queso Ají de gallina
Papa con ocopa Mondonguito a la italiana
Rocoto relleno Tallarín verde
Ceviche Cau Cau
Patasca
Responder:
• ¿Cuántas relaciones de Entrada - Segundo
hay en el cartel "A?
• ¿Cuántas relaciones de Entrada - Segundo
hay en el cartel "B"?
• ¿Cuántas relaciones comunes de Entrada -
Segundo hay en "A" y "B"?](https://image.slidesharecdn.com/lgebra4-240617025348-2ba3a9a6/85/Algebra_4-pdf-TEMAS-SELECTOS-DE-PREPARACION-148-320.jpg)



![Capítulo
152
Colegios
TRILCE Central: 6198-100
Aplica lo comprendido
1. Hallar "x" en la siguiente igualdad:
–
a b
a b a b
x
2 3
2
3
6
+
+
=
e e
o o
a) 4 b) 5 c) 6
d) 7 e) 8
2. Dada la matriz: A =
2
0
1
1
e o; además:
P(x) = x2 – 5x+2; hallar la suma de los elemen-
tos de "P(A)".
a) 8 b) 6 c) –6
d) –8 e) –4
3. Hallar "x" en:
... x
x
1
1
0
0
1
1
1
0
1
1
1
0
0
2
1
2
0
1
1
1
0
0
3
1
3
0
1
1
1
0
0
1
0
1
+ + + + =72
a) 9 b) 8 c) 11
d) 10 e) 7
4. Resolver:
x =
3+
– 5
x
–
1
1
2
2
0
2
1
1
0
–
x
x
8
0
a) 8 b) 3 c) 4
d) 6 e) 10
5. Sea: x ∈ [5 ; 7]; indicar el intervalo de:
g(x) = x2 – 4x + 9
a) [5; 30] b) [7; 30] c) [10; 30]
d) [14; 30] e) [15; 30]
6. Si: x ∈ +, hallar el mínimo valor de:
G = x
x
8
200
+
a) 8 b) 9 c) 10
d) 11 e) 12
7. Resolver:
• x2 (x – 3) – 16(x – 3) = 0
• x2 – 2x – 35 ≤ 0
• 16x–3 > 64x+2
•
–
( – )( )
x
x x
1
6 5
+
≤ 0
8. Resolver:
(x - 3)5(x – 4)6(x2 – x – 6) > 0
a) ] – 2 ; + ∞ [ b) ] - 2 ; + ∞ [ – {3}
c) [2 ; + ∞] d) ] - ∞ ; – 2[
e) ] - 2 ; + ∞[ – {3 ; 4}
9. Resolver:
x x
x x
4 3
2
2
2
+ +
- - ≤ 0
a) ] – 3 ; – 1[ ∪ ]1 ; 2]
b) ] – 3 ; – 1]
c) ] – 3 ; – 1[ ∪ ] – 1 ; 2]
d) ] – 1 ; 2]
e) ] – 3 ; 2[
10. Determine el C.S. de:
x
x x
1
6
2
4 2
-
- - ≤ 0
a) ] – 1 ; 1[ b) [3 ; +∞[
c) ]– ∞ ; – 2[ d) [- 3 ; 3 ]
e) [– 3 ; –1[ ∪ ]1 ; 3 ]
25](https://image.slidesharecdn.com/lgebra4-240617025348-2ba3a9a6/85/Algebra_4-pdf-TEMAS-SELECTOS-DE-PREPARACION-152-320.jpg)
![Álgebra
153
www.trilce.edu.pe Cuarto año de secundaria
Aprende más
1. Sean las matrices: A=
4
2
3
1
= G y B=
5
7
6
8
= G
Hallar la traza de la matriz: 2A – B+I, donde
"I" es la matriz identidad.
a) – 4 b) – 5 c) – 1
d) 1 e) 2
2. Dadas las matrices:
A =
–
–
2
3
1
2
3
4
= G ; B =
1
2
1
1
3
2
> H
Calcular la suma de los elementos de la matriz: A×B.
a) 8 b) 9 c) 6
d) 5 e) 4
3. Sean las matrices:
A =
–
x y x
y
3
1
= G ; B =
–
–
y
x
2
1
6
6
= G ; C =
– –
4
2
8
3
= G
Si: A=B, calcular: 2B+C.
a)
0
4
2
5
= G b)
0
5
3
4
= G c)
2
5
0
4
= G
d)
1
4
0
5
= G e)
0
5
1
4
= G
4. Dada la matriz: A =
–
2
3
1
1
= G
Calcular la traza de: A2 + 2A.
a) 13 b) 2 c) 11
d) 10 e) 9
5. Luego de resolver la ecuación:
–
–
x
x x
2
1
3
1
4
0
0
=
Indicar la suma de soluciones.
a) 1 b) 2 c) 3
d) 0 e) – 3
6. Calcular el valor de:
– –
4
31
74
0
1
1
0
1
2
3
2
1
0
2
0
0
4
6
+
a) 36 b) 32 c) 38
d) 40 e) – 36
7. Resolver:
(x – 5)(x+3)+
–
x 8
1 >(x – 6) (x + 4)+
–
x 8
1
a) x ∈ φ b) x ∈ c) x ∈ {5}
d) x ∈ – {8} e) x ∈ 〈0;+∞〉 – {8}
8. Si: x ∈ [4 ; 7], ¿entre qué límites varía la expre-
sión:
–
–
x
x
2
2 1
2
1
+ ?
a) 〈
2
5 ; 2〉 b) [
2
5 ; 4〉 c) [2; 4]
d) [
2
5 ; 4] e) 〈–
2
5 ; 4〉
9. Resolver: x2 – 4x+1 ≤ 0
a) x ∈ [2 – 3 ; 2+ 3 ] b) x ∈ [1– 3 ; 1+ 3 ]
c) x ∈ [– 3 ; 3 ] d) x ∈ f
e) x ∈
10. Si: {x; y} ⊂ +, hallar la variación de:
E =
y
x
x
y
+ + 5
a) E ≥ 5 b) E ≥ 2 c) E ≥ 7
d) E ≤ 7 e) E ≤ 2
11. Hallar el valor mínimo de:
F(x) =
–
–
x
x x
1
2 2
2
+ ; ∀ x > 1
a) 2 b) 3 c) 2
d) 1 e) 3
12. Resolver: x3 – 5x2+6x ≥ 0
a) [0 ; 2] ∪ [3 ; +∞〉
b) 〈– ∞ ; 0] ∪ [ 2 ; 3]
c) [– 2 ; 3〉
d) 〈–2 ; 3]
e) [– 2 ; 0] ∪ [3 ; +∞〉
13. Resolver: (x – 4)x3 ≤ 9x(x – 4)
a) 〈– ∞ ; – 3] ∪ [0 ; 3]
b) 〈– ∞ ; – 3] ∪ {3 ; 4}
c) [– 3 ; 0] ∪ [3 ; 4]
d) 〈– ∞ ; – 3] ∪ [0 ; 3] ∪ [4 ; +∞〉
e) [– 3 ; 3] ∪ [4 ; +∞〉](https://image.slidesharecdn.com/lgebra4-240617025348-2ba3a9a6/85/Algebra_4-pdf-TEMAS-SELECTOS-DE-PREPARACION-153-320.jpg)
![Capítulo
154
Colegios
TRILCE Central: 6198-100
a) 〈– ∞ ; 2] ∪ [3 ; + ∞〉
b) 〈– ∞ ; – 3〉 ∪ [2 ; + ∞〉
c) 〈– ∞ ; – 3〉 ∪ [2 ; + ∞〉
d) 〈– 3 ; 2] ∪ {3} – {–1}
e) 〈– ∞ ; 2] ∪ {3} – {1}
18. Si se verifica: ax2 – (a – 1)x – 1 > 0 ; ∀ x ∈ ,
¿qué se puede afirmar de "a"?
a) + b) c) –
d) + – {1} e) Ø
19. Si la siguiente inecuación:
–ax2+2x>2x2 – ax+1>x2+x – a
Se verifica para todo "x" que pertenece a
los reales, entonces "a" ¿en qué intervalo se
encuentra?
a) 〈– ∞ ; – 2〉 b) Ø c) 〈– ∞ ; 1〉
d) 〈0 ; + ∞〉 e) 〈3 ; + ∞〉
20. Si: x ∈ 〈0 ; 2〉 , entonces: 2x2 – 12x+19, ¿en qué
intervalo se encuentra?
a) [1 ; + ∞〉 b) [1 ; 19〉 c) [– 4 ; 8〉
d) 〈3 ; 19〉 e) 〈0 ; 19〉
14. Indicar un intervalo solución de:
–
–
x
x
x
x
3
2 2
+
c `
m j ≤ 0
a) 〈 0 ; 3〉 b) [–2 ; 2] c) 〈 0 ; 2]
d) 〈– 2 ; 0] e) [– 2 ; 0〉
15. Indicar la suma de los valores enteros que no
satisfacen la inecuación fraccionaria siguiente:
– –
–
x x
x
3 10
2 11
2
1
2
#
a) 5 b) 7 c) 6
d) 3 e) 8
16. Sean los conjuntos:
A = {x ∈ / –
x
3 1 > – 2}
B = {x ∈ / – –
x x x
2 1
3 2
3
$
+ }
Indicar el conjunto: A ∩ B.
a) [–1 ; 3] b) [–1;3]–{
3
1} c) [–1 ;
3
1]
d) [
3
1 ; 3] e) 〈
3
1 ; 3]
17. Indicar el C.S. de la siguiente inecuación:
( ) ( ) ( )
( – ) ( ) ( – )
x x x
x x x
1 3 1
3 1 2
3 37 4
50 7 23
+ + +
+
≤ 0
1. Si: C=
–
2
1
3
2
= G
Hallar la traza de: C2.
2. Si:
–
–
5
m
A
4
1
2
5
2
5
1
1
+
+ =
Hallar: |A|.
3. Calcular:
–
–
–
3
2
1
4
5
7
6
4
2
4. Resolver e indicar el mayor valor de "x" en:
–
–
x
x x
3
2
10
1
1
3
1
+
= 6
5. Si:
A =
0
4
3
5
= G ; B =
–3
4
1
2
= G
Hallar: 2At – 3B+5I.
6. Resolver: (5+2x)(3 – 4x) ≥ 0
7. Calcular el mayor número entero "m" que
satisface la desigualdad:
2x2 – 4x+1>2m 6 x ∈ .
8. Si: |x| ∈ [ ;
3
1
3
2 ], indicar la suma del mayor y
menor valor de:
x
x
2 1
+
9. Resolver: 2x+8(x+1)>3(2x+1)+15
25
Practica en casa](https://image.slidesharecdn.com/lgebra4-240617025348-2ba3a9a6/85/Algebra_4-pdf-TEMAS-SELECTOS-DE-PREPARACION-154-320.jpg)
![Álgebra
155
www.trilce.edu.pe Cuarto año de secundaria
1. Encontrar el valor de verdad de las siguientes proposiciones:
I. –1 < – x < e ⇒ x2 ∈ [0 ; e2〉
II. – 5 ≤ x2 < 4 ⇒ x ∈ 〈– 2 ; 2〉
III. x2 > 1 ⇒ x ∈ 〈1 ; +∞〉
a) V V F b) F V V c) F F F d) V V V e) V F F
2. Calcular el mayor número real "m" tal que:
x
x
1
2
2
2
+
+ ≥ 2m ; ∀ x ∈ .
a) – 1 b) 0 c) 1 d) 2 e) 3
3. Resolver en : –
x 3 1
+ < 2x – 7.
a) [–
2
7 ;
2
7 ] b) [
2
7 ; 51] c) 〈
2
7 ; +∞〉 d) 〈
4
17 ; +∞〉 e) – [
2
7 ]
4. Resolver:
bx a
x 1
+
+ >
a
2 , si: a>2b>0.
a) 〈– ∞ ;
–
a b
a
2
〉 b) 〈–
b
a ;
–
b a
a
2
〉 c) 〈–
b
a ;
–
–
b a
a
2
〉 d) 〈
–
b a
a
2
; –
b
a 〉 e) 〈 –
b
a ;
–
b a
a
2
〉
5. Resolver: – – – –
x x
3 4 1 <0
a) [– 15 ; 1] b) [– 15 ; 1 〉 c) 〈 0 ; 1] d) 〈– 15 ; 1 〉 e) 〈– 1 ; 1]
10. Hallar el conjunto solución de la inecuación:
40[2(x–2)+7]<6[6{2(x–1)+2}]+160
11. Si: {a ; b} ∈ , resolver:
xa2 – (a+b)2 ≥ a2 – 2ab+b2 – xb2
12. Al resolver: (a+1)x+1<ax+8<(a+2)x–2
el C.S. de "x" es 〈m ; n〉. Hallar "m+n", si: a ∈
.
13. Hallar el conjunto solución de:
–
x x
3 6 8
2
+ > – 4
14. Calcular "xy" en la igualdad:
; – ;
x y x
3 27 12 3
+ = +
^ ^
h h
15. Si: A = {–2; 0; 2} y R = {(x; y) ∈ A2/x2=y2}
hallar el número de elementos de "R".
Tú puedes](https://image.slidesharecdn.com/lgebra4-240617025348-2ba3a9a6/85/Algebra_4-pdf-TEMAS-SELECTOS-DE-PREPARACION-155-320.jpg)

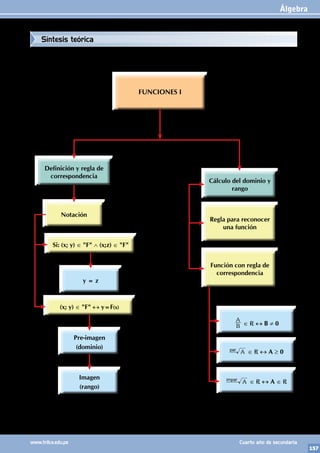
![Capítulo
158
Colegios
TRILCE Central: 6198-100
Aplica lo comprendido
Saberes previos
1. Relacionar las reglas de correspondencia y los
pares ordenados:
F(x)=x2+x – 2 A (–1;1)
G(x)=2x+1 B (–1;2)
H(x)=2x2 – 1 C (1;0)
I(x)=x2+1 D (–1;–1)
2. Indicar verdadero (V) o falso (F):
• F={(1;2),(3;5),(1;2)} es función............... ( )
• G={(0;1),(2;1),(4;1)} es función.............. ( )
• H={(–1;1),(–1;–1),(1;–1)} es función...... ( )
3. Completar correctamente:
• Un conjunto de pares ordenados se obtiene
al relacionar dos conjuntos por medio del
producto .....................
• En una función a cada primer componente le
corresponde solo una ..................
• Se llama función ................... a aquella cuya
regla de correspondencia es de primer grado.
4. Dada la función: F(x)= x 2
+
Calcular: F(–1)+F(7) – F(14)
5. En la función: F(x)={(2;7), (1;8), (6;1), (8;5)}
Calcular: S=F[F(1)] + F[F(6)]+F[F(8)–3]
1. Si: A={1; 2}, B={3; 5}, indicar por extensión:
• A×B = _______________________
• A2= __________________________
2. Si: A = {x ∈ / x ∈ [2 ; 5]}
B = {y ∈ / y ∈ 〈0 ; 3〉}
Indicar:
• n(A×B) = ________________________
• n(A2)= ___________________________
3. Resolver:
• (x – 1; 5) = (3; y+2) → xy=
• (x+y; x – y)= (6; 4) → xy=
4. Si: P(x) = x2+3x+2, calcular:
• P(1) + P(2) = _____________________
• P(–3) + P(0) = ____________________
5. Si: P(x) = 2x+5; calcular:
• P(x – 1)= __________________________
• P(3x+1) = _________________________
26](https://image.slidesharecdn.com/lgebra4-240617025348-2ba3a9a6/85/Algebra_4-pdf-TEMAS-SELECTOS-DE-PREPARACION-158-320.jpg)
![Álgebra
159
www.trilce.edu.pe Cuarto año de secundaria
Aprende más
1. Relacionar correctamente, respecto al dominio
de las funciones:
F(x)= –
x 4 A x ∈ –{±2}
G(x)=
–
–
x
x
4
2
B x ∈ [–2; 2]
H(x)= –x
4 2 C x ∈ –{4}
I(x)=
–
x 4
1
2 D x ∈ [4; +∞〉
2. Indicar verdadero (V) o falso (F) según corres-
ponda, dada la función: F(x)= –x
9 2
• F(0) = 3 .................................................( )
• No existe "F(4)"......................................( )
• ( 5 ; 2) ∈ F............................................( )
• (– 8 ; 1) ∈ F.........................................( )
3. Completar:
• Toda función es una ......................
• A la ................ solo le corresponde una
segunda componente
• El dominio de la función es el conjunto de
.....................
4. Calcular la suma de los elementos del dominio
de la función:
F={(3;4), (n+1;7), (n;1), (3;n2), (2;9)}
a) 5 b) –2 c) 2
d) –4 e) 0
5. Sea la función:
F= {(3;5), ; a
4
2
` j, (5;2), (4;9), ; b
3
4
c m}
Calcular "a – b"
a) –6 b) –2 c) 2
d) 18 e) 38
6. Sea "f" y "g" dos funciones donde:
0
1
2
–1
1
3
1
2
4
f g
Calcular: f[g(3)]+g[f(2)]+g[f(0)]
a) 0 b) 1 c) 2
d) 3 e) 4
7. Indicar el rango de: F(x)= – –
x x
7 7
+
a) {0;7} b) {0} c) {7}
d) {2} e) { }
8. Indicar el dominio de: G(x)=
–
x
x
9
7
2
+
a) – {3} b) –{9} c) –{3;–3}
d) e) { }
9. Indicar el rango de: H(x)=
–
–
x
x
3 4
6 5
a) – {
3
4 } b) – {4} c) – {2}
d) e) { }
10. Indicar cuántos valores enteros pertenecen al
dominio de: F(x)= –x
4 2
a) 6 b) 4 c) 3
d) 2 e) 5
11. Indicar la suma de los elementos del dominio
de la función:
F={(7; 4), (m–1; 9), (m; 6), (7; m+3)}
a) 8 b) 11 c) 10
d) 9 e) 12
12. Si (2;m) y (n;7) pertenecen a la función:
F(x)=4x+3, calcular "mn".
a) 16 b) 11 c) 4
d) 9 e) 8
13. Si el dominio de la función: F(x)= –x
1 2
+x–1
es de la forma: [a ; b] – {c}, hallar ab+ac+bc.
a) –3 b) –2 c) –1
d) 0 e) 1](https://image.slidesharecdn.com/lgebra4-240617025348-2ba3a9a6/85/Algebra_4-pdf-TEMAS-SELECTOS-DE-PREPARACION-159-320.jpg)
![Capítulo
160
Colegios
TRILCE Central: 6198-100
Practica en casa
14. Si la producción inicial es de 30 artículos y se
sabe que en los primeros 12 meses aumenta
la cantidad de artículos producidos en forma
lineal; además en el cuarto mes se produjo 190
de ellos. Obtener:
• La expresión que define la producción "P"
en función al tiempo "x" en meses.
• La producción al año.
15. Para niños cuyas edades están entre seis y diez
años, la altura en pulgadas "y" en promedio es
una función lineal de la edad en años "t". La
altura de un niño es 48 pulgadas a la edad de
seis años y de 50,5 pulgadas a la edad de siete
años.
• Expresar "y" en función de "t".
• ¿Qué altura en promedio tiene un niño de ocho
años?
1. Relacionar correctamente, dada la función:
F(x)= ;
;
x x
x x
2 5
1 5
<
2
$
+
+
)
F[F(1)] A 26
F[F(3)] B 37
F[F(4)] C 3
F[F(–1)] D 5
2. Indicar verdadero (V) o falso (F) según
corresponda, dada la función: F(x)=x2–x+2
• (2; 2) ∈ F ...............................................( )
• (–1; 4) ∈ F .............................................( )
• F(1) – F(0) = 0 .......................................( )
• F[F(–2)]+F[F(2)]=0 .................................( )
3. Completar:
• En un par ordenado que proviene de una
regla de correspondencia, a la primera
componente se le denomina pre imagen y a
la segunda .......................
• La abscisa se obtiene de la primera
componente y la ....................... se obtiene
de la segunda componente.
• Se llama función ............. a aquella cuya regla
de correspondencia es de segundo grado.
4. Calcular "ab" en la función:
F = {(2; 7), (6; a–b), (6; 1), (2; a+b)}
5. Calcular "n" en la función:
F={(5; 9), (3; 6), (n; 1), (5; n2)}
6. Dadas las funciones "f" y "g" definidas en los
siguientes diagramas:
1
2
5
4
5
2
2
5
4
6
3
5
f g
Hallar el valor de:
f(1) + g(2)
f[g(4)] + g[f(2)]
7. Hallar el dominio de: F(x) =
–
x
x
2
1
+
8. Hallar el dominio de la función:
F(x) = – –
x x
3 3
4 8
+
9. Sabiendo que:
F(x) = ;
– ;
x x
x x
3 4 0
2 3 0
<
$
+
)
Calcular: E = F[F(1)] – F[F(0)]
10. Si el rango de la función:
F(x) =
x 9
8
2
+
es: 〈a+1 ; b+1] , calcular:
b
a .
11. Hallar el rango de la función:
F(x) = 4+2x – x2 ; x ∈ [–2; 3〉.
12. Determinar el rango de la función:
G(x) =
x
x
1
4
2
+
26](https://image.slidesharecdn.com/lgebra4-240617025348-2ba3a9a6/85/Algebra_4-pdf-TEMAS-SELECTOS-DE-PREPARACION-160-320.jpg)
![Álgebra
161
www.trilce.edu.pe Cuarto año de secundaria
Tú puedes
1. Dada la función "F" tal que: F(4)=1; 2F(2)=3F(3).
Además: F(x) = ax+b. Luego podemos afirmar:
a) F(2)=2 b) F(3)=1 c) F(10)=5
d) F(–2)=7 e) F(2)+F(8)=3
2. Si: F(x+y)=F(x)+F(y) ; F(2)+F(5)=42
Calcular la pendiente de la función lineal "F"
a) 7 b) 4 c) 12
d) 21 e) 6
3. La gráfica de la función: f(x)=mx2+nx –
3
20
intersecta al eje "x" en los puntos (–2; 0) y
(5; 0); al eje "y" en el punto (0; p). Hallar el
valor de: m – 3n+p
a) –2 b) –1 c) 0
d) 1 e) 2
4. Un hombre dispone de 40 m de alambre para
cercar un jardín rectangular. Sabiendo que solo
debe colocarlo sobre tres lados porque el cuarto
limita con su casa, determinar el área máxima
que puede cercar.
a) 120 m2 b) 180 c) 200
d) 300 e) 240
5. Hallar el rango de: F(x) = ex + e–x – 2
Si: e = 2,7182
a) [– 2 ; +∞〉 b) [ 2 ; +∞〉 c) [ 2 ; 2]
d) [2– 2 ; +∞〉 e) [2+ 2 ; +∞〉
13. Si el dominio de:
F(x) =
– –
–
x x
x x
7 12
5 6
2
2
+
es: [a ; b〉 – {c}, calcular "a+b+c".
14. Un vendedor tiene un sueldo mensual de
S/.1000 más el 40% de comisión sobre el monto
vendido en ese mes; entonces:
• Hallar la expresión que defina el ingreso "I"
mensual del vendedor en función del monto
(x) vendido en el mes.
• Si en un mes vendió S/.3500, ¿cuál fue su
ingreso en ese mes?
15. Para niños cuyas edades están entre 5 y 11
años, la altura en pulgadas "y" en promedio es
una función lineal de la edad en años "t". La
altura de un niño es 42 pulgadas a la edad de
cinco años y de 58 pulgadas a la edad de siete
años.
• Expresar "y" en función de "t".
• ¿Qué altura en promedio tiene un niño de
ocho años?](https://image.slidesharecdn.com/lgebra4-240617025348-2ba3a9a6/85/Algebra_4-pdf-TEMAS-SELECTOS-DE-PREPARACION-161-320.jpg)

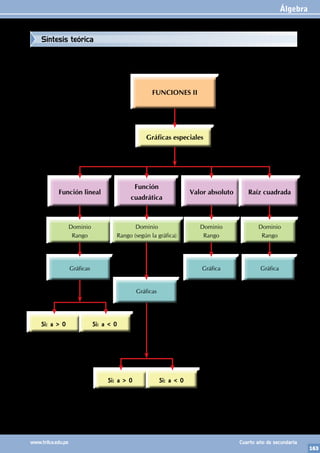

![Álgebra
165
www.trilce.edu.pe Cuarto año de secundaria
Aprende más
1. Relacionar correctamente las tablas respecto a
la gráfica y el cuadrante en el que se definen.
F(x)= x A I y II C
G(x)=x2 B I y III C
H(x)=– x2 C I C
I(x)=x3 D III y IV C
2. Indicar verdadero (V) o falso (F) según corres-
ponda:
• La gráfica de: y=(x – 1)2 – 1 es una
parábola ................................................. ( )
• El mínimo valor de: y = x es cero........ ( )
• La gráfica de: y=5 es una recta............... ( )
• La gráfica de: x=5 no corresponde al de una
función.................................................... ( )
3. Completar:
• F(x) = – x+6 es decreciente y ..............
sobre el origen.
• G(x)=x2 tiene mínimo valor en el punto ............
• H(x)= –x se define en el ............ cuadrante.
4. Al graficar: F(x) = 2x – 4, se obtiene:
y
x
a
b
F
Hallar "a×b".
a) –6 b) –10 c) –4
d) –8 e) –9
5. Hallar los interceptos con el eje "x", en la gráfica
de la función: F(x)=x2+2x–15.
a) –5 y 3 b) –3 y 5 c) 5 y 3
d) –5 y –3 e) 0 y –5
6. Indica cuántas gráficas corresponden a funcio-
nes:
I. II.
y
x
y
x
III. IV.
y
x
y
x
a) 1 b) 4 c) 0
d) 2 e) 3
7. Al graficar: F(x)=x2 – 4, calcular "m.n+p".
y
x
n
m
p
F
a) –10 b) –12 c) –8
d) 6 e) –6
8. Bosquejar la gráfica de: F(x)=x – 3, si: x ∈ [4 ; 6].
a) b)
y
x
y
x
c) d)
y
x
y
x](https://image.slidesharecdn.com/lgebra4-240617025348-2ba3a9a6/85/Algebra_4-pdf-TEMAS-SELECTOS-DE-PREPARACION-165-320.jpg)

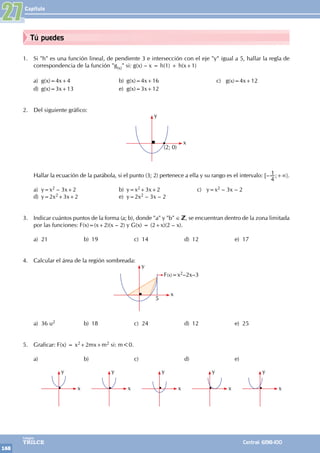












![Capítulo
184
Colegios
TRILCE Central: 6198-100
Practica en casa
1. Relacionar correctamente:
log816 A –2
log8127 B –3
log0,2125 C
3
4
log0,01 D
4
3
2. Indicar verdadero (V) o falso (F):
• El (log20,5) es negativo ..........................( )
• El (log0,10,01) es positivo .......................( )
• No existe [log(log10)] ............................( )
• No existe [log(log0,1)] ...........................( )
3. Completar correctamente:
• La base del logaritmo decimal es .................
• El logaritmo de la .............. siempre es cero.
• El logaritmo equivale a 1 cuando la ............
y el ........... son iguales.
4. Calcular: log0,25+log0,52+log0,254
5. Calcular:
, ,
, ,
log log
log log
0 25 0 04
0 2 0 5
2 5
25 4
+
+
6. Calcular:
log log log
8 81 64
3 4
+ +
2 9
3
8
4
7. Calcular:
log log
6
1
6
1
2 108
+
8. Calcular: (1+log53)(1+log35) – log53 – log35
9. Calcular:
log
log
log
log
log
log
12
4
12
2
12
18
3
3
7
7
5
5
+ +
10. Si x=log23, calcular: log62.
11. Calcular:
8
2 4
log
log log
16
6
4 4 2 2
+
+ +
3 3
3
12. Calcular:
5
36
log
log
4
5
3
3
13. Calcular:
log log log
yz xz xy
1
1
1
1
1
1
x y z
+
+
+
+
+
14. Si "P" representa el precio de venta de un
artículo, y "x" es la demanda correspondiente
en cantidad vendida por día, entonces la
relación entre "P" y "x" se puede expresar,
algunas veces, mediante: P=P0e–ax , donde
"P0" y "a" son constantes positivas. Exprese "x"
como función de "P".
15. La ley de Pareto para países capitalistas, afirma
que la relación entre el ingreso anual "x" y
el número "y" de individuos cuyo ingreso es
mayor que "x" es: logy=logb – klogx, donde
"b" y "k" son constantes positivas. Despeje "y"
de esta ecuación.
30](https://image.slidesharecdn.com/lgebra4-240617025348-2ba3a9a6/85/Algebra_4-pdf-TEMAS-SELECTOS-DE-PREPARACION-184-320.jpg)









![Capítulo
194
Colegios
TRILCE Central: 6198-100
Aplica lo comprendido
1. Hallar el dominio de la función:
f(x) = –15+8x – x2
a) x∈[1;2 ] b) x∈[2; 3] c) x∈[3; 4]
d) x∈[3; 5] e) x∈[3; 6]
2. Sea la función "f" cuya regla de correspondencia
es: f(x)=x3 – 2x+1; calcular el rango de "f", si el
Dom(f)={–2; 0; 3}.
a) {–11; 1; 22} b) {–3; 1; 22}
c) {0; 1; 22} d) {–8; 0; 27}
e) {1; 13; 22}
3. Sea: f(x)=log3(x – 4) y g(x)=logx
Calcular:
f(85)+f(31)+f(7)
g(100)+g(1000)–g(10)
a) 0 b) 1 c) 2
d) 3 e) 4
4. Graficar: F(x)=2x+3
a) b) c)
y
x
y
x
y
x
d) e)
y
x
y
x
5. Se tiene la función: F(x)=ax+6; si la gráfica
pasa por el punto (2; 8), calcular: F(7)
a) 8 b) 10 c) 11
d) 13 e) 14
6. Obtener el valor de:
S = 0,25+(0,25)2+(0,25)3+...
a) 1 b)
1
2 c)
1
3
d)
1
4 e)
1
5
7. Tres números consecutivos de una progresión
aritmética creciente tienen como suma 42 y
como producto 2688. Hallar el tercer término.
a) 11 b) 12 c) 13
d) 22 e) 16
8. Indicar el quinto término de una P.G. creciente
de siete términos, si la suma de los tres primeros
es 26 y la suma de los tres últimos 2106.
a) 42 b) 152 c) 144
d) 162 e) 216
9. Sabiendo que el conjunto de pares ordenados:
F={(3; a2), (3; 1), (5; 4), (5;a+b), (b; 4)}
Representa una función, indicar la suma de
elementos del dominio.
a) 3 b) 5 c) 8
d) 13 e) 11
10. Calcular el área de la región sombreada limitada
por las funciones indicadas.
y
x
H(x)=6–|x–2|
G(x)=4
a) 24 u2 b) 32 c) 48
d) 16 e) 20
32](https://image.slidesharecdn.com/lgebra4-240617025348-2ba3a9a6/85/Algebra_4-pdf-TEMAS-SELECTOS-DE-PREPARACION-194-320.jpg)


![Álgebra
197
www.trilce.edu.pe Cuarto año de secundaria
Practica en casa
1. Resolver:
x
( )
log
log log
x
x
5
5 4
= – colog23
2. Calcular la suma de soluciones de:
9log8x + 2logx8 = 9
3. Calcular el logaritmo en base 16 del logaritmo
de 2 2 en base 8.
4. Calcular:
E=
–
log log Ln
Ln
2 5
1
1 9
1
3
25
3 45
+
c c c
m m m
5. La suma de los tres primeros términos de
una P.A. es la raíz positiva de la ecuación:
x2–17x–84=0. Siendo el sexto término 15,
hallar la razón.
6. Determinar el mayor de los cinco primeros
términos en una P.A., sabiendo que la suma
de los tres últimos es igual al duplo de los tres
primeros, y que la suma de estos cinco términos
es 90.
7. Hallar la suma de todos los números de dos
cifras que son múltiplos de 3.
8. Dado el conjunto: A={1; 2; 3; 4} y dadas las
funciones "F" y "G", definidas de "A" en " "
por:
F(x)=mx – b
G = {(1; a), (1; 7), (2; 5), (m; 6), (4; b), (4; 8)}
Calcular: F(2)+a
9. Hallar el dominio de la función "F", si:
F(x)= – –
x x
2 1
4
10. Sea la función: F(x)=7 – x2
Calcular: Dom(F) – Ran(F)
11. Sea "F" una función cuyo rango es un conjunto
unitario, además:
F={(x+y;y), (xy; x–y), (x–y; y), (4y; x–1)}.
Hallar la suma de los elementos del dominio de
"F".
12. Calcular el valor de "x" que satisface:
logx 343
10
1
20
=
13. Determinar la suma de las soluciones de la
ecuación:
9
log9 [log(x2+x+4)]
=1
14. Se quiere construir un jardín de forma
rectangular de perímetro 60 m. ¿Cuál sería el
área máxima que tendría este jardín?
15. La figura muestra un terreno en forma de
trapecio sobre el cual, se desea construir una
pileta circular de área máxima. Hallar dicha área
si: B=8 – H, b=
H
2
; (H : Altura del trapecio).
b
B
r
o](https://image.slidesharecdn.com/lgebra4-240617025348-2ba3a9a6/85/Algebra_4-pdf-TEMAS-SELECTOS-DE-PREPARACION-197-320.jpg)
![Capítulo
198
Colegios
TRILCE Central: 6198-100
Tú puedes
1. Dada la función: F(x)=
–
– –
x
x
x
x
1
1
1
1
+
+
, hallar su dominio.
a) 〈–1 ; 0] ∪ 〈1 ; +∞〉 b) 〈– 1 ; 1〉 c) 〈– ∞ ; – 1〉 ∪ 〈1 ; + ∞〉
d) 〈–1 ; +∞〉 e) 〈– ∞ ; –1〉
2. Sabiendo que: f(x)=
x 1
1
+
, calcule: f(1)+f(2)+...+f(10)+f(1–1)+f(2–1)+...+f(10–1)
a)
10
1 b) 100 c) 8 d) 10 e) 20
3. Si el dominio de la función "f", cuya regla de correspondencia es: f(x)= – – –
x x a
x
x
3 2
1
2
2
+
+
; a ∈
tiene solo cinco elementos enteros, señale el número de valores enteros de "a".
a) 1 b) 2 c) 3 d) 4 e) 5
4. Dada la función: F(x)=
–
– –
x x
x x x x
3 3
6 15 18 11
2
4 3 2
+
+ + , determine el rango.
a) [2 2 ; +∞〉 b) [1; +∞〉 c) [3; +∞〉 d) [ 2 ; +∞〉 e) [0; +∞〉
5. Dada la función: F(x)= – – –
x x x
9 2 20 5
2
+ +
Halle el mayor elemento de su rango.
a) 1 b) 2 c) 4 d) 3 e)
2
3
32](https://image.slidesharecdn.com/lgebra4-240617025348-2ba3a9a6/85/Algebra_4-pdf-TEMAS-SELECTOS-DE-PREPARACION-198-320.jpg)