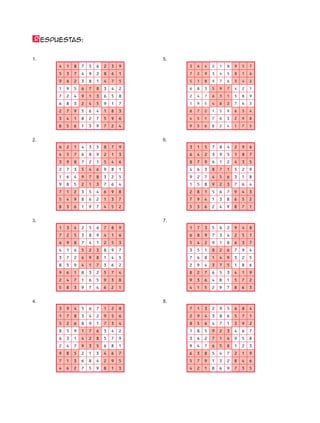
El documento presenta un libro de álgebra dividido en cuatro unidades. Cada unidad contiene temas como leyes de exponentes, ecuaciones de primer y segundo grado, y funciones. Cada tema incluye secciones para aplicar los conceptos, ejercicios de práctica y maratones matemáticas.

1. Álgebra
Actividades

3. Contenido
T
emas Páginas
PRIMERA
UNIDAD
Leyes de la teoría de exponentes I
Aplicamos lo aprendido
Practiquemos
6
8
Leyes de la teoría de exponentes II
Aplicamos lo aprendido
Practiquemos
10
12
Ecuaciones trascendentes
Aplicamos lo aprendido
Practiquemos
14
16
Expresiones algebraicas - Monomios
Aplicamos lo aprendido
Practiquemos
18
20
Polinomios
Aplicamos lo aprendido
Practiquemos
22
24
Maratón matemática 26
SEGUNDA
UNIDAD
Productos notables
Aplicamos lo aprendido
Practiquemos
29
31
División de polinomios
Aplicamos lo aprendido
Practiquemos
33
35
Factorización
Aplicamos lo aprendido
Practiquemos
39
41
Radicación
Aplicamos lo aprendido
Practiquemos
43
45
Racionalización
Aplicamos lo aprendido
Practiquemos
49
51
Maratón matemática 53
TERCERA
UNIDAD
Ecuaciones de 1.er
grado - Planteo de ecuaciones
Aplicamos lo aprendido
Practiquemos
56
58
Sistema de ecuaciones lineales
Aplicamos lo aprendido
Practiquemos
61
63
Ecuaciones de 2.
o
grado - Planteo de ecuaciones
Aplicamos lo aprendido
Practiquemos
66
68
Desigualdades e inecuaciones
Aplicamos lo aprendido
Practiquemos
70
72
Maratón matemática 74
CUARTA
UNIDAD
Valor absoluto
Aplicamos lo aprendido
Practiquemos
76
78
Logaritmos
Aplicamos lo aprendido
Practiquemos
81
83
Funciones
Aplicamos lo aprendido
Practiquemos
85
87
Progresiones
Aplicamos lo aprendido
Practiquemos
90
92
Maratón matemática 94
Sudoku 95

4. Unidad 1

5. Reflexiona
Recuerda
Muhammad Ibn Musa Al-Jwarizmi
Matemático árabe, vivió por los años 780 d.C. y 850 d.C.
Escribió una obra titulada Libro de la reducción, cuya versión
latina tuvo gran influencia en la matemática europea hasta
mediados del siglo XV. En ella indicó las primeras reglas del
cálculo algebraico: la transposición de los términos de uno a
otro miembro de una ecuación, previo cambio de signo, y la
anulación de términos idénticos en ambos miembros. También
estudió las ecuaciones de segundo grado y otras cuestiones
matemáticas. La latinización de su nombre dio lugar a la
palabra «guarismo».
Poco sabemos acerca de la vida de este astrónomo, geógrafo
y matemático musulmán del siglo IX. Era natural de Juwarizmi
(Jhiva), y residió en Irak, en la corte del califa abasida Al-
Namun (813-833).
Con su Kitab al-yabr wa-I-mugaballa o Libro del álgebra
(literalmente, Libro de la reducción, o bien “de la integración”
o “compensación”), Al-Jwarizmi inició la literatura matemática
de los musulmanes. Traducido al latín por Rodolfo Chester y
Gherardo da Cremona (en el siglo XII), ejerció grandísima
influencia en los matemáticos europeos hasta el siglo XV.
De la popularidad de este libro dan prueba dos términos de
nuestro más común lenguaje matemático. En primer lugar, la
palabra “algoritmo”, que hoy, después de haber pasado
por varios significados, indica un “procedimiento constante
de cálculo” y que deriva evidentemente del nombre de Al-
Jwarizmi (igualmente la palabra “guarismo”). Y en segundo
lugar, la misma palabra “álgebra”, introducida en Occidente
por medio de este tratado árabe, en el que el término “Al-
yéber” designa la conocida operación por la que un término
pasa de un miembro a otro de una ecuación, cambiando de
signo. En realidad, esa palabra tiene su raíz más antigua en la
forma babilónica “gabru-inaliaru” que significa “parangonar”,
“confrontar”, “poner en ecuación”.
En la obra de Al-Jwarizmi se estudian no solo las ecuaciones
de primer grado, sino también las de segundo (por ejemplo:
x2
+ 10x - 39 = 0), con un método que substancialmente no
difiere del actual. Las ecuaciones de primer grado cuyas
soluciones han de estar en números enteros (porque se
refieren a problemas que admiten solo tales soluciones, como,
por ejemplo, cuando se busca un número de hombres, o de
caballos, etc.) son tratados con el método de “falsa suposición”
o, como se dice comúnmente, “falsa posición”.
• La fortuna solo sonríe a los audaces, fríos
y prudentes, a aquellos a quienes las
espontaneidades de la imaginación no
son suficientes para lanzarse al peligro.
• Uno de los secretos para disfrutar
de una vida larga y feliz es amar el
trabajo que hacemos.
• Si amas tu profesión descubrirás que
nunca tendrás que volver a trabajar en
tu vida.
• ¡Derrota tu negativismo y halla en
todas las cosas simples motivos de
ilusión!
¡Razona...!
En la figura, ¿cuántos cerillos como mínimo
se deben mover para que dicha operación sea
correcta?
A) 1
B) 2
C) 3
D) 4
E) 5

6. Aplicamoslo aprendido
6 Intelectum 1.°
1 Calcula:
7
A 340
=
A) 343 B) 49 C) 7
D) 247 E) 81
2 Efectúa:
5 8 7 16
S 2
0 1 2 0
=- + + -
A) 40 B) 39 C) 42
D) 43 E) 36
3 Calcula:
4 16
A 2 16
4 2 0 0
= - - + +
_ i
A) 2 B) 3 C) 4
D) 6 E) 5
4 Calcula:
7 9 8 6
A 5
0 0 0 2 0
=- + + + -
A) 2 B) 3 C) 6
D) 1 E) 5
5 Calcula:
5
E 230
=
A) 5 B) 1 C) 25
D)
5
1 E) 10
6 Calcula:
7 8
E 8 7
0 0
= +
A) 20 B) 21 C) 16
D) 22 E) 15
TEMA 1: LEYES DE LA TEORÍA DE EXPONENTES I

7. Claves
7
ÁLGEBRA - ACTIVIDADES UNIDAD 1
7 Efectúa:
A 6 5
3 0 5
6 3 0
= +
_ _
i i
: :
D D
A) 11 B) 1 C) 2
D) 125 E) 126
8 Calcula:
a
a
a
a
a
a
2 3
3
5
8
10
13
15
+ +
A) 4a2
B) 5a2
C) 6a2
D) 7a2
E) 8a2
9 Calcula:
-(-2x6
) por - (-3x4
)(-2x2
)
A) 3x2
B) 6x12
C) -12x12
D) -3x2
E) -6x2
10 Calcula:
2x3
x4
x5
+ 7x6
x6
+ 6x10
x2
A) 13x10
B) 12x15
C) 15x12
D) 9x8
E) 6x7
11 Calcula:
8 5 9
A 5 2 3 1
0 0 0 0 0
= + + - - + +
_ _
i i
A) 9 B) 8 C) 12
D) 10 E) -8
12 Calcula: N =
. .
. .
30 35 6
48 14 15
2 3 4
3 5
A) 2 B) 8 C) 12
D) 6 E) -8
13 Halla: A =
ab2
a3
b4
a5
b6
a7
b8
2b4 ; si ab = 1.
A)
2
1 B)
3
1 C)
4
1
D)
5
1 E)
6
1
14 Efectúa:
P =
a
b
a
b
b
a
( )
a b
a b
2
2
2
- +
-
d
d d
n
n n
A) 5 B) 4 C) 3
D) 2 E) 1
1.
A
2.
A
3.
A
4.
E
5.
C
6.
E
7.
C
8.
C
9.
C
10.
C
11.
D
12.
A
13.
A
14.
E

8. Practiquemos
8 Intelectum 1.°
Nivel 1
Comunicación matemática
1. Escribe verdadero (V) o falso (F) según
corresponda:
▪
▪ Al multiplicar (-3x5
) por -(-2x3
.x2
)
resulta -6x10
.
▪
▪ Luego de reducir (2a + 3a - 4a) '
(8a + 6a - 13a) se obtiene -1.
▪
▪ El resultado de: a2a
+ a3a
cuando
aa
= 2 es la mitad de 24.
▪
▪ Luego de reducir a a a
2 3 2 2
3 2
- -
_ _
i i
el
exponente de a es 2.
2. Efectúa la expresión:
R =
4
1
2
1
2 3
+
- -
d d
n n
Siguiendo un orden operativo, lo primero
es convertir los exponentes negativos en
positivos:
R = 4 + 2
Luego la potencia resultante de cada
sumando es como sigue:
R = +
Obteniéndose finalmente como respuesta:
` R =
Razonamiento y demostración
3. Demuestra que el resultado de operar en:
B = . .
y y y
2 2 1 2 3
0 2 2
2 2
10
- -
-
_ _
_
i i
i
es: y-9
Demostración:
Tomamos de dos en dos los exponentes
de arriba hacia abajo, se tiene:
B = y y y
2 2 1 2 3
0 2 2
2 2
10
- -
-
_ _
_
i i
i
B = (y-2
)2
y y
1 2 3
4 2
-
_ i
Igual que el paso anterior tomamos de dos
en dos de arriba hacia abajo:
B = (y-2
) (y-1
) y3
En los dos primeros factores usa la
ley: potencia de potencia (am
)n
= amn
mientras que en el último factor efectúa el
exponente de y.
B = y-2 .
y-1 .
y
A bases iguales, sumamos exponentes:
B = y y y = y + +
` B =
4. Reduce:
. .
.
E
7 7 7
7 7 7
5
9 7
= -
A) 42 B) 40 C) 36
D) 30 E) 56
5. Efectúa:
S = 7
2
1
10
1
1 1
0
+ +
- -
d d
n n
A) 12 B) 11 C) 14
D) 8 E) 13
6. Efectúa:
M
5
1
6
1
2 2
= +
- -
d d
n n
A) 52 B) 61 C) 62
D) 53 E) 71
7. Simplifica:
A = .3
3
1
3
5
7
6
+
d n
A) 1 B) 2 C) 3
D) 4 E) 5
8. Si xn
= 3, reduce: x3n
- 100
A) -71 B) -72 C) -73
D) -74 E) -75
9. Reduce:
Z =
2
2 4
a
a a
2 2
2 1 1
+
-
+ -
A) 6 B) 3 C) 4
D) 8 E) 9
10. Sabemos que: A = 9 2 1
- -
y B = 814 1
-
Halla el valor de A . B
A) 5 B) 4 C) 3
D) 2 E) 1
NIVEL 2
Comunicación matemática
11. Marca con un aspa las igualdades
verdaderas:
.
5 5
5 5 126
4
8 5
+ =
3 3
3 3 3
24
n
n n
1
3
-
=
-
+
_
_
i
i
. . .
x x x x
x x x x
x
x
4
4
4
+ + + =
b d
l n
222
+ (-1)2
- (-3)3
+ (-1)3
52
= 19
12. Escribe: = o ! según corresponda:
I.
.
x
x x
2 5
2 3 3 4
_
_ _
i
i i 2 3
3 360
II. 1 1 3 1
2 3 0 5
- - - + - -
_ _ _
i i i
2
1
2 1 2 2 1
2 + - +
_ _
i i
III. 16 x x
2 6 6 5 5
1
+ -
- - 3 1
101
-
_ i
Razonamiento y demostración
13. Calcula:
. .
P
2
2 2 2
3 4
3 4 5
=
_ i
A) 1 B) 2 C) 3
D) 4 E) 5
14. Calcula:
.
Q
8
2 16
8
16 2
=
A) 1 B) 2 C) 4
D)
2
1 E)
4
1
15. Efectúa:
. .
M
2
2 2 2
12 2
8 10 7
=
_ i
A) 1 B) 2 C) 4
D) 8 E) 16
16. Luego de reducir:
5
5n n
n
3
3
+
_ i
; n ! N
Indica el exponente final de 5
A) 5n
B) 4n
C) 3n
D) 2n
E) n
17. Calcula:
E
2
2 2
n
n n
3
1 2
= +
+
+ +
A)
3
4
B)
1
2
C) 1
D) 2 E)
2
3
18. Efectúa:
2009
A
5
1
3
1
2 3
0
= + +
- -
d d
n n
A) 25 B) 24 C) 53
D) 37 E) 41

9. 9
ÁLGEBRA - ACTIVIDADES UNIDAD 1
NIVEL 3
Comunicación matemática
19. Subraya la proposición correcta:
a) En la resolución de (56
24
)4
'(53
22
)7
▪
▪ El exponente de cinco es tres.
▪
▪ El exponente de dos es tres.
b) Al resolver:
3
1
4
1
5
1
1 2 3
+ +
- - -
d d d
n n n
▪
▪ La suma de cifras de la respuesta es tres.
▪
▪ La suma de cifras de la respuesta es par.
c) Si: E = 9 2 1
- -
y M = 814 1
-
▪
▪ El valor de E . M = 5
▪
▪ El valor de E . M = 20120
20. Relaciona cada expresión con su respuesta.
(12)4
36
67
46
27
Si: mm
= 3
Calcula: 2m2m
5 3
15 5
4 5
6 2
-
7
1
5
1
3
1
1 2 3
+ +
- - -
d d d
n n n
59
3
18
(3.22
)1.7
Razonamiento y demostración
21. Si: xx
= 5
halla:
T xx x x
1
= + +
A) 57
B) 253
C) 254
D) 5 E) 1
22. Para n !N, simplifica:
3
3 3
n
n n
2
1
+
- +
- - +
A)
5
4 B)
9
4 C) 4
D)
9
5 E)
4
3
23. Efectúa:
W = x x xy 1 4 1 2
1
- - - -
_
b i l
( 2
A) xy B) y/x C) y2
/x2
D) x2
/y2
E) x/y
24. Al reducir:
. ; 0
a a a a
9
3 2
2
Indica el exponente final de a.
A) 1 B) 2 C) 3 D) 4 E) 5
25. Al multiplicar:
.
.
x y
x y
x y
x y
4 2
3 3 3
2 2
3 5
- -
f f
p p
Se obtiene:
x
y m
-
b l
Determina el valor de mm + 1
A) 2 B) 8 C) 4 D) -3 E) -2
26. Calcula el producto de los dígitos del valor de la expresión:
I =
3 3
3 3
3
1 3 1
+
+
- - -
< F
A) 49 B) 56 C) 36 D) 32 E) 81
27. Si: x2n
+ 4 = 29; calcula: xn
� 3
A) 2 B) 3 C) 6 D) 4 E) 8
28. Simplifica:
E
5 5
5 5
n n
n n
3 2
4 3
=
+
+
+ +
+ +
A) 1 B) 4 C) 5 D) 8 E) 7
29. Simplifica:
64 8
64 8
m
m m
2
1 2
1 2 1
'
-
+
+ +
A) 209 B) 324 C) 294
D) 448 E) 298
Claves
Nivel 1
1.
2.
3.
4. A
5. E
6. B
7. B
8. C
9. E
10.E
Nivel 2
11.
12.
13.a
14.a
15.b
16.e
17.a
18.c
Nivel 3
19.
20.
21.B
22.b
23.C
24.D
25.B
26.E
27.A
28.C
29.D

10. Aplicamoslo aprendido
10 Intelectum 1.°
TEMA 2: LEYES DE LA TEORÍA DE EXPONENTES II
1 Efectúa:
P = 27 36
3
1
2
1 1
+
- -
-
b l
A) 2 B) 3 C) 6
D) 3 E) 2
2 Halla el valor de E:
E =
8 81
16 27
5
3
3
4
7
4
4
3
A) 6 B) 10 C) 12
D) 4 E) 16
3 Simplifica:
A = x x x
2 3
3
A) 9
1
x B) 4
3
x C) 3
4
x
D) 9
8
x E) 8
9
x
4 Calcula:
B = . .
54 128 250
3 3 3
A) 80 B) 100 C) 104
D) 110 E) 120
5 Halla el exponente final de a:
E = aa a
a 1
1 -
-
_ i
A) -1 B) 3 C) 2
D) 0 E) 1
6 Reduce:
M = 8
3 5
2 2 2 2 0
+ -
A) 6 B) 9 C) 10
D) m E) 7

11. Claves
11
ÁLGEBRA - ACTIVIDADES UNIDAD 1
7 Efectúa:
.
64 1024
2
4
A) 4 B) 8 C) 2
D) 6 E) 16
8 Calcula P:
P = .
x x x
5 1 5 1
5
5 5
- + -
A) x B) x3
C) 1
D) 0 E) x2
9 Calcula:
V =
16
1
300 192 48
27 75
+ +
+
d n
A) 9 B) 1/11 C) 11
D) 1/9 E) 3
10 Efectúa:
K = . . . .
x x x x x
3 4
3 5
4 6
5 2
3
A) x B) x2
C) x-1
D) x-2
E) x3
11 (UNT - 1984 - B)
Calcula el valor de:
2 2
2
3 5
5
3
f p
A) 250
29
B) 2 40
113
-
C) 1
D) 2 E) 2 200
49
-
12 Resuelve:
2 2 16
8 64
3
5 3
4
A)
2
1
4 B)
3
1
4 C)
4
1
4
D)
5
1
4 E)
6
1
4
13 Calcula:
3 27 81
3
4 25
24
b l
A) 0,5 B) 1 C) 2
D) 1,5 E) 3
14 Reduce:
45 95
9 19
m m
m m
m
+
+
A)
3
1 B)
4
1 C) 5
1
D)
6
1 E)
7
1
1.
E
2.
C
3.
D
4.
E
5.
E
6.
E
7.
A
8.
A
9.
B
10.
A
11.
E
12.
A
13.
E
14.
C

12. Practiquemos
12 Intelectum 1.°
Nivel 1
Comunicación matemática
1. Escribe = o !según estimas conveniente:
I.
18
8 32
+ .
2 2 128
4
3 12
II. 25 11
2 1
+
-
8 32 128
+ +
50 18
+ -
III. 4a
a b
-
4b
a b
-
Razonamiento y demostración
2. Efectúa:
T
8
50 18
= -
A) 1 B) 2 C) 3
D)
2
1 E)
3
2
3. Calcula:
U
20 5
20 45 500
=
-
+ +
A) 10 B) 8 C) 20
D) 4 E) 15
4. Calcula:
D
2
128 54
3
3 3
= +
A) 8 B) 7 C) 9
D) 5 E) 4
5. Calcula:
I
64 1
8 125 27
3 3
3 3 3
=
+
+ +
A) 2 B) 1 C) 3
D) 4 E) 5
6. Efectúa:
S 8 32 50 18
= + + -
A) 6 2 B) 9 2 C) 2
D) 9 E) 8 2
7. Calcula:
A 12 27 48 3
'
= + +
_ i
A) 6 B) 9 C) 8
D) 12 E) 11
8. Efectúa:
L 500 20 45 5
'
= - +
_ i
A) 11 B) 9 C) 10
D) 8 E) 7
Nivel 2
Comunicación matemática
9. Dada la expresión:
1 49 19 64
a a
+ + +
Marca con una “X” si es verdadero (V) o
falso (F) según las condiciones dadas.
I. Si el índice: a = 2, el resultado final es:
2 2 3 3
+ V F
II. Si el índice: a = 3, el resultado final es:
1 V F
10. De la siguiente expresión:
2
128
3
48
a b
2
+
d n
Marca si es verdadero (V) o falso (F)
según corresponda:
I. Si los índices a = 3 y b = 4, entonces
obtenemos: 36 V F
II. Si los índices: a = 6 y b = 4, entonces
obtenemos: 17 V F
Razonamiento y demostración
11. Efectúa:
M
4
32
2
50
3
2
= +
d n
A) 64 B) 36 C) 49
D) 4 E) 9
12. Calcula:
E 5 16 9 25
= + + -
A) 7 B) 8 C) 9
D) 5 E) 4
13. Efectúa:
S 49 27
2 3
1 1
= -
- -
A) 1 B) 2 C) 3
D) 4 E) 5
14. Calcula:
S
10
1000
5
40
3
2
= -
d n
A) 49 B) 81 C) 64
D) 4 E) 9
15. Calcula:
A 3 25 1 64
3
= + + +
A) 6 B) 7 C) 9
D) 5 E) 4
16. Calcula:
L 6 100 400 7
4 3
= + + +
A) 6 B) 5 C) 7
D) 8 E) 9
17. Calcula:
R
3
27
10
40
7
56
3
2
= + +
d n
A) 36 B) 49 C) 64
D) 100 E) 81
Nivel 3
Comunicación matemática
18. Si:
N = 81 49 144 225
3
+ + +
S = 1 3 25 6 5 4
3
+ + +
Luego, calcula
S
N .
Escribe en los recuadros los valores co-
rrespondientes para hallar la solución:
Primero, resolvemos la expresión N:
N 9 7
2 2
2 2
3
= + + +
N = + + +
N
2 3
3
= +
N = +
N =
Luego, resolvemos la expresión S:
S 1 3 5 6 5
2
2
3
= + + +

13. 13
ÁLGEBRA - ACTIVIDADES UNIDAD 1
. .
S 1 3 6 5
3
= + + +
S
2 2
3
= +
S
3
3
=
S =
Nos piden:
S
N = `
S
N
2
7
=
19. Si: x = 37
1
marca verdadero (V) o falso (F) según corresponda:
...
x x x x
16 9 16
2
2 4 30 2
30 3
30 20
30
1 1 1
+ + =
- - -
¿ V o F ?
Razonamiento y demostración
20. Calcula:
E
2
54 16
3
3 3
= +
A) 3 B) 5 C) 8
D) 6 E) 7
21. Efectúa:
R
2
54
3
24
3 3
6
= -
d n
A) 68 B) 64 C) 1
D) 8 E) 729
22. Reduce:
.
3 3 3
2 4
3
5 20
15
A) 3 B) 9 C) 27
D) 312
E) 320
23. Calcula el exponente final de x:
. .
x x x
3 2 4
4 -
A) 2 B) 5/3 C) 3
D) 2/3 E) 2/7
24. Efectúa:
. . ...
V a a a a
11 2
11 3
11 10
11
=
A) a10
B) a C) a2
D) a20
E) a5
25. Halla el exponente final de x:
P =
veces
30
1 2 3
4
4 4
4
...
...
x x x
x x x
veces
3
3
4 3
4 3
4
40
3 6 7 8
444 444
A) 7 B) 8 C) 9
D) 11 E) 5
26. Calcula:
27 5 4 7
3 2
3 1 1
+ + +
- -
A) 6 B) 7 C) 5
D) 8 E) 4
27. Reduce la expresión:
.
.
V
x x
x x
2 2
3
3
3 3
=
A) x x13
36
B) x x10
36
C) x x15
36
D) x2
E) x
C
l
a
ve
s
Nivel
1
1.
2.
A
3.
E
4.
B
5.
A
6.
E
7.
B
8.
A
Nivel
2
9.
10.
11.
C
12.
D
13.
B
14.
C
15.
D
16.
B
17.
B
Nivel
3
18.
19.
20.
B
21.
C
22.
B
23.
D
24.
E
25.
E
26.
C
27.
A

14. Aplicamoslo aprendido
14 Intelectum 1.°
TEMA 3: ECUACIONES TRASCENDENTES
1 Si: m2X - 3
= m7
, calcula: x2
+ x + 1
A) 29 B) 30 C) 31
D) 33 E) 35
2 Halla n.
5n - 4
= 25
A) 7 B) 6 C) 8
D) 9 E) 12
3 Halla x.
a2x -1
= a3 5
_ i
A) 6 B) 9 C) 8
D) 10 E) 11
4 Calcula x.
5x + 7
= 125
A) -3 B) 3 C) 5
D) -5 E) -4
5 Calcula n.
b3n - 3
= b7 3
_ i
A) 6 B) 7 C) 8
D) 9 E) 10
6 Halla el valor de x en:
2 512
3 x
3 4
=
-
A) 0 B) 1 C) 2
D) 3 E) 4

15. Claves
15
ÁLGEBRA - ACTIVIDADES UNIDAD 1
7 Calcula x.
A A8
2x x
8 6
=
- -
A) 6 B) 7 C) 5
D) 4 E) 9
8 Halla n.
27n + 10
= 81n - 10
A) 80 B) 50 C) 60
D) 70 E) 90
9 Resuelve:
a a
5 625
x
3 8
=
-
A) 6 B) 7 C) 8
D) 9 E) 4
10 Halla n.
Si: b b
n 7 112
2
=
_ i
A) 2 B) 4 C) 6
D) 8 E) 10
11 Halla: x
2 16
xx
=
A) 1 B) 2 C) 4
D) 7 E) 8
12 Si (x + 3)x + 3
= 27, calcula x.
A) 0 B) 1 C) 2
D) 3 E) 4
13 Si m2
m3
= 32, halla: m6
A) 2 B) 4 C) 16
D) 32 E) 64
14 Resuelve:
x15
= (343)5
A) 1 B) 3 C) 5
D) 7 E) 9
1.
C
2.
B
3.
C
4.
E
5.
C
6.
C
7.
C
8.
D
9.
E
10.
B
11.
B
12.
A
13.
E
14.
D

16. Practiquemos
16 Intelectum 1.°
Nivel 1
Comunicación matemática
1. Relaciona las ecuaciones exponenciales con sus soluciones:
7
1 5
x
x
2 3
2 3
=
+
+
d n
512
x x 1
x
=
+
_ i
a a
3 9
x x
1 3
=
- -
b b
3 4 108
x
=
_ i
5
3
2
2
3
-
2. Relaciona las ecuaciones exponenciales con sus soluciones:
5x - 10
= 52x - 14
(2x + 8)18
= 2418
(x - 2)(x - 2)
= 99
a3x - 4
= a2x + 8
(3x + 7)3x + 7
= 2525
Analogía
Bases iguales
Exponentes iguales
Razonamiento y demostración
3. Halla x.
A A
7 343
x
2 9
=
-
A) 5 B) 4 C) 6
D) 7 E) 8
4. Calcula x.
ax
. ax
. ax
= a2x + 5
A)
2
5 B)
5
2 C)
3
5
D) 1 E) 5
5. Calcula n.
b2n
. bn + 1
= b19
A) 6 B) 5 C) 7
D) 8 E) 9
6. Halla x.
.
b
b b b
x
3
6
5 3
= _ i
A) 12 B) 10 C) 14
D) 15 E) 18
7. Halla x.
.
a
a a a
x
x x
2
2 4
20
=
+
+
A) 8 B) 9 C) 10 D) 7 E) 11
8. Halla n.
.
. .
a a
a a a a
n
n
3 5
7 8
39
n
5
=
A) 4 B) 5 C) 6 D) 7 E) 8
9. Halla: n
2 .2 2
2
n
4
3
2
2
=
A) 1 B) 2 C) 8 D) 16 E) 10
Nivel 2
Comunicación matemática
10. Emily, Sandra y Estela resolvieron los ejercicios de ecuaciones
exponenciales dejadas en clase. Relaciona el tipo de ejercicio
con su respectiva solución realizada por las alumnas.
,
x 0 5
x 4
=
3 279
3x x 5
=
-
7
21 3
x
x
x
15
3 5
15
=
+
+
+
9 27 81
x x x
1 1 3
=
+ - +
x 2 8
x x 2
x 2
= - -
-
Emily: x = 9
Sandra: x = 2-4
Estela: x = 13
Razonamiento y demostración
11. Calcula x.
a
a x
3
5 8
+
= a20
. a15
A) 9 B) 8 C) 7 D) 6 E) 10
12. Calcula x.
b
b b
x
x
8
14 2
= _ i
A) 4 B) 3 C) 5 D) 2 E) 6

17. 17
ÁLGEBRA - ACTIVIDADES UNIDAD 1
13. Halla y.
A6y + 10
. A2 - 4y
= A2 3 4
_ i
: D
A) 6 B) 5 C) 7
D) 8 E) 10
14. Resuelve:
3125x - 2
= 625x + 1
A) 13 B) 12 C) 14
D) 11 E) 15
15. Resuelve la ecuación:
16 8
x 3 2 4 3
=
_ _
b
i i l
A) 5 B) 8 C) 9
D) 4 E) 6
16. Halla x en:
2
2
2
2 16
x
x
2
4
=
+
-
_ i
A) 1 B) 2 C) 3
D) 4 E) 5
17. Resuelve:
81 274
3 x x
2 2
=
A) 2 B)
2
1 C)
4
1
D)
3
1 E)
8
1
Nivel 3
Comunicación matemática
18. Resuelve las siguientes ecuaciones exponenciales para x:
75x + 1
= 49x - 10
8 16
4 3
x x
2 2
=
(x2
)x
(xx
)23
= (x5
)4
(x3
)2
(x1
)-1
3x
9x + 1
27x + 2
= 32x - 1
92x - 3
272x - 5
3 27
27 9
x x
3 3
=
+ +
2 4
16 4
x x
2 1
=
- -
3
3
1
3 9
1
3
1
x
5
9
1
3
1
3
=
-
-
d
d d
f f
n
n n
p p
(x + 2)x + 2
= 256
Según la representación de las letras con los resultados forma el
apellido de un famoso matemático alemán.
D O K D E N I
1
2
1
- -2 2 5 -1
2
7
E D M
2
1 -7 0
Razonamiento y demostración
19. Calcula n.
272n - 1
= 812n + 1
A)
2
3
- B)
2
7
- C)
2
1
-
D)
2
1
- E)
2
3
20. Halla x.
x
2 2
x 2
2
=
_ i
A) 2 2 B) 1
2 - C) 2
2 1
-
D) 2
2 1
+
E) 2
4
21. Resuelve:
4 2
8 2
x x
3 2 7 1
=
+ -
A) 9 B) 10 C) 11
D) 12 E) 13
22. Halla a en:
5
58 4 16
–
a a 60
=
_ i
A) 210 B) 240 C) 200
D) 180 E) 120
23. Resuelve:
16 2
32 2
x x
2 2
=
- +
A)
5
2 B)
2
5 C)
3
5
D)
5
3 E)
3
4
Claves
Nivel 1
1.
2.
3. C
4. E
5. A
6. A
7. B
8. A
9. c
Nivel 2
10.
11.D
12.A
13.A
14.C
15.E
16.C
17.B
Nivel 3
18.
19.b
20.C
21.c
22.B
23.B

18. Aplicamoslo aprendido
18 Intelectum 1.°
1 El siguiente monomio
T(x) = x x
a
a a
a
a
a a
tiene como grado 3.
Determina el valor numérico de:
R(x) = xa + 3
; cuando x = 2.
A) 31 B) 32 C) 33
D) 34 E) 35
2 Determina el valor numérico de la expresión:
J =
.
.
x
x
x x
x x
a
a
a
a
a
1 2
5
2
10 2
1
3
+
d
b
_
b
n
l
i l
Cuando: x = 3
A) 9 B) 10 C) 11
D) 12 E) 27
3 Si el monomio:
M(x) = 8 x
2 a
4 3
-
es de grado 19.
Halla: a
A) -4 B) -3 C) -2
D) -5 E) -6
4 Halla el grado absoluto del monomio:
M(x) = xb
1
xa
1
Si se cumple: a - b = 8 / ab = 4
A) 1 B) 2 C) 4
D) 0 E) 6
5 Halla n si Q es de segundo grado:
Q x
x
x x
n
n n
12
1
3
2
7
$
= +
-
_ i
A) 7 B) 6 C) 8
D) 5 E) 9
6 Halla a, si el grado absoluto del monomio es 6:
; ; ;
M x y w z
y w
x z
a
a a
5
2
10
37
4
2 2
3
2 3
=
- +
_ i
A) 24 B) 10 C) 14
D) 12 E) 8
TEMA 4: Expresiones algebraicas - monomios

19. Claves
19
ÁLGEBRA - ACTIVIDADES UNIDAD 1
7 Halla (p + q + r) si el monomio:
; ; 15
M x y z x y z
p q r p q r p q r
2 2 2 3 3 3
= + + + + + +
_ i
es de grado absoluto 180.
A) 20 B) 40 C) 50
D) 30 E) 10
8 Si el monomio: M(x) = 4 5 xa + 20
es de grado 24, halla a.
A) 2 B) 3 C) 4
D) 5 E) 6
9 Halla el grado del siguiente monomio:
M(x; y) = .
x y
12
4 9
3
A) 3 B) 6 C) 12
D) 18 E) 16
10 Hallar a si la expresión es de octavo grado.
[( ) . ]
[( ) . ] .
M
x x
x x x
a
a a
2 4 2
2 3 2 3 2 10
=
- -
A) 6 B) 4 C) 2
D) 8 E) 5
11 Reduce:
P x x y xy x
4 1 1 8 5
- - + + -
= +
_ _
i i
A) 3 B) 6 C) 5
D) 7 E) 2
12 Calcula:
S x x x
5 5 3 3 8 1 8
5 - - -
= + + +
_ _ _
i i i
A) 2 B) 1 C) 3
D) 5 E) 6
13 Halla el valor de P.
P = - x2
+ 2x2
- 3x2
+ 4x2
- ... + 80x2
A) 30x2
B) 60x2
C) 120x2
D) 40x2
E) 28x2
14 Efectúa:
( ) ( ) ( )
M
b b b
a b a b a b
2 3
3 4 7
+ +
+ + - - -
=
A) 0 B) 2 C)
b
a
D) 1 E) b
1.
B
2.
E
3.
D
4.
B
5.
A
6.
D
7.
D
8.
C
9.
B
10.
B
11.
E
12.
A
13.
D
14.
D

20. Practiquemos
20 Intelectum 1.°
Nivel 1
Comunicación matemática
1. Escribe verdadero (V) o falso (F) según corresponda:
▪
▪ Al operar: x + x + ... + x se obtiene: x3
x veces
▪
▪ Luego de reducir:
R =
a a b
b b a b a
4 4 4
3 2
- + +
- + - +
_
b il
obtenemos 1.
▪
▪ Al efectuar:
2x(x + 1) - x(2x - 1) obtenemos: 4x.
2. Efectúa la expresión:
GR x GR z
GA P GR y
+
+
_ _
_ _
i i
i i
de:P(x; y; z) = 17x5
y4
z3
Veamos:
Los grados absolutos de “x”; “y”; “z” del monomio son:
▪
▪ GR(x) = ; GR(y) = ; GR(z) =
El grado absoluto también es igual a:
GA(P) = GR(x) + GR(y) + GR(z)
= + +
▪
▪ GA(P) =
Reemplazamos los grados en la expresión solicitada tenemos:
( ) ( )
( ) ( )
GR x GR z
GA P GA y
+
+
=
+
+ = =
Razonamiento y demostración
3. Calcula:
E = (x + 6)(x + 4) - (x + 8)(x + 2)
A) 6 B) 2 C) 1 D) 5 E) 8
4. Efectúa:
S = x(3x + 6) - 3(x2
+ x)
A) 2x B) 3x C) 4x D) 0 E) x
5. Calcula:
R=(5+5+5+...+5) + (4 + 4 + 4 + ... + 4)
10 veces 8 veces
A) 56 B) 64 C) 72 D) 70 E) 82
6. Efectúa:
A=(3 . 3 . 3 . 3 . ... . 3) - (9 . 9 . 9 . 9 . ... . 9)
20 veces 10 veces
A) 38
B) 920
C) 312
D) 0 E) 914
7. Calcula:
S =9 +3(3y - 1) +4(4y - 1) +2(2y - 1)
A) 29 B) 29y C) 0 D) -29 E) -20
8. Efectúa:
N
x y
x x x y
2
2
-
- +
=
+ _ i
: D
A) 0 B) 1 C)
y
x D)
x
y
E) 2
9. Demuestra que el resultado de efectuar la expresión:
Z = 2x(x3
+ 1) - x4
(2 - x) - 2x es x5
.
Resolución de problemas
10. Si el monomio:
M(x; y) = (n3
- 27)x3n + 2
. y8 - n
,
posee un coeficiente igual a 98. Calcula GA (M) + GR (y).
A) 22 B) 25 C) 20 D) 23 E) 24
11. En el siguiente monomio P(x; y), el grado relativo respecto a x,
es 4 y el grado relativo respecto a y es 4.
P(x; y) = 23xa
yb + 1
Calcula: a b
2 2
+
A) 11 B) 13 C) 4 D) 5 E) 7
Nivel 2
Comunicación matemática
12. Marca con un aspa las igualdades verdaderas:
(x + 3)(x + 2) - (x + 4)(x + 1) = 2
(x + 3)(x2
- 3x + 9) - x3
= 28
(a + 2)(a2
- 2a + 4) - (a3
- 3) = 11
13. Escribe = o ! según corresponda:
(x - 2)(x2
+ 2x + 4) (x3
- 10)
((6+6+6+6+6) (2.2.2.2.2))
(7 . 7 . 7 ... 7)4
(49 . 49 ... 49)
15 veces 30 veces
6(a - 1) + 5(a - 1) 11(a - 1)
Razonamiento y demostración
14. Efectúa:
R = (3a + 3a + 3a + ... + 3a) - (a + a + ... + a )
40 términos 110 términos
A) 12a B) 14a C) 5a D) 10a E) 8a

21. 21
ÁLGEBRA - ACTIVIDADES UNIDAD 1
15. Calcula: 1
S +
S = 4(3a + 2) + 3(2a + 1) + 5(6a - 3)
+ 48(1 - a) + 5
A) 9 B) 10 C) 11
D) 12 E) 8
16. Reduce:
3 3 3
...
3
M x x x x x
8
veces
24
3
3
= + + + + +
b l
1 2 3
44444 44444
A) 0 B) 10x C) 9x
D) 12x E) 15x
17. Demuestra que el resultado de operar la
expresión:
B = x x x x x
3
2
6 2
3
11
12
11
21
- + + +
d d
n n es: 5x
Resolución de problemas
18. Dados los monomios de varibles x; y:
A = 3x2
y3
B = 7xy2
C = 2x2
y3
Realiza con ellos las siguientes operaciones
A - C; 3A - 2C;
B
A , y da como resultado
el mayor grado absoluto.
A) 5 B) 4 C) 3
D) 2 E) 1
19. Halla el valor numérico de los polinomios
dando un valor positivo y otro negativo a
las variables:
a) Z(x; y) = 2x2
y3
b) T(x) = - 5x3
¿Cómo son los resultados que se
obtienen?
Nivel 3
Comunicación matemática
20. Relaciona cada expresión con su
respuesta:
1
-2
2
3
6
0
2 3 4
9 3
a b a b a b
a b
+ + - + +
- -
_ _ _
i i i
(x + 6)(x + 1) -(x + 4)(x + 2) - x
Si: R(x; y) = 3x3
yb
Q(x; y) = 10xa + 1
y4
Son términos semejantes
& a + b es:
21. Con los siguientes datos completa la tabla
si para cada caso GR(x) = 14 y GR(y) = 8
Expresión algebraica m + n
( ; )
P x y x y
3 n m
8 2 4
= - -
( ; )
Q x y x y
2 n m
25 6 2 2
= - +
( ; ) 7
T x y x y
n
m
2
1 5
8 4
3
=-
+
-
22. Relaciona cada monomio con su
coeficiente:
( ; )
P x y xy xy
2 2 2
2 4
=- +
( )
Q x a x a x a x
2 4
5 5 5
= - +
( ; )
R x z xz xz xz
4
7
2
7
2
28
3 3 3
= + -
4
7
-
3
2
a
3
4
Razonamiento y demostración
23. De la expresión de tercer grado, calcula el
valor de “a”:
( )
T x
x
x x
a
a a
2 1
4
2 1 4
9
7
=
+
-
A)
70
801 B)
7
800 C) 1
D) 0 E)
801
70
24. Determina el valor de “a” si el monomio
( )
T x
x
x x
a
a a
3
2 9
4
5
=
-
es de primer
grado.
A) 4 B) 5 C) 100
D) 0 E) 1
25. Cuánto es el grado relativo de “y” en el
monomio:
T(x; y; z) =
x y z
x y z
p p r
p p p
3 4 2 3 1
3 1 2 7 3
r
p
- + -
+ + -
Si el grado relativo a “z” es 2012.
A) 4 B) 3 C) 2
D) 1 E) 0
Resolución de problemas
26. Escribe dos monomios de tercer grado
y verifica que se cumpla la propiedad
distributiva:
(A(x) + 7B(x)) . B(x) /A(x)B(x) + 7B(x)B(x)
27. ¿En cuánto excede el área del rectángulo
(I) al área del rectángulo (II)?
I
x + 2
2x + 4
II
x + 4
2x
A) 4 B) 6 C) 8
D) 10 E) 2
28. El grado absoluto de M(x; y; z) es 100
M(x; y; z) =
yz xz
xz yz
b
a a
a
b
b
5
5
b
a
a
b
_
b _
b
_
b _
b
i l i l
i l i l
Halla el grado relativo respecto a z.
A) 20 B) 30 C) 40
D) 50 E) 60
29. Determina: a + b + c si el grado absoluto
del monomio es 91.
A(x;y;z)=31xa+4b+3c
y3a+2b+2c
z3a+b+2c
A) 11 B) 12 C) 13
D) 14 E) 15
30. Determina “m” en el polinomio:
M(x) = 7x. Si. M(M(m)) = 343
A) 0 B) 1 C) 7
D) 3 E) 4
C
l
aves
NIVEL
1
1.
2.
3.
E
4.
B
5.
E
6.
D
7.
B
8.
B
9.
10.
D
11.
D
NIVEL
2
12.
13.
14.
D
15.
E
16.
B
17.
18.
A
19.
NIVEL
3
20.
21.
22.
23.
A
24.
A
25.
A
26.
27.
C
28.
D
29.
C
30.
C

22. Aplicamoslo aprendido
22 Intelectum 1.°
1 Si: P(x + 3) = x
Halla: P(4) + P(5)
A) -3 B) 2 C) -5
D) 3 E) 9
2 Sea P(x) = xa
+ x2
+ x + 1 un polinomio de tercer grado.
Calcula: P(2)
A) 9 B) 4 C) 6
D) 5 E) 15
3 Sea el polinomio: P(x) = x3
+ ax + b, si la suma de coeficientes
es 10 y su término independiente es 4. Halla: ab
A) 20 B) 30 C) 40
D) 50 E) 60
4 Sea el polinomio: P(x) = (3x - 1)n
+ 5x + 1, donde la suma de
coeficientes es 70.
Halla: n + 2
A) 1 B) 2 C) 4
D) 8 E) 10
5 Si el polinomio P(x) es tal que:
2P(x - 1) + P(2x - 1) = 3x + P(x + 1) + P(x - 2)
Además su término independiente es 18; halla la suma de
coeficientes.
A) 12 B) 10 C) 16
D) 8 E) 14
6 Si: P(x) = 2x + 4 / P(F(x)) = 8x + 10
Halla: F(9)
A) 30 B) 39 C) 36
D) 28 E) 30
TEMA 4: POLInomios

23. Claves
23
ÁLGEBRA - ACTIVIDADES UNIDAD 1
7 Sea: P(x) = 2x + 1
Halla: P(P(x))
A) 2x + 3 B) 5x + 1 C) 4x + 3
D) 5x + 7 E) 3x - 1
8 Si: P(x) = xa - 4
+ x2a - 3
- x2a - 4
Calcula: GA(P)
A) a - 4 B) 2a - 3 C) 2a - 4
D) 2a + 5 E) 3a - 1
9 Si: P(x) = 8x8
- 7x6
+ 10x12
- 7
Calcula: GA(P)
A) 8 B) 6 C) 12
D) 13 E) 10
10 Calcula mn, si en el polinomio
R(x; y) = 5xm + 1
yn - 2
+ 4xm + 3
yn - 3
- 6xm + 1
yn - 1
el grado relativo a x es 5 y el grado relativo y es 8
A) 5 B) 7 C) 18
D) 12 E) 11
11 Si: M(x) = (3x5
+ 8)(4x2a
- 4) + x2
- 6
Calcular: GA(M)
A) a - 4 B) 2a - 3 C) 2a - 4
D) 2a + 5 E) 2a - 1
12 En el siguiente polinomio:
M(x) = (x - 3)(x + 3)(x2
- 4)
El términos independiente es:
A) 13 B) -13 C) 36
D) 28 E) 2
13 En el siguiente polinimio hallar la suma de coeficientes:
R(x) = (2x + 3)(4 - x) + 2x2
A) 17 B) 12 C) 13
D) 25 E) 5
14 Al efectuar:
(x + 2)(x + 3)(x + 4)
uno de sus términos es:
A) 8x2
B) 26x C) 9x3
D) 24x E) 1
1.
D
2.
E
3.
A
4.
D
5.
A
6.
B
7.
C
8.
B
9.
C
10.
C
11.
D
12.
C
13.
A
14.
B

24. Practiquemos
24 Intelectum 1.°
Nivel 1
Comunicación matemática
1. Subraya la proposición correcta:
a)Del siguiente polinomio:
P(x; y) = 54
x18
y - 45
x2
y12
• El grado del polinomio es 19.
• El grado relativo respecto a x es 2.
• El grado relativo respecto a y es 1.
b)Dado el polinomio:
P(x; y) = xa - 2
y2a + 7
x2 - a
y4a + 1
Si: GR(y) = 9
• El valor de “a” es un número negativo.
• El valor de “a” es un número impar.
• El valor de “a” es un número par e igual a dos.
c) Se tiene: F(x) = x3
+ x2
- 2x + 3
• El valor de: F(1) + F(2) es 13.
• El valor de: F(2) + F(3) es 44.
• El valor de: F(4) - F(3) es 1.
2. Relaciona cada proposición con su respuesta:
11
8
6
-11
10
-7
12
Sea P(x) = 8x8
- 7x6
+ 10x12
- 7
GA(P) es:
Dado: P(x) = x2
+ x - 1
P(3) es:
Dado:
P(x) = (xm
+ 3)(xm
+ 1)(xm
+ 2)
Grado de P(x) = 24 & m es:
Razonamiento y demostración
3. Muestra que: F(F(4)) = 32 a partir de:
F(x) = 3x - 1
4. Dado: P(x + 1) = 2x + 1
Halla: P(5)
A) 9 B) 7 C) 10 D) 6 E) 4
5. Siendo: F(x) = 2x + 1
P(x) = 3x - 2
Calcula: F(P(4))
A) 23 B) 21 C) 24 D) 26 E) 27
6. Halla el grado del siguiente monomio:
P(x; y) =
7
4 x6m + 10
y3 - 6m
A) 10m B) 6 C) 3 D) 16
E) 13
7. Calcula a, si GR(x) = 4 en:
M(x; y) = 5xa
+ xa+3
y6
+ 6xa
y8
A) 1 B) 2 C) 3 D) 4 E) 5
8. Si: P(x; y) = 2x9
y - 7x2
y9
+ x8
y3
Calcula: GR(x) + GR(y)
A) 15 B) 16 C) 17 D) 18 E) 20
9. Si: F(x) = 5(x - 1) + 1
calcular: F(F(2))
A) 28 B) 26 C) 32 D) 36 E) 21
10. Si: ( )
F x x
7
4 8
= +
Calcula: S F 5 4
-
= ^ h
A) 5 B) 3 C) 1 D) 2 E) 0
Resolución de problemas
11. Si el coeficiente principal de A(x) es 5, calcula su término
independiente.
P(x) = x2
+ (a + 3)x3
+ 2x + a
A) 2 B) 4 C) 0 D) 1
E) 3
12. Si P(x) = x2
+ x - a2
Además: P(a) = 3
Calcula el término independiente de P.
A) 1 B) 3 C) 9 D) 2 E) -9
13. Dados los polinomios:
; 2 3 7
P x y x y x y x y
a b b a a b
1 1 1 2 1
= + +
- - - + -
_ i
; 5 7 6
Q x y x y x y x y
a b b a a b
2 1 2 1 2
= + +
+ - - - -
_ i
si el grado absoluto de P es 10 y el grado absoluto de Q es 6,
halla ab
.
A) 216 B) 316 C) 108 D) 96 E) 128
14. Si: P(x; y) = x y x y y
3
7
7
a b a b
5 7 7
- +
+ +
Donde GR(x) = 5, calcula: a
A) 0 B) 1 C) 2 D) 3 E) 5

25. 25
ÁLGEBRA - ACTIVIDADES UNIDAD 1
Nivel 2
Comunicación matemática
15. Emily, Lucio y Estela resolvieron los
siguientes ejercicios. Identifica el tipo de
ejercicio con su respectiva respuesta.
Ejercicio 1:
A(x) = x2
+ 2x2
+ 3x2
+... + 10x2
Scoef.(A) = ?
Ejercicio 3:
Q(x) =
.
.
.
.
x x
x x
x x
x x
5 5
7 4
4 4
6 3
+
Q(5) = ?
Ejercicio 2:
P(x; y) = - xa - 2
y10 - a
+ 13xa - 8
y10 - a
El GA(P) = ?
Ejercicio 4:
Si F(x) = x2
+ 2x - 3x + x2
+ 3
Determina: R = ( )
F 2 4
- -
Ejercicio 5:
Si P(x; y) = 7x2
+ 3xy - 7x2
Calcula: P(-2; 3)
Emily
Lucía
Estela
Rpta.: -18
Rpta.: 8
Rpta.: 3
Razonamiento y demostración
16. Demuestra que la suma de los grados
relativos respecto a x e y del polinomio:
P(x; y) = x7
y3
+ x8
y2
- x5
y5
P(x; y) es 13.
17. Calcula el término indepediente del
siguiente polinomio:
Y(a) = (2a + 7)(a - 5) - 2(a2
- 20)
A) 5 B) 7 C)9
D) 8 E) 3
18. Calcula GA(K) en:
K(x) = (x9
+ 3)(x5
- x + 1) - x2
(x + 2)
A) 10 B) 5 C) 20
D) 9 E) 14
19. Calcula la suma de coeficientes en:
M(n) = n(n + 1)(n + 2) - n3
+ 2n2
A) 8 B) 5 C) 10
D) 3 E) 7
20. Calcula el grado absoluto del siguiente
polinomio:
E(x) = (x2
- 2)12
+ (x2
+ x4
+ 2)
A) 40 B) 24 C) 30
D) 25 E) 10
21. Si: P(y) = y2a+3
- ya+1
+ y2a+2
Donde GR(y) = 7, halla a
A) 2 B) 3 C) 4
D) 5 E) 7
Resolución de problemas
22. Determina el valor de a2
en el polinomio:
P(x) = 9xa + 8
+ 2x2a + 9
- 3xa + 5
+ 4x
Si sabemos que es de grado 7.
A) 9 B) 2 C) 1
D) 3 E) 4
23. Si se cumple que P(x) + Q(x) = R(x)
donde: P(x) = 7x2
- 8x + 4
R(x) = 10x2
- 2x + 5
calcula la suma de coeficientes de Q(x)
A) 8 B) 15 C) 12
D) 9 E) 10
Nivel 3
Comunicación matemática
24. Escribe verdadero (V) o falso (F) según
corresponda al resolver:
• F(1 - x-1
) = 4x2
- 2x - 5
Para F(3) = -4
• Dado: F(x) = 2(x2
- x) + x - 1
Para: F(F(-1)) se obtiene 5.
• Del polinomio
P(x, y) = xm - 2
y5 - m
+ xm - 3
y9 - m
Si:
GR(x) - GR(y) = -3 & m = 4
Razonamiento y demostración
25. Sea P(x) un polinomio:
P(x - 2) = (2x - 1)10
- (7x - 11)10
+ 3x + 1
Halla el término independiente.
A) 7 B) 8 C) 12
D) 13 E) 14
26. Dado:
P(x) = x(ax + 2c) + bx2
- c
si la suma de coeficientes es cero,
determina: ab + bc + b2
.
A) 1 B) -1 C) 3
D) 0 E) 2
27. Sea P(x) = ax2
+ bx + c; c !0
Además: P(1) = 0
Calcula:
c
a b
+
A) 1 B) -1 C) 2
D) -2 E) 3
Resolución de problemas
28. Cuál será el valor de m en el polinomio:
P(2x - 1) = (5x - 1)m
+ (2x + 1)m
- 2x + 1
Si la suma de coeficientes y el término
independiente de P(x) suman:
24 +
2
3
m
d n + 2m
A) 1 B) 2 C) 3
D) 4 E) 5
29. Dado el polinomio:
F(z + 2) = z2
- 5z + m
Si el término independiente es 6; calcula la
suma de coeficientes.
A) -2 B) -1 C) 0
D) 1 E) 2
30. Dados los polinomios:
P = 2x2
- 5x + 1; R = -x2
- 2 + 6xy
T = -4 + 6x2
- 5x
Realiza las siguientes operaciones:
3R - 2P; 3T - 2R; T + R - P
C
l
a
ve
s
Nivel
1
1.
2.
3.
4.
a
5.
b
6.
E
7.
A
8.
D
9.
B
10.
E
11.
A
12.
E
13.
A
14.
A
Nivel
2
15.
16.
17.
A
18.
E
19.
E
20.
B
21.
A
22.
C
23.
E
Nivel
3
24.
25.
A
26.
D
27.
B
28.
B
29.
A
30.

26. 26 Intelectum 1.°
Matemática
1. Desarrolla y determina los valores de x.
I. 3x
. 3x
... 3x
= 912
& 3 = 3
12 veces x =
II. m2x - 7
= m3
& 2x - 7 = 3 & x =
III.
a
a a ax
3 1
=
-
& a = a & x =
IV. 2-x
=
4
1 &
2
1
2
1
= & x =
2. Determina M.
M =
x
x x x
x
x
3
4
7 3
8
18
$
- +
A) 2x B) x3
C) x2
D) x E) x
2
3. Halla el área del cuadrado de lado (x - 4).
A) x2
- 16 B) x2
- 4x - 16
C) x2
+ 4x + 16 D) x2
- 8x + 16
E) x2
+ 8x + 16
4. Efectúa e indica uno de los términos de:
(x - 3)(x - 7)(2x + 5)
A) 8x B) -15x2
C) 2x2
D) 25x E) 50
5. Si: Los siguientes términos de los polinomios P y Q son
semejantes, determina: a + b
P(x; y) / 7xy3
; Q(x; y) / 3xa - 4
yb + 1
A) 4 B) 6 C) 7
D) 3 E) 10
6. Indica el valor de GA(P) + GR(x)
P(x; y) = 7x8
y7
+ 2y8
x10
- 3x3
y12
A) 30 B) 28 C) 15
D) 18 E) 12
7. Determina el valor de x en:
2 32
x
x 17 3
=
-
A) 1 B) 5 C) 4
D) 7 E) 2
8. Encuentra el valor de m:
318
= mm
A) 3 B) 18 C) 9
D) 6 E) 81
9. Encuentra un polinomio de grado 3 que sea divisible entre
(x2
+ 1), y cuya suma de coeficientes sea nulo, además,
P(-2) = 15.
A) x3
- 3x2
+ 3x - 6 B) 3x3
- x2
+ 3x - 9
C) x3
- 3x2
+ 6x - 3 D) 3x3
- 3x2
+ 3x - 3
E) x3
+ 5x2
+ x + 9
10. Calcula el valor de a, si el siguiente monomio es de grado 30.
N(x; y; z) =
6
-
x y
3
a
a a
2
3
10 1
+ -
w z
A) 5 B) 8 C) 12
D) 10 E) 20
11. Dado el siguiente polinomio P(x) = x2
- x + b, determina el valor
de b, si: P(3) = 12
A) 3 B) 6 C) 8
D) 12 E) 4
12. Dado el polinomio Q(x) = 7x - 5. Si Q(P(x)) = 12x + 2, halla el
valor numérico de P(-7).
A) -53 B) -82 C) -1
D) -11 E) 4
13. Si: f(x + 4) = ax + b; f(-1) = -32 y f(2) = -11
Determina a - b.
A) 5 B) 10 C) 4
D) -4 E) -2
Si xx
= 3, determina:
E =
x
x
x
x x
2
3 x 1
+ +
Desarrollando:
E =
x
( )
( ) ( )
x
x x
x
x x
x
x
x
x x x
2
3
2
3 x
x 1
$ $
=
+
Reemplazamos xx
= 3, en E:
E =
3
3 3
3
3
2
3 3
2
6
$ = = 34
`E = 81
Resolución:

27. Unidad 2

28. Recuerda
DIOFANTO DE ALEJANDRÍA
Matemático griego. Cronológicamente se le sitúa en la segun-
da mitad del siglo II d. C. Sus escritos contribuyeron de forma
notable al perfeccionamiento de la notación algebraica y al
desarrollo de los conocimientos del álgebra de su época. Me-
diante artificios de cálculo supo dar soluciones particulares a
numerosos problemas, y estableció las bases para un posterior
desarrollo de importantes cuestiones matemáticas.
Perteneció a la escuela alejandrina, nació hacia el 250 y murió
a los ochenta y cuatro años.
Por su originalidad y sus aportaciones, Diofanto fue llamado
por los historiadores el padre de los algebristas modernos. En
una época de decadencia y de pura exégesis, como era el si-
glo en que vivió, su obra constituye una notabilísima excep-
ción. Generalmente se le atribuye la introducción del cálculo
algebraico en las matemáticas. Según parece, inició el empleo
sistemático de símbolos para indicar potencias, igualdades o
números negativos.
De la obra de Diofanto se conserva los seis primeros libros y
un fragmento del séptimo de un tratado titulado Aritmética,
integrado originariamente por trece. Los libros conservados
contienen un tratado sobre las ecuaciones y sobre sistemas de
ecuaciones determinadas e indeterminadas, en el que se bus-
ca, de modo sistemático, la solución en números racionales.
Reflexiona
• Solo puedes volverte un profesional
consumado en algo que te fascine. No
hagas del dinero tu meta. Mejor haz las
cosas que te encantan, y hazlas tan bien
que no dejes de llamar la atención.
• Ten el valor de seguir tu pasión, y si no
sabes cuál es, comprende que una razón
de tu existencia en la Tierra es descubrirla.
• El trabajo de tu vida consiste en encontrar
el trabajo de tu vida, y luego tener la
disciplina, la tenacidad y la dedicación
necesarias para ejercerlo.
¡Razona...!
¿Cuántos palitos debes de mover como mínimo para que el caballito
mire al lado opuesto?
A) 2
B) 3
C) 4
D) 5
E) 1

29. Aplicamoslo aprendido
29
ÁLGEBRA - ACTIVIDADES UNIDAD 2
tema 1: productos notables
1 Efectúa:
M = (x + 1)3
+ (x - 1)3
- (2x3
- x)
A) 10x B) 12x C) 6x
D) 6 E) 7x
2 Reduce:
G = (x - 5)2
- (x - 7)(x + 2) + 9 + 5x
A) 45 B) 48 C) 47
D) 46 E) 49
3 Efectúa:
N = (x + 2)2
- (x + 1)2
- 3
A) 0 B) 2x C) 3x
D) x E) 5
4 Efectúa:
xy
x y x y
2
2 2
+ - -
_ _
i i
A) 3 B) x C) 2
D) xy E) 6
5 Efectúa:
A = (x + 1)(x - 1)(x2
+ 1) + 1
A) x2
B) x4
C) x3
D) x8
E) 0
6 Si: 5; 3
x y xy
+ = =
Halla: x3
+ y3
A) 125 B) 100 C) 80
D) 50 E) 25

30. Claves
30 Intelectum 1.°
1.
e
2.
b
3.
b
4.
c
5.
b
6.
c
7.
a
8.
a
9.
C
10.
a
11.
d
12.
b
13.
e
14.
A
7 Efectúa:
E = (a + 4)(a2
- 4a + 16) - 26
A) a3
B) a2
C) 0
D) a6
E) 2
9 Efectúa:
A
b
a
a
b
b
a
a
b
2 2
= + - -
d d
n n
A) 2 B) 3 C) 4
D) 12 E) 8
11 Efectúa:
M = (2x + 5)(2x + 3) - 4x2
- 15
A) 8 B) 8x C) 7x
D) 16x E) 10
13 Halla P:
P = (x + 1)(x2
- x + 1) - x3
A) 0 B) 2x C) -2x
D) 2 E) 1
8 Efectúa:
A = (x + 4)2
- (x - 2)2
- 12x
A) 12 B) 8 C) 6
D) 5 E) 4
10 Calcula N:
1
N x x
1 1
6 6
6
= + - +
_ _
i i
A) x2
B) x C) 0
D) 1 E) -x
12 Si: a3
- b3
= 28 y a - b = 4
Calcula: ab
A) -2 B) -3 C) -4
D) 3 E) 2
14 Efectúa:
( 2) 2
P 3 3 1 3
2 2
= + + - -
_ i
A) 11 B) 10 C) 12
D) 9 E) 8

31. Practiquemos
31
ÁLGEBRA - ACTIVIDADES UNIDAD 2
Nivel 1
Comunicación matemática
1. Relaciona cada proposición con su respuesta.
Si: x = 3 1
+
Calcula: x2
- 2x + 1
Si: x - y = 2 / xy = 3
Halla: x2
+ y2
Efectúa:
(2a-3b)(4a2
+6ab+9b2
)+27b3
7a3
8a2
3
-3
10
11
8a3
A.
B.
C.
2. Coloca los signos matemáticos adecuados de tal manera que se
cumplan las siguientes identidades:
(a - b)3
= a3
3a2
b 3ab2
b3
(x - a)(x - b) = x2
(a b)x ab
(a b)(a - b) = a2
b2
(a b)(a2
ab b2
) = a3
- b3
Razonamiento y demostración
3. Calcula: Z = (x + 2)2
+ (x + 3)2
- 2x(x + 5)
A) 11 B) 9 C) 16
D) 14 E) 13
4. Efectúa: M = (x + 5)2
+ (x - 4)2
- 2x(x + 1)
A) 51 B) 43 C) 31
D) 41 E) 37
5. Efectúa: M = [(x + 2y)2
- x2
- 4y2
] ' xy
A) 1 B) 2 C) 3
D) 4 E) 8
6. Si: a + b = 7 / a2
- b2
= 42
Calcula: a - b
A) 3 B) 5 C) 6
D) 7 E) 9
7. Efectúa:
K =
a
a
a
a
4
16
2
4
2 2
+
- +
+
-
A) 0 B) a - 8 C) 2a - 6
D) 2a - 8 E) 3a - 6
8. Efectúa: A = (a - 1)(a2
+ a + 1) - a3
A) -a B) -1 C) 2a
D) -2 E) -2a
9. Efectúa:
R = (x + 2)(x2
- 2x + 4) - 8
A) 2x B) x3
C) 2x - 3
D) 2x + 3 E) x2
Resolución de problemas
10. Reduce:
ab
a b a b
2 2
+ - -
_ _
i i
A) 0 B) 1 C) 2
D) 3 E) 4
11. La expresión: a8
- b8
se puede escribir como:
A) (a2
+ b2
)2
(a2
- b2
)2
B) (a - b)8
C) (a4
+ b4
)(a4
- b4
)
D) (a5
+ b5
)(a3
- b3
)
E) (a - b)(a7
+ b7
)
Nivel 2
Comunicación matemática
12. Marca la igualdad correcta:
A) (a - b)3
= (b - a)3
B) (a - 1)3
= a3
- 3a + 1
C) ( a + 9)(a - 9) = a2
- 80
D) (a + 3)2
+ (a - 3)2
= 2a2
+ 18
E) (x + 2)(x - 3) = x2
+ x + 6
13. Marca con un aspa las igualdades verdaderas:
(c + 1)3
- (c - 1)3
= 2(1 + 3c2
)
(x3
+ bb
)(x3
- aa
) = x6
+ (bb
- aa
)x3
+ aa
. bb
(a + b)(a - b) = a2
+ b2
(x2
+ y2
)2
= x2
+ y2
+ 2xy
(x + y + 3)(x + y - 3) = x2
+ y2
+ 2xy - 9
Razonamiento y demostración
14. Efectúa:
(x + 2)2
- (x + 2)(x - 2) - 4x
A) 6 B) 4 C) 8
D) 10 E) 12
15. Efectúa:
(a + b)2
- (a + b)(a - b) - 2b2
A) 2ab B) ab C) 3ab
D) -ab E) -2ab

32. 32 Intelectum 1.°
16. Efectúa:
(x + 2)(x + 6) - (x + 4)2
A) -10 B) -2 C) -4 D) -6 E) -8
17. Reduce:
M 7 3 7 3
2 2
= + + -
_ _
i i
A) 10 B) 13 C) 20 D) 18 E) 36
18. Efectúa:
Q a a
2 2 4
4 4
8
= + - +
_ _
i i
A) 1 B) a4
C) a2
D) 0 E) a
19. Efectúa:
[(2 )(2 )(3 )(3 )]
M 3 3 2 2 2
= + - + -
A) 64 B) 81 C) 25 D) 36 E) 49
20. Si: a - b = 4; ab = 2; halla: a3
- b3
A) 64 B) 76 C) 88 D) 100 E) 52
21. Efectúa:
A = (x - 3)(x2
+ 3x + 9) - (x3
- 30)
A) 2 B) 1 C) 6 D) 0 E) 3
Resolución de problemas
22. Si: x = (a + b)4
;
y = (a - b)4
;
z = a2
+ b2
Calcula: ab
A)
x y
4
-
B)
x y
8
-
C)
z
x y
8
-
D)
y
x E) x2
+ y2
23. Calcula: E = 5
2 1 2
3
+ -
_ i
A) 8 B) 9 C) 10 D) 6 E) 7
Nivel 3
Comunicación matemática
24. Determina la operación efectuada correctamente.
A) (x - 7)(x - 3) = x2
- 10x - 21
B) (x + aa
)(x - bb
) = x2
+ (aa
- bb
)x - aa
bb
C) (a + 2)2
+ (a - 2)2
= (a2
+ 4)
D) (a2
+ 32
)(x2
+ 22
) = (ax + 6)2
+ (2a + 3x)2
E) (a + 2)3
- (a - 2)3
= 4(4 + 3a3
)
25. Ordena los productos notables según su número de términos
algebraicos dados en el segundo miembro, de menor a mayor.
A) (a + b)2
/ a2
+ 2ab + b2
B) (a + b + c)2
/ a2
+ b2
+ c2
+ 2(ab + ac + bc)
C) (a - b)3
/ a3
- b3
- 3ab(a - b)
D) a2
- b2
/ (a + b)(a - b)
E) (a + b)2
- (a - b)2
/ 4ab
Razonamiento y demostración
26. Efectúa:
( 3) (4 ) 2
A 5 5 5
2 2
= + + - +
A) 32 B) 36 C) 34 D) 29 E) 35
27. Efectúa:
A= (2x + 3)2
+ (3x + 1)2
- 13x(x + 1) - 10
A) 5x B) 4x C) 16 D) 8x E) 8
28. Efectúa:
R = 3
5 1 2 5
2 2
+ - - +
_ _
i i
A) 6 5 B) 4 C) 0 D) 4 5 E) 10
29. Efectúa:
A = (a2
- 5b3
)2
+ 10a2
b3
- 25b6
A) 2a4
B) a4
C) 8 D) 0 E) 1
30. Efectúa:
R = (x8
+ 3)(x8
- 3) - (x16
- 10)
A) 2 B) 3 C) 4 D) 0 E) 1
31. Efectúa:
A = (x + 1)(x2
- x + 1)(x - 1)(x2
+ x + 1)
A) 2x6
- 1 B) x6
C) x6
+ 1 D) x6
- 1 E) 4
Resolución de problemas
32. Desarrolla:
Z=(m+n)2
(n+p-m)(m+p-n)+(m-n)2
(m+n+p)(m+n-p)
A) mnp B) m2
n2
p2
C) 2mnp2
D)
4
1 mnp2
E) 4mnp2
33. Simplifica: E = (x2
+ x + 1)(x2
- x + 1) - x2
(x2
+ 1)
A) - 2 B) -1 C) 0 D) 1 E) 2
Claves
Nivel 1
1.
2.
3. e
4. d
5. d
6. c
7. c
8. b
9. b
10. e
11. C
Nivel 2
12. d
13.
14. c
15. A
16. c
17. c
18. e
19. E
20. c
21. e
22. C
23. E
Nivel 3
24. B
25.
26. e
27. A
28. a
29. b
30. e
31. d
32. e
33. D

33. Aplicamoslo aprendido
33
ÁLGEBRA - ACTIVIDADES UNIDAD 2
tema 2: DIVISIÓN DE POLINOMIOS
1 Calcula la suma de coeficientes del cociente que resulta de
dividir.
x x
x x x
2 1
5 10 10
2
3 2
+ +
+ + +
A) 7 B) -3 C) 4
D) -4 E) 0
2 Calcula el resto en la división:
a a
a a a
1
2 1
2
4 2
+ +
- - -
A) -2 B) -1 C) 0
D) 1 E) 2
3 Halla P si la división, es exacta.
x x
x x x P x
2 3
4 5
2
2 3 4
- + +
- + + +
A) -13 B) -14 C) -15
D) -16 E) -17
4 Calcula A . B, si la división:
x x
x x x Ax B
7 2 1
7 12 18
2
4 3 2
+ +
- + + +
deja como resto: 4x + 5
A) 60 B) 61 C) 62
D) 63 E) 64
5 Halla la suma de coeficientes del cociente de:
x
x x x x
3
2 3 9 11 33
4 3 2
-
- - - +
A) 0 B) -3 C) -4
D) -5 E) -6
6 Calcula el cociente de:
x
x x x
1
4 7 12
3 2
+
- + +
A) x2
- 5x + 12 B) x2
- 5x -12 C) x2
+ 5x + 12
D) x3
- 5x -12 E) x3
- 5x + 12

34. Claves
34 Intelectum 1.°
1.
c
2.
c
3.
c
4.
e
5.
e
6.
a
7.
d
8.
a
9.
b
10.
d
11.
e
12.
E
13.
e
14.
d
7 Divide y señala el cociente:
x
x x x
2 1
16 24 28 5
4 3 2
-
- + -
A) 8x3
- 8x2
+ 5 B) 8x3
-1
C) x3
- 8x2
+ 10x + 5 D) 8x3
- 8x2
+ 10x + 5
E) 8x3
+ x + 5
9 Halla n, si en la siguiente división el residuo es 40.
x
x x x x n
2
4 3 2
-
+ + + +
A) 8 B) 10 C) 12
D) 14 E) 2
11 En la división:
x
x x x
3 3
6 12 8 9
2
3 2
+
- + -
Halla el término independiente del resto.
A) 1 B) 2 C) 5
D) 4 E) 3
13 Halla el residuo en la siguiente división:
x x
x
1
2
4
- +
A) x B) -2x C) x - 1
D) 2x E) -x
8 Calcula el cociente de:
x
x x x
3 5
3 2 11 10
3 2
+
+ - -
A) x2
- x - 2 B) x2
+ 3x + 1
C) 2x2
+x-1 D) 2x2
- x + 4
E) x2
- 2x + 3
10 Halla el resto en:
x
x x
6
5 1
2009 2
-
- + +
_ i
A) 30 B) 35 C) 37
D) 38 E) 41
12 Señala el coeficiente del término lineal del cociente en:
x x
x x x x
4 3 1
8 6 23 15 4
2
4 3 2
- +
+ - + +
A) 1 B) 2 C) 3
D) 4 E) -4
14 Si:
x x
x x q
1
5
2
4 2
+ +
+ +
Deja como resto - 4x + 3. Halla: q
A) 10 B) 1 C) 2
D) 8 E) -1

35. Practiquemos
35
ÁLGEBRA - ACTIVIDADES UNIDAD 2
Nivel 1
Comunicación matemática
1. Del siguiente esquema de Ruffini:
2 9 7 10 a b
-4 -8 c d 8 -48
2 1 3 -2 12 -50
Calcula: a + b - 3c + d
A) 1 B) 2 C) 3
D) 4 E) 5
2. Del esquema de Ruffini:
3 18 -26
6 28 0
3
Halla la suma de coeficientes del cociente.
A) 25 B) 20 C) 26
D) 28 E) 15
Razonamiento y demostración
3. Divide:
x x
x x x x x
3 2 4
6 13 13 23 34 25
2
5 4 3 2
- -
- + + - -
y halla el valor del residuo.
A) 1 B) 2 C) 3
D) 4 E) 5
4. Divide:
x x
x x x x x
2 2
2 2 3 7 11 8
3
5 4 3 2
- -
- + + + -
Da como respuesta la suma de coeficientes del residuo.
A) 10 B) 15 C) 20
D) 25 E) 30
5. Divide:
x x
x x x x
3 5 3
6 15 24 7
2
4 3 2
+ -
+ - + -
Halla el valor del residuo.
A) x - 1 B) x + 5 C) x - 5
D) 5x - 1 E) 5x + 1
6. Divide:
x x
x x x x
2 4 2
6 2 4 5 3
2
4 3 2
- +
+ - - +
y da como respuesta la suma de coeficientes del cociente.
A) 17 B) 18 C) 19
D) 20 E) 21
7. Divide:
x x
x x x
2 3 5
4 8 15 6
2
3 2
- +
- + -
Indica el residuo.
A) 2x - 1 B) 2x + 1 C) 3x - 2
D) 3x + 2 E) 5x - 1
8. Divide:
x x
x x x
3 2
6 4 3
2
4 3
+ +
- - -
Indica el cociente.
A) 2x2
+ x + 1
B) 2x2
- x - 1
C) 2x2
+ 3x + 1
D) 2x2
- 3x - 1
E) 2x2
- 5x + 3
9. Da como respuesta la suma de coeficientes del cociente de la
siguiente división:
x x
x x x x
3 2
2 5 3 1
2
4 3 2
+ +
+ + + +
A) 6 B) 7 C) 1
D) 3 E) 5
10. Divide:
x
x x x x
4
5 12 37 24 32
4 3 2
+
+ - - -
y señala el menor coeficiente del cociente.
A) 5 B) -8 C) -5
D) -4 E) -10
11. En la división, halla el cociente.
x
x x x
1
3 3 1
3 2
+
+ + +
A) 1 B) x2
+ 1 C) x2
+ 2x + 1
D) x2
- 2x + 1 E) x2
+ 2x - 1
12. Encuentra el cociente de:
x
x x x
1
5 2 2 1
3 2
-
- - -
A) 5x2
+ 3x + 1 B) 5x2
- 3x + 1
C) 4x2
+ 3x + 12 D) 5x3
+ 3x + 2
E) 5x2
- 3x - 1
13. En la división:
x
x x x x
2
2 3 2 12 3 2 2
4 3 2
-
+ - + -
Calcula el término independiente del cociente.
A) 2 B) 2 2 C) 3 2
D) 4 2 E) 0

36. 36 Intelectum 1.°
14. Halla el resto en:
x
x x x
2
2 4 7 10
3 2
-
- + -
A) 14 B) -10 C) 4
D) -4 E) -8
15. Calcula m + n, si:
x
x mx nx
1
1
3 2
-
+ + +
es exacta.
A) 0 B) -1 C) -2
D) -3 E) -4
16. Divide:
x
x x x
3
27 81 5 19
425 424
+
+ - -
y calcula el residuo.
A) 0 B) -1 C) -2
D) -3 E) -4
17. Luego de dividir se obtuvo de residuo 12;
calcula el valor de a.
x
x x x a x a
2
4 3 12 4
4 3 2
-
- - + + +
_ i
A) 1 B) 3 C) 2
D) 4 E) 5
18. En la siguiente división, halla el resto:
x
x x x
2
2 30
4 3 2
+
+ + -
A) 3 B) 2 C) -3
D) -2 E) -6
19. Halla el resto al dividir:
x
x x x
1
2 3
3 2
+
+ + +
A) -1 B) 0 C) 1
D) 2 E) -2
20. Calcula el resto en la siguiente división:
x
x x x
1
5 3 2 15
3 2
+
- + +
A) -2 B) 1 C) 3
D) 5 E) 7
Resolución de problemas
21. Determina el valor de:
Z =
( )
a b
a b ab
ab
+
+ - , , R
a b
a b 0
! !
!
Si:
a2
+ 11a + 2 = 0
b2
+ 11b + 2 = 0
A)
121
7 B)
121
9 C)
120
1
D)
9
7 E)
121
13
-
22. Al dividir el polinomio P(x) entre
(x2
+ 1)(x - 3) se obtuvo como resto:
x2
+ 4x - 6. ¿Cuál será el resto de
dividir P(x) ' (x - 3)?
A) 12 B) 11 C) 10
D) 15 E) 20
Nivel 2
Comunicación matemática
23. Del esquema de Ruffini:
10 12 -5
25 5 0
'
5
Calcula la suma de coeficientes del
cociente.
A) 6 B) 7 C) 5
D) 9 E) 4
24. Indica verdadero (V) o falso (F), en la
siguiente división:
x
x x
1
2 1
3
5
+
- -
1. El grado del dividendo es 3. ( )
2. El cociente es de grado igual a 2. ( )
3. El grado del resto puede ser 2. ( )
A) FVF B) FFV C) VVF
D) FFF E) FVV
Razonamiento y demostración
25. Divide:
x x
x x x x x x
2 3 1
6 9 4 3 2
3 2
7 6 4 3 2
+ -
+ + + + - +
Indica el coeficiente del término
cuadrático del residuo.
A) 3 B) 2 C) -1
D) 4 E) 5
26. Halla el cociente en la división:
x x x
x x x x x
3 3 1
5 10 10 5 1
3 2
5 4 3 2
- + -
- + - - +
A) x2
+ x + 1
B) x2
- 2x + 1
C) x2
+ 2x + 1
D) x2
- x + 1
E) x2
+ x - 1
27. Determina el valor de (m + n), si la
siguiente división es exacta:
x x
x x x mx n
3 5
2 7
2
4 3 2
- +
+ - + +
A) 16 B) 15 C) 30
D) 31 E) 32
28. Halla m si la división:
x x
x mx mx
2 4
2 4 8
2
3 2
- +
- + - es exacta.
A) 1 B) 2 C) 3
D) 4 E) 5
29. Calcula a b
3
+ , si la división es exacta.
x x
x x ax b
3 3 2
3 5
2
4 2
+ +
+ + +
A) 1 B) 2 C) 3
D) 4 E) 5
30. Halla (a + b) en la siguiente división
exacta:
x x
x x x ax b
2 1
4 6
2
4 3 2
+ +
+ + + +
A) 1 B) 2 C) 3
D) 4 E) 5
31. La siguiente división:
x px
x x x x q
1
4
3
4 3 2
+ -
+ - + +
tiene un resto de la forma: 2x2
+ 8x + 5
Halla: p + q
A) 2 B) 1 C) 0
D) -1 E) -2
32. Divide:
x x
x x x
4 2
6 5 10
2
3 2
- +
- + +
Da como respuesta el resto.
A) x + 7 B) 0 C) 2x + 1
D) 5x - 2 E) -5x + 14
33. Indica la suma de coeficientes del cociente
que se halla al dividir.
x
x x x x
2 1
4 4 11 6 6
4 3 2
-
+ - + -
A) 2 B) 3 C) -4
D) 1 E) -1
34. Halla el coeficiente mayor del cociente al
dividir:
x
x x x
5 3
20 3 16 6
4 3 2
+
- + -
A) 4 B) 5 C) 6
D) -5 E) -4

37. 37
ÁLGEBRA - ACTIVIDADES UNIDAD 2
35. Halla el cociente al dividir:
x
x x x
2
2 5
3 2
+
+ + -
A) x2
- 1 B) x2
+ 1 C) x2
+ x + 1
D) x2
+ 2 E) x2
- x + 1
36. Halla el residuo de dividir:
x
x x x x x
2
4 32 6 12 5 1
78 75 41 40 4
+
+ + + + +
A) 81 B) 82 C) 83
D) 84 E) 85
37. Calcula n, si al dividir:
( )
x
x x n x nx
2
32 1 10
100 95 3 2
+
+ + + + +
deja como residuo 14.
A) - 2 B) - 3 C) - 4
D) - 5 E) - 6
38. Cuando se divide:
( ) ( )
x
x x x m
7
2 7 2 7 15 15 7
3 2
-
+ - - + - + +
Se obtiene como resto (3m - 8). Encuentra el valor de m.
A) 2 B) 4 C) 6
D) 8 E) 10
39. Halla el residuo de:
x
x x x
2 1
2 9 3 4
5 4
-
- + -
A) -8 B) -6 C) 4
D) 7 E) -3
Resolución de problemas
40. Efectúa:
x x
x x x x
4 3
27 3 5 2
2
9 6 2
- +
- + - +
Luego indica la suma del coeficiente principal y el término
independiente del residuo.
A) -44 B) -28 C) -26
D) -42 E) 28
41. Al dividir un polinomio P(x) entre el producto:
(x + 4)(x - 5)(x + 6) el resto obtenido es: x2
- 7x + 2. Encuentra
cuáles son los restos que se obtienen al dividir P(x) entre:
I. x + 4 II. x - 5 III. x + 6
A) 45; -7; 81 B) 50; -1; 90 C) 1; -1; 2
D) 30; -20; 10 E) 46; -8; 80
Nivel 3
Comunicación matemática
42. Luego de dividir:
x x
x x x x
2 3
4 2 3 5 1
3 2
5 4 2
+ -
- + - +
Indica verdadero (V) o falso (F), según corresponda:
1. El cociente es: Q(x) = 2x2
- 2x + 1 ( )
2. El residuo es: R(x) = 3x + 4 ( )
3. El coeficiente principal del residuo es -3. ( )
A) VVV B) FFF C) VVF
D) VFV E) FFV
43. Del esquema:
7 -14 1 -100
a 14 0 c
b 0 1 -98
Calcula: S = ab c
14
2
A) 0 B) 1 C) -1
D) 15 E) 14
44. En el siguiente esquema de Horner, halla la suma de los números
que debemos escribir en los recuadros vacíos.
2 1
3 5
1 24 8
5 35 13
A) 30 B) 35 C) 40
D) 44 E) 48
45. En el siguiente cuadro de Ruffini, halla la suma de los números
que debemos escribir en los recuadros vacíos.
1 3 2 -4
-3 -3 30 -87
1 0 2 -10 29 -93
A) -10 B) -11 C) -13
D) -14 E) -15
Razonamiento y demostración
46. Encuentra el resto de dividir:
( ) ( ) ( )
x ax b
x a x a b x b x ax b
1 1
2
5 4 3 2
+ +
+ + + + + + + +
A) 1 B) 2 C) 0
D) 4 E) 8

38. 38 Intelectum 1.°
47. Indica un valor de m para que:
4x4
- 5x2
+ 2mx
sea divisible por: 2x2
- mx + 2
A) 3 B) 4 C) 5
D) 7 E) 8
48. Si la siguiente división es exacta.
x x
px qx x x
2
6
2
4 3 2
- +
+ + - -
halla: p y q
A) 1 y 3 B) -1 y 3 C) 1 y -3
D) -1 y -3 E) 2 y 1
49. ¿Qué valor adquiere
k
n
1
2
+
+ ; si la división es exacta?
x x
x nx k
2 1
2
19
- +
- +
A) 1 B) 2 C) 19 D) 38 E) 4
50. Determina el resto en la división:
x
x x x
1
1
2
4 6 2
+
+ + +
A) 1 B) 3 C) 0 D) 2 E) 4
51. Halla n si la división:
x n
x n x x
2
8 2 4
4 2 2
-
- + - tiene por residuo 1.
A) 8 B) 10 C) 12 D) 14 E) 16
52. Si la siguiente división es exacta:
( ) ( )
x y
x y x my
3 4 2
5 5 5
+
+ - -
Calcula el valor de m.
A) 30 B) 31 C) 32 D) 33 E) 34
53. Calcula:
m q
n p
2
5
+
+
_
_
i
i
Si el residuo al dividir:
x x
x x x x mx n
3 2 1
6 4 5 8
2
5 4 3 2
+ +
+ + + + +
es: px + q.
A) 0 B) 2 C) 1 D) 3 E) 8
Resolución de problemas
54. Halla el resto en:
x x
x x
3 4
3 4 6
80 71
- -
- + - +
_ _
_ _
i i
i i
A) 1 B) 2x C) 3x + 1
D) 2x - 1 E) 2x + 1
55. Da el valor de (m + n + p + q) si la división:
x x
mx nx px x q
2 3 1
4
2
3 2 4
+ -
+ + + +
es exacta, además los coeficientes del cociente aumentan de 3
en 3 a partir del primero.
A) 50 B) 52 C) 54
D) 56 E) 58
56. Sea el polinomio:
P(x) = 2x4
+ x3
- 18x2
- 29x + 6
¿cuánto hay que aumentarle al coeficiente de x3
, para que sea
divisible por (x - 3)?
A) 1 B) 3 C) 2
D) 4 E) 5
57. Se tiene un polinomio entero en "x" de tercer grado que se anula
para x = 9 y para x = -7 y al dividirlo entre x - 11 da como resto
2160. Si el primer coeficiente del polinomio es 5, halla el resto de
dividirlo entre x - 1.
A) -640 B) 640 C) 300
D) -300 E) 1
C
l
a
ve
s
Nivel
1
1.
b
2.
D
3.
c
4.
b
5.
d
6.
c
7.
a
8.
b
9.
a
10.
b
11.
c
12.
a
13.
a
14.
c
15.
c
16.
e
17.
d
18.
d
19.
c
20.
d
21.
e
22.
d
Nivel
2
23.
C
24.
e
25.
d
26.
b
27.
d
28.
b
29.
b
30.
e
31.
e
32.
e
33.
a
34.
b
35.
B
36.
a
37.
b
38.
b
39.
E
40.
c
41.
e
Nivel
3
42.
d
43.
e
44.
d
45.
c
46.
c
47.
A
48.
C
49.
B
50.
C
51.
B
52.
D
53.
c
54.
d
55.
D
56.
C
57.
a

39. Aplicamoslo aprendido
39
ÁLGEBRA - ACTIVIDADES UNIDAD 2
1 Indica el número de factores primos:
P(x) = x3
+ x2
- 4x - 4
A) 1 B) 2 C) 3
D) 4 E) 5
2 Factoriza por el método del factor común:
F(x) = (x - 3)(x - 2) - (x - 2)(1 - x) + 1 - x
A) (x + 3)(2x - 1) B) (x + 5)(2x - 3)
C) (x - 3)(2x - 3) D) (x - 7)(2x - 3)
E) (x - 3)(x + 3)
3 Factoriza:
F(a; b) = a3
b3
+ a2
b4
+ 3a2
b3
A) a2
b2
(a + b + 3) B) ab2
(a + b + 3)
C) a2
b(a + b - 3) D) a3
b(a + b + c)
E) a2
b3
(a + b + 3)
4 Factoriza:
P(x; a) = ax4
- ax2
Luego, indica un factor primo.
A) x2
- 1 B) ax2
- 1 C) x + 1
D) x - 2 E) x2
+ 1
5 Factoriza: 2a3
b2
c4
d - 3ab4
c5
+ 7a2
b2
c4
d2
A) a2
bc4
d(2a - 3b + d2
)
B) ab2
c4
d(2a2
d - 3b2
c + 7ad2
)
C) ab2
c4
(2a2
d - 3b2
c + 7ad2
)
D) abcd(2a + 3b + 7d)
E) abcd(2a - 3b + 7d)
6 Factoriza: P(x) = (5x - 3)2
- (2x - 7)2
Da como respuesta la suma de coeficientes de un factor primo.
A) -3 B) 7 C) -4
D) 6 E) A o B
tema 3: FACTORIZACIÓN

40. Claves
40 Intelectum 1.°
7 Factoriza:
P(x; y) = x5
y + 2x4
y2
+ x3
y3
Indica un factor primo.
A) x + y B) x - y C) x - 2y
D) x + 2y E) x - 3y
9 Factoriza:
M(x; y) = x6
- x2
- 8x - 16
Da el número de factores primos.
A) 6 B) 2 C) 3
D) 4 E) 5
11 Factoriza:
6x2
+ 19x + 10
Indica la suma de sus factores primos.
A) x - 3 B) 3x + 5 C) 5x + 7
D) 2x + 7 E) 5x + 2
13 Factoriza cada expresión por aspa simple:
• x2
- 3x - 4
• x2
+ 2x + 1
• x2
- 6x - 7
• x2
+ 5x + 6
8 Factoriza:
M(x; y) = (3x + y)2
- (3y - x)2
Da el número de factores primos.
A) 1 B) 2 C) 3
D) 4 E) 5
10 Si: x - y = 5
Halla: x2
- 2xy + y2
A) 15 B) 10 C) 20
D) 30 E) 25
12 Factoriza:
6x2
- 4x - 2
Indica un factor primo.
A) 3x B) 2x - 1 C) 3x + 2
D) 2x + 3 E) 3x + 1
14 Factoriza cada expresión por aspa simple:
• a2
+ 8a + 16
• n2
- 5n - 6
• x2
- x - 2
• x2
- 2x - 3
1.
c
2.
b
3.
e
4.
c
5.
c
6.
e
7.
a
8.
b
9.
b
10.
e
11.
c
12.
e
13.
14.

41. Practiquemos
41
ÁLGEBRA - ACTIVIDADES UNIDAD 2
Nivel 1
Comunicación matemática
1. Encuentra el valor de (a + b)2
en la siguiente factorización
efectuada por aspa simple:
27x2
+ 42x - 49
3x 7
ax b
2. Calcula el valor de A en la siguiente factorización efectuada por
aspa simple:
7x2
- Ax - 18
7x -3
x 6
Razonamiento y demostración
3. Factoriza e indica la suma de los términos independientes de los
factores primos.
P(a; b) = 4a2
+ 4ab2
+ b4
- 1
A) 1 B) -1 C) 2
D) 2 E) 0
4. Factoriza e indica un factor primo.
w2
x5
+ 3w2
- t3
x5
- 3t3
A) x5
+ 3 B) x3
+ t3
C) w2
+ t3
D) t2
- 3 E) w5
- 3
5. Factoriza e indica un factor primo.
P(x) = 8x2
- 2x - 3
A) 2x - 1 B) 3x - 4 C) 4x - 3
D) 8x - 1 E) 8x - 3
6. Factoriza e indica un factor primo.
3m4
+ 7m2
+ 4
A) 3m2
- 4 B) m2
+ 3 C) m2
+ 4
D) m2
+ 1 E) m2
+ 7
7. Factoriza: R(x) = 8a3
- x3
Indica el término independiente del factor primo con mayor
coeficiente.
A) 4 B) 2ax C) x2
D) 2a E) 4a2
Resolución de problemas
8. Factoriza y da como respuesta la mayor suma de coeficientes
de un factor de:
A(t) = t5
+ 3t3
+ 2t
A) 0 B) 1 C) 2
D) 3 E) 4
9. Encuentra el coeficiente que aparece al factorizar:
(a - c)2
- (a - b)2
- (b - c)2
A) -3 B) -2 C) -1
D) 0 E) 2
Nivel 2
Comunicación matemática
10. Luego de factorizar el polinomio:
T(a; b) = 4a19
b5
- 4a18
b6
+ a17
b7
Indica verdadero (V) o falso (F), en las siguientes proposiciones:
( ) T(a; b) posee 2 factores primos.
( ) (a - 2b) es factor de T(a; b)
( ) a es factor primo de T(a; b)
A) VFV B) FFF C) VVV
D) VVF E) FFV
11. Del siguiente polinomio:
A(x; y; z) = xyzw(x + 7)(w - 10)(y - 3)(z - 20)
Indicacorrecto(C)oincorrecto(I)enlassiguientesproposiciones:
( ) A(x; y; z) tiene 6 factores primos.
( ) Un factor primo de A tiene término independiente -10.
( ) Un factor primo de A tiene suma de coeficientes -19.
A) ICI B) CCI C) ICC
D) CIC E) CCC
Razonamiento y demostración
12. Factoriza cada caso:
▪
▪ ax + bx + cx
▪
▪ mn2
+ m2
n + mn
▪
▪ a2
b - 2ab2
▪
▪ 5a + 5b + 3a + 3b
▪
▪ x3
y - x2
y3
+ x2
y
▪
▪ 2xa - a + 2xb - b
13. Indica un factor primo de:
P(a; b) = a2
- 2ab + b2
- 1
A) a - b + 1 B) a + b - 1 C) a + b + 1
D) a + b E) a - b
14. Factoriza:
P(m) = m2
- 3m - 4
Indica la suma de sus factores primos.
A) m - 1 B) 2m + 1 C) m + 3
D) 3m + 1 E) 2m - 3
15. Factoriza:
2x4
+ 17x2
+ 21 y luego señala el producto de los términos de
un factor.
A) 2x2
B) 3x2
C) 6x2
D) 5x2
E) 21x2

42. 42 Intelectum 1.°
16. Factoriza e indica un factor primo.
P(x) = x3
- 2x2
- x + 2
A) x + 2 B) x - 1 C) x + 3
D) x - 4 E) x + 4
17. Factoriza e indica el número de factores primos:
F(x; y) = x2
y2
+ x2
y + xy2
+ xy
A) 2 B) 3 C) 4
D) 5 E) 6
18. Factoriza en R:
H(x) = x4
- 5x2
- 14
Indica luego, el número de factores primos.
A) 4 B) 5 C) 1
D) 2 E) 3
19. Factoriza en R:
S(q) = q4
- 9q2
+ 18
Luego indica la suma de sus factores primos.
A) 2q2
- 9 B) 2 C) -4q
D) 4q E) 5q2
- 1
Nivel 3
Comunicación matemática
20. Lee el siguiente texto 3 veces, y luego responde las preguntas
planteadas.
La factorización es un proceso mediante el cual un polinomio
se expresa como la multiplicación indicada de factores primos.
Por lo general la FACTORIZACIÓN se realiza en el campo de
las EXPRESIONES ALGEBRAICAS RACIONALES ENTERAS,
esto referido a las variables y con respecto a los coeficientes
se define respecto al conjunto de los números RACIONALES
(Q) salvo excepciones de poder abandonar éste conjunto y
considerar, por ejemplo, el campo de los números REALES (R)
o el conjunto de los números COMPLEJOS (C).
MarcaconunaCdecorrectooIdeincorrecto,segúncorresponda
a los enunciados:
A) La FACTORIZACIÓN permite expresar un
polinomio en función de sus divisores.
B) SilasvariablessonEXPRESIONESALGEBRAICAS
IRRACIONALES, estas son factorizables en el
campo de los números racionales.
C) Según como los coeficientes se expresan en un
conjunto numérico, estos son factorizables en
dicho conjunto numérico.
21. Identifica cuál(es) de las expresiones presentadas es(son)
factor(es) del siguiente polinomio:
P(x) = 21x2
+ 11x - 2
I. 7 II. 7x + 1 III. 3x + 2 IV. 7x - 1
A) Solo I B) Solo II C) I y II
D) III y IV E) II; III y IV
Razonamiento y demostración
22. Factoriza e indica un factor primo.
M(x; y) = ab(x2
- y2
) + xy(a2
- b2
)
A) ay - y B) -ax + y C) -by + a
D) bx + ya E) a2
+ b2
23. Indica el número de factores primos de:
P(x) = yx2
+ 7xy + 12y
A) 1 B) 2 C) 3
D) 4 E) 5
24. Factoriza e indica el término independiente de uno de sus
factores primos.
15a2
+ 14a + 3
A) 2 B) 3 C) 5
D) -1 E) -3
25. Indica el número de factores primos del siguiente polinomio:
P(x) = x4
- 3x2
+ 1
A) 1 B) 2 C) 3 D) 4 E) 0
26. Factoriza e indica un factor primo.
M(x; y; z) = xm+a
+ xm
yb
+ xa
yn
+ yn+b
+ zp
xa
+ zp
yb
A) xm
+ yn
B) xm
- yn
C) xa
+ yb
D) xm
+ yn
- zp
E) xa
- yb
Resolución de problemas
27. Luego de factorizar:
T(m) = m7
- m4
a3
- m3
a4
+ a7
Indica el término independiente del factor repetido.
A) (m - a)2
B) (m + a) C) a2
D) m2
+ a2
E) 1
28. Factoriza:
P(x; y) = x3
- x2
+ 3x2
y - y2
- 2xy + y3
+ 3xy2
Da como respuesta la diferencia de sus factores primos.
A) -1 B) 1 C) ! 1
D) 0 E) -2
Claves
Nivel 1
1.
2.
3. e
4. a
5. c
6. d
7. e
8. d
9. E
Nivel 2
10. e
11. D
12.
13. A
14. E
15. C
16. B
17. C
18. E
19. D
Nivel 3
20.
21. D
22. d
23. b
24. b
25. b
26. c
27. c
28. c

43. Aplicamoslo aprendido
43
ÁLGEBRA - ACTIVIDADES UNIDAD 2
tema 4: RADICACIÓN
1 Calcula:
2
2
85
3
100
3
A) 2 B) 8 C) 16
D) 32 E) 64
2 Calcula:
x x
35
14 30
12
+
A) x35
B) x C) 2 x5
D) x6
E) x7
3 Calcula:
.
7
2
49
4
3 3
A)
7
2 B)
7
4 C)
4
7
D)
7
2
3 E)
7
2
4 Calcula:
816
4
3
A) 2 B) 4 C) 6
D) 8 E) 16
5 Simplifica:
M x y
1024 8 10
3
=
A) x y xy
8 2
2 2 3 B) xy xy
10 5
3
C) x y xy
5 3
5 5 3 D) x y xy
3 2
3 3
E) x y x y
8 2
2 3 2
3
6 Calcula:
S =
32
8
A)
5
2 B)
2
1 C)
3
1
D)
4
1 E)
7
3

44. Claves
44 Intelectum 1.°
7 Efectúa:
M x y x y
125 256
12 6
3 8 4
= +
A) 20xy B) 10xy2
C) 3x2
y
D) 7xy E) 21x4
y2
9 Calcula:
M 11 512 5 1 1 16
2 3 3 3 6 4
3
= + - + + +
A) 2 B) 1 C) 3
D) 4 E) 5
11 Efectúa:
P = 6
3 2 5 10
2
+ -
_ i
A) 24 B) 26 C) 32
D) 33 E) 23
13 Efectúa:
2 3 1 3 3 2 9
4
+ - +
_ _
i i
A) 2 3 B) 8 C) 4
D) -3 E) 16
8 Efectúa:
P 81 7 64 64 10
3 3 2
4
= + + - -
A) 4 B) 2 C) 3
D) 6 E) 8
10 Calcula:
R 64 3 512 5 27
3 4 3 2 3
= + - - -
A) 7 B) 6 C) 8
D) 9 E) 11
12 Calcula:
R 2 3 2 2 3 2
2 2
= + + -
_ _
i i
A) 28 B) 24 C) 32
D) 36 E) 40
14 Después de efectuar, se obtiene:
.
3 2 5 2 6
4
+ -
A) 1 B) 3 C) 2
D) 3 E) 6
1.
d
2.
c
3.
a
4.
b
5.
E
6.
B
7.
E
8.
A
9.
a
10.
a
11.
e
12.
A
13.
e
14.
a

45. Practiquemos
45
ÁLGEBRA - ACTIVIDADES UNIDAD 2
Nivel 1
Comunicación matemática
1. Indica verdadero (V) o falso (F):
a b a b
+ = + ...( )
ab a b
$
= ...( )
a b a b
2 2 2 2
- = - ...( )
b
a
b
a
= ...( )
2. Si: m = ; ;
n p
2
6
5
15
3
27
= =
Indica lo correcto:
A) mn = p2
B) m + n = 3p C)
n p
m n 2
+
+ =
D) pn = m E) mnp = 27
Razonamiento y demostración
3. Calcula:
E 1 4 9 16 25
= + + + +
A) 13 B) 14 C) 15
D) 16 E) 18
4. Efectúa:
.
P 125 64
3 3
=
A) 20 B) 21 C) 23
D) 24 E) 25
5. Reduce:
3 4
2 2
+
A) 4 B) 5 C) 6
D) 7 E) 8
6. Halla:
. .
A 1 4 9 16
= +
A) 14 B) 16 C) 18
D) 20 E) 21
7. Calcula:
6 7 4
+ +
A) 3 B) 4 C) 5
D) 6 E) 7
8. Calcula:
2 2 2 2 1
0 1 2 3
+ + + +
A) 1 B) 2 C) 4
D) 8 E) 16
9. Efectúa:
R = . .
3 2 24
A) 2 B) 6 C) 12
D) 18 E) 24
10. Efectúa:
S 16 25 36 49
= + + +
A) 4 B) 15 C) 22
D) 41 E) 126
11. Efectúa:
k 12 300 75 48
= + + -
A) 12 3 B) 10 3 C) 13 3
D) 9 3 E) 0
12. Efectúa:
4 2 8 3 9
4 3 6
+ - + -
A) 0 B) 1 C) 3
D) 5 E) 2
13. Reduce:
( )
E 3 4 5 6
0 0 0 0
5
5
= + + +
A) 0 B) 1 C) 2
D) 3 E) 4
14. Calcula:
3 2 3 18
0 3 3
+ - +
A) 1 B) 0 C) 2
D) 3 E) 4
15. Efectúa:
4 8 16
3 4
+ +
A) 4 B) 6 C) 5
D) 3 E) 4
16. Reduce:
3 3 3 3 9
0 1 2 3
+ + + +
A) 5 B) 6 C) 7
D) 8 E) 9
17. Efectúa:
M 50 8 18 200
= + + -
A) 4 2 B) 3 2 C) 2
D) 0 E) 2 2
Resolución de problemas
18. Calcula:
E
a b
a b
a b
a b a b
a b
a b
2 2
=
-
+
+
- + -
-
+
_ _
i i
; a > b > 0
Luego determina el cuadrado de E disminuido en uno.
A) a + b B) a2
- b2
C) 1
D) a b
2 2
- E) 2

46. 46 Intelectum 1.°
19. Determina la suma de los cuadrados de M y T.
Sabiendo que:
M 4 27 100 8 25
3 3 3
= + - + +
T 900 2 125 16 64
6 3 3
= + - - -
A) 100 B) 140 C) 145
D) 2 E) 1
Nivel 2
Comunicación matemática
20. Memoriza durante 1 minuto los radicales de las casillas. Tápalos
y a continuación llena el recuadro de abajo.
75
20 m m m
10 9
2
10 2
10 2
10
+ -
; ;
7 9 10
3 3 3
x27
3
9
53
2
92
7
125
64
3
. ;
8 2
25
1
3
273
2
Verifica si ha tenido aciertos, comparando los dos cuadros.
21. Completa con mayor que ( 2 ) o menor que ( 1 ) los resultados
de efectuar:
125
3
- 64
3
-
343
3
1000
3
.
3 27 312
3
4
4
3
30
5
3
c m
8
125
3
Razonamiento y demostración
22. Reduce:
P x x
72
36 40
20
= +
A) x3
B) 3x3
C) x2
D) x5
E) 2x2
23. Calcula:
E
9
25
25
9
= -
A)
3
7 B)
16
15 C)
15
16
D)
3
2 E)
7
3
24. Efectúa:
E
27
8
64
27
3 3
= +
A)
7
13 B)
17
12 C)
12
17
D)
3
17 E)
27
8
25. Reduce:
M
3
3
100
140
20
=
A) 8 B) 9 C) 10
D) 29 E) 30
26. Reduce:
M 8 27 64
3 3 3
= + +
A) 9 B) 10 C) 11 D) 12 E) 13
27. Efectúa:
P
9
1
27
8
3
3
= +
A) 0 B) 1 C) 2 D) 3 E) 4
28. Calcula:
A 8 27 125
3 3 3
= + +
A) 10 B) 12 C) 1
D) 16 E) 18
29. Calcula:
1 8 27 64
3 3 3 3
+ + +
A) 9 B) 10 C) 13
D) 12 E) 11
30. Calcula:
A 10 2 10 2
2 2
= + + -
_ _
i i
A) 24 B) 10 C) 60
D) 50 E) 40
31. Efectúa:
P = x y
32 4
4
A) xy B) x2
y C) xy8
1
D) x y
2
1
E) x3
y3
32. Simplifica:
F
x
x
x
x
1
1
1
1
3
=
-
+
+
-
A)
x
x
1
1
2
2
3
-
+
_
_
i
i
B)
x
x
1
1
3
-
-
C) 1
D)
y
x E)
x
x
2
2
3
-
+

47. 47
ÁLGEBRA - ACTIVIDADES UNIDAD 2
33. Efectúa:
16
9
27
8
3
+
A)
17
13 B)
17
12 C)
12
17
D)
7
4 E)
5
7
34. Efectúa:
9
1
25
1
+
A)
8
7 B)
8
15 C)
15
8 D)
7
8 E) 6
35. Efectúa:
E
4
9
9
16
= +
A)
15
7 B)
17
6 C)
6
17 D)
3
4 E) 0
36. Calcula:
P 8 27 64
3 3 3
= - +
A) 1 B) 2 C) 3 D) 4 E) 5
37. Calcula:
64 216 125
3 3 3
+ +
A) 4 B) 6 C) 12 D) 15 E) 25
38. Efectúa:
K = 4
2 6 3 18
2
- +
_ i
A) 29 B) 30 C) 32 D) 36 E) 27
39. Simplifica:
N =
b
a
a
b
2 3
8
A)
b
a
5
3 B) a2
- b2
C)
b
a
3
2
D) a b
2 2
- E)
b
a
Resolución de problemas
40. Se presenta el polinomio que es un cuadrado perfecto.
Determina el valor de l2
.
25x20
+ lx18
- 70x10
+ 49 + 4x16
- 28x8
A) 400 B) 500 C) 600
D) 700 E) 800
41. Aque es igual el cuádruple de “m” disminuido en 9 de la siguiente
relación:
m n m n 3 0
+ - - - =
A) n
20
16 B) n
4
3 C) n
9
4
D) n
2
E) n
2
2
Nivel 3
Comunicación matemática
42. Observa los radicales durante un minuto:
a a a
n
m
m
n n m
= = _ i
a a
8 2
2
3 2
3
=
5 6
x x x
a a a
3 3 3
- =-
a a
2 2
5 5
5
=
.
2 8 2 8 4
= =
7 7 7
.
20
4
5 20
5 4
= =
16
100
16
100
4
10
2
5
= = =
, ,
x y x y
3 4 4
12 3
12
"
Luego tápalos y escribe el nombre de las propiedades aplicadas
para su respectiva solución en los casilleros, pero en el orden
inverso al que tenían.
43. ¿Cuál es la alternativa correcta?
I. x x x x x x
3 10 5 3 10 5
9 2
9 4
9 2 4
9
+ - = + -
II. 10 R R R R R R
3
2 2 10
3
2 2
2
3 2
3 2 2
3 2 2
3
- + + = - + +
_ c
i m
R R R R
12
3
2
3
34
2 2
3 2 2
3
= - + = +
c c
m m
III. R R R R
10
3
2 2
2
3 2
3 2 2
3
- + + =
_ i
R R R R
10
3
2 3
3 2
3
2 2 3 2
3
1
- + + =
^ c _
e h m i o
10
3
2 2
R R
3
3
2 3 3
2
- + +
^ c _
e h m i o
IV. x y x y x y x y x y
2 2 2
2 3 3
5 5 10 5 3 3
5 5 13 8
5
= =
x y
32 13 8
5
=
A) Solo I B) I y II C) II y IV
D) I y III E) Todas
Razonamiento y demostración
44. Siendo:
2 16
x 4
=
Halla el valor de xx
.
A) 5 B) 4 C) 3 D) 2 E) 1
45. Efectúa y luego da el valor de x.
2
16 x
4 2
= +
A) -2 B) -1 C) 0 D) 1 E) 2

48. 48 Intelectum 1.°
46. Calcula:
M 16 81 1
4 4 4
= + +
A) 2 B) 3 C) 4
D) 5 E) 6
47. Efectúa:
E
3
3
4
4 9
3
5
8
10
= + -
A) 1 B) 2 C) 3
D) 4 E) 5
48. Calcula:
( )
2 2 2
n
n
2 3 4
+ +
A) 26 B) 27 C) 28
D) 29 E) 30
49. Calcula:
M 2 2
k
k 2 32
16
= +
A) 7 B) 8 C) 9
D) 10 E) 11
50. Efectúa:
4 9 16 1
36 49 81 100
+ + -
+ + +
A) 3 B) 4 C) 5
D) 6 E) 7
51. Calcula:
a b
a b
10 15
20 25
5
A) ab2
B) a2
b2
C) ab
D)
b
a E)
a
b
52. Calcula:
S 8 16 2 1000 2 400
3 8 3 4
8
= + + - - +
A) 3 B) 4 C) 2
D) 1 E) 6
53. Calcula:
6 8 4
N
3
2
81
16
12
1
4
9 18
3 3 3 3 3
= + + - -
A) 1 B) 2 C) 0
D) 3 E) 4
54. Halla el equivalente de:
3 5 2 7 2 6 35
+ +
A) 18 35
4 4
+ B) 15 14
4 4
+
C) 45 28
+ D) 45 28
4 4
+
E) 18 35
+
55. Calcula:
M
a
a
5
4
3
3
24
10
8
6
=
a k
A) 0 B) 2 C) 5
D) 1 E) 10
56. Calcula:
M 9 512 5 100 1 8
2 3 2 4 3
3
= + + + - +
A) 4 B) 8 C) 10
D) 5 E) 15
57. Calcula el valor de k
k = .
20 14 2 20 14 2
7
21 2
6
+ -
^ ^
h h
A) 5 B) 6 C) 7
D) 4 E) 2
Resolución de problemas
58. Si:
a
3
2
= ; b
2
3
= ; c
5
6
= ; d
6
5
=
Calcula:
E
c d d c
a b b a
2 2
2 2
=
-
+
A) 3 B) 5 C) 6
D) 30 E) 5 5
59. Calcula: V x 1
2
= +
Si: ; 0
x
b
a
a
b b a
2
1 < <
= -
< F
A)
ab
a b
2
- B)
ab
a b
+ C)
ab
a b
2
+
D)
a b
ab
2
+
E)
a b
ab
+
Claves
Nivel 1
1.
2. a
3. c
4. a
5. B
6. A
7. a
8. C
9. c
10. c
11. c
12. A
13. e
14. B
15. B
16. C
17. d
18. C
19. C
Nivel 2
20.
21.
22. E
23. C
24. C
25. B
26. A
27. b
28. a
29. b
30. a
31. C
32. A
33. C
34. C
35. C
36. C
37. D
38. E
39. C
40. A
41. C
Nivel 3
42.
43. C
44. E
45. B
46. E
47. D
48. c
49. B
50. B
51. B
52. c
53. c
54. D
55. D
56. D
57. e
58. e
59. C

49. Aplicamoslo aprendido
49
ÁLGEBRA - ACTIVIDADES UNIDAD 2
tema 5: racionalización
1 Racionaliza:
3
15
5
A) 5 9
5
B) 10 3
5
C) 3 3
3
D) 15
3
E) 5 81
5
2 Racionaliza:
3 5
5
A) 3 5 B)
3
5 C) 5
D) 1 E)
2
5
3 Racionaliza:
3
12
5
A) 4 81
5
B)
5
6 81
3
C)
5
3 36
3
D) 4 27
5
E) 2
4 Racionaliza:
2
6
3
A) 2 4
3
B) 8 4
3
C) 4
3
D)
2
4
3
E) 3 4
3
5 Luego de racionalizar y simplificar
75 45
5
-
; el
denominador resulta:
A) 1 B) 3 C) 5
D) 6 E) 15
6 Simplifica:
3 2
2
3 2 2 3
12
-
-
-
e indica el denominador racionalizado.
A) 1 B) 2 C) 3
D) 4 E) 5

50. Claves
50 Intelectum 1.°
1.
e
2.
B
3.
A
4.
E
5.
D
6.
A
7.
C
8.
D
9.
C
10.
D
11.
b
12.
A
13.
A
14.
c
7 Calcula el equivalente de:
3 3
6 12
-
+
A) 1
3 - B) 2 3
- C) 1 3
+
D) 2 3
+ E) 2 3
9 Racionaliza: M
3 5 8
5
=
+ -
Indica el denominador.
A) 2 B) 4 C) 6
D) 8 E) 10
11 Racionaliza:
5 3 2
5
+ -
e indica el denominador.
A) 13 B) 12 C)16
D) 14 E) 15
13 Racionaliza:
5
5
3
A) 25
3
B) 5
3
C) 10
3
D) 11
3
E) 1
8 Calcula:
8
S
1
8
3
1
=
+
+
A) 3 2 B) 8 2 C) 3
D) 6 2 E) 2
10 Señala el denominador racionalizado:
2 3 2 1
1
2 2
+ + +
_ _
i i
A) 56 B) 89 C) 67
D) 34 E) 17
12 Calcula: M
3 2
2
2 3 2
5
3 2 2 3
3
=
-
-
-
+
-
A) 0 B) 1 C) 2
D) 3 E) 4
14 Efectúa:
3
2
10 2
-
A) 5 2 B) 6 2 C) 2 2
D) 2 E) 1

51. Practiquemos
51
ÁLGEBRA - ACTIVIDADES UNIDAD 2
Nivel 1
Comunicación matemática
1. Marca la veracidad o falsedad, según corresponda:
( ) Al factor racionalizante también se le denomina factor
opuesto del denominador.
( ) Se pueden racionalizar también a los numeradores de una
fracción.
( ) En la racionalización de la forma:
c
A
b
a
se debe cumplir: a < b
A) FFF B) VVF C) FFV
D) FVF E) FVV
2. De los radicales cuadráticos, relaciona con su conjugado:
I.
II.
III.
IV.
V.
3 2
- 11 5
- +
1
10 + x y
4 3
5
x y
3 2
5 10 1
-
xy2
5 3 2
+
5 11
+ x y
2 3
5
Razonamiento y demostración
3. Racionaliza:
3 2
8
A)
6
2 B)
3
2 C)
5
6 2
D) 2 E)
3
4 2
4. Racionaliza:
2 3
12
A) 1 B)
2
3 C)
3
3
D) 2 3 E) 3
5. Racionaliza:
3
2
3
3
A)
3
9
3
B)
2
27
3
C)
3
18
3
D)
3
16
3
E)
3
2 6
3
6. Racionaliza:
3 7
2
-
A) 3 7
+ B) 2 7
+ C) 2 7
-
D) 3 7
- E) 6 2 7
+
7. Racionaliza:
5 2
1
-
A) 2 5
- B) 1 5
+ C) 5 2
+
D) 5 2
- E) 5 2
+
8. Racionaliza:
8
2
A) 2 8 B) 8 C) 2
D)
2
2 E) 3 8
Resolución de problemas
9. Determina el cuádruple del denominador racionalizado.
10 2
3
-
A) 4 B) 5 C) 6
D) 7 E) 8
10. Determina la suma de los valores (para cada valor de m), de los
denominadores racionalizados.
Para: m = 5 y 7
m 3
1
+
A) -6 B) 5 C) 2
D) 1 E) 0
Nivel 2
Comunicación matemática
11. Racionaliza cada caso e indica lo incorrecto:
A)
5
5 625
3
7
7
=
B) 1
7 1
6 7
-
= +
C) 10
5 6
10 6 5
-
- = -
_ i
D)
10
1
10
4
10
10
- =-
12. “Racionalizar el denominador _________ de una fracción
es transformarla en otra fracción ________ de denominador
________ racional”.
A) x5
3
- igual - x
B) Más una constante - similar - con la constante.
C) O el numerador - equivalente - o numerador.
D) x3
5
- diferente - x
E) 10 5
+
_ i - desigual - 5
10 -
_ i
Razonamiento y demostración
13. Efectúa:
A
3
3 3
= -
A) 3 B) 2 3 C) 0
D) 3 E) 9

52. 52 Intelectum 1.°
14. Efectúa: M
2
5
2
3 2
= +
A) 0 B) 2 C) 3 2
D) 2
- E) 4 2
15. Racionaliza:
A
5 2
2 2
=
-
A)
3
2 10 4
+
B)
3
5
C)
3
5 4
+
D)
2
10 4
+
E)
4
2 5
+
16. Racionaliza:
15 10
5
+
A) 15 10
+
B) 5
C) 10
D) 75
15 10
-
_ i
E) 15 10
-
17. Efectúa: S
3
5
3
7 3
= +
A) 3 B)
3
5 3 C)
3
2 3
D) 6 3 E) 4 3
18. Efectúa:
8
V
2
16 2
= -
A) 4 2 B) 6 2 C) 5 2
D) 7 2 E) 0
Resolución de problemas
19. Determina la suma de los exponentes del
denominador racionalizado:
a b c d
1
5 2 3
7
A) 3 B) 4 C) ab
7
D) cd
7
E) 2
20. Si luego de racionalizar se obtiene una
cantidad subradical de la forma: 7tm - p
:
7
1
m 5
3
5
; m > 1
Determina:
p
t
A) 1 B) 2 C) 3
D) 4 E) 5
Nivel 3
Comunicación matemática
21. Indica lo correcto:
I.
7
7
7
7
7
7
7
7 7
7
7 7 7
7
3 7
3 3 7
3
3 7
3
3
3
4
3
4
3
4
3
= =
= =
-
- -
-
-
f p
II.
11
10
11
10
11
11
11
10 11 10 11
9
4 9
4 9 4
4
9 4
4
14
4
5
4
9
4
=
= =
-
-
-
f p
III.
( )
32 2
8
32 2
8
32 2
32 2
34 2 8
8 32 2
25
20 2
+
=
+ +
+
=
+
+
=
d
_
n
i
IV.
a b c
a b c
a b c
a b c
a b c
a b c
a b c
100 373 81
481
10 10 10
100 373 81
481
10 10 10
381 108 400
481
381 108 400
481
9 9 9 381 108 400
481
=
a b c
=
f p
22. Escribe mayor que (2) o menor que (1),
según corresponda:
I.
x y x y
7 7
3 2
7 2
7
; 6 x, y ! N
II.
3 2
1
3 2
1
- +
III.
a b c a b c
4 4
7 9 3
3 4 9 3
3
; 6a,byc!N
IV.
11 2
9
11 3
8
+ -
Razonamiento y demostración
23. Simplifica:
3
3
5 3
2
+
+
A) 2 B) 3 C) 4
D) 5 E) 15
24. Simplifica:
5 2 7 2
15 14 35
+ -
+ -
_ _
i i
A) 2
10 - B) 1
7 - C) 2
D) 1 E) 3
14 -
25. Efectúa:
A
3
17
3
5 3
= -
A) 6 3 B) 8 3 C) 4 3
D) 3 E) 0
26. Halla el valor equivalente de:
3 3
6 12
-
+
A) 1
3 - B) 1
3 + C) 2
3 +
D) 2
3 - E) 3 2
+
27. Simplifica:
75 50
5 24 75 50
-
- +
_ _
i i
A) 3 B) 1 C) 5
D) 10 E) -3
28. Simplifica:
T
7
28
7
7
3
3
2 6
= - -
d d
n n
A) 7 B) 9 C) 15
D) 36 E) 59
Resolución de problemas
29. Luego de racionalizar, determina 4
7
A .
A
8
4
3
7
=
A) 2
4
B) 5 2
4
C) 2 2
4
D) 2
2
1 4
E) 1
30. Calcula la suma del numerador y
denominador luego de racionalizar:
5 3
8 2 15 5 3
-
- +
_ _
i i
es:
A) 3 B) 2 C) 1
D) 5 E) 0
Claves
Nivel 1
1. D
2.
3. e
4. d
5. C
6. a
7. c
8. d
9. E
10. A
Nivel 2
11. c
12. C
13. C
14. e
15. a
16. E
17. E
18. e
19. B
20. C
Nivel 3
21.
22.
23. D
24. A
25. c
26. B
27. B
28. D
29. C
30. A

53. maraton Matemática
53
ÁLGEBRA - ACTIVIDADES UNIDAD 2
1. Con respecto a la siguiente división:
x
x x x
1
6 8
3 2
-
+ + - = 6x2
+ mx + 8 / P(x)
Responde verdadero (V) o falso (F), según corresponda:
I. Es una división exacta de cociente de segundo grado.
II. Aplicando el método de Ruffini se demuestra que m = 7.
III. Es posible resolverlo por el método Horner.
IV. El valor numérico de P(6) = 256.
V. La suma de coeficientes de P(x) es 21.
2. Factoriza e indica el número de factores primos.
(a - b - c)x2
+ (b + c - a)y2
A) 2 B) 3 C) 4
D) 1 E) 0
3. Al factorizar: 7x2
- 5x - 2 se obtiene (ax + 2)(x - b).
Determina: a - b
A) 3 B) 5 C) 6
D) 8 E) 10
4. Si la división
x x
x x x Mx N
7 2 4
7 2 45
2
4 3 2
+ -
+ + + + es exacta, determina
M/N.
A) -1/2 B) 1/2 C) 2
D) 4 E) 28
5. Determina el resto luego de dividir:
x x
x x x
2 1
2 2
2
4 3 2
+ -
+ - -
A) -2 B) x + 2 C) x - 2
D) 1 E) 2
6. Determina a qué opción es equivalente:
6 3
+
A) 6 9
+ B) 9 18
+ C) 9 2 18
+
D) 36 3
+ E) 7 5
+
7. Efectúa:
( )( )
5 24 2 3 2 3
4 4 4 4
+ + - +
A) 2 B) 2 2 C) 3
D) 2 3 E) 5
8. Reduce la siguiente expresión:
( ) ( )
a b a b
2 2
2 2
-
-
+
+ 2b2
+ (a + b)(a - b)
A) (a + b)2
B) (a - b)2
C) a2
+ 2ab
D) b2
+ 2ab E) a2
+ b2
9. Reduce:
8 28 6 20
2
+ - +
_ i
A) 10 + 5 B) 8 6
+ C) 12 + 2 35
D) 12 - 2 35 E) 3 5
10. Determina el resto de dividir:
( )( )
x x
x x x
1 1
3 7
18 10 2
+ -
+ +
A) 6 B) 7 C) 11
D) 22 E) 10
11. Indica el factor de multiplicidad 2 en:
M(x) = x3
+ 5x2
+ 3x - 9
A) 2x B) 2x - 2 C) x + 3
D) x - 6 E) x
Racionaliza la siguiente expresión y determina el valor numérico
para cuando x = 1.
R(x) =
x
x x
1
2 1
-
- -
Racionalizamos el numerador y denominador:
R(x) =
( ) ( )
x
x x
x
x
x x
x x
1
2 1
1
1
2 1
2 1
$ $
-
- -
+
+
- +
- +
R(x) =
( )( )
( )( )
( )( )
( )( )
x x x
x x x
x x x
x x
1 2 1
2 1 1
1 2 1
1 1
- - +
- - +
=
- - +
- +
( )
( )( )
( )( )
R x
x x x
x x
1 2 1
1 1
=-
- - +
- +
R(x) =
( )
x x
x
2 1
1
- +
- +
Evaluamos en x = 1:
& R(1) =
2
2
-
` R(1) = -1
Resolución:

54. Unidad 3

55. Reflexiona
Recuerda
T
artaglia [Niccolo Fontana]
(Brescia, actual Italia,
1499 - Venecia, 1557)
Matemático italiano,
de origen muy humil-
de, su familia no pudo
proporcionarle ningún
tipo de educación,
de modo que el jo-
ven Tartaglia tuvo que
aprenderlo todo por
su cuenta. Ya adulto,
se ganó la vida como
profesor itinerante (se-
gún permiten conocer sus obras, vivió en Verona, Mantua y Ve-
necia) y a través de su participación en concursos matemáticos.
En uno de ellos se planteó la resolución de diversas ecuaciones
de la forma x3
px q; Tartaglia consiguió averiguar la solu-
ción general y obtuvo el premio. Más adelante reveló su méto-
do a Gerolamo Cardano, bajo la firme promesa de mantener
el secreto, pero este acabó publicándolo en su Ars magna de
1545.
Después de que Gerolamo Cardano rompiera su promesa
de mantener en secreto su resolución de las ecuaciones de
tercer grado, Tartaglia se decidió publicar la importante obra
Problemas e invenciones varias (1546), cuyos cuatro primeros
libros se refieren a la balística y al arte militar, el quinto a la
topografía, y los tres siguientes a las fortificaciones y a la
estática; muy interesante resulta el noveno, que trata del
álgebra y de la resolución de las ecuaciones de tercer grado
y de los problemas correspondientes. La parte dedicada al
arte de la fortificación fue la que atrajo más la atención de sus
contemporáneos: a consecuencia de la invención de la pólvora
pírica, el arte de la guerra había experimentado profundas
transformaciones que hacían necesarios nuevos medios de
ofensiva, y un estudio que sirviese para aumentar su potencia y
la precisión en relación con la nueva técnica de fortificar.
• Una valía propia saludable surge de
la personalidad, la competencia y un
conjunto de decisiones acertadas.
• Una vez que sepas lo que quieres
hacer con tu vida, tus metas, sueños
y propósitos, de ahí vendrá tu energía
y dejarás de obsesionarte por la
apariencia física.
• No te obsesiones con la apariencia;
esfuérzate por lucir lo mejor que puedas
y destacar tus rasgos naturales.
¡Razona...!
Completa la siguiente multiplicación y da como
respuesta la suma de cifras del producto.
A) 24 B) 25 C) 27
D) 18 E) 22
* 1 * ×
3 * 2
* * *
* * 2 *
* 2 * *
* * * * 3 0

56. Aplicamoslo aprendido
56 Intelectum 1.°
tema 1: ECUACIONES DE 1.ER
GRADO - PLANTEO DE ECUACIONES
1 Resuelve la siguiente ecuación:
x
2
1
- - 2 = 5
A) 12 B) 13 C) 17
D) 9 E) 15
2 Resuelve la siguiente ecuación:
x x
3
1
4
2
- + =
A) 1 B) 2 C) 3
D) 4 E) 5
3 Calcula x en:
2x + 3 = 7x - 7
A) 0 B) 1 C) 2
D) 3 E) 4
4 Calcula x en:
x x
5
1
3
3 9
+ = -
A) 0 B) 4 C) 2
D) 3 E) 7
5 Halla el valor de x en:
x x x
2 5
3
2
6
- = -
A) 5 B) 17 C) 2
D) 4 E) 3
6 Resuelve la siguiente ecuación:
(x + 4)(x + 1) = (x + 2)2
A) 1 B) 3 C) 6
D) 5 E) 0

57. Claves
57
ÁLGEBRA - ACTIVIDADES UNIDAD 3
1.
E
2.
D
3.
C
4.
B
5.
A
6.
E
7.
B
8.
A
9.
A
10.
D
11.
D
12.
E
13.
A
14.
B
7 Resuelve la siguiente ecuación:
(x + 3)(x + 2) = (x - 2)(x + 1)
A)
3
2
- B)
3
4
- C)
2
1
-
D) 2 E) -2
8 Resuelve:
(x - 2)2
= 1 + (3 - x)2
A) 3 B) 2 C) 1
D) 0 E) 7
9 El quíntuplo de un número, aumentado en 8 es igual al triple
del mismo aumentado en 6. Halla el valor de dicho número.
A) 5 B) 1 C) 2
D) 9 E) 7
10 La suma de un número con su cuádruple, resulta igual a 75.
¿Cuál es dicho número?
A) 10 B) 13 C) 12
D) 15 E) 20
11 Halla el valor de x en la ecuación:
x
x
4
2 3
9
7
+
- =
A) 4 B) 9 C) 8
D) 5 E) 6
12 Resuelve la siguiente ecuación:
x x x
2 3 4
26
+ + =
A) 18 B) 19 C) 20
D) 17 E) 24
13 Uno de dos ángulos complementarios tiene 2/3 de la medida
del otro. Calcula las medidas de los dos ángulos.
A) 36° y 54° B) 20° y 70° C) 30° y 60°
D) 15 y 75° E) 10° y 80°
14 Los ángulos agudos de un triángulo rectángulo están en la
relación de 5 a 13. Halla el valor del mayor de dichos ángulos.
A) 70° B) 65° C) 75°
D) 60° E) 78°

58. Practiquemos
58 Intelectum 1.°
NIVEL 1
Comunicación matemática
1. Búsqueda de palabras:
C F Y B N J A C I O N K O Z S
T A R D Q D A D L A U G I C A
W I T A Y I P Q C G R S Z I X
H C D E C K T L D T R A S D K
N V B V F C H A B G L F B E I
O S E R P E I N Q X F R M N X
I N O I C I S O P S N A R T S
C I D E N O E I N K F N A I L
A C A X Z J B C Y A Q U V D T
U D P L E C U A C I R G L A H
C E F O S P H R O R M I V D Y
E A D W M L G R P N A T A N J
O I N V O G N I T A I R G Q T
K H X J Z M E I V Y G I H S Z
N E T N E D N E C S A R T J M
IDENTIDAD ECUACIÓN IRRACIONAL
INCÓGNITA IGUALDAD TRANSPOSICIÓN
FRACCIONARIA TRASCENDENTE
2. Luego de resolver la siguiente ecuación:
2x + 3 = 28 - 3x
Se afirma que:
I. La solución o raíz es 5. ...( )
II. Transponiendo términos se obtiene: 5x = 25 ...( )
III. Es una ecuación fraccionaria. ...( )
Luego, la alternativa correcta es:
A) FVF B) VFV C) VVF D) FFF E) FFV
Razonamiento y demostración
Determina el valor de x para cada caso:
3. (3x + 2) - (-x - 1) = (2x + 4) + (x + 3)
A) 3 B) 6 C) 8 D) 10 E) 4
4. 2(3x - 6) = 2x + 8
A) 5 B) 6 C) 7 D) 8 E) 12
5. 12
x
2
5
- =
A) 26 B) 27 C) 28 D) 29 E) 30
6. 4x + 9 = 2x - 3 + x
A) -12 B) -6 C) -18 D) -20 E) 20
7. 4(x + 3) = 9x + 7
A) 2 B) 3 C) 1
D) -3 E) -6
8. 3(x + 2) - 5(4 - 7x) = 8
A)
13
11 B)
19
7 C)
7
11
D)
11
7 E)
19
11
9. 5x + 3(x - 1) = 4(x - 2)
A)
5
4
- B)
4
5
- C) 4
D) -4 E) -3
10. 3(2x + 5) = 2(4x + 5) + 9
A) 2 B) -3 C) -2
D) 3 E) 4
11. x
3
8 - 5 = 1 + 3 + 5 + 2
A) 6 B) 7 C) 8
D) 9 E) 12
12. 4x - 8 + 9 = 7x + 18
A) -
3
17 B)
7
15
- C) -3
D) -2 E) -1
13. 4(x - 1) + (x + 3)2 - 5(x - 1) = 10
A) 3 B) 2 C) 5
D) 8 E) 9
Resolución de problemas
14. ¿Cuál es el número que aumentado en 8 unidades produce un
resultado igual al que se obtiene dividiéndolo entre 3/5?
A) 10 B) 12 C) 14
D) 16 E) 18
15. Un taxista cobra t soles por los r primeros kilómetros y s soles
por cada kilómetro adicional. ¿Cuántos kilómetros recorrió si
cobró v soles? (v > t)
A) t
s
v r
+
-
^ h
B) r
s
v t
+
-
^ h
C) r
s
v t
-
-
^ h
D) r
s
v t
+
+
^ h
E) t
s
v r
+
+
^ h
16. Un ángulo agudo de un triángulo rectángulo mide la mitad del
otro ángulo, menos 30°. Calcula las medidas de los dos ángulos.
A) 5° y 85° B) 20° y 70° C) 80° y 10°
D) 1° y 89° E) 75° y 15°

59. 59
ÁLGEBRA - ACTIVIDADES UNIDAD 3
NIVEL 2
Comunicación matemática
17. De la ecuación:
5 7
x x
3
9
2
4
- = +
Se afirma que:
I. La solución o raíz es -12. ...( )
II. El MCM de los denominadores es 6. ...( )
III. Es una igualdad condicional. ...( )
Luego, la alternativa correcta es:
A) VVF B) FVF C) VFV
D) FFV E) VVV
18. Relaciona cada ecuación con su respectiva raíz.
A. x
2
7 21
- = x = 14 - 21
B. 21
x
2
7 = x =
7
6
C. x
2
3 7
= x = 6 - 7
D. x
2
3 7
+ = x = 14 - 3
E.
x
2
7 3
+ = x = 6
F.
x
2
7 3
= x = 7 - 42
G.
x
2
21 7
+ = x =
3
14
H.
x
2
21 7
= x
3
2
=
Razonamiento y demostración
Halla el valor de x en cada caso:
19. 1 17
x
5
6 - =
A) 18 B) 20 C) 24 D) 30 E) 15
20. x
3
1
- - 4 = 2
A) 36 B) 49 C) 64 D) 19 E) 25
21.
x
x
1
2 3
8
11
+
- =
A) 8 B) 4 C) 2 D) 6 E) 7
22. (x + 2)2
- 3 = x2
+ 17
A) 3 B) 1 C) 6 D) 5 E) 4
23. (x + 7)(x + 1) = (x + 2)(x + 5)
A) 1 B) 4 C) 6 D) 5 E) 3
24. x x x
2 5
3
2
6
- = -
A) 1 B) 2 C) 3 D) 4 E) 5
25.
x
x
4
3
7
8
-
- =
A) 10 B) 9 C) 11 D) 7 E) 0
26. x
2
7 + 3 = 24
A) 5 B) 6 C) 7 D) 9 E) 10
27. Calcula el valor de x:
(x + 3)2
- 5x = x2
+ 15
A) 5 B) 6 C) 3 D) 1 E) 9
Resolución de problemas
28. Si compro 15 pantalones y 7 camisas, gasto S/.415. Sabiendo
que el precio de cada pantalón excede en S/.13 al de una
camisa. ¿Cuánto cuesta un pantalón?
A) S/.10 B) S/.17 C) S/.23 D) S/.25 E) S/.28
29. Un ángulo de un triángulo mide 12° menos que el segundo. El
tercer ángulo mide 18°, más que el complemento del segundo
ángulo. Calcula las medidas de los tres ángulos.
A) 1°; 5°; 174° B) 30°; 20°; 130° C) 40; 40°; 100°
D) 84°; 72°; 24° E) 96º; 60º; 24º
NIVEL 3
Comunicación matemática
30. La ecuación:
x
x x
x
2 2
1
2
8
5
5
2
1
3
- - = - -
Según su estructura algebraica se clasifica como una:
I. Ecuación fraccionaria. ...( )
II. Ecuación irracional. ...( )
III. Ecuación trascendente. ...( )
Luego, la alternativa correcta es:
A) VFV B) VVF C) VFF
D) FFV E) FVV
31. Resuelve cada ecuación. Las incógnitas determinadas ubícalas
en su respectivo recuadro del valor de su raíz, de esta manera
formarás el nombre por el cual se le conoce a una ciudad.
A. 5(A + 1) - 5 = 2(A - 3) + 12
B. (L + 1) = -31L + 3(2 + 5L) + 8
C. 2(O - 1) + 2 = (O - 2) - 5 - 2(O + 3) + 28
D. 7(N + 2) - 10 = 2(N + 1) + 19 - (3N - 1) + 6

60. 60 Intelectum 1.°
E. 5(N + 2) + 7 = 2N - 1 - (N + 1) + 20
F. 5{S - 2[3(S - 1) + 10(S + 1)]} = 55
G.
2 1
5 3
A
A
7
2
+
- =
H.
11
52
E
E
2
5
-
+ = I.
17
10
R
R
7
2
+
- =-
J.
8 7
1
A
A
11
1
+
- = K.
2 1
12 25
B
B 5
+
+ =
L.
16
6
T
T
3
1
+
- =
M. 3
5
5
6
I
I
I
I
1
7
-
+ +
-
+ =
N. 3 7
L
L
L
L
1 6
-
+ -
+
-
O. 2
C
C
C
C
3
1
1
-
+ =
-
+
P. 56
T T
3
17
33 11
70
+ = +
¿A qué ciudad se le
conoce con este nombre?
17
11
- 2
39
55
4
1 -5 5
4
13
2
1 4 6
25
3 -1
31
23 -10 1 -7
Razonamiento y demostración
Determina el valor de x para cada caso:
32. 4
x x
3
2
7
4
- =
A) 40 B) 42 C) 84
D) 80 E) 86
33.
bx
ax
b
a
1
1
-
- =
A)
ab
a b
2
+ B) a b
2
+ C) ab
D)
a b
ab
-
E)
a b
ab
+
34. 8 13
x
5
2
4
+
- =
A) 111 B) 211 C) 312
D) 316 E) 202
35.
x
x
4 3
3 6
5
3
+
- =
A) 55 B) 12 C) 32
D) 15 E) 13
36.
x
x
2 1
3 4
8
7 1
+
+ =
-
c m
A) 1 B) -3 C) -4
D) -2 E) -6
37. x
5
2 1
7
15
7
2
+ =
A) 3 B)
6
1 C) - 2
D) 2 E)
6
1
-
38. (x + 5)2
= (x + 3)2
+ 36
A) 1 B) 2 C) 3
D) 4 E) 5
39. (4 - 5x)(4x - 5) = (10x - 3)(7 - 2x)
A) 1/15 B) 2/35 C) 1/35
D) 4/9 E) 3/17
40. (x - 2)2
= (x + 3)2
+ 5
A) -2 B) -1 C) 0 D) 3 E) 5
Resolución de problemas
41. Un carpintero vende la cuarta parte de sus muebles. ¿Cuántos
muebles tenía inicialmente, si al final se quedó con 21 muebles?
A) 12 B) 16 C) 25
D) 28 E) 32
42. Un ángulo de un triángulo mide 6° más que el segundo. El tercer
ángulo mide 4° menos que tres veces la suma de las medidas
de los otros primeros ángulos. Calcula las medidas de los tres
ángulos.
A) 1°; 10° y 169° B) 20°; 50° y 110° C) 30°; 60° y 90°
D) 17°; 37° y 126° E) 20°; 26° y 134°
Claves
Nivel 1
1.
2. C
3. E
4. a
5. D
6. A
7. C
8. E
9. B
10. C
11. A
12. A
13. A
14. B
15. B
16. C
Nivel 2
17. D
18.
19. E
20. D
21. E
22. E
23. E
24. E
25. C
26. B
27. B
28. C
29. D
Nivel 3
30. C
31.
32. B
33. A
34. E
35. E
36. C
37. E
38. E
39. C
40. B
41. D
42. E

61. Aplicamoslo aprendido
61
ÁLGEBRA - ACTIVIDADES UNIDAD 3
tema 2: SISTEMA DE ECUACIONES LINEALEs
1 Halla x:
x + y = 12
x - y = 4
A) 4 B) 6 C) 9
D) 8 E) 3
2 Halla y:
x + y = 60
x - y = 48
A) 5 B) 6 C) 8
D) 4 E) 7
3 Halla y:
7x - 2y = -1
4x + 3y = 16
A) 4 B) 1 C) 2
D) 3 E) 6
4 Halla x:
8x + 2y = 13
8x - 2y = 3
A) 2 B) 0 C) 3
D) 4 E) 1
5 Halla y:
7x + 3y = 60
7x - 3y = 12
A) 7 B) 10 C) 8
D) 9 E) 4
6 Halla y:
x + 2y = 28
x - 3y = 8
A) 10 B) 20 C) 18
D) 5 E) 4

62. Claves
62 Intelectum 1.°
7 Halla y:
6x + y = 20
6x - y = 8
A) 5 B) 7 C) 4
D) 6 E) 9
9 Halla x en:
2x + y = 12
3x - y = 23
A) 3 B) 4 C) 5
D) 6 E) 7
11 Resuelve:
.
x y
x y
e indica xy
2 3 9
4 8
- =
- =
*
A) -2 B) -3 C) -5
D) 2 E) 6
13 Determina el valor de: xy
3x + 9y = 15
x - y = 1
A) -2 B) 1 C) 8
D) 2 E) 3
8 Halla a:
9a - b = 29
4a - b = 14
A) -2 B) 2 C) 4
D) 3 E) -3
10 Halla x en:
3x + y = 21
7x + 2y = 47
A) 3 B) 4 C) 5
D) 6 E) 7
12 En el sistema:
2x + y = m + 3
3x - y = 8
Halla m, si x = 5.
A) 10 B) 8 C) 6
D) 12 E) 14
14 En el sistema:
4x + y = 19
5x - ny = 14
Halla: n; si y = 3
A) 2 B) 1 C)3
D) 0 E) 4
1.
d
2.
b
3.
a
4.
e
5.
c
6.
e
7.
d
8.
d
9.
e
10.
c
11.
B
12.
e
13.
d
14.
a

63. Practiquemos
63
ÁLGEBRA - ACTIVIDADES UNIDAD 3
NIVEL 1
Comunicación matemática
1. En esta sopa de letras se han perdido los 3 métodos de solución
para sistemas lineales
¡ENCUÉNTRALOS!
A E J B E K Y C I F Z J A
F N O I C A L A U G I M L
R G H D B F S C O G T L H
S N O I C U T I T S U S X
U I P X M E H P N E Q N G
S P D E R J D O V R O D T
T Q S Y D T I Y N Q W O Z
Q S U S T C N R W D E R L
Z M S T C M Z L U I V W A
X B A U A C V C Y Z K R U
L R D U F I G U A L G H G
X E U I B S J V T K R S I
R W K R E D U C C O N P W
2. Completa en los recuadros en blanco lo que corresponda,
siguiendo la secuencia para llegar a la solución.
Determinamos el valor de (y - x) del sistema:
x y
3
3
4
4
0
- -
-
= ...(1)
x y
2
4
5
2
3
- +
+
= ...(2)
▪
▪ De (1), eliminamos los denominadores:
(x - 3) - (y - 4) = 0
4x - y = 0 ...(3)
▪
▪ Haciendo lo mismo con (2):
(x - 4) + (y + 2) = 3 . 10
x+ 2y = 46 ...(4)
▪
▪ Ala ecuación (3) la multiplicamos miembro a miembro por
2 y a la ecuación (4) por 3 también miembro a miembro,
obteniendo:
8x - y = 0 ...(5)
x + 6y = 46 . ...(6)
▪
▪ Sumamos (5) y (6):
(8 + )x = 46 .
x =
x = 6 ...(7)
▪
▪ Reemplazamos (7) en (3):
y = x
4
y =
.
3
4
y = ...(8)
▪
▪ Nos piden:
y - x = - =
Razonamiento y demostración
3. Halla y:
x + y = 5
x - y = 1
A) 2 B) 1 C) 3
D) 4 E) 6
4. Halla y:
x + y = 20
x - y = 8
A) 5 B) 4 C) 6
D) 7 E) 8
5. Halla x:
x + y = 3
5x - 2y = 8
A) 1 B) 3 C) 2
D) 4 E) -4
6. Halla x:
4x + 3y = 30
4x - 3y = 18
A) 5 B) 4 C) 9
D) 6 E) 10
7. Halla a:
5a - 4b = 24
a + b = 3
A) -1 B) 1 C) -4
D) 3 E) 4
8. Halla x:
x + 3y = 8
x - 3y = 2
A) 6 B) 5 C) 7
D) 10 E) 12
9. Halla y:
x + y = 60
x - y = 24
A) 14 B) 18 C) 16
D) 20 E) 12
10. Halla x:
6x + 8y = 60
6x - 8y = 12
A) 6 B) 8 C) 12
D) 14 E) 9

64. 64 Intelectum 1.°
11. Resuelve:
x y
x y
e indica xy
2 4
5
- =
+ =
* .
A) 4 B) 12 C) 6
D) 8 E) 10
Resolución de problemas
12. La diferencia de dos números es 328, el cociente es 12 y el
residuo es 20. Halla la suma de dichos números.
A) 358 B) 384 C) 356
D) 346 E) 406
13. La suma de dos números es 103, el residuo y el cociente de su
división son 5 y 13 respectivamente. ¿Cuál es el número mayor?
A) 13 B) 65 C) 96
D) 100 E) 103
NIVEL 2
Comunicación matemática
14. Examen de Admisión UNI 2008-II (matemática).
▪
▪ Para los enteros positivos a y b se define:
a # b = a2b - 1
▪
▪ Si x e y son enteros positivos:
x # y = 32
¿Cuál de los siguientes números podrían ser el valor de y?
I. 1 II. 2 III. 3
A) Solo I B) Solo III C) I y III
D) II y III E) I; II y III
15. Qué sistema lineal es el adecuado para dar solución al problema:
La suma de dos números es 84. El triple del menor excede en 12
al mayor. Determina el menor de dichos números.
Siendo x e y los números, donde: x > y
I. x + y = 84
3x - y = -12
II. x + y = 84
3x = y + 12
III. x + y = 84
3y = x + 12
IV. x + y = 84
3y + x = 12
Razonamiento y demostración
16. Halla x:
7x - 5y = 23
2x + y = 9
A) 4 B) 3 C) 6
D) 1 E) 8
17. Halla y:
3x - 5y = -11
2x - 8y = - 26
A) 3 B) 4 C) 5
D) 6 E) 8
18. Halla y:
8x + y = 2
4x - 3y = -34
A) 10 B) -1 C) 2
D) 3 E) 4
19. Calcula el valor de a:
9b - 2a = 17
12b + a = 41
A) 4 B) 3 C) 5
D) 8 E) 12
20. Halla x:
5x - 4y = 14
6x - y = 51
A) 9 B) 12 C) 10
D) 18 E) 20
21. Halla m:
8m - 2n = 20
7m + 3n = 65
A) 5 B) 10 C) 12
D) 8 E) 20
22. Halla x:
12x - y = 50
8x + 3y = 70
A) 6 B) 10 C) 8
D) 5 E) 12
23. Halla m:
3m + 2n = 24
5m - n = 27
A) 8 B) 7 C) -7
D) 6 E) -8
24. Halla y:
9y + 2x = 42
7y - x = 25
A) 3 B) 6 C) 5
D) 4 E) 8
Resolución de problemas
25. La diferencia de dos números es 40. Si el mayor se disminuye
en 4, se obtiene el cuádruple del menor. Halla el producto de los
números dados.
A) 620 B) 624 C) 324
D) 402 E) 604

65. 65
ÁLGEBRA - ACTIVIDADES UNIDAD 3
26. Un alumno le dice a otro: “Si quiero comprar 15 chocolates me
faltan 10 soles, pero comprando tan solo 10 me sobra 15 soles”.
¿Cuánto dinero tenía?
A) S/.30 B) S/.40 C) S/.50
D) S/.65 E) S/.70
NIVEL 3
Comunicación matemática
27. Verifica el valor de verdad (V) o falsedad (F), según corresponda:
I. x + y = 12 El valor de xy x - y = 6 es 27.
II. x + 2y = 3
No es cierto que 4x + 5y = 6 yx
valga 1/2.
III. x + y = 10
y
x vale -2.
x - y = 20
IV. x + 3y = 15
y
x vale - 6.
x + 5y = 5
V. 2x + y = 12
El valor de xyx
es 1.
x - y = 6
VI. 2x + y = 20
x-y
vale 125.
2x + 5y = 12
28. Relaciona cada sistema de ecuaciones con sus soluciones:
A.
2x + y = 10
3x - y = 5
x = 3 / y = 1
B.
3x + y = 10
2x - y = 5
x =
a d
c e
+
+ ; y = cte
C.
2x + y = 5
3x - y = 10
x =
d a
e c
-
- ; y = cte
D. 3x + y = 5
2x - y = 10
x = 3 / y = -4
E. ax + by = c
dx - by = e
x=
b a
cb ae
2 2
-
- ; y = cte
F. dx + by = c
ax + by = e
x = 3 / y = 4
G. dx + by = e
ax + by = c
x = 3 / y = -1
H. bx + ay = c
ax + by = e
x
d a
c e
=
-
- ; y = cte
Razonamiento y demostración
29. Resuelve por el método de igualación si:
18x - 15y = -27
20x + 15y = 65
Halla: x2
+ y
A) 1 B) 3 C) 5
D) 4 E) 7
30. Resuelve: 1
a
x
b
y
+ = ; 1
b
x
a
y
- = ; a / b ctes.
e indica el numerador del valor de x.
A) ab(a + b) B) a2
+ b2
C) ab - 1
D) ab + 1 E) a + b
31. Halla y:
4x + 5y = 25
7x - y = 34
A) 0 B) 6 C) 7 D) -4 E) 1
32. Halla x:
6x - 4y = 10
3x + y = 11
A) 1 B) 0 C) 8 D) 3 E) 6
33. Halla x:
4x + y = 10
2x + 3y = 0
A) 2 B) -3 C) 4 D) 3 E) -2
34. Halla a:
6a + 7b = 15
8a - 5b = -23
A) -3 B) 3 C) -1 D) 4 E) 6
Resolución de problemas
35. Pedro dice: “Tengo el doble de hermanas que de hermanos,
pero mi hermana tiene la mitad de hermanas que de hermanos”.
¿Cuántos hijos somos?
A) 2 B) 4 C) 6 D) 7 E) 8
36. Al resolver el sistema:
5x - 4y = -14
2x + 3y = k
Se halla que y es el triple de x, entonces ¿cuál es el valor de k?
A) 21 B) 25 C) 2 D) 5 E) 22
Claves
Nivel 1
1.
2.
3. a
4. c
5. c
6. d
7. E
8. B
9. B
10. A
11. C
12. B
13. C
Nivel 2
14. C
15.
16. A
17. B
18. A
19. C
20. C
21. A
22. D
23. D
24. D
25. B
26. D
Nivel 3
27.
28.
29. D
30. A
31. E
32. D
33. D
34. C
35. B
36. E

66. Aplicamoslo aprendido
66 Intelectum 1.°
tema 3: ECUACIONES DE 2.º GRADO - PLANTEO DE ECUACIONES
1 Resuelve:
3x2
+ 4x + 1 = 0
Indica la menor raíz.
A) -1 B) -
3
1 C) -3
D) 1 E)
3
1
2 Resuelve:
x2
- 7x - 1 = 0
A) 5 57
! B)
2
5 53
! C)
2
5 51
!
D) 4 59
! E)
2
7 53
!
3 Resuelve: x2
+ (1 + i)x + i = 0
A) {-1; -i} B) {1; i} C) {-1; i}
D) Ø E) {1; 0}
4 Resuelve:
x2
- 5x + 5 = 0 e indica su menor raíz.
A)
2
5 5
+ B)
2
5 5
- C)
3
5 5
+
D) 5 5
+ E) 5 5
-
5 Resuelve e indica la mayor raíz de:
2x2
- 11x + 14 = 0
A) 2 B) 3 C) 3,5
D) -7 E) -2
6 Resuelve e indica la mayor raíz de.
-x2
- 3x + 1 = 0
A)
2
13 3
- B)
2
13 3
- - C)
2
5 1
-
D)
2
5 1
+ E) 2 1
5 -

67. Claves
67
ÁLGEBRA - ACTIVIDADES UNIDAD 3
7 Resuelve:
x2
- 7x + 4 = 0
A)
2
7 51
! B)
2
7 51
!
- C)
2
7 33
!
D)
2
7 33
!
- E)
2
3 51
!
9 Resuelve:
2x2
- x - 3 = 0 e indica la mayor raíz.
A) 1 B) -1 C)
3
2
D)
2
3 E)
2
5
11 Resuelve e indica las raíces:
2x2
- 3x - 5 = 0
A) ;
1
3
5
-
( 2 B) ;
1
2
5
( 2 C) ;
0
3
5
( 2
D) ;
1
2
5
-
( 2 E) ;
3
5 2
- -
( 2
13 En la siguiente ecuación: 2x + 8x2
= 4x + 5, indica la suma
de raíces.
A)
4
1 B)
4
1
- C)
3
6
D)
3
4 E)
3
4
-
8 Resuelve e indica la mayor raíz.
x2
- x = 1
A)
2
5 1
+ B)
2
3 1
+ C)
2
2 1
+
D)
2
5 2
- E)
2
5 3
-
10 Resuelve:
2x2
- x - 15 = 0 e indica la mayor raíz.
A)
5
2 B) -3 C) 3
D) -6 E)
2
5
12 Halla dos números consecutivos naturales cuyo producto sea
182:
A) 10; 11 B) 9; 10 C) 20; 21
D) 13; 14 E) 1; 2
14 Resuelve e indica su CS:
3x2
- 507 = 0
A) {8} B) {-8; 8} C) {-13; 13}
D) {13} E) {-13}
1.
a
2.
e
3.
a
4.
b
5.
c
6.
a
7.
c
8.
a
9.
D
10.
C
11.
D
12.
D
13.
a
14.
c

68. Practiquemos
68 Intelectum 1.°
NIVEL 1
Comunicación matemática
1. Búsqueda de palabras
A M T N R A I C X E S B I K B
S G R A D O L R K A T O L U H
Z Z G O Y C U A D R A T I C O
Q D Y N F D E D P X R V N H C
S Q O L Q I Q K D J M G D F I
O R N R S S S P O R C R E S T
L T I D L C O X F E O A P F G
U P M A I R L I S U C M E N Y
J E R U N I U J E I N A N F I
B F E C E M C X C V Z E D J M
H E T N A N I M I R C S I D R
P I Z G L G O S A E O C E N E
J S G Y V L N E R N B E N K T
K A C L O V E G H I H X T B U
O D N U G E S U M L U M E D A
▪
▪ DISCRIMINANTE
▪
▪ INDEPENDIENTE
▪
▪ SOLUCIONES
▪
▪ CUADRÁTICO
▪
▪ RAÍCES
▪
▪ TÉRMINO
▪
▪ LINEAL
▪
▪ SEGUNDO
▪
▪ GRADO
Plantea las ecuaciones respectivas que mejor representen a los
siguientes enunciados:
2. Determina dos números positivos cuya diferencia es 11 y la
suma de sus cuadrados sea 2581.
3. Halla dos números sabiendo que su diferencia es 10 y su
producto 119.
4. El cuadrado de un número positivo más el doble de su opuesto
es 528. Determina tal número.
5. La suma de un número natural y su cuadrado es 110. ¿De qué
número se trata?
6. Encuentra dos números cuya suma sea 20 y su producto 99.
Razonamiento y demostración
7. Resuelve:
x2
= -5x - 6
A) {-3; -2} B) {2; 3} C) {1; 6}
D) {-1; 6} E) {-1; -6}
8. Resuelve:
x2
- x - 2 = 0 e indica la menor raíz.
A) 2 B) -2 C) 1 D) -1 E) 0
9. Resuelve:
x2
+ x - 6 = 0 e indica la mayor raíz.
A) -3 B) 3 C) -2
D) -6 E) 2
10. Resuelve:
x2
- 4x - 5 = 0 e indica la menor raíz.
A) 1 B) 5 C) -5
D) 4 E) -1
11. Resuelve:
x2
+ 3x - 4 = 0 e indica la mayor raíz.
A) -4 B) 4 C) -1
D) 1 E) -3
12. Resuelve:
x2
+ 7x + 12 = 0 e indica la menor raíz.
A) 3 B) -3 C) 12
D) 6 E) -4
Resolución de problemas
13. La hipotenusa de un triángulo rectángulo mide 3 m más que uno
de sus catetos. Determina el valor del cateto mayor si el menor
mide 4 m.
A) 33 m B) 2 m C) m
33
D) 5 m E) 10 m
14. Un número excede a otro en 2; y su producto es 24. Determina
el mayor positivo.
A) 5 B) 6 C) 9
D) 2 E) 1
NIVEL 2
Comunicación matemática
15. Relaciona cada ecuación con su respectivo conjunto solución (CS).
x
x
3
2
2
4
+ =
-
x
x
2
3
4
2
+ =
-
x
x
3
2
2
4
=
7x2
+ 8x = 0
8x2
+ 7x = 0
9x2
+ 2x = 2x2
- 6x
,
CS 3 3
= -
# -
,
CS
7
8 0
= -
' 1
,
CS
8
7 0
= -
' 1
CS = {-4,4}
,
CS
2
1 65
2
1 65
= - +
' 1
A.
B.
C.
D.
E.
F.

69. 69
ÁLGEBRA - ACTIVIDADES UNIDAD 3
16. Indica verdadero (V) o falso (F) en las
siguientes proposiciones:
( )
2
1 es raíz de 2x2
- x + 1 = 0
( ) Toda ecuación cuadrática tiene
2 soluciones.
( ) La suma de las raíces de:
3x2
- 6x + 12 = 0 es 4.
A) FFF B) FFV C) FVF
D) FVV E) VVV
Según como se muestra las condiciones del
enunciado, traducirlas al lenguaje algebraico
mediante una ecuación correctamente
planteada.
17. Determina un número que sumado con el
cuádruple de su raíz cuadrada da 21.
18. El producto de dos números es 891, y
si el mayor se divide por el menor, el
cociente es 3 y el residuo 48. Determina
los números.
19. El producto de dos números es 270 y su
cociente 1 5
1
. Determina los números.
Razonamiento y demostración
20. Resuelve:
x2
- 7x + 12 = 0
A) {3; 4} B) {-3; -4} C) {2; 6}
D) {-2; -6} E) {5; -1}
21. Indica la menor raíz, luego de que
resuelvas:
x2
+ 9x - 10 = 0
A) 1 B) -1 C) -9
D) -10 E) 10
22. Resuelve: x2
+ 4x - 21 = 0
indica la menor raíz.
A) 3 B) -7 C) -3
D) 4 E) -4
23. Resuelve e indica la mayor raíz de:
x2
+ 8x - 9 = 0
A) 9 B) -9 C) -3
D) -8 E) 1
24. Resuelve e indica la menor raíz de:
x2
+ x - 20 = 0
A) 4 B) -4 C) 5
D) -5 E) -1
25. Resuelve:
2x2
+ 6x - 1 = 0
A)
3
3 11
! B)
2
3 11
!
C) -1 11
! D)
2
3 11
!
-
E) 2 11
!
Resolución de problemas
26. En la siguiente ecuación: 3x2
-3x+6=0,
las raíces son x1 y x2. Halla: x1
2
+ x2
2
A) -1 B) -2 C) -3
D) -4 E) -5
27. Un número es 4 más que el doble del otro
y el producto de tales números es 70.
Determina el menor positivo.
A) 10 B) 1 C) 7
D) 5 E) 15
NIVEL 3
Comunicación matemática
28. Indica verdadero (V) o falso (F) en las
siguientes proposiciones:
( ) (-2) es raíz de ax2
+ 3x + 2 = 0; a ! 0.
( ) 4x2
- 4x + 1 = 0 tiene raíces iguales.
( ) Si T = 4, entonces la ecuación
cuadrática no tiene solución.
A) VVF B) VFF C) VVV
D) FFF E) FVF
29. De la ecuación:
( )( )
x x x
x
10 7 2 7 0
+ + - =
c m
Se puede afirmar que:
I. Posee raíces complejas conjugadas.
II. Posee 4 soluciones reales.
III. Es incompatible.
IV. El producto de raíces en R diferentes
de 0 es -2.
V. La suma de sus soluciones en R es
-47.
Razonamiento y demostración
30. Resuelve:
x2
+ x - 42 = 0 e indica la mayor raíz.
A) -7 B) 7 C) 6
D) -6 E) 8
31. Resuelve: P(x) = x2
- 22x + 57 = 0,
Indica luego la diferencia positiva de las
soluciones.
A) 21 B) 22 C) 19
D) 16 E) 17
32. Resuelve: 3x2
+ 10x - 2 = 0
A)
3
5 31
!
- B) 3 29
!
-
C) 3 29
! D)
3
3 29
!
E)
2
5 31
!
33. Resuelve: x2
- 10x - 24 = 0 e indica la
suma de las raíces entre dos.
A) 24 B) -24 C) 10
D) -2 E) 5
34. Resuelve e indica la división entre el
producto y la suma de las raíces.
x2
+ 12x + 32 = 0
A) -8 B) 8 C) -8/3
D) 4/3 E) 12
Resolución de problemas
35. Halla el valor de k en la ecuación para que
unadelasraícesseaelrecíprocodelaotra.
(k-1)x2
-5x+3k-7=0,si:x1.x2=
k
k
1
3 7
-
-
A) 3 B) 4 C) 7
D) 8 E) 5
36. La base de un rectángulo es 2 m más que
su atura y su diagonal 2 m más que su
base. Determine el valor de su base.
A) 10 m B) 21 m C) 8 m
D) 5 m E) 2 m
C
l
a
ve
s
Nivel
1
1.
2.
3.
4.
5.
6.
7.
a
8.
d
9.
E
10.
E
11.
D
12.
E
13.
C
14.
b
Nivel
2
15.
16.
A
17.
18.
19.
20.
A
21.
d
22.
b
23.
e
24.
D
25.
D
26.
c
27.
d
Nivel
3
28.
e
29.
Iv
30.
c
31.
D
32.
A
33.
E
34.
C
35.
A
36.
c

70. Aplicamoslo aprendido
70 Intelectum 1.°
tema 4: desigualdades e inecuaciones
1 Resuelve: (3x - 1)2
+ 20 # (9x - 1)(x + 2)
A) ]1; + 3[ B) [1; + 3[ C) [-1; + 3[
D) ]-1; + 3[ E) [-1; 1]
2 Halla el intervalo de x tal que:
x x
x x
7 10 5 18
3
8 1 7
>
<
- -
+ +
*
A) ]-2; 2[ B) ]-4; 2[ C) ]-2; 4[
D) ]-4; 4[ E) ]-4; 12[
3 Sean los intervalos:
A = [-12; 9]; B = ]-4; 11[
Halla el número de valores enteros de A + B.
A) 12 B) 11 C) 13
D) 10 E) 14
4 Determina el mayor valor entero que verifica:
2
x x
22
13
13
22 <
- + -
A) 30 B) 32 C) 33
D) 34 E) 35
5 Si A = ]16; +3[ ; halla A’.
A) ]-3; 16] B) ]-3; 16[ C) ]16; +3[
D) [-3; 16] E) [-3; -16[
6 Si:
A = {x ! r / -7 < x # -3}
B = G-3; 4H
C = {x ! r / x > 4},
halla: C’- (A , B)’
A) ]-7; -4[ B) ]-7; -3[ C) ]-7; 4[
D) ]-7; 4] E) ]-7; -4]

71. Claves
71
ÁLGEBRA - ACTIVIDADES UNIDAD 3
1.
b
2.
d
3.
c
4.
d
5.
a
6.
c
7.
a
8.
e
9.
d
10.
c
11.
a
12.
e
13.
c
14.
b
7 Si x > 2, halla la variación de:
x
x x
9 6 1
2
2
+ +
A) ;
9
4
49 B) G3; 9H C) ;
3
4
49
D) ;
0
4
49 E) ;
4
49
3
-
8 Si x ! [2; 5], indica el menor valor que toma la expresión:
x
x
1
2
-
+
A)
7
4 B)
4
1 C)
7
2
D)
2
7 E)
4
7
9 Si x ! ;
2
1 1
< <, entonces:
x
2
4 3
2
- , pertenece al intervalo:
A) ]-1/2; 1] B) [-1/2; 3/2[ C) [-1; 1/2]
D) [-1; 1/2[ E) ]1/2; + 3[
10 Encuentra el mayor valor entero que satisface:
2
x
x
3
2
3
4
<
-
+
A) 3 B) 4 C) 5
D) 6 E) 7
11 Sea: A = {x ! Z / x + 2 < 2x + 1 # x + 5}
y F(x) =
0, si x " A
1, si x ! A halla el valor de: kF k
k 0
10
=
_ i
/
A) 9 B) 10 C) 11
D) 12 E) 55
12 Resuelve:
x x
5
3 6
14
5 7
1
- +
A) G-3; 3H B) G-2; 14H C) G-8; +3H
D) G7; +3H E) G-3; 7H
13 Resuelve:
6x + 5 < 5x + 3 < 4x + 3
A) x ! G-3; -6H B) x ! G-3; -2]
C) x ! G-3; -2H D) x ! R
E) x ! Q
14 Resuelve:
5x + 1 < 6x + 3 < 7x + 9
A) x ! [-6; +3] B) x ! G-2; +3H
C) x ! [-2; +3H D) x ! G-3; -6]
E) x ! G-3; 2H

72. Practiquemos
72 Intelectum 1.°
NIVEL 1
Comunicación matemática
1. ¿Es verdadero 3 $ 3?
2. ORDÉNALAS
Algunas palabras del concepto de desigualdad se han
desordenado. Ubícalas en su lugar.
Se denomina .......................... a la
relación de ............... que se establece
entre dos .................................. que
poseen .............. valor.
orden desigualdad
cantidades diferente
Razonamiento y demostración
3. Si A = ]-13; 18] y B = [-6; 30]
Halla A , B; A + B
A) ]-13; 30] y [-6; 18] B) [-13 y 30[ y ]-6; 8]
C) ]-10; 20] y [-5; 1] D) ]-2; 1] y [3; 4]
E) [-20; 5] y [-30; 18]
4. Resuelve:
2x - 5 # 3x - 11
A) x $ 6 B) x < 6 C) x > -6
D) x # -6 E) x ! Q
5. Resuelve:
6 - 2x $ 7
A) G-1; +3H B) G-3; 1/2H C) G-1; 2]
D) G-3; -1/2] E) [-1/2; +3H
6. El mayor valor entero de x que cumple con: x x
5
4 1
3
3 2
$
- -
es:
A) 3 B) 1 C) 2
D) -2 E) 5
7. Resuelve el sistema (en Z):
-x < -2 + x > 0 + x < 5
A) {1} B) {3; 4} C) {0; 1}
D) {4; 5} E) {0}
8. Resuelve y señala la menor solución entera:
-5 < 3x + 4 < 5
A) -5 B) -4 C) -3
D) -2 E) -1
Resolución de problemas
9. Si (x2
+ 7) ! [11; 32]
Halla en qué intervalo se encuentra x, si x > 0.
A) ]4; 9] B) ]1; 7] C) [2; 5] D) [3; 6] E) ]0; 3]
10. ¿Cuál es el valor de a de tal manera que
x2
+ ax + 6 < 0 tenga como conjunto solución a ]-3; -2[?
A) 2 B) 3 C) 4 D) 5 E) 7
NIVEL 2
Comunicación matemática
11. Para los números reales afirmamos que:
I. Si a > 0 & a2
> 0
II. Si a > 0 & a +
a
1 # -2
III. Si 0 < a < b & 0 <
b a
1 1
<
Son verdaderas:
A) Todas B) Solo I C) I y III
D) II y III E) I y II
12. Indica verdadero (V) o falso (F), según corresponda:
( ) Si x > y &
x y
1 1
<
( ) Si -x > -y > 0 & xy < 0
( ) Si y > 0 &
y
1 < 0
A) FVF B) FVV C) FFF D) VFV E) VVF
Razonamiento y demostración
13. Si (2x - 1) ! [-5; 4H entonces; ¿a qué intervalo pertenece
(3 - 5x)?
A) Q B) G1; 4H C)
2
19 ;13
- F
D) G1; 2H E) G2; 8H
14. Resuelve:
x x
4
3 4
+ +
_ i
< 2(x + 1)
A) x < -1 B) x > 4 C) x > 3
D) x > 1 E) x < -2
15. Si: /
z
A x x x x x
5
3
2
6
4
4
3
5 4
<
d
= - + - + - + -
+
( 2
Calcula la suma de elementos de A.
A) 20 B) 28 C) 30 D) 35 E) 47
16. Si x ! [-3; 2H, a qué intervalo pertenece la siguiente expresión:
(x2
- 6)2
A) [16; 81] B) [4; 25] C) [4; 9]
D) [0; 36] E) [-9; 4]

73. 73
ÁLGEBRA - ACTIVIDADES UNIDAD 3
17. Si: x ! [-3; 2[
Halla el intervalo de: x2
+ 4x + 5
A) [2; 17] B) [-3; 2[ C) [0; 20]
D) [1; 17[ E) [1; -17[
18. Si: x ! ;
1
2
3
F , halla el intervalo de: 2x – 3.
A) G0; 1] B) G-2; -1H C) G-1; 0H
D) G-1; 0] E) ∅
Resolución de problemas
19. Luego de que resuelvas la inecuación: x2
- mx + n < 0 se
obtiene como conjunto solución ]-8/3; 3[
Calcula el valor de mn
4
.
A) 3 B) 6 C) 8 D) 9 E) 10
20. Si n > 0; respecto a:
n
n
12
3
+ podemos afirmar que su mínimo
valor es:
A) 6 B) 2 C) 3 D) 4 E) 8
NIVEL 3
Comunicación matemática
21. Si a < b / ab < 0; indica cuál(es) es (son) verdadera(s):
I. a < 0 / b > 0
II. 1
a
b <
III. a2
b < b2
a
A) I y III B) II y III C) Solo II
D) Solo I E) I y II
22. Indica verdadero (V) o falso (F), según corresponda:
( )-5 < x < 8 & 25 < x2
< 64
( )-7 < x < -3 & 9 < x2
< 49
( )-4 < x < 9 & 0 # x2
< 81
A) VVV B) VFV C) FFV
D) FVV E) FVF
Razonamiento y demostración
23. Si 3 # x # 7; halla la variación de:
M =
x
x
2 5
2 1
-
+
A) [5; 7] B) [1/5; 7H C) [5; 10]
D) G-1; 2] E) [5/3; 7]
24. Si
-10 < a < -5; -2 < b < -1; 2 < c < 5
Halla la variación de:
c
ab
A) [1; 9] B) [-2; 3H C) ]1; 10[ D) G1; 10] E) G1; 2H
25. Resuelve:
7ax - 1 < 7a - x
Si a <
7
1
- .
A) x > 1 B) x < 2 C) x > a
D) x < a E) x > 2a + 1
26. Resuelve:
x
x x
3
3 4
2
2
+
- < 3
A) G-3; 0H B) G-5; - 3H C) R
D) G-3; 0H E) G-9/4; +3H
27. Resuelve:
15x - 2 > 2x +
3
1 ... (1)
2(x - 4) < x
2
3 14
- ... (2)
A)
9
7 < x < 2 B)
38
39 < x < 2 C)
9
7
- < x < 2
D)
39
7 < x < 2 E)
39
7
- < x < 2
28. Calcula el mayor valor de m y el menor valor de n, tal que:
4x2
- 12x + 1 $ m
x x
2 5
1
2
+ +
# n
Indica el valor de mn.
A) 1 B) -2 C) 2
D) 4 E) -4
Resolución de problemas
29. ¿Qué valor deberá tomar m > 0 para que la desigualdad:
5x - 2 <
m
m x
3 2
+ tenga solución ]-3; 2[?
A)
5
4 B)
5
2 C)
3
2
D)
3
5 E) 2
30. Determina la cantidad de números enteros mayores que 1 que
cumplen con la condición que su octava parte más 21 sea mayor
que su séptima parte más 3.
A) 100 B) 1000 C) 1005
D) 1006 E) 1008
Claves
Nivel 1
1.
2.
3. A
4. A
5. d
6. C
7. B
8. D
9. C
10. D
Nivel 2
11. c
12. c
13. C
14. D
15. B
16. D
17. d
18. d
19. d
20. d
Nivel 3
21. E
22. D
23. E
24. C
25. A
26. E
27. D
28. B
29. A
30. D

74. 74 Intelectum 1.°
Matemática
1. De cada figura determina x.
I. Rectángulo de perímetro 100 m de lado mayor 4x y lado
menor x.
4x
x
A) 4 m B) 8 m C) 12 m
D) 10 m E) 6 m
II. Cuadrado de área 144 m2
y lado (x - 3).
x - 3
A) 14 m B) 15 m C) 17 m
D) 10 m E) 12 m
2. Halla las raíces de la ecuación:
x2
+ 6x - 16 = 0
A) {4; 8} B) {2; 6} C) {-8; 2}
D) {-4; 1} E) {2; 3}
3. Resuelve:
x(4x + 1) = 3x2
+ 42; e indica la suma de sus raíces.
A) 0 B) 1 C) 4
D) -1 E) 3
4. En el siguiente sistema, determina los valores de x e y,
respectivamente:
3x + 2y = 22
2y - 7x = 2
A) 1 y 2 B) 3 y 4 C) 2 y 8
D) 7 y 6 E) 2 y 6
5. Lidia vende cuadernos de 2 precios S/.4 y S/.5. Si obtuvo una
recaudación de S/.192 al vender 40 libros, ¿cuántos de cada
precio vendió?
A) 20 y 20 B) 24 y 16 C) 13 y 27
D) 18 y 22 E) 20 y 18
6. Forma la ecuación cuadrática de raíces x1 = 3 y x2 = -1.
A) x2
+ 2x + 7 = 0 B) x2
+ x - 3 = 0 C) x2
- 2x - 3 = 0
D) 2x2
+ 5x + 2 =0 E) x2
+ 3x - 2 = 0
7. Halla las raíces de las siguientes ecuaciones e indica la suma
de todas ellas.
x2
- 7x + 6 = 0 y x2
+ 7x + 6 = 0
A) 7 B) -7 C) 1
D) -1 E) 0
8. Sean los conjuntos:
A = /
R
x x x
3
7 2 1
<
! + -
( 2
B = /
R
x x x
5
4 3
>
! -
% /
Determina: (A , B)C
A) G-10; 3H B) ;
3
40 2 C) ;
7
10 2
-
; E
D) G2; +3H E) G-2; -10/7H
9. Indica el valor de x que verifica:
x
x
x
x
3
1
2
5
-
+ =
-
+
A) 7/2 B) 6 C) 8/3
D) 12/7 E) 13/3
10. Se definen las siguientes operaciones:
a = b = (a + b)2
- (a - b)2
a T b = a2
- b2
Determina los valores que toma x en:
x = 2 = x T 3
A) {1; 8} B) {3; 7} C) {1;-9}
D) {-1; 3} E) {-1; 4}
Cuatro hermanos se reparten las ganancias de la semana que
suman S/.1500. A Hugo le toca S/.200 más que a Luis, a quien le
toca
5
3 de lo que le corresponde a Ximena, a quien le toca S/.300
más que a Bruno. ¿Cuánto recibe Ximena?
Sea: H lo que le toca a Hugo, L a Luis; X a Ximena y B a Bruno.
& De acuerdo a la premisa: H = 200 + L ... (I)
L = X
5
3 ...(II)
X = 300 + B ...(III)
Sabemos que: H + L + X + B = 1500 ... (IV)
Como piden lo que le toca a Ximena, ponemos todo en función de X.
& De I y II: H = 200 + X
5
3
L =
5
3 X
& De (III): B = X - 300
Reemplazamos en (IV):
200 + X
5
3 + X
5
3 + X + X - 300 = 1500
Efectuamos: 16X = 1600 . 5
X = 500
` Ximena recibe S/.500.
Resolución:

75. Unidad 4

76. Aplicamoslo aprendido
76 Intelectum 1.°
1 Encuentra el valor de la expresión que se da a continuación
para x = -4; y = 3; z = -5:
|x| - |y| + |z|
A) 4 B) 5 C) 6
D) 3 E) 2
2 Encuentra el valor de la expresión que se da a continuación
para x = -3; y = 2; z = -1:
.
z
x y
A) 4 B)
5
2
- C)
4
5
-
D) -6 E) 5
3 Resuelve:
x x
2 3 9
- = -
A) {-6; 4} B) {-6} C) {4}
D) {6} E) {-4}
4 Encuentra el valor de la expresión que se da a continuación
para x = 1; y = -7; z = -3:
2
x y z
- + -
A) -2 B) 10 C) 0
D) 1 E) 2
5 Halla la suma de las soluciones de:
4
x
8 - =
A) 14 B) 15 C) 16
D) 17 E) 18
6 Resuelve:
(|x| + 3)2
+ 16x = 0
A) {-1; 9} B) {-9; -1} C) {-9; 1}
D) {1; 9} E) {-10; 1}
tema 1: valor absoluto

77. Claves
77
ÁLGEBRA - ACTIVIDADES UNIDAD 4
1.
c
2.
D
3.
a
4.
b
5.
c
6.
B
7.
a
8.
a
9.
c
10.
a
11.
e
12.
A
13.
E
14.
C
7 Resuelve:
x x
4 2
2
$
- +
A) G-3; -2] B) G-3; -2] , [2; + 3H
C) [2; +3H D) [-2; 2]
E) G-3; -1H
8 Resuelve:
|5x - 2| = 4
A) ;
5
2
5
6
-
( 2 B) ;
4
1 3
-
( 2 C) [2; +3H
D) [-2; 2] E) G-3; -1H
9 Resuelve e indica uno de los intervalos de:
13
x
3 2
- =
A) {0; 2} B) {5} C)
3
11; 5
-
' 1
D) {-2; 1} E) {3; 5}
10 Resuelve:
x x
2 9 6
+ = +
A) {-3; -5} B) {-1; 1} C) {-1; 2}
D) {4; 5} E) {-2; 5}
11 Halla el conjunto A por extensión si:
A = {x ! R / |x3
- 1| = |x2
+ x + 1|}
A) {-2; 4} B) {-1; 2} C) {0; 4}
D) {-1; 2; 3} E) {0; 2}
12 Resuelve:
(|x - 1| + |x - 2|)(|1 - x| - |2 - x|) = 7
A) {5} B) {4} C) {3}
D) {9} E) {7}
13 Resuelve:
x
x
1
3 1 4
-
+ =
A) ;
7
2 5
( 2 B) ;
7
3 4
( 2 C) ;
7
2 2
( 2
D) {1; 3} E) ;
7
3 5
( 2
14 Resuelve: |2x + 1| = |x + 3|
A) {-4; 2} B) {-1; 2} C) ;
3
4 2
-
( 2
D) ;
3
1 2
-
( 2 E) {-7; 5}

78. Practiquemos
78 Intelectum 1.°
NIVEL 1
Comunicación matemática
1. Completa en los recuadros en blanco lo que corresponda para
llegar a la solución.
Determina la suma de soluciones que se obtiene a partir de:
x
4
1
4
13
+ =
Resolución:
De acuerdo a la definición:
x
4
1
+ = 0 x
4
1
+ =-
x
4
= - 0 x
4
=- -
x
4
=
0 x
4
=-
x =
0 x =
Nos piden: suma de soluciones = + =
2. De acuerdo a las proposiciones podemos afirmar:
A) |-3| - |2| = |-5|
B) |-2| + |-3| = |-5|
C) -|-3| = |3|
D) |2| - |3| = |-1|
E) |2| + |-2| = |0|
Razonamiento y demostración
3. Resuelve |2x - 1| = 5 e indica la menor solución.
A) -2 B) -1 C) 2 D) 3 E) 4
4. Resuelve:
|2x - 3| = 7
A) {2; 5} B) {-5; 2} C) {-2; 5}
D) {-5; -2} E) Ø
5. Resuelve:
|5x - 20| = 30
A) CS = {-2; 9} B) CS = {-1; 9} C) CS = {-9; 9}
D) CS = {-2; 10} E) CS = {-2; -9}
6. Resuelve la siguiente ecuación:
|2x - 4| = 6
A) CS = {1; 5} B) CS = {0; 5} C) CS = {-1; 5}
D) CS = {-1; 5} E) CS = {-2; -1}
7. Resuelve:
|x - 2| = 4; siendo su CS = {-a; b}
Indica: a + b
A) -6 B) -8 C) -4 D) 8 E) 4
8. Resuelve:
2
x 1
1
-
=
A) {1} B)
2
1
( 2 C)
2
3
( 2
D) ;
2
1
2
3
( 2 E) { }
Resolución de problemas
9. El valor absoluto del quíntuplo de un número, menos tres es el
doble de dicho número, menos tres. Determina el número.
A) 5 B) 12 C) x ! f D) -1 E) 20
10. El valor absoluto de la suma del cuadrado de un número con dos
es igual a la suma de uno con el doble del número.
Determina la mitad del número.
A)
2
1 B) 1 C) 2 D) 4 E) 10
NIVEL 2
Comunicación matemática
11. El valor absoluto de un número x se define como aquel
número real que se denota por ; donde:
x; si x $ 0
= 0; si x = 0
-x ; si x < 0
A) Complejo - no negativo - |x| -
x ; si x $ 0
|x| = 0 ; si x = 0
-x ; si x < 0
B) Real - no negativo - |x| -
x ; si x < 0
|x| = 0 ; si x = 0
-x ; si x $ 0
C) Real - no negativo - |x| -
x ; si x $ 0
|x| = 0 ; si x = 0
- x ; si x < 0
D) Irracional - positivo - |x| -
x ; si x $ 0
|x| = 0 ; si x = 0
-x ; si x < 0
12. Cálculo.
Luego de realizar las operaciones con valor absoluto dentro de
las fichas, trace una curva recta para separar las fichas en dos
grupos de 5 cuya suma sea idéntica.
|-3 - 2|
3
|-7|
|6 + 3|
|-23
|
1
|-1 - 7| |-3|2
|2||3|
2

79. 79
ÁLGEBRA - ACTIVIDADES UNIDAD 4
Razonamiento y demostración
13. Resuelve e indica una solución:
x x
4 5 2
- = -
A) 6 B) 5 C) 4
D) 3 E) 2
14. Resuelve: 0
x x
2 1
- - =
A) ;
1
3
1
- -
( 2 B) ;
1
3
1
-
( 2 C) ;
3
1 1
( 2
D)
3
1
( 2 E) {1}
15. Indica la suma de soluciones de la ecuación:
|x2
- 5x| = 6
A) 1 B) 2 C) 3
D) 6 E) 10
16. Resuelve:
0
x x
2 1
+ - =
A) {-1} B) {1} C)
3
1
-
( 2
D) ;
1
2
1
( 2 E) ;
1
3
1
- -
( 2
17. Resuelve |x - 2| = |3 - 2x| e indica el producto de soluciones.
A) 1 B) 5/3 C) 5
D) 3 E) 15
18. Resuelve:
|2x - 1| = -x
A) ;
1
3
1
- -
( 2 B) ;
1
3
1
-
( 2 C)
3
1
( 2
D) ;
1
3
1
( 2 E) { }
19. Resuelve:
7
x x
3 1
- = +
A)
2
3
-
( 2 B) {4} C) ;
2
3 4
( 2
D) ;
2
3 4
-
( 2 E) R
20. Resuelve:
|2x - 7| = x - 5
A) {2} B) {3} C) {11}
D) {5} E) No tiene solución
Resolución de problemas
21. Halla el conjunto solución de la siguiente desigualdad:
x x x
1 1 $
- + +
A) ;
5
4
5
4
-
; E B) ; ;
1
5
4
5
4 1
,
- - <
=
C) ; ;
1
5
4
5
4 1
,
- -
; <
E D) G-1; 1H
E) [-1; 1]
22. El número de raíces de la ecuación:
x x x
1 9 2 1 9
2 2
- = - es igual a:
A) 0 B) 1 C) 2
D) 3 E) 4
NIVEL 3
Comunicación matemática
EL MANUSCRITO MISTERIOSO:
23. A continuación se tiene un teorema en clave. ¡Descífralo! ten en
cuenta que cada casilla que tiene un número representa a una
letra del alfabeto. 1 = A; 2 = B; ... ; no considere (Ñ; LL; CH).
19 4 19 13 18 15
,
15 15 14 12 19 7 14
21 22 12 18 5
, ,
9 21 1 19 5 4 3 18
5 12 5 19 6 18 14 9 14
19 15 21 20 15
|-x| = |x| 6 # ! R.
24. Compara según sea el caso con: > ; < o = considerando el
menor de las soluciones para cada ecuación con valor absoluto:
▪
▪ |x2
- 4| = 2 - x
x
x
2 3
5 9
+
-
▪
▪ |3 - x | = 4 |3x - 5| = 7 - x
▪
▪ |x + 1|2
- 5|x + 1| + 6 = 0 |x - 6| = |3 - 2x|
Razonamiento y demostración
25. Resuelve (2 - x)|x2
- 9| < 0 e indica la menor solución entera.
A) 1 B) 2 C) 3
D) 4 E) 5

80. 80 Intelectum 1.°
26. Encuentra el valor de la expresión que se da a continuación para
x = -4; y = 3; z = -5:
x y z
x y z
+ +
+ +
A) -1 B) -2 C) 0
D) 3 E) 5
27. Halla el menor valor de x que satisface:
3|x - 2| = |x + 4|
A) 1/2 B) 1 C) 3/2
D) 2 E) 3
28. Resuelve: |x + 5| = 2x - 4, e indica la suma de las raíces
obtenidas.
A)
3
28 B)
3
26 C) 9
D)
3
1
- E)
3
28
-
29. Resuelve e indica la suma de soluciones, multiplicando por 4.
1
x
x
5 3
10
-
-
=
A) 1 D) 2 C) 3
D) 4 E) 5
30. Halla las soluciones negativas:
|x - 1|2
- 2|x - 1| - 15 = 0
A) {-1; -2} B) {-2; -4} C) {-1; -4}
D) {-4} E) {-2}
31. Halla el producto de los elementos del CS de la siguiente
ecuación:
7
x
x
3
3
+
- =
A) 5 B) 4 C) -4
D) 9 E) –9
32. Resuelve: 2x2
- 7|x| + 3 = 0
A) ; ;
2
2
1 3
( 2 B) ;
2
1
2
1
-
( 2 C) ; ;
1 0
3
1
-
( 2
D) ; ; ;
3 1 2
2
1
-
( 2 E) ; ; ;
3
2
1
2
1 3
- -
( 2
Resolución de problemas
33. De la ecuación: |3x+ 2| = 2x - 11, determina el valor de:
5x1 + x2, siendo x1, x2 sus soluciones; x1 > x2.
A) -1 B) -2 C) -3
D) -4 E) -5
34. El valor absoluto de un número disminuido en dos, menos el
valor absoluto del triple del mismo número, aumentado en cuatro
obtenemos una diferencia que si lo dividimos entre cinco restado
del cuádruple del número, formamos en este caso una división
que es cuanto menos cero. Determina el número (mayor valor
entero y positivo).
A) 5 B) 2 C) 7
D) 1 E) 3
35. Si la suma de los valores absolutos de un número, con 7 restado
del triple del valor absoluto del mismo número; es cuanto menos
5. Determina los valores permisibles del número.
A) CS = G-3; -3] , G0; 6]
B) CS = G-3; -2] , [0; 1] , [7; +3H
C) CS = G-3; -3] , [0; 1] , [3; +3H
D) CS = ;
4
1
4
1
-
< F
E) CS =
4
1 ; 7
-
<
C
l
a
ve
s
Nivel
1
1.
2.
b
3.
A
4.
C
5.
D
6.
C
7.
D
8.
D
9.
C
10.
A
Nivel
2
11.
C
12.
13.
D
14.
c
15.
e
16.
E
17.
B
18.
E
19.
d
20.
E
21.
E
22.
C
Nivel
3
23.
24.
25.
D
26.
B
27.
A
28.
B
29.
E
30.
d
31.
D
32.
E
33.
D
34.
D
35.
C

81. Aplicamoslo aprendido
81
ÁLGEBRA - ACTIVIDADES UNIDAD 4
1 Halla a:
( )
( )
2
log
log
a a
a
3 3
1 4
2
2
+ - -
+ -
=
A) 1 B) 2 C) 5
D) 8 E) 10
2 Halla:
12 5
( )
log x 4
=
-
12
A) 7 B) 8 C) 4
D) 5 E) 9
3 Calcula x en:
x = log3243
A) 4 B) 5 C) 6
D) 7 E) 3
4 Halla y:
logx3x6
= y
A) 5 B) 1 C) 6
D) 3 E) 2
5 Calcula:
. .
log log log
M 3 6 5
25 27 36
=
A) 16 B) 12 C) 27
D) 24 E) 18
6 Calcula:
A = logab5
. logca3
. logbc2
A) 10 B) 5 C) 20
D) 30 E) 12
tema 2: logaritmos

82. Claves
82 Intelectum 1.°
1.
C
2.
e
3.
b
4.
e
5.
b
6.
d
7.
c
8.
e
9.
a
10.
c
11.
b
12.
c
13.
c
14.
c
7 Calcula el número cuyo logaritmo de base 2 es igual a -6.
A)
2
1 B) 6 C)
8
1
D) 2 E)
3
1
8 Calcula:
2 3 5
A log log log
3 2 4 2 6 2
2 3 5
= + +
+ + +
_ _ _
i i i
A) 190 B) 192 C) 194
D) 196 E) 198
9 Calcula el valor de m en:
m -1 = log32
A) log36 B) 2 C) 63
D) log63 E) 1
10 Calcula el valor de:
64 36
M log log
3 3
1
4 6
1
= +
A) 34 B) 35 C) 36
D) 37 E) 38
11 Calcula:
4 5 6
M log log log
3 2 1 4 2
4 5 6
= + +
+ +
_ _
i i
A) 156 B) 157 C) 158
D) 159 E) 160
12 Si log62 = a, ¿cuánto vale log63 en función de a?
A) 2a B) a C) 1 - a
D) 1 + a E) 2a - 1
13 Calcula x en:
7 11 2
log log log
x
9 49
7 11 2
+ =
A) 20 B) 30 C) 40
D) 50 E) 60
14 Calcula:
4
A . . ...
log log log log
5 6 7 50
4 5 6 49
=
A) 48 B) 49 C) 50
D) 51 E) 52

83. Practiquemos
83
ÁLGEBRA - ACTIVIDADES UNIDAD 4
NIVEL 1
Comunicación matemática
1. Indica el valor de verdad o falsedad en:
I. log215 = log2(-5) + log2(-3) ( )
II. 2 2
log log
2
3 3
= ( )
III. 7
log
log 5
1
5
7
= ( )
A) FVF B) VFV C) VVV
D) FFV E) FFF
2. Relaciona cada logaritmo con su respectiva respuesta.
log71
log28
log3 3
3
1/2
0
log216
log5050
1
4
Razonamiento y demostración
3. Calcula x en:
2 5 343; 1
x a
7log log
x 7
a a 2
+ =
_ _
i i
A) a B) a2
C) a3
D) a4
E) a5
4. Calcula:
E 25 243
log log
125
5
1
5
1
3
1
= - -
_ a
i k
A) 5 B) 25 C) 3
D) 9 E) 27
5. Calcula el valor de m en:
log m
32
1
2 =
d n
A) -1 B) 2 C) -5
D) 4 E) 3
6. Reduce:
B = log216 + log327 + log5625
A) 14 B) 13 C) 12
D) 11 E) 10
7. Si: c = ab
Calcula x en:
log log log
N
x
N N
1 1
c b a
= +
A) 1 B) 2 C) 3
D) 4 E) 5
8. Calcula:
A = log log log log
3 3 5 4
9 2 27 25
3
_ _ _ _
i i i i
A) 2 B)
2
1 C) 3
D)
3
1 E) 4
Resolución de problemas
9. El cuádruple del logaritmo de un cierto número excede en 4 al
duplo del logaritmo del mismo número. Halla el número.
A) 1000 B) 200 C) 100
D) 256 E) 300
10. El quíntuplo del logaritmo de un cierto número excede en 8 al
triple del logaritmo del mismo.
Determina el número.
A) 10 B) 102
C) 103
D) 104
E) 105
NIVEL 2
Comunicación matemática
11. Indica verdadero (V) o falso (F), según corresponda:
I. log3x = 4 & x = 81 ( )
II. log(-2)(-2) = 1 ( )
III. log35 + log32 = log37 ( )
A) VVV B) VFF C) VVV
D) VFV E) FVF
12. Completa los recuadros con los números respectivos de tal
manera que lleguemos al resultado correcto.
Calcula el equivalente de:
Z = log425 log37 log59 log74
La expresión se puede escribir de la siguiente manera:
Z = log45 log37 log53 log74
Z = log45 log37 log53 log74
Z = log45 log 3 log 7 log 4
Z = log44 = . 1 =
Razonamiento y demostración
13. Resuelve:
7
log log 4
x x
7
=
A) 2 B) 4 C) 2
7
D) 7 E) 4
7

84. 84 Intelectum 1.°
14. Resuelve:
log3(x + 5) + log3(x + 3) = log3(16x) y
señala el producto de sus soluciones.
A) 15 B) 8 C) 9
D) 10 E) 17
15. Si m es el valor de x que verfica:
5
x
log x
3
1
= +
-
3
_ i
Calcula el valor de m .
A) 2 B) 4 C) -1
D) 3 E) 1
3 -
16. Si: log35 = a / log32 = b
Halla log3(2,7) en función de a y b.
A) a + b - 2 B) a - b + 1
C) a - b + 3 D) 3 - a - b
E) a + b + 1
17. Calcula:
N = (log28)(log92)(log85)(log2527)
A)
2
1 B)
4
3 C)
5
7
D)
2
3 E)
4
5
18. Si b2
= ac, calcula x en:
log log log
N
x
N N
1 1
b a c
= +
A) c B) a C) ac
D) 1 E) 2
19. Calcula:
A = (log26)(log36) - log32 - log23
A) 0 B) 1 C) 2
D) 3 E) 4
Resolución de problemas
20. El logaritmo decimal de 27 veces el
cubo de un número es 7,4512. Calcula
el cuadrado del logaritmo decimal del
número, más 1.
Considere: log 3 = 0,47713
A) 5,5555 B) 4,4444 C) 3,1841
D) 3,0211 E) 5,0266
21. El logaritmo decimal de 16 veces un
número es 5,89882. Calcula el logaritmo
decimal del cubo de dicho número.
Considere: log 2 = 0,30103
A) 15,0877 B) 13,0711 C) 14,0841
D) 9,9977 E) 14,0700
NIVEL 3
Comunicación matemática
22. Indica el valor de verdad de las siguientes
proposiciones:
I. log2(xy) = log2|x| + log2|y| / xy > 0
II. log 2 (x + y) = log log
x y
2 2
+ ,
solo si: 1
x y
1 1
+ = ; x, y ! r+
III. log2(-2)4
= 4log2|-2| = 4
A) VFF B) VFV C) FFV
D) VVV E) VVF
23. Compara mediante >, < o = las siguientes
alternativas:
log164 log93
log32187 log41024
log642 log339
Razonamiento y demostración
24. Si: 8
log 7 3
n
10 2 21 + =
+ _
_ i
i
Resuelve: x n
xx
=
A) 2 B) 3 C) 7
D) 10 E) 2
25. Reduce:
log 2
5
log 3
log 6 2
log
log
2
5
7
2
49
3
d n
A) 7 B) 49 C) 36
D) 42 E) 28
26. Al resolver:
2 2
( )
Inx Iny
25 5
2
x y
=
=
*
Halla: x + y
A) 2 B)
8
7 C)
4
3
D)
4
1 E)
4
5
27. Calcula:
2
log log log
M
16
75
9
5
243
32
= - +
d d d
n n n
A) log 6 B) 1 C) log 3
D) log 5 E) log 2
28. Calcula:
B = (log210)(log510)- log25 - log52
A) 6 B) 5 C) 4
D) 3 E) 2
29. Si: log35 = a
Calcula: log1581
A) (4 + a)-1
B) 3(2 + a)-1
C) 2(1 + a)-1
D) 4(1 + a)-1
E) (1 + a)-1
30. Si:
a b ab
a b
1 1 2
+ = -
Halla: 0,5
log
E a
b
3
=
A) 1 B) 2 C) 3
D) 4 E) 5
Resolución de problemas
31. La suma de los cuadrados de dos números
enteros es 29 y la suma de sus logaritmos
(en base 10) es 1. Dichos números son:
A) -2 y 5 B) 4 y 5 C) 2 y -5
D) 2 y 5 E) 3 y 20
32. Si al cuadrado de 343 veces un número
se le toma el logaritmo decimal se obtiene
como resultado 9,8143. Determina el
cuadrado del logaritmo decimal del
número menos 1.
Considere: log7 = 0,8451
A) 1,8820 B) 2,8820 C) 3,8820
D) 11,8820 E) 5,8820
C
l
a
ve
s
Nivel
1
1.
d
2.
3.
B
4.
A
5.
C
6.
d
7.
A
8.
b
9.
C
10.
D
Nivel
2
11.
b
12.
13.
C
14.
A
15.
A
16.
D
17.
B
18.
E
19.
C
20.
E
21.
C
Nivel
3
22.
D
23.
24.
E
25.
C
26.
C
27.
e
28.
E
29.
D
30.
C
31.
D
32.
A

85. Aplicamoslo aprendido
85
ÁLGEBRA - ACTIVIDADES UNIDAD 4
1 De las siguientes relaciones indica la que es una función:
A) R1 = {(1; -7), (2; -7), (3; 5)}
B) R2 = {(3; -7), (3; -3), (2; 5)}
C) R3 = {(1; 5), (2; -3), (2; -7)}
D) R4 = {(2; -5), (2; -7), (2; -3)}
E) R5 = {(2; 3), (5; -1), (5; -7)}
2 Si f es una función de A en B:
B
f
A
3
7
8
6
Determina: f(7) . f(3)
A) 21 B) 48 C) 22
D) 42 E) 52
3 En la siguiente función determina el valor de b.
g = {(7; 17), (3; 5), (4; 14), (7; b - 7)}
A) 17 B) 14 C) 24
D) 21 E) 5
4 Dada la función:
f = {(2; 6), (1; a - b), (1; 4), (2; a + b), (3; 4)}
Determina: a . b
A) 3 B) 7 C) 8
D) 10 E) 5
5 Sean M = {3; 7; 1} y N = {49; 1; 3} dos conjuntos y
f(x) = {(x; y) ! M # N / y = x2
} una función.
Completa f(x) = {(...; 49), (1; ...)} e indica Dom(f) / Ran(f).
A) {7; 49} / {1; 1} B) {7; 1} / {49; 1}
C) {7} / {49} D) {-1; 1} / {7; 49}
E) {49} / {1}
6 Si: g(x + 2) = x + 9 y f(x - 2) = x 9
+
Determina:
( )
( )
f
g
14
3
A) 3 B) 9 C) 14
D) 2 E) 1
tema 3: FUNCIoNes

86. Claves
86 Intelectum 1.°
1.
a
2.
B
3.
c
4.
E
5.
b
6.
D
7.
A
8.
D
9.
10.
D
11.
C
12.
B
13.
A
14.
A
7 Si el dominio de g(x) = 6x - 12 es {7; 4; 2}, determina su rango
e indica la suma de sus elementos.
A) 42 B) 13 C) 18
D) 32 E) 52
8 Determina el rango de f(x) = 7x - 5
Si: Domf ! 14; 7]
A) [23; 49] B) ]23; 49] C) [2; 7]
D) ]23; 44] E) [-1; 3]
9 Grafica: y = 4x - 3 10 Dados los conjuntos:
A = {1; 7; 6; 4} y B = {1; 35; 0; 48}
Determina la función g(x) de A en B Si:
g(x) = {(x; y) ! A # B / y = x2
- 1}
Indica la suma de los elementos del rango.
A) 72 B) 82 C) 64
D) 83 E) 18
11 Si f(x) es una función lineal; calcula.
f(-2), además: f(0) = 3 y f( 6) = 9.
A) 3 B) 4 C) 1
D) 5 E) 0
12 De la gráfica, halla m + n.
x
y
2 4
4
n
m
8
A) 6 B) 3 c) 4
D) 9 E) 1
13 Sea una función f: R " R definida por:
f(x) = ax + b, donde a y b son constantes.
Si: f(1/3) = 4 y f(2) = -1, halla a y b.
A) a = -3; b = 5 B) a = 2; b = -3
C) a = 2; b = -3 D) a = 1; b = 1
E) a = 3; b = 4
14 Del gráfico, halla m . n.
x
9
2
6
n
m
y
3/2
A) 36 B) 48 C) 24
D) 72 E) 12

87. Practiquemos
87
ÁLGEBRA - ACTIVIDADES UNIDAD 4
NIVEL 1
Comunicación matemática
1. Responde con una (V) o (F) si las premisas son verdaderas o
falsas, respectivamente:
A)
5
4
6
7
3
f1
1
B)
4
2
6
g1
3
1
f1 es una función. ( ) g1 no es función. ( )
C) Si f = {(3; 7), (7; 3), (4; 5)} & f es una función. ( )
D) Si g = {(6; 9), (3; 7), (3; 17)} & g es una función. ( )
E) Si f(x) es una función, & f(x) es una relación. ( )
A) FVFVV B) FFVVF C) VVFFV
D) VVVFF E) VVVFV
2. A) Según el diagrama cartesiano completa en el diagrama sagital.
B
1 2
4
6
7
3 A
2
3
f
B
A
B) Dadas las funciones:
f
3
2
5
2
1
6
B
A
g
6
1
7
3
2
5
A
M
Calcula:
C =
( ( ))
( ( )) ( ( ))
f g
f g f g
6
1 7
+
A) 2 B) 4 C) 6
D) 8 E) 10
Razonamiento y demostración
3. Si F = {(3; a + 2), (1; 7), (3; 4)} es una función; determina a2
.
A) 16 B) 4 C) 2
D) 1 E) 9
4. Si el conjunto:
G = {(a; 3b); (a; a + b); (2b; 12)}
es una función, halla a - b.
A) 2 B) 3 C) 4
D) 5 E) 6
5. Sean las funciones F y G:
F = {(3; 6), (9; 11), (13; 17)}
8
5
2 6 x
y
G(x)
Determina:
( )
( ) ( ( )) ( )
G
F G F F
2
9 3 3
+ +
A) 3 B) 2 C) 4
D) 6 E) 5
6. Si A = {1; 2; 3} y B = {4; -6; 9} y
F = {(x; y) ! A # B / y = 4x}; indica el rango de F.
A) {-3} B) {4} C) {(1; 4)}
D) {-6} E) Q
7. Determina el rango de:
f(x) = 4x + 3; si: Domf(x) = [2; 6]
A) [8; 12] B) [11; 24] C) [11; 27]
D) R+
E) R
8. Halla la suma de los valores del dominio de la función:
f(x) = 3x - 2; si Ranf(x) = {4; 1; 7; 13}
A) 11 B) 14 C) 17
D) 6 E) 5
Resolución de problemas
9. Dados los conjuntos:
A = {x / 2 # x # 7, x ! N}
B = {x + 2 / 0 # x < 7, x ! N}
Determina la siguiente función como par ordenado
f = {(x; y) ! A # B / y = 2x - 2}
A) f = {(2; 2); (3; 4); (5; 8)}
B) f = {(6; 10), (7; 12)}
C) f = {(2; 2), (3; 4)}
D) f = {Q}
E) f = {(2; 2), (3; 4), (5; 8), (6; 10)}
10. Joanna lee 10 páginas de una obra por día, representa en una
función y que indique el n.° de páginas que lee por x semanas.
A) y = 10x B) x = 10y C) y = 70x
D) x =
x
70 E) y = 10 + 7x
11. Una empresa de viajes ofrece un tour de S/.800 para un máximo
de 40 personas. Si solo asisten x personas; x < 40, cuánto
pagará cada persona.
A) 3200x B) 40x C) 800/x
D) 400/x E) 300/x

88. 88 Intelectum 1.°
NIVEL 2
Comunicación matemática
12. Observa y determina cuántas funciones hay.
f = {(2; 3), (4; 7), (4; 9), (7; 5)}
g = {(13; 4), (7; 2), (6; 1), (11; 3)}
x
y
f1
x
y
f2
x
y
g1
x
y
g2
A) 1 B) 2 C) 3 D) 4 E) 5
13. a) Relaciona las siguientes proposiciones:
I. Función lineal y = f(x)
II. Producto cartesiano y = kx
III. Función inversamente proporcional A # B
IV. Función directamente proporcional y =
x
k
V. Regla de correspondencia y = ax + b
b) Completa las siguientes tablas:
y = -5x
x 1 4
y -5 -15 -30
y =
x
4
x 2 4
y 1/2 2/5
y = 6x - 2
x 4 5
y -2 16 28
Razonamiento y demostración
14. Dada la función f = {(2; 3), (3; 4), (4; 1)}
Calcula: M = f(f(2)) + f(f(3))
A) 7 B) 9 C) 6 D) 8 E) 5
15. Sea la función: H = {(a; 4), (1; 7), (a; b), (1; a)}. Determina: a2
- b2
A) 33 B) 28 C) 16 D) 5 E) 49
16. Dados los conjuntos:
A # B = {(1; 2), (1; 3), (1; 4), (2; 2), (2; 3), (2; 4)} y
C = {1; 5; 6}
Determina f = {(x; y) ! A # C} e indica Ran(f) + Dom(f).
A) {1; 2} B) {2} C) {1} D) {3; 4; 1} E) {4}
17. Halla el rango de la función f(x) = -4x + 10
Si: x ! [2; 5]
A) [-4; 3] B) [-11; 1] D) [8; 20]
D) [0, + 3H E) R
18. Halla el dominio y el rango de la siguiente función:
F = {(2; 5), (-1; -3), (2; 2a - b), (-1; b - a), (a + b2
; a)}
Luego, indica: Dom(f) + Ran(f)
A) {3} B) {-1} C) {2} D) {5} E) Q
19. Sea la función h(x) = 3x - 2; Ranh(x): ]7; 13], determina su
dominio.
A) [3; 5] B) ]3; 5] C) [-2; 3]
D) [3; 7] E) ]19; 37]
20. Si f(x) =
x
x
1
1
2
+
- ; determina: f(f(2))
A) 3 B) 2 C) 1 D) 0 E) 1
Resolución de problemas
21. La medida del diámetro de un círculo es el doble que la de su
radio (r), expresalo en una función f(r) e indica cuánto mide su
diámetro si el radio mide 25 cm.
A) f(r) = 2r; 30 cm B) f(r) = r; 25 cm
C) f(r) = r2
; 25 cm D) f(r) = r; 50 cm
E) f(r) = 2r; 50 cm
22. El área de un triángulo es 12 m2
. Determina como varía su altura
h(x) en función a su base (x).
A) h(x) = 12x B) h(x) =
x
12 C) h(x) =
x
24
D) h(x) = 24x E) h(x) = 12
NIVEL 3
Comunicación matemática
23. Resuelve:
I) Dados los conjuntos: A = {7; 1; 8; 3; 4; 5; 6; 5}
B = {c; d; a; c}
Determina: n(A # B) = . =
II) Sea el conjunto M # N:
M
N
3 4 5
4
6
8
3
5
7
2
2 6 7

89. 89
ÁLGEBRA - ACTIVIDADES UNIDAD 4
R = {(x; y) ! M # N / y es primo / x es par}
Halla: Dom(R) + Ran(R)
A) {2; 8; 3; 7} B) {2; 3} C) {8; 7}
D) { } E) {2; 7}
III) Completa: y = . x +
x -1 0 7
y 4 12 14
IV)Mediante una gráfica representa la función costo, que
depende del volumen de leche, si 1 litro cuesta S/.3.
V) Si M = 1 es DP a N = 7; cuánto vale M cuando N es 28.
24. Responde verdadero (V) o falso (F):
I) (2; 3) ! a la función f(x) = x2
- 1 ( )
II) g g: es una función ( )
III) Si A DP B y B DP C & A DP C. ( )
IV)El dominio de f(x) =
x
x
1
1
-
+ es R. ( )
V) La gráfica de f(x) = 3 es una recta horizontal. ( )
A) VVVFF B) VFVFF C) FVFVV
D) VFVFF E) VFVVV
Razonamiento y demostración
25. Si A = {3; 5; 6; -2} y B = {1; 5; 13; -3; 0}
Halla f = {(x; y) ! A # B / y = 2x + 1}
A) f = {(3; 7), (5; 11)} B) f = {(3; 7), (6; 7)}
C) f = {(5; 1), (6; 13)} D) f = {(6; 13), (-2; -3)}
E) f = {(3; 7), (5; 13), (-2; -3)}
26. Si f(x) es una función lineal, además f(0) = -3 y f(2) = 1
Halla la regla de correspondencia de f(x).
A) f(x) = 3x - 6 B) f(x) = 4x - 7 C) f(x) = 2x - 3
D) f(x) = x + 6 E) f(x) = x - 1
27. Si Df = [-3; 2] halla el conjunto solución para el rango de la
función: f(x) = x2
+ 1.
A) [5; 9] B) [1; 10] C) [3; 5]
D) [-3; 5] E) [0; 10]
28. Halla el dominio de: f x
x
x
x
x
3
2
3
1
=
+
- +
-
+
_ i
A) Df = R -{3} B) Df = R -{!3} C) Df = R
D) Df = R-{0} E) Df = { }
29. Halla el rango de la función: f(x) = -2x + 5; x ! ]-4; 2]
A) [-3; 9] B) ]-3;9[ C) [1; 13]
D) ]-3; 13[ E) ]-1; 5[
30. Si f(x) = 3x - 5 y g(x) = 2x2
- 1; determina g(f(3)).
A) 21 B) 13 C) 31 D) 17 E) 13
31. Si (3; 1) ! f(x), siendo f(x) = ax - 8 determina f(4).
A) 4 B) 5 C) 7 D) 9 E) 1
32. De la gráfica determina el dominio y rango de h(x); si h(-2) = -1
10
-2
9 x
y
h(x)
A) [-2; 9] y [9; 10] B) [-1; 9] y [9; 10]
C) [-1; 9] y [-2; 10] D) [-2; 9] y [-1; 10[
E) N. A.
33. Sea la función:
G(x) =
2x - 1; si x $ 6
4; si x 1 6
Calcula: E
G G
G G
5 2
7 9 2
=
+
+ +
_ _
_ _
i i
i i
A)
4
15 B)
2
15 C) 4 D) 8 E) 31
Resolución de problemas
34. 3 trabajadores hacen 200 m de carretera en un día si se duplica
el trabajo y se enferma 1 trabajador en cuántos días realizan
dicho trabajo. (Día laboral 8 h).
A) 2 días B) 3 días C) 4 días
D) 5 días E) 1 día
35. Un tanque de agua tiene una capacidad de 36 m3
; qué tiempo en
horas tomará en llenarse (1 m3
= 1000 L).
I. A un caudal de 60 L/min.
II. A un caudal de 25 L/min.
A) 14 y 18 B) 12 y 20 C) 15 y 18
D) 10 y 24 E) 25 y 60
Claves
Nivel 1
1. e
2. D
3. B
4. C
5. e
6. B
7. C
8. A
9. C
10. c
11. c
Nivel 2
12. c
13.
14. e
15. A
16. C
17. B
18. C
19. B
20. D
21. E
22. C
Nivel 3
23. D
24. B
25. D
26. C
27. B
28. B
29. C
30. C
31. A
32. D
33. C
34. B
35. d

90. Aplicamoslo aprendido
90 Intelectum 1.°
1 En la PA determina el valor de x.
: 6; x; 10; ...
A) 7 B) 8 C) 9
D) 5 E) 3
2 Determina el término de lugar 50 de la siguiente progresión:
: 2; 5; 8; ...
A) 130 B) 140 C) 150
D) 149 E) 139
3 En la siguiente PA:
: 2; 4; 6; ...; 198.
halla a14.
A) 26 B) 28 C) 30
D) 32 E) 34
4 Halla a25 ' a15, en la siguiente PA:
: 5; 10; 15; ...
A) 5 B) 3 C)
3
5
D)
5
3 E) 8
5 Halla la suma de términos en la siguiente PA:
: 2; 4; 6; 8; ... ; 68
A) 1000 B) 1190 C) 2190
D) 1290 E) 1128
6 Identifica cuál(es) es(son) PG:
A) 3; 7; 11; ...
B) 6; 12; 24; ...
C) 2/3; 1/3; 1/6; ...
D) ab; a2
b2
; a3
b3
; ...
E) xy; x3
y; xy2
; ...
A) A B) B; C C) C; D
D) B; C y D E) Todas
tema 4: progresiones

91. Claves
91
ÁLGEBRA - ACTIVIDADES UNIDAD 4
1.
b
2.
d
3.
b
4.
c
5.
b
6.
d
7.
D
8.
c
9.
c
10.
c
11.
c
12.
C
13.
A
14.
B
7 Halla el número de términos de 28; 32; 36; 40;... ; 208.
A) 32 B) 36 C) 42
D) 46 E) 16
8 Halla T15 en la PA.
: (n - 1); (n + 3); (3n - 1); ...
A) 19 B) 16 C) 59
D) 57 E) 4
9 Halla la siguiente suma:
4 1
S
4
1
16
1
64
1 $$$
= + + + + +
A) 16 B) 3 C)
3
16
D)
16
3 E)
4
3
10 En una PG se conoce que:
S6 = 28(S3)
Halla la razón q.
A) 1 B) 2 C) 3
D) 4 E) 5
11 La suma de n términos de una progresión aritmética es:
Sn = 3n2
- 5. Halla t21.
A) 220 B) 198 C) 218
D) 88 E) 118
12 En la siguiente PG:
:: ; 1; ;...
3
2
2
3
Calcula a8.
A)
2
3 B)
2
3 3
d n C)
2
3
6
6
D)
3
2 6
d n E)
3
2
13 Halla la suma: ...
10
1
10
2
10
3
10
4
2 3 4
+ + + +
A)
81
10 B)
10
1 C)
90
1
D)
90
7 E)
10
7
14 El producto de los tres primeros términos consecutivos de una
progresión aritmética es 162 y la razón es 3, halla el cuarto
término.
A) 10 B) 12 C) 14
D) 9 E) 15

92. Practiquemos
92 Intelectum 1.°
NIVEL 1
Comunicación matemática
1. En las siguientes progresiones aritméticas completa.
I) : m - 2; m + 1 ; + ; ...
II) : 7 ; ; 17; ...
III)
n = (n.° términos)
r = (razón)
PA
10
35
IV): 2 + 3 ; 3; 3 - ; ...
20 términos
V) : 2; ...; 35 ; ... ; ...;
12 términos
30 términos
2. A) Determina x si:
I) : 4x; 5x + 1; 4x + 10; ... es una PA & x =
II) ::
x
16 ; 7; 3x + 1; ... es una PG & x =
B) Relaciona correctamente:
PA decreciente
PG oscilante
PG creciente
PG creciente
2; 7/2; 5; 13/2
:: ; ; ;...
2 8 32
: a + 1; a + 11 ; a + 21; ...
:: 4; -12 ; 36; - 108 ; ...
: 13; 11; 9; 7; ...
sucesión finita
Razonamiento y demostración
3. Demuestra que la suma de los n primeros números naturales es
( )
n n
2
1
+
.
4. Sea la PA: 10; 14; 18; ... encuentra el término de lugar 20.
A) 38 B) 58 C) 70 D) 50 E) 86
5. Determina el primer término de una progresión aritmética de 29
términos de razón 4 cuyo último término es 119.
A) 14 B) 7 C) 0 D) 4 E) 29
6. Halla el número de términos de: 28; 32; 36; 40;... ; 208.
A) 36 B) 30 C) 46 D) 50 E) 56
7. Calcula: S = 27 + 30 + 33 + ... + 333
A) 10 050 B) 18 540 C) 30 000
D) 5040 E) 3700
8. Halla a20 ' a10, en la siguiente progresión:
:: 4 ; 8 ; 16 ; ...
A) 512 B) 1024 C) 256
D) 64 E) 16
Resolución de problemas
9. La suma de los términos de una PA es 425 y su término central
17. El número de términos es:
A) 15 B) 25 C) 30 D) 35 E) 50
10. El tercer término de una PA es 18 y el séptimo 30. Calcula la
suma de los 17 primeros términos.
A) 600 B) 610 C) 611 D) 612 E) 630
11. Las edades de 3 personas están en PG siendo el producto de
las edades 27 000. ¿Cuál es la edad de la persona intermedia?
A) 15 B) 20 C) 30 D) 40 E) 25
NIVEL 2
Comunicación Matemática
12. 1
3
5
55
De la figura responde:
I) Las filas corresponden a una PA creciente de razón .
II) La fila n.° 17 tiene bolitas.
III) El n.° total de bolitas del arreglo es .
13. Completa los pasos adecuadamente.
...
M
4 2 1
2
1
4
1
4 8 16 32 64 128
=
+ + + + +
+ + + + +
í ó 1/2
é min
M
Suma l mite de una PG de raz n
Suma de PG de t r os
6
=
.
S
S
1
2
L
6
=
-
=
+
f p
=
` M =
Razonamiento y demostración
14. Determina la razón de la progresión aritmética:
: m + 3 ; m - 2; ...
A) m B) m - 1 C) 5
D) -5 E) 7

93. 93
ÁLGEBRA - ACTIVIDADES UNIDAD 4
15. Sea una PA donde a5 = 4 de razón 1/2, determina el término de
lugar 15.
A) 9 B) 7 C) 16 D) 17 E) 15/2
16. En la siguiente progresión geométrica:
:: 2–2
; 2-1
; ...
Calcula a49.
A) 242
B) 244
C) 246
D) 248
E) 235
17. El cuarto término de una PG es 2 y el décimo es 128. Calcula el
valor de la razón.
A) 1 B) 2 C) 3 D) 4 E) 5
Resolución de problemas
18. El cociente entre el quinto y el primer término de una PG es 16
y su suma es 51. Determina el tercer término de la progresión.
A) 10 B) 8 C) 12 D) 4 E) 1/2
19. El quinto término de una PG es 24 y el segundo 81. Halla el
número de términos enteros de la progresión.
A) 5 B) 6 C) 12 D) 25 E) 83
20. Halla cinco números enteros en PG creciente cuya suma es 31 y
su producto 1024. Proporciona la suma de la razón con el primer
término de dicha progresión.
A) 3 B) 4 C) 5 D) 2 E) 6
NIVEL 3
Comunicación matemática
21. En un triángulo sus ángulos internos siguen una PA. Si el menor
mide 10°, determina el ángulo mayor.
A) 50°
10°
B) 60°
C) 110°
D) 100°
E) 70°
22. En el siguiente arreglo se tiene 12 filas:
3 Fila 1
3 3
3 6 3
3 9 9 3
3 12 18 12 3
...
.
.
.
.
.
.
Determina:
I) La suma de los números de la fila 10.
t10 =
II) ¿Cuánto suman todos los números del arreglo?
S12 =
Razonamiento y demostración
23. Halla la suma de los infinitos términos de:
...
7
1
7
2
7
1
7
2
2 3 4
+ + + +
A)
24
9 B)
16
3 C)
16
5
D)
16
9 E)
24
5
24. Determina la suma de los múltiplos de 5 comprendidos entre
50 y 149.
A) 199 B) 2000 C) 1900
D) 750 E) 500
25. En la siguiente PG:
:: 2 ; 2; ...
Determina:
a
a
5
10
A) 25 B) 2 C) 2
3
D) 4 2 E) 2 2
26. Si:
:: (a + b), (4a - 3b); (5b + 3a), ... es una PA; luego a/b es:
A) 3 B) 4 C) 5 D) 7 E) 2
Resolución de problemas
27. La suma de los infinitos términos de una PG decreciente es 8 y
la suma de los dos primeros términos es 6. ¿Cuál es el valor del
primer término?
A) 1 B) 2 C) 3 D) 4 E) 6
28. El quinto término de una PA es igual a 19 y el décimo es 39.
¿Cuántos términos hay que tomar para que su suma sea 465?
A) 18 B) 12 C) 20 D) 10 E) 15
29. La suma de los 10 términos de una PA creciente es 60, la
diferencia de los extremos es 18, halla el término 10.
A) 15 B) 18 C) -3 D) 10 E) 8
Claves
Nivel 1
1.
2.
3.
4. e
5. b
6. c
7. b
8. b
9. b
10. d
11. c
Nivel 2
12.
13.
14. d
15. A
16. C
17. B
18. C
19. A
20. A
Nivel 3
21. C
22.
23. B
24. C
25. D
26. A
27. d
28. E
29. A

94. 94 Intelectum 1.°
Matemática
1. Completa cada caso:
a)
Ecuaciones Valor (es) de x
|x - 3| = 4 x1 = x2 =
logx9 = 2 x =
log3(x + 2) + log39 = 1 x =
b) Si F(x) = 7x - 3
F(x) 11 46 -17
x 2 4 3
c) :: 1 + 3 + ... + 38
+ 39
: -3 + 4 + ... + 95 + 102
Sn = 3 1
-
Sn = - + 1
=
2. Determina el rango de la función:
f(x) =
x
x
1
7
+
- , si x ! G0; 5]
A) [1/3; 7H B) ;
4
7 4
< C) G5; 7]
D) G5; 7] E) ;
3
2 7
<
3. Encuentra el conjunto solución de:
|x - 3| = 3
A) CS: {0; 3} B) CS: {1; 3} C) CS: {
3
1 ; 7}
D) CS: {0; 6} E) CS: {2; 4}
4. Resuelve la siguiente ecuación:
4x
- 2x + 2
- 32 = 0
e indica un valor real de x.
A) 2 B) 1 C) 3
D) 4 E) -2
5. Dada una progresión aritmética. Si su undécimo término y cuarto
término son 25 y 11, respectivamente, determina la razón.
A) 2 B)
2
1 C) 3
D) 4 E) 6
6. Determina el valor de a.
Si: log(xy) = a y logx2
+ logy2
= 10
A) 10 B) 100 C) 5
D) 4 E) 1
7. En la siguiente progresión aritmética determina x + y si:
: -5; -1; 3; ... ; x; ... ; y
12 términos
20 términos
A) 102 B) 84 C) 100
D) 110 E) 124
8. En una función de proporcionalidad f(x), se cumple:
f(3) + f(2) = 30
Determina:
( )
( ) ( )
f
f f
3
7 8
+
A) 5 B) 4 C) 3
D) 7 E) 8/3
9. Determina un valor de x.
logx - 3(x - 1) = 2
A) 4 B) 2 C) 6
D) 5 E) 3
10. En una reunión cada 5 minutos se reciben 7 invitados, luego
10, luego 13 y así sucesivammente hasta que al final llegan 37
invitados. ¿Cuánto tiempo transcurrió? En minutos.
A) 33 B) 77 C) 55
B) 45 E) 25
11. Elena lee una obra literaria, el primer día lee 10 páginas, el
segundo 14 páginas, el tercer día, 18 páginas... ¿Qué día
culminará la lectura si empezó el 12 de abril y la obra posee
960 páginas?
A) 19 de abril B) 29 de abril C) 8 de mayo
B) 5 de mayo E) 3 de mayo
Determina en la figura A + B; si la recta ON es una función de
proporcionalidad directa y la curva NP representa una función de
proporcionalidad inversa.
A
y
10/3
O
B
4 6 10
N
P
x
Como ON es función de proporcionalidad directa se cumple:
A
4
3
10
6
= & A = 5
NP es curva de una función de proporcionalidad inversa, entonces:
A . 6 = B . 10 & 5 . 6 = B . 10
& B = 3
` A + B = 8
Resolución:

95. Instrucciones: completa los tableros subdivididos en 9 cuadrados llenando las celdas vacías con los números del 1 al 9, sin que se repita ninguna
cifra en cada fila, ni en cada columna, ni en cada cuadrado.
1.
4 1 5 2 9
5 4
2 8 1 7
9 6 7 8 4
8 2 4 5 1
7 5 6 1
7 6
8 6 3 2 4
2.
5 7
7 6 2 1
3 9 8 4 6
5 4 1
6 4 7 3 2
9 1 3
7 1 6 9 8
4 9 2 1
3 1
3.
1 3 5 7 9
3 4 6
6 9 1
6 5 3 9
3 9 5
5 4 7 3
8 7 4
2 7 5
5 3 7 2 1
4.
9 6 1 2 8
8 3 5
5
8 9 1 7 4
1 4 2 8 5
4 3 5 6 1
7
1 4 2
4 6 2 5 1
5.
4 1 8 5
2 9 4 8 6
5 1
6 9 7 4
6 1
5 4 8 3
3 4
4 1 6 2 9
3 8 2 1
6.
3 9 6
6 4 1 8
7 9 6 4
8 7 1 5
4 5 6
8 9 2 3
1 7 9 4
9 4 5 2
5 3 1
7.
2 4
6 8 3 4 5
2 1 6
3 5 2
6 8 1 4 9 3 2
7 8 6
7 5 4
3 4 8 7 2
1 2
8.
7 2 4
9 8 6 5 7
5 6 7 3
8 7
6 2 1 9 5
9 2
8 4 2 1
7 9 1 3 4
4 9 5

96. 1.
4 1 8 7 5 6 2 3 9
5 3 7 4 9 2 8 6 1
9 6 2 3 8 1 4 7 5
1 9 5 6 7 8 3 4 2
7 2 4 9 1 3 6 5 8
6 8 3 2 4 5 9 1 7
2 7 9 5 6 4 1 8 3
3 4 1 8 2 7 5 9 6
8 5 6 1 3 9 7 2 4
2.
6 2 1 4 3 5 8 7 9
4 5 7 6 8 9 2 1 3
3 9 8 7 2 1 5 4 6
2 7 3 5 4 6 9 8 1
1 6 4 9 7 8 3 2 5
9 8 5 2 1 3 7 6 4
7 1 2 3 5 4 6 9 8
5 4 9 8 6 2 1 3 7
8 3 6 1 9 7 4 5 2
3.
1 3 4 2 5 6 7 8 9
7 2 5 3 8 9 4 1 6
6 9 8 7 4 1 2 5 3
4 1 6 5 2 3 8 9 7
3 7 2 6 9 8 1 4 5
8 5 9 4 1 7 3 6 2
9 6 1 8 3 2 5 7 4
2 4 7 1 6 5 9 3 8
5 8 3 9 7 4 6 2 1
4.
3 9 4 5 6 7 1 2 8
1 7 8 3 4 2 9 5 6
5 2 6 8 9 1 7 3 4
8 5 9 1 7 6 3 4 2
6 3 1 4 2 8 5 7 9
2 4 7 9 3 5 6 8 1
9 8 5 2 1 3 4 6 7
7 1 3 6 8 4 2 9 5
4 6 2 7 5 9 8 1 3
5.
3 6 4 2 1 8 9 5 7
7 2 9 3 4 5 8 1 6
5 1 8 9 7 6 3 4 2
6 8 3 5 9 7 4 2 1
2 4 7 6 3 1 5 8 9
1 9 5 4 8 2 7 6 3
8 7 2 1 5 9 6 3 4
4 5 1 7 6 3 2 9 8
9 3 6 8 2 4 1 7 5
6.
3 1 5 7 8 4 2 9 6
6 4 2 3 9 5 1 8 7
8 7 9 6 1 2 4 3 5
4 6 3 8 7 1 5 2 9
9 2 7 4 5 6 3 1 8
1 5 8 9 2 3 7 6 4
2 8 1 5 6 7 9 4 3
7 9 4 1 3 8 6 5 2
5 3 6 2 4 9 8 7 1
7.
1 7 3 5 6 2 9 4 8
6 8 9 7 3 4 2 5 1
5 4 2 9 1 8 6 3 7
3 5 1 8 2 6 7 9 4
7 6 8 1 4 9 3 2 5
2 9 4 3 7 5 1 8 6
8 2 7 6 5 3 4 1 9
9 3 6 4 8 1 5 7 2
4 1 5 2 9 7 8 6 3
8.
7 1 3 2 9 5 6 8 4
2 9 4 3 8 6 5 7 1
8 5 6 4 7 1 3 9 2
1 8 5 9 2 3 4 6 7
3 6 2 7 1 4 9 5 8
9 4 7 6 5 8 1 2 3
6 3 8 5 4 7 2 1 9
5 7 9 1 3 2 8 4 6
4 2 1 8 6 9 7 3 5