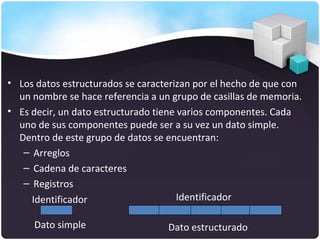
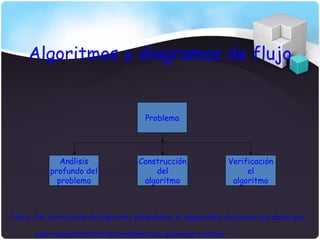
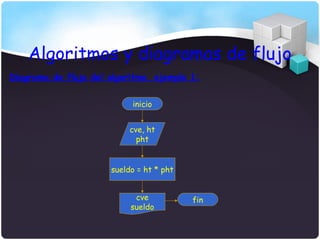
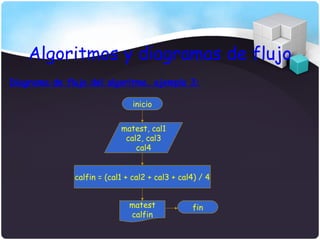
El documento describe los tipos de datos, expresiones, algoritmos y diagramas de flujo. Explica datos simples como enteros, reales y caracteres, así como datos estructurados como arreglos y registros. También cubre conceptos como identificadores, constantes, variables, operaciones aritméticas y lógicas, y las reglas para desarrollar algoritmos secuenciales usando diagramas de flujo.

2. OBJETIVO
El alumno comprenderá los tipos de datos y
expresiones mas comunes, el concepto y
características de lo que es un algoritmo, así
como las reglas y aspectos básicos de un
diagrama de flujo, además de adquirir la
habilidad de desarrollar un algoritmo
secuencial.

3. CONTENIDO
• Tipos de Datos y Expresiones
• Conceptos de Algoritmos
• Diagramas ( reglas y símbolos básicos)
• Algoritmos Secuenciales

4. Tipos de datos
• Los datos a procesar por una computadora pueden clasificarse
en:
– Simples
– Estructurados
• Los datos simples se caracterizan porque ocupan sólo una casilla
de memoria, por lo tanto una variable simple hace referencia a
un único valor a la vez. dentro de este grupo de datos
encontramos:
– Enteros
– Reales (flotantes)
– Caracteres
– Cadena de caracteres

5. • Los datos estructurados se caracterizan por el hecho de que con
un nombre se hace referencia a un grupo de casillas de memoria.
• Es decir, un dato estructurado tiene varios componentes. Cada
uno de sus componentes puede ser a su vez un dato simple.
Dentro de este grupo de datos se encuentran:
– Arreglos
– Cadena de caracteres
– Registros
Identificador Identificador
Dato simple Dato estructurado

6. Datos simples
• Enteros.- son números que no contienen componentes
fraccionarias y, por lo tanto, no incluyen el punto decimal, pueden
estar precedidos del signo + o --. Por ejemplo:
465 -387 9 99 -1578 125550
• Reales (flotantes).- son números que contienen una parte
fraccionaria y, por lo tanto, incluyen el punto decimal, pueden esta
precedidos del signo + o --. Por ejemplo:
125.87 -124.0 158000.75 -38.5879
• Carácter.- contiene un solo carácter y va encerrado entre comillas
simples. Por ejemplo:
‘a’ ‘A’ ‘$’ ‘#’ ‘7’ ‘+’ ‘h’ ‘H’

7. Algoritmos y diagramas de flujo
Cadena de caracteres.- contiene un conjunto de caracteres alfabéticos,
numéricos, y especiales, que sirven para representar y
manejar datos como: nombres, descripciones de artículos,
direcciones, etc. Van encerrados entre comillas dobles, por
ejemplo:
“abc” “Carlos Jiménez” “83-15-24-65” “$8#2”
Booleanos.- toma los valores de verdadero (true) o falso (false), no
puede ser leído o escrito, sólo asignado, es útil para
plantear cierto tipo de condiciones en el manejo de las
estructuras lógicas de control.

8. Algoritmos y diagramas de flujo
Identificadores, constantes y variables
Identificadores.- son nombres que se usamos para referirnos a
variables, constantes, funciones o cualquier objeto
definido por el usuario.
Un identificador se forma de acuerdo a ciertas reglas
básicas:
» El primer carácter que forma un identificador debe ser
una letra o el símbolo de subrayado ( _ ).
» Los demás caracteres pueden ser letras, dígitos o
símbolo de subrayado.
» La longitud del identificador depende del lenguaje de
programación a utilizar.

9. Algoritmos y diagramas de flujo
Constantes
• Son datos que no cambian durante la ejecución de un programa.
Existen tipos de constantes como tipos de datos, por lo tanto, puede
haber constantes enteras, reales (flotantes), de carácter, de
cadenas de caracteres, booleanas, etc.
Variables
• Es un identificador que puede cambiar su valor durante la ejecución
de un programa.
• Se utiliza para representar un dato tipo entero, real (flotante), o una
constante de carácter. Por ejemplo:
Variable i es de tipo entero
variable prom es de tipo real (flotante)
Variable opción es de tipo carácter

10. Algoritmos y diagramas de flujo
Operaciones aritméticas
• Para poder realizar operaciones aritméticas necesitamos de
operadores aritméticos.
• Estos operadores nos permiten realizar operaciones aritméticas
entre operandos: números, constantes o variables. El resultado de
una operación aritmética es un número.
• A continuación presentamos en una tabla los operadores aritméticos,
la operación que puede realizar y, un ejemplo de su uso y su
resultado:

11. Algoritmos y diagramas de flujo
Operadores Aritméticos
Operador Aritmético Operación Ejemplo Resultado
** Potencia 3**2 9
* Multiplicación 5.25*3 15.75
/ División 17/4 4.25
+ Suma 58+79 137
- Resta 25.96 -11.25 14.71
Mod Módulo (residuo) 21 mod 2 1
div División entera 19/3 6

12. Algoritmos y diagramas de flujo
• Al evaluar expresiones que contienen operadores aritméticos
debemos respetar la jerarquía en el orden de aplicación. Es decir, si
tenemos en una expresión más de un operador, debemos aplicar
primero el operador de mayor jerarquía, resolver esa operación y así
sucesivamente.
Jerarquía de los operadores aritméticos
Operador Jerarquía Operación
** (Mayor) Potencia
*, /, mod, Multiplicación, división, módulo, división entera
div
+, - Suma, resta
(menor)

13. Algoritmos y diagramas de flujo
Reglas para resolver una expresión aritmética:
1. Si una expresión contiene subexpresiones entre paréntesis, éstas
se evalúan primero, respetando claro la jerarquía de los operadores
aritméticos en esta subexpresión.
Si las subexpresiones se encuentran anidadas por paréntesis,
primero se evalúan las subexpresiones que se encuentran en el
último nivel de anidamiento.
2. Los operadores aritméticos se aplican teniendo en cuenta la
jerarquía y de izquierda a derecha.

14. Algoritmos y diagramas de flujo
Por ejemplo:
• Dados los siguientes casos, resolver cada caso aplicando las reglas
correspondientes:
1). 7 + 5 – 6 2). 9 +7 * 8 – 36 / 5 3). 7 * 5 ** 3 / 4 div 3
1 1 1
12 – 6 9 + 56 – 36 / 5 7 * 125 / 4 div 3
2 2 2
=6 9 + 56 – 7.2 875 / 4 div 3
3 3
65 – 7.2 218.75 div 3
4 4
= 57.8 = 72

15. Algoritmos y diagramas de flujo
4). 7 * 8 * (160 mod 3 ** 3) div 5 * 13 – 28 3640 - 28
1 7
7 * 8 * (160 mod 27) div 5 * 13 – 28 = 3612
2
7 * 8 * 25 div 5 * 13 – 28
3
56 * 25 div 5 * 13 – 28
4
1400 div 5 * 13 – 28
5
280 * 13 – 28
6

16. Algoritmos y diagramas de flujo
Expresiones lógicas
• Las expresiones lógicas o booleanas, están constituidas por números,
constantes o variables y operadores lógicos o relacionales. El valor
que pueden tomar estas expresiones es de verdadero o falso.
Se utilizan con frecuencia en las estructuras selectivas y en las
estructuras repetitivas.
Operadores relacionales
• Son operadores que permiten comparar dos operandos, los operandos
pueden ser números, caracteres, constantes o variables.
Las constantes o variables, a su vez, pueden ser de tipo entero, real
(flotante), carácter o cadena de caracteres.

17. Algoritmos y diagramas de flujo
El resultado de una expresión con operadores relacionales es
verdadero o falso.
Operadores Relacionales
Operador Operación Ejemplo Resultado
== Igual que “lalo” == “lola” Falso
< > Diferente a ‘x’ < > ‘y’ Verdadero
< Menor que 14 < 25 Verdadero
> Mayor que 35 > 10 Verdadero
< = Menor o igual que 5 <= 6 Verdadero
>= Mayor o igual que 15 >= 7 Verdadero

18. Algoritmos y diagramas de flujo
Operadores lógicos
• Son operadores que permiten formular condiciones complejas a partir de
condiciones simples.
• Los operadores lógicos son de:
Conjunción (y).- relaciona dos operandos booleanos. Proporciona un
valo verdadero (V), si los dos son verdaderos; en caso
contrario da un resultado falso (F).
Disyunción (o).- relaciona dos operandos booleanos. Proporciona un
valor verdadero (V), si uno de los dos es verdadero; en
caso contrario da un resultado falso (F).
Negación (No).- este operador relaciona sólo un operando booleano y
da como resultado un valor opuesto al que tenga
el operando.

19. Algoritmos y diagramas de flujo
Operadores Lógicos
Operador Jerarquía Expresión lógica
No (~) (Mayor) No P Jerarquía de todos los
Operadores
Y (^) P y Q Operadores Jerarquía
o P o Q ( ) (Mayor)
(Menor) **
Tabla de verdad de los Operadores *, /, div, mod
Lógicos
==, < >, <, >, < =,
P Q P ^ Q P o Q ~ P ~ Q > =
V V V V F F No ( ~ )
V F F V F V y ( ^ )
F V F V V F o
(Menor)
F F F F V V

20. Algoritmos y diagramas de flujo
Por ejemplo:
• Dados los siguientes casos, resolver cada caso aplicando las reglas
correspondientes:
1). A = 5, B = 16 2). X = 6, B = 7.8
(A ** 2) > (B * 2) (X * 5 + B ** 3 / 4) < = (X ** 3 div B)
1 1
25 > (B * 2) (X * 5 + 474.552 / 4) < = (X ** 3 div B)
2 2
25 > 32 (30 + 474.552 / 4) < = (X ** 3 div B)
3 3
(30 + 118.638) < = (X ** 3 div B)
Falso 4
Continua

21. Algoritmos y diagramas de flujo
Continuación 2)
148.638 < = (X ** 3 div B)
5
148.638 < = (216 div B)
6
148.638 < = 27
Falso
3). ~(15 > = 7 ** 2) o (43 – 8 * 2 div 4 < > 3 * 2 div 2)
1
~(15 > = 49) o (43 – 8 * 2 div 4 < > 3 * 2 div 2)
2 3 Continua

22. Algoritmos y diagramas de flujo
Continua 3).
~ Falso o (43 – 16 div 4 < > 3 * 2 div 2) Verdadero o Verdadero
4 10
~ Falso o (43 – 4 < > 3 * 2 div 2) Verdadero
5
~ Falso o (43 – 4 < > 6 div 2)
6
~ Falso o (43 – 4 < > 3)
7
~ Falso o (39 < > 3)
8
~ Falso o Verdadero
9

23. Algoritmos y diagramas de flujo
Concepto de algoritmo
• Los seres humanos realizamos una serie de pasos, procedimientos o
acciones que nos permiten alcanzar un resultado o resolver un
problema, esto se repite innumerables veces durante el día. En
realidad estamos aplicando un algoritmo para resolver un problema.
Definición de Algoritmo.- secuencia ordenada y cronológica de pasos
que llevan a la solución de un problema o a la ejecución de una tarea (o
actividad).

24. Algoritmos y diagramas de flujo
• El algoritmo debe tener las siguientes características:
 Tener un principio
 Ser simples, claros, precisos, exactos.
 Tener un orden lógico.
 Debe ser finito.
 Tener un fin.
• La definición de un algoritmo debe describir tres partes:
 Entrada.
 Proceso.
 Salida

25. Algoritmos y diagramas de flujo
• La serie de pasos, procedimientos o acciones que nos permiten
alcanzar un resultado o resolver un problema a través de algoritmos,
los desarrollamos por medio de pseudocódigo.
• El pseudocódigo describe un algoritmo utilizando una mezcla de
frases en lenguaje común, instrucciones de programación y palabras
clave que definen las estructuras básicas.
• El objetivo del pseudocódigo es permitir que el programador se
centre en los aspectos lógicos de la solución, evitando las reglas de
sintaxis de los lenguajes de programación.
• No siendo el pseudocódigo un lenguaje formal, los pseudocódigos
varían de un programador a otro, es decir, no hay un pseudocódigo
estándar.

26. Algoritmos y diagramas de flujo
Diagramas de flujo
• Un diagrama de flujo representa la esquematización gráfica de un
algoritmo.
• En realidad muestra gráficamente los pasos o procesos a seguir para
alcanzar la solución de un problema.
• Su correcta construcción es sumamente importante porque, a partir
del mismo se escribe un programa en algún lenguaje de programación.
• Si el diagrama de flujo está completo y correcto, el paso del mismo a
un lenguaje de programación es relativamente simple y directo.
• A continuación, presentamos los símbolos que utilizaremos y una
explicación de los mismos. Estos satisfacen las recomendaciones de la
ISO y la ANSI.

27. Algoritmos y diagramas de flujo
Símbolo utilizado para marcar el inicio y el fin del diagrama flujo.
Símbolo utilizado para introducir los datos de entrada. Expresa
lectura.
Símbolo utilizado para representar un proceso. En su interior se
expresan asignaciones, operaciones aritméticas, cambios de valor
de celdas en memoria, etc.
Símbolo utilizado para representar una decisión. En su interior se
almacena una condición y dependiendo del resultado de la evaluación
de la misma se sigue por una de las ramas o caminos alternativos:
verdadero o falso.

28. Algoritmos y diagramas de flujo
Símbolo utilizado para representar la impresión de un resultado.
Expresa escritura.
Símbolo utilizado para expresar conexión dentro de una misma
página.
Símbolos utilizados para expresar la dirección del flujo del
diagrama
Símbolo utilizado para expresar conexión entre páginas diferentes.

29. Algoritmos y diagramas de flujo
Símbolo utilizado para representar una decisión múltiple. En su interior
se almacena un selector y dependiendo del valor de dicho selector se
sigue por una de las ramas o caminos alternativos.

30. Algoritmos y diagramas de flujo
Estructura y diseño de un algoritmo
• Existe una gran cantidad de problemas que requieren de un análisis
profundo y de un pensamiento flexible y estructurado para la
solución.
• La idea es ofrecer un conjunto de técnicas y herramientas
metodológicas que permitan flexibilizar y estructurar el
razonamiento utilizado en la solución de problemas, esto provocará
finalmente la construcción de algoritmos eficientes.
• A continuación en la figura podemos observar las etapas que debemos
seguir para la solución de un problema

31. Algoritmos y diagramas de flujo
Problema
Análisis Construcción Verificación
profundo del del el
problema algoritmo algoritmo
Nota.- Por verificación del algoritmo entendemos el seguimiento del mismo con datos que
sean representativos del problema que queremos resolver

32. Algoritmos y diagramas de flujo
• La secuenciación es una estructura de control que permite a la
computadora ejecutar una acción, después otra, luego la que sigue y
así sucesivamente hasta la última.
• Dichas acciones pueden consistir en operaciones primitivas
elementales como declaraciones de variables, leer datos, imprimir
datos o calcular alguna expresión.
• Es conveniente etiquetar cada acción con números desde el uno en
forma ascendente de uno en uno, para denotar el orden secuencial.
• Por lo tanto los elementos básicos que integran la estructura de un
algoritmo son:

33. Algoritmos y diagramas de flujo
1. Encabezado.- todo algoritmo debe tener un encabezado como
identificación, el cual debe empezar con la palabra Algoritmo
seguida por una descripción del problema a resolver.
2. Inicio.- todo algoritmo debe empezar con la etiqueta 1, que marca
el inicio del mismo.
3. Declaraciones.- después de marcar el inicio se debe hacer las
declaraciones que se necesiten como: variables, constantes, tipos
de datos, etc.
4. Leer, calcular e imprimir.- los siguientes pasos pueden consistir en
acciones tales como: leer datos, calcular algunas expresiones
aritméticas e imprimir datos tantas veces como se requiera y en el
orden apropiado para resolver el problema en cuestión.

34. Algoritmos y diagramas de flujo
5. Fin del algoritmo.- el último paso del algoritmo consiste en incluir
la indicación fin.
Ejemplo No 1 de algoritmos secuenciales
Calcular e imprimir el sueldo de un empleado, se pedirá la clave del
empleado, las horas trabajadas y el pago por hora trabajada.
Algoritmo Calcular el sueldo de un empleado
1. Inicio 5. Imprimir cve, sueldo
2. Declaración de variables: 6. Fin
cve, ht: entero
pht, sueldo: real (flotante)
3. Leer cve, ht, pht
4. sueldo = ht * pht

35. Algoritmos y diagramas de flujo
Ejemplo No 2.- desarrollar un algoritmo que permita leer un número
en radianes e imprima su equivalencia en grados; así mismo, leer un
número en grados e imprima su equivalencia en radianes.
Algoritmo Convierte radianes a grados y grados a radianes
1. Inicio
2. Declaración de variables:
PI = 3.145926536: real (flotante)
rad, grad, numrad, numgrad: real (flotante)
3. Leer rad, grad
4. numgrad = rad * (180 / PI)
5. numrad = grad * (PI / 180)
6. Imprimir numgrad, numrad
7. Fin

36. Algoritmos y diagramas de flujo
Ejemplo No 3.- desarrollar un algoritmo para calcular el promedio de
un estudiante, se pedirá la matricula del estudiante y cuatro
calificaciones de los exámenes. Se imprimirá la matricula del
estudiante y el promedio.
Algoritmo calcular promedio de un estudiante
1. Inicio
2. Declaración de variables
matest: entero
cal1, cal2, cal3, cal4, calfin: real (flotante)
3. Leer matest, cal1, cal2, cal3, cal4
4. calfin = (cal1 + cal2 + cal3 + cal4) / 4
5. Imprimir matest, calfin
6. Fin

37. Algoritmos y diagramas de flujo
Reglas para la construcción de diagramas de flujo
• Debemos recordar que un diagrama de flujo debe ilustrar
gráficamente los pasos o procesos a seguir para alcanzar la solución
de un problema.
• Los símbolos colocados adecuadamente, permiten crear una
estructura gráfica flexible que ilustra los pasos a seguir para
alcanzar un resultado específico.
• El diagrama de flujo facilitará más tarde la escritura del programa
en algún lenguaje de programación.
Reglas
1. Todo diagrama de flujo debe tener un inicio y un fin.

38. Algoritmos y diagramas de flujo
2. Las líneas utilizadas para indicar la dirección del flujo del diagrama
deben ser rectas, verticales y horizontales.
3. Todas las líneas utilizadas para indicar la dirección del flujo del
diagrama deben estar conectadas. La conexión puede ser a un
símbolo que exprese lectura, proceso, decisión, impresión, conexión
o fin de diagrama.
4. El diagrama de flujo debe ser construido de arriba hacia abajo
(top-down) y de izquierda a derecha (right to left).
5. La notación utilizada en el diagrama de flujo debe ser
independiente del lenguaje de programación.
6. Es conveniente cuando realizamos una tarea compleja poner
comentarios que expresen o ayuden a entender lo que hicimos.

39. Algoritmos y diagramas de flujo
7. Si el diagrama de flujo requiere más de una hoja para su
construcción, debemos utilizar los conectores adecuados y
enumerar las páginas convenientemente.
8. No puede llegar más de una línea a un símbolo.

40. Algoritmos y diagramas de flujo
Diagrama de flujo del algoritmo, ejemplo 1:
inicio
cve, ht
pht
sueldo = ht * pht
cve fin
sueldo

41. Algoritmos y diagramas de flujo
Diagrama de flujo del algoritmo, ejemplo 2:
inicio
rad
grad
numgrad = rad * (180 / PI)
numgrad
numrad = grad * (PI / 180) fin
numrad

42. Algoritmos y diagramas de flujo
Diagrama de flujo del algoritmo, ejemplo 3:
inicio
matest, cal1
cal2, cal3
cal4
calfin = (cal1 + cal2 + cal3 + cal4) / 4
matest fin
calfin

43. 3. Algoritmos y Diagramas de Flujo
Actividades:
• El alumno evaluara diferentes expresiones aritméticas
simples y compuestas, haciendo énfasis en el uso del
estatuto de asignación
• Ejercicios para el diseño y desarrollo de algoritmos y
diagramas de flujo secuenciales