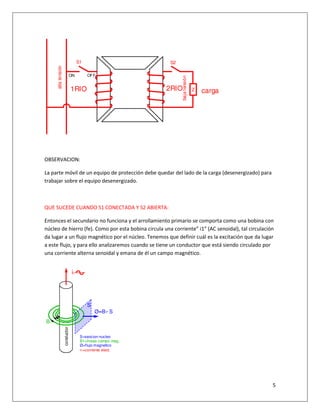
1. El documento describe las leyes fundamentales del transformador, analizando el circuito eléctrico y magnético. 2. Explica que cuando solo el primario está conectado, la corriente magnetizante (ix) crea un flujo magnético (Ø) en el núcleo. La permeabilidad determina el valor de ix. 3. Determina la expresión para ix usando la ley de Ohm magnética, mostrando que ix depende solo de la permeabilidad y está en fase con el flujo Ø.

1. 1
fb
ib ib
fb
ib
fb
ib ib
fb
ib
w
fb
fb
1
2
3
4
5
6
7
wvu
vu
URIVERSIDAD AUTONOMA GABRIEL RENE MORENO
CARRERA INGENIERIA ELECTROMECANICA
TEXTO DE MAQUINAS DE CORRIENTE ALTENA 1 - ELT 260
DOCENTE: ING. LUCIO RONALD LINO CUELLAR

2. 2
INDICE GENERAL
EL TRANSFORMADOR 1
GENERALIDADES 1
LEYES FUNDAMENTALES DEL TRANSFORMADOR 2
TRANSFORMADOR IDEAL 3
ANALISIS DEL PRIMARIO 3
QUE SUCEDE CUANDO S1 CONECTADA Y S2 ABIERTA 3
MAGNETIZACION: 5
DETERMINACION DE LA CORRIENTE MAGNETIZANTE (IX) 5
RESUMEN DEL PRIMARIO 9
VALORES EFICACES: 10
ANALISIS DEL SECUNDARIO 11
QUÉ PASA SI CERRAMOS “S2” 13
RESUMEN DEL SECUNDARIO 14
TRANSFORMADOR REAL 16
TENSION INDUCIDA EN EL SECUNDARIO EN VACIO (E20) 17
ANALISIS TEORICO DE IX (CORRIENTE MAGNETIZANTE) 19
POTENCIAS QUE ENTRAN EN JUEGO TRANSFORMADOR 20
POTENCIA MAGNETIZANTE Y PERDIDA DE VACIO 21
ANALISIS TEORICO (IX = CORRIENTE MAGNETIZANTE) 22

3. 3
FLUJO DE DISPERSION (ØS) 31
VALORES REFERIDOS Y DIAGRAMA FASORIAL 32
DIAGRAMA FASORIAL 33
ENSAYO DE TRANSFORMADOR EN VACIO 34
ENSAYO DE CORTO CIRCUITO 36
DIAGRAMA DE TRANSFORMADOR CON CARGA RESISTIVA 37
DIAGRAMA DE TRANSFORMADOR CON CARGA R-L 38
DIAGRAMA DE TRANSFORMADOR CON CARGA R-C 38
REGULACION O CONMUTACION (TAP) 39
TRANSFORMADORES TRIFASICOS 41
TRANSFORMADOR TRIFASICO TEMPLO 43
CONEXIÓN DE BOBINADO 44
FORMA DE CONECTAR DOS BOBINAS 44
CONEXIONES TRIFASICAS 46
CONEXIÓN DELTA O TRIANGULO (D) 47
CONEXIÓN ESTRELLA (Y) 48
CONEXIÓN ZIG - ZAG (Y) 48

4. 4
EL TRANSFORMADOR
El transformador tiene 2 tipos de circuitos, uno eléctrico, otro magnético; el magnético está
constituido por láminas de hierro de la siguiente manera:
LEYES FUNDAMENTALES DEL TRANSFORMADOR
Para analizar estas, vamos a analizar el transformador más simple, el transformador didáctico, lo
consideraremos con su núcleo rectangular, con un yugo inferior y un yugo superior; con dos
columnas.
El transformador tiene 2 tipos de circuitos:
-Un eléctrico (bobinas)
-Un magnético (núcleo Fe)
Sobre las columnas se colocan los arrollamientos:
-Primario (alta tensión)
-Secundario (baja tensión)
Mediante una llave S1 conectamos los arrollamientos del primario a la red
Mediante una llave S2 conectamos los arrollamientos del secundario a la carga.
yugo superior
yugo superior (fe)
columnaizquierda
columnaderecha
ventana

5. 5
OBSERVACION:
La parte móvil de un equipo de protección debe quedar del lado de la carga (desenergizado) para
trabajar sobre el equipo desenergizado.
QUE SUCEDE CUANDO S1 CONECTADA Y S2 ABIERTA:
Entonces el secundario no funciona y el arrollamiento primario se comporta como una bobina con
núcleo de hierro (fe). Como por esta bobina circula una corriente” i1” (AC senoidal), tal circulación
da lugar a un flujo magnético por el núcleo. Tenemos que definir cuál es la excitación que da lugar
a este flujo, y para ello analizaremos cuando se tiene un conductor que está siendo circulado por
una corriente alterna senoidal y emana de él un campo magnético.
S1 S2
Z carga
ON OFF
altatensión
bajatensión
1RIO 2RIO
i1
Ø=B1* S
S
B1
S=seccion nucleo
B1=lineas campo mag.
Ø=flujo magnetico
i1=corriente elect.
conductor

6. 6
La inducción se puede dar de dos maneras:
-Flujo en movimiento y espira en reposo
-Flujo en reposo y espira en movimiento
Principales actores: Faraday, Lenz, Gauss, Maxwell, Ampere.
La circulación de corriente (i1)(magnetizante), da origen al campo magnético (B1), este se suma en
la parte del núcleo y la ventana, se anula en la parte de vecindad.
Los flujos en cada espira se anulan a un lado de la misma (vecindad), y se suman en el lado interior
dando resultado a un flujo principal (Øp), cuyas líneas están trazadas dentro del núcleo, sobre el
circuito magnético.También se suman en el lado de la ventana, a este flujo lo llamamos flujo de
dispersión(Øs).
Como lacorriente que circula es la misma en todas las espiras, el flujo es generado por una
excitación igual “n” veces la corriente circulan
fmm(Ɵ) = i1xN1
S1 S2
Z
carga
ON OFF
altatensión
B1
B1
Ø
Vind=V2
bornes
bornes
i1

7. 7
En nuestro caso la superficie (S=sección transversal del núcleo) es constante, por lo que se
obtienen la siguiente ecuación:
Ø = B * S S=constante, (Unidades: Ø (Wb), B (T), S (m2
))
Si hago el análisis para una espira n = 1 entonces:
e1 =
Ø
,e1=tensión espira, (unidades: e1(V), Ø(Wb), t(seg))
-tensión inducida (en) es la derivada del (Ø) con respecto al (t).
Excitación: es la corriente que circula por “n” espiras, es la que impulsa al flujo (Ø) a circular por el
núcleo.
Ɵ = N1 * i1 N1=numero vueltas 1rio, i1=corriente del primario
Ɵ=fuerza magneto motriz (fmm)
MAGNETIZACION:
Significa que al circular un flujo magnético (Ø) a través del núcleo, el flujo producido por esta
excitación, tendrá una magnitud determinada, según cual sea el camino que recorra. Para tener
una idea vamos a valorar la permeancia del circuito magnético (Λ, viene de permitir). La
S1 S2
Z
carga
altatensión
B1
B1
i1
B1
B1
B1
B1
B1
B1
Øp
Øs
Øp=flujo principal
Øs=flujo secundario
responsable de
creacion reacctan-
cias X1 y X2

8. 8
permeancia es la inversa de la reluctancia magnética, o sea da idea de la capacidad de conducción
del flujo por ese medio, por lo que llegamos a la siguiente ecuación:
Fmm= Ɵ = Ɽ* Ø = * Ø LEY DE OHM MAGNETICA (V = i x R, Ohm)
Ɽ = Ɽ=reluctancia mag. (Unidad: Hy, (Wb/A, V*seg/A)
Λ=permeancia, mide cuanto flujo puede circular por circ.mag.
La fmm que impulsa al flujo a circular por el circuito magnético y este circuito está representado
por la permeancia.
i1*N1 = *Ø Condición: >>
I1~ = I1R + jI1x, (I1x=corr. Magnetiza núcleo, I1R=calentamiento bobina)
DETERMINACION DE LA CORRIENTE MAGNETIZANTE – (ix):
Supongamos el transformador monofásico con llave S1 cerrado al cual le estamos aplicando una
tensión senoidal, esta hace que circule una corriente senoidal “i1”, que a su vez produce un flujo
senoidal. Si el flujo es senoidal, significa que su valor varía en el tiempo, si recordamos la 2da Ley
de Maxwell tenemos lo siguiente:
S1
altatensión
i1
Øp=B *S
U1
Øs

9. 9
Si la ecuación general de la 2da Ley de Maxwell, se expresa mediante derivadas parciales, significa
que el campo magnético depende de más de una sola variable, que son la superficie y el flujo. En
nuestro caso la superficie por la que obtengo la siguiente ecuación inducida en una espira:
en =
Ø
Considerando que cada espira concatena el mismo Ø, podemos decir que la tensión inducida en la
bobina es la siguiente:
E = N * en , (en , vale lo mismo en 1rio y 2rio)
E1 = N1 *
Ø
, E1 = Tensión inducida en el primario
Despreciando la caída o pérdida por dispersión (Øs), la tensión aplicada tiene que ser igual a la
tensión inducida:
V1 = E1 = N1 * en
La tensión aplicada determina el valor del flujo primario, según cuanto valga la tensión resultara el
valor del flujo.
Hemos dicho que el flujo es senoidal y podemos admitir como flujo la siguiente ecuación senoidal:
Ø = ØV*sen(wt) → Ix
E1 = N1 *
Ø
= N1* ØV*w*cos(wt) , (Ê1 = N1* ØV*w)
E1 = Ê1*cos(wt)
S1
altatensión
B1
B1
i1
B1
B1
B1
B1
B1
B1
Øp
U1 E1=N1*en

10. 10
Como podemos ver la corriente magnetizante y el flujo, están en fase y la tensión esta adelantada
90° (∏/2), (por qué Ø α Ix), además ix, depende únicamente de la permeancia. Podemos escribir lo
siguiente:
V1 = E1 = Û1*cos (wt)
Podemos ahora a partir de la LEY DE OHM MAGNETICA, determinar el valor de la corriente
magnetizante Ix, que es la parte reactiva de la I1 y es la corriente que magnetiza al núcleo: significa
que es la corriente que crea el flujo.
Ê1 = N1* ØV*w
→ØV =
̂
∗ω
“A partir de la ley de OHM MAGNETICA”, determinamos el valor de la corriente magnetizante (Ix):
ix*N1 = * Ø , (Fmm= Ɵ = Ɽ* Ø = * Ø)
ix =
ØV
∗
*sen(wt) =
∗ ∗
*sen(wt) , (L =Λ*N12
)
ix =
∗
*sen(wt) , (XL = L*w)
ix = *sen(wt)
2
w t
E1 Ix
XL
ix
V1=Ix*XL
LVIS=tension adelanta corriente
L
E1
E1
E1

11. 11
Ø = ØV*sen (wt)
ix = *sen (wt) , U1 = Û1*cos (wt)
Como podemos observar, la corriente magnetizante esta en fase con el flujo, y depende
únicamente de la permeancia, ya que las otras magnitudes son impuestas:
ix =Ψ(
1
) ,corriente para magnetizar el núcleo o hacer circular el flujo (Ø) por circuito
ix =
∗ ∗ ∗
*sen(wt) ,(L =Λ*N12
), (XL = wL)
CONCLUSION:
1) La inductancia propia de una bobina, viene dada por el producto al cuadrado del número de
espiras por la permeancia del circuito magnético:
L = fe*N12
2) El flujo es impuesto por la tensión aplicada, dice que si la tensión aplicada es sinusoidal, el flujo
resultante es sinusoidal; si la tensión es rectangular el flujo es triangular por que se rige por la
ecuación:
e =
Ø
U1
Ø
ix
U1
U1

12. 12
3) Para que exista el flujo, es necesario que existan las corrientes magnetizantes, “en” es la tensión
inducida por la espira o tensión espira, consideremos que cada espira concatena el mismo flujo,
tenemos entonces la tensión inducida en toda la bobina y es la siguiente:
E1 = en * N1, entonces E1 = N1*
Ø
(tensión inducida en toda la bobina, n veces la de espira)
Despreciando la caída (las perdidas por dispersión), la tensión aplicada es igual a la tensión
inducida
Perdidas del circuito: Resistencia de contacto, resistencia de conductores.
E1 = N1*
Ø
despresiando perdidas: U1 = E1 = N1*
Ø
, (U1=tensión aplicada)
La tensión aplicada determina el valor primario del flujo, según cuanto valga la tensión será el
valor del flujo.
Hemos dicho que el flujo es senoidal y podemos admitir como flujo la siguiente ecuación:
Ø = ØV*sen(wt), E1 = N1*
Ø
Entonces: E1 = N1*ØV*w*cos(wt) , (N1*ØV*w= Ê1)
E1 = Ê1*cos(wt)
La tensión adelanta 90º al flujo, como hemos considerado que la tensión aplicada es igual a la
tensión inducida, podemos escribir lo siguiente:
U1 = E1
U1 = Û1*cos(wt)
De ahí podemos advertir que la tensión adelanta 90º a la corriente, porque (Øαi).
S1
altatensión
B1
B1
i1
B1
B1
B1
B1
B1
B1
Øp
U1 E1=N1*en

13. 13
Podemos ahora a partir de la “ley de Ohm magnética”determinar el valor de la corriente
magnetizante (ix, que es la parte reactiva de la i1) y es la corriente que magnetiza al núcleo,
significa que es la corriente que crea al flujo:
Ê1 = N1* ØV*despejando: ØV =
̂
∗
VALORES EFICACES:
Podemos trabajar con: 1)Valores máximos, 2)Valores eficaces; (magnitudes sinusoidales seno-cos)
Trabajando con VALORES MAXIMOS obtenemos la siguiente ecuacion:
Û = NØV*(como: Û = √2*Uef, también:2∏f, y como: ØV = B*S)
√2*Uef= NØV*2∏f
Uef = 4,44 N ØV*f = 4,44 N*f* B*S
Û1 = √2 ∗U1 ef = √2 ∗E1 ef (Û1=Ê1, despreciando perdidas)
2
w t
E1
w t
U1
U1ef
2 2
23

14. 14
Como: Û1 = N1* ØV*
Entonces: √2 ∗E1 ef = N1* ØV*2∏f
√2 ∗E1 ef = N1*ØV*2∏f , ( Ø = B * S , ØV =BV * S)
E1 ef =
∏
√
*f*N1*BV*S , ( cte =
∏
√
= 4,4 )
E1 ef = 4,4*f1*N1* BV *S
E2ef = 4,4* f1*N2* BV *S , ( f = la frecuencia no cambia)
Estas ultimas expresiones nos dan el valor de la tensión efectiva, es importante analizar las
unidades en que se miden:
B ( ) , S (m2
) , Si quiero asumir S (cm2
) asumo: Ø = B * S *10-8
ANALISIS DEL SECUNDARIO:
Sabemos que la ley de inducción: e =
Ø
, es genérica y por lo tanto válida para cualquier
arrollamiento, esto significa que con el arrollamiento secundario hay también una tensión-espira
inducida.
Tensión-espira: e1n =
Ø
,
Condición: e1n = e2n =
Ø
, (E1 = e1n*N1 , E2 = e2n*N2).
La tensión “e2n” inducida que significa lo siguiente:
Tensión inducida en el secundario: E2 = e2n*N2 =
Ø
N2
Si indicamos con los valores eficaces de la tensión-espira, podemos llegar a una relación,
consideremos antes algo importante: E1 y E2 son tensiones que están en fase, pues son inducidas
por el mismo flujo:
Condiciones:
e1n = e2n = en =
Ø
, (E1 =e1n * N1 y E2 = e2n * N2)
Entonces: =
∗
∗
, como resultado : = = constante

15. 15
Esta relación de tensiones nos da un valor, un coeficiente que debe ser el mismo valor de la
relación del numero de espiras y lo probamos con un ensayo de T.T.R. (transformerturns
ratio)(relacio de vueltas del transformador).
1er Calculo: =
∗
∗
, como resultado : = = constante
2do Calculo: P1 = P2 , U1* i1 = U2 * i2 : reemplazando =
!
!
=cte, =
!
!
= cte
RELACION DE TRANSFORMACION:
= = =
!
!
= kt = cte ,kt (constante de transformación)
Qué pasa si serramos “S2”:
Cuando esto sucede comienza a circular por el secundario, una corriente “i2” y se cumple que:
U2 = E2 = i2 * Z (despreciando las perdidas)
w
V1
V2
Ix
2 2
3 2

16. 16
Al circular “i2” (corriente inducida) por el secundario aparece una fuerza magneto motriz (fmm)
capaz de producir un flujo, el cual haría que en el arrollamiento secundario se produzca una
tensión inducida que crearía un flujo de reacción, el cual se opondría a quien lo creo (Øp), pero
como la tensión primaria esta dada por la red, esto no puede cambiar y por lo tanto el flujo no
puede cambiar. Físicamente los sentidos de la corriente del 1rio y 2rio se oponen, por lo tanto es
necesario que el 1rio tome de la red los amperios-vuelta suficiente para contrarrestar los efectos
del 2rio (reacción del 2rio).
E2 → i2 → Øreacción
Øp - Øreac = 10000 (gauss) - 1000 (gauss) = 9000 (gauss), Esto no puede suceder
Øp - Øreac = 11000 (gauss) - 1000 (gauss) = 10000 (gauss), Queda así
S1
Z
carga
ON OFF
altatensión
B1
B1
Ø
i1 S2
ON OFF
i2

17. 17
Esto significa que los amper-vuelta del 1rio y 2rio, se componen para mantener su flujo constante,
lo que matemáticamente significa lo siguiente:
.fmm = i1*N1 = amper-vuelta = Ø
.ix*N1 tienen que mantenerse constante, para que el flujo no varie (ix=corriente magnetizante).
Le pide a la red los amper-vuelta suficiente para contrarrestar el efecto del 2rio:
.i1*N1 + i2*N2 = ix*N1
S1
Z
carga
altatensión
Øp
i1 S2
i2
REACCION DEL SECUNDARIO
E1 E2V1
Øreaccion
V2
ix*N1 =
N1
*i1
N2*i2
N1 * i1
N2 * i2
1
fe
Ø
fmm

18. 18
La posición fasorial de la corriente depende de la impedancia de carga, como la corriente i1 no
puede variar su módulo y ante la imposibilidad que i1 varie, se debe ubicar sobre el arco de
circunferencia de tal forma que se mantenga ix pequeño respecto a los valores i1, incluso para los
transformadores grandes, tienen un valor del 1% del valor de la corriente i1 nominal, esto permite
se desprecie el valor de ix para poder escribir la siguiente ecuación:
Resumen del secundario:
1)El transformador en vacio absorbe de la red una corriente magnetizante ix, la cual produce una
fuerza magnetomotriz (fmm), que produce un flujo senosoidal, que a su vez produce una fuerza
E1 = en*N1
2)La tensión producida en el primario (E1), equilibra una tensión aplicada (U1), la equilibra
totalmente en el caso del transformador ideal, pero en general ponemos E1 = U1 porque la
corriente magnetizante produce perdidas en el 2rio, cuando entramos en vacio la tensión inducida
es igual a la tensión en bornes.
3)Cuando el secundario se conecta a una carga “Z”, comienza a circular una corriente i2, que se
calcula de la siguiente manera:
i2 = "
4)Los amper-vuelta producida por la corriente 2ria o sea i2 y N2 se compensan con los amper-
vuentasdel 1rio, para que se mantenga constante el valor del flujo.
Z
carga
Øp
S2
i2
E2
Øreaccion
V2
tension induc.
en el vacio
tension
en bornes

19. 19
Ø, ix, N1*ix, están en fase
E1, E2, están en fase, pero 90o
delante de N y ix (en bobina U adelanta 90o
a i)
.i1*N1 y i2*N2 se componen de manera de tener al Ø = constante.
ix*N1 =
N1
*i1
N2*i2 N1 * i1
N2 * i2
1
fe
Ø
fmm
E2
E1

20. 20
TRANSFORMADOR REAL
El hecho de calificarse como real al transformador, significa que vamos a considerar la
IMPEDANCIA propia de los arrollamientos, consideramos la resistencia óhmica de los
arrollamientos R1 y R2 del PRIMARIO Y SECUNDARIO respectivamente; como asitambie sus
REACTANCIAS X1 Y X2.
PRIMARIO SECUNDARIO CARGA
V1 = tensión
E1 = tensión inducida
R1 = Resistencia
X1 = reactancia inductiva
N1 = número de vueltas 1rio
V2 = tensión
E2 = tensión inducida
R2 = Resistencia
X2 = reactancia inductiva
N2 = numero de vueltas 2rio
Z2= impedancia
En estas condiciones y tomando en cuenta la ley de KIRCHOFF, podemos escribir las siguientes
ecuaciones:
V1 = E1 + ER1 + EX1
V1 = E1 + ER2 + EX2
E1 y E2 estan en fase, ya que es el mismo flujo el que las produce.
Z2
altatensión
Øp
i1
i2
E1 E2V1 V2
R1
X1
R2
X2

21. 21
Analizamos lo que sucede en el triangulo de corrientes, debemos considerar que si (Ix) representa
la magnetización del nucleo, debe existir la representación del calentamiento del nucleo, a la cual
la denominamos CORRIENTE VATADA: (Iv (W=Watts)).
Donde (Iv)(W), representa el calentamiento del nucleo cuando circula el flujo magnético. Se mide
en POTENCIA ACTIVA y el calentamiento del nucleo se debe representar en un circuito como una
RESISTENCIA, y la circulación del flujo se debe representar como una INDUCTACIA.
I1 →Ix : corriente de magnetización del nucleo, significa que hace circular el Ø por el circuito
magnético (nucleo Fe).
CIRCUITO ABIERTO O DE VACIO CORTO CIRCUITO
Se representa con C.O.
R =
I = 0
Se representa con C.C.
R = 0
IK =
En el secundario en vacio, la tension es igual a la tension en bornes:
R1 X1 R2 X2
Ro
Xo
Iv Ix
V2V1
V2
CIRCUITO ELECTRICO EQUIVALENTE

22. 22
U2 (400/231), (380/220)
U20 (400/231)
TENSION INDUCIDA EN EL SECUNDARIO EN VACIO (E20):
3)Cuando el SECUNDARIO se conecta a una carga Z2 comienza a circular I2 por el secundario y se
calcula de la siguiente manera:
I2 =
#
"
4)Los amper-vueltas producidas por las corrientes del SECUNDARIO I2 = f.m.m., se compensan por
los amper-vueltas producidos por el PRIMARIO, para que se mantenga el valor del flujo.
DONDE:
Ix = Corriente magnetizante
Iv = Corriente watada
Io = Corriente en vacio
Z2
S2 (abierto)
V2 E20
Ø
Ix
Iv
I2N2
I1N1
E1
E2
Io

23. 23
E1 = tension inducida PRIMARIO
E2 = tension inducida SECUNDARIO
.fmm = I1N1
.fmm = I2N2
Ø = flujo magnético
El circuito magnético esta constituido por dos materiales: (hierro y aire)
Las chapas de hierro pueden ser de grano orientado a laser o soplo magnético
Rm =
1
, (Rm = reluctancia magnetica)
Rm =
1
$!%
ANALISIS TEORICO DE - Ix (Corriente magnetizante).
La inducción magnética B, se genera por la acción de densidad o fuerza del campo magnético Ĥ, se
mide en amper-metro (A/m) y B en (Wb/m2
).
Ĥ = intensidad de campo magnético
B = inducción magnética
aire
yugo superior (fe)
ventana
aire
(fe)
+ - + - + - + - + -
+ -+ -
+-

24. 24
Veamos cual es la relación entre B y H, comenzamos estudiando en el vacio donde se cumple:
Bo = µo* H
Donde: µo = 4∏x10-6
(Wb/m2
).
Por otra parte sabemos que cuando existe una inducción B atraves de una superficie determinada:
E = 4,44 N*f*B*S
Ø = B*S
B =
Ø
&
, densidad de induccionmagnetica
Ademas sabemos que:
' ( ∗ )* = Ɵf.m.m. ; Ley Ohm mag.:Ɵ = N* I =
1
Ø (A) ; Ley Ohm mag.: V = R* I ; I =
V
,
' ( ∗ )* = N* Ix
H**= N* Ix
Ademas sabemos que existe una analogia entre la ley de Ohm MAGNETICA y la ley de Ohm
ELECTRICA:
Potencial eléctrico:
V = e** (v) , Û =
e
ᵨ
=
campo electrico
% 9!9 !:! $
Donde:
V = potencial eléctrico
.e = campo eléctrico
* = longitud
POTENCIAS QUE ENTRAN EN JUEGO EN UN TRANSFORMADOR
Las maquinas absorben una potencia
activa de la red: P1 = V1*I1*cos(ⱷ)
reactiva: Q1 = V1* I1*sen(ⱷ1)

25. 25
POTENCIA CONSUMIDA ACTIVA
POTENCIA DE LA RED
activa: P1 = V1* I1*cos(ⱷ1)
reactiva: Q1 = V1* I1*sen(ⱷ1)
POTENCIAS ACTIVAS POTENCIAS REACTIVAS
I12
*R1
I22
*R2
Iv*U1 = Iv2
*Ro
I2*U2*cos(ⱷ2)
I12
*X1
I22
*X2
Ix*U1 = Ix2
*Xo
I2*U2*sen(ⱷ2)
Z
altatensión
Øp
i1
i2
E1 E2V1 V2
R1
X1
R2
X2
R1 X1 R2 X2
Ro
Xo
Iv Ix
V1
CIRCUITO ELECTRICO EQUIVALENTE
i1 i2
Z
Iv
I2N2
I1N1
Iv*U1
I1*R1
S=V1*I1(kVA)
ACTIVAS
REACTIVAS
2
I2*R2
2
I2*U2*cos( 2)
I1*X1
2
I2*X2
2
Ix*U1I2*U2*sen( 2)
P1=I1*U1*cos(1)

26. 26
POTENCIA MAGNETIZANTE Y PERDIDA DE VACIO
La potencia magnetizante, esta ligada a la corriente magetizante. Sabemos que si el transformador
fuera IDEAL no necesitaríamos una corriente magnetizante para que circule el flujo, por otra parte
sabemos que la permeabilidad magnética del hierro ( ), es mucho mas alta que la del aire
( ); y por lo tanto mucho mas facil que circule por el hierro (Fe) un flujo magnetico
(Ø), que por le aire.
Quiere decir, que si el nucleo magnético del transformador fuera de aire, la corriente
magnetizante fuera mucho mayor que la del hierro.
Como el caso es REAL, se plantea la existencia de la corriente magnetizante y teniendo en
cuenta lo dicho anteriormente, es que siempre hay que tratar que la corriente
magnetizante (Ix) sea lo mas pequeña posible para los TRANSFORMADORES REALES.
La corriente (Ix) lo mas pequeña posible, se consigue construyendo un nucleo que
aseguren la máxima permeabilidad para el flujo (Ø), estos nucleos están hechos de 0,35 –
0,50 mm de espesor. También se han perfeccionado las chapas, con diferentes
tecnologías.
Circuito magnético con 2 materiales (hierro, aire)
fe ˃˃ aire (Rm =
Λ;<
, Rm =
Λ=>?<
, Rm =reluctancia magnetica)
Ƞ = 97% (Si y C)
Ƞ = 99% Fe(grano orientado con laser)
Ƞ = 99,9% Fe(grano orientado con soplo magnetico)
aire
yugo superior (fe)
ventana
aire
(fe)
+ - + - + - + - + -
+ -+
-
+-

27. 27
ANALISIS TEORICO (Ix = Corriente magnetizante)
La inducción magnética (B), se genera por la accionde la intensidad de campo o fuerza de
campo magnético (H) que se mide en (amper/metro), y (B) se mide en (Wb/m2).
B҃ = densidad de inducción magnética (Wb/m2).
H҃ = intensidad de campo magnético (A/m).
Veamos cual es la relación entre B y H, comenzaremos estudiando en el vacio, donde se
cumple que:
Bo = µo*H , (µo = 4∏x10-6 (V*seg/A*m)
Por otra parte sabemos que cuando tenemos una inducción uniforme a través de una
superficie determinada, podemos obtener:
Ø = B*S
Además, sabemos que:
' ( ∗ )* = Ɵf.m.m. ; Ley Ohm mag.:Ɵ = N* Ix =
1
Ø (A) ; Ley Ohm elect.: V = R* I ; I =
V
,
Ɵ = N* Ix
H**= N* Ix
Además sabemos que existe una analogía entre la ley de Ohm MAGNETICA y la ley de Ohm
ELECTRICA:
S
dl*H

28. 28
Potencial eléctrico:
V = e** (v) , Û =
e
ᵨ
=
campo electrico
% 9!9 !:! $
Donde:
V = potencial eléctrico
.e = campo eléctrico
* = longitud
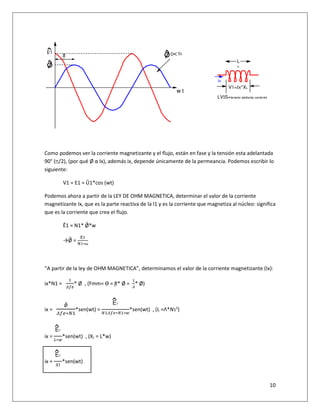
Haciendo una analogía que la fuente fem es igual a la intensidad del campo que impulsa al flujo a
un elemento del circuito:
Fmm = Ɵ = ʃ H*dl = N*Ix
Fem = N*Ix
El campo eléctrico por longitud, es igual a la corriente magnetizante en el bobinado que
me crea una fuerza electromotriz (fem)
Ɵ = N*Ix = Ø = H*l , (como: Ø = B*S y H = B/µo), (l = línea que recorre el campo)
B*S =
@
µA
*l ( = mide cuanto flujo puede circular por el circ. Mag., =R=reluctanciamag.)
=
&
* µo ,[ Unidad:
B
B
*
#∗9 C
D∗B
=
EF
D
= (Hg)], (µo=permeabilidad vacio(Hg/m))
Esta ultima expresión nos dice que la permeancia del aire, es proporcional a la sección, e
inversamente proporcional a la línea que recorre el campo.
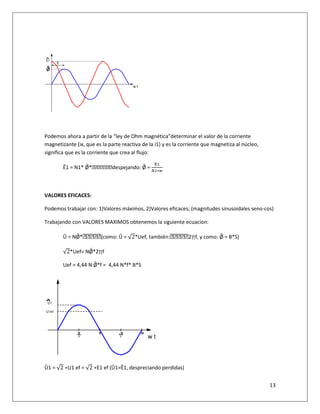
Ahora bien, la corriente de vacio (Io) tiene en realidad 4 componentes:
1),2)Corriente de excitación(disipación) del hierro, corriente magnetizante capaz de hacer
circular elel flujo por el núcleo de hierro(Ixfe) y el entre hierro (Ixair).
3),4)Por otra parte están las corrientes vatadas que producen las perdidas por
histéresis(IH) y focaul(IF).

29. 29
El subíndice (0), sale de que los valores del nucleo se hacen con ensayo de vacio(Pfe, Io, Ixo, Iv).
N1*Ix = N1*Ixfe + N1*Ixa
N1*Ix = Hfe*lfe + Ha*la
H = f(I)
Vamos a tratar de buscar el valor de Ix:
El valor de H, esta vinculado por B, mediante la expresión:
B = µo*H , (Ba = µo*Ha),(Bfe = µfe*Hfe), (µo = 4∏x10-7 (V*sg/A*m))
fe α µfe
El problema surge cuando se requiere encontrarIxfe, hay que recurrir a B = f(H), con la cual
trabajamos, como vemos no es constante.
Curva de Histéresis:
Ba = f(Ha), utiliza la curva del nucleo con una perdida:
R1 X1 R2 X2
Ro
Xo
Iv Ix
V1
i1 i2
Z
E1=E2
V2
Ø
Ix
Iv
I2
I1
E1
E2
Io
Ixfe Ixair
IH
IF
H(int.camp.mag.)
B(camp.mag.)
12000
15000
23000
clasicas(fe-si)
grano orientado
a laser
soplo magnetico

30. 30
0,5% material clásico normal
0,2% grano orientado a laser
0,0% orientado a soplo magnético
El campo B, tiene una forma senoidal, si la Ix es senoidal, no puede ser modificada, pues esta
impuesta por la tensión senoidalrígida de la red. Tiene ruido internamente, no es una senoidal
pura, tiene un fuerte contenido del tercer armónico.
Ix = √G1H + G3H + G5H , Se estudia con los armónicos que intervienen en la principal, el fabricante
garantiza el valor efectivo fundamental (valor que da el amperímetro).
Cuando representamos a Ix en un diagrama fasorial lo hacemos según el valor de la
FUNDAMENTAL, si la midiéramos con un amperímetro nos daría un valor EFECTIVO.
A los fines practicos, es necesario el VALOR EFECTIVO, de la FUNDAMENTAL, el fabricante lo
garantiza.
Recién aquí aparece el concepto de POTENCIA MAGNETIZANTE con una necesidad masespecifica,
se trata de la potencia necesaria para hacer circular el flujo senoidal con el valor máximo del
campo Bmax = f(kg fe). Con este dato de la pot. Magnetizante se tiene 2 formas de calculo:
CALCULO DE Ix (PRIMER METODO):
Como se ve, trabajamos con valores efectivos, hace falta hacer una aclaración, como el espesor del
entre hierro que es tan pequeño (0,1mm) que consideramos que el flujo que pasa por el nucleo
del hierro es igual al que pasa por el entre hierro.
wt
Ix
2 2
3 2
resultante
1er armonico
3er armonico
Ief

31. 31
Por otra parte Hfeesta en función de B máximo y lo obtengo de la grafica del ciclo de histéresis:
Ix*N1 = Ha*la + Hfe*lfe , (Ha =
@$
µ$
, Baef =
@B$L
√
)
Ix =
@$
∗µ$
*la +
M ∗
, (como: Ix = Ixa + Ixfe , Hfe = f(Bmax))
Ix = Ixa + Ixfe =
@$
∗µ$
*la +
M ∗
CALCULO DE Ix (SEGUNDO METODO):
En este caso lo hacemos conociendo la potencia magnetizante Px.
Px = Ix*U1 , (U1 = E1, despreciando perdidas)
Px = Ix*E1 , (Ix = Ixa + Ixfe)
Px = E1*Ixa + E1*Ixfe
Análisis 1:
E1*Ixfe = X*Gfe
aire
(fe)
(air)
H(Wb)
B(T)
Bmax
Hfe

32. 32
Datos del fabricante:
X = perdidas por el peso del hierro (W/kg)
Gfe = peso del hierro (kg)
Análisis 2:
Por la ley de inducción de Faraday:
E1 =
∏
√
*f1*N1* BV *S
De la igualdad de Ix:
Ixa =
@$
∗µ$
*la =
@B$L
√
∗
$
∗µ$
, (µa = µo)
Reemplanzando:
E1*Ixa =
∏
√
*f1*N1* BV *la)*(
@B$L
√
∗
$
∗µ$
)
E1*Ixa =
∏
µA
*f1* BV2
*la*S
Ix =
NO
=
∗ PO= Q ∗PO;<
=
∏∗; ∗ ∗ RS∗
TU
µV
Q ∗W
PERDIDAS POR HISTERESIS Y CORRIENTES PARASITAS:
Para hablar de estas pérdidas, debemos recordar la corriente vatada(Iv), si bien por la presencia
del hierro hablamos de corrientes magnetizaste (Ix), que magnetiza el núcleo de hierro y por cierto
que al realizar esta acción el núcleo de hierro consume una cierta potencia vatada(Pv), y se
constituye el precio que hay que pagar por (Ix).
Entonces de la I1 que se toma de la red, hay una parte reactiva Ix, que se desprende de I1 como si
se apartara (consideramos ramal paralelo), esta Ix que magnetiza el núcleo y debido a esta hay
una potencia que se consume en el hierro (Fe), esta potencia es activa y se manifiesta con el
calentamiento del nucleo, se mide en (Watt), de ahí su nombre de vatada.
La corriente vatada es la suma de perdidas por histéresis mas las perdidas por corrientes parasitas
o focault.

33. 33
Ix → (Ix y Iv), Ix→ Q(calentamiento)
Perdida por Histéresis:
Se hace el estudio con el diagrama simplificado (1er cuadrante, línea llena) de campo magnético
en función de la “H”, hacemos el estudio solo con el diagrama simplificado, por que en realidad se
trata de un diagrama cíclico, el cual el fabricante nos proporciona los valores.
Las perdidas por histéresis son proporcionales al área que encierra el ciclo de histéresis, de ahí que
a menor área existe menor perdida.
Por otra parte el ciclo de histéresis es proporcional a la potencia necesaria para conseguir la
inducción magnética B.
Z
altatensión
Øp
i1
i2
E1V1 V2
R1
X1
R2
X2
R1 X1 R2 X2
Ro
Xo
Iv Ix
V1
i1 i2
Z
Ø
Ix
Iv
I2
I1
E1
E2
Io
Ixfe Ixair
IH
IF
,Ix

34. 34
Las perdidas dependen de la calidad del material y además de la inducción y la frecuencia, se la
calcula matematicament mediante la formula empírica siguiente:
UH = Kh*f *Bn
(perdidas por histéresis)
Kh = factor de histéresis, que tiene en cuenta las dimensiones, la calidad y unidades usadas
n.= exponente empírico, que depende de la calidad del material, chapas clásicas n=0, grano
orintado laser n=2, modernas n=2,5.
Perdidas por corrientes parasitas:
Estas dependen de la geometría del material.
UP= Kp*
1
ᵨ
*a2
*f2
*B2
Vamos a realizar un análisis que nos llevara a concluir, que si pretendiéramos construir un
transformador de nucleomaciso o por el que circula un flujo senoidal no lo podríamos conseguir,
debido a la acción de las corrientes parasitas, estas corrientes parasitas no permitirán la
circulación del flujo.
Partamos del supuesto del flujo senoidal que esta circulando por el núcleo con una variación
temporal, del mismo se produce una tensión inducida en la sección transversal del nucleo y esta a
su vez produce una corriente inducida, que según la ley de Lenz, debe producir un flujo que se
H(int.camp.mag.)
B(camp.mag.)
ciclo de
histeresis

35. 35
oriente de tal suerte que se oponga a quien lo creo, este flujo de oposición es generado y mas
intenso en el centro que en la periferia del nucleo, a tal punto que anula la penetración del flujo
transversal.
Problema:
Supongo que el núcleo es maciso, entonces se genera Iinducida en la sección transversal del
nucleo, se llama corriente parasita (Focault).
Solución para evitar la IF:
Se lamina el núcleo, disminuyendo la sección, de tal manera que aumenta la resistencia a la
circulación de If a tal punto que se anule, por la relación de resistencia:
R = ᵨ&
, como S=baja, R=aumenta al paso de la Iparasita (Ip) , hasta hacerlo despreciable.
Con esta solución eliminamos el flujo paradito (Øp).
No solo existe el problema de la imposibilidad de la penetración del campo, sino que además se
produce calentamiento, debido a esto la Ix aumenta y se reduce la permeabilidad del hierro.
Cuando laminamos el nucleo, tenemos que aislar una parte de la otra, lo que conseguimos reducir
la tensión Vi parasita, esta disminución produce la anulación de If y por lo tanto anula Ø de
reacción.
Ø
Ø
Ei
Eind.
iind=ipars
Øparasito
NUCLEO MACISO
Ø
Ø
NUCLEO LAMINADO
solucion

36. 36
Conocidos los valores de la pérdida del Fe, puedo calcular la llamada PERDIDA TEÓRICA DE FE, de
acuerdo a la siguiente formula:
UFE= UH+ UP
U FE = Kh*f *Bn
+ Kp*
1
ᵨ
*a2
*f 2
*B2
= (Kh*f + Kp*
1
ᵨ
*a2
*f 2
)B2
Esto medice que conociendo la inducción, puedo conocer la perdida, ya que lo dentro del
paréntesis es una constante y se lo denomina factor de perdida a 10000 Gauss(U 10).
U FE = XXXX
*B2
*U 10
Conociendo los valores de la perdida de hierro puedo calcular la llamada perdida de tensión
teorica del hierro de acuerdo con la siguiente formula:
PFE = U FE * G (watt*kg/kg), (watt), se verifica con ensayo de vacío.
G = peso del hierro
El valor de las perdidas teóricas debe ser afectada por un factor que lo incrementa entre 5 a 20%.
En la zona de las ventanas el camino de U es menor, por lo tanto esta aumenta, en nuestro caso se
considera U constante, por otra parte la aislación no es perfecta y existe una fuerte conectividad
de chapas.
Los armónicos de Ix en oportunidades produce alteraciones de flujo, dice la energía necesaria para
contrarestar la perdida son suministradas por la red.
PFE = Iv*V1
FLUJO DE DISPERSION:
Analizando físicamente el transformador es un problema complejo, la complejidad se basa en la
existencia de otros flujos:
- magnético, galvánico, térmico y mecánico.
No todos los flujos son deseables, desde el punto de vista técnico, o sea apuntando a un
transformador optimo del mismo, es por ello que se hace necesario analizar los flujos en cuestión,
asegurando a los flujos útiles caminos de circulación fácil, y a los flujos inútiles impidiendo su
circulación.

37. 37
*Flujo Galvánico: es la circulación de la corriente eléctrica por la bobina(arrollamiento 1rio y2rio),
y es necesario que se lo analice óptimamente. El I1 es un flujo galvánico UTIL
*Flujo Magnético
principal(Øp): se lo canaliza en el circuito magnético, (UTIL)
dispersión (Øp): es un flujo difícil de controlar, pues se hace camino por cualquier medio del
transformador, por el aire, hierro, por el cubo, etc. Es el causante de la reactancia del circuito
eléctrico.(INUTIL).
Flujo parasito(creado por Ifocoult): debo tratar de eliminarlo (INUTIL)
*Flujo térmico: es un flujo inútil y hay que sacarlo (INUTIL)
*Flujo mecánico:
VALORES REFERIDOS Y DIAGRAMA FASORIAL
VALORES REFERIDOS
Cuando se trabaja con un transformador se prefiere una referencia, se toma valores del primario
como referencia y todos los demás valores del transformador se refiere al primario. Igual o ídem al
secundario.
Ejemplo:
Cuanto vale U2 viendo desde el primario, o sea referenciar los valores del secundario hacia el
primario.
Problema:
No se puede trabajar en el transformador con los valores referidos a sus propios niveles de
tensión, o sea al 1rio se refiere al 1rio y el 2rio se refiere al 2rio.
R1 X1 R'2 X'2
Ro
Xo
Iv Ix
i1
i2
V2
+ +- -
I1R1 I1X1
++ --
I2R2I2X2Io
N1/N2
V'2

38. 38
Solucion:
Se debe poner todo en una misma base de tensión “U base”, se debe referir todo al primario
Ejemplo: Cuanto vale U2 vista desde el primario?
= , entonces: U’2 = U2*
*Si a U2 lo multiplico Kt( ), la estoy transfiriendo al 1rio: U’2 =U1 = U2*
I2:
Y
Y
= , entonces: I’2 = I1 = I2*
R2:
,
,
=( )2
, entonces: R’2 = R1 = R2*( )2
X2: =( )2
, entonces: X’2 = X1 = X2*( )2
ENSAYO DE TRANSFORMADOR EN VACIO:
En este ensayo se busca las pérdidas del circuito magnético (perdida nominal de vacío, estas están
en el hierro, perdida del hierro Pfe).
69kv 10,5kv
1rio 2rio
R1 X1 R2 X2
Ro
Xo
Iv Ix
i1
V1
+ +- -
I1R1 I1X1
++ --
I2R2I2X2Io
Z2 =
I2 = 0
CIRCUITO EQUIVALENTE DE VACIO
altatensión
Øp
i1 = io
E1V1
E1=4,44*N1*f1*Ø

39. 39
R1 y X1, los despreciamos porque son pequeños frente a Ro y Xo.
Ro = resistencia ficticia, se disipe en (W), igual a la perdida en hierro.
Xo = reactancia inductiva, que origina el flujo.
*Se le aplica al primario la tensión U1 nominal (U1n).
*Perdidas en el hierro vienen dadas por la expresión:
Pfe =
#
,A
→ Ro =
#
Z
(U1 = tensión de la red, Pfe = dato fabrica)
Tambien:
Pfe = U1n*Ivo → Ivo =
Z
#
(por Ohm: Ivo =
#
,A
)
Luego:
Io = √G2[ + G2H , (condición: I1 = Io, Io es dato de ensayo)
Ixo = √G2 − G2[ , (Ixo = corriente de magnetización)
R1 X1
Ro
Xo
Iv Ix
i1
V1
+ +- -
I1R1 I1X1 Io
CIRCUITO EN VACIO
Ro
Xo
Iv Ix
i1
V1
Io = I1
CIRCUITO PARA ENSAYO

40. 40
DATOS PLACA TRANSFORMADOR
Fabricante Rhome S.A.
Aumento de temperatura 55 oC
Tensión primario 69000 V
Tensión secundario 13800 V
Derivaciones primario 69000 +/- 10% en 18 pasos
Liquido aislante aceite mobilent 35,18950 lt
Peso total 50200 kg
Potencia 25000 KVA
Fases 3
Polaridad Yd11
Corriente primaria 209 A
Corriente secundario 1046 A
Número de serie 17890
Frecuencia 50 Hz
Impedancia 10% a 75 oC
Conexión primario Estrella
Ø
Ix
Iv
E1=E2
Io=I1
U1
I1R1
I1X1

41. 41
Conexión secundario Delta
ENSAYO DE CORTO CIRCUITO:
Sirve para calcular las perdidas en el cobre Cu, medido en watt (Pcu(W)).
La impedancia de corto circuito Zcc o Zk, viene dada en la placa del transformador, el ensayo que
se realiza es para verificar el dato de la placa.
Ejemplo placa de transformador:
El ensayo se realiza de la siguiente forma:
*Se corta circuita el secundario con una sección del conductor igual o mayor que la de baja tensión
o secundario.
*Se aplica una tensión en el PRIMARIO: Vk o Vcc variable, que va desde cero hasta
aproximadamente 5% de la U1 nominal, cuando esta tensión de corto circuito hace circular la I1
nominal, paramos el ensayo y se toman los datos de Vcc, I1n y Pcc, (I1n=corr.1rio nominal).
Donde: Vk o Vcc = tension corte circuito (V)
V1 = tensión primario (V)
I1n = corriente primario nominal (A)
Pcc = potencia de corto circuito (W)
Pcu = potencia del cobre (W), (Pcu ˂ dato fabrica)
Zk = Z1 = R1 + R’2 + J(X1+X’2) , (RI = R1 + R’2 , XI = X1 + X’2)
Vk = se define como la tensión aplicada en corte circuito, hace que circule la corriente nominal I1n,
esta tensión es importante y viene dada en la placa del transformador.
R'2 X'2
i1
Vcc=Vk
I1
CIRCUITO ENSAYO CORTO CIRCUITO
R1X1
A
RI XI
I1n
Vcc=Vk

42. 42
Vk = I1n * Zk , (porcentual: Vk(%) =
#^
#
*100)
La impedancia Zk, como cualquier impedancia tiene un anguloⱷk, angulo de corto circuito.
Zk2
= RI2
+ XI2
→ XI = √_` − aG
Donde: Zk =
#^
Y
, RI =
Zbc
Y
, (dato placa: Vk, Pcu, I1n)
DIAGRAMA DE TRANSFORMADOR CON CARGA RESISTIVA PURA:
DIAGRAMA DE TRANSFORMADOR CON CARGA R-L:
Ø
Ix
Iv
I2
I1
E1=E2
Io
U1
I2 X2
I2Rc2
I2Rc2
I2R2
I1R1
I1X1
I2X2
R1 X1 R2 X2
Ro
Xo
Iv Ix
i1 i2
V1
+ +- -
I1R1 I1X1
++ --
I2R2I2X2Io
Rc2
E1=E2

43. 43
DIAGRAMA DE TRANSFORMADOR CON CARGA R-C:
REGULACION O CONMUTACION (TAP):
Ø
Ix
Iv
I2
I1
E1=E2
Io
U1
I2X2
I2Rc2
I2Rc2I1R1
I1X1
I2X2
R1 X1 R2 X2
Ro
Xo
Iv Ix
i1
i2
V1
+ +- -
I1R1 I1X1
++ --
I2R2I2X2Io
Rc2
E1=E2
Xc2
I2R2
I2Xc2
I2R2
I2Xc2
Ø
Ix
Iv
I2
I1
E1=E2
Io
U1
I2X2
I2Rc2
I2Rc2
I1R1
I1X
1
I2X2
R1 X1 R2 X2
Ro
Xo
Iv Ix
i1
i2
V1
+ +- -
I1R1 I1X1
++ --
I2R2I2X2Io
Rc2
E1=E2
Xcap I2R2
I2Xcap
I2R2
I2Xcap

44. 44
Para entender claramente cual es el motivo por el cual se hace necesario la carga de regulación, es
necesario saber cual es la característica de carga, la cual puede ser completamente INDUCTIVA o
hasta completamente CAPACITIVA, pasando por RESISTIVA PURA.
Si pretendemos tener la tensión en bornes del secundario de forma constante (Un2), se debería
variar el valor de U1, como U1 proviene de la red rígida, no podemos pensar en variarla, desde ahí
es que se hace el proceso de regulación.
La regulación consiste en variar de a saltos el numero de espirar que tiene alguno de los
arrollamiento, lo cual se consigue mediante contactos deslizables, motivo por el cual se elige el
arrollamiento que posee de menor corriente circulante para colocar el conmutador en esa bobina,
pues de esta manera es menor el riesgo de arco(chispa) en el proceso de conmutación.
En general se usa en el arrollamiento de mayor tensión porque tiene menor corriente, implica
chispa menor.
69kv10,5kv
1rio2rio
Regulacion a 10,5 kv
400/231 vol. (2rio en vacio)
380/220 vol. (2rio en carga)
Quiere decir que van a caer
20 (V), en la distancia hasta
el ultimo usuario.

45. 45
Por relación de transformación se tiene:
= → U1 = U2* , (U’1 = U2↑ = U1* ↓
OBS.: Si tomo menos espiras tengo mayor tensión U2 a la salida de la carga.
Ejemplo:
(+5%) → 24,9 + (0,05*24,9) = 26,145 kv
(+2,5%) → 24,9 + (0,05*24,9) = 25,5225 kv
dV = 26,145 – 25,5225 = 0,6225 kv
(-5%) → 24,9 - (0,05*24,9) = 24,2775kv
(-2,5%) → 24,9 - (0,05*24,9) = 23,655kv
dV = 24,2775 – 23,655 = 0,6225 kv
24,9kv10,5kv
1rio2rio
Regulacion a 10,5 kv
400/231 vol. (2rio en vacio)
380/220 vol. (2rio en carga)
Quiere decir que van a caer
20 (V), en la distancia hasta
el ultimo usuario.
AT BT
N1 N2
- 5%
- 2,5%
Unominal
+ 5%
+ 2,5%
U1n
U1+dU1
U1-dU1
chispa
U2

46. 46
TRANSFORMADORES TRIFASICOS:
La mayoría de las redes de distribución son TRIFASICAS, también un gran numero de usuarios del
tipo comercial e industrial. Por lo tanto la importancia que tiene la transformación trifásica para
alimentar este tipo de usuarios.
La energía de un sistema TRIFASICO, se puede transformar, ya sea por tres transformadores
monofásicos (yustapuestos) formando un banco trifásico, o bien por el uso de un transformador
trifásico.
NOMENCLATURA:
Si esta en el PRIMARIO: MAYUSCULAS “D”(triangulo), “Y”(estrella)
Si esta en el SECUNDARIO: MINUSCULA“d”(triangulo), “y”(estrella)
*Se muestra el transformador con un bobinado estrella(Y), que debe cumplir con los siguientes
requisitos del requerimiento trifásico:
CONEXION TRIANGULO-TRIANGULO CONEXION ESTRELLA-ESTRELLA CONEXION TRIANGULO-ESTRELLA
U
V
W
ULY
UFY
ILY
IFY
ULY = 1,732*UFY
UFY = ULY
3
ILY = IFY

47. 47
*Se muestra el transformador con un bobinado delta (D), que debe cumplir con los siguientes
requisitos del requerimiento trifásico:
*Las potencias serán:
PT = P1 + P2 + P3
PTD = 3*PF , ILD =
Ze
f∗√g
, IFD =
Y f
√g
PTY = 3*PF , ILY =
Ze
h∗√g
, ILY =IFY
U
V
W
ULD
ILD
IFD
IFD U
FY
ULD = UFD
ILD = 3
IFD =
*IFD
ILD
3
U
V
W
UL
IL
IF
IF U
F
U
V
W
UL
UF
IL
IF

48. 48
TRANSFORMADOR TRIFASICO TEMPLO:
*Estuvo en funcionamiento un tiempo. Luego se suprimió la columna central, después de
comprobar que por ella no circulaba ningún flujo(Ø), esto se evidencio colocando un galvanómetro
detector de circulación de flujo y se vion que no registraba, por ende se podría retirar dicha
columna.
a)tres transformadores independientes.
b)Si unimos magnéticamente una columna en común, circulara en cada momento por esta
columna el resultante de todas ellas, ahora bien, la suma algebraica de los valores instantáneos de
tres flujos senoidales, es constantemente nulo. Por eso suprimimos la columna central.
c)Alineamos la culata 1 y 3 y la 2 acortarla a cero, con ello se produce un ligero desequilibrio en la
corriente de magnetización que en las 3 fases, pero conduce a una construcción plana de los
núcleos del transformador.
120°
120°
120°
G
120°
120°
120°
= O
carga
1
2
1
2
1
2
a) b) c)
w2 2
3 2
120° 120° 120°
DIAGRAMA CARTESIANO
V
W U
LASUMADE
FLUJOSCERO
DIAGRAMA FASORIAL
=O

49. 49
CONEXIÓN DE BOBINADO:
Se determina el sentido de la siguiente manera:
1)Bobina a derecha (Ld): si el sentido de avance de la corriente es el mismo que el sentido de
avance del flujo.
b)Bobina a la izquierda (Li): El sentido de avance de la corriente esta invertido 180°, al sentido de
avance del flujo.
FORMA DE CONECTAR DOS BOBINAS:
Si quiero unir dos bobinas del mismo sentido (significa dos bobinas a derecha), entonces debo unir
extremos de nombres distintos.
a)Unir en serie dos bobinas del mismo sentido: Ld, Ld: uno extremos de nombre distinto.
I
I

50. 50
b)Unir en paralelo dos bobinas de distinto sentido: Ld y Li: uno extremos de nombre distinto.
c)Unir en serie dos bobinas de distinto sentido: Ld y Li: unir extremos del mismo nombre.
I
j
s
I
j
s
Donde:
i = inicio de la bobina
s = salida de la bobina
Ld
Ld
I
j
s
I
j
s
Donde:
i = inicio de la bobina
s = salida de la bobina
Ld
Li

51. 51
d)Unir en paralelo dos bobinas del mismo sentido: Ld y Ld: uno extremos de nombre igual
CONEXIONES TRIFASICAS:
La base inicial correcta del grupo de conexión, esta en construir el diagrama fasorial de manera
correcta, tanto para el primario como para el secundario. Fijamos una regla para la construcción
del mismo:
I
j
s
I
j
s
Ld
Li
I
j
s
I
j
s
Ld
Ld

52. 52
Diagrama Fasorial:
*Primero nombramos un fasor de referencia V, a 120° de atraso a W y 240° a U.
*Denominamos a los bornes de alta tensión(AT): U, V, W.
*Denominamos a los bornes de baja tensión(BT): u, v, w.
*Seguimos la flecha de fondo de bobina a principio de bobina(borne)(el fondo de la bobina
coincide con la cola de la flecha).
a)Fijamos una base de referencia. Se ubica el fondo de la bobina(Fb), Ubicamos el principio de
bobina (ib) como una punta (o con los subíndices superior o inferior).
Recorremos la bobina de final a principio de bobina y marcamos el fasor correspondiente con el
desfasaje correspondiente.
b)Fijamos los desfases de 120° y se fija la fase de referencia y esta fase de referencia marcara el
grado cero (0°).
c)Se busca un centro gravitacional (geométrico real) al que se denomina neutro (0), o neutro
ficticio, a partir de ahí se traza una recta que pase por la punta del fasor de referencia, o sea el
fasorV.
d)Iden para la baja tensión.
e)Luego se superponen los fasores de referencia, que va del neutro a la punta de la flecha del fasor
V y se mide el desface angular.
*Los mas usados 0, 1,5, 11.

53. 53
Conexión delta o triangulo (D):
Conexión estrella (Y):
U V W
fb
ib
fb
ib
fb
ib
wvu
fb
ib
fb
ib
fb
ib
0°
relog=12h
V W
U
vu
w
60°
60°
1 2
SOLUCION
D d 2

54. 54
Conexión Zig - Zag (Y):
Solo se conectan en el secundario en baja tensión. Se bobina la mitad en una fase y la otra mitad
en otra fase.
Pasos a seguir para diagrama fasorial:
1)y2)trazo el fasor v/2 y a continuación trazo el fasor u/2
3)como no tengo otro fasor vuelvo a tierra(0)
4)y5)trazo el fasor w/2 y a continuación trazo el fasor v/2
6)como no tengo otro fasor vuelvo a tierra(0)
7)y8)trazo el fasor u/2 y a continuación trazo fasor w/2
9)como no tengo otro fasor vuelvo a tierra(0)
U V W
fb
ib ib
fb
ib
fb
ib ib
fb
ib
wvu
V
WU
uw
v
relog
0-12h
1
2
3
4
56
SOLUCION
Y y 6

55. 55
10)trazo una envolvente y cierro mi diagrama fasorial.
fb
ib ib
fb
ib
fb
ib ib
fb
ib
wvu
fb
fb
1
2
3
4
5
6
7
0
1-2
4-5
7-8
v/2
v/2
u/2
u/2
w/2
w/2
wvu

56. 56
U VW
u v w
u v w
U V W
U V W
u v w
V
U
W D d 11
u
v
w
V
WU
Y y 6
D d 5
U
V
W
u
v
w
u
v
w

57. 57
D d 0
D d 11U
U
V
V
Y d 1
V
U W
W
W
v
u
w
U V W
u v w
U V W
u v w
u v w
U V W
w
u
v
v
w

58. 58
u v w
D y 11
D y 6
Y d 5
U V W
u v w
u
U V W
U V W
V
W
U
v
wu
V
U
W
uw
v
V
U W
u

59. 59
u v w
UV W
UV W
uv w
uv w
u v w
UV W
v
w
V
WU
v
w
u
V
WU
V
W
U
Y d 1
Y d 11
D z 11
w
v
u

60. 60
U V W
UV W
UV W
uv w
uv w
D z 0
Y z 11
v/2
v/2
v/2
v/2
W
V
U
v/2
v/2
V
WU
V
U
W

61. 61
uv w
v/2
v/2

62. 62
Efectos de campo eléctrico de líneas aéreas y subestaciones transformadoras.-
Todas las líneas áreas y los est. Transformaron, generan un C.E. contra tierra – a medio que crece la
tensión, crece el C.E y se hace necesario evaluar con el ambiente de humanos y animales.
Normalmente las distancias mínimas entre las áreas y tierra, se eligen en función de los que se
permiten efectuar debajo de las líneas por ej. Agricultura, transito de gentes y vehículos, etc.
Todo línea aérea creo, restricciones al dominio (no se puede edificar dibujo de una línea, en ciertas
condiciones). La dist de servidumbre de la línea está entre 22 y 23 mts de ancho.
Se estudió el periodo de trabajo en estaciones transformadoras y se llegó a conclusión importantes
en lo que respecto a la integridad física de los operarios.
Se dieron normas que dan el periodo de trabajo bajo la acción del campo eléctrico: (normas dados
por Rusia.)
E [kv/m] periodo de trabajo
5 kv/m ilimitado
10 kv/m 180 minutos
15 kv/m 90 minutos
10 kv/m 10 minutos
25 kv/m 5 minutos
La corriente eléctrica a través del cuerpo humano.-
Tanto en C.A. como en C.C. se pueden presentar estados: transitorios y estaciones permanentes y
los efectos se pueden dividir en tres causas: corriente de bajo percepción, shock primario y shock
secundario.
Las ǂ partes de cuerpo tiene ǂ sensibilidad – la 1ra sensación se percibe en C.A. es de pincho
duro, mientras que en C.C., la sensación es de calor.
Los umbrales de percepción están en C.C.:
5,2 Ma p/hombres y 3,4 mh p/mujeres en C.A.; 1,8 Ma y 0,8 mA (corriente estacionario y
permanente).

63. 63
La corriente de shock 2do:
Ya se relaciona con sensaciones de dolor o molestia.
En C.A. se vuelven objetables alrededor de los 2Ma, minutos que en C.C. estaciones en 1Ma
p/hombre y 6Ma p/mujeres.
Lo corriente de shock 1ro:
Incrementando los ítems de la corriente permanente se llegó a un punto en el que no es posible
controlar los muebles por donde circule (no se puede soltar la mano del objeto). Este es el nivel de
corriente de Shock 1ro o de fuga desde donde incrementándose a un más la corriente, puede
producirse la fabricación vehicular, (depende del peso de la persona, de la magnitud y duración de
la corriente).
Dalziel.-
Define esta corriente para una probabilidad del 5% con valores 62 Ma p/hombre en C.C., y 9 Ma
hombres, 6Ma mujeres en C.A.
Se estima en C.A., un valor de 5Ma, como la corriente de fuga para niños
Lo más inaceptable es la descarga de chispas:
Que se presentan cuando se ponen en contacto 2 cuerpos de ǂ potencial y luego se separan, Ej.
Operario en una escalera aislado y tocando una estructura metálica en forma alternativa.
Con el nombre de stress:
Se engloba cualquier experiencia intensa en humanos, sea grata o ingrata que provoca trastornos
en el cuerpo humano.
Calculo de las tensiones inducidas:
Se pueden distinguir 3 casos principales:
• Perona aislada tocando un objeto contra tierra (una estructura)
• Perona a tierra tocando un objeto aislado (un vehículo)
• Perona a tierra tocando un objeto aislado
Lo que se trata de determinar es la carga sobre un objeto dentro de un campo eléctrico.

64. 64
Cog capacidad de objeto contra tierra:
I= jw. Eh Cog si hemos los signos da:
G = jk l. ln
jℎ . pqn
l
Jw Es E- la densidad de desplazamiento
En el caso de corriente inducidas:
Grs = tu v. v. w.Tomando valores absolutos y reemplazando el Es y w, vamos a tener pero So p
r x
Grp =
l. y
3.6 H 10|
} / 60 p
r ⁄ → Grp =
l. y.
3. 10|
p• l ‚`[
ƒx „ → Grp = …ƒ†‡
Determinación de la tensión inducido según el tipo de objeto
Considerando los alambrado y cercas bajo una línea
En los alumbrados: pq =
ˆ A
‰Š
‹Œ
•
L = log del alambre
H= altura del alambre
R= radio del alambre
La corriente en este caso:
G = Ž. l. ℎ.
2. • l
ln
2ℎ
q= E.h. Cog h- altura efectivo del objeto
La corriente valle J= jWq

65. 65
Encendido de combustible
La descarga entre 2 cuerpos conductores puede encender una mezcla compatible. Cuando se
hicieron las pruebas de UHV, se empleó una manguera (como conductor) contra un recipiente llama
de no fta y se encontró que la fórmula de la tensión de encendido.
‘pp
= 4.6. p“X.g
r” ” •r • ) • •) ) * ” • ) * p” ); r r * p*p ) •—•”, * ‘pp r ƒ •
p • p ) ) r • …• ™‡
− Humanos 100.-
− Humanos y herramientas 150.-
− Pequeños vehículos 700.-
− Automóviles compactos 800.-
− Camionetas 900.-
− Autom. Grandes 1000.-
− Camiones con plemios 1000.-
− Furgones 1200.-
− Camiones grandes 1200.-
Distancias típicas en líneas de EHV y UHV contra tierra
• 362 Kv : 5,5 mts (basado en el criterio de los 5mA)
• 950 Kv : 8,25 mts (argentino)
• 800 Kv : 11,3 mts 500 Kv : 8,5 m
• 1200 Kv : 16,8 mts 132 Kv : 7 m
• 1500 Kv : 21,1 2 MT : 6m

66. 66
Conclusión
a) No hay razones para suponer un efecto biológico directo bajo líneas aéreas o estaciones
transformadores.
b) En casos prácticos, cada con diez desfavorables se pueden desarrollo síntomas de stress, o
consecuencia del dolor producido por el shock
c) La sensibilidad de personas a descargas o chispas respectivas puede ser eliminado con
zapatos de suelos resistivos.
d) Las alturas mínimas sobre el suelo pueden determinarse en diferentes zonas como ser zonas
rurales, etc.
e) Es conveniente entre para cualquier estructura metálica dentro de la zona de influencia sea
conectado a tierra.
f) Como consecuencia de y este tipo de una do puede permanecer en la tierra por unos
segundos, está clasificado como sobre temporal aunque su pies inicial tiene que
permanecer a la categoría de maniobra