Este documento describe el análisis de circuitos eléctricos sinusoidales en estado estacionario. Explica que las bobinas hacen que la corriente se retrase 90° con respecto a la tensión, mientras que los condensadores hacen que la corriente se adelante 90° con respecto a la tensión. Introduce el concepto de fasores para representar magnitudes sinusoidales, donde la amplitud es el módulo del fasor y la diferencia de fase es el ángulo entre fasores. Finalmente, define la impedancia como la relación entre tens

1. PARTE 2PARTE 2
ANÁLISIS DE CIRCUITOS SINUSOIDALESANÁLISIS DE CIRCUITOS SINUSOIDALES
EN ESTADO ESTACIONARIOEN ESTADO ESTACIONARIO
Jorge Patricio Muñoz Vizhñay
CIRCUITOS
ELÉCTRICOS II

2. INTENSIDAD DE CORRIENTEINTENSIDAD DE CORRIENTE
Y TENSIÓN SENOIDALESY TENSIÓN SENOIDALES
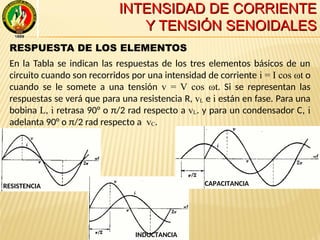
RESPUESTA DE LOS ELEMENTOS
Sea una bobina L recorrida por una corriente i = I cos (ωt + 45°) (A) [ver
Figura]. La tensión entre sus extremos es:
Comparando vL e i se observa que la intensidad de corriente está retrasada
90° o π/2 rad respecto a la tensión.

3. INTENSIDAD DE CORRIENTEINTENSIDAD DE CORRIENTE
Y TENSIÓN SENOIDALESY TENSIÓN SENOIDALES
RESPUESTA DE LOS ELEMENTOS
En la Tabla se indican las respuestas de los tres elementos básicos de un
circuito cuando son recorridos por una intensidad de corriente i = I cos ωt o
cuando se le somete a una tensión v = V cos ωt. Si se representan las
respuestas se verá que para una resistencia R, vL e i están en fase. Para una
bobina L, i retrasa 90° o π/2 rad respecto a vL. y para un condensador C, i
adelanta 90° o π/2 rad respecto a vC..
RESISTENCIA
INDUCTANCIA
CAPACITANCIA

4. INTENSIDAD DE CORRIENTEINTENSIDAD DE CORRIENTE
Y TENSIÓN SENOIDALESY TENSIÓN SENOIDALES
RESPUESTA DE LOS ELEMENTOS

5. INTENSIDAD DE CORRIENTEINTENSIDAD DE CORRIENTE
Y TENSIÓN SENOIDALESY TENSIÓN SENOIDALES
RESPUESTA DE LOS ELEMENTOS
Ejemplo Circuito RL
Por el circuito serie RL representado en la Figura circula una corriente
i = I sen ωt. Determinar la diferencia de potencial total que se produce
entre los elementos del circuito y representar v e i.

6. INTENSIDAD DE CORRIENTEINTENSIDAD DE CORRIENTE
Y TENSIÓN SENOIDALESY TENSIÓN SENOIDALES
RESPUESTA DE LOS ELEMENTOS
Ejemplo Circuito RL
Por el circuito serie RL representado en la Figura circula una corriente
i = I sen ωt. Determinar la diferencia de potencial total que se produce
entre los elementos del circuito y representar v e i.
Como la corriente es una función seno y
Igualando los coeficientes de los términos semejantes de las ultimas
expresiones, se tiene:
v=V sen(ω t+θ )=V senω t cosθ +V cosω t senθ
v=RI senω t+ω LI senω t cos90+ω LI cosω t sen90

7. INTENSIDAD DE CORRIENTEINTENSIDAD DE CORRIENTE
Y TENSIÓN SENOIDALESY TENSIÓN SENOIDALES
RESPUESTA DE LOS ELEMENTOS
En la Figurase han representado las funciones v e i. El angulo de fase ϴ,
angulo que i retrasa respecto a v, esta dentro del rango 0 ≤ ϴ ≤ 90, cuyos
limites se dan cuando ωL « R y cuando ωL » R, respectivamente. Si el
circuito tuviera una tensión de alimentación v = V sen ωt, la corriente
resultante seria:
donde ϴ = tg -1
(ωL / R)

8. INTENSIDAD DE CORRIENTEINTENSIDAD DE CORRIENTE
Y TENSIÓN SENOIDALESY TENSIÓN SENOIDALES
RESPUESTA DE LOS ELEMENTOS
Ejemplo Circuito RC
Por el circuito serie RC serie circula una corriente i = I sen ωt. Determinar la
diferencia de potencial total que se produce entre los elementos del circuito
y representar v e i.

9. INTENSIDAD DE CORRIENTEINTENSIDAD DE CORRIENTE
Y TENSIÓN SENOIDALESY TENSIÓN SENOIDALES
RESPUESTA DE LOS ELEMENTOS
En la Figura se han representado las funciones v e i. El angulo de fase ϴ,
angulo que i adelanta respecto a v. El angulo de fase esta limitado dentro
del rango 0 ≤ ϴ ≤ 90. Para (1/ ωC) « R el angulo ϴ = 0 y para (1/ωC) » R el
angulo ϴ = 90:

10. INTENSIDAD DE CORRIENTEINTENSIDAD DE CORRIENTE
Y TENSIÓN SENOIDALESY TENSIÓN SENOIDALES
FASORES
La simple observación de las sinusoides de tensión e
intensidad en los ejemplos anteriores muestra que las
amplitudes y las diferencias de fase son los dos
parámetros principales.
Un fasor o vector, giratorio en el sentido de las agujas del
reloj a velocidad angular constante ω (rad/s), como el
representado en la Figura, tiene una proyección en el eje
horizontal que corresponde a los valores de la función
coseno.
La longitud del fasor o su módulo es la amplitud o valor
máximo de la función coseno. El ángulo entre dos
posiciones del fasor es la diferencia de fase entre los
puntos correspondientes en la función coseno (se usara
esta función como referencia).

11. INTENSIDAD DE CORRIENTEINTENSIDAD DE CORRIENTE
Y TENSIÓN SENOIDALESY TENSIÓN SENOIDALES
FASORES
Véanse los ejemplos de la Tabla. Obsérvese que los fasores, .que tienen
naturaleza de segmentos dirigidos o vectores, están indicados con
mayúsculas en negrita, es decir, V e I. El ángulo de fase de la función
coseno es el ángulo del fasor.
La frecuencia f (Hz) y la pulsación ω (rad/s) no aparecen generalmente pero
deben ser tenidas en cuenta, ya que están presentes implícitamente en
cualquier problema de circuitos sinusoidales estacionarios.

12. INTENSIDAD DE CORRIENTEINTENSIDAD DE CORRIENTE
Y TENSIÓN SENOIDALESY TENSIÓN SENOIDALES
FASORES
Los fasores pueden ser tratados como números complejos. Cuando el eje
horizontal se identifica con el eje real de un plano complejo, los fasores se
convierten en números complejos y son aplicables sus reglas habituales.

13. INTENSIDAD DE CORRIENTEINTENSIDAD DE CORRIENTE
Y TENSIÓN SENOIDALESY TENSIÓN SENOIDALES
IMPEDANCIA Y ADMITANCIA
La tensión y la intensidad de corriente se pueden escribir, respectivamente:
La relación entre el fasor de tensión V y el de intensidad I se define como
impedancia Z; es decir, Z = V/I Ω. El inverso de la impedancia se denomina
admitancia Y, esto es, Y = 1/Z (S), donde 1 S (siemens) = 1 Ω-1
. Tanto Y
como Z son números complejos.
Dominio de la
frecuencia

14. INTENSIDAD DE CORRIENTEINTENSIDAD DE CORRIENTE
Y TENSIÓN SENOIDALESY TENSIÓN SENOIDALES
IMPEDANCIA Y ADMITANCIA
Cuando la impedancia se expresa en forma cartesiana, la parte real es la
resistencia R y la parte imaginaria es la reactancia X. El signo de la parte
imaginaria puede ser positivo o negativo: cuando es positivo, X se
denomina reactancia inductiva o inductancia, y cuando es negativo, X se
denomina reactancia capacitiva o capacitancia. Cuando la admitancia se
escribe en forma cartesiana, la parte real es la conductancia G y la parte
imaginaria es la susceptancia B. El signo positivo en la susceptancia indica
que es capacitiva y un signo negativo indica que es inductiva.

15. INTENSIDAD DE CORRIENTEINTENSIDAD DE CORRIENTE
Y TENSIÓN SENOIDALESY TENSIÓN SENOIDALES
IMPEDANCIA Y ADMITANCIA
R
jXL Z
R
-jXC Z
+ ϴ
- ϴ