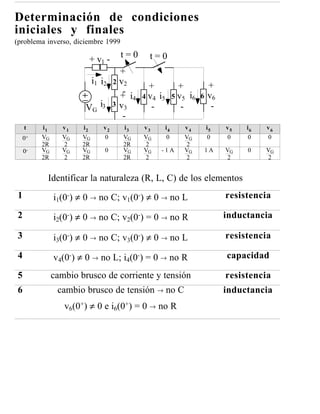
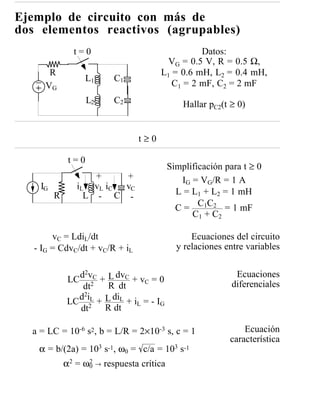
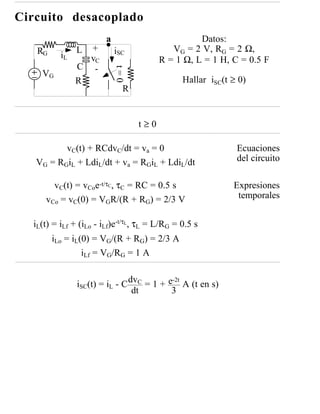
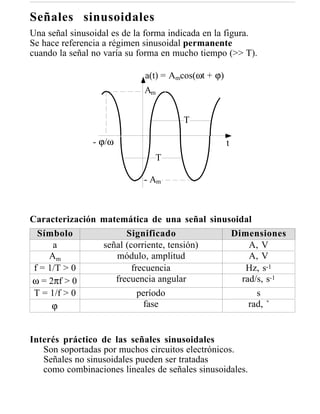
Este documento presenta transparencias para la asignatura de Análisis de Redes. Incluye conceptos básicos sobre análisis de circuitos, elementos ideales, leyes de Kirchhoff, y procedimientos para simplificar el análisis como elementos en serie y paralelo. El objetivo es calcular corrientes, tensiones, potencias y energía en circuitos eléctricos.

1. Departamento de Teoría de la Señal y Comunicaciones
Escuela Técnica Superior de Ingenieros de Telecomunicación
UNIVERSIDAD DE VIGO
web: www.tsc.uvigo.es/DAF/Investigacion/index.html
web: www.tsc.uvigo.es/Docencia/FichasAsignaturas/ar.php
Análisis de redes
Transparencias de clase
Enrique Sánchez
Artemio Mojón
Vigo, enero 2003
Escuela Técnica Superior de Ingenieros de Telecomunicación. Lagoas-Marcosende, s/n. 36200 VIGO
Tfno.: 986812142. Fax: 986812116. Correo electrónico: esanchez@tsc.uvigo.es, amojon@tsc.uvigo.es

3. Análisis de redes
Transparencias de clase
Índice
Conceptos básicos ....................................................................................... 1
Régimen transitorio .................................................................................... 25
Régimen sinusoidal permanente.................................................................... 79
Cuadripolos ............................................................................................... 169

5. Análisis de redes
Transparencias de clase
Conceptos básicos
Conceptos básicos - 1: páginas 3-9
Conceptos básicos - 2: páginas 10-22
Ejercicios de repaso: página 23

7. Los sistemas electromagnéticos se analizan
utilizando las ecuaciones de Maxwell.
Se requiere un proceso de cálculo complejo para determinar
las intensidades de los campos eléctrico y magnético.
Se utilizan simplificaciones matemáticas
(teoría de circuitos, teoría de líneas de transmisión).
Aproximación básica
de la teoría de circuitos (análisis de redes)
Las dimensiones de los elementos del sistema son mucho menores
que la menor de las longitudes de onda de las señales.
Consecuencia
Las magnitudes a calcular son
Magnitud Símbolo Unidades
voltaje / tensión v(t) voltios (V)
corriente i(t) amperios (A)
potencia |p(t)| = |v(t)i(t)| watios (W)
t2
energía w= p(t)dt julios (J)
t1
En general, estas magnitudes varían con el tiempo (t).
Análisis: se supone que el sistema está formado
por elementos ideales y se aplican las leyes de Kirchhoff.

8. Elementos ideales
Esquema i
funcionales
terminales
relaciones
v = f (i)
(bornes)
+
v
- i = f-1 (v)
Características
Un elemento ideal no puede descomponerse en otros.
Sólo tiene dos terminales.
Los terminales pueden estar a distinta tensión.
La corriente que entra por un terminal es igual
a la que sale por el otro.
La corriente y la tensión están relacionadas
por una función (distinta en cada elemento).
En el cálculo de la potencia se aplica el convenio pasivo.
Se clasifican en activos y pasivos.
Convenio pasivo de signos
Se asignan arbitrariamente la polaridad de la tensión (+ -)
y el sentido de la corriente (-> <-).
- v + = + -v - i -i
=
i i i i
+ v - + v - - v + - v +
p = vi p = - vi p = - vi p = vi
Si p < 0, el elemento libera energía.
Si p > 0, el elemento absorbe energía.

9. Elementos activos (fuentes, generadores)
Representan la excitación que se aplica al resto del circuito.
Clasificación
Por la magnitud: de tensión, de corriente.
Por la relación con otros elementos:
independientes,
dependientes (su valor depende de otros elementos).
Por la relación con el tiempo:
continuas (el valor no cambia con el tiempo),
variables (el valor cambia con el tiempo).
Representación gráfica
+ - + -
Fuente de tensión Fuente de tensión Fuente de tensión
independiente independiente independiente
(continua o variable) continua sinusoidal
Fuente de corriente Fuente de corriente Fuente de tensión
independiente dependiente dependiente
(continua o variable) (continua o variable) (continua o variable)
Fuente de tensión
Impone en sus bornes la tensión indicada
por la relación funcional; soporta cualquier corriente.
Fuente de corriente:
Impone en sus bornes la corriente indicada
por la relación funcional; soporta cualquier tensión.

10. Elementos pasivos
Soportan la excitación proporcionada por las fuentes.
Caracterización de los elementos pasivos
Esquema Elemento Relación Observaciones
y unidades funcional
+ i Resistencia
v v = Ri Ley de Ohm
- R Ohmios (Ω)
+ i Conductancia
v i = Gv Ley de Ohm
- G Siemens (S)
+ i Inductancia No soporta
v v = L di cambios bruscos
- L Henrios (H) dt de corriente
+ i Capacidad No soporta
v i = C dv cambios bruscos
- C Faradios (F) dt de tensión
+ i
Cortocircuito v=0 Soporta
- R=0 cualquier corriente
+ i
Circuito i=0 Soporta
- R=∞ abierto cualquier tensión
Si se cambia el sentido de la corriente con relación a la tensión,
hay que utilizar un signo menos
en el segundo miembro de la relación funcional.
L y C son elementos reactivos; almacenan y liberan energía.
R y G son elementos resistivos; disipan energía.

11. Análisis
Analizaremos exclusivamente circuitos lineales
(los elementos pasivos tienen valores positivos, constantes con el
tiempo, e independientes de los valores de cualquier otro elemento),
con lo que podremos aplicar el principio de superposición.
Principio de superposición
Si en un sistema lineal
la respuesta a una excitación xk (k = 1, 2,... n) es una salida yk,
la respuesta a una excitación compuesta
por una combinación lineal de las excitaciones xk
es una salida que es la misma combinación lineal
de las excitaciones xk.
sistema
xk yk k = 1, 2,... n
lineal
sistema
Σ a kx k Σ a kyk
lineal
ak = cte, para todo k
La linealidad (y el principio de superposición)
sólo se mantiene si las salidas son tensiones o corrientes,
y no si las salidas son potencias o energías.

12. Leyes de Kirchhoff
Definiciones
Nudo: punto en el que se conectan dos o más elementos.
Malla: conjunto cerrado de elementos conectados
uno a uno que puede recorrerse
sin pasar dos veces por ninguno de ellos.
Ley de las corrientes en los nudos
La suma algebraica de las corrientes en un nudo es nula.
Σ ik = 0, k = 1, 2,... n
n: número de elementos conectados al nudo
Ley de las tensiones en las mallas
La suma algebraica de las tensiones en una malla es nula.
Σ vk = 0, k = 1, 2,... n
n: número de elementos que forman la malla
Análisis de redes
Analizar un circuito consiste en calcular
las corrientes y las tensiones en sus elementos
(y, en caso necesario, potencias y energías).
Para ello hay que:
plantear las leyes de Kirchhoff en los nudos y en las mallas;
relacionar la corriente y la tensión en cada elemento
mediante su correspondiente relación funcional.

13. Ejemplo de análisis de redes
Conocidos los valores de vg, R1, R2, y R3,
R1 se desea hallar los valores
de las corrientes y las tensiones
R2 en todos los elementos del circuito.
vg
R3
a + v1 - b Se identifican los nudos (a, b, c, y d)
y las mallas (abcd) del circuito.
i1 R1
+ Se asignan tensiones y corrientes
ig i2 v2 arbitrarias a los distintos elementos
vg R2 - (excepto para la fuente,
R3 i3 el sentido de cuya tensión
ya está especificado).
d + v3 - c
nudo a: ig - i1 = 0 Se aplica la ley de las corrientes
nudo b: i1 + i2 = 0 a los nudos
nudo c: i2 - i3 = 0 (una ecuación por cada nudo).
nudo d: i3 + ig = 0
malla abcd: Se aplica la ley de las tensiones
vg - v1 - v2 + v3 = 0 a las mallas
(una ecuación por cada malla).
v1 = R1i1 Se consideran las relaciones
v2 = - R2i2 funcionales de los elementos
v3 = R3i3 (una relación por elemento).
A partir del sistema de ecuaciones es posible
hallar las corrientes y las tensiones buscadas.

14. Refinamientos del análisis de redes
El análisis de un circuito mediante la aplicación directa
de las leyes de Kirchhoff puede ser muy complicado.
Para resolver este problema pueden utilizarse
simplificaciones y procedimientos derivados,
sin aproximaciones matemáticas, de las leyes de Kirchhoff.
Simplificaciones
Elementos en serie.
Elementos en paralelo.
Equivalencia ∇-Y (∏-T) entre agrupaciones de resistencias.
Divisores de tensión.
Divisores de corriente.
Procedimientos
Análisis por mallas.
Análisis por nudos.
Otros aspectos (también derivados de las leyes de Kirchhoff)
Equivalentes de Thèvenin y Norton.

15. Elementos en serie
Se dice que dos elementos están en serie cuando
tienen un nudo común,
y a este nudo no se conecta ningún otro elemento.
a b c Los elementos a, b y c
están en serie
La corriente que circula por un conjunto de elementos en serie
es igual en todos ellos. Por tanto:
no es posible conectar en serie
fuentes de corriente de distintos valores;
si los elementos en serie son idénticos en naturaleza y valor,
la tensión es igual en ellos.
Elementos en serie de igual naturaleza pueden agruparse.
E1 En Eeq
i1 = = = in = i i
Elementos de igual naturaleza en serie Elemento equivalente
n
Fuentes de tensión vk (k = 1, 2,... n) veq = ∑ vk
k=1
n
Resistencias Rk (k = 1, 2,... n) Req = ∑ Rk
k=1
n
Inductancias Lk (k = 1, 2,... n) Leq = ∑ Lk
k=1
n
Capacidades Ck (k = 1, 2,... n) 1 = ∑ 1
Ceq k = 1 Ck

16. Elementos en paralelo
Se dice que dos elementos están en paralelo
cuando los terminales de todos ellos se conectan a los mismos nudos.
a b c Los elementos a, b y c
están en paralelo
La tensión en un conjunto de elementos en paralelo
es igual en todos ellos. Por tanto:
no es posible conectar en paralelo
fuentes de tensión de distintos valores;
si los elementos en paralelo son idénticos en naturaleza y valor,
la corriente es igual en ellos.
Elementos en paralelo de igual naturaleza pueden agruparse.
+ + +
v1 E1 vn En v1 = ... = vn = v v Eeq
- - -
Elementos de igual naturaleza en paralelo Elemento equivalente
n
Fuentes de corriente ik (k = 1, 2,... n) ieq = ∑ ik
k=1
n
Resistencias Rk (k = 1, 2,... n) 1 = ∑ 1
Rk
eq k=1
n
Inductancias Lk (k = 1, 2,... n) 1 = ∑ 1
Lk
eq k=1
n
Capacidades Ck (k = 1, 2,... n) Ceq = ∑ Ck
k=1

17. Divisor de tensión
+ v1 - R1
v1 = v
+ R 1 + R2
R1
v2
v R2 - v2 = v R2
R 1 + R2
Divisor de corriente
R2
i1 = i
R1 i1 R 2 i2 R 1 + R2
i
i2 = i R1
R 1 + R2
Transformación de generadores
a a
R R
v b i b
Desde la perspectiva de un circuito externo
conectado a los terminales a y b, ambos esquemas son iguales
si se cumplen las relaciones indicadas más abajo.
Sin embargo, téngase presente que para cálculos de corrientes y
tensiones en el conjunto generador-resistencia
la equivalencia no se mantiene en general.
v = Ri i = v/R

18. Utilización de las simplificaciones
vg = 60 V, ig = 5.6 mA,
+ R1 = 30 kΩ, R2 = 60 kΩ,
R1 R3 R5
v6 R3 = 5 kΩ, R4 = 100 kΩ,
vg R2 ig R4 R6 - R5 = 1 kΩ, R6 = 4 kΩ
Hallar v6
+ Transformación de fuente
R3 R5 vg
v6 i1 =
i1 R1 R2 ig R4 R6 - R1
+ Agrupación de resistencias
R3 R5 en paralelo
v6
ig
i1 R12 R4 R6 - R12 = R1R2
R 1 + R2
+ Transformación de fuente
R12 R3 R5 v12 = R12i1
v6
v12 ig R4 R6 -
+ Agrupación de resistencias
R123 R5 en serie
v6
v12 ig R4 R6 - R123 = R12 + R3
+ Transformación de fuentes
i2 R5
v6 i2 = v12
R123 ig R4 R6 - R123

19. Utilización de las simplificaciones
Agrupación de resistencias en paralelo
R1234 = R123R4
+
R5
v6 R123 + R4
i3 R1234 R6 - Agrupación de fuentes en paralelo
i 3 = ig - i2
+ Transformación de fuente
R1234 R5 v1234 = R1234i3
v6
v1234 R6 -
+ Agrupación de resistencias
R12345 en serie
v6
v1234 R6 - R12345 = R1234 + R5
+ Divisor de tensión
R12345 R6
v6 v6 = v1234 = 12.8 V
v1234 R6 - R12345 + R6

20. Equivalentes de Thèvenin y Norton
Un circuito puede conectarse a una red externa
a través de dos o más terminales.
Si una red externa está conectada a un circuito
a través de dos terminales,
el comportamiento del segundo puede representarse
mediante los equivalentes de Thèvenin y Norton.
Un circuito tiene tantos equivalentes distintos
como parejas de terminales se consideren.
Equivalentes de Thèvenin y Norton en continua
a a a
RTh
VTh IN RN
b b b
Circuito original Equivalente Equivalente
de Thèvenin de Norton
Entre los equivalentes se cumplen las relaciones
(transformación de fuentes)
RTh = RN VTh = RNIN IN = VTh
RTh
Si entre los terminales a y b se conecta una resistencia
RL = RTh
la potencia disipada en dicha resistencia es la máxima posible,
y vale
2
VTh
pmax =
4RTh

21. Análisis por mallas
Identificación de mallas
En un circuito hay r - (n - 1) mallas independientes.
n: número de nudos esenciales.
nudo esencial: conecta tres o más elementos.
r: número de ramas esenciales.
rama esencial: camino entre dos nudos esenciales
que no pasa por otro nudo esencial.
Sistema de ecuaciones
A cada malla independiente se asigna una corriente.
Se formula una ecuación por cada malla independiente
(refleja la ley de Kirchhoff de las tensiones en la malla).
Las incógnitas son las corrientes de las mallas.
Ecuaciones adicionales
Debe formularse una ecuación adicional por:
cada fuente independiente de corriente,
cada fuente dependiente.
Las incógnitas de las ecuaciones adicionales
están relacionadas con los elementos que las introducen.
Nota
Las corrientes de malla no tienen existencia real.
Las corrientes que tienen sentido físico y pueden medirse
son las corrientes de rama.
En una rama no compartida entre dos mallas
la corriente coincide con la de la malla
de la que forma parte la rama.

22. Ejemplo de análisis por mallas
R1 R3 R2 Datos:
v a , vb , R1 , R2 , R3 , R4 , R5
i3
va vb Hallar i3
R4 R5 i3 = ia - ib
R1 + v1 - R3 + v2 - R2 Asignación de corrientes
+ de malla (sentido arbitrario)
v3 y tensiones (polaridad arbitraria)
va ia - i3 ib vb
R4 + v 4 - + v 5 - R5
v a - v1 - v3 + v4 = 0 Ley de Kirchhoff
v 3 - v2 - vb + v 5 = 0 de tensiones en las mallas
v3 = R3i3 = R3(ia - ib) Relaciones funcionales
v1 = R1ia, v4 = - R4ia
v2 = R2ib, v5 = - R5ib
va - R1ia - R3(ia - ib) - R4ia = 0 Ecuaciones de malla
R3(ia - ib) - R2ib - vb - R5ib = 0
va = ia(R1 + R3 + R4) - ibR3 Ecuaciones de malla
vb = iaR3 - ib(R3 + R2 + R5) (ordenadas)
Prescindiendo de signos:
suma algebraica fuentes tensión independientes en malla =
= corriente de malla X suma resistencias malla +
+ suma algebraica (resistencia compartida X
X corriente en resistencia compartida)
Los signos dependen de las relaciones entre:
corrientes y fuentes en una malla,
corrientes en las ramas compartidas.

23. Ejemplo de análisis por mallas
R1 R3 Datos:
vd = ri2,
i2 ig, r, R1, R2, R3
ig R2 vd
Hallar potencias en las fuentes
R1 R3 Identificación de incógnitas
+
vg i2
- ig ia ib vd
R2
vg = ia(R1 + R2) - ibR2 Ecuaciones de malla
vd = - iaR2 + ib(R2 + R3)
vd = ri2 = r(ib - ia) Ecuación adicional
para la fuente dependiente
i a = ig Ecuación adicional
para la fuente de corriente
p g = - vg i g , pd = - vd i b Cálculos

24. Análisis por nudos
Identificación del nudo de referencia
Se escoge arbitrariamente un nudo esencial
como referencia y se le asigna una tensión arbitraria.
Suele escogerse el nudo con más conexiones
y suele asignársele una tensión nula.
Indicación del nudo de referencia con tensión nula
(conexión a tierra, a masa).
Sistema de ecuaciones
A cada nudo esencial se asigna una tensión
con relación al de referencia.
Se formula una ecuación por cada nudo
(refleja la ley de Kirchhoff de las corrientes en el nudo).
Las incógnitas son las tensiones en los nudos
(excepto la del de referencia).
Ecuaciones adicionales
Debe formularse una ecuación adicional por:
cada fuente independiente de tensión,
cada fuente dependiente.
Las incógnitas de las ecuaciones adicionales
están relacionadas con los elementos que las introducen.
Nota
Las tensiones en los nudos no tienen existencia real.
Las tensiones que tienen sentido físico y pueden medirse
son las diferencias de tensiones entre los nudos
y el de referencia.

25. Ejemplo de análisis por nudos
Datos:
Rc i 1 , i2 , R a , R b , R c
i1 Ra Rb i2 Hallar la potencia en Rc
ic
v1 v2 Identificación de nudos
y asignación de tensiones (vo = 0 V).
Rc
Asignación arbitraria del sentido
i1 ia R a R b ib i2 de las corrientes de rama.
vo
i 1 - ia - ic = 0 Ley de Kirchhoff
i 2 - ib - ic = 0 de corrientes en los nudos
ia = (v1 - vo) / Ra = v1/Ra Relaciones funcionales
ic = (v1 - v2) / Rc
ib = (vo - v2) / Rb = - v2/Rb
i1 - (v1/Ra) - (v1 - v2) / Rc = 0 Ecuaciones de nudo
i2 - (- v2/Rb) - (v1 - v2) / Rc = 0
i1 = v1 1 + 1 - v2 Ecuaciones de nudo
Ra Rc Rc (ordenadas)
- i 2 = - v1 + v 2 1 + 1
Rc Rb Rc
pc = ic(v1 - v2) Cálculo
suma algebraica fuentes corriente independientes en nudo =
= tensión de nudo X suma conductancias nudo -
- suma algebraica (conductancia compartida X
X tensión en otro nudo de conductancia compartida)
Los signos de las fuentes se toman positivos
si sus corrientes entran en el nudo considerado.

26. Ejemplo de análisis por nudos
+ vb - Datos:
id = gvb,
R1 R2
v g, g, R1, R2, R3
vg R3 id
Hallar potencia
en la fuente independiente
v1 + vb - v2 Identificación de nudos
y asignación de tensiones
R1 R2 (vo = 0 V)
vg ig R3 id
vo
- ig = v1 1 + 1 - v2 Ecuaciones de nudo
R1 R2 R2
id = - v1 + v2 1 + 1
R2 R2 R3
id = gvb = g(v1 - v2) Ecuación adicional
para la fuente dependiente
v 1 = - vg Ecuación adicional
para la fuente de tensión
p g = - vg i g Cálculo

27. CONTINUA 2003/1
ID R4
VG = 5 V, IS = - 1 mA, ID = gV3,
R1 R2
g = 1 mS, R1 = R2 = R3 = R4 = 1 kΩ x y
El circuito de la figura funciona en régimen perma- +
nente continuo. Hallad las potencias en las tres fuentes (indi- V3
cando si liberan o absorben energía) y la tensión entre x e y. VG - R3 IS
CONTINUA 2003/2 R1
R2
R3
VG = 1 V, IS = 250 mA, +
R1 = R2 = R3 = R4 = 2 Ω V4
El circuito de la figura funciona en régimen VG IS R4 -
permanente continuo. Hallad la tensión V4.

29. Análisis de redes
Transparencias de clase
Régimen transitorio
Transitorio-1: páginas 27-40
Ejercicios para resolver en clase: página 41
Transitorio-2: páginas 42-51
Transitorio-3: páginas 52-69
Ejercicios para resolver en clase: página 70
Transitorio-4: páginas 71-78

31. En el régimen permanente
la excitación mantiene sus características mucho tiempo;
la excitación fue aplicada hace mucho tiempo.
En régimen permanente, las salidas del circuito (corrientes,
tensiones) son de la misma forma que la excitación.
Una excitación continua provoca salidas continuas.
Una excitación sinusoidal provoca salidas sinusoidales.
El régimen transitorio es el que se produce inmediatamente después
de que se aplique o se suprima una excitación.
y elementos
elementos
excitación
asociados
Interruptor cerrado: cortocircuito.
otros
t = ta
Interruptor abierto: circuito abierto.
En régimen transitorio, las salidas del circuito
no son de la misma forma que la excitación.
Ello se debe a la presencia de elementos reactivos
(sus relaciones funcionales implican dependencias del tiempo).
En un circuito puramente resistivo no hay régimen transitorio.
Condiciones de estudio
del régimen transitorio
La excitación que se aplica al circuito o se suprime de él es continua.
Sólo se analizan respuestas de circuitos
con dos elementos reactivos como mucho.
Los cálculos se realizan mediante análisis integro-diferencial.

32. Elementos reactivos en régimen transitorio
Relaciones funcionales
+ v -
LoC
i
vL = L diL iC = C dvC
dt dt
Consecuencias
La corriente no puede variar bruscamente (en un tiempo nulo)
en una inductancia (provocaría tensión infinita).
La tensión no puede variar bruscamente (en un tiempo nulo)
en una capacidad (provocaría corriente infinita).
La tensión en una inductancia y la corriente en una capacidad
sí pueden variar bruscamente.
(Las resistencias admiten cambios bruscos de corriente y tensión).
En continua
la inductancia se comporta como un cortocircuito
(tensión nula ya que la corriente es constante);
la capacidad se comporta como un circuito abierto
(corriente nula ya que la tensión es constante).
Condiciones iniciales y finales
Iniciales (t = 0): las que hay en el circuito cuando cesa
el permanente (t = 0-) y empieza el transitorio (t = 0+).
Finales (t = ∞): las que hay en el circuito
cuando cesa el transitorio y se llega al permanente.

33. Determinación de condiciones
iniciales y finales
(aplicación de excitación, cálculo directo, septiembre 1999)
Datos:
iC + + IG (continua), R, L, C
vC t = 0 R iL vL
IG C - R L - Hallar condiciones en
t = 0-, t = 0+, y t = ∞
iC(0-) = 0 C es un circuito abierto en continua
vL(0-) = 0 L es un cortocircuito en continua
iL(0-) = 0 L no está conectada a la excitación
vC(0-) = RIG toda corriente fuente se va por R paralelo C;
las tensiones en R y C son iguales
vC(0+) = vC(0-) = RIG tensión en C no cambia bruscamente
iL(0+) = iL(0-) = 0 corriente en L no cambia bruscamente
vL(0+) = RIG en la malla que contiene a L
vC (0+) = RiL(0+) + vL(0+)
iC(0+) = 0 vC (0+) = vC (0-) →
toda corriente fuente se va por R paralelo C
manteniendo la tensión en C
iC(∞) = 0 C es un circuito abierto en continua
vL(∞) = 0 L es un cortocircuito en continua
iL(∞) = IG/2 toda corriente fuente se reparte entre R y R
(iC (∞) = 0) igual entre ambas
vC(∞) = RIG/2 tensión en C igual a tensión R paralelo C

34. Determinación de condiciones
iniciales y finales
(aplicación de excitación, cálculo directo, junio 2001)
Datos:
R t=0 iC + avL R iL + IG (continua), a, R, L, C
vC vL
IG C - L - Hallar: condiciones en
t = 0-, t = 0+, y t = ∞;
wL (0 ≤ t ≤ ∞)
iC(0-) = 0 C es un circuito abierto en continua
vL(0-) = 0 L es un cortocircuito en continua
iL(0-) = 0 iL(0-) + iC(0-) = 0
vC(0-) = 0 vC(0-) = avL(0-) + RiL(0-) + vL(0-)
vC(0+) = vC(0-) = 0 tensión en C no cambia bruscamente
iL(0+) = iL(0-) = 0 corriente en L no cambia bruscamente
iC(0+) = IG iC(0+) = IG - vC(0+)/R - iL(0+)
vL(0+) = 0 vC(0+) = avL(0+) + RiL(0+) + vL(0+)
iC(∞) = 0 C es un circuito abierto en continua
vL(∞) = 0 L es un cortocircuito en continua
iL(∞) = IG/2 toda corriente fuente se reparte entre R y R
(iC (∞) = 0) igual entre ambas
vC(∞) = RIG/2 vC(∞) = avL(∞) + RiL(∞) + vL(∞)
∞ ∞ ∞
d iL(t)
wL = pL(t)dt = vL(t)iL(t)dt = iL(t)L dt = L i2 (∞) - i2 (0)
dt 2 L L
0 0 0

35. Determinación de condiciones
iniciales y finales
(aplicación de excitación, cálculo directo, diciembre 2002)
t=0 Datos:
+ iL + IG (continua), a, R, L, C
R
iC vC vL
IG C - aiC L - Hallar: condiciones en
t = 0-, t = 0+, y t = ∞;
wL (0 ≤ t ≤ ∞)
iC(0-) = 0 C es un circuito abierto en continua
vL(0-) = 0 L es un cortocircuito en continua
iL(0-) = 0 L no está conectada a la excitación
vC(0-) = 0 vC(0-) = vL(0-)
vC(0+) = vC(0-) = 0 tensión en C no cambia bruscamente
iL(0+) = iL(0-) = 0 corriente en L no cambia bruscamente
iC(0+) = IG/(1 - a) IG = vC(0+)/R + (1 -a)iC(0+) + iL(0+)
vL(0+) = 0 vL(0+) = vC(0+)
iC(∞) = 0 C es un circuito abierto en continua
vL(∞) = 0 L es un cortocircuito en continua
iL(∞) = IG IG = vC(∞)/R + (1 -a)iC(∞) + iL(∞)
vC(∞) = 0 vC(∞) = vL(∞)
∞ ∞ ∞
d iL(t)
wL = pL(t)dt = vL(t)iL(t)dt = iL(t)L dt = L i2 (∞) - i2 (0)
dt 2 L L
0 0 0

36. Determinación de condiciones
iniciales y finales
(supresión de excitación, cálculo directo, julio 1999)
+ vL - Datos:
L iC + VG (continua), R, L, C
iL t=0 vC
VG R R C - Hallar: condiciones en
t = 0-, t = 0+, y t = ∞;
wC (0 ≤ t ≤ ∞)
iC(0-) = 0 C es un circuito abierto en continua
vL(0-) = 0 L es un cortocircuito en continua
iL(0-) = 2VG/R iC (0-) = 0 → VG = vL(0-) + (R//R)iL(0-)
vC(0-) = VG VG = vL(0-) + vC(0-)
vC(0+) = vC(0-) = VG tensión en C no cambia bruscamente
iL(0+) = iL(0-) = 2VG/R corriente en L no cambia bruscamente
iC(0+) = - VG/R iC(0+) + vC(0+)/R = 0
vL(0+) = - VG VG = vL(0+) + RiL(0+)
iC(∞) = 0 C es un circuito abierto en continua
vL(∞) = 0 L es un cortocircuito en continua
iL(∞) = VG/R vL(∞) = 0
vC(∞) = 0 iC(∞) + vC(∞)/R = 0
∞ ∞ ∞
d vC(t)
wC = pC(t)dt = vC(t)iC(t)dt = vC(t)C dt = C v2 (∞) - v2 (0)
dt 2 C C
0 0 0

37. Determinación de condiciones
iniciales y finales
(supresión de excitación, cálculo directo, junio 2000)
t=0 Datos:
iC + IG (continua), a, R, L, C
R + avC R iL
vC vL
IG C - R L - Hallar condiciones en
t = 0-, t = 0+, y t = ∞
iC(0-) = 0 C es un circuito abierto en continua
vL(0-) = 0 L es un cortocircuito en continua
iL(0-) = IG(1 - a)/(3 - a) IG = vC(0-)/R + iC(0-) + vC(0-)/R + iL(0-)
vC(0-) = RIG/(3 - a) vC(0-) = avC(0-) + RiL(0-) + vL(0-)
vC(0+) = vC(0-) tensión en C no cambia bruscamente
iL(0+) = iL(0-) corriente en L no cambia bruscamente
iC(0+) = IG(2 - a)/(3 - a) IG = iC(0+) + vC(0+)/R
vL(0+) = RIG(a - 2)/(3 - a) 0 = RiL(0+) + vL(0+) + avC(0+) + RiL(0+)
iC(∞) = 0 C es un circuito abierto en continua
vL(∞) = 0 L es un cortocircuito en continua
vC(∞) = RIG IG = iC(∞) + vC(∞)/R
iL(∞) = - aIG/2 0 = RiL(∞) + vL(∞) + avC(∞) + RiL(∞)

38. Determinación de condiciones
iniciales y finales
(aplicación de excitación, cálculo directo, otras variables, septiembre 2002)
+ v1 - Datos:
R + IG (continua), a, R, L, C
R t=0 Ri
L iC v C
VG L RiL C - Hallar: v1, vC, iL e iC
en t = 0-, t = 0+, y t = ∞
iL(0-) = 0 L no está conectada a la excitación
v1(0-) = 0 v1(0-) = RiL(0-)
iC(0-) = 0 C es un circuito abierto en continua
vC(0-) = 0 RiL(0-) = RiC(0-) + vC(0-)
iL(0+) = iL(0-) = 0 corriente en L no cambia bruscamente
v1(0+) = 0 v1(0+) = RiL(0+)
vC(0+) = vC(0-) = 0 tensión en C no cambia bruscamente
iC(0+) = 0 RiL(0+) = RiC(0+) + vC(0+)
iL(∞) = VG/(2R) VG = (R + R)iL(∞) + vL(∞), vL(∞) = 0
v1(∞) = VG/2 v1(∞) = RiL(∞)
iC(∞) = 0 C es un circuito abierto en continua
vC(∞) = VG/2 RiL(∞) = RiC(∞) + vC(∞)

39. Determinación de condiciones
iniciales y finales
(aplicación de excitación, cálculo directo, otras variables, junio 2002)
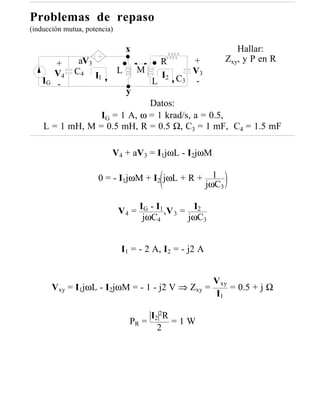
+ v1 - Datos:
+ IG (continua), g, R, L, C
R t=0 R iL R i2
vC
VG C - gvC L R Hallar: v1, vC, iL e i2
en t = 0-, t = 0+, y t = ∞;
wG (0 ≤ t ≤ ∞)
v1(0-) = 0 v1(0-) = RiC(0-), iC(0-) = 0
vC(0-) = 0 C no está conectada a la excitación
iL(0-) = 0 gvC(0-) = iL(0-) + i2(0-)
i2(0-) = 0 vL(0-) = 0 → iL(0-) = i2(0-)
iL(0+) = iL(0-) = 0 corriente en L no cambia bruscamente
vC(0+) = vC(0-) = 0 tensión en C no cambia bruscamente
v1(0+) = VG/2 v1(0+) = RiC(0+), VG = (R + R)iC(0+) + vC(0+)
i2(0+) = 0 gvC(0+) = iL(0+) + i2(0+)
v1(∞) = 0 v1(∞) = RiC(∞), iC(∞) = 0
vC(∞) = VG VG = (R + R)iC(∞) + vC(∞)
iL(∞) = gVG/2 gvC(∞) = iL(∞) + i2(∞)
i2(∞) = gVG/2 vL(∞) = 0 → iL(∞) = i2(∞)
∞ ∞ ∞
dv C(t)
wG = pG(t)dt = - VGiC(t)dt = - VGC dt = - CVG[vC(∞) - vC(0)]
dt
0 0 0

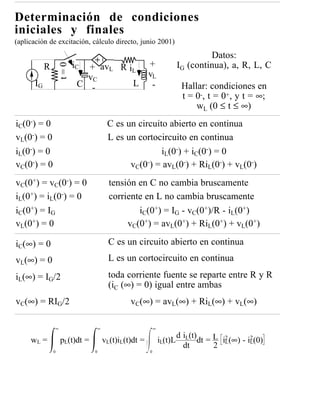
40. Determinación de condiciones
iniciales y finales
(cálculo directo, otras variables, junio 1998)
t=0 + +
t=0
RG i1 i2 i4 i5 i6 i7 v 7
i3 v3
VG L1 C2 R3 - gVG R4 C5 R6 L7 -
Datos: VG (continua), g, RG, L1, C2, R3, R4, C5, R6, L7
Hallar las variables que se indican en negrita
v3(0+) = vC2(0+) = vC2(0-) = vL1(0-) = 0
i1(0+) = i1(0-) = [VG - vL1(0-)]/RG = VG/RG
i3(0+) = v3(0+)/R3 = 0
i2(0+) = - i1(0+) - i3(0+) = - VG/RG
i7(0+) = i7(0-) = 0
v7(0+) = vC5(0+) = vC5(0-) = gVGR4
i6(0+) = vC5(0+)/R6 = gVGR4/R6
i5(0+) = gVG - i4(0+) - i6(0+) - i7(0+) =
= gVG - vC5(0+)/R4 - i6(0+) - i7(0+) = - gVGR4/R6
v7(∞) = 0
i7(∞) = gVG - i4(∞) - i5(∞) - i6(∞) =
= gVG - vC5(∞)/R4 - vC5(∞)/R6 = gVG
Una vez conocidas las variables fundamentales (iL, vC)
para un instante dado, es posible obtener
cualquier otra corriente o tensión para el mismo instante.

41. Determinación de condiciones
iniciales y finales
(cálculo de derivadas, septiembre 2000)
+ vL - Datos: IG (continua), R, L, C
R L RiL +
iL t=0 iC vC Hallar las derivadas
IG R R C - que se indican en negrita
iL(0+) = 2IG , vC(0+) = - RIG
3 3
- RiC(0+) = RiL(0+) + vC(0+) →
+) = - IG → dv C iC(0+)
→ iC(0 = = - IG
3 dt 0 + C 3C
vL(0+) + RiL(0+)
IG = + iL(0+) → vL(0+) = - RIG →
R 3
+)
→
diL = vL(0 = - RIG
dt 0 + L 3L
El cálculo de la corriente y la tensión en t = 0+
se hace como se indicó en problemas anteriores.
Las derivadas de cualquier variable
en régimen permanente continuo son nulas.

42. Determinación de condiciones
iniciales y finales
(influencia de distintas condiciones iniciales, diciembre 1994)
- vC +
Ra + +C IG
t=0
t=0
i1 v1 i2 v2 iC
gvC L1 - L2 - Rb
Datos: IG (continua), g, Ra, Rb, L1, L2, C
Hallar i1(∞) e i2(∞)
Solución aparente: i1(∞) = i2(∞) = 0.
Es falsa porque i1 e i2 tienen corrientes distintas en t = 0.
t=∞ 0 = iC(∞) = i1(∞) + i2(∞) (1)
t≥0 v1(t) = v2(t) → L1 di1 = L2 di2 →
dt dt
→ L1 di1 dt = L2 di1 dt → L1i1(t) = L2i2(t) + K
dt dt
t = 0+ L1i1(0+) = L2i2(0+) + K
i1(0+) = gRbIG, i2(0+) = 0 → K = L1gRbIG (2)
t=∞ L1i1(∞) = L2i2(∞) + K (3)
gRbIGL2 Combinando (1-3)
i1(∞) = = - i2(∞)
L 1 + L2
El cálculo de las corrientes en t = 0 se hace
como se indicó en problemas anteriores.

43. Determinación de condiciones
iniciales y finales
(influencia de distintas condiciones iniciales, diciembre 1996)
+ v1 - + v2 - Datos:
R + VG (continua), r, R, C1, C2, L
iL v L i1 C 1 i2 C 2 R
VG L - t=0 riL Hallar v1(∞) y v2(∞)
Solución aparente: v1(∞) = v2(∞) = 0
(C1 y C2 están entre dos cortocircuitos).
Es falsa porque v1 y v2 tienen tensiones distintas en t = 0.
t=∞ 0 = vL(∞) = v1(∞) + v2(∞) (1)
t≥0 i1(t) = i2(t) → C1 dv1 = C2 dv2 →
dt dt
→ C1 dv1 dt = C2 dv2 dt → C1v1(t) = C2v2(t) + K
dt dt
t = 0+ C1v1(0+) = C2v2(0+) + K
(2)
v1(0+) = 0, v2(0+) = - rVG → K = C2rVG
R R
t=∞ C1v1(∞) = C2v2(∞) + K (3)
v1(∞) = C2rVG = - v2(∞) Combinando (1-3)
(C1 + C2)R
El cálculo de las tensiones en t = 0 se hace
como se indicó en problemas anteriores.

44. Determinación de condiciones
iniciales y finales
(problema inverso, diciembre 1999
t=0 t=0
+ v1 -
1
+
i1 i2 2 v 2
+ + +
-
+ i4 4 v 4 i5 5 v 5 i6 6 v6
VG i3 3 v3 - - -
-
t i1 v1 i2 v2 i3 v3 i4 v4 i5 v5 i6 v6
0+ VG VG VG 0 VG VG 0 VG 0 0 0 0
2R 2 2R 2R 2 2
0- VG VG VG 0 VG VG -1A VG 1A VG 0 VG
2R 2 2R 2R 2 2 2 2
Identificar la naturaleza (R, L, C) de los elementos
1 i1(0-) ≠ 0 → no C; v1(0-) ≠ 0 → no L resistencia
2 i2(0-) ≠ 0 → no C; v2(0-) = 0 → no R inductancia
3 i3(0-) ≠ 0 → no C; v3(0-) ≠ 0 → no L resistencia
4 v4(0-) ≠ 0 → no L; i4(0-) = 0 → no R capacidad
5 cambio brusco de corriente y tensión resistencia
6 cambio brusco de tensión → no C inductancia
v6(0+) ≠ 0 e i6(0+) = 0 → no R

45. Ejercicios para resolver en clase
TRANSITORIO- + v3 -
CONDICIONES 2003/A i1 iC + +
+ kv R iL
t=0
C
vC v2 vL
El circuito de la figura funciona en IG R C - R - L -
régimen permanente continuo.
Hallad los valores de i1, iC, v2, y vL Son datos los valores
de todos los elementos del circuito.
para t = 0-, t = 0+, y t = ∞.
TRANSITORIO- + v1 - - vL +
CONDICIONES 2003/B + L gvC
R R iL
t=0 iC vC i2
El circuito de la figura - R
VG C R
funciona en régimen permanente
continuo. Son datos los valores
Hallad los valores de v1, vC, de todos los elementos del circuito.
i2, e iL para t = 0-, t = 0+, y t = ∞.
TRANSITORIO- + vL -
CONDICIONES 2003/C + L + Ri +
t=0
iL L
v1 v3 i vC
El circuito de la figura funciona C
- R IG R R - C -
en régimen permanente continuo.
Hallad los valores de v1, vL, v3, y Son datos los valores
vC para t = 0-, t = 0+, y t = ∞. de todos los elementos del circuito.

46. Respuesta en régimen transitorio
Se entiende por respuesta de un circuito en transitorio
la evolución temporal de sus corrientes y tensiones
entre dos estados permanentes.
La respuesta de un circuito en régimen transitorio
es igual para todas sus corrientes y tensiones
(excepto cuando son variables desacopladas).
Es decir, un circuito tiene un único tipo de respuesta
en régimen transitorio.
Tipos de respuestas
natural: la que se tiene cuando se suprime la excitación;
forzada: la que se tiene cuando se aplica la excitación.
Objeto del análisis en régimen transitorio
Hallar las expresiones temporales (ecuaciones que reflejan
la variación de corrientes y tensiones con el tiempo)
que caracterizan matemáticamente la respuesta.
Metodología de estudio
Análisis de respuestas en circuitos con un solo elemento reactivo.
Análisis de respuestas en circuitos con dos elementos reactivos.
Caso particular: circuitos con variables desacopladas.
Circuitos con cambios sucesivos.

47. Respuesta natural de un circuito RL
t=0
RG + iL
vL Datos: IG (continua), RG, L, R
IG - L R
Se pretende encontrar la respuesta del circuito para t ≥ 0.
En esas condiciones la parte de interés (la que contiene a L)
está caracterizada por la ecuación de malla
vL + RiL = 0 → L diL + RiL = 0
dt
Se trata de la ecuación diferencial que caracteriza
la evolución temporal de iL para t ≥ 0.
Por ser una ecuación diferencial de primer orden
con segundo miembro nulo, la solución es de la forma
iL(t) = Ae-t/τ, constante de tiempo: τ = L/R
Esta ecuación es la expresión temporal de iL para t ≥ 0
y caracteriza la respuesta del circuito.
Para que la expresión temporal esté completa
es necesario determinar el valor de la constante A.
Para ello se tienen en cuenta las condiciones iniciales.
Por el circuito Por la expresión temporal
iL(0+) = iL(0-) = IG iL(0) = A →A = IG
La respuesta del circuito es
iL(t) = IGe-t/τ

48. Significado de la constante de tiempo
iL(t)
respuesta para
IG ritmo de descenso
constante
respuesta Representación gráfica
0.37I G natural de la expresión temporal
0.007IG que caracteriza
la respuesta natural
de un circuito RL
τ 5τ t
La constante de tiempo es una medida
de lo rápido que desaparece el régimen transitorio.
Puede decirse que el nuevo régimen permanente
se establece una vez que ha transcurrido un tiempo
igual a cinco constantes de tiempo
(pasado ese tiempo apenas hay variaciones
en la respuesta del circuito).
Esto valida la suposición de que
el circuito está en régimen permanente
antes del cambio de posición del interruptor
(se supone que el circuito ha permanecido en el mismo estado
mucho tiempo antes de que se produzca dicho cambio).

49. Ejempo de respuesta natural en circuito RL
t=0 Datos:
VG = 24 V, L = 5 mH,
RG + R + iL RG = 12 Ω, R1 = 6 Ω,
2
v1 vL R3
R2 = 4 Ω, R3 = 10 Ω
VG - R1 - L
Hallar:
v1(t ≥ 0) y wR3(0 ≤ t ≤ ∞)
t≥0
vL + i + vL = 0 Ecuación de nudo
R1 + R2 L R3
+ 1 diL + iL = 0
1 Ecuación diferencial
L
R1 + R2 R3 dt
iL = Ae-t/τ, τ = L 1 + 1 = 1 ms Expresión temporal
R1 + R2 R3
Por circuito Por expresión temporal
iL(0+) = iL(0-) = iL(0) = A
→A =1A
V GR 1
= =1A
RG(R1 + R2) + R1R2
vL(t) = L diL = - 5e-t V (t en ms)
dt
R1 = - 3e-t V (t en ms)
v1(t) = divisor de tensión = vL
R 1 + R2
∞ ∞ ∞
vL(t)
wR3 = pR3(t)dt = vR3(t)iR3(t)dt = vL(t) dt = 1.25 mJ
R3
0 0 0

50. Respuesta natural de un circuito RC
t=0
RG + iC
vC Datos: IG (continua), RG, C, R
IG - C R
Se pretende encontrar la respuesta del circuito para t ≥ 0.
En esas condiciones la parte de interés (la que contiene a C)
está caracterizada por la ecuación de nudo
iC + vC = 0 → C dvC + vC = 0
R dt R
Se trata de la ecuación diferencial que caracteriza
la evolución temporal de vC para t ≥ 0.
Por ser una ecuación diferencial de primer orden
con segundo miembro nulo, la solución es de la forma
vC(t) = Ae-t/τ, constante de tiempo: τ = RC
Esta ecuación es la expresión temporal de vC para t ≥ 0
y caracteriza la respuesta del circuito.
Para que la expresión temporal esté completa
es necesario determinar el valor de la constante A.
Para ello se tienen en cuenta las condiciones iniciales.
Por el circuito Por la expresión
temporal
vC(0+) = vC(0-) = IG(RG//R) vC(0) = A →A = IG(RG//R)
La respuesta del circuito es
vC(t) = IG(RG//R)e-t/τ

51. Ejempo de respuesta natural en circuito RC
t=0 Datos:
VG (continua), RG, R, C1, C2
RG + iC2
vC Hallar vC(t ≥ 0)
VG iC1 C1 - R C2
t≥0
iC1 + vC + iC2 = 0 Ecuación de nudo
R
(C1 + C2) dvC + vC = 0 Ecuación diferencial
dt R
vC = Ae-t/τ, τ = R(C1 + C2) Expresión temporal
Por circuito Por expresión temporal
vC(0+) = vC(0-) = vC(0) = A → A = VG R
= VG R RG + R
RG + R
El circuito contiene dos elementos reactivos,
pero, como pueden ser agrupados en un solo,
el circuito es del tipo RC.

52. Respuesta forzada
en circuitos RL y RC (t ≥ 0)
t=0 t=0
RG R RG R +
iL vC
VG L VG C -
L descargada para t ≤ 0 C descargada para t ≤ 0
Ecuación diferencial que caracteriza la evolución temporal
L diL + (RG + R)iL = VG (RG + R)C dvC + vC = VG
dt dt
Por ser una ecuación diferencial de primer orden
con segundo miembro no nulo, la solución es de la forma
iL(t) = B + (A - B)e-t/τ vC(t) = B + (A - B)e-t/τ
τ= L τ = (RG + R)C
RG + R
Esta ecuación es la expresión temporal para t ≥ 0
y caracteriza la respuesta del circuito.
Es necesario determinar las constantes A y B.
Para ello se consideran condiciones iniciales y finales.
Circuito Circuito
iL(0+) = iL(0-) = 0 vC(0+) = vC(0-) = 0
→ A = 0 → A=0
Ex. temporal Ex. temporal
iL(0) = A vC(0) = A
Circuito Circuito
→ B =
iL(∞) = VG vC(∞) = VG
→ B = VG
RG + R = VG
Exp. temporal RG + R Exp. temporal
iL(∞) = B vC(∞) = B

53. Respuesta forzada de circuitos
con un solo elemento reactivo (t ≥ 0)
La ecuación diferencial que caracteriza la evolución temporal
es de la forma (x = iL; x = vC)
dx + x = K ⇔ τ dx + x = Kτ = xf
dt τ dt
La expresión temporal que representa la respuesta
es de la forma (x = iL; x = vC)
x(t) = xf + (xo - xf)e-t/τ
xo = x(t = 0), xf = x(t = ∞)
Respuesta general de circuitos
con un solo elemento reactivo (t ≥ 0)
La respuesta natural es un caso particular
de la respuesta forzada en el que
K = 0 = xf
Procedimiento de análisis en régimen transitorio
Formular ecuaciones de mallas o de nudos.
Establecer la ecuación diferencial relativa
a la variable fundamental (iL, vC).
Obtener la expresión temporal.
Determinar la(s) constante(s) de la expresión temporal
comparando lo que ocurre en el circuito
(condiciones inicial y final) con la expresión temporal.

54. Ejemplo de respuesta forzada
t=0 Datos: IG (continua), R1, R2, L1, L2
R1 + R2
i1 vL i2 Hallar i1(t ≥ 0)
IG L1 - L2
t≥0
R iL + Simplificación para t ≥ 0
vL
IG L - L = L1L2 , R = R1R2
L 1 + L2 R 1 + R2
IG = iL + vL Ecuación de nudo
R
L diL + iL = IG Ecuación diferencial
R dt
iL = iLf + (iLo - iLf)e-t/τ, τ = L/R Expresión temporal
circuito 0 = iL(0) = iLo exp. temporal
circuito IG = iL(∞) = iLf exp. temporal
iL = IG(1 - e-t/τ), τ = L/R Respuesta
circuito L1 di1 = L2 di2 = L diL circuito
original dt dt dt simplificado
L1 di1 dt = L diL dt → L1i1 = LiL + K
dt dt
t = 0 → i1 = 0 = iL → K = 0 →
→ i1(t) = LiL(t)/L1

55. Ejemplo de respuesta forzada
t=0 t=0 Datos:
VA = 2 V = VB, C = 1µF,
+ R2 R1 = R2 = R3 = 2 Ω
R1 iC vC
VA C - R3 iB VB
Hallar potencia
en VB para t ≥ 0
t≥0
iB = VB - vC = iC + vC Ecuación de nudo
R2 R3
R2C dvC + R2 + R3 vC = VB Ecuación diferencial
dt R3
vC = vCf + (vCo - vCf)e-t/τ Expresión temporal
τ = R2R3C/(R2 + R3) = 1 µs
circuito 2 V = VA = vC(0) = vCo exp. temporal
circuito 1 V = VBR3/(R2 + R3) = vC(∞) = vCf exp. temporal
vC = 1 + e-t V (t en µs) Respuesta
VB - vC(t)
pB(t) = - VBiB(t) = - VB = - 1 + e-t W (t en µs)
R2

56. Respuesta en régimen transitorio
de circuitos con dos elementos reactivos
distintos, o iguales pero no agrupables
t=0 + vL -
L + Caracterización de la respuesta
R
iL iC vC para t ≥ 0
VG C -
(1) VG = RiL + vL + vC Ecuaciones del circuito
(2) vL = L diL , iL = iC = C dvC Relaciones entre variables
dt dt
Sustituyendo (2) en (1),
d2vC + RC dvC + v = V (3) y (4) son
(3) LC 2 C G
las ecuaciones diferenciales
dt dt
que caracterizan
Despejando vC en (1) la evolución temporal
y sustituyendo en (2), de vC e iL para t ≥ 0
d2iL + RC diL + i = 0
(4) LC 2 L
dt dt
La respuesta de un circuito con dos elementos reactivos
se caracteriza por dos ecuaciones diferenciales
de segundo orden
(al igual que la de un circuito con un elemento reactivo
se caracteriza por una ecuación diferencial
de primer orden).

57. Respuesta de circuitos
con dos elementos reactivos
Las ecuaciones diferenciales que caracterizan
la evolución temporal son de la forma (x = iL; x = vC)
2
a d x + b dx + cx = K
dt2 dt
Los coeficientes a, b y c son iguales para todas
las variables fundamentales del circuito
(corrientes en inductancias, tensiones en capacidades)
excepto en el caso de variables desacopladas.
El valor de K puede ser distinto para cada variable.
La solución general (expresión temporal) de la ecuación
diferencial (ecuación diferencial de segundo orden
en una sola variable con coeficientes constantes)
es de la forma (x = iL; x = vC)
x(t) = xf + xh(t)
xf = x (t = ∞), (= 0 si K = 0)
xh(t): solución de la ecuación homogénea

58. Solución de la ecuación homogénea
Ecuación característica:
as2 + bs + c = 0 (aunque K ≠ 0)
Raíces de la ecuación característica:
- b ± b2 - 4ac
s1,2 = = - α ± α2 - ω0
2
2a
Coeficiente de amortiguamiento: α s-1 = b/(2a)
Frecuencia angular de resonancia: ω0 rad/s = s-1 = c/a
Caso 1 (respuesta supercrítica o sobreamortiguada):
(s1 y s2 reales y < 0) y (s1 ≠ s2) ⇔ ω0 < α2
2
xh(t) = Aes1t + Bes2t
Caso 2 (respuesta crítica o amortiguada):
(s1 y s2 reales y < 0) y (s1 = s2) ⇔ ω0 = α2
2
xh(t) = Ate-αt + Be-αt
Caso 3 (respuesta subcrítica o subamortiguada):
(s1 y s2 complejas) y (s1 = s2) ⇔ ω0 > α2
* 2
xh(t) = Ae-αtcos(ωdt) + Be-αtsen(ωdt), ωd = + ω2 - α2
0

59. Procedimiento de análisis
de circuitos con dos elementos reactivos
Formular dos ecuaciones de circuito
aplicando las leyes de Kirchhoff.
Formular relaciones entre variables.
Transformar las ecuaciones de circuito
en dos ecuaciones diferenciales
(una por cada variable fundamental).
Seleccionar una de las variables fundamentales.
Obtener la solución de la ecuación homogénea
correspondiente a la variable seleccionada.
Obtener las soluciones generales (expresiones temporales)
correspondientes a las dos variables.
Determinar las constantes de las soluciones generales
comparando lo que ocurre en el circuito
(condiciones iniciales y finales)
con las expresiones temporales (soluciones generales).

60. Ejemplo de análisis de circuitos
con dos elementos reactivos
(respuesta supercrítica)
t=0 t=0 Datos:
a VG = 1 V, k = - 1,
R R R = 1 Ω, L = 1 H, C = 1 F
VG
R
+ kiL + Hallar:
iC vC iL vL iL(t ≥ 0) y vC(t ≥ 0)
C - L -
t≥0
(1) RiC + vC = va = RiL + vL Ecuaciones del circuito
(2) kiL = iC + va/R + iL
(3) vL = LdiL/dt Relaciones entre variables
(4) iC = CdvC/dt
Combinando (1-4),
d2vC + (3 - k)RC + L dvC + (2 - k)v = 0 Ecuaciones
2LC 2 C
dt R dt diferenciales
d2iL + (3 - k)RC + L diL + (2 - k)i = 0
2LC 2 L
dt R dt
a = 2LC = 2 s2, b = (3 - k)RC + L/R = 5 s, c = 2 - k = 3 Ecuación.
característ.
α = b/(2a) = 5/4 s-1, ω0 = c/a = 3/2 s-1
α2 > ω0 → respuesta supercrítica
2

61. Ejemplo de análisis de circuitos
con dos elementos reactivos
(respuesta supercrítica)
(5) vC(t) = vCf + Aes1t + Bes2t Expresiones
temporales
s1,2 = - α ± α2 - ω0
2 → s1 = - 1 s-1, s2 = - 1.5 s-1
Sustituyendo (5) en (4), y el resultado en (2),
iL(t) = 1 ×
k-1
× vCf + A 2Cs1 + 1 es1t + B 2Cs2 + 1 es2t =
R R R
= - vCf + Ae 1 + Bes2t
st
2 2
circuito 1 V = VG = vC(0) = vCf + A + B exp. temporal
circuito 0 = vC(∞) = vCf exp. temporal
circuito 0 = iL(0) = - vCf + A + B exp. temporal
2 2
vCf = 0, A = 2 V, B = - 1 V
vC(t) = 2e-t - e-1.5t V (t en s) Respuesta
iL(t) = e-t - e-1.5t A (t en s)

62. Circuitos con dos elementos reactivos
(respuesta crítica, diciembre 1997)
t=0 t=0 Datos:
a IG = 2 A, R = 1 Ω,
R R R L = 1 H, C = 1 F
IG R IG
+ + Hallar:
iC vC
pG
iL vL iL(t ≥ 0), vC(t ≥ 0);
L C - L - pG(t ≥ 0)
t≥0
(1) RCdvC/dt + vC = va = RiL + LdiL/dt Ecuaciones del circuito
(2) IG = CdvC/dt + va/R + iL y relaciones
d2vC + (3RC + L ) dvC + 2v = RI Ecuaciones
2LC 2 C G
dt R dt diferenciales
d2iL + (3RC + L ) diL + 2i = I
2LC 2 L G
dt R dt
a = 2LC = 2 s2, b = 3RC + L/R = 4 s, c = 2 Ecuación
α = b/(2a) = 1 s-1, ω0 = c/a = 1 s-1 característica
α2 = ω0 → respuesta crítica
2
(3) vC(t) = vCf + Ate-αt + Be-αt Expresiones
Combinando (1-3), temporales
iL(t) = IG - vCf + A 2αC - 1 te-αt +
R R
+ -2CA + B 2αC - 1 e-αt =
R
= 2 - vCf + Ate-αt + (B - 2A)e-αt (t en s, vCf en V)

63. Circuitos con dos elementos reactivos
(respuesta crítica, diciembre 1997)
circuito 2 V = RIG = vC(0) = vCf + B exp. temporal
circuito 1 V = RIG/2 = vC(∞) = vCf exp. temporal
circuito 1 A = IG/2 = iL(0) = 2 - vCf + B - 2A exp. temporal
vCf = 1 V, A = 0.5 V/s, B = 1 V
vC(t) = 1 + 0.5te-t + e-t V (t en s) Respuesta
iL(t) = 1 + 0.5te-t A (t en s)
pG(t) = - va(t)IG = - RiL + L diL IG = - (2 + e-t) W (t en s)
dt

64. Circuitos con dos elementos reactivos
(respuesta subcrítica, septiembre 1999)
Datos:
t=0 IG = 2 A, R = 1 Ω,
+ + L = 1 H, C = 1 F
R
iC v C R iL vL
IG C - L - Hallar:
iL(t ≥ 0), vC(t ≥ 0);
wC(0 ≤ t ≤ ∞)
t≥0
(1) vC = RiL + LdiL/dt Ecuaciones del circuito
(2) IG = CdvC/dt + vC/R + iL y relaciones entre variables
d2vC + (RC + L ) dvC + 2v = RI
LC 2 C G
dt R dt Ecuaciones
d2iL + (RC + L ) diL + 2i = I diferenciales
LC 2 L G
dt R dt
a = LC = 1 s2, b = RC + L/R = 2 s, c = 2 Ecuación
característ.
α = b/(2a) = 1 s-1, ω0 = c/a = 2 s-1
α2 < ω0 → respuesta subcrítica, ωd = ω2 - α2 = 1 s-1
2
0
(3) iL(t) = iLf + Ae-αtcos(ωdt) + Be-αtsen(ωdt) Expresiones
Sustituyendo (3) en (2), temporales
-αt (R - αL)cos(ω t) - ω Lsen(ω t) +
C(t) = RiLf + Ae d d d
+ Be-αt (R - αL)sen(ωdt) + ωdLcos(ωdt) =
= iLf - Ae-tsen(t) + Be-tcos(t) (t en s, iLf en A)

65. Circuitos con dos elementos reactivos
(respuesta subcrítica, septiembre 1999)
circuito 0 = iL(0) = iLf + A exp. temporal
circuito 1 A = IG/2 = iL(∞) = iLf exp. temporal
circuito 2 V = RIG = vC(0) = iLf + B exp. temporal
iLf = 1 A, A = - 1 A, B = 1 A
iL(t) = 1 - e-tcos(t) + e-tsen(t) A (t en s) Respuesta
vC(t) = 1 + e-tsen(t) + e-tcos(t) V (t en s)
∞ ∞ ∞
d vC(t)
wC = pC(t)dt = vC(t)iC(t)dt = vC(t)C dt =
dt
0 0 0
= C v2 (∞) - vC(0) = - 1.5 J
C
2
2
(los valores de vC para t = 0 y t = ∞ se obtienen
directamente de la correspondiente expresión temporal)

66. Circuitos con dos elementos reactivos
(respuesta crítica)
R iL Datos:
L VG continua; RC = τ = L/R
C
+ vC - R Hallar:
VG
t=0
R iL(t ≥ 0), vC(t ≥ 0)
t≥0
(1) VG = RiL + LdiL/dt + R(iL + CdvC/dt) Ecuaciones del circuito
(2) VG = RCdvC/dt + vC + R(iL + CdvC/dt) y relaciones
d2vC + (3RC + L ) dvC + 2v = V Ecuaciones
2LC 2 C G
dt R dt diferenciales
d2iL + (3RC + L ) diL + 2i = VG
2LC 2 L
dt R dt R
RC = τ = L/R → (RC)(L/R) = τ2 = LC Ecuación
característica
a = 2LC = 2 τ2, b = 3RC + L/R = 4 τ, c = 2
α = b/(2a) = 1/τ, ω0 = c/a = 1/τ
α2 = ω0 → respuesta crítica
2
(3) vC(t) = vCf + Ate-αt + Be-αt Expresiones
Sustituyendo (3) en (1), temporales
iL(t) = IG - vCf + A 2αC - 1 te-αt +
R R
+ -2CA + B 2αC - 1 e-αt
R

67. Circuitos con dos elementos reactivos
(respuesta crítica, diciembre 1997)
circuito 0 V = vC(0) = vCf + B exp. temporal
circuito VG/2 = vC(∞) = vCf exp. temporal
circuito 0 A = i (0) = VG - vCf - 2CA + B 2αC - 1 exp. temporal
L
vCf = VG , A = 0 V/s, B = VG
2 2
vC(t) = VG (1 - e-t/τ) Respuesta
2
iL(t) = VG (1 - e-t/τ)
2R

68. Ejemplo de circuito con más de
dos elementos reactivos (agrupables)
t=0 Datos:
VG = 0.5 V, R = 0.5 Ω,
R L1 = 0.6 mH, L2 = 0.4 mH,
L1 C1
VG C1 = 2 mF, C2 = 2 mF
L2 C2 Hallar pC2(t ≥ 0)
t≥0
t=0
Simplificación para t ≥ 0
+ + IG = VG/R = 1 A
IG iL v L iC vC
R L - C - L = L1 + L2 = 1 mH
C = C1C2 = 1 mF
C 1 + C2
vC = LdiL/dt Ecuaciones del circuito
- IG = CdvC/dt + vC/R + iL y relaciones entre variables
d2vC + L dvC + v = 0 Ecuaciones
LC 2 C
dt R dt diferenciales
d2iL + L diL + i = - I
LC 2 L G
dt R dt
a = LC = 10-6 s2, b = L/R = 2×10-3 s, c = 1 Ecuación
característica
α = b/(2a) = 103 s-1, ω0 = c/a = 103 s-1
α2 = ω0 → respuesta crítica
2

69. Ejemplo de circuito con más de
dos elementos reactivos (agrupables)
iL(t) = iLf + Ate-αt + Be-αt Expresiones
vC(t) = L A(1 - αt)e-αt - αBe-αt temporales
circuito 0 = iL(0) = iLf + B exp. temporal
circuito - 1 A = - IG = iL(∞) = iLf exp. temporal
circuito 0 = vC(0) = L(A - αB) exp. temporal
iLf = - 1 A, A = 103 A/s, B = 1 A
iL(t) = - 1 + te-t + e-t A (t en ms) Respuesta
vC(t) = - te-t V (t en ms)
C dvC = iC = C2dvC2 → CdvC dt = C2dvC2dt → C2vC2(t) = CvC(t) + K
dt dt dt dt
CvC(t)
t = 0 → vC2 = 0 = vC → K = 0 → vC2(t) =
C2
CvC(t) dvC t(1 - t)e-2t
pC2(t) = vC2(t)iC(t) = C = W (t en ms)
C2 dt 2

70. Circuitos con dos elementos reactivos
(problema inverso-directo, junio 1999)
Datos:
+ vL - t=0 VG = 2 V, R = 1 Ω,
+ α = 1 s-1, ω0 = 1 rad/s
L i
L
R R iC vC
VG C - Hallar:
L y C; vC (t ≥ 0) e iL (t ≥ 0)
t≥0
iL = vC(1/R + 1/R) + CdvC/dt Ecuaciones del circuito
VG = LdiL/dt + vC y relaciones entre variables
d2vC + 2L dvC + v = V Ecuación diferencial
LC 2 C G
dt R dt
a = LC, b = 2L/R, c = 1 Ecuación
1 s-1 = α = b/(2a) = 1/(RC) → C = 1 F característica
1 s-1 = ω0 = c/a = 1/ LC → L = 1 H
α2 = ω0 → respuesta crítica
2
vC(t) = vCf + Ate-αt + Be-αt Expresiones
iL(t) = 2vCf + A(1 + t)e-αt + Be-αt A (vCf en V, t en s) temporales
circuito 0 = vC(0) = vCf + B exp. temporal
circuito 2 V = VG = vC(∞) = vCf exp. temporal
circuito 2 A = VG/R = iL(0) = 2vCf + A + B exp. temporal
vCf = 2 V, A = 0, B = - 2 V
vC(t) = 2 - 2e-t V (t en s) Respuesta
iL(t) = 4 - 2e-t A (t en s)

71. Circuitos con dos elementos reactivos
(problema inverso-directo, septiembre 1999)
t=0 Datos:
IG = 2 A, R = 1 Ω,
+ R + α = 1 s-1, ω0 = 2 rad/s
iC v C R iL vL
IG C - L -
Hallar: L y C;
vC (t ≥ 0) e iL (t ≥ 0)
t≥0
vC = RiL + LdiL/dt Ecuaciones del circuito
IG = CdvC/dt + vC/R + iL y relaciones entre variables
d2vC + (RC + L ) dvC + 2v = RI Ecuación diferencial
LC 2 C G
dt R dt
a = LC, b = RC + L/R, c = 2 Ecuación
característica
1 s-1 = α = b/(2a) = 1/(2RC) + R/(2L) L=1H
→
2 s-1 = ω0 = c/a = 2/(LC) C=1F
α2 < ω0 → respuesta subcrítica, ωd = ω2 - α2 = 1 s-1
2
0
vC(t) = vCf + Ae-αtcos(ωdt) + Be-αtsen(ωdt) Expresiones
L(t) = (2 - vCf) + Ae-tsen(t) - Be-tcos(t) V (vCf en V, t en s) temporales
circuito 2 V = RIG = vC(0) = vCf + A exp. temporal
circuito 1 V = RIG/2 = vC(∞) = vCf exp. temporal
circuito 0 = iL(0) = 2 - vCf - B exp. temporal
vCf = 1 V, A = 1 V, B = 1 V
vC(t) = 1 + e-tsen(t) + e-tcos(t) V (t en s) Respuesta
iL(t) = 1 - e-tcos(t) + e-tsen(t) A (t en s)

72. Circuitos con dos elementos reactivos
(problema inverso, diciembre 1999)
Datos (t ≥ 0, t en s):
R vC = (1 - t)e-t V
t=0 t = 0 iL +
+ iL = 0.5te-t A
iC vC R L vL
VG C - - Hallar: α y ω0;
L
VG (continua), R, L y C
t≥0
vC = LdiL/dt Ecuaciones del circuito
0 = CdvC/dt + vC/R + iL y relaciones entre variables
d2iL + L diL + i = 0 Ecuación diferencial
LC 2 L
dt R dt
a = LC, b = L/R, c = 1 Ecuación característica
La respuesta es crítica, ya que en las expresiones temporales
figuran términos de la forma te-t.
En la respuesta crítica α es el coeficiente del exponente
en el término exponencial; luego α = 1 s-1.
En la respuesta crítica α2 = ω0; luego ω0 = 1 s-1.
2
(circuito) VG = vC(0) = 1 V (exp. temporal) → VG = 1 V
e-t - te-t = vC = diL = 0.5e-t - 0.5te-t → igualando → L = 2 H
L L L dt términos
1 s-1 = ω0 = c/a = 1/ LC → C = 0.5 F
1 s-1 = α = b/(2a) = 1/(2RC) → R = 1 Ω

73. Circuitos con dos elementos reactivos
(problema inverso, septiembre 1996)
t=0 + vL - Datos (t ≥ 0, t en s):
vC = 10 - 5e-9000t - 5e-9000t V
L +
R iL = 9e-9000t + e-1000t mA
iL iC vC
VG C - Hallar: α y ω0;
VG (continua), R, L y C
t≥0
iL = CdvC/dt Ecuaciones del circuito
VG = LdiL/dt + vC + RiL y relaciones entre variables
d2vC + RC dvC + v = V Ecuación diferencial
LC 2 C G
dt dt
a = LC, b = RC, c = 1 Ecuación característica
La respuesta es supercrítica, ya que en las expresiones
temporales figuran dos términos exponenciales distintos.
En la respuesta supercrítica los coeficientes
de los exponentes son las raíces de la ecuación característica.
s1 = - 9000 s-1, s2 = - 1000 s-1
α = - s1 + s2 = 5000 s-1
s1,2 = - α ± α2 - ω0 →
2 2
ω0 = + α 2 - s1 - s2 = 3000 s-1
2
2
(circuito) VG = vC(∞) = 10 V (exp. temporal) → VG = 10 V
0.009e-9000t + 0.001e-1000t = iL =
C C C
igualando
= dvC = 45000e-9000t + 5000te-1000t → → C = 200 nF
dt términos
3000 s-1 = ω0 = c/a = 1/ LC → L = 5/9 H
5000 s-1 = α = b/(2a) = R/(2L) → R = 50/9 kΩ

74. Ejercicios para resolver en clase
TRANSITORIO-RESPUESTA 2003/A R R R
iL +
El circuito de la figura funciona en régimen permanente L vC
C VG
continuo. Llegó al estado indicado en ella en t = 0; en ese -
momento, la corriente en la inductancia y la tensión en la VG = 2 V,
capacidad valían I0 y V0, respectivamente. Con posterioridad, V0 = 1 V, I0 = 2 A,
el circuito no experimenta más cambios. Hallad la expresión R = 1 Ω,
temporal de la potencia en la fuente para t ≥ 0. L = 1 µH, C = 1 µF
TRANSITORIO-RESPUESTA 2003/B L +
iL
R R vC
El circuito de la figura funciona en régimen IG C -
permanente continuo. Llegó al estado indicado en ella en
t = 0; en ese momento, la corriente en la inductancia y la IG = 2 mA,
tensión en la capacidad valían I0 y V0, respectivamente. V0 = 2 V, I0 = 2 mA,
Con posterioridad, el circuito no experimenta más R = 1 kΩ,
cambios. Hallad la expresión temporal de la potencia en L = 1 mH, C = 1 nF
la fuente para t ≥ 0.
TRANSITORIO-RESPUESTA 2003/C +
iL R
vC
El circuito de la figura funciona en régimen IG C -
L R
permanente continuo. Llegó al estado indicado en ella en
t = 0; en ese momento, la corriente en la inductancia y la IG = 1 A,
tensión en la capacidad valían I0 y V0, respectivamente. V0 = 1.62 V, I0 = 0 A,
R = 1 Ω,
Con posterioridad, el circuito no experimenta más
L = 2.62 µH, C = 0.38 µF
cambios. Hallad la expresión temporal de la potencia en
la fuente para t ≥ 0.

75. Circuitos con dos elementos reactivos
parcial o totalmente desacoplados
(julio 1999)
+ vL - Datos:
L iC + VG (continua), R, L, C
iL t=0 vC
VG R R C - Hallar iL(t ≥ 0) y vC(t ≥ 0)
t≥0
VG = LdiL/dt + RiL Ecuaciones
0 = CdvC/dt + vC/R del circuito
iL(t) = iLf + (iLo - iLf)e-t/τL Expresiones
temporales
Lo = iL(0) = 2VG /R, iLf = iL(∞) = VG/R, τL = L/R
vC(t) = vCf + (vCo - vCf)e-t/τC
vCo = vC(0) = VG, vCf = vC(∞) = 0, τC = RC
Para t > 0 los dos elementos no se influyen entre sí
(las variables son independientes -están desacopladas-).
A cada variable fundamental le corresponde
una ecuación diferencial de primer orden.
Puede haber influencia de un elemento en otro
sin que el segundo influya en el primero
(circuito parcialmente acoplado -desacoplado).
A la variable independiente le corresponde
una ecuación diferencial de primer orden.
A la variable acoplada le corresponde
una ecuación diferencial de segundo orden.
En circuitos parcial o totalmente desacoplados
no hay respuesta única.

76. Circuito desacoplado
a Datos:
RG L + iSC VG = 2 V, RG = 2 Ω,
iL vC R = 1 Ω, L = 1 H, C = 0.5 F
C -
t=0
VG
R Hallar iSC(t ≥ 0)
R
t≥0
vC(t) + RCdvC/dt = va = 0 Ecuaciones
VG = RGiL + LdiL/dt + va = RGiL + LdiL/dt del circuito
vC(t) = vCoe-t/τC, τC = RC = 0.5 s Expresiones
vCo = vC(0) = VGR/(R + RG) = 2/3 V temporales
iL(t) = iLf + (iLo - iLf)e-t/τL, τL = L/RG = 0.5 s
iLo = iL(0) = VG/(R + RG) = 2/3 A
iLf = VG/RG = 1 A
iSC(t) = iL - C dvC = 1 + e A (t en s)
-2t
dt 3

77. Circuito parcialmente acoplado
(junio 2000)
t=0 Datos:
I = 2 A, k = 1, R = 1 Ω,
iC + R + G
kvC iL vL L = 1 H, C = 1 F
R vC R
IG C - L -
Hallar i (t ≥ 0) y v (t ≥ 0)
L C
t≥0
(1) IG = vC/R + CdvC/dt Ecuaciones
del circuito
(2) 0 = (R + R)iL + LdiL/dt + kvC
(3) vC(t) = vCf + (vCo - vCf)e-t/τC, τC = RC = 1 s Cálculo
de vC(t)
Co = vC(0) = RIG/(3 - k) = 1 V, vCf = vC(∞) = RIG = 2 V
Despejando vC de (2) y sustituyendo en (1),
d2iL + 2RC + L diL + 2i = - kI Ecuación
LC 2 L G
dt R dt diferencial de iL
a = LC = 1 s2, b = 2RC + L/R = 3 s, c = 2 Ecuación
α = b/(2a) = 1.5 s-1, ω0 = c/a = 2 s-1 característica
α2 > ω0 → respuesta supercrítica
2
(4) iL(t) = iLf + Aes1t + Bes2t Expresión
s1,2 = - α ± α2 - ω0 → s1 = - 1 s-1, s2 = - 2 s-1
2 temporal de
iL(t)
(5) (4) en (2) → vC(t) = - 2iLf - Ae-t V (iLf en A, t en s)
(3) = (5) → iLf = - vCf/2 = - 1 A, A = - (vCo - vCf) = 1 A
(circuito) 0 = iL(0) = iLf + A + B (exp. temporal) → B = 0
vC(t) = 2 - e-t V, iL(t) = - 1 - e-t A (t en s)

78. Circuito parcialmente acoplado
(septiembre 2000)
t=0 Datos:
VG = 2 V, R = 1 Ω,
R i L + L = 4 H, C = 1 F
L
R RiL vC
VG R C -
Hallar iL(t ≥ 0) y vC(t ≥ 0)
t≥0
(1) VG = (R + R)iL + LdiL/dt Ecuaciones
del circuito
(2) 0 = RCdvC/dt + vC + RiL
(3) iL(t) = iLf + (iLo - iLf)e-t/τL, τL = L/(2R) = 2 s Cálculo
de iL(t)
iLo = iL(0) = 2VG/(3R) = 4/3 A, iLf = iL(∞) = VG/(2R) = 1 A
Despejando iL de (2) y sustituyendo en (1),
d2vC + 2RC + L dvC + 2v = - V Ecuación
LC 2 C G
dt R dt diferencial de vC
a = LC = 4 s2, b = 2RC + L/R = 6 s, c = 2 Ecuación
α = b/(2a) = 3/4 s-1, ω0 = c/a = 1/ 2 s-1 característica
α2 > ω0 → respuesta supercrítica
2
(4) vC(t) = vCf + Aes1t + Bes2t Expresión
s1,2 = - α ± α2 - ω2 → s1 = - 1 s-1, s2 = - 0.5 s-1 temporal de
0
vC(t)
(5) (4) en (2) → iL(t) = - vCf - 0.5Be-0.5t A (vCf en V, t en s)
(3) = (5) → vCf = - iLf = - 1 V, B = - 2(iLo - iLf) = - 2/3 V
(circuito) - 2/3 = vC(0) = vCf + A + B (exp. temporal) → A = 1 V
-0.5t
iL(t) = 1 + e A, vC(t) = - 1 + e-t - 2e
-0.5t
V (t en s)
3 3

79. Circuitos con cambios sucesivos
La evolución de un circuito en régimen transitorio
está determinada por
las constantes de tiempo de las expresiones temporales
correspondientes a variables independientes;
los términos exponenciales de las expresiones temporales
correspondientes a variables acopladas.
En un circuito pueden producirse cambios en distintos instantes.
La evolución del circuito se calcula como se indicó anteriormente,
con algunas peculiaridades:
El circuito no sabe que va a producirse un cambio;
en consecuencia, tras cada cambio evoluciona
como si fuera a alcanzar el régimen permanente.
Las condiciones iniciales correspondientes a un intervalo
se obtienen de las expresiones temporales
que caracterizan el intervalo anterior.
La variable t ha de ser sustituida por t - t0,
donde t0 es el instante final del intervalo anterior.

80. Circuitos con cambios sucesivos
(junio 1997)
1 2 3
R iC R R
+
C vC R iL
- kvC
VA L VB
1 2 3
t<0 Abierto Abierto Abierto
0 ≤ t < t1 Cerrado Abierto Abierto
t1 ≤ t < t2 Cerrado Cerrado Abierto
t ≥ t2 Cerrado Abierto Cerrado
Datos:
VA = 200 mV, VB = 2 V, t1 = 1 s, t2 = 2 s,
R = 0.5 kΩ, L = 0.5 H, C = 2 µF, k = 2
Hallar dvC , dvC , iL(1.1 s), e iL(t ≥ t2)
dt 0+ dt 100 ms

81. Circuitos con cambios sucesivos
(junio 1997)
dvC iC(0+) 1 VA - vC(0+) -
1 VA - vC(0 ) = VA = 200 V/s
= = =
dt 0+ C C R C R RC
0 ≤ t < t1 → VA = RCdvC/dt + vC → τC = RC = 1 ms << 100 ms
Esto indica que la parte del circuito formada por VA, R y C
ha alcanzado el régimen permanente para t = 100 ms
(no hay cambios en el circuito entre 0 y 100 ms), con lo que
iC(100 ms) = cte = 0 → dvC =0
dt 100 ms
Por el mismo motivo, vC (para todo t > 5τC = 5 ms) = cte = VA.
Así, en la parte del circuito que contiene a L,
t1 ≤ t < t2 → kvC = kVA = LdiL/dt + RiL → τL1 = L/R = 1 ms << 100 ms
Esto indica que la parte del circuito que contiene a L
ha alcanzado el régimen permanente para t = 1.1 s
(no hay cambios en el circuito entre 1 y 2 s), con lo que
iL(1.1 s) = cte = kVA/R = 0.8 mA = iL(2 s)
t ≥ t2 → VB = 2RiL + LdiL/dt →
→ iL(t ≥ t2) = iLf + (iLo - iLf)e- (t - t2)/τL2, τL2 = L/(2R) = 0.5 ms
+ -
iLo = iL(t2 ) = iL(t2) = 0.8 mA, iLf = iL(∞) = VB/(2R) = 2 mA

82. Circuitos con cambios sucesivos
(diciembre 1998)
t=0 t = t1 Datos:
1 2 0 ≤ t ≤ t1 →
6
L R → α = 10 s-1, ω 0 = 8 rad/s
R t = t1
+
vC 3 VB en malla 123451
C
VA - R
Hallar:
5 4 vC(t1 = 100 s),
tipo de respuesta
en malla 126451
para t > t1
0 ≤ t ≤ t1, malla 123451
α2 > ω0 → respuesta supercrítica
2
α = 10 s-1 → s = - α ± α2 - ω2 → s1 = - 16 s-1
ω0 = 8 s-1 1,2 0
s2 = - 4 s-1
vC(t) = vCf + Aes1t + Bes2t
vCf = vC(∞) = 0
ya que el circuito no sabe que va a haber cambio en t = t1
e s 1 t 1 ≈ 0 ≈ es 2 t 1
→ vC(t1) ≈ 0
vCf = vC(∞) = 0
Para t ≥ t1, la malla 126451 es de la misma forma
que la malla 123451; los elementos R, L y C siguen en serie,
con los mismos valores,
y la presencia de la fuente no afecta al tipo de respuesta.
Luego ésta es también supercrítica.

83. Análisis de redes
Transparencias de clase
Régimen
sinusoidal permanente
Sinusoidal-1: páginas 81-89
Sinusoidal-2: páginas 90-101
Sinusoidal-3: páginas 102-107
Sinosoidal-4: páginas 108-115
Sinusoidal-5: páginas 116-123
Sinusoidal-6: páginas 124-139
Ejercicios para resolver en clase: 140
Sinusoidal-7: páginas 141-167
Ejercicios para resolver en clase: 164

85. Señales sinusoidales
Una señal sinusoidal es de la forma indicada en la figura.
Se hace referencia a régimen sinusoidal permanente
cuando la señal no varía su forma en mucho tiempo (>> T).
a(t) = Amcos(ωt + ϕ)
Am
T
- ϕ/ω t
T
- Am
Caracterización matemática de una señal sinusoidal
Símbolo Significado Dimensiones
a señal (corriente, tensión) A, V
Am módulo, amplitud A, V
f = 1/T > 0 frecuencia Hz, s-1
ω = 2πf > 0 frecuencia angular rad/s, s-1
T = 1/f > 0 período s
ϕ fase rad, ˚
Interés práctico de las señales sinusoidales
Son soportadas por muchos circuitos electrónicos.
Señales no sinusoidales pueden ser tratadas
como combinaciones lineales de señales sinusoidales.

86. Respuesta de un circuito
a una señal sinusoidal permanente
t=0 Datos:
R, L,
R vg(t) = Vmcos(ωt + ϕv)
vg L
i
Hallar i(t > 0)
L di + Ri = Vmcos(ωt + ϕv) Ecuación diferencial
dt que caracteriza la evolución
del circuito para t > 0
i(t) = - Imcos(ϕi)e-t/τ + Imcos(ωt + ϕi)
respuesta = transitorio + permanente
(desaparece para t > 5τ)
Consideraremos únicamente la respuesta permanente.
Características de la respuesta
La respuesta es una señal sinusoidal
de la misma frecuencia que la excitación.
El módulo y la fase de la respuesta
dependen del módulo y la frecuencia de la excitación,
y de los elementos del circuito.
, ϕ i = ϕ v - arctg ωL
Vm
Im = 2 + ω2L2
R R
Objeto del análisis en régimen sinusoidal permanente
Calcular el módulo y la fase de la respuesta.

87. Tratamiento matemático
Las corrientes y las tensiones se tratan mediante fasores
(el concepto de fasor deriva de las identidades de Euler).
Los elementos pasivos se tratan como impedancias.
Se aplican técnicas de análisis por mallas y nudos.
Identidades de Euler
Un número complejo, z, verifica las identidades (a y b reales)
z = a + jb ≡ kejθ ≡ k∠θ ≡ kcos(θ) + jksen(θ)
unidad de los números imaginarios: j ≡ - 1
módulo: k = a2 + b2 , fase: θ = arctg b
a
Re z = a ≡ kcos(θ) ≡ kRe ejθ , Im z = b ≡ ksen(θ) ≡ kIm ejθ
complejo conjugado de z: z* ≡ a - jb ≡ ke-jθ

88. Fasores
A cualquier señal (corriente, tensión) sinusoidal
se le puede asociar un fasor.
señal: a(t) = Amcos(ωt + ϕ) (1)
fasor: A ≡ A ≡ Amejϕ
Un fasor no tiene entidad real.
En un circuito sólo tienen significado físico
señales caracterizadas por expresiones temporales como (1).
Conocido un fasor, la señal a la que aquél está asociado
se obtiene como
a(t) = AmRe ej(ωt + ϕ) = Re Amej(ωt + ϕ) =
= Re Amejϕejωt = Re Aejωt
Dado que la respuesta en régimen sinusoidal permanente
es una señal con la misma frecuencia que la excitación,
su cálculo se reduce a la determinación
del fasor asociado a la respuesta.
En otras palabras, el fasor combina en un solo parámetro
la información de módulo y fase,
que son las incógnitas a calcular.
Obsérvese que a la derivada de la señal, da/dt,
le corresponde el fasor jωA.

89. Impedancias
Caracterización de elementos pasivos en régimen sinusoidal
Elemento Corriente y Fasores
(R, L, C) tensión reales asociados
+ v(t) = Vmcos(ωt + ϕv) V = Vmejϕv
i v
- i(t) = Imcos(ωt + ϕi) I = Imejϕi
Relaciones funcionales en régimen sinusoidal
Elemento Relación Equivalencia Relación
funcional en términos entre fases
de fasores
R v = Ri V = RI ϕv = ϕi
L v = Ldi/dt V = jωLI ϕv = ϕi + 90 ˚
C i = Cdv/dt I = jωCV ϕv = ϕi - 90 ˚
Cualquier elemento pasivo puede representarse
por una impedancia asociada
V = ZI = I/Y I = YV = V/Z Ley de Ohm generalizada
Impedancia: Z Ω = R + jX (R: resistencia; X: reactancia)
Admitancia: Y S = G + jB (G: conductancia; B: susceptancia)
Z=R Z = jωL Z = 1/(jωC)
R → Y = 1/R , L → ,C →
Y = 1/(jωL) Y = jωC

90. Técnicas de análisis
El circuito se caracteriza en términos
de fasores e impedancias.
Se aplican las leyes de Kirchhoff
∑ Vk = 0, k = 1, 2,... n (n: elementos en una malla)
k
∑ Ik = 0, k = 1, 2,... n (n: elementos en un nudo)
k
y las simplificaciones del análisis de redes
(elementos en serie y paralelo, agrupación de elementos,
divisores de tensión y de corriente, equivalentes,...).
El análisis se hace aplicando
la técnica de corrientes en las mallas;
la técnica de tensiones en los nudos.
Obtenido el fasor correspondiente a la respuesta,
se determina la expresión temporal.
Si el circuito es lineal,
es posible aplicar el principio de superposición.

91. Agrupación de elementos
Elementos pasivos
Se agrupan teniendo en cuenta sus impedancias
Agrupación en serie
Z eq = Z1 + ... + Zn, 1 = 1 + ... + 1
Yeq Y1 Yn
Agrupación en paralelo
Y eq = Y1 + ... + Yn, 1 = 1 + ... + 1
Zeq Z1 Zn
En régimen sinusoidal permanente es posible agrupar
elementos pasivos de distinta naturaleza
(resistencias y/o inductancias y/o capacidades)
una vez que cada uno de ellos ha sido caracterizado
por su impedancia correspondiente;
de ahí que la impedancia sea compleja en general.
Elementos activos
Pueden agruparse siempre que
sean independientes;
sean de la misma naturaleza;
tengan la misma frecuencia.
Agrupación de fuentes de corriente en paralelo
Ieq = I1 + ... + In
Agrupación de fuentes de tensión en serie
V eq = V 1 + ... + V n

92. Ejemplo de análisis por mallas
Datos:
ig R = 1 Ω, L = 1 µH, C = 1 µF,
RL RC Rig RL = 3 Ω, RC = 1 Ω, Ro = 1 Ω,
Ro vg(t) = Vmcos(ωt + ϕv), Vm = 2 V,
vg L C
ω = 1 Mrad/s, ϕv = 45 °
Hallar po(t)
Simplificación del circuito
y caracterización en términos
RIg de fasores e impedancias
Ig Vg = Vmejϕv = 1 + j V
I1 I2
Vg Z Ro ZL = RL + jωL = 3 + j Ω
Z C = RC + 1 = 1 - j Ω
jωC
1 = 1 + 1 → Z = ZLZC = 1 - j0.5 Ω
Z ZL ZC Z L + ZC
V g = I1Z - I2Z Ecuaciones de mallas
0 = - I1Z + I2(Z + Ro) + RIg
Ig = I1 Ecuación adicional
para la fuente dependiente
Io = 0.3 - j0.1 A → io(t) = Re Ioejωt = 0.1cos(ωt + ϕo) A
Vo = RoIo = 0.3 - j0.1 V → vo(t) = Re Voejωt = 0.1cos(ωt + ϕo) V
po(t) = vo(t)io(t) = 0.1cos2(ωt + ϕo) W, ϕo = arctg - 0.1
0.3

93. Ejemplo de análisis por nudos
Datos:
ig R = 1 Ω, L = 1 µH, C = 1 µF,
RL RC Rig RL = 3 Ω, RC = 1 Ω, Ro = 1 Ω,
Ro vg(t) = Vmcos(ωt + ϕv), Vm = 2 V,
vg L C
ω = 1 Mrad/s, ϕv = 45 °
Hallar po(t)
Simplificación del circuito
y caracterización en términos
Vz RIg de fasores e impedancias
Ig Z Vg = Vmejϕv = 1 + j V
Io Ro
Vg ZL = RL + jωL = 3 + j Ω
Z C = RC + 1 = 1 - j Ω
jωC
1 = 1 + 1 → Z = ZLZC = 1 - j0.5 Ω
Z ZL ZC Z L + ZC
Ig = Vz/Z + Io Ecuación de nudo
V z = V g = RIg + RoIo Ecuaciones adicionales
para las fuentes
Io = 0.3 - j0.1 A → io(t) = Re Ioejωt = 0.1cos(ωt + ϕo) A
Vo = RoIo = 0.3 - j0.1 V → vo(t) = Re Voejωt = 0.1cos(ωt + ϕo) V
po(t) = vo(t)io(t) = 0.1cos2(ωt + ϕo) W, ϕo = arctg - 0.1
0.3

94. Inducción mutua
En general, la tensión en una inductancia depende de
la corriente que circula por ella (autoinducción);
la corriente que circula por inductancias próximas
con las que está acoplada (inducción mutua).
Está regida por
la ley de Ampère
(una corriente tiene un campo magnético asociado);
la ley de Faraday-Henry
(el voltaje inducido es proporcional
a la variación del campo magnético).
Dos inductancias (L1, L2) acopladas se caracterizan por
el coeficiente de acoplamiento, k (0 ≤ k ≤ 1);
el coeficiente de inducción mutua, M
M H = + k L1L2
En continua no hay fenómenos de inducción mutua
ya que no hay variación de corriente, ni, por tanto,
del campo magnético creado por aquélla.

95. Inducción mutua
La tensión total en una inductancia es la suma algebraica
de las debidas a la autoinducción y a la inducción mutua.
Caracterización de la autoinducción
+ -
va v'a va = L di = - L di' = - v'a
i' i dt dt
L - +
Caracterización de la inducción mutua
Si la corriente entra en (sale de) uno de los elementos
por el terminal marcado con el punto,
la tensión inducida en el otro es positiva (negativa)
en el terminal marcado con el punto.
i'1 i1 i2 i'2 v1m = M di2 = - M di'2 = - v'1m
- + + - dt dt
v'1m v1m M v2m v'2m
+ - L1 L2 - + v2m = M di1 = - M di'1 = - v'2m
dt dt
Tensión total en L1 v1 = v1a + v1m = v1a - v'1m =
= - v'1a + v1m = - v'1a - v'1m = - v'1
Tensión total en L2 v2 = v2a + v2m = v2a - v'2m =
= - v'2a + v2m = - v'2a - v'2m = - v'2
En régimen sinusoidal permanente
Tensión total en L1 V1 = V1a + V1m = - V'1a - V'1m = - V'1
V1m = jωMI2 = - jωMI'2 = - V'1m
Tensión total en L2 V2 = V2a + V2m = - V'2a - V'2m = - V'2
V2m = jωMI1 = - jωMI'1 = - V'2m

96. Circuito con inducción mutua
(septiembre 1992)
Hallar
L4 R3
M12 L2 M34 L5 I1, I2, e I3
L1 M45
I1 Vg L3 C2 R2 I3
R1
C1 I2 Is C3
Datos:
V g = 35 + j77 V, Is = 1 A,
R1 = 100 Ω, R2 = 10 Ω, R3 = 15 Ω,
ωL1 = 4 Ω, ωL2 = 9 Ω, ωL3 = 1 Ω, ωL4 = 25 Ω, ωL5 = 25 Ω,
ωM12 = 4 Ω, ωM34 = 3 Ω, ωM45 = 20 Ω,
(ωC1)-1 = 5 Ω, (ωC2)-1 = 7 Ω, (ωC3)-1 = 10 Ω
V s: tensión en la fuente de corriente
(positiva en el extremo por el que sale la corriente)
0 = I1 1 + jωL1 + jωL2 + R1 - I2R1 - I1jωM12 - I1jωM12
jωC1
ec. malla 1 sin inducción mutua L1 en L2 L2 en L1
- Vg = -I1R1 + I2 R1 + jωL3 + 1 + R2 + Vs + I3jωM34
jωC2
ec. malla 2 sin inducción mutua L4 en L3
1 + I2jωM34 + I3jωM45 + I3jωM45
V s = I3 jωL4 + R3 + jωL5 +
jωC3
ec. malla 3 sin induc. mutua L3 en L4 L4 en L5 L5 en L4
Is = I3 - I2 ecuación adicional para la fuente de corriente
I1 = - 2 A, I2 = - 2 A, I3 = - 1 A

97. Circuito con inducción mutua
(septiembre 1996)
Datos:
V g = 9 + j30 V,
R1 L1 + R2 R1 = 3 Ω, R2 = 5 Ω,
M V2 I2
V g I1 L2 - L3 ωL1 = 1 Ω, ωL2 = 4 Ω,
ωL3 = 1 Ω, ωM = 1 Ω
Hallar k y V 2
k= ωM = 0.5
(ωL1)(ωL2)
Vg = I1(R1 + jωL1 + jωL2) - I2jωL2 - I1jωM - (I1 - I2)jωM
ec. malla 1 sin inducción mutua L1 en L2 L2 en L1
0 = - I1jωL2 + I2(jωL2 + R2 + jωL3) + I1jωM
ec. malla 2 sin inducción mutua L1 en L2
I1 = 5 + j5 A, I2 = j3 A
V2 = (I1 - I2)jωL2 - I1jωM = - 3 + j15 V = I2(R2 + jωL3)

98. Transformadores
Son dispositivos que incluyen dos inductancias acopladas
electromagnéticamente (afectadas por inducción mutua).
transformador
excitación primario Esquema
+ otros general
otros elementos de un
elementos transformador
bobinas secundario
acopladas
Un transformador modifica las condiciones en las que
una excitación llega a una carga (conjunto de elementos
pasivos) con relación a las que existen en ausencia de aquél.
Tipos
Transformador lineal.
Transformador ideal.
Serán analizados sólo en régimen sinusoidal permanente.
Un transformador no funciona como tal en continua
ya que en dichas condiciones no hay inducción mutua
(las inductancias que lo constituyen
se comportan como simples cortocircuitos).
Un transformador elimina la componente continua
de una excitación combinada.

99. Transformador lineal
transformador lineal
ZG Z1 Z2 ZL Esquema
M
VG IG L1 L2
excitación carga
ZG: impedancia asociada a la excitación
Z1: impedancia de pérdidas asociada al primario
Z2: impedancia de pérdidas asociada al secundario
ZL: impedancia de carga
En un transformador lineal se cumple (con independencia de las
posiciones de los puntos en las inductancias)
VG = IG(ZG + Z), Z = ZP + ZR
impedancia del primario: ZP = Z1 + jωL1
(ωM)2
impedancia reflejada en el primario: ZR =
ZTS
impedancia total en el circuito secundario: ZTS = ZS + ZL
impedancia del secundario: ZS = Z2 + jωL2
El transformador altera las condiciones
en las que la excitación v e la carga.
Si no estuviera el transformador, se cumpliría
VG = IG(ZG + ZL)

100. Ejemplo de transformador lineal
(diciembre 1996)
Datos:
ZG L2 + V G = 1 + j V,
M VL
VG L1 C2 ZL - Z G = 0.75 Ω,
ωL1 = 1 Ω, ωL2 = 1 Ω,
Hallar V L ωM = 0.5 Ω, ωC2 = 1 S,
ZL = 1 + j Ω
ZG ZTS = jωL2 + 1 //ZL = 1 Ω
jωC2
(ωM)2
VG
IG Z ZR = = 0.25 Ω
ZTS
Z = jωL1 + ZR = 0.25 + j Ω
VG = IG(ZG + Z) → IG = 1 A
+ 1 = jωC2 + 1 → Z2L = 1 - j Ω
L2 I2 Z2L ZL
M VL
Z2L -
= IG jωM + I2(jωL2 + Z2L) → I2 = - j0.5 A
VL = I2Z2L = - 0.5 - j0.5 V

101. Ejemplo de transformador lineal
(febrero 1992)
Z1 Z2 Datos:
M12
I2 I3 V G = - j54 V, Z1 = 2 - j4 Ω,
I1
G L1 L2 M23 L3 Z3 ωL1 = 4 Ω, ωL2 = 9 Ω,
ωM 12 = 4 Ω, Z2 = 8 - 65 Ω,
Hallar: ωL3 = 36 Ω, ωM23 = 10 Ω,
I1, I2, e I3;
Z3 = 23 - j36 Ω
impedancia total del secundario
VG = I1(Z1 + jωL1) + I2jωM12
0 = I2(jωL2 + Z2 + jωL3) - I3jωL3 +
+ I1jωM12 + I2jωM23 + (I2 - I3)jωM23
0 = - I2jωL3 + I3(jωL3 + Z3) - I2jωM23
I1 = - j25 A, I2 = - 1 A, I3 = - j2 A
VG = I1(Z1 + jωL1 + ZR) → ZR = 0.16 Ω
(ωM12)2
ZR = → ZTS = 100 Ω
ZTS

102. Transformador ideal
Es un transformador lineal llevado al límite.
k = 1, L1 = ∞ = L2
Se caracteriza por la relación de transformación.
a = n2/n1; ni: número de espiras de la bobina i, i = 1, 2
Los voltajes en los terminales de las inductancias
incluyen los efectos de autoinducción e inducción mutua.
i'1 i1 i2 i'2 Esquema
1:a
- + + -
v'1 v1 v2 v'2 v2 = i1 = n2 = a
v1 i2 n1
+ - n1 n2 - +
1/a:1
Caracterización matemática
Relación de voltajes: positiva
si ambos tienen la misma polaridad en los puntos
v2 = av1 = - av'1, v'2 = - av1 = av'1
Relación de corrientes: negativa
si ambas entran o salen simultáneamente por los puntos
i1 = - ai2 = ai'2, i'1 = ai2 = - ai'2
En régimen sinusoidal permanente
V 2 = aV 1 = - aV'1, V'2 = - aV 1 = aV'1
I1 = - aI2 = aI'2, I'1 = aI2 = - aI'2

103. Transformador ideal
ZG
1:a
IG ZL Esquema
G
ZG: impedancia asociada a la excitación
ZL: impedancia de carga
En un transformador ideal se cumple (con independencia
de las posiciones de los puntos en las inductancias)
VG = IG(ZG + ZR)
impedancia reflejada en el primario: ZR = Z2L
a
El transformador altera las condiciones
en las que la excitación v e la carga.
Si no estuviera el transformador, se cumpliría
VG = IG(ZG + ZL)
Obsérvese que, si se refleja la impedancia del primario
en el secundario, se tiene
Z R = a2 Z G
Es decir, el transformador ideal es asimétrico,
mientras que el lineal es simétrico.

104. Ejemplo de transformador ideal
(febrero 1992)
R1 1:a1 R2
1/a2:1 R3
+ + + + +
Ia V1 V2 Ib V3 V4 Ic VS Hallar V S
VG - - - - IS -
Datos:
V G = 600 V, IS = 12 A, a1 = 6, a2 = 1/3,
R1 = 24 Ω, R2 = 18 Ω, R3 = 2 Ω
V G = I aR 1 + V 1 Ecuaciones de mallas
V 2 = IbR 2 + V 3
V 4 = I cR 3 + V S
Ic = - IS Ecuación adicional para la fuente
V 2 = a1 V 1 , I a = a1 I b Ecuaciones de los transformadores
V 4 = - a2 V 3 , I b = - a2 I c
VS = 0 V

105. Ejemplo de transformadores
(septiembre 1999)
1:a
R bVL C R C +
R
L M ZL VL
I1 I2 L I3
VG -
Son datos las características de todos los elementos.
Escribir un sistema algebraico de tres ecuaciones
cuyas incógnitas sean únicamente las corrientes de malla.
1 R + jωL + 1 + (ωM)2
VG = R + 2 I1 + bZLI3
a jωC R + jωL + 1 + Z
L
jωC
impedancia reflejada
en el primario del lineal
impedancia reflejada en el primario del ideal
I1 = aI2
0 = I3 R + jωL + 1 + ZL + I2jωM
jωC
Nota
No se puede reflejar impedancias en el primario
si el secundario contiene fuentes
(a menos que se trate de fuentes independientes
que estén desactivadas).

106. Potencia en régimen sinusoidal
Potencia instantánea (real): p(t) = v(t)i(t) (¡signos!)
Caso particular
v(t) = Vmcos(ωt + ϕ) ↔ V, i(t) = Imcos(ωt) ↔ I
Potencia media W : P = VmIm cos(ϕ), factor de potencia: cos(ϕ)
2
Potencia reactiva VAR (voltio-amperio reactivo) : Q = VmIm sen(ϕ)
2
Potencia instantánea: p(t) = VmIm cos(ϕ) + VmIm cos(ϕ)cos(2ωt) -
2 2
- VmIm sen(ϕ)sen(2ωt) = P + Pcos(2ωt) - Qsen(2ωt)
2
Potencia compleja VA (voltio-amperio) : S = P + jQ = VI*
2
Siempre
Potencia media Potencia reactiva
en un elemento resistivo puro en un elemento reactivo puro
V 2 I 2R V 2 I 2X
P= = Q= =
2R 2 2X 2
Conclusiones
La potencia instantánea tiene frecuencia doble.
R → ϕ = 0 ° → p(t) = P + Pcos(2ωt) ≥ 0 para todo t
(la resistencia siempre absorbe energía)
L → ϕ = 90 ° → p(t) = - Qsen(2ωt)
(absorbe-libera energía en cada ciclo)
C → ϕ = - 90 ° → p(t) = - Qsen(2ωt)
(absorbe-libera energía en cada ciclo)

107. Valores eficaces
(rms, root mean square -valor cuadrático medio-)
Valor eficaz de una función f(t) de período T:
Feff = 1 f2(t)dt
T
T
En régimen sinusoidal permanente
V I
ensión eficaz: Veff = Vm = , corriente eficaz: Ieff = Im =
2 2 2 2
fasores eficaces: Veff = V , Ieff = I
2 2
potencias:
S = VeffI*eff
P = VeffIeffcos(ϕ)
Q = VeffIeffsen(ϕ)

108. Cálculos de potencias
(septiembre 2001)
- VG +
Ia IG R2 + 1:a + Ic Hallar
M V2 V3
Ib V G y pL1(t)
V S L1 L2 - - R3
Datos:
V S = 2 + j2 V, IG = - j2 A, ω = 100 krad/s, a = 2,
R2 = 5 Ω, R3 = 4 Ω,
L1 = 10 µH, L 2 = 50 µH, M = 10 µH
V S = I ajωL1 + IbjωM Ecuaciones de mallas
0 = I ajωM + Ib(jωL2 + R2) - VG + V 2
V 3 = I cR 3
Ib = IG Ecuación adicional
fuente de corriente
Ib = - aIc, V 3 = - aV 2 Transformador ideal
Ia = 2 A, Ib = - j2 A, VG = 10 - j10 V
IajωL1 + IbjωM = VL1 = V S = 2 + j2 V
*
VL1Ia = 2 + j2 VA
∠VL1 ≠ 0 °, ∠Ia = 0 ° → SL1 =
2
P = Re SL1 = 2 W, Q = Im SL1 = 2 VAR
pL1(t) = 2 + 2cos(2ωt) - 2sen(2ωt) W

109. Cálculos de potencias
(junio 2001)
1:a
RM M VG R1 C1 + + Ra +
V1 V2 Ia VS Hallar
CMIM L2 L1 I1 - - IS - pV1(t)
Datos:
V G = 10 V, IS = j A, ω = 100 krad/s, a = 5,
RM = 1 Ω, R1 = 1 Ω, Ra = 50 Ω, CM = 5 µF, C1 = 5 µF,
L1 = 20 µH, L2 = 20 µH, M = 10 µH
0 = IM 1 + RM + jωL2 - I1jωM Ecuaciones
jωCM de mallas
V G = I1 1 + R1 + jωL1 - IMjωM + V1
jωC1
V 2 = I aR a + V S
Ecuación adicional
Ia = - IS
fuente de corriente
I1 = aIa, V 2 = aV 1 Transformador ideal
I1 = - j5 A, IM = 5 A, V1 = 10 + j10 V
∠V1 ≠ 0 °, ∠I1 ≠ 0 ° → caso general
i1(t) = 5cos(ωt - 90 °) A, v1(t) = 10 2cos(ωt + 45 °) V
pV1(t) = v1(t)i1(t)

110. Cálculos de potencias
(diciembre 2000)
a:1 Hallar
C2 L2 R1 L1 C1 las potencias
L3 media y reactiva
IG VG en la fuente
Datos:
VG = 2 + j2 V, ω = 100 krad/s, a = 10,
R1 = 1 Ω, C1 = 10 µF, C2 = 50 nF,
L1 = 10 µH, L2 = 1 mH, L3 = 2 mH
Reflejando impedancias,
V G = IG 1 + jωL1 + R1 + 1 jωL2 + 1 + jωL3 → IG = 2 A
jωC1 a2 jωC2
*
V GIG = - 2 - j2 VA
∠V G ≠ 0 °, ∠IG = 0 ° → SG = -
2
PG = Re SG = - 2 W, QG = Im SL1 = - 2 VAR

111. Cálculos de potencias
(junio 1997)
Hallar
C1 L1 R2 1:a pG(t)
R1 M L3
R3 (se supone
I1 L2 I2
C3 ω conocida)
VG
Datos:
V G = - j2 V, a = 0.5,
R 1 = 2 Ω, R2 = 4 Ω, R3 = 0.5 Ω,
ωL1 = 3 Ω, ωL2 = 1 Ω, ωL3 = 2 Ω,
(ωC1)-1 = 6 Ω, (ωC2)-1 = 0.75 Ω, ωM = 1 Ω
Reflejando impedancias,
V G = I 1 R1 + 1 + jωL + jωL - I jωL + I jωM + (I - I )jωM
1 2 2 2 1 1 2
jωC1
0 = - I1jωL2 + I2 jωL2 + R2 + jωL3 + 12 R3 + 1 - I1jωM
a jωC3
I1 = - j0.75 A
∠VG ≠ 0 °, ∠I1 ≠ 0 ° → caso general
i1(t) = 0.75cos(ωt - 90 °) A, vG(t) = 2cos(ωt - 90 °) V
pG1(t) = - vG(t)i1(t)

112. Equivalente Thèvenin
en régimen sinusoidal permanente
Dado un circuito su comportamiento hacia el exterior,
desde la perspectiva de dos de sus terminales,
puede ser caracterizado mediante
los equivalentes de Thèvenin y Norton.
Equivalentes de Thèvenin y Norton
a a a
ZTh
VTh IN ZN
b b b
ZTh = ZN VTh = ZNIN IN = VTh/ZTh
Procedimientos para calcular el equivalente (a-b)
V Th: tensión de circuito abierto entre a y b.
IN:: corriente de cortocircuito de a a b.
ZTh:
cociente entre V Th e IN.
Desactivación de fuentes independientes,
aplicación de V aux (positivo en a),
cálculo de Iaux (sale por el positivo de V aux),
y ZTh = V aux/Iaux.
Si no hay fuentes dependientes,
desactivación de fuentes independientes,
y ZTh = impedancia total entre a y b.

113. Máxima transferencia de potencia
ZTh = RTh + jXTh Dado un circuito caracterizado
ZL = RL + jXL
a por su equivalente Thèvenin,
se trata de determinar la carga
que debe conectarse
VTh entre sus terminales.
b
Si
ZL = Z*Th ⇔ RL = RTh, XL = - XTh
la potencia media en la carga es la máxima posible y vale
VTh 2
PL = Pmax =
8RTh
Casos particulares
RL y XL no pueden tomar valores cualesquiera,
sino algunos fijados previamente:
se escoge el valor de XL lo más próximo posible a - XTh,
se escoge el valor de RL lo más próximo posible a
RTh + (XL + XTh)2
2
La fase de ZL no puede ser cualquiera, sino una fija:
se escoge el módulo de ZL lo más próximo posible al de ZTh.

114. Cálculo de equivalente Thèvenin
(cálculo completo, septiembre 1997)
c + V5 - Hallar
1:a eq. Th.
C1 R2 C5
M entre
bV5 L3 L4 IG cyd
d
Datos:
IG = - j5 A, a = 2, b = 2,
ωL3 = 2 Ω, ωL4 = 8 Ω, ωM = 2 Ω,
(ωC1)-1 = 0.5 Ω, (ωC5)-1 = 0.5 Ω, R2 = 2 Ω
Cálculo de la tensión de circuito abierto
c + V5 -
1:a
C1 + + R2 + C5
V1 V2 V M
bV5 - - I2 -3L3 L4 IG
d
V 1 = bV 5 = b - IG = 5 V, V 2 = aV 1 = 10 V
jωC5
V2 = I2(R2 + jωL3) + IGjωM → I2 = 0 A
I2jωL3 + IGjωM = V3 = VTh = Vcd = V2 - I2R2 = 10 V

115. Cálculo de equivalente Thèvenin
(cálculo completo, septiembre 1997)
Cálculo de la corriente de cortocircuito
c + V5 -
1:a
C1 + + R2 C5
V1 V2 I3 M
bV5 - - I2 L3 L4 IG
d
V 1 = bV 5 = b - IG = 5 V, V2 = aV 1 = 10 V, I2 = V 2 = 5 A
jωC5 R2
0 = Vcd = - I3jωL3 + IGjωM → I3 = - j5 A
Icd = IN = I2 + I3
Cálculo de la impedancia equivalente
ZTh = VTh = 1 + j Ω
IN

116. Cálculo de equivalente Thèvenin
(cálculo de impedancia con fuente auxiliar, junio 1999)
1:a +
R C R C bVL R
M VL
IG L L ZL -
Datos:
IG = - j5 A, ω = 1 Mrad/s, a = 2, b = 0.25,
R = 1 Ω, L = 2 µH, M = 1 µH, C = 500 nF
Hallar el valor de ZL para que disipe la máxima potencia
Se desactiva la fuente de corriente (queda en circuito abierto)
con lo que el primario del transformador lineal no actúa.
El cálculo se hace sin ZL ya que es la impedancia a calcular.
Se aplica una fuente auxiliar.
1:a
R C bVL + + R Vaux +
I2 V2 V3 VL
L - - Iaux -
0 = I2 jωL + R + 1 - bVaux + V2
jωC
Vaux = IauxR + V3, V3 = - aV2, I2 = aIaux
Eliminando I2, V 2, y V 3,
a jωL + R + 1 - R
jωC a
ZTh = Vaux = = 3.33 Ω
Iaux b+a 1
ZL = ZTh = 3.33 Ω
*

117. Cálculo de equivalente Thévenin
(cálculo agrupando impedancias, febrero 1994)
1:a
R C R
M L
VG L ZL
Se suponen conocidos los datos de todos los elementos.
Hallar ZL para que disipe la máxima potencia
El cálculo se hace sin ZL ya que es la impedancia a calcular.
Se desactiva la fuente de tensión (queda en cortocircuito)
y se van reflejando impedancias.
1:a 1:a
R C R C R R
M L L ZR2
L ZR1
ZTh = R + ZR2 = R + a2 ZR1 + jωL + 1 =
jωC
2
=R+a 2 (ωM) + jωL + 1
R + jωL jωC
*
ZL = ZTh

118. Cálculo de equivalente Thèvenin
(cálculo completo, junio 2002)
I3 I2 x Hallar
y eq. Thèvenin
+ + C L VG
V3 V2
2 entre x e y
M
L3 - - L1 I1
I1, I2 e I3
Datos: son corrientes
V G = j5 V, a = 2, ω = 100 krad/s, de rama
L1 = 40 µH, L2 = 20 µH, L3 = 160 µH,
M = 10 µH, C = 5 µF
Cálculo de la tensión de circuito abierto
Se considera el circuito tal y como está
VG = I1jωL1 + I2jωM, V3 = I3jωL3
I1 = 1 A
VG = I1jωM + I2 jωL2 + 1 ⇒
jωC I2 = 1 A
V 3 = aV 2, I2 = aI3
VTh = Vxy = I2 jωL2 + 1 + I1jωM = j V
jωV

119. Cálculo de equivalente Thèvenin
(cálculo completo, junio 2002)
Cálculo de la corriente de cortocircuito
I3 I2 IN x
y
+ + C L2 VG
V3 V2 M
L3 - IP - L1 I1
a:1
IP = V 2 = V G = 5 A
jωL3 jωL3 4
a2 a2
VG = I1jωL1 + I2jωM
I1 = 0 A
0 = Vxy = I1jωM + I2 jωL2 + 1 ⇒
jωC I2 = 5 A
IN = IP - I2 = - 15 A
4
Cálculo de la impedancia equivalente
ZTh = VTh = - 4 Ω
IN 15

120. Aplicación
del principio de superposición
Cuando un circuito soporta distintas excitaciones,
una o más continuas
y/o una o más sinusoidales de distintas frecuencias,
el análisis se realiza aplicando el principio de superposición.
Si las excitaciones están simbolizadas
en una sola fuente independiente
(sólo es posible si las excitaciones
son de igual naturaleza -corrientes o tensiones-),
se realiza un análisis separado
para cada una de las excitaciones.
Si las excitaciones están simbolizadas
en más de una fuente independiente,
se realiza un análisis para cada una de ellas,
estando las restantes fuentes independientes desactivadas.
Desactivación de fuentes
Desactivar una fuente de corriente
supone sustituirla por un circuito abierto.
Desactivar una fuente de tensión
supone sustituirla por un cortocircuito.

121. Ejemplo de aplicación
del principio de superposición
(diciembre 2000)
Datos:
vg(t) = VD + VAcos(ωt),
D = 2 V, VA = 26 V, ω = 2 rad/s,
R C
vg R L R R = 2 Ω, L = 2 H, C = 5/8 F
Hallar pC(t)
El circuito tiene una componente continua (VD)
y una componente sinusoidal. La respuesta es
vC(t) = VCD + VCAcos(ωt + ϕv), iC(t) = ICD + ICAcos(ωt + ϕi)
+ Continua
R ICD En continua la inductancia y la capacidad
VCD
VD R C - son, respectivamente, un cortocircuito
y un circuito abierto.
VCD = VDR = 1 V, ICD = 0 A
R+R
Sinusoidal
R
ICA Z = 1/(jωC) + (jωL)//R = 1.6 Ω
VA IG R Z
VA∠0 ° = VA = IG(R + R) - ICAR
0 = - IGR + ICA(R + Z)
ICA = 5 A → ICA = 5 A, ϕi = 0 °
VCA = ICA/(jωC) = - j4 V → VCA = 4 V, ϕv = - 90 °
Respuesta
pC(t) = vC(t)iC(t) = 1 + 4cos(ωt - 90 °) 5cos(ωt) W

122. Ejemplo de aplicación
del principio de superposición
(febrero 1994)
Datos:
vg(t) = VC +
L1 + V1cos(ω1t) + V2cos(ω2t + 270 °),
C1
+
R1 C2 ω1 = 1 Mrad/s, ω2 = 2 Mrad/s,
R2 vO
vg L2 VC = 3 V, V1 = 1 V, V2 = 2 V,
- L1 = 1 µH, L 2 = 2 µH,
C1 = 1 µF, C 2 = 2 µF,
R1 = 1 kΩ, R2 = 2 kΩ
Hallar vO(t)
El circuito tiene una componente continua (VC)
y dos componentes sinusoidales de distintas frecuencias.
Ha de ser analizado aplicando el principio de superposición.
La respuesta es
vO(t) = VOC + VO1cos(ω1t + ϕ1) + VO2cos(ω2t + ϕ2)
Continua
Dado que en continua la inductancia y la capacidad son,
respectivamente, un cortocircuito y un circuito abierto,
el circuito queda reducido a la fuente y a las dos resistencias.
Por tanto,
VOC = de tensión = VCR2 = 2 V
divisor
R 1 + R2

123. Ejemplo de aplicación
del principio de superposición
(febrero 1994)
Régimen sinusoidal
Hacemos las siguientes agrupaciones de elementos:
L1/C1
Z1(ω) = R1 + (jωL1)// 1/(jωC1) = R1 +
jωL1 + 1/(jωC1)
R2 jωL2 + 1/(jωC2)
Z2(ω) = R2// jωL2 + 1/(jωC2) =
R2 + jωL1 + 1/(jωC1)
con lo que la respuesta para cualquier frecuencia es
divisor VkZ2(ωk)
VOk∠ϕk = VOk = de tensión = ; k = 1, 2
Z1(ωk) + Z2(ωk)
En consecuencia,
respuesta para la frecuencia 1:
k = 1 → V1 = V1ej0 ° = 1 V → VO1 = 0 V
respuesta para la frecuencia 2:
k = 2 → V2 = V2ej270 ° = - j2 V → VO2 = 0 V
Respuesta total
La respuesta es continua, ya que son nulas
las componentes sinusoidales.

124. Ejemplo de aplicación
del principio de superposición
Datos:
R R iA(t) = IAcos(ωt),
vD L
- vR + R IA = 1 A, ω = 1 rad/s,
R L + vD(t) = VD = 2 V,
C vd
R R GvR R = 1 Ω, G = 2 S,
iA C - L = 1 H, C = 1 F
Hallar vd(t)
El circuito tiene una componente continua (vD(t))
y una componente sinusoidal. La respuesta es
vd(t) = VdD + VdAcos(ωt + ϕv)
Continua
R + Se desactiva la fuente independiente
VD VdD de corriente (se sustituye por un circuito abierto),
R con lo que vRD = 0 V.
-
En consecuencia, y teniendo en cuenta
que en continua la inductancia
VDR = 1 V y la capacidad son, respectivamente,
VdD =
R+R un cortocircuito y un circuito abierto,
el circuito queda como se indica
en la figura adjunta.

125. Ejemplo de aplicación
del principio de superposición
Sinusoidal
R R Se desactiva la fuente
- VRA + de tensión (se sustituye por un
R
Z2 cortocircuito).
+
GVRA
R
R VdA
I Z1
A R -
Z1 = jωL + 1 = 0 Ω (cortocircuito)
jωC
Z2 = (jωL)// 1/(jωC) = ∞ Ω (circuito abierto)
VRA = - IAR, VdA = GVRA R + (R + R)//(R + R) →
→ VdA = 4 V → VdA = 4 V, ϕv = 0 °
Respuesta
vd(t) = 1 + 4cos(ωt) V

126. Ejemplo de aplicación
del principio de superposición
(septiembre 2000)
Datos:
vg(t) = VD + VAcos(ωt),
R L VD = 3 V, VA = 4 V, ω = 1 rad/s,
vg R C R R = 1 Ω, L = 0.5 H, C = 1 F
Hallar pL(t)
El circuito tiene una componente continua (VD)
y una componente sinusoidal. La respuesta es
vL(t) = VLD + VLAcos(ωt + ϕv), iL(t) = ILD + ILAcos(ωt + ϕi)
+ VLD - Continua
R ILD En continua la inductancia y la capacidad
son, respectivamente, un cortocircuito
VD R R y un circuito abierto.
ILD = VD = 1 A, VLD = 0 V
3R
Sinusoidal
R
ILA Z = jωL + R// 1/(jωC) = 0.5 Ω
VA IG R Z
VA∠0 ° = VA = IG(R + R) - ILAR
0 = - IGR + ILA(R + Z)
ILA = 2 A → ILA = 2 A, ϕi = 0 °
VLA = ILAjωL = j V → VLA = 1 V, ϕv = 90 °
Respuesta
pL(t) = vL(t)iL(t) = 1 + 2cos(ωt) cos(ωt + 90 °) W

127. Ejemplo de aplicación
del principio de superposición
Datos:
vG(t) = cos(ωGt) V, ωS = 1 Mrad/s,
R L iL R iS(t) = 2cos(ωSt - 45 °) A, ωS = 1 krad/s,
iS R C vG R = 1 Ω, L = 1 mH, C = 1 mF
Hallar iL(t)
El circuito tiene dos componentes sinusoidales de distintas
frecuencias. La respuesta es
iL(t) = ILScos(ωSt + ϕS) + ILGcos(ωGt + ϕG)
R L Componente ωs
R
IS R
ILS I3S 0 = - ISR + ILS R + jωL + 1 - I3S
C jωC jωC
IS = 2 ∠- 45 ° A 0 = - ILS + I3S R + 1
jωC jωC
ILS = 4 A ⇒ ILS = 4 A, ϕS = 0 °
L Componente ωG
R
VG
R
ILG I3G 0 = ILG R + jωL + 1 - I3G
C jωC jωC
VG = 1 V V G = ILG - I3G R + 1
jωC jωC
ILG ≈ 0 A ⇒ ILG = 0 A

128. Problemas de repaso
(cortocircuito en inductancia mutua, diciembre 1994)
Isc L Son datos las características
1 b
a de todos los elementos
R1
M I2
ZG L2
Escribir un sistema algebraico
I1 ZL de ecuaciones cuyas incógnitas
R2 sean las corrientes de malla
VG
Podría pensarse que no circula corriente por R1 y L1
ya que el cortocircuito impone una tensión nula
en los extremos de esa rama.
Sin embargo hay tensión en L1 debido al efecto de inducción mutua.
Esa tensión debe ser compensada por otra igual y de signo opuesto
en R1 y L1 para que la tensión total sea nula.
Y, si hay tensión en la resistencia, también hay corriente en ella.
En consecuencia el sistema de ecuaciones es
Vab = I1(R1 + jωL1) - Isc(R1 + jωL1) - (I1 - I2)jωM = 0
VG = I1(ZG + R2 + jωL2) + Vab - I2(R2 + jωL2) - (I1 - Isc)jωM
0 = - I1 (R2 + jωL2) + I2(ZL + R2 + jωL2) + (I1 - Isc)jωM

129. Problemas de repaso
(inducción mutua, potencia)
x Hallar:
+ aV3 R + Zxy, y P en R
L M
V4 C4 I
1 I2 C 3 V 3
IG - L -
y
Datos:
IG = 1 A, ω = 1 krad/s, a = 0.5,
L = 1 mH, M = 0.5 mH, R = 0.5 Ω, C3 = 1 mF, C4 = 1.5 mF
V4 + aV3 = I1jωL - I2jωM
0 = - I1jωM + I2 jωL + R + 1
jωC3
V 4 = IG - I1 ,V 3 = I2
jωC4 jωC3
I1 = - 2 A, I2 = - j2 A
Vxy
Vxy = I1jωL - I2jωM = - 1 - j2 V ⇒ Zxy = = 0.5 + j Ω
I1
I2 2R
PR = =1W
2

130. Problemas de repaso
(inducción mutua, potencia)
x y Hallar:
L C Zxy, y la potencia
+
M instantánea en la
V1 I1 I2
IG - C L aV1 fuente independiente
Datos:
IG = 1 A, ω = 1 krad/s, a = 0.5,
L = 1 mH, M = 0.5 mH, C = 1 mF
V1 = I1(jωL + jωL) - I2jωL + I1jωM + (I1 - I2)jωM
0 = - I1(jωM + jωL) + I2 jωL + 1 + aV1
jωC
V 1 = IG - I1
jωC
I1 = - 0.5 A, I2 = 0 A
Vxy
Vxy = I1jωL + (I1 - I2)jωM = - j0.75 V ⇒ Zxy = = j1.5 Ω
I1
V 1 = IG - I1 = - 1.5 V ⇒ v1(t) = 1.5cos(ωt - 90 °) V
jωC
IG = 1 A ⇒ iG(t) = cos(ωt) A
pG(t) = - v1(t)iG(t)

131. Problemas de repaso
(inverso a partir de potencia, febrero 1995)
ZG + R
Datos: R = 3 kΩ, ZG = 300 + j21 kΩ,
V V = Vmejϕ, Vm = 5 V,
VG - jX
arctg(4/3) = ϕ ∈ primer cuadrante;
Hallar V G X absorbe 2 mVAR
y minimiza la potencia media en R
La corriente que circula por el circuito es
V Vm
I= V → I = =
R + jX R + jX R 2 + X2
La potencia absorbida en el elemento reactivo es
I 2X 2
QX = = VmX 2 → X = 4 kΩ
2 2(R2 + X ) X = 2.25 kΩ
La potencia media en R es
I 2R 2
VmR
PR = =
2 2(R2 + X2)
PR mínima → I mínimo → X máximo = 4 kΩ
Vm = Re2 V + Im2 V
Im V
V = Re V + jIm V = tg(ϕ) = = 3 + j4 V
Re V
ϕ primer cuadrante
I = V/(R + jX) = 1 mA, VG = IZG + V = 303 + j25 V

132. Problemas de repaso
(equivalente Thèvenin, junio 2001)
1:a x
R M VG R C + RS
V1
C L L - IS
y
Datos:
V G = 10 V, IS = j A, ω = 100 krad/s, a = 5,
R = 1 Ω, RS = 50 Ω, C = 5 µF, L = 20 µH, M = 10 µH
Hallar el equivalente Thèvenin entre x e y
Aplicando las propiedades de los transformadores,
(ωM)2
V G = - aI S + R + jωL + 1 + V 1 → V 1 = 10 + j10 V
R + jωL + 1/(jωC) jωC
VTh = Vxy = aV1 + ISR = 50 + j100 V
Desactivando las fuentes,
y reflejando y agrupando impedancias,
(ωM)2
ZTh = Zxy = RS + a2 + R + jωL + 1 = 100 Ω
R + jωL + 1/(jωC) jωC

133. Problemas de repaso
(potencia, equivalente Thèvenin, septiembre 2002)
L1 L2 x 1:a Hallar:
la potencia instantánea
R1 M C en L1, y el equivalente
I1 R2
VG Thèvenin entre x e y
y
Datos:
V G = 4 V, ω = 100 krad/s, a = 2, R1 = 1 Ω, R2 = 4 Ω,
L1 = 40 µH, L 2 = 40 µH, M = 10 µH, C = 1 µF
Reflejando impedancias en el transformador ideal,
VG = I1 R1 + jωL1 + jωL2 + j2ωM + 1 + R2 ⇒ I1 = 2 A ⇒
2
jωC a
⇒ i1(t) = Re I1ejωt = 2cos(ωt) A
VL1 = I1(jωM + jωL) = j10 V ⇒
⇒ vL1(t) = Re VL1ejωt = 10cos(ωt + 90 °) V
pG(t) = vL1(t)i1(t)
Decir “equivalente entre x e y” es lo mismo que “equivalente en el
primario del transformador ideal”.
La tensión de circuito abierto se calcula en las condiciones de la
figura.
VTh = Vxy = I1R2 = 2 V
a2
Cuando hay un cortocircuito entre x e y, la tensión es nula en el
primario.
V G = IN R1 + jωL1 + jωL2 + j2ωM + 1 ⇒ IN = 4 A
jωC
ZTh = VTh = 0.5 Ω
IN

134. Problemas de repaso
(equivalente Thèvenin, diciembre 2002)
x 1:a Hallar la impedancia
RS RG CG R4 que hay que colocar
LS M LG entre x e y para que
IS VG C4 en ella se disipe la
y máxima potencia
Datos:
V G = - 1 + j V, IS =1 A, ω = 100 krad/s, a = 2,
RS = 1 Ω, RG = 1 Ω, R4 = 1 Ω,
LS = 20 µH, L G = 20 µH, M = 10 µH, C G = 5 µF, C 4 = 10 µF
Desactivando las fuentes y reflejando impedancias,
(ωM)2
ZTh = Zxy = jωLS + = 1 + j2 Ω
jωL2 + RG + 1
jωCG
ZL = ZTh = 1 - j2 Ω
*

135. Problemas de repaso
(equivalente Thèvenin, máxima potencia con limitación de impedancias)
1:a1 1:a2 1:a3
R1 C R2 R3
VG ZL
Son datos las características de todos los elementos
Hallar el valor que ha de tomar ZL para que en ella
se disipe la máxima potencia posible
sabiendo que tal valor sólo puede ser resistivo
Se desactiva la fuente.
El cálculo se hace sin ZL ya que es la impedancia a calcular.
Se reflejan impedancias.
ZTh = R3 + a3 R2 + a2 1 + a1R1
2 2 2
jωC
En principio debería ser ZL = Z*Th,
pero ello resultaría en una impedancia compleja.
Puesto que la impedancia ha de ser resistiva,
ello significa que hay una limitación de fase (0 ˚).
En consecuencia
ZL = ZTh

136. Problemas de repaso
(equivalente Thèvenin, problema inverso, junio 1998)
1:a
R + L M M R
VC I1 I2
VG IG - C IC L IL bVC RL
Demostrar que V C no depende de RL
Hallar R sabiendo que a = 2, RL = 4 Ω,
y que en RL se disipa la máxima potencia media posible
Sabiendo que V C = (IG - IC)/(jωC) y reflejando impedancias,
el circuito queda descrito por el sistema de ecuaciones
V G = I G R + 1 - IC
jωC jωC
0 = - IG + IC 1 + j2ωL + j2ωM - IL(jωL + jωM)
jωC jωC
b(IG - IC)
0 = - IC(jωL + jωM) + IL jωL + jωM +
jωC
b(IG - IC)
= I1 R + R2 , I1 = - aI2
L
jωC a
Las tres primeras ecuaciones conforman un sistema cerrado
del que es posible obtener IG e IC independientemente de RL.
En consecuencia V C también puede ser obtenida
independientemente de la resistencia.

137. Problemas de repaso
(equivalente Thèvenin, problema inverso, junio 1998)
Equivalente Thèvenin
Sustituyendo RL por un circuito abierto,
I2 = 0 → I1 = 0 → VTh = - abVC
Sustituyendo RL por un cortocircuito,
I1 = bVC → IN = - I1 = - bVC
a
R aR
Puesto que V C es igual en ambos casos ya que no depende de RL (en
general sí cambiaría),
RL = RL = ZTh = VTh = a2R → R = 1 Ω
*
IN

138. Problemas de repaso
(equivalente Thèvenin, problema inverso, junio 1996)
1:a
ZG Z2 Hallar ZG
M ZL
VG L L
Datos:
V G = 5 - j V, ω = 1 Mrad/s, L = 1 µH, M = 0.5 µH,
a = 2, Z2 = 1 - j5 Ω, ZL = 0.25 - j Ω;
en ZL se disipa la máxima potencia media posible
Desactivando la fuente, prescindiendo de ZL,
y reflejando impedancias,
(ωM)2
*
ZL = ZTh = jωL + → ZG = j Ω
jωL + Z2 + a2ZG

139. Problemas de repaso
(superposición, septiembre 2001)
Hallar la potencia instantánea
RG C C en la capacidad en serie con RG
vG L RC
Datos:
vG(t) = V1 + V2cos(ωt), V1 = 12 V, V2 = 5 V, ω = 1 rad/s,
L = 1 H, C = 1 F, RG = 2 Ω, RC = 2 Ω
El circuito tiene una componente continua (V1)
y una componente sinusoidal. La respuesta es
vC(t) = VCD + VCAcos(ωt + ϕv), iC(t) = ICD + ICAcos(ωt + ϕi)
Continua
RG C La inductancia y las capacidades son,
vG respectivamente, un cortocircuito y circuitos
abiertos.
ICD = 0 A, VCD = V1 = 12 V
Vale el circuito del Sinusoidal
enunciado, con V G = V2 Z1 = RG + jωC = 2 - j Ω
Z2 = jωL // RC + jωC = 0.5 + j Ω
V G = 2 A ⇒ I = 2 A, ϕ = 0 °
ICA = CA i
Z 1 + Z2
VCA = ICA = - j2 V ⇒ VCA = 2 V, ϕv = - 90 °
jωC
Respuesta
pC(t) = vC(t)iC(t)

140. Problemas de repaso
(superposición)
1:a Datos:
L1 L2 +
C vC vg(t) = VD + VAcos(ωt),
vg - VD = 46 V, VA = 220 2 V,
R1 R2 R3 R 1 = 6.5 Ω, R2 = 5 Ω, R3 = 45 Ω,
ωL1 = 10.8 Ω, ωL2 = 22 Ω,
(ωC)-1 = 2 Ω, a = 10
Hallar vC(t)
Por haber dos excitaciones de distinta naturaleza,
vC(t) = VCD + VCAcos(ωt + ϕ)
+ Continua
R1 Excitación sinusoidal desactivada
VCD
VD R2 - L = cortocircuito, C = circuito abierto
VCD = VDR2 = 20 V
R 1 + R2

141. Problemas de repaso
(superposición)
1:a Sinusoidal
L1 + + L2 + Excitación continua desactivada
V1 V2 VCA
VA - - C -
I1 I2
R1 R2 R3
VA = I1(R1 + jωL1 + R2) + V1 - I2R2
0 = - I1R2 - V2 + I2 R2 + jωL2 + 1 + R3
jωC
I1 = aI2, V 2 = aV 1
I2 = 2(1 - j) A, VCA = I2 = - 2 2(1 + j) V
jωC
Respuesta
vC(t) = 20 + 4cos(ωt + 225 °) V

142. Problemas de repaso
(superposición)
Hallar la expresión temporal
L L R
C de la potencia en la capacidad
vG R iS
Datos:
vG(t) = 4 V, iS(t) = 2cos(ωt) A, ω = 1 krad/s,
L = 2 mH, C = 0.5 mF, R = 2 Ω
El circuito tiene una componente continua (vG)
y una componente sinusoidal. La respuesta es
vC(t) = VCD + VCAcos(ωt + ϕv), iC(t) = ICD + ICAcos(ωt + ϕi)
+ Continua
VCD Excitación sinusoidal desactivada
vG - R L = cortocircuito, C = circuito abierto
VCD = vG = 4 V, ICD = 0 A

143. Problemas de repaso
(superposición)
+ L Sinusoidal
R Excitación continua desactivada
VCA I3 C I2
- L R IS
IS = 2 A
(IS - I2)R = I2 jωL + 1 - I3
jωC jωC
0 = I3 jωL + 1 - I2
jωC jωC
I2 = 0 A, I3 = - j2 A
ICA = I2 - I3= j2 A ⇒ ICA = 2 A, ϕi = 90 °
VCA = ICA = 4 V ⇒ VCA = 4 V, ϕv = 0 °
jωC
Respuesta
pC(t) = vC(t)iC(t)

144. Ejercicios para resolver en clase
SINUSOIDAL 2003/A R R R +
v3
vG(t) = 1.8cos(ω 1t + 33.69 ˚) + 2cos(ω 2t) V, L C L -
vG
ω 1 = 1 krad/s, ω 2 = 1 Mrad/s,
L = 1 mH, C = 1 mF, R = 1 Ω Hallad la expresión temporal de v3.
SINUSOIDAL 2003/B y x
M R gVR
+ C
El circuito de la figura, en cuya VG
VR
representación se ha utilizado - L L C
notación fasorial, funciona en
régimen sinusoidal permanente. V G = 1.5 V, ω = 1 krad/s,
Hallad la impedancia entre x e y, L = 1 mH, M = 0.5 mH, C = 1 mF,
justificando el signo del resultado, y R = 0.5 Ω, g = - 1 S
la potencia reactiva en la fuente
dependiente.
SINUSOIDAL 2003/C x y
gV2 C L +
Hallad el equivalente Thèvenin entre x L V2
e y. VG M -
Se desea colocar entre tales puntos una
El circuito de la figura, en cuya
impedancia en la que se disipe la máxima
representación se ha utilizado notación
potencia media posible, pero las partes real
fasorial, funciona en régimen sinusoidal
e imaginaria de dicha impedancia sólo
permanente.
pueden tomar valores (positivos o
negativos) iguales a múltiplos enteros de
V G = 0.75 V, ω = 1 krad/s,
0.5 Ω.
L = 1 mH, M = 0.5 mH, C = 1 mF, g = 4 S
Determinad los elementos que han de
constituir esa impedancia.

145. Respuesta en frecuencia
Función de transferencia es una expresión matemática
que relaciona los fasores correspondientes
a la salida y a la entrada de un circuito.
La función de transferencia depende de
las características de los elementos del circuito,
la frecuencia de operación del circuito.
La función de transferencia suele representarse como T(jω).
Función de transferencia en resonadores ideales
Resonador RLC paralelo Resonador RLC serie
Vo = Vo∠ϕ
IG = IG∠0 °
V G = VG∠0 °
+
Vo = Vo∠ϕ
+
L C
R
R L C-
-
T(jω) =
Vo
= Zeq = 1 (jω) = V o = R = R
IG 1 + 1 + jωC V G Z eq R + jωL + 1
R jωL jωC
ω → 0 ⇒ Zeq ≈ jωL → j0 ω → 0 ⇒ Zeq ≈ 1/(jωC) → - j∞
ω → ∞ ⇒ Zeq ≈ 1/(jωC) → - j0 ω → ∞ ⇒ Zeq ≈ jωL → j∞
ω intermedia ⇒ Zeq no despreciable ω intermedia ⇒ Zeq finita

146. Resonador paralelo ideal
(para el serie son aplicables consideraciones similares)
Vo BW ϕ Frecuencia central
Vomax
90 ° ω0 = 1
LC
0° T(jω0) máximo
- 90 ° ∠T(jω0) = 0 °
ω1 ω0 ω2
Zeq(ω0) = R
ω creciente →
Frecuencia de resonancia
Suele denominarse frecuencia de resonancia
a la frecuencia central; es decir, la frecuencia
para la que se cumplen las tres condiciones indicadas.
Sin embargo, las tres condiciones sólo se dan a la vez
en los resonadores ideales.
Para nosotros, frecuencia de resonancia es aquélla
para la que la impedancia del circuito es resistiva
(los efectos inductivos y capacitivos
se cancelan mutuamente).
Zeq(ω0) = 0 Ω
ω0 = 1 L C
LC (cortocircuito)
ω0 = 1 Zeq(ω0) = ∞ Ω
LC L C
(circuito abierto)

147. Banda de paso
Conjunto de frecuencias en las que se cumple
T(jω0)
T(jω) ≥
2
Ancho de banda
Intervalo de frecuencias correspondiente a la banda de paso.
Se representa por BW.
Ancho de banda relativo
bw = BW
ω0
Factor de calidad
Q = ω0 = 1
BW bw
Cuanto mayor es Q, más afilada es la curva
de la función de transferencia.
En resonadores ideales
Paralelo ω0 = 1 = ω1ω2
LC
BW = ω2 - ω1 = 1 , Q = ω0RC
RC
Serie ω0 = 1 = ω1ω2
LC
BW = ω2 - ω1 = R , Q = 1
L ω0RC
La frecuencia de resonancia depende
sólo de los elementos reactivos.
La resistencia influye en el ancho de banda.

148. Otras observaciones sobre
la respuesta en frecuencia
Para unos valores dados de L y C
ω 0 ∞
Z = 1/(jωC) - j∞ Ω - j0 Ω
(circuito abierto, (cortocircuito,
fase = - 90 ˚) fase = - 90 ˚)
Z = jωL j0 Ω j∞ Ω
(cortocircuito, (circuito abierto,
fase = 90 ˚) fase = 90 ˚)
Para un valor dado de ω
Z = 1/(jωC) C → 0 ⇒ Z → - j∞ Ω C → ∞ ⇒ Z → - j0 Ω
(circuito abierto, (cortocircuito,
fase = - 90 ˚) fase = - 90 ˚)
Z = jωL L → 0 ⇒ Z → j0 Ω L → ∞ ⇒ Z → j∞ Ω
(cortocircuito, (circuito abierto,
fase = 90 ˚) fase = 90 ˚)

149. Ejemplo de respuesta en frecuencia
(función de transferencia, junio 2001)
+ Si la función
R L C de transferencia es
Vo
VG C R L - T(jω) = V o
VG
Datos: hallar los valores
características de los elementos, a los que tienden
∠V G = 0 ° su módulo y su fase
para ω → 0, ω = 1/ LC,
yω→∞
T(jω) = V o = Z2
V G Z 1 + Z2
Z1 = R + jωL + 1/(jωC), Z2 = 1/R + 1/(jωL) + jωC -1
ω → 0 ⇒ Z1 → - j/(ωC), Z2 → jωL ⇒ T(jω) → - ω2LC ⇒
⇒ T(jω) → ω2LC, ∠T(jω) → 180 °
ω = 1/ LC ⇒ Z1 = R, Z2 = R ⇒ T(jω) = 1/2 ⇒
⇒ T(jω) = 1/2, ∠T(jω) = 0 °
ω → ∞ ⇒ Z1 → jωL, Z2 → - j/(ωC) ⇒ T(jω) → -1/(ω2LC) ⇒
⇒ T(jω) → 1/(ω2LC), ∠T(jω) → 180 °

150. Ejemplo de respuesta en frecuencia
(función de transferencia, septiembre 1993)
Si la función
R1 L1 C1
de transferencia es
R2 L2 C2 + T(jω) = V o
Vo VG
VG Ro - se pide dibujar
la variación cualitativa de
Son datos las características su módulo
de todos los elementos. Además,
las bandas de paso de los dos en función de ω.
resonadores están muy separadas, y
ω2 = 1 >> 1 = ω1, R1 > R2
L2C2 L1C1
T(jω) = V o = Ro ; Zi = Ri + jωLi + 1 , i = 1, 2
V G Ro + Z1//Z2 jωCi
T(jω) Si el circuito incluyera
Ro sólo el resonador 1 (2),
R2 + Ro la gráfica buscada sería
total la marcada en la figura
Ro como res 1 (res 2), ya que
res 1
res 2
R1 + Ro es un resonador serie ideal.
ω1 ωc ω2 ω
La posición relativa de las curvas deriva de los datos
(bandas de paso muy separadas, frecuencia de resonancia
más elevada en el segundo, etc.).

151. Ejemplo de respuesta en frecuencia
(función de transferencia, septiembre 1993)
Para cualquiera de los dos resonadores se tiene
ω << ωi → Zi ≈ - j∞ (por la capacidad)
ω ≈ ωi → Zi ≈ Ri (por estar en resonancia)
ω >> ωi → Zi ≈ j∞ (por la inductancia)
Sea ωc una frecuencia cualquiera mucho mayor (menor)
que las correspondientes a la banda de paso
del resonador 1 (2).
Cuando están presentes los dos resonadores se tiene
Z1(- j∞) Ro
ω << ωc → Z = Z1//Z2 ≈ ≈ Z1 → T(jω) ≈
Z1 - j∞ R o + Z1
ω ≈ ω 1 → R o + Z1 ≈ R o + R 1
j∞(- j∞)
ω≈ ωc → Z = Z1//Z2 ≈ ≈ ∞ → T(jω) ≈ 0
j∞ - j∞
(j∞)Z2 Ro
ω >> ωc → Z = Z1//Z2 ≈ ≈ Z2 → T(jω) ≈
j∞ + Z2 R o + Z2
ω ≈ ω 2 → R o + Z2 ≈ R o + R 2
Luego la curva pedida es la marcada como total en la figura.

152. Ejemplo de respuesta en frecuencia
(función de transferencia, septiembre 1998)
+ Si la función de transferencia es
C
Vo T(jω) = V o
VG L R - VG
hallar:
Son datos los valores a los que tienden
las características su módulo y su fase
de todos los elementos para ω → 0, ω = 1/ LC, y ω → ∞;
las condiciones para que el módulo
sea superior a la unidad.
T(jω) =
Vo
=
R//(jωL)
= - ω2LRC =
N(ω)
V G 1/(jωC) + R//(jωL) R(1 - ω2LC) + jωL D(ω)
ω → 0 ⇒ T(jω) ≈ - ω2LC ⇒ T(jω) ≈ ω2LC, ∠T(jω) ≈ 180 °
ω = 1/ LC ⇒ T(jω) = jR C/L ⇒ T(jω) = R L/C, ∠T(jω) = 90 °
ω → ∞ ⇒ T(jω) ≈ 1 ⇒ T(jω) ≈ 1, ∠T(jω) ≈ 0 °
T(jω) =
N(ω) N(ω)
= = ω2RLC
D(ω) D(ω) R2(1 - ω2LC)2 + (ωL)2
T(jω) ≥ 1 → N(ω) ≥ D(ω) → (ω2LRC)2 ≥ R2(1 - ω2LC)2 + (ωL)2 →
→ ω ≥ ωm = R → L < 2R2C
L(2R2C - L)

153. Ejemplo de respuesta en frecuencia
(función de transferencia, junio 2000)
Datos:
características de los elementos,
∠V G = 0 °
R +
L
Vo Hallar:
VG R C R - módulo y fase de V o
para ω → 0 y para ω → ∞;
frecuencia de resonancia.
V GR
Vo =
R(3 - 2ω2LC) + jω(R2C + 2L)
ω → 0 ⇒ Vo → VG/3 ⇒ V o → V G /3, ∠V o → 0 °
ω → ∞ ⇒ Vo → - VG/(2ω2LC) ⇒ V o → V G /(2ω2LC), ∠Vo → 180 °
La impedancia que v e la fuente es
Z = R + R//Z1
+ j ωL - ωR 2
2C
Z1 = jωL + R// 1/(jωC) = R
(ωRC)2 + 1 (ωRC) + 1
ω = ω0 → Z resistiva → Z1 resistiva → Im Z1 = 0 →
→ ω0L -
ω0R2C R 2C - L
= 0 → ω0 =
(ω0RC)2 + 1 LR2C2

154. Ejemplo de respuesta en frecuencia
(función de transferencia, junio 1999)
I R, L y C datos; ¿∠V - ∠I para ω → 0?
+
R R, L y C datos; ¿ ω (≠ 0) para ∠V = ∠I?
C V
L R, L y ω = ωa datos; ¿ C para ∠I = ∠V + 45 °?
-
R + jωL N(ω)
V = IZ, Z = (R + jωL)// 1/(jωC) = =
(1 - ω2LC) + jωRC D(ω)
ω → 0 ⇒ Z → R ⇒ ∠V = ∠I
∠V = ∠I → ∠N(ω) = ∠D(ω) → ωL = ωRC → ω= 1 - R2LC
R 1 - ω2LC LC
∠V = ∠I + ∠Z = ∠V + 45 ° + ∠Z → ∠Z = - 45 °
N(ω) N(ω)D*(ω) ya que
Z= = , ∠Z = - 45 ° → →
D(ω) D(ω)D*(ω) D(ω)D*(ω) real
→ Re N(ωa)D*(ωa) = - Im N(ωa)D*(ωa) → C = L2 + R/ωa2
R + ωa L
2

155. Ejemplo de respuesta en frecuencia
(resonancia, junio 2002)
R R
Datos:
R, L, C, a, IG (real) ig iC C aiC L
ig = IGcos(ωt)
El circuito funciona en régimen +
sinusoidal permanente. R R
VG
IG = IG - IG IC C aIC L
Impedancia que ve la fuente independiente
IG + aIC = V G + VGjωC + V G ⇒ IG = V GY = V G
R R + jωL Z
Y = 1 + j(1 - a)ωC + 1 ,Z= 1
R R + jωL Y
Módulo y fase de la tensión en la fuente dependiente
para ω ≈ 0 rad/s y ω ≈ ∞ rad/s
La tensión en ambas fuentes es igual
V G → IG R
2
ω → 0 rad/s ⇒ Y → 2 ⇒ V G → IGR ⇒
R 2
∠V G → 0 °
ω → ∞ rad/s ⇒
IG
VG →
IG (1 - a)ωC
⇒ Y → j(1 - a)ωC ⇒ VG → - j ⇒
(1 -a)ωC ∠V G → - 90 °

156. Ejemplo de respuesta en frecuencia
(resonancia, junio 2002)
Frecuencia angular (ω0 ≠ 0 rad/s) para Z puramente resistiva;
condiciones para que exista
Z resistiva ⇒ Im Y = 0 Ω ⇒ (1 - a)ω0C - 2 ω0L 2 = 0 ⇒
R + (ω0L)
0 rad/s (no vale)
L - (1 - a)R2C
⇒ ω0 = ; condición: 2C
> 0 s-2
(1 - a)L
L - (1 - a)R2C
+
(1 - a)L2C
Hallar iC(t) para C = ∞ F
C = ∞ F ⇒ VG = 0 V ⇒ IG + aIC = IC ⇒
I cos(ωt)
⇒ IC = IG ⇒ iC(t) = Re ICejωt = G
1-a 1-a

157. Ejemplo de respuesta en frecuencia
(superposición, junio 2002)
Datos:
R R
R, L, C, a, ID (real), IA (real), ω = ω0
ig iC C aiC L
Hallar la potencia en la capacidad ig(t) = ID + IAcos(ωt)
Continua + R
C = circuito abierto; L = cortocircuito VGD
- ID ICD R
ICD = 0 A, VGD = ID(R // R) = IDR
2
Sinusoidal + R R
Y(ω0) = 1 + 2 R real VGA
R R + (ω0L)2 - IA ICA C aICA L
VGA = IA ⇒ vGA(t) = Re VGAejω0t = IA cos(ω0t)
Y(ω0) Y(ω0)
jIAω0C I ωC
CA = VGAjω0C = ⇒ iCA(t) = Re ICAejω0 t = G 0 cos(ω0t + 90 °)
Y(ω0) Y(ω0)
Respuesta total
iC(t) = ICD + iCA(t), vC(t) = VGD + vGA(t), pC(t) = vC(t)iC(t)

158. Ejemplo de respuesta en frecuencia
(resonancia, septiembre 2002)
iL L R
Datos: R C
R, L, C, a, IG (real) ig aiL
ig = IGcos(ωt)
El circuito funciona en régimen + IL L C
sinusoidal permanente. VG
- IG R aIL R
IG = IG
Impedancia que ve la fuente independiente
IG + aIL = V G + VGjωC + V G ⇒ IG = V GY = V G
R R + jωL Z
Y = 1 + jωC + 1 - a , Z = 1
R R + jωL Y
Valor de a para Z imaginaria pura
= 0 ⇒ a = 2 + ωL
(1 - a)R 2
Z imaginaria ⇒ Re Y = 0 Ω ⇒ 1 + 2
R R + (ωL)2 R

159. Ejemplo de respuesta en frecuencia
(resonancia, diciembre 2002)
iL R C
iC
Datos:
R, L, C, a, IG (real) ig L aiL R
ig = IGcos(ωt)
Hallar iC(t) para C = ∞ F y L = ∞ H
El circuito funciona en régimen sinusoidal permanente.
C = ∞ F ⇒ C es un cortocircuito
L = ∞ H ⇒ L es un circuito abierto ⇒
⇒ la fuente dependiente es un circuito abierto
La corriente proporcionada por la fuente independiente se reparte
por igual entre las dos resistencias
i (t)
iC(t) = g
2

160. Ejemplo de respuesta en frecuencia
(frecuencia para entrada y salida en fase)
Son datos
las características
RL + de todos los elementos
RG RC aIL IL
R Vo Hallar la frecuencia angular
C para la que V o y V G
VG L -
están en fase
aIL = V o - V G + V o + Vo + IL, IL = Vo
RG R RC + 1/(jωC) RL + jωL
Vo = 1 1
=
VG jωRGC (1 - a)RG D(ω)
1+ + RG +
1 + jωRCC R RL + jωL
Puesto que el numerador es real,
también ha de serlo el denominador.
2
RLC + (a - 1)L
∠V o = ∠V G → Im D(ω) = 0 → ω =
(1 - a)RCLC2 - L2C
2

161. Ejemplo de respuesta en frecuencia
(frecuencia para entrada y salida en fase)
C 1:a R +
C
IG M I1 I2 Vo
VG L L -
Son datos Hallar la frecuencia angular
las características para la que V o y V G
de todos los elementos están en fase
Reflejando impedancias,
X = ωL - 1/(ωC), Z = jX + R/a2, ZG = jX + (ωM)2/Z
IG = V G/ZG, I1 = IGjωM/Z, I 2 = I1/a
VGjωRM V GjωRM
V o = I2R = =
aZGZ a (ωM)2 - X2 + jXR/a2
Puesto que el numerador es imaginario,
también ha de serlo el denominador.
(ωM)2 - X2 = 0
∠Vo = ∠VG →
X > 0 → 1/(ωC) < ωL
ω = - X/M Incompatible con la
(ωM)2 - X2 =0→ condición indicada
ω = X/M Solución correcta

162. Ejemplo de respuesta en frecuencia
(frecuencia para tensión máxima)
+ VR -
R1 R2 C L3
M
IG L1 L2
Son datos las características Hallar la frecuencia angular
de todos los elementos para la que es máximo
el módulo de V R
Transformando la fuente y reflejando impedancias,
2
I G R 1 = I R 1 + R2 + 1 + jωL1 + (ωM) = IZ
jωC jωL2 + jωL3
VR = IR2, I = IGR1/Z
V R máximo → I máximo → Z mínimo →
(R1 + R2)2 + ωL1 - 1 - ωM
2 2
→ mínimo →
ωC L2 + L3
→ Im Z = 0 → ω = 1
C L1 - M/(L2 + L3)
La parte real de Z no depende de ω.
Z sólo puede hacerse mínima
actuando sobre su parte imaginaria.

163. Ejemplo de respuesta en frecuencia
(frecuencia para tensión máxima)
IC C
R + 1:a + +
IG I1 V 1 V2 I2 IL VL
VG - - -
Son datos las características Hallar la frecuencia angular
de todos los elementos para la que es máximo
el módulo de V L
V G = IGR + V 1, V 1 = IC + V2, V2 = ILjωL
jωC
IG = I1 + IC, IC = I2 + IL, I1 = - aI2, V 2 = aV 1
VG
VL = = VG
1 + j (1 - a2)ωRC - aR D(ω)
a a ωL
VL máximo → D(ω) mínimo → Im D(ω) = 0 →
→ ω= a
(1 - a) LC
La parte real de D no depende de ω.
D sólo puede hacerse mínima
actuando sobre su parte imaginaria.

164. Ejemplo de respuesta en frecuencia
(frecuencia para impedancia resistiva, diciembre 1998)
- VC +
+ a:1
R L + + R L C
VD M I2 V 2 V1
I1 VG
- gVC L - -
Son datos Hallar la frecuencia angular
las características para la que la impedancia
de todos los elementos que v e la fuente independiente
es puramente resistiva
VD = gVC(R + jωL) + I2jωM
0 = gVCjωM + I2jωL + V2
VG = I1 R + jωL + 1/(jωC) + V 1
VC = I1/(jωC), V2 = aV1, I1 = - aI2
VG = I1 R - gM/(aC) + j ωL(1 + 1/a2) - 1/(ωC) = I1Z
Z resistiva → Im Z = 0 → ω = a
(a2 + 1)LC

165. Ejemplo de respuesta en frecuencia
(frecuencia para potencia máxima, septiembre 1998)
R IR 1:a
2C R Rd
M
IG C L L/2 L L bIR
Son datos Hallar la frecuencia angular
las características para la que la potencia media
de todos los elementos en Rd es máxima
bIR 2Rd
PRd = máxima → IR máxima
2
El módulo de IR será máximo cuando toda la corriente
de la fuente independiente circule por R.
Ello ocurrirá cuando las corrientes en L y C se compensen;
es decir, cuando L y C estén en resonancia.
Para que eso suceda ha de ser
Z C = - ZL → ω = 1
LC

166. Ejemplo de respuesta en frecuencia
(frecuencia para corriente máxima, junio 1996)
+ Son datos las características
L de todos los elementos
V1
VG
n1 - R
+ Hallar la frecuencia angular
V 2 I2 para la que es máximo el módulo de I2
I1
n2 - C
V G = I1jωL + V 1 + V 2, V 2 = I2 R + 1/(jωC)
V2/V1 = n2/n1 = a, I1/(I1 - I2) = - n2/n1 = a
aVG/(1 + a)
I2 = = VG
R + 1/(jωC) + a2jωL/(1 + a)2 D(ω)
I2 máximo → D(ω) mínimo →
→ R2 + a2ωL/(1 + a)2 - 1/(ωC) 2 mínimo →
→ Im D(ω) = 0 → ω = 1 + a
aLC
La parte real de D no depende de ω.
D sólo puede hacerse mínima actuando sobre su parte imaginaria.

167. Ejemplo de respuesta en frecuencia
(impedancia mínima y corriente máxima, problema inverso)
R1 Son datos IG, ω, R1, C1, R2 y L2
I1
IG R2 Hallar el valor de L1 que minimiza
el módulo de la impedancia de su rama,
C2 L1 L2 y el valor de C2 que maximiza
el módulo de I1
C1
1 2
Z1 = R1 + jωL1 + → Z1 = R2 + ωL1 - 1
ωC1
1
jωC1
Z1 mínimo → Im Z1 = 0 → L1 = 1/(ω2C1)
La parte real de Z1 no depende de L1.
Z1 sólo puede hacerse mínima
actuando sobre su parte imaginaria.
El módulo de I1 será máximo cuando toda la corriente
de la fuente circule por R1 y R2.
Ello ocurrirá cuando las corrientes en L2 y C2 se compensen;
es decir, cuando L2 y C2 estén en resonancia.
Para que eso suceda ha de ser
ZC2 = - ZL2 → C2 = 1
ω2L2

168. Ejercicios para resolver en clase
RESPUESTA
R L +
EN FRECUENCIA 2003/A R vO
iG R C -
Hallad los valores hacia los que tienden el
módulo y la fase de vO cuando ω tiende a 0 rad/s
iG(t) = IGcos(ωt)
y cuando ω tiende a ∞ rad/s.
Son datos IG (real, > 0), R, L y C.
Hallad la frecuencia angular de resonancia.
RESPUESTA R +
R
EN FRECUENCIA 2003/B L R vO
iG C -
Hallad los valores hacia los que tienden el
módulo y la fase de vO cuando ω tiende a 0 rad/s
iG(t) = IGcos(ωt)
y cuando ω tiende a ∞ rad/s.
Son datos IG (real, > 0), R, L y C.
Hallad la frecuencia angular de resonancia.
RESPUESTA
R L +
EN FRECUENCIA 2003/C R vO
iG R C -
Hallad los valores hacia los que tienden el
módulo y la fase de vO cuando ω tiende a 0 rad/s
iG(t) = IGcos(ωt)
y cuando ω tiende a ∞ rad/s.
Son datos IG (real, > 0), R, L y C.
Hallad la frecuencia angular de resonancia.

169. Ejemplo de respuesta en frecuencia
(circuito resonante, equivalente Thèvenin)
R x L VG C
R ZL
1:a Son datos
las características
m L n
C de todos los elementos
excepto ZL
R R
y
Hallar la frecuencia angular para la que
el módulo de la corriente en la rama x y es mínimo
Puede observarse que a la frecuencia de resonancia del secundario
éste presenta una impedancia infinita, con lo que también es infinita
la reflejada en el primario, haciendo así nulo el módulo de la
corriente en él. Luego
ω = 1/ LC
Para la frecuencia calculada hallar ZL para que disipe
máxima potencia y el valor de dicha potencia
En las condiciones indicadas
R VG el circuito se reduce al de la figura.
m x n La impedancia equivalente se calcula
R
desactivando la fuente
R y R y agrupando resistencias.
*
ZL = ZTh = R + (R + R)//R * = 5R/3
VTh = Vxn = Vmn = VG - VGR = 2V G
3R 3
Pmax = VTh 2/ 8Re ZTh = V G 2/(30R)

170. Ejemplo de respuesta en frecuencia
(superposición, resonancia, inverso a partir de expresiones temporales, diciembre 1996)
+
R R
L C
bvP R Hallar a y b
1:a
iS + L V G vP (reales)
vL
RL - C -
Datos:
iS(t) = IScos(ωt), IS = 8 mA, ω = π krad/s, VG = 30 V,
R = 1 kΩ, RL = 250 Ω, L = π-2 H, C = 1 µF,
vL(1 ms) = - 6 V, vL(4 ms) = - 4 V
Por haber dos fuentes de distinta naturaleza,
vL(t) = VLD + VLAcos(ωt + ϕ) (1)
+ Continua
R + R VG
VLD Fuente corriente desactivada
vPD
RL - bVPD R - IG L = c.c., C = c.a.
VLD = - bVPD = - b(VG - IG R) = - b VG - VGR = - 10 b (2)
R + R//R

171. Ejemplo de respuesta en frecuencia
(superposición, resonancia, inverso a partir de expresiones temporales, diciembre 1996)
bVPA R Sinusoidal
+ RL + 1:a + + Fuente tens. ind. desactivada
I2 V L-C serie = c.c.
VLA I V1 V2 PA
IS - IL 1 - - R - y L-C paralelo = c.a.
por ser ω = 1/ LC
IS = IL + I1, I1 = aI2, V 2 = aV 1, V PA = V 2/2
8 (2 - ab)
LRL = VLA = bV PA + V1 → V LA = = VLA∠0 ° (3)
a2 + 4(2 - ab)
Respuesta combinada
Ya que la fase de la componente sinusoidal es nula, de (1)
vL(1 ms) = VLD - VLA = - 6 V VLD = - 5 V
vL(4 ms) = VLD + VLA = - 4 V VLA = 1 V
Igualando estos resultados a (2-3),
b = 0.5, a = - 4 o a = 2
El valor negativo de a es posible; equivaldría a invertir
la posición de uno de los puntos en el transformador.

173. Análisis de redes
Transparencias de clase
Cuadripolos
Cuadripolos-1: páginas 171-175
Cuadripolos-2: páginas 176-187

175. Cuadripolos
Un circuito se reduce a una caja negra con dos puertas.
La caracterización del circuito como cuadripolo
pretende describir su comportamiento
en función de lo que ocurre en las puertas.
circuito No hay fuentes
i1 i2 independientes
excitación
entrada
+ + en el cuadripolo.
salida
carga
v1 v2
- - Sin excitación externa
no hay energía
i1 cuadripolo i2 almacenada
en el cuadripolo.
Clasificación
Pasivos: la potencia entregada a la carga
es siempre igual o inferior
a la que la excitación entrega a la entrada.
Activos: la potencia entregada a la carga
puede ser mayor que la que la excitación entrega
a la entrada del cuadripolo.

176. Caracterización de un cuadripolo
Se hace en función de un juego de cuatro parámetros
(parámetros característicos)
que relacionan las corrientes y tensiones
en la entrada y la salida del cuadripolo.
Parámetros Ecuaciones Matrices
Impedancia v1 = z11i1 + z12i2 v1 = z11 z12 × i1
v2 = z21i1 + z22i2 v2 z21 z22 i2
Admitancia i1 = y11v1 + y12v2 i1 = y11 y12 × v1
v2
i2 = y21v1 + y22v2 i2 y21 y22
Híbridos (h) v1 = h11i1 + h12v2 v1 = h11 h12 i
× v1
i2 = h21i1 + h22v2 i2 h21 h22 2
Híbridos (g) i1 = g11v1 + g12i2 i1 = g11 g12 × v1
v2 = g21v1 + g22i2 v2 g21 g22 i2
Transmisión v1 = Av2 - Bi2 v1 = A B × v2
i1 = Cv2 - Di2 i1 C D - i2
En continua los parámetros de impedancia y admitancia son,
respectivamente, de resistencia y conductancia.
En régimen sinusoidal permanente
la caracterización puede ser expresada en términos de fasores.
Cuadripolos z12 = z21, y12 = y21,
recíprocos h12 = - h21, g12 = - g21, AD - BC = 1
Cuadripolos Son recíprocos y, además,
simétricos z11 = z22, y11 = y22,
h11h22 - h12h21 = 1, g11g22 - g12g21 = 1, A = D

177. Obtención de parámetros
Caso general: aplicando las definiciones
z11 = v1 impedancia de entrada
i1 i2 = 0 con la salida en circuito abierto
h21 = i2 ganancia de corriente directa
i1 v2 = 0 con la salida en cortocircuito
A = v1
v2 i2 = 0 ganancia inversa de tensión
con la salida en circuito abierto
Caso particular
Si se conoce el interior del cuadripolo,
se puede caracterizar el comportamiento del circuito
mediante dos ecuaciones e identificar sus términos
con los de las ecuaciones de los parámetros deseados.
Equivalencia entre parámetros
Conocido un juego de parámetros es posible obtener otro
manipulando las ecuaciones del primero.
i1 = z22 v1 - z12 v2 y11 = z22 , y12 = - z12
v1 = z11i1 + z12i2 → ∆z ∆z → ∆z ∆z
v2 = z21i1 + z22i2 z21 v + z11 v z z11
i2 = - 1 2 y21 = - 21 , y22 =
∆z ∆z ∆z ∆z
∆z = z11z22 - z12z21

178. Utilización práctica
i1 i2
v G = i1 Z G + v1
+ +
ZG v 2 = - i2 Z L
v1 cuadripolo v2 ZL
vG - - dos ecuaciones
de parámetros
Utilizando las cuatro ecuaciones
es posible encontrar cualquier relación deseada en el circuito
Zin = v1 = z11 - z12z21 impedancia de entrada
i1 z22 + ZL al cuadripolo
i2 = y21 transconductancia
vG 1 + y22ZL
*
ZL = v2 = B + DZG
* impedancia de carga
i2 A + CZG para máxima potencia
(prescindiendo de excitación)
Gi = i2 = h21 ganancia de corriente
i1 1 + h22ZL

179. Interconexión de cuadripolos
Conexión Esquema Resultado
Cascada 1 2 ABCD =
= ABCD 1 × ABCD 2
1
Serie z = z1+ z2
2
1
Paralelo y = y1+ y2
2
1
Serie- h = h1+ h2
paralelo 2
1
Paralelo- g = g1+ g2
serie 2
Supondremos que las reglas son válidas en todos los casos,
aunque estrictamente hablando
sólo lo son en el caso de la agrupación en cascada.

180. Problemas de cuadripolos
(parámetros a partir de definición, junio 1998)
I1 I2 Régimen sinusoidal;
+ + son datos las características
Z de los elementos
V1 1 V2
- Z2 Z3 -
Hallar los parámetros indicados
z11 = V 1 = Z1 + Z2//Z3 V1 = I1(Z1 + Z2//Z3)
I1 I2 = 0
h21 = I2 I2 se va por Z1, ya que,
=-1
I1 V2 = 0 de lo contrario, V 2 ≠ 0
B = - V1 = Z1 V 1 = I1Z 1 = - I2Z 1
I2 V2 = 0
y22 = I2 = 1/(Z1//Z2//Z3)
V2 V1 = 0

181. Problemas de cuadripolos
(parámetros y a partir de definición, junio 1999)
I1 I2 Régimen sinusoidal;
+ + son datos las características
Z de los elementos
V1 1 V2
- Z2 Z3 -
Hallar los parámetros de admitancia,
y las condiciones
de reciprocidad y simetría
y11 = I1 = 1
V1 V2 = 0 Z1 V 1 = I1Z 1
y12 = I1 V 1 = I1Z 1 + V 2
=- 1
V2 V1 = 0 Z1
y21 = I2 I2 se va por Z1, ya que,
=- 1
V1 V2 = 0 Z1 de lo contrario, V 2 ≠ 0
y22 = I2 = 1/(Z1//Z2//Z3) = 1 + 1 + 1
V2 V1 = 0 Z1 Z2 Z3
recíproco → y12 = y21
se cumple siempre, independientemente de los valores
de las impedancias
simétrico → y11 = y22 → Z2 = - Z3

182. Problemas de cuadripolos
(parámetros z a partir del circuito, relaciones, potencias, septiembre 1996)
I1 + V4 - I2
ZG
+
R1 R2
+ n4 +
V1 M V3 V2 ZL
VG - L1 L2 I3 - n3 -
Régimen sinusoidal permanente;
son datos las características de todos los elementos
Hallar los parámetros de impedancia del cuadripolo,
I2, y las potencias media y reactiva en ZL
V 1 = I1(R1 + jωL1) - I3jωM, 0 = - I1jωM + I2(R2 + jωL2) + V 3
V3 = V4 + V2, V4/V3 = - n4/n3, (I3 + I2)/I2 = - n4/n3
V1 = I1(R1 + jωL1) + I2jωM(1 + n4/n3)
⇔
V2 = I1jωM(1 + n4/n3) + I2(R2 + jωL2)(1 + n4/n3)2
⇔ V1 = I1z11 + I2z12 →
V2 = I1z21 + I2z22
z11 = R1 + jωL1, z12 = jωM(1 + n4/n3)
→
z21 = jωM(1 + n4/n3), z22 = (R2 + jωL2)(1 + n4/n3)2
V1 = I1z11 + I2z12, V2 = I1z21 + I2z22 →
V G = I 1 Z G + V 1 , V 2 = - I2Z L
→
z21VG
I2 = -
(ZG + z11)(ZL + z22) - z12z21
SL = - V2I*2/2 = - I 2 2ZL/2 → PL = Re SL , QL = Im SL

183. Problemas de cuadripolos
(parámetros z a partir del circuito, simetría, parámetros abcd, junio 2002)
¿Qué condiciones han de C1 C2
cumplirse para que sea simétrico? + +
V1 I1 I2 V 2
Hallar los parámetros abcd - L -
Régimen sinusoidal permanente;
son datos las características de
todos los elementos
1 + jωL + I2jωL
V 1 = I1
jωC1 ⇔ V1 = I1z11 + I2z12 ⇒
V2 = I1jωL + I2 1 + jωL V2 = I1z21 + I2z22
jωC2
z11 = 1 + jωL, z12 = jωL recíproco (z12 = z21 siempre)
⇒ jωC1 ⇒
z21 = jωL, z22 = 1 + jωL simétrico si z11 = z22 ⇒ C1 = C2
jωC2
I1 = z 2 - Izz22
V 2
V1 = I1z11 + I2z12 ⇔ 21 21
⇒
V2 = I1z21 + I2z22 V2z11 - I2(z11z22 - z12z21)
V1 = z z21
21
+L 1 + 1- 1
a = z11 = 1 - 2 1 , b = z11z22z z12z21 = ω 1C2
- C1 C2 2C
⇒
z21 ω LC1 21 jωL
c = z1 = 1 , d = z21 = 1 - 2 1
21 jωL z21 ω LC2

184. Problemas de cuadripolos
(parámetros ABCD a partir del circuito, agrupación, diciembre 1998)
I1 I2 Cuadripolo en continua;
+ R2 + son datos
R
V1 1 V2 las características
- gVV2 g II 1 - de todos los elementos
Hallar parámetros ABCD
I2 = gII1 + V2 gv - R1 - R1 gI
R2 ≡ V1 = AV2 - BI2 → ABCD = gIR2
I1 = CV2 - DI2
V 1 = R1 I 1 + gv V 2 - 1 1
-g
gIR2 I
gv y (1/R2) despreciables;
se conectan en cascada k cuadripolos idénticos
Hallar los parámetros ABCD del cuadripolo resultante
0 - R1
gI
gv, (1/R2) despreciables → ABCD ind = →
0 -g1
I
0 (- 1)k Rk1
→ ABCD k = ABCD k = gI
ind
0 (- 1)k 1k
gI

185. Problemas de cuadripolos
(parámetros ABCD a partir del circuito, agrupación, diciembre 1998)
Se carga el cuadripolo resultante del apartado anterior
con una resistencia RL
Hallar el valor de k para que el módulo de I2/I1
valga al menos GI
En un cuadripolo cargado,
I1 = CV2 - DI2, V2 = - I2RL → I2 = - 1
I1 CRL + D
Sustituyendo los resultados del apartado anterior
en esta expresión,
I2 = - 1 = gk log(GI)
GI ≤ I → k≥
I1 D (- 1)k log( gI )

186. Problemas de cuadripolos
(parámetros ABCD a partir de medidas, agrupaciones, junio 1997)
I1 I2 Datos:
+
continua, cuadripolo simétrico;
+
V1 V2 medida: V1 = 8 V, I1 = 6 A,
- - V2 = 2 V; I2 = 0 A
Hallar parámetros ABCD
V1 = AV2 - BI2, I1 = CV2 - DI2
A = V1 = 4, C = I1 =3S
V2 I2 = 0 V2 I2 = 0
simétrico (y recíproco) → D = A = 4, B = (AD - 1)/C = 5 Ω
I1 I2 R=1Ω
1
+ +3 Hallar parámetros ABCD
R
V1 V2 del cuadripolo 1234;
2 - - 4 ¿es recíproco, simétrico?
Se trata de la agrupación en cascada de dos cuadripolos:
el original y el constituido por la resistencia. En el segundo,
V1 = V2 + I1R → A = 1, B = R = 1 Ω, C = 0 S, D = 1
I 1 = - I2
ABCD 1234 = ABCD × ABCD R = 4 S9 Ω 3 7
AD - BC = 1 (recíproco), A ≠ D (no simétrico)

187. Problemas de cuadripolos
(parámetros ABCD a partir de medidas, agrupaciones, junio 1997)
Se conectan en paralelo-serie dos cuadripolos 1234
Hallar los parámetros g del cuadripolo resultante;
¿es recíproco, simétrico?
V2 = V1 + BI2 I = g11V1 + g12I2
V1 = AV2 - BI2 A A
→ ≡ 1
I1 = CV2 - DI2 CV1 + BC - D I V2 = g21V1 + g22I2
I1 = 2
A A
0.75 S - 0.25
g 1234 =
0.25 2.25 Ω
Por tratarse de una conexión paralelo-serie,
1.5 S - 0.5
g = g 1234 + g 1234 =
0.5 4.5 Ω
g12 = - g21 (recíproco), g11g22 - g12g21 ≠ 1 (no simétrico)

188. Problemas de cuadripolos
(parámetros z a partir de medidas, potencias, septiembre 1997)
I1 I2
Hallar RL para máxima
+ +
RG transferencia de potencia,
V1 V2 RL
VG y la potencia
- -
en el cuadripolo
Datos: VG = 8 V, RG = 11 Ω, continua,
cuadripolo recíproco, parámetros z positivos;
medida 1: V1 = 100 V, I1 = 20 A, I2 = 0 A;
medida 2: V1 = 0 V, I1 = 8 A, V2 = 2 V;
medida 3: I1 = 0 A, V2 = 3 V, I2 = 1 A
V1 = I1z11 + I2z12 (1)
V2 = I1z21 + I2z22 (2)
Despejando I2 de (2) y sabiendo que z12 = z21 (recíproco),
2
V1 = I1(z11 - z12/z22) + V2z12/z22 (3)
medida 1 en (1) → z11 = 5 Ω
medida 3 en (2) → z22 = 3 Ω
medida 2 en (3) → z12 = z21 = 4 Ω, - 3.75 Ω (no vale)
V1 = I1z11 + I2z12, V2 = I1z21 + I2z22 →
V G = I1 R G + V 1
V2
→ RL = RTh = = z22 - z12z21 = 2 Ω
I2 VG = 0 RG + z11
p(VG) = - VGI1 = - 5 W , p(RG ) = I2RG = 4.3 W, p(RL) = I2RL = 0.5 W
1 2
p(VG) = p(RG) + p(RL) + pcuad → pcuad = 0.2 W

189. Problemas de cuadripolos
(parámetros ABCD a partir de un cuadripolo mayor, simetría, septiembre 1998)
Un cuadripolo tiene los parámetros de transmisión
A B = 7 12 Ω
C D 4S 7
Es el resultado de agrupar en cascada
dos cuadripolos idénticos con parámetros
a b
c d
tales que b = 3c y a es un entero positivo.
Hallar a, b, c y d
A B = a b × a b = a2 + bc b(a + d)
C D c d c d c(a + d) d2 + bc
El cuadripolo original es simétrico (AD - BC = 1, A = D);
por tanto,
A = D ⇒ a2 = d2 → a = - d (no vale, a = que → B = 0 = C)
ya
d
Teniendo en cuenta esto, y que b = 3c,
4 = C = c(a + d) → c = 2/a
7 = A = a2 + bc = a2 + 3c2 = a2 + 12/a2 →
a = 2 → b = 3 Ω, c = 1 S, d = 2
→ a = -2 (ha de ser positivo)
a = ± 3 (ha de ser entero)

190. Problemas de cuadripolos
(parámetros h a partir de un cuadripolo mayor, simetría, septiembre 2001)
Un cuadripolo es el resultado de la conexión serie-paralelo
de otros dos idénticos y simétricos.
En el cuadripolo se hacen dos medidas con la salida en cortocircuito:
medida 1: V1 = VX, I1 = YVX
medida 2: I1 = IX, I2 = GIX
Hallar los parámetros h de los cuadripolos individuales.
En conexión serie-paralelo
H11 H12 = h11 h12 h11 h12
+ =
H21 H22 h21 h22 h21 h22
recíproco ⇒ h12 = - h21 2h11 2h12
= = 2
simétrico ⇒ h11h22 - h12h21 - 2h12 2 1 - h12
h11
A partir de la definición de los parámetros h y de las medidas se tiene
V1 = H11I1 + H12V2, I2 = H21I1 + H22V2; V2 = 0 V
H11 = V1 = 1 = 2h11 ⇒ h11 = 1
I1 V2 = 0 V Y 2Y
H21 = I2 = G = - 2h12 ⇒ h12 = - G = - h21
I1 V2 = 0 V 2
1 - h12 = Y(4 - G2) ⇒ h = Y(4 - G2)
2
2h22 = H22 = 2 22
h11 2

191. Problemas de cuadripolos
(parámetros h, equivalente Thèvenin, junio 2001)
De un cuadripolo, que funciona en régimen sinusoidal permanente,
se conocen sus parámetros híbridos.
A su entrada se conecta una fuente (V G)
con una impedancia en serie (ZG).
Hallar el equivalente Thèvenin en la salida.
Tensión de circuito abierto
I2 = h21I1 + h22V2 = 0 A ⇒ I1 = - h22 V 2
h21
h (Z + h11)
VG = I1ZG + V1 = I1(ZG + h11) + h12V2 = h12 - 22 G V2 ⇒
h21
h21VG
⇒ V2 = = VTh
h12h21 - h22(ZG + h11)
Corriente de cortocircuito
V2 = 0 V ⇒ I2 = h21I1
VG = I1ZG + V1 = I1(ZG + h11) = - ZG + h11 I2 ⇒ I2 = - h21VG = IN
h21 ZG + h11
Impedancia equivalente
ZTh = VTh = ZG + h11
IN h22(ZG + h11) - h12h21