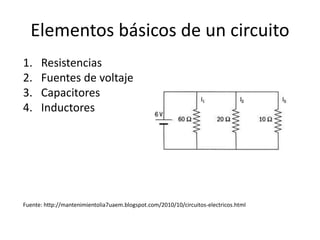
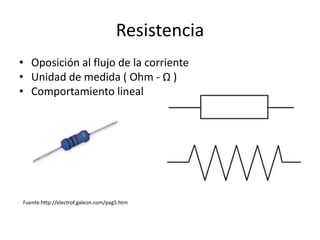
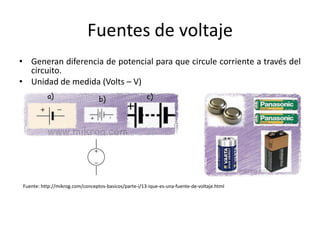
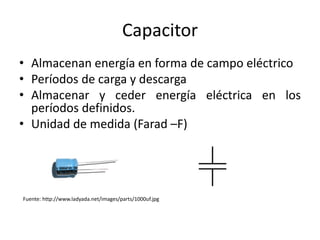
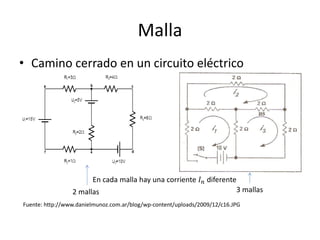
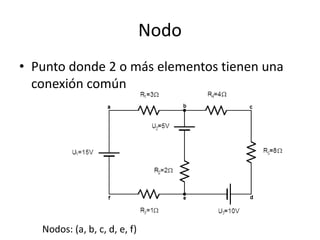
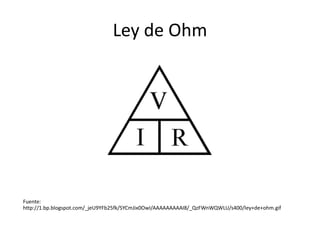
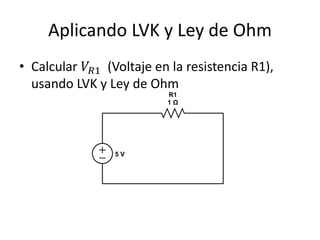
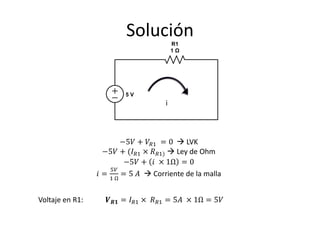
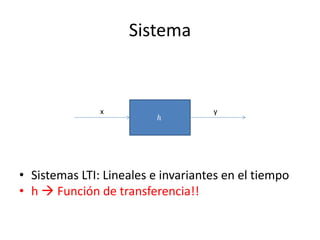
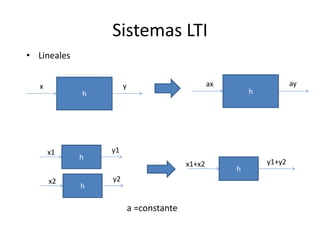
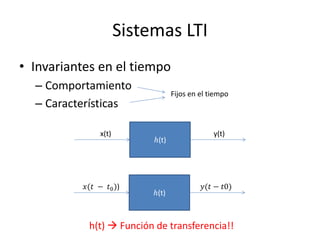
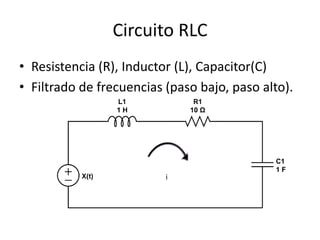
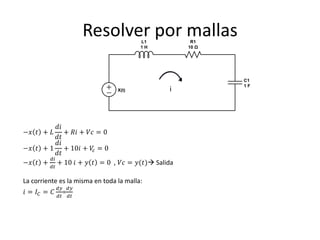
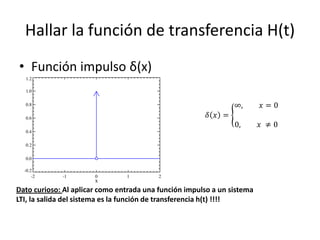
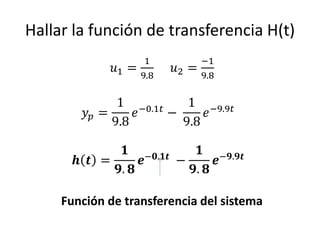
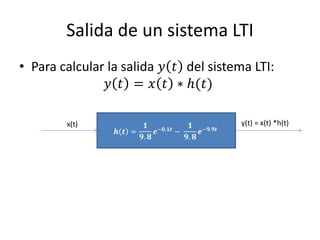
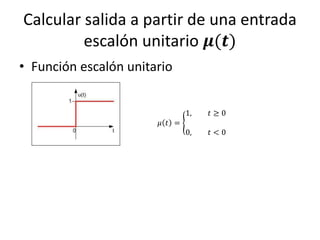
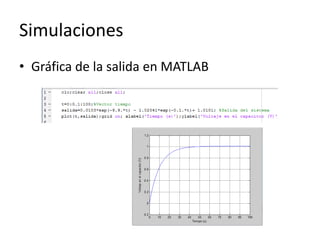
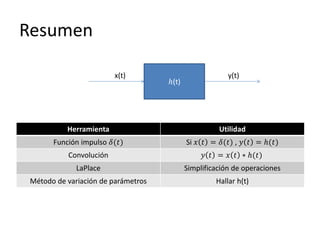
Este documento resume los elementos básicos de un circuito eléctrico como resistencias, fuentes de voltaje, capacitores e inductores. Explica conceptos clave como mallas, nodos, leyes de Kirchhoff y la ley de Ohm. Además, introduce el modelado de circuitos con ecuaciones diferenciales de orden superior, describiendo sistemas lineales e invariantes en el tiempo y cómo resolverlos mediante la función de transferencia.

1. Modelado de circuitos con ED de
orden superior
JUAN CAMILO SACANAMBOY
UNIVERSIDAD ICESI

2. Elementos básicos de un circuito
1. Resistencias
2. Fuentes de voltaje
3. Capacitores
4. Inductores
Fuente: http://mantenimientolia7uaem.blogspot.com/2010/10/circuitos-electricos.html

3. Resistencia
• Oposición al flujo de la corriente
• Unidad de medida ( Ohm - Ω )
• Comportamiento lineal
Fuente:http://electrof.galeon.com/pag5.htm

4. Fuentes de voltaje
• Generan diferencia de potencial para que circule corriente a través del
circuito.
• Unidad de medida (Volts – V)
Fuente: http://mikrog.com/conceptos-basicos/parte-i/13-ique-es-una-fuente-de-voltaje.html

5. Capacitor
• Almacenan energía en forma de campo eléctrico
• Períodos de carga y descarga
• Almacenar y ceder energía eléctrica en los
períodos definidos.
• Unidad de medida (Farad –F)
Fuente: http://www.ladyada.net/images/parts/1000uf.jpg

6. Inductor
• Almacenan energía en forma de campo
magnético
• Se oponen a los cambios bruscos de la corriente
• Unidad de medida (Henrio – H)
• Fuente: http://www.clker.com/cliparts/6/9/a/8/1223615567190235753rsamurti_RSA_IEC_Inductor_Symbol-
1.svg.med.png

7. Partes de un circuito
1. Mallas
2. Nodos

8. Malla
• Camino cerrado en un circuito eléctrico
En cada malla hay una corriente 𝐼 𝑛 diferente
2 mallas 3 mallas
Fuente: http://www.danielmunoz.com.ar/blog/wp-content/uploads/2009/12/c16.JPG

9. Nodo
• Punto donde 2 o más elementos tienen una
conexión común
Nodos: (a, b, c, d, e, f)

10. Ley de Ohm
Fuente:
http://1.bp.blogspot.com/_jeU9YFb25fk/SYCmJix0OwI/AAAAAAAAAI8/_QzFWnWQWLU/s400/ley+de+ohm.gif

11. Leyes de Kirchhoff
• Ley de voltajes (LVK)  Método de mallas
• Ley de corrientes (LCK)  Método de nodos

12. LVK-Ley de Voltajes
• La suma de voltajes en una malla es igual a cero.
Fuente: http://es.wikipedia.org/wiki/Leyes_de_Kirchhoff

13. Aplicando LVK y Ley de Ohm
• Calcular 𝑉 𝑅1 (Voltaje en la resistencia R1),
usando LVK y Ley de Ohm

14. Solución
i
−5𝑉 + 𝑉 𝑅1 = 0  LVK
−5𝑉 + (𝐼 𝑅1 × 𝑅 𝑅1)  Ley de Ohm
−5𝑉 + 𝑖 × 1Ω = 0
5𝑉
𝑖 = 1 Ω = 5 𝐴  Corriente de la malla
Voltaje en R1: 𝑽 𝑹𝟏 = 𝐼 𝑅1 × 𝑅 𝑅1 = 5𝐴 × 1Ω = 5𝑉

15. ¿Por qué se usan ED para modelar
circuitos?
• Cuando se involucran componentes que no tienen un
comportamiento lineal (Capacitores e inductores).

16. Sistema
x y
ℎ
• Sistemas LTI: Lineales e invariantes en el tiempo
• h  Función de transferencia!!

17. Sistemas LTI
• Lineales
x y ax ay
h h
x1 y1
h
x1+x2 y1+y2
h
x2 y2
h
a =constante

18. Sistemas LTI
• Invariantes en el tiempo
– Comportamiento
Fijos en el tiempo
– Características
x(t) y(t)
ℎ(t)
𝑥(𝑡 − 𝑡0 )) 𝑦(𝑡 − 𝑡0)
ℎ(t)
h(t)  Función de transferencia!!

19. Circuito RLC
• Resistencia (R), Inductor (L), Capacitor(C)
• Filtrado de frecuencias (paso bajo, paso alto).
i

20. Fórmulas
Resistencia Capacitor Inductor
𝑉𝑅 = 𝐼 𝑅 × 𝑅 𝑅 1 𝑑𝑖
𝑉𝐶 = 𝑖 𝑡 𝑑𝑡 𝑉𝐿 = 𝐿
𝐶 𝑑𝑡
𝑉𝑅 𝑑𝑉 1
𝐼𝑅 = 𝐼𝐶 = 𝐶 𝐼𝐿 = 𝑉 𝑡 𝑑𝑡
𝑅𝑅 𝑑𝑡 𝐿

21. Resolver por mallas
i
𝑑𝑖
−𝑥 𝑡 + 𝐿 + 𝑅𝑖 + 𝑉𝑐 = 0
𝑑𝑡
𝑑𝑖
−𝑥 𝑡 + 1 + 10𝑖 + 𝑉𝑐 = 0
𝑑𝑡
𝑑𝑖
−𝑥 𝑡 + + 10 𝑖 + 𝑦 𝑡 = 0 , 𝑉𝑐 = 𝑦(𝑡) Salida
𝑑𝑡
La corriente es la misma en toda la malla:
𝑑𝑦 𝑑𝑦
𝑖 = 𝐼𝐶 = 𝐶 =
𝑑𝑡 𝑑𝑡

22. Reemplazando
𝑑2 𝑦 𝑑𝑦
−𝑥 𝑡 + + 10 + 𝑦 𝑡 =0
𝑑𝑡 2 𝑑𝑡
𝒅𝟐 𝒚 𝒅𝒚
+ 𝟏𝟎 + 𝒚 𝒕 = 𝒙 𝒕 ED que representa al
𝒅𝒕 𝟐 𝒅𝒕
sistema
x(t)  Entrada del sistema
i) Homogénea
𝑑2 𝑦 𝑑𝑦
+ 10 + 𝑦 𝑡 =0
𝑑𝑡 2 𝑑𝑡
Ecuación auxiliar
𝑠 2 + 10𝑠 + 1 = 0
𝑟1 = −0.1 𝑟2 = −9.9
Solución del homogéneo
𝒚 𝑪 𝒕 = 𝑪 𝟏 𝒆−𝟎.𝟏𝒕 + 𝑪 𝟐 𝒆−𝟗.𝟗𝒕

23. Hallar la función de transferencia H(t)
• Método de variación de parámetros
𝑑2 𝑦 𝑑𝑦
– Ecuación + 𝑘 𝑑𝑥 + +𝑞𝑦 = 𝑓(𝑥) , Raíces: 𝑦1 y 𝑦2
𝑑𝑥
– Hallar solución particular 𝑦 𝑝 = 𝑢1 𝑦1 + 𝑢2 𝑦2 , donde:
′ 𝑊1 ′ 𝑊2
𝑢1 = 𝑢2 =
𝑊 𝑊
𝑦1 𝑦2
𝑊= 𝑦1 ′ 𝑦2 ′
0 𝑦2
𝑊1 =
𝑓(𝑥) 𝑦2 ′
𝑦1 0
𝑊2 =
𝑦1 ′ 𝑓(𝑥)

24. Hallar la función de transferencia H(t)
– Retomando:
𝑑2 𝑦 𝑑𝑦
+ 10 + 𝑦 𝑡 = 𝑥 𝑡
𝑑𝑡 2 𝑑𝑡
𝑦1 𝑡 = 𝑒 −0.1𝑡 𝑦2 𝑡 = 𝑒 −9.9𝑡
𝑊= 𝑒 −0.1𝑡 𝑒 −9.9𝑡 −𝑡
+ 0.1𝑒 −𝑡 = −9.8𝑒 −𝑡
−9.9𝑡 = −9.9𝑒
−0.1𝑒 −0.1𝑡 −9.9𝑒
0 𝑒 −9.9𝑡
𝑊1 = = −𝑥(𝑡)𝑒 −9.9𝑡
𝑥(𝑡) −9.9𝑒 −9.9𝑡
𝑒 −0.1𝑡 0
𝑊2 = = 𝑥(𝑡)𝑒 −0.1𝑡
−0.1𝑒 −0.1𝑡 𝑥(𝑡)

25. Hallar la función de transferencia H(t)
′ −𝑥 𝑡 𝑒 −9.9𝑡 ′ 𝑥 𝑡 𝑒 −0.1𝑡
𝑢1 = 𝑢2 =
−9.8𝑒 −𝑡 −9.8𝑒 −𝑡
−𝑥 𝑡 𝑒 −9.9𝑡 𝑥 𝑡 𝑒 −0.1𝑡
𝑢1 = 𝑑𝑡 𝑢2 = 𝑑𝑡
−9.8𝑒 −𝑡 −9.8𝑒 −𝑡
−𝛿 𝑡 𝑒 −9.9𝑡 𝛿 𝑡 𝑒 −0.1𝑡
𝑢1 = 𝑑𝑡 𝑢2 = 𝑑𝑡
−9.8𝑒 −𝑡 −9.8𝑒 −𝑡
Se pone como entrada 𝑥(𝑡), a la función impulso
(también llamada función delta de dirac) 𝛿(𝑡)

26. Hallar la función de transferencia H(t)
• Función impulso δ(x)
∞, 𝑥=0
𝛿 𝑥 =
0, 𝑥 ≠0
Dato curioso: Al aplicar como entrada una función impulso a un sistema
LTI, la salida del sistema es la función de transferencia h(t) !!!!

27. Hallar la función de transferencia H(t)
• Propiedad de la función impulso δ(t)
𝛿 𝑡 − 𝑡0 𝑓 𝑡 𝑑𝑡 = 𝑓(𝑡0 )

28. Hallar la función de transferencia H(t)
1 −1
𝑢1 = 𝑢2 =
9.8 9.8
1 −0.1𝑡 1 −9.9𝑡
𝑦𝑝 = 𝑒 − 𝑒
9.8 9.8
𝟏 −𝟎.𝟏𝒕 𝟏 −𝟗.𝟗𝒕
𝒉 𝒕 = 𝒆 − 𝒆
𝟗. 𝟖 𝟗. 𝟖
Función de transferencia del sistema

29. Representación del sistema LTI
x(t) 𝟏 −𝟎.𝟏𝒕 𝟏 −𝟗.𝟗𝒕 y(t)
𝒉 𝒕 = 𝒆 − 𝒆
𝟗. 𝟖 𝟗. 𝟖

30. Salida de un sistema LTI
• Teniendo la función de transferencia ℎ(𝑡), se puede determinar cual es la
salida del sistema 𝑦(𝑡) , dada una entrada 𝑥(𝑡) , por medio de la
convolución
• Convolución
∞
𝑟 𝑡 ∗ 𝑠 𝑡 = −∞
𝑟 𝜏 𝑠 𝑡 − 𝜏 𝑑𝜏
Convolución de un pulso
cuadrado (entrada) ante el impulso
de un condensador
Salida del sistema
Fuente: Wikipedia

31. Salida de un sistema LTI
• Para calcular la salida 𝑦 𝑡 del sistema LTI:
𝑦 𝑡 = 𝑥 𝑡 ∗ ℎ(𝑡)
x(t) 𝟏 −𝟎.𝟏𝒕 𝟏 −𝟗.𝟗𝒕 y(t) = x(t) *h(t)
𝒉 𝒕 = 𝒆 − 𝒆
𝟗. 𝟖 𝟗. 𝟖

32. Calcular salida a partir de una entrada
escalón unitario 𝝁(𝒕)
• Función escalón unitario
1, 𝑡≥0
𝜇 𝑡 =
0, 𝑡<0

33. Calcular salida a partir de una entrada
escalón unitario 𝝁(𝒕)
• Hallando la salida 𝑦 𝑡
𝑦 𝑡 = 𝑥 𝑡 ∗ ℎ 𝑡 𝜇 𝑡 = 𝜇 𝑡 ∗ ℎ 𝑡 𝜇 𝑡
Se añade una función escalón a la función de
transferencia, para indicar que no se tenga en
cuenta los valores donde t<0

34. Calcular salida a partir de una entrada
escalón unitario 𝝁(𝒕)
∞
𝑦 𝑡 = 𝜇 𝜏 ℎ 𝑡 − 𝜏 𝜇(𝑡 − 𝜏)𝑑𝜏
−∞
La función 𝜇(𝑡), indica que sólo se debe calcular la integral a partir de
𝑡≥0
La función 𝜇 𝑡 − 𝜏 , indica que sólo se debe calcular la integral para
𝜏≤ 𝑡
𝜇 𝑡 − 𝜏 = 1 cuando 𝑡 − 𝜏 ≥ 0
Con esto, cambian los límites de integración.

35. Calcular salida a partir de una entrada
escalón unitario 𝝁(𝒕)
𝑡
𝑦 𝑡 = ℎ 𝑡 − 𝜏 𝑑𝜏
0
𝑡
1 −0.1(𝑡−𝜏) 1 −9.9 𝑡−𝜏
𝑦 𝑡 = 𝑒 − 𝑒 𝑑𝜏
9.8 9.8
0
𝑡 𝑡
1 −0.1𝑡 0.1𝜏 1 −9.9𝑡 9.9𝜏
𝑦 𝑡 = 𝑒 𝑒 𝑑𝜏 − 𝑒 𝑒 𝑑𝜏
9.8 9.8
0 0
𝑡 𝑡
1 −0.1𝑡 1 −9.9𝑡
𝑦 𝑡 = 𝑒 𝑒 0.1𝜏 𝑑𝜏 − 𝑒 𝑒 9.9𝜏 𝑑𝜏
9.8 9.8
0 0
1 −0.1𝑡 1 −9.9𝑡 1 9.9𝑡 1
𝑦 𝑡 = 𝑒 10𝑒 0.1𝑡 − 10 − 𝑒 𝑒 −
9.8 9.8 9.9 9.9
𝒚 𝒕 = 𝟎. 𝟎𝟏𝟎𝟑𝒆−𝟗.𝟗𝒕 − 𝟏. 𝟎𝟐𝟎𝟒𝒆−𝟎.𝟏𝒕 + 𝟏. 𝟎𝟏𝟎𝟏
Salida del sistema ante una entrada escalón

36. Simulaciones
• Gráfica de la salida en MATLAB

37. Simulaciones
• Simulación del sistema en Simulink, usando la
transformada de LaPlace para representar H(t)

38. Resumen
x(t) y(t)
ℎ(t)
Herramienta Utilidad
Función impulso 𝛿(𝑡) Si 𝑥 𝑡 = 𝛿(𝑡) , 𝑦 𝑡 = ℎ(𝑡)
Convolución 𝑦 𝑡 = 𝑥 𝑡 ∗ ℎ(𝑡)
LaPlace Simplificación de operaciones
Método de variación de parámetros Hallar h(t)