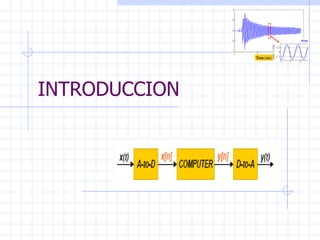
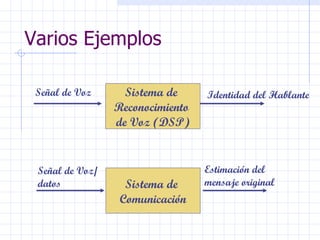
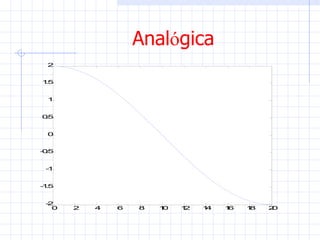
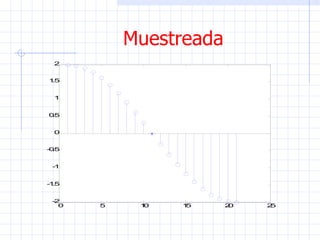
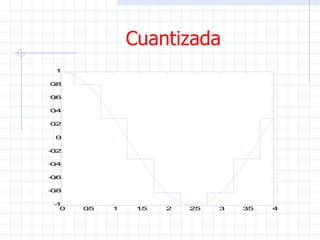
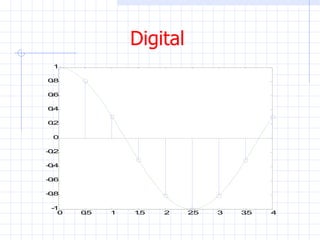
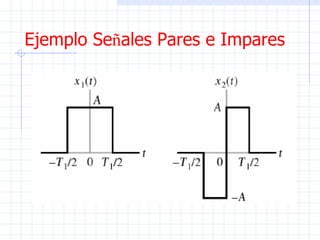
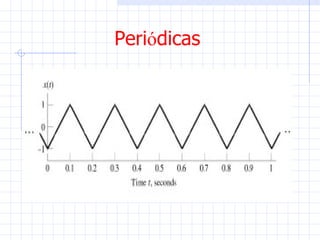
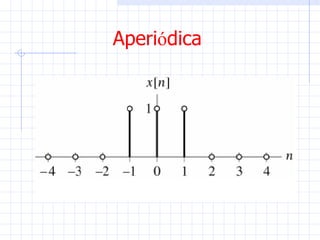
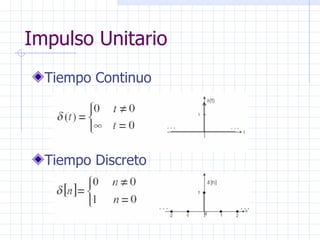
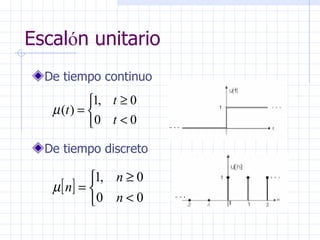
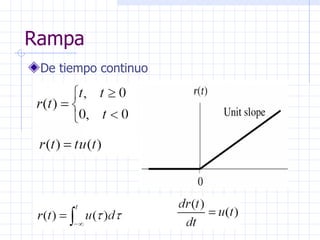
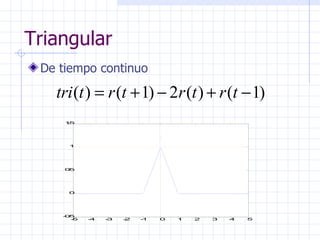
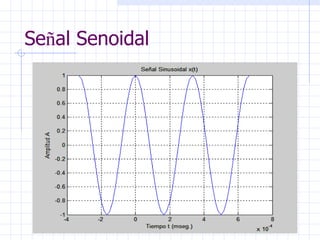
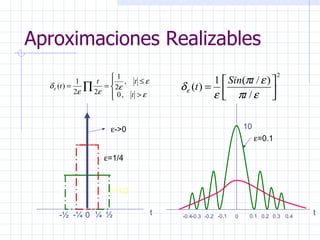
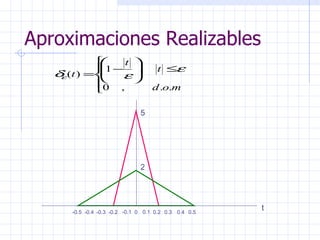
Este documento introduce conceptos básicos sobre señales y sistemas. Explica que una señal es una función que transporta información sobre un fenómeno físico y un sistema manipula señales de entrada para producir señales de salida. Luego clasifica las señales en diferentes categorías como continuas, discretas, determinísticas, aleatorias, periódicas y no periódicas. Finalmente, describe algunas señales elementales como impulso, escalón, rampa y senoidal.

1. SE Ñ ALES Y SISTEMAS http://www.espol.edu.ec/

2. INTRODUCCION

3. SE Ñ ALES Y SISTEMAS Entre los objetivos del curso de Se ñ ales y Sistemas est á conseguir las herramientas matem á ticas que nos permiten representar las se ñ ales y sus efectos al excitar cualquier sistema, es decir se desea: Representar "x" Representar al sistema. Obtener la salida "y" SISTEMA x y

4. ¿ Que es una se ñ al? ¿ Que es un sistema? Ejemplo de sistemas espec í ficos Como se clasifican las se ñ ales Se ñ ales singulares o elementales Aproximaciones de la Se ñ al Impulso Operaciones b á sicas con se ñ ales

5. ¿ Que es una Se ñ al? Funci ó n de una o mas variables que transporta informaci ó n acerca de la naturaleza de un fen ó meno f í sico. (Haykin) Cualquier cantidad f í sica que varia con el tiempo, espacio o cualquier otra variable o variables independientes. (Proakis) La informaci ó n de una se ñ al esta contenida en un patr ó n de variaciones que presenta alguna forma determinada.

6. Ejemplo de Se ñ ales Comunicaci ó n humana mediante se ñ ales de voz. Im á genes visuales de nuestro entorno Internet: Correo electr ó nico, informaci ó n diversa, chat, VOIP, etc. Se ñ ales biol ó gicas humanas: Electrocardiogramas, Presi ó n sangu í nea, temperatura, electroencefalograma).

7. Ejemplo de Se ñ ales (cont.) Pronostico del tiempo: Temperatura, humedad, velocidad y direcci ó n del viento). Fluctuaciones en los mercados (bolsa de valores): Mercanc í as en los mercados mundiales, divisas, valor de acciones Sondas Espaciales: Informaci ó n sobre perfiles de la superficie del planeta, im á genes infrarrojas que portan informaci ó n sobre la temperatura, im á genes ó pticas que reflejan nubosidades alrededor de los planetas.

8. ¿ Que es un Sistema ? Es una entidad que manipula una o mas se ñ ales para llevar a cabo una funci ó n, produciendo de ese modo nuevas se ñ ales Sistema Señal de Entrada Señal de Salida x(t) y(t)=H {x(t)}

9. Ejemplo de Sistemas Sistemas Biol ó gicos: Mecanismo de generaci ó n de voz humana O í dos y v í as auditivas en el cerebro Sistema Electr ó nico: Reconocimiento de voz humana Sistema de Comunicaci ó n Sistema de Aterrizaje de avi ó n

10. Varios Ejemplos Sistema de Reconocimiento de Voz (DSP) Señal de Voz Identidad del Hablante Sistema de Comunicación Señal de Voz/datos Estimación del mensaje original

11. Clasificaci ó n de Se ñ ales Real vs Compleja Monodimensional vs Multidimensional Tiempo Discreto o Continuo Pares e Impares Peri ó dicas y no peri ó dicas Determin í sticas y aleatorias De energ í a y potencia

12. Clasificaci ó n de Se ñ ales Se ñ ales reales o complejas: Por ejemplo: Esta se ñ al tiene parte real e imaginaria. Es decir es una funci ó n compleja. Cuando la parte imaginaria es cero se dice que la se ñ al es real .

13. Clasificaci ó n de Se ñ ales Monodimensional Es de una dimensi ó n Es funci ó n de una sola variable. Multidimensional De dos o mas variables. De dos o mas dimensiones. Ejemplo im á genes, fotograf í as blanco y negro.

14. Clasificaci ó n de Se ñ ales De tiempo continuo (Continuas) Son se ñ ales continuas en el tiempo Definidas por una sucesi ó n continua de valores Si su amplitud es continua se conocen como anal ó gicas De tiempo discreto (Discretas) Se define solo en instantes de tiempo discreto Se derivan de se ñ ales continuas muestreadas a una tasa uniforme. Se representan por una secuencia de n ú meros Si su amplitud es discreta se llaman digitales

15. Clasificaci ó n de Se ñ ales De acuerdo a la naturaleza de la amplitud (A) y a las caracter í sticas de la variable independiente que generalmente es el tiempo (t) en : Se ñ ales continuas o anal ó gicas : t y A son variables continuas. Se ñ ales discretas o de tiempo discreto (Muestreadas) : t discreto , A continua. Se ñ ales cuantizadas : t contin ú o, A discreta. Se ñ ales digitales : t y A son variables discretas

16. Tipos de Se ñ ales Anal ó gica : Amplitud y Tiempo continuos x(t) Muestreada : Tiempo Discreto, Amplitud continua x s (nT s ) Cuantizada : Tiempo Continuo, Amplitud discreta x q (nT s ) Digital : Tiempo Discreto, Amplitud discreta x q (nT s ) Continuar

17. Anal ó gica

18. Muestreada

19. Cuantizada

20. Digital

21. Clasificaci ó n de Se ñ ales De acuerdo a su simetr í a: Simetr í a Par: x(t) = x(-t) Simetr í a Impar: x(t) = -x(-t) Una se ñ al no sim é trica puede siempre expresarse como la suma de una funci ó n par x e (t) y una funci ó n impar x o (t) : x e (t) = (x(t)+x(-t))/2 x o (t) = (x(t)-x(-t))/2

22. Ejemplo Se ñ ales Pares e Impares

23. Clasificaci ó n de Se ñ ales De acuerdo a su periodicidad Peri ó dicas Aperi ó dicas Para se ñ ales de t continuo, si x(t) = x( t + kT) para todo valor de k entero, se dice que x(t) es peri ó dica con per í odo T. Si una se ñ al discreta x(n) = x(n + kN) para k entero, se dice que x(n) es peri ó dica con per í odo N . Continuar

24. Peri ó dicas

25. Aperi ó dica

26. Clasificaci ó n de Se ñ ales De acuerdo a la certidumbre de su descripci ó n: Determin í sticas y Aleatorias Aleatorias: Es impredecible, no sobre el valor de la se ñ al en todo tiempo, no se puede describir mediante una ecuaci ó n simple. Determin í sticas: Pueden ser modeladas completamente por una funci ó n del tiempo espec í fica. Puede ser descrita por una ecuaci ó n matem á tica explicita. Donde A y B son constantes. Otro ejemplo de una señal determinística que no es función continua en el tiempo es la función pulso unitario.

27. Clasificaci ó n de Se ñ ales Una se ñ al se dice que es de energ í a si E x es finito, lo que implica que P x es 0. Ej. Pulsos limitados en el tiempo. Una se ñ al se dice que es de potencia si P x es finito, lo que implica que E x es infinito. Ej. Una se ñ al peri ó dica. De acuerdo a la potencia o energía: Energía de una señal: Potencia de una señal:

28. Clasificaci ó n de Se ñ ales De acuerdo a su duraci ó n: Causales: Son 0 para t<0 . Se definen s ó lo para el eje positivo de t . Anticausales: Son 0 para t>0 . Se definen s ó lo para el eje negativo de t . No causales: Se definen para ambos ejes de t . Continuas: Se definen para todo tiempo t . Peri ó dicas: xp(t) = xp(t±nT), donde T es el periodo y n es un entero.

29. Se ñ ales B á sicas o Elementales

30. Se ñ ales Elementales Impulso Escal ó n Pulso Unitario Rampa Triangular Exponenciales Senoidales

31. Impulso (Delta) La funci ó n Delta tiene las siguientes caracter í sticas: y Sin embargo, es imposible para cualquier funci ó n convencional tener estas propiedades, pero es posible aproximarla considerando el l í mite de una funci ó n convencional cuando el par á metro sea aproxima a cero.

32. Impulso Unitario Tiempo Continuo Tiempo Discreto

33. Escal ó n unitario De tiempo continuo De tiempo discreto

34. Rampa De tiempo continuo

35. Triangular De tiempo continuo

36. Se ñ al exponencial real de tiempo continuo Caso a <0: Decaimiento exponencial Caso a > 0: Crecimiento exponencial Caso a=0: Se ñ al constante, igual a B

37. Se ñ al exponencial compleja De tiempo continuo De tiempo discreto

38. Se ñ al Senoidal Tiempo Continuo Tiempo Discreto

39. Se ñ al Senoidal

40. Funci ó n Impulso Aproximaciones y Propiedades

41. Aproximaciones Realizables  =1/4  =1/2  ->0 t ½ ¼ -¼ -½ 0 t 10  =0.1 0.1 -0.1 -0.2 0 0.2 -0.3 -0.4 0.3 0.4

42. Aproximaciones Realizables 0.1 -0.1 -0.2 0 0.2 -0.3 -0.4 -0.5 0.3 0.5 0.4 t 5 2

43. Propiedades de la Funci ó n Delta

44. Operaciones B á sicas sobre se ñ ales Sobre la variable dependiente Suma Escalamiento en amplitud Multiplicaci ó n Diferenciaci ó n Integraci ó n

45. Operaciones B á sicas sobre se ñ ales Sobre la variable independiente Escalamiento: Compresi ó n o Expansi ó n Reflexi ó n: Inversi ó n en el tiempo Corrimiento (desplazamiento en el tiempo)