Analisis estructural

C
o
f,:
,{)
*
c'
{
p
. UNIV]ERSIDAD AUTONO¡4A
TOMAS FRIAS
INGENIERIA CIVIL
ANAI,I§$ N§TNUüIUNAI,
APUNTIS Y PNOBI,IMA§
clll 204
fng. Nelson áonzález Villanueva
R.N.r. 5277
Potosí,"2007

APU¡rls§ y Pluulel¡¡as uÉ E§lluu(uta5 nlPgE§latlcs
CAP.1 rlflrRoDuccroN
1.1 CONCSPTO DE ESTRÜCTI'RA SIPTRESTATICA
Una estructura hiperestática es aquella en 1a cua1, las
ecuaciones de 1a estática en el plano o en eI espacio, no son
suficientes para determinar 1as reacciones en 1os aPoyos o
las fuerzas internas en una sección cualquiera'
En e1 ca.so cie '7igas en e1 plano:
ESTRUCTU8A ISOSTÁTICA ESTRUCTURA HIPERESTATIC¿
Ec. EstáEica = 3
Incógnitas = 3
Redundanies = 0
Para marcos en eI Plano:
Ec est,ática = 3
Incógnitsas = 4
Redundantses = 1
ESTRUCTURA ISOSTÁTICA
Ec. Estálica = 3
Incógnitas = 3
RedundanEes = 0
ESTRUCTUR.A. HIPERESTATICA
Ec esEáti.ca = 3
IncógniE,as = 6
Redundantes = 3

L.2 CONCEPTO DE }ÍUDO COIflITNUO
Para anali-zar estructuras hiperestáticas se deben utilizar,a1 margen de las ecuaciones de la estáticas, otras que
permi-tan estabr-ecer las deformaciones (rotacionales y
traslacionales) de sus elementos constituyentes y utilizardichas defo¡maciones como expresiones a. .on,putitiriaua.
En toda estructura se presentan zonas donde las barras que 1a
componen se unen entre si de forma r-orc1i: j r-:a (hcrrnigón
armado) o a travé.s de dispositivos de unión con posibrliciaci
de rotación (estructuras de madera o metá'r i cas) . E"tu.u zonas
de uni-ón se denominan nudos.'
APUnIUS y lIUUtet[as uc ESUUUtUtá§ n¡petE§rauks
Los estudios realizados en Resistencia de plateri-ares muestran
que las barras someti_das a cargas externas, sufren
deformaciones rotaciona-les y tra.slaci-ona1es.
Las ddformaciones rotaciona.l-es de un nudo continuo se
consideran, sin error apreciabl e, como rotaciones
ortogonales, 1o cual significa que los ejes de cada uaa de
1as barras que concurren aI nudc, giran un ángu1o similar.
lng. N. González V. OZOOZ

APU[ttrs y ptuuterua§ uc tr§uuutuf á§ nt!.JcrE5(aIES
L.2 CONCEPTO DE NI'DO CONEINUO
Para analizar estructuras hiperestáticas se deben utilizar,
al margen de 1as ecuaciones de la estáticas, otras que
permitan establecer las deformaciones (rotacionales y
traslacionales) de sus elementos constituyent_es y utilizar
dichas deformaciones como expresiones de comp.atibilidad.
En toda estructura se presentan zonas donde las barras que 1a
componen se unen eatre sí de forma :r.orcli:i r:a (hcrrnigón
armado) o a travé.s de dispositivos de unión con posibii-idaci
de roiación (estructuras de madera o m.etáricas). Estas zonas
de unión se denorninan nudos.
Los estudios realizados en Resistencia de llateriales muestran
que las barras sometidas a cargas externas, sufren
deforrnaciones rotacional-es y tra.slacional-es.
Las ddformaci-ones rotacionales de un nudo continuo se
consideran, sin error apreciabl e, como rotaciones
ortogonales, Lo cual significa que los ejes de cada una de
1as barras que concurren al nudc, giran ue ángulo similar.
l"S Ñ=or,zález V. O 200?

^puilrtss
y pruurErilas uE E§Íuulura§ nrfJcrcJ(auG§
1;3 GRJADOS DE LIBERTAD
La posibilidad de traslación o rotación de un punto
componente de una estructura se denomj-na grado de libertad.
En el pl-ano, los grados de libertad de ufr' punto son dos:
traslación y rotación; pudiendo descomponerse 1a traslación
en do,s direccibnes,
En eI espacj-o, un punto puede trasladarse en tres direcciones
(x,y,z) y puede rotar también en tres direcciones (alrededor
de Ios ejes x,y,z), contándose por consiguiente con seis
grados de libertad.
z
LTres grados de libertad
en el plano
Seis grados de libertad
en el espacio
L.4 GEOMETRTA DE ESTRUCTI'RAS
Las estructuras se encuentran constitui-das por elementos que
euentan con dimensiones, siendo ellas longitud, altura y
espesor, Por eIIo deben ser consideradas como elementos
tridimensionales; sin embargo, para efectos de idealización,
se l-as consideran representadas por 1a longitud de los ejes
de los elementos,
LAS

AWll(6 y frma¡Eni C H.r¡r.-as n.tEEEtr,A
"r+
Eqt
trt
ad,ESTRUCTURA R§¡I,
ESÍRUCTI'RA REAL
ESTRUCTURA REAL
ESTRUCTSR;A, IDEATTZSDA
ESTRUCTI'RA TDEALTZADA
ESTRUCfl'RA IDEALIZADA
1.5 c¿RilcrERrsrrcAs epouárnrcas DE r,As sEccroNEs
En e1 análisis estructurar se define como sección transváisar.
de un elemento al área de ra sección que se enc*entra
definida perpendicularmente a su eje longitudinal.
P
I
El eje mostrado
en la sección
transversal,
corresponde al
eje respecto del
cual se produce
la rotación por
flexión.
I
i
Eg

ApuÍrltss y P¡uulEltlas ue Esuuutulas nlpclcstauq§
1.5 EQUIVATENCIA
1 lb = 0.45359 kp
1 lb = 4.44818 N
DE UNIDADES
I kP = I'9966 N
1 kP = 2'264530 ,O
1N = 0.22481 1
1 N = 0.101972
tb
kp
1 N/m = 0.101972 kp/m
1N/m = 0.06852247 lb/pie
1kp/m = 9.8066 N/m
1lb/pie = f4F.Qa72$)5o i'¡i¡rt
1 kp i cmz = 2048.172138 lb / Pie2
1 kp / cm2 = 14.2?341755 lb ti¡2
iPa = I N/m2
1 Pa = 0.00000001 O1972kp I mm2
1 Pa = 0.00001019721412kp t crnz
1 Pa = 0.02088565 lb / pie2
1 Pa = 0.0000145039235 lb / in2
I kPa = 0.098066 kp t cm2
'l kPa = O.OOOOI 01972 kp / mm2
,
I kPa = 0.01019721412 kP/on-
1 kPa = 20.88564984 lb lpie2
1 kPa = 0.145039235 lb / in2
l MPa = 1N/mm2
)
1 MPa = 0.1019721412 kP / mm-
1 MPa = 10.19721412kp I cm2
1 MPa = 145.039235 lb / in2
l GPa = 1kN/mm2
1 GPa = 1O'l.97214'l2kp/mm2
1 GPa = 101g7.21412kp / cm2
1 GPa = 20885649.84 lb tpiez
1 GPa = 145039.235 lb / in2
T.7 PROPIEDADES DE f,OS MAIERIATES
Los materiales utilizados en la construcción Presentan
caracteristicas particulares frente a solicitaciones de
tracción, compresión, flexión, corte, torsión y temperatura'
Estas caracteristicas son estudiadas con deLalle en materias
como Resistencia de Nlaterial.gs..-y Materiales de construcción,
y.se verifican a través de experimentación en laboratori'o'

APUIttsS y ptuuttsiltas qs E§uGUrás ntpEtE§lduk§
¿
d
cá
é
d
dq
d
é
eé
d
PROP:3D}DES FÍSICAS DE üOS U¡TERIAIJES
MATERIAL
E G c
Kplcm
psi
GPa
Kp/m
Psi
Gtr¡
1 t'c
1 t'F
Acero laminado en cal¡enie
(0.2 9á de carbono)
2.,l x 10-
30 x '106
2C0
8.4 x l0'
12 x 10-
82
,l1.7x10-6
6.5 x 1o-5
Acero laminado en fríoro ram¡nado en frio i
(0.2%ciecarbon;) | soxto" I ,.,..-' | )oo I oo' 6.5 x
Acero laminado en calienle
(0.8 % de carbono)
2.'l x 10'
30 x 10"
200
8.4 x 10-
12x,.6
82
'!j.l x 10-6
Hierro forjado 1.99 x 10"
27 x 1Q6
ls0
7.03 x 10o
10 x to6
69
12 x 10'6
6.7 x 10€
Hierro colado maleable
1.77 x 10"
25 x 106
173
8.79 x l0e
12.5 x l06
86
1 1.8 x 10€
6.6 x 10{
Cobre de fundición
9.14 x 10
l3 x 106
90
4.22 x 1Ar
6 x to6
16.7 x 10
6
9.3 x l0€
Cobre estirado en frío
1.12 x 10
17x 1co
1't0
4.22 x'lo-
6
6 x 10
16.7 x 10-6
9.3 x 1o-5
A¡uminio de fundición
(99 % de a,umin¡o)
7.03 x'10"
10 x 106
2.81 x 10s
6
4x10
23.1 x 10-6
12.8 x'10-6
Magnesio lroquelado
4.55 x l0e
6.5 x 106
45
1.76 x 10-
2.5 x 106
26.1 x 10-6
14.5 x 10-6
Latón de fundición
(60% cobre, 40o/o zioc)
9.14 x 10"
13 x lo5
3.52 x 10o
5 x 1co
ls.7 x 10'6
lo.4 x 10-6
Bronce
(90% cobre, 10% sstaio)
8.44 x l0r
l2 x 106
83
4.60 x 10'
l8 x 10'6
10 x 10-6
Hormigón
2.18 x 105
3.1 x 106
25-30
9.9 x 1 0-6
5.5x10-
Madera 1 .12 - 1.43 x 't0
1.6 - 2 x lo6
't1 - 14
5.50 x 1O-
5.8x10-
.E
3.2x10-
Gran¡io
5.1 x 10-
7.3 x lo6
50
Duralu..ninio
8.44 x 10o
12 x 106
óJ
2.70 x l0o
lng. N. González V. @ 200,

APUiltCS y PrUurgrila§ UC ESUUUIUTa§ nrPgC5UU€5
1.8 BARRAS PRIS}4ÁTTCAS Y NO PRIS},ÍÁIICAS
Las barras prismáticas son aquellas
transversal constante a los largo
barras también reciben eI nombre
constante -
EARR§, PRISMATICA
Las barras no prismáticas varian su sección
largo de su extensión, esta variación puede
lineal-, parabólica o de otro tipo.
gue
de
de
mantienen su sección
su extensión, estas
barras de inercia
transversal a 1o
ser escalonada,
BARRA NO PRIS}'IATICA ESCAIONADA
BARRA NO PRISMATICA LINEAI B.ARRA NO PRIS¡,ÍATICA PARABOI.ICA
1. 9 ESTRUCTI'RAS TRASI,ACIONATES
EI efecto de las cargas externas, variaciones en su geometria
(sección transversaf) y eI asentami-ento de apoyos, originan
sobre las estructuras desplazamientos en algunas dj-recciones,
1os cuales definen a e1la como una estructura traslacional.

APU¡rttsS y fJtuutEiltirs uE ESUUUiUa§ n¡pctcsrau€§
1.10 TEORIA GENERAL DE BARRAS SOMETTDAS A FT'ERZA NOR!4AL
Para barras sometiCas a fuerzas normales que originanesfuerzos l_nternos que no superar e1 l_imite álástico, sepresentan deformaciones rongitudin"l."
_-
;"
-iL""io.,
ocompresión iguales a:
I;=¡r I
IE.Ai
donde:
1.11 TEORTA GENERJA]-
TA}¡GENCIAI,ES
dx
+----------r-
FT
llrlv I
t l-l
'-r- i I
"-.il-r
^
Módulo de elasticidad
área de 1a sección transversal
DE ELEMENTOS SO},ETIDOS A II'ERZAS
é
é,
e
e
U
e
é
€
é
€
€
e
é
I
vl
Por la Ley de
además:
ent.onces:
Aislando un trozo de barra
sometida a flexión, el
V esfuezo originado para .....
fuezas tangenciales es:
dy
V.S
l.b
flooke:
donde:
r = G.7
tr
u--
2.(1 + ¡r)
_ V.S
G.t.b
1
G
,=dY dY
r-di
dvv: Kr !-
dx ' G.A
V.S A.S V
G.t.b t.b G.A
donde: k.=4-l' l.b
lng. N. González V. @ 2007

A¡JUilrES y PrUorCilras uÉ csuuutula§ nlPeltssEr¡k5
donde:
L.I2 TEORIA GENERAI
FLECTORES
Aplicando momentos flectores
en el eje de las barras:
k1 = coeficiente de forma. (depende de'la seCción
transversal).
k1 = 1.2 para secciones rectangulares
kr = f9 Dara secc¡ones c¡rculares
'9
k1 = 1 Para secciones WF
G = módulo de elasticidad a cortante
A = área de la sección transversal
!r = módulo de Poisson
DE ELEMENTOS SOMETIDOS A MOME}CTOS
a barras, se produce curvatura
M(
Aislando un trozo de bana
somet¡da a Rexión, el
esfuer¿o or¡g¡nado para esta
solicitación es:
t=
Por Ia Ley de Hooke:
o
E
M
l.b
M_1
E'l p
M = moménto f1éqtor.... ,.i.: ... ,.:
E = módulo'de elasticidad.
I = momento estático de segundo orden.
de_
dx
donde:
además:

APUilteS y pf uutgttEs ug EStruqtuta5 ntpctesrauÉs
1.13 TEORIA GENERJAT DE ELEMENTOS SOMEÍIDOS A TORSION
Aplicando momentos torsores a barras de sección transversal
circular, en 1as cuales no se produce alabeo:
(
E
q
q
q
q
q
q
q
(
(
{
(
(
{
{
q
f
t{
{
q
q
I
tII
T
q
II
I
t
Aislando una sección
sometida a torsión, el
esfuezo originado para
esta solicitación es:
a=rd0 l
Id0
¡ Y=r' '
a=vdx I dx
,)
do: T.dx
G.J
t = G'y
T
G.J
tdO
'GdxPor ]a Ley de Hooke:
además:
donde:
de
r.-dx
L_ moÍ'.ento torsor.
módulo de el-asticidad a cortante.
momento de i-nercia torsional de 1a sección
transversal respecto del eje y.
módulo de Poisson
lng. N. González V. @ 2007 - 10

ApurtES y ptuutcil¡a5 ug tr§t¡uutura§ ntptstB§tdrrÉs
Valores de1 momento torsional
secc:.on:
.f para diferentes formas de
Sección circu].ar:
Sección eliptica:
Sección triangu!-ar eguilátera:
Sección rectangr.rlar :
@1" I.r= *.aa I
I 32 I
|l-'---.------'---l
l- a'.b' I
I a2+02 |
rÍifEa{4rz
'2b
Jz"
donde:
hJ," f-:+;l
I
a
t:::.:.:::.:.:.:.:.:.:l:.:.:.:::::t:::::::.: I I
.-..*-.t!-*..Ji
I
+_---E+
l- _
^Z-
3
,'-1? 3,,,iu É "'n#,

Apunrc§ y Pruurcfilé5 uc Esuuutula§ n¡Pcltr§talluas
CAP. 2 TRABAiIO Y ENERGIA
2.L §OtICITACIONES EN ELEMEI{TOS ESTRUCTURA],ES
Cuando se aplican cargas sobre cuerpos elástj-cos, se originan
en el1os esfuerzos internos tales como tracción, compresión,
corte, flexión y torsión, según los planos en 1os que actúen
dichas solicitaciones internas.
E1 gráfico adjunto muesEra esEas solicitaciones:
e"T
2.2 TR;A3AJO
Al actuar una fuerza constante
originar sobre e1la un movimiento
por eI desplazamiento 6, genera un
mediante la expresión:
F sobre una partÍcu1a y
de traslación determinado
trabajo /(externo) definido
F----------+o--.. w = F.6 + dvq = F.d6
-+-----------t-
6
Cuando actúa un momento constante M sobre una particula y
origina sobre ella un movimiento de rotación definido por e1
ángulo de rotación 0, origina un trabajo externo definido por:
¡¡ (o,,:....
/ 6
I,I = 'M. 0 dW = M.d0

^PUil(tsS
y P¡Uurelila5 Ur trSUUUtUra§ nrPErtsSHUgS
2.2 -L TR,LB.EJO EXTERNO DE UNA EUERZA NORMAI,
Aplicando una fuerza gradual P sobre una barra prismática, se
origina una deformación A determinada por 1a Ley de Hooke a
través de Ia relación:
EI trabajo exLerno originado por
esta fuerza es:
PL
a=- +EA
we = J e.oa
w" = tEA.¡.a¡ =El 12 =
áL 2L
p=El oI
EAA A
f;t;I (rey de C].al}eyron)
I
I
I
l
1
1
i
2,2.2 TR,A3A.'O EXTERNO DE UNA FUERZA TANGENCIAT
l"ü
d
v
v=9 A
v
k.x -
E1 t,rabajo exLerno es: We =J V'AY
*" =
}H y oy =
e-:l ,'=?Y ;

Alruiltcs y ptuutEt¡¡a§ uc trSuuutula§ nrpetc§ta§(z§
i;J;;l2l
2.2.4 TELABA.'O EXTERNO DE I'N MOMENTO TORSOR
2.2.3 TRABAiIO EXTERNO DE
Generalizando 1as
fuerzas normales,
e1 trabajo externo
T'N MOMENTO FLECTOR
tr-t
M=-'.0x
trabajo externo es: .- We = J ff4.Oe
A
w" = i E--L.e.ae =El.e2 - E'l'€ e
J x x x' 2
T =
G'J.e
x
EI trabajo externo es: We = J f.Oe
w" = ?9-{ e .de = 9:¿. e2 - G'J'e . e
áx x x z
deducciones para un elemento
cortantes, momentos flectores
se determina mediante:
sometido a
y torsores,
,|
We =
7.I
N.A+V¿.2+V¡ .x+M* :g, a¡¡..0¿ +T.0y I

AFTUiltCS y lIUUtCtItaJ ue trsüUUtUtA§ ntpErE§tát¡G§
2.3 ENERCTA DE DEFOR!,IACION
En el- estudio de Ia energ:ia, se establece que ella no se
pierde, sino que se transforma; en el caso de un elemento
sometiCo a un sistema general de fuerzas, e1 trabajo Ce todas
1as fuerzas se transforma en energia interna de deftrmación.
Esfuerzos normales: Considerando un elemento e1ástico
diferenci-al : W:U
Para esfuerzos normales:
we = 1'P'6
2
además,o"=? 3 p=Gn.A
^t =r- = A- e.L
deformación es:
u =1(or,.A) (r,L) L
2
on. E. L. A
Siendo V=A.L (volumendelelemgnto): U= 1 o..r.,
considerando ]as tres d.i¡nensiones der elemento diferencial:
dUonx
dUonr
dUom
1
2
1
2
1
2
onx. gx. dx
ony. Ey. dx
onz . tz. dx
dy dz
dy dz
dy dz

AfJUil(CS y ptUU|CIta5 Ue E§uuututaS ntpctestauÉ§
La energia total de deformación para esfuerzos normales será.:
dU:dU6n**dUonvldUo.z
O, :
I I G.*.r* r ony.ey+ onz,rz ] dx dy dz
u = i llf "",.'6x
* 6nv'€y* or,,'e, I dv
Esfuerzos tang'enciales :
Para fuerzas tangenciales:
Considerando un elemento e1ástico
diferenci-al : W:U
P1ano x-y:
uyx - l,xy
x
P
^vx
t=rxydxdz
Av* = y*, dy
1
owe=-
2
por otra parte:
dx.dz
, :A'*rxY ¡trr
trabajo externo será:
1-
dwe = 1r,,.. dx dz y.... dv
1
i'"-Y T*Y dx dy dz

AfJUlrtcs y pluulÉilras (lc Esuuurulá§ nlPslcstauE§
Considerando las tres dimensiones de} elemento
{
I
{
(
{
-t
(
I
{
{
(
{
I
il
1
{
I
!
{
{
{
{
{
I
(
I
(
(
{
{
!
{
{
dU
du = it
duirxy = : f* T* dx dy dz
duirr, = ] fy, Ty" dx dy dz
duir*, = ] a*, ^l*, c--: di. dz ,"
escribirse de otra forma, ello
Ley generalizada de Hooke, 1a
sonetido a esfuerzos normal-es Y
diferencial:
La energía total de deformación para esfuerzos tangenciales
será:
- dUir*y + dUilr, + CUil*,
7* T* + xy, Ty, * a*, T*, I dx dY cz
IJ= 1
2 fff,t", ^{xy * ayz Ty. + rxz Yxzl dv
Si ahora determinamos la
elemento sometido tanto a
La energia total interna
diferencial se obtiene su¡r'ando
energia total d'e deformación Para u=
esfuerzos normales y tangenciales:
a lmacenada por
ambos efectos:
eI elemento
Esta expresión también Puede
se consigue recurriendo a Ia
cual se aplica a un el-emento
i IIf Gnx rx + ony Ey + on, t. I ., - t
fJJ,t*v
Y*v + rvz^lvz+ rxz Yxzl dv
u=
tangenciales:

APU¡rtE§ y ptuutc[tas uE ESUuututa§ ntpcr€§ra[a5
Esfuerzos norma]-es:
Según el eje x:
Según el
donde:
donde:
donde:
on*
ty=-p
e.:-$
6ny
"y ¡1
t*:-Fty
6, = -lr Ey
tx
ex
e]e y:
z
eJe
z
on,
¿_ - I-
E*:-PEz
Ey: -$Ez
il,j
!
l

<I4
4é
G
J
G
G
J
G
G
C
J
C
ó
*
t'*
ta
C
j
J
J
j
c
J
J
rj
r¡
C
J
3
C
Txy
,xy tr
Txz
4' _-
lxz- G
ay.
_ ---(JTr"
AuuiltES y PtuulHlES us E§uucturás ntPerEsrauES
Esfuerzos taagencfales :
Según plano xy:
A
I
I
x
segúl plano xz:

APU|ltEs y PluulEllla§ uc ESUUUrUlaS nlpElts§tétlG§
Sumando las defornaciones producldas por los esfuerzos en Ias
tres direcciones:
I o.* - !t( ory + o., ))
I ony - F( on* + on, ) J
I o., - F( o.* + on, )J
Txy
Y"v=T
1y,
Tv, = -€
f*,
T*.: T
1
-E
1
1
=t
t8
gy
gz
Reemplazando las deformaciones unitarias longitudinales y las
deformaciones angulares por cortantes en 1a expresión general
de energia interna se obtiene una expresión que permite
expresar }a energia interna del elemento en función de las
component.es de toáos 1os esfuerzos que actúan sobre él '
La expresiones de energia interna de deformación por
esfuerzos normales y tangenciales' se evalúan, mediante
integrales triples, 1o cual, representa integrales de volumen
e" fá fegión Linitada por eI elemento que se analiza'
":fff
c2nx. + c2 ¡1y + c2 n7 - 2Y(o ¡xony * o onz + onxonz **y+4y+r2u 1¿v

A[ruIttss y ptuutcillir§ ue csuuurutas nt¡Jete§táuua§
2.4 ENERGIA DE DEFORI,ÍACIóN EN BARRAS
La energía interna se puede determinar para 1os casos máscomunes de solicitación áe ta
"iá"ll"a. manera:
2.4.1 Barras sometid.as a fuerza norma]-
,|
Uru=j.e a ::> dui{=i.,-.cl
Por la Ley de Hooke:
fuerza tangencial
u, =*r., =) duy =1y.6,
Por 1a Ley d.e Hooke:
or=H*
oa==!..0'
o2
u¡¡ =fr..o u"
=i ou¡¡ =
]ur.ce
Hooke:
a ¡nomanto flector
u¡, =
]M
e
Por la Ley de' ( r-------¡) ,
ds
do = -!t ¿.
EI
PE,
¡
I D "^2duN =
áP
.
E;o' =
7ff o.
2.4.2 Barras sometidas a
l,I
dy
2.4.3 Barras sometiCas
or, =*u.g#"=**á
f ,. uv = JlIv' .ds
,* =lrh o'
aunr=*u#0.=j$0.

A¡JUnttss y lruurBilras uc cstluotu¡a5 nlfJelc5tau€s
2.4.4 Barras sometidas momento torsor
¿ur =-1'r'
r d.=t'f10.2 G.J 2 G.J
La energia total de deformación es:
UT=IT,2
Por 1a
u., : t p2't
" " 2.E.4
.o + ¿ur=1r.¿e,2
Lgi de Hooke:
de= T ds
G.J
-2
Ur=[ ' ds. J 2.G.J
u=[ P2 ¿.*[k1 'V2d.*f M2 d.*[ T.',0,
- )2.E.A r2.G.A rz.E.l J2.G.J
De acuerdo a} tipo de solicitación que actúa
estudiadas, se pueden efectuar 1as siguientes
prácticas:
sobre las barras
consideraciones
En armaduras, predominan las fuerzas normales,
consecuencia Ia energia interna es:
predominan l-as
por flexi-ón, en
solicitaciones
consecuencia:
uM :
f-u1
o,

Apuf rrES y PruurEilla§ us E§Uuululas nlPettssEUGs
En ménsulas cortas o voladizos, predominan 1as
originadas Por
tangenciales (cortantes), Por el10:
d
N
Ll!E}s§,, Predominan
r¡nsecuencia:
solicitaciones
los esfuerzos
f kl'V2 .¿.
J 2.G.A
kr : factor de forma
Ias solicitaciones por torsión, en
--2u,=J*ro'
EL::.'.;;r'+ se presentan dos casos: cuando eI arco es plano
(rebajado) predomina Ia flexión y cuando el arco
es peraltado predominan la flexión y fuerza
normal:
I
I
/ l'
O.2 Arco pJano: u, : ffi.u"
0.2 Arco pera ttado: , =
f,$ o, *
J-N1'6.
f
L-
f.
-L
lng. N. Gonzáiez V. @ 2007 -23 -

ApuiltE§ y PruulElf la§ uc E§uuulula§ nlPclts§raue5
Ejemplo: Encontrar e1 factor de
rectangular.
forma para una sección
La Ley de Hooke para cortante indica:
El esfuerzo cortante por flexión es: . V'S,.
'=kó,
1 t2 V2 .S*
:
z o= zsV;./-
de giro se define mediante la
t.rabajo externo se puede escribir
-t Sr2 . V2
- (71;
b" ) z'c'e
.G
El trabajo externo para fuerza cortante se determina a través
de la expresión de ClaPeYron:
9le:
1
--f-v2'
Por otra parte, eI radio
2lrelación r-=Á entonces el
como:
v2'sr2
We=
2.G.A-12 'lr.br2
f,re = k1 r$l
donde k1 un coeficiente que caracteriza Ia desuniformidad de
Ia distribución de tensiones tangenciales en. 1a sección
transversal de Ia barra y que depende de la forma geométrica
de elIa.

^PUiltE§
y PtUUtEiltáS Us E§UUCIUra§ ntpqc§tauE§
Ejempl.o: Encontrar eI factor de forma k1 para una seccj.óo
rectangular maciza.
v
.f
,l
I
hl
,l
o2
t, = fl--'¡ ,-dA
' 'Y
9i!22
donde: Sx = momento estático de primer orden
r = radio de giro
I = momento de inercia del área
bx = ancho de 1a fibra consj.derada
En este caso particular:
h
sx=u 1!-y) o.+=f,r$-rrt, o=* ;
zh2
12
eI factor de forma k1 se determina integrando la expresión
dentro de La región definida por 1os limites:
bbhhx = -
2 , x = Z, Y = - 2, y :
,
12 12
f-,=-l {
{
{
{
n"

AIJUI¡tss y IJluulclllas uE EsUUCtUlas nlpElts§tatl*S
EjempJ.o:
e interiores b6 x hs-
Encontrar el factor de forma k1 para una secqlon
rectangular hueca de dimensiones exteriores b x h
v
I
bo:bo
ai)
+---j-------+-
]----¿--#
b¡b
;;
Para Ias
dA1 = 5.'6,
alas:
bx =b
h
;
h
I
+
hol
:llt
I
' "'I'
hol
-;l
T
-dv
I'
lx
sr
= !rf -v2r
Para el alma:
dA2=(b-be)dY ; by =(b-bo)
^ bh2 -boho2 b -bo ..2
"2=-----l-,
h
*,=4r?
lx' ho
2
*,*-,"'._-e__
h
xr=4 r 'r r*-r'r'| ¿ 4 ,' .+
rx o6
f ,¡n2
-!ono2 _b -!o ,272
¿v*f #b-bo)'d,l
ó (b - bo)'
'{
-v2aYl
ho
dy*b-;bo Í-o
2
Resolviendo las integrales:
bo
Denominando: ffi =- Y
b-
Sección rectangular donde:
Sección rectangular donde:
I
bo= ho
.bDo:1,
m:p=
1
m=D=-'2
ho
n
.hno=i i
0= kt=L'2
+ kr = 1.548

^puiltE§
y PluulEllla§ uc Est¡usula§ ñlPelEsEu(jus
Ejeaplo: Hallar la energia interna por flexión y fuerzas
tangenciales para Ia viga cargada con carga
concentrada y determinar la deflexión en el punto B'
8T
Energía j.nterna por flexión:
6.0
--+
. ,M¿
ui :J¡fr.4s
en el corte: M = -8x
8T
,(#
Energia interna
8T
' L-* ---*
r-8.x2) . ur.ra lu 2304
-r-.6¡ |
: -El
z1l 6El to
por cortante: ui =¡S'os
en eI corte: V = 8
6 a ^ 16
rri :"1 ki'(8)2."" - 64'k1'x3 | - rsz'rr
J zoa 2GA lo GA
0
6
ui:J
0
La energia interna total (energia,de deformación) será:
Para hall-ar la
trabajo externo
2304 192,k1l!¡
=
-!
EI GA
deflexión en eI punto B, determinamos
efeciuado por Ia fuerza en ese punto, asi:
8T
e1
lng. N.
?4^B

APUlltE§ y Pluultlllas UC E§uuutulaS nlpclc§láuq5
Por f]-exión:
Por e1 PrinciPio
1 .-.
W. : - (u)
-2
de conservación
4Aa
energia:
^i=
de la We:Ui
2304
4 ae :-ET- =
Por fuefzas Eangenciales (cortantes) :
W.: l tal ao
2-
:4ae
Por el princiPio de conservación de 1a energia: We:Ui
, a 192.k1
GA
Si Ia viga en estudio
rectangular constante de
E : 2. 1.107 'rlm2 Y módulo
A = 0.30'0.60 = 0.18 m2
una sección transversal
un móduIo de elasticiciad
= 8.4 . 106 T,/m2 :
GA= 1.512'1067
Et =1.134.105Tm2
tuviese
30 x 60 cm,
de corte G
I =
0.30'-(9.60)3
= 0.0054 m4
Las energias internas para cada solicitación serán:
Por Elexión:
Por Cortante:
2304
-=o.o2o3174Tm
1.134.10"
192 1
- =o.ooo1269Tm
1 .512 . 1ob
Ui =0.0204443Tm
Ui=
Ui=
Energia interna total:

Apuilte§ y Pruulelllas uE Esuuutulas nlFElE§lauG§
De Ios resul-taCos encontramos
energfia interna:
1os sigui-entes Porcentajes de
Solicitación Ui t
Elexión 0.0203174 99 38
Cortanl:.e 0 . 00012 69 o .62
Totai 0.0204443 100 . 00
En este caso se deiermina que 1a energia j-nterna por fuerzas
tangenciales es irsi cni'. 1.:¡::'e i:':ri¡ - --. -.:-¿y'-- -¡"""":ldl
por flexión, por ello en 1a mayoria .cie los casos se Ia
desprecia. En otros casos esta energia puede ser iBportante.
Las deformaciones en e1 punto B serán:
q
q
q
q
€
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
T
q
T
T
T
f
¡
I
Por Flexión:
^B:-
j76-=0.005079
rn :
1.134.10-
Pcr cortante: Ao: 48
= =0.000032 m =
- 1.512.100
La deformación total:
^B
: 5.08 + 0.03
De 1os resultados encontramos los siguientes
energia interna:
5. 08 mrn
0.03 mm
= 5.11 mm
porcentajes de
Solicitación As t
Flexión 0 . 00507 9 99.38
Cortante 0.000032 0 .62
Total 0.005111 100. 00
En este caso particular se determina que }a deformación por
flexión es mucho mayor en comparación con 1a' defor¡nación
originada por corte, por ello en 1a mayoría de 1os casos se
desprecia Ia deformación por cortante.
E3enplo: Hallar 1a energia de deformación Por flexión
para la viga cargada con carga concentrada y
determinar Ia deflexión en eI punto B.
10
r-' rM2
Energia interna: ,t :J
2r,
O"
en el corte: M = -10
m_
a--
3.0
-------------+
,Mr--
-X
----+
10
T-*
)
lng. N- González V. @ 2007

APUlItts y ptoutuf Es uE ESUUqUtaS n!¡ESEIES
Ejemplo: Hal}ar 1a energia de deformación Por flexión
para'-}a-t'iq" '--cargada
con carga concentrada y
determinar Ia deflexión en el punto B'
cM2
Energia interna:. uí =J,r, Ot1o
T-'
+_- 3.0 ------------+
10
T-,
ft¡l- ) en eI corte:
._x ___-f f
ui=J c:!r' .o* = H l: +ó -' ro
3 . 0 --------f
8T
I
vL---J
i-..+
M.= -IU i.
-..
. .. :
:'
-4.
Para hallar Ia rotación en eI punto B' determj-namos e}
trabajo externo "f.ti"t¿"
por la fuerza en ese punto' asi:
10
) (10)-^B=50e
Por el Prj-nciPio de conservación de Ia energia: We : Ui
1
w^=-'2
50e=#
AI igual que en caso anterior
fuerza cortante, sin embargo
flexión Pura, las fuerzas
deformación también será nula'
Ejemplo: HaIIar la energia de deformación Por fuerzas
cortantes para la viga sometj-da a carga
concentrada y determinar Ia deflexión en el punto B
puede efectuarse análisÍs
L., este caso, tratándose
cortantes son nulas Y
por
Ld
Enersia j.nterna: ur =JS'os
en el corte¡ V = B
-

3
ui =f
0
,3
kr't8l2 64tr''i-
_ñ;_ ox = _7ffi_
i
_
,o
Para hallar 1a
trabaio exte=no
<iefle:<iór, en
efeclu:Jc 5;or
eI Purlto B, de-'ernir'a:rcs
ia íuer¿a en ese P''Irrio, asi:
Pcr e1 !-rin:lpio cte conservación Ce = L¡i
':ó k1
GA
E jenplo: Deterainar La ene'rgia por fuerza nor:nal
acumula en sistena' ccnsiderar Af = 5
a
ri2 = 6 puigz y 1a iongit':ci ci¿ las barras 10 pies '
que::..;+
Fu19- t
i/?
}IAB
,^o -
.. -' - t
30" -," I
i
.a
NBc ^kó
10'
¡! -
^^q¡.;3
¡¡.r.a . sen
t 'Áa
I'lpL- . cos
tlr,. ' sert
; Ns,:
^^O
?no -o
300
300+

Aputrtcs y Pluulclllas ut Estlugtula§ nlPslsstauH5
Barra
Barra
La energia total
Ejesplo:
EjemgJ.o:
AB: u* = rN1
L,
=
U:
:',! ='T',
2'E'A 2'E'5 E
Bc : ,* = $'! =
t^o
i'^o =
o3o
2,E.A 2.E.8 E
de deformación es:
HaIlar la
flexión.
16r
Hallar la energia del
fuerzas tangenciales.
16r
energÍa de1 sistema considerando
Tomando en cuenta que ds = 5 d0
sistema considerando las
en el corte: M: - l-6(5)'senO: -
fi
:^
,r. _ f 8oz .sen'o'(5)
¿6 : 4ooo'¡
J 2EI EI
0
Tomando en cuenta que ds = 5 d0
I
I
!
s'j.¡4-l
en el corte: V = 16 cosO
,l
ui = j*,.19' :":1'otdt=l!%:Ú
0
':íeid0 ::.. i
a:. !
.--...-....-.-l

¿
r!i = lu.t"¡
0
162 .cos2 o (5) ,. -
160'k1 ';
2GA GA
Ejenplo: Iiallar ia energÍ a ie1
Íuer-zas nc:;:.ai¿s, fue=uas
sis--e=a ccnsid¿ra¡:ic
^..1-r.
z---r 1., il ¿:i.:-¡i :¿ú--:v'-'
r
20'
Tor:lendo en cuenEa cue: cis = r - ciü
e: eI ccrte: ¡; - -20 seri0
tr : ! gC,5Q
i"i - lul r serrO
I
I
¡
Dfr,
liornal:
...,...0
d0'::.
Co!tante:
l{órni¿nt,o:
l; .1
r'", = ?(:?0-r-t*1qi¿2
rldil
= -1t0:i ?="nru.oo = :?-'-1
-'r J 2EA :EA J EA
0C
ñÍ
"r
u,, = ?..ki:(1-l -c.cs!----------------l?
r <r0
- aY? k:i I ?"o.ro ci6 = lg-il ki-r
-r'-J :GA :GA I GA
0fJ
Ílf
'aa
,,^, = ?(:,1 r.senü)- r._0
=
*cl.13 fr"nz,.¿¿=
5c'n r3
-rv¡ J :El :.=l I El
0 -- 0
La enerEla to¿ales l-a siil¡.a cie f"s tres c,b:+ai(ies,
5C; r' 50.x.k,.r 50; 13
Ui =U,.¡+Uy+U¡.1 =-ElÁ-"-6A--= il
Si el- ar-co tierle sección t:l:ánsversal rectani''r1ar (kr - 1^' 2 )
10 ,< 30 c;r., un r.Ódulc de elastj-cr'lacl E = 2.1'10' T/m' 'J
nócurc ce ccrte G = B .i.loo i/^2;
F. = 0.10 . 0.30 = 0.03 m2
q
q
q
q
q
q
q
q
q
,t
q
t
un
irg. N. Gcn:áez V. @ 2007
; GA = 2.52 105 T

^yurrrE§
y Prugrc¡ié) uc E§(¡ul(qtas n¡pEtÉStduks
r (o) U¡ Uy I4.r U tóta1
3 .00 0.000748
0.08r
0.002244
o.25*,
0.897s98
99.6't
0.9005590
100.00*
2.00 0.000499
0.19*
0. 0014 96
0.56*
0.2659s5
99.26r
0.267950
100.00*
1.00 0.000249
0. ?3*
0.000?48
2.18t
0 .033244
97.09r
0.034242
100.00*
0.50 0.000125
2.681
0.000374
8.04t
0.004156
89.293
0 . 004 654
100.00*
0.10 0.000025
18.75t
0.000075
56.25%
0.000033
25 . 00r
0.000133
100.00t
0 .05 0.000012
23.08r
0.000037
69.23*,
0.000004
7.69i
0.000054
100.00*
Ejemplo: Hallar la energia totaL del sistema.
Por proporcionalj_dad de triángulos:m
f¡ ft
h+m m
+dv
I;l-
lrrr-
h+m-y m
h.r.
IIT
-
-
't2-t1
fc-fi . h.I¡
|-----:_.t--y,
n f2-11
UN=J
u^, = P2 'h
" 2n.E.q.r2

ApuilrÉs y Pluultsltta§ uE cÚt¡u(lulas nl¡'glE§rarss
p2.n2
UN =-------- "2nÉ(r2-rfi'
th dv
Jg;12't1
,*=;Éh
Ejemplo: Halfar 1a energia
para Ia barra AB,
total de deformación elástica
sin consi-derar 1a barra BC'
x
1-----F T
Las solicitaciones internas Para
Cortante:
Momento flector:
Momeato torsor:
AffiGr
Ia barra AB son:
V=P
M:-Px
T=Pa
,v=t¿s{.o*=! É'
,r=i#o*={#
,.='J#o*=*#
Energia Por
Energia Por
cortante:
flexión:
Energia Por torsión:
La energia total de deformación elástica es:
u=u¡,1 +uv+ur

Ejetuplo: Determinar Ia energia interna
mostrada consj-derando que las
están dadas por eI estado tensionaL
una constante. La sección tlene 1as
longitud de la barra es L.
para l_a barra
solicitaciones
ony=.zrdondekes
dimensiones b,h y la
i i.. L.i,:i|,: ¡"...,
j.: ji# - l-.
12.L.b.h3
24.E
h
-.- -. v
/ L----------J
El estado tensional- refleja que 1os esfuerzos se producen porflexión' utilizando 1a exprlsión que reraciona ár potencialde ta ba=a en función de 1as tensiones ii;;-;";ializada deHooke) :
-2u= [:!¿-6yJ 2.E
^/)
¡
^ta
u = fll k¿ 'z¿'dz'dt'dx
JJJ 2'E
-b/2 o -h/2
Ejemplo: Ha1lar Ia energia total de deformacÍón
barra contenida en uñ plano horizontal.
z
de la

Apuilres y [ruulcillas uc csuuuutá§ nrPsrs§taüEs
G
q
Iq
q
c
é
4q
á !
q
G
C
q
C
!
q
q
{E
G
G
G
G
G
(É
G
q
G
G
á
I
¡
€
VNT
1800
:-8 0 54
18 0 36
Tramo Origea LÍmlEes !,f
DC D 0-3 -18x
CB C 0-2 -18x
BA B 0 - 4 -18(3+x)
EnergÍa por f,qerza uormal:
A1 no existir ning"una soliciE,ación por fuerza normal, Ia
energÍa acumulada para est,a solicit.ación es nu1a.
UN=0
EnergÍa por f1exlón:
3. 324.x2 2,
3%* ¿**}
gz¿.(g+x)2
axuM=J ,Er 'dx+J 2Er '^*J -- 2E:¡
,r=TF
,, 2¡324.9
,...4t3!!d*
'. =
J zo¡
o'*
J-
zc.r -^
.. 5508
ljr=-.GJ
de deformación eIástica
Energía por corte:
u., =t ki.324
dx+t k1.324
dx+t kr.324
o*
'dzGA d2GA d2GA
u., _ 1458.kl
'GA
Energía por Eorsión:
La energía toEal será:
€

ApuiltE§ y ptuuttsilta§ ue trSuuututa§ ntrJetEstáuE5
Ejemplo: Ha11ar 1a energia
un arco de raCio 4
total del sistema formado por
m contenido en el plano x-y.
de
'' _ __':1:::::::::::::: "::::- '_ _"_'_'
....:::::::..^i::::;'."-"
-
.......
"' -"'¡ y
-"
^kN¿
Sobre el plano x-y
Momento flector:
Cortante
Momento torsor:
Por fLexión:
=-BsenOFJ
T
)."
=4d0
'"=f
B(1 - cosO)
/1
(-B sen0)'(q)a0
2Et
32¡
EI
0
x/2
I r,(g)2ralao
üv= l:=,o
4 krzr
LrA
Por cortante:

Apu[rcs y pruulerilas us ESUucrutas ntpErESrauG§
Por flexión:
Por cortante:
Por torsión:
(-8 sea0)t(a)ae
ry - 2EI
uv:
/2
Ur=
k1(8)2(4)de
------zGE-
l-8 (1-cos0)12(a)og 32 (3a-B)
----GJ--
las energiias
32 ¡r
-Ef-
_ 4krn
GA
J0
j ZG¿
es 1a suma deL:- ..,:ergia total de deformación
obtenidas:
U:U*+Uv+Ur
rT _ 4'k1 .r.32.r,32(3r-8)
GA EI GJ
En este problema, Ia energia por fuerza normal es nul-a.
2.5 LEYES DE RECTPROCIDAD
2.5.1 Ley de Betti.- Esta Ley se refiere al trabajo
reciproco de las fuerzas.
EI trabajo de un sistema de fuerzas gradual "Pi" debiCo a los
desplazamj-entos que en sus puntos de aplicación le produce
otro sistema de fuerzas giradual "Pj", es igual a1 trabajo de
1as fuerzas gradua!-es deI segundo sistema debidc a 1a
aplicación gradual del prim.er sj-stema de fuerzas".
a) Aplicando eI sistema gradual de fuerzas 'tPi't sobre 1a
vj-ga, se origina un trabajo igual a:
1
Wi = Z. Pi . §i
(Trabajo real)

AputtttsS y Ptuurcilras uc c§uuululas nlPtsrcsr¿uÉs
vrj P: .6j (Trabajo real)
. Aij (Trabajo virtual)$I,. = Pr
efectuado por ambos sistemas de fuerzas
1
2
E1 trabajo total
graduales será:
w=
1
w :Z- Pi ,6;.
i.l= + $I. =.) L)
'Pr '6j +
gradual
Sli +
1
+z Pi 'aij
de fuerzas "Pj ", e1
wj:1
Z
P:'61 (Trabajo real)
Aplicando a continuaci-ón
mantenj-endo aplicado eI
será:
D. D.!1
de fuerzas gradual "Pi",
fuerzas "Pj ", e1 trabajo
P:" - 6i (Trabajo real)
'Ajr (Trabajo virtual)
eI sistema
sistena de
Ili
Jr
=1'.;¿
=P.
EI trabajo total efectuado por ambos sistemas de fuerzas
graduales será:
t^]=
wj*
*1
z
1
z
I^]=
'Pi'6t
w. + t¡l-.¡ Jr
.P, .6- + P, ,4,..) ) r rJ
6i Ajl

lPU¡ttEs y ptuuteiltas qB rsr¡uurutas ntpEtr§tau(as
E1 trabajo total efectuado
graduales será:
por ambos sistemas de fuerzas
w=Illj+[rli+W¡i
[,¡=1.pi.5i +1.pj.6: *
2Z
El trabajo total no depende del orden
cargas graduales, en consecuencia ambos
es decir:
'lr
á.tt.¡, É.Pi.6j + pr.aij =i.rr.u,
Pi,^ij : Pi*Aii
2.5.2 Ley de Maxwell
Es un caso particular
sistemas de fuerzas son
de la Ley de
iguales ( pi =
Pi:Pr:¡>
P*^ij = p*A1t
P. ..^.,¡ r_J
de aplicáción de 1as
trabajos son iguales,
,l
*á.ri.6j + pi.Aij
Betti, en
Pi ).
la eue, O4pos

Apuntes y problemas de Estructuras Hiperestáticas
CAP.3 PRINCIPIO DEL TRABAJO VIRTUAL
3.1 CONSERVACIóU OP LA ENERGIA
Est,ablecidos 1os procedimientos para determinar e1 trabajo
producido por una solicitación externa aplicada sobre un
cuerpo y Ia energiÍa j-nterna acumulada ..por dicho cuerpo,
veremos cómo de pueden aplj-car dichos procedimienEos .para
esLablecer desplazamientos y rotaciones de un punto de una
estructura
Ej emplo : Hallar e1 desplazami-ento
flexión del punE.o donde se
Aislando
p somet.ida
verti.cal debido
aplica 1a carga P.
un trozo de viga
a flexión:
el trabajo
M=-Px,
y 1a energía interna de
deformación es:
.M2ds LrP2 ,) . P2L3
LT1 = l- = l-X-.dX=
-
r z1t d2El 6El
EI trabajo externo de 1a
fuerza es:
w" = 1.p.¡
2
Por eI principio de Ia conservación de 1a energia,
externo y Ia energia interna son iguales, asi:
1p¡ -
P2t-3
2 6El
Se observa que Ia solución deI problema es directa y que Ia
aplicación deI procedimiento se limita solo a algunos
problemas, Do pudiendo generalizarse para otro tipo de
cargas, e1Io debj-do a que solo se puede utilizar una ecuación
de t.rabajo para 1a viga.
PL3
3Et

= €
.
q
q
q
q
a
ó
4
G
G
G
1,
q
q
q
q
q
C
G
G
G)
G
C
q
C
C
G
IG
til
ffi
llr
tI
ti
ll'
lt
i
H
I
i
i
t
Apuntes y problemas de Estructuras H,perestát¡cas
3.2 PRINCIPIO DEt TRABA.]O VIRTUAI
E1 principio de1 Erabajo virtual fue desarrol-Iado por 'Juan
Bernculli en L7L7 y también es conocido con eI nombre de
Método de la Carga UniEaria.
A1 igual que oEros métodos de cáIcu1o para estructuras
hi-peresEáEicas, se basa en e1 principio de 1a conservación de
1a energía (We = Ui), de esta manera permiE.e establecer un
medio general para obtener un desplazamiento o rotación cie
a1gún punto de una estructura.
1o) Si sobre un cuerpo deformable aplicamos una serie de
cargas externas P, elJ.as se transmiten a 1a estructura,
originando 1a aparición de fuerzas internas u.
2") Es necesario que 1as cargas exEernas P y 1as fuerzas
inlernas u queden relacionadas por ecuaciones de
equilibrio.
3o) Las cargas P, en sus puntos de aplicación, origin:n
desplazamientos externos A y 1as cargas internas rr
originan desplazamientos internos 6 en cada punto de
carga j.nterna.
4') Los desplazamientos e:.:ternos y los desplazamientos
internos deben estar relacionados entre si por
ecuaciones de conpatibilidad de desplazamientos.
EI principio de Erabajo y energía esEablece. '"':-oE
Trabajo de 1as cargas ext.ernas = P, A
Trabajo de 1as cargas internas = u - 6
Por e1 principio de conservación de la energÍa, e1 t.rabajo
que efectúan las cargas externas es igual a1 t.rabajo de 1as
cargas in"ernas, cumpliéndose que:
»P'^ = Xu.6
Estudiando un cuerpo sometido a cargas externas reales P,
suponiendo gue los soportes del cuerpo no pueden contar con
pcsibilidad de desplazamienlo, pero que eI material puede
deformarse de manera irrest.rict,a más allá de su 1Ímite
elást.ico:

Apuntes y problemas de Estructuras H¡perestát¡cas
Como ninguna de 1as cargas externas actúa directamente sobre
el punto A y menos en l-a dirección A, e1 desplazamiento A
puede ser determinado colocando sobre el cuerpo primero una
fuerza ficticia Pt actuando en Ia misma direcci-ón A (por
conveniencia se escoge para 1a fuerza fictÍcia un valor
unitario P'= 1). §sta fuerza Pr se denomina fuerza virtual,
para indicar que el}a no es real (es imaginarj-a).
Esta carga virtual genera una
elemento representativo.
Trabajo externo
Trabajo interno
carga virtual interna u en un
Como resultado de esas cargas, el cuerpo
y el elemento experimentarán un
desplazamiento virtual debido a las fueza
P'.
Una vez que se aplican las cargas
virtuales P' y que el cuerpo está sometido
a las cargas reales, el punto A se desplaza
una magnitud A, ocasionando que el
elemento se deforme una magnitud dL.
Como consecuencia de ello, la fueza
virtual externa P' y las cargas virtual
interna u viajan a los largo de A Y dL
respectivamente y efectúan una trabajo
virtual externo sobre el cuerpo y un'trabajo
virtual interno sobre el elemento iguales a:
(sobre eI cuerpo)
(sobre e1 elemento)
1'a
u.dL
lng. N. González V. @ 2007 -44-

Apuntes y problemas de Estructuras H¡perestáticas
Por e1 principio de conservación de Ia energ:ía, e1 trabajo
virtual externo es igual a1 trabajo interno ejecutado sobre
todos 1os element,os de1 cuerpo, en consecuencia:
cargas virtuales
ttYV
1.^ =Eu.diAA
lrdesplazamientsos reales
donde:
P' = 1 = carga virtual unitaria, que actúa según la dirección A
u = carga virtual interna, que actÚa sobre el elemento en la dirección dL.
A = desplazam¡ento externo origioado por las cargas reales.
dL = deformación interna del elemento causada por las cargas reales.
I
1.
(3 .1)
(3.2)
uniEario en ese punto. Este momento concentrado orig:ina una
carga virt,ual interna u0 en uno de los elementos del cuerPo'
suponiendo gue 1as cargas reales deforman aI elemento en una
magnitud dL, Ia rotación 0 puede enconErarse a partir de 1a
ecuación dei trabajo virtual:
cargas virtuales
Si el anáIisis se cenEra
rotacional o pendiente <ie
esLructura, se aPlicará
desplazamienE.os reales
en determinar el desPlazaniento
1a tangenEe en un Punto de r¡na
un mo¡¡.eato viríuaT tft dé walor
I
0 =Xug.dIJ
rt
M' = 1 = momento v¡rtual un¡tario, que actúa según la dirección 0
ue = carga virtual interna, que actúa sobre el elemento en la d¡recc¡ón dL
a = desplazamiento rotacionai externo or¡ginado por las cargas reales'
dL = deformación ¡nterna del elemento causada por las cargas reales'

3.3 TRABAJO VIRrUAJ, APLÍCADO A AR¡,ÍADURAS
Las armaduras principalmente están sometidas a fuerzas
normales, aunque también pueden estar sometidas a efectos
provenientes de cambios de temperatura y defectos de
fabricación.
3.3.1 EI'ECTO DE ETIERZAS NOR},Í¡ILES
Las fuerzas normales actúan sobre una
alargamiento o acortamiento, en función
tracción o compresión.
Para eI caso g:eneral de una barra eIástica,
determina mediante la Ley de Hooke,
barra originando
que eIlas sean de
1a deformación se
donde:
^' - N'L
E.A
entonces Ia expresión de1 trabajo virtual queda en 1a forsa:
(3 .3)
donde:
'l = carga unitaria virtual externa que actúa sobre el
nudo de la armadura, en la dirección A estipulada.
n = fueza normal virtual interna en el miembro de la
armadura, causada por la carga virtual unitaria externa.
A = desplazamiento externo del nudo, causado por las cargas
reales en la armadura.
§ = fueza normal interna en la barra de una armadura,
causada por las cargas reales.
| = longitud del elemento.
f = módulo de elasticidad lineal del mater¡al
fi = área de la sección transversal del elemento.
3.3.2 E¡'ECTOS DE TEMPER;§,TURA
Cuando los miembros de una armadura están sometidos a canücios
de temperatura, modifican su longitud mediante 1a expresión:
l,l=;!.r! I
| "l j__i
AL=oLAT
-46-

en consecuencia Para determinar e1 desplazamiento de un nudo
específico de una armadura, la expresión de1 trabajo virLual
puede ser escrita en 1a siguiente forma:
1.4= rn.cr.L.AT (3.4)
donde:
| = carga un¡taria v¡rtual externa que actúa sobre el nudo
de la armadura, en la dirección A estipulada.
n = fueza normal virtual interna en el m¡embro de la
^
= desplazamiento externo del nudo, causado porel cambio
de temPerature.
c! = coeficiente de dilatación térmica del material.
| = longitud del elemento.
AT = variación de temPeratura.
3.3.3 EFECTOS DE ERRORES DE FABRICACION
Si los miembros de una armadura presentsan defecEos &
fabricación referidos a su longiE'ud o Por razones
construcEivas se desea lograr combeo (flechas o
conEraflechas) durante eI funeionamiento de 1a armadura, e1
anáIisis deI desplazamienEo de nudos específicos se logra a
Eravés de La expresión de trabajo virtual siguiente:
(3.5)
doade:
'l =
n=
^=
c[=
AL=
I t.l = In.AL I
l-l
carga unitaria virtual externa que actúa sobre el
fueza normal virtual interna en el miembro de la
desplazamiento externo del nudo, causado por
el error de fabricación.
coeficlente de dilatación térmica del material'
variación de longitud del miembro, respecto
del tamaño estipulado.
lng. N. González V. @ 2007 -47

Apuntes y problemas de Estructuras Hiperestát¡cas
Ejemplo:
El análisis se
considerando eI
considerando una
hacia abajo.
efectúa bajo
efecto de las
carga vj-rtual
Hallar eI deéplazamiento vertical del nudo
1a armadura de 1a figura, considerando
29,000 ksi
l)
Bde
§=
,.
I
t
dos situaciones, Ia primera
cargas reales y Ia segunda
Pr: 1K actuando en eI nudo B,
a) Fuerzas reales (N)
t¿
15"
JU
Los resultados de ambos aná1isis
tabla:
b) E¡erzas virtuales (n)
L
1''
se muestran en la siguiente

en consecuencia para determinar e1 desplazamiento de un nudo
específico de una armadura, 1a expresión de1 t.rabajo wirEual
puede ser escriEa en la siguiente forma:
1'A= In.cr.L.lT (3.4)
donde:
| = carga unitaria virtual externa que actúa sobre el nudo
de la armadura, en la dirección
^
estipulada.
n = fueza normal virtual interna en el miembro de la
armadura, causada por la carga virtual un¡taria externa'
^
= desplazamiento externo del nudo, causado por el cambio
de temPeratura.
cr = coeficiente de dilatación térmica del material.
l- = longitud del elemento.
AT = variación de temperatura.
3.3.3 EFECTOS DE ERRORES DE FABRICACION
si 1os miembros de una armadura presentan defectsos de
fabricación referidos a su longiE,ud o por razone§¡
constructivas se desea lograr combeo (flechas o
contraflechas) duranEe eI funcionamiento de 1a armadura, eI
análisis de1 desplazamiento de nudos especÍficos se logra a
través de 1a expresión de Erabajo virtual siguienEe:
(3. s)
donde:
t-
n=
^=
(l=
AL=
I r.n = rn.aL I
l-l
carga unitaria virtual externa que actúa sobre el
fueza normal virtual interna en el m¡embro de ¡a
armadura, causada por la carga virtual unitaria externa'
desplazamiento externo del nudo, causado por
el error de fabricación.
coeficiente de dilatación térmica del material.
variación de longitud del miembro, respecto
del tamaño estipulado.
lng. N. González V. @ 2007 -47 -

Ejemplo:
E1 análisis se
considerando e1
considerando una
hacia abajo.
efectúa bajo
efecto de 1as
carga virtual
Hallar eI deéplazamiento vert.i.cal del nudo B de
la armadura de 1a figura, considerando B =
29,000 ksi
15
l(
20R
D
7.z',
30k
7.2',
I
I
s4 I
I
la-i-
7.z'.
38
dos situaciones, 1a primera
carqas reales y la segunda
Pr: 1K actuando en el nudo B,
Fuerzas reales (N)
15
k
2ok
^^kJÓ
Los resultados de ambos análisis
tabla:
b) Fuerzas virtuales (n)
1k
se muestran en 1a siguiente
E
B c
F

Apuntes y probtemas de Estructuras H¡persstáticas
Traao
N n L A NNL/A
kips k].ps inch inch2 k2linch
AB 69.3333 0.8889 86.40 8.00 665.60
Br 6B.UUUU 0.4444 86.40 8.00 326.40
CD 6U.UOUU o.4444 86.40 8.00 326.40
AE -86.6667 -1.1111 '108.00 10.00 1C40.00
BE 37.0000 0.6667 64. 8.00., 1
BF 1.6667 0.5556 108.00 8.00 12.50
CF 30.0cc0 0.,.-rCr10 ñ4.AC I ?.00
108-00 r
- -lu.uñ
0.00
)F -85.0000 -0.5556 ¡ lñ nñ
szz¿aEF -69.3333 -0.8889 86.40 't0.00
Aplicando 1a exPresión del
k
1r
I = 3613.18
trabajo vj-rtual:
361 3.1 IAD
" 29000
AB, = 0.1246 inch = 0.32 cm = 3.20 mm
I
Ejeurplo: Ha11ar eI desplazamiento vertsical del ando B &
Ia armadura de Ia figura, si las barras ¿'1
cordón inferior sufren un cambio de Eerq)eratura de L:lt'F-
considerar Gg = 0.000006 1,/"F
,rl^
E1 aná1isis se efeeEúa bajo dos siEuaciones, Ia primera
tomando en cuenta 1as cargas reales y 1a segunda considerando
1a carga virtual P'= 1 k actuando en B.
-é,
é
Cq
C,
G
C
G,
C
G
á
4
G
If
q
{r
={t
;
¡
q
q
q
q
q
q
q
(
(
(
(
(
{
It
a) Fuerzas reales (N) b) FuerzaE virtuales (n)

Tramo
N n L
^r
noL^T
kips kips inch r k ' inch
AB 0.000 0.8889 86.40 't 20.00 0.055296
BC 0.000 0.4444 86.40 120.00 o.o27648
CD 0.000 0.4444 86.40 120.00 o.o27648
AE 0.000 1.1111 108.00 0 0
BE 0.000 0.6667 64.80 0 o
BF 0.000 0.5556 't08.00 o, 0
CF 0.000 0.0000 64.80 0 0
DF 0.000 -0.5556 108.00 0 0
EF 0.000 -0.8889 86.40 0 0
t = 0.110592 k.inch
Aplicando la expresj-ón del trabajo virtual:
1K'AB' =0.110592
AB, = g.116592 inch = 0.2809 cm = ,;;;l
Ejemplo: Hal-lar eI desplazamiento vertical- del nudo B de
Ia armadura Ce la figura, si 1a barra BE es 0.20"
más corta de los establecido en 1a geometria real de la
estructura.
,.1
^tl7.2'
El aná1isis de Ia armadura
la primera tomando en cuenta
Ia segunda considerando una
eI nudo B,, hacia abaio.
a) Fuerzas reales (N)
7.2'
se efectúa bajo dos situaciones,
el efecto de 1as cargas reales Y
carga vj-rtua1 P'= 1 k actuando en
b) Euerzas virtuaLes (n)
7.2',

Los resultados se muestran en 1a siguienEe tabla:
E =-0.1111 k-inch
Apli-cando Ia expresión del trabajo virtual:
1k'AB* =-0'1111
,/.ide:
Tra.[lo
}I n
^r
n Ar,
kiDs kips inch k. inch
AB 0.00 u.566v 0 .00 0
BC U. UU o.4444 0.00 0
CD u. uu 0 .4444 o.00 0
AE 0 .0u -1.1111 o. o0 0
DT U. UU o.6667 U. UU 0
BF 0 .00 u.555b -0.20 -0.1L11
CF o.00 0,0000 o.00 0
DF 0.00 -u.555b 0.00 0
EF U. UU -o.8889 0.00 0
ae, = -6.11f inch = -0.2822
"n't
= -*rnl
3.4 TRABAJO VIRTUAL API.ICADO A MARCOS Y VIGAS
:-,llosmarcosyvigaspredorni-nanlassolicitacicnespor
flexión. de esta forma, si- nuestro obietivo es determirrar eI
desplazamiento
^
del punto A, debemcs aplicar u:ra carga
viriual unitaria en ese punto, según 1a dirección del
desplazamiento que deseamos determinar.
Los marcos y vigas principalmente están someLidos a flexión'
aunque también pueden estar sometidas a efectos provenienEes
de cambios de temperatura y defectos de fabricación'
'#
xdx
CARGA REAL
I
MOMENTO REAL
¡-) *
_L.-i
lx
CARGA VIRTUAL MOMENTO VIRTUAL

donde:
M = momento flector originado por 1as cargas reales '
m = momento flector originado por Ia carga virtual'
EI trabajo externo efectuado por 1a carga virtual es:
1.^
EI .trabajo interno
m es:
efectuado por el momento virtual unitario
¡n'd0
Además, en flexión
donde:
'l =
m=
¿=
ffi=
E-L-
l=
m do : *'Md*
EI
ae:üas =EI
Aplicando eI principio de conservación de 1a energia:
lrle = Wi entonces:
¡ffI 'M
1.4= l-.dxJ E.I
(3. 6)
carga un¡taria virtual externa que actúa sobre la viga o marco,
en la dirección
^
estipLrlada.
momento v¡rtual interno en la v¡ga o marco, en función
de x, y que se origina por la carga virtual unitaria externa.
desplazamiento externo del punto, causado por las cargas
reales sobre la viga o marco.
momento interno en la viga o marco, en función de x,
causado por las cargas reales.
módulo de elasticidad del material.
momento estático de segundo orden de la sección transversal'
respecto del eje neutro. (momento de inercia).
para determinar 1a rotación angular 0 de Ia tangente trazada a
un punto de 1a viga o marco, se aplica un momento virtual
unitario en ese punto, según la dirección de 1a rotación que
se desea determi_nar, obteniéndose un momento mo en ese punto.
lng. N. Goñzález V. @ 2007

'4
..d0:
:
,)*
rns d0 : '9j[ a*
Ia enerqia:
1
I
1 t rr.=-1 +- x ---+
CARCA REAL
1
MOLÍETflTO REAL
C¿RCA VIRTUAL MOMENEO /IRTUAI,
externo efectuado por e1 momento virtual es:
1.0
interno efectuado por e1 momento virtual unitario
El trabajo
EI trabajo
r0 es:
Además, en
Aplicando
Ejemplo:
ug.d0
ao : -14- ax =E.t
flexión:
eI principio de conservación de
We = Wi, entonces:
q
Frecha, M(ffi M=
Encontrar Ia flecha
B. (El=cte) .
1'o = ['o'M.o*J E.I
12--o x
2'
(3.7)
y rotación de1 extrem.o libre
¡ng. N. González V. @ 2007 -53-

x .(-o't-1'q'*21
¿dx
EI
L
- q.fr3.o*
z1l )
o
1
me f ).q = -1- +-x---+1"
r3
q .j
"2.d*=
Q'r
2EI J 6EI
o
1AB:
Ejenplo:
Flecha: M C
_ q.L4
8El
L
J
o
q12
Arrgulo: M f*trtrtrm M : -79x
| x ----r
L (-1).t-*.q *21
1eB: I
='¡
o*=
o
F-"=-ql
1a flecha yEncontrar
(EI=cte) .
rotación
P
0<x<b: M:-Px
b<x<L: M=-Px
de1 punto B.
P
I
v
+-x-J
CB:
BA:
1
,l I o
- t- x ----t
1 ae : Jtol
(-I'*1.0,
0
CB: 0 < x S b: m = 0
BA: b<x<L: *:-(x-b)
I rr-ur.r-p.rl P2t3
- lj--------.!Y=
-
.l E.t 6El
0
P -14 b.L2 b3.
Ae = EJiT--z 'o '
_+__ a ----f---- b ---------+

AngrrJ-o:
1oe
E1 trabajo de
EI trabajo de
Por eI
además,
I
lr
ftr
--;7-
+_x_t
: ltol.t-t.rl.o*
ó Er
* l(-,r.(-p.r).0* -
á E'l
CB:
BA:
0<xl
b<xS
m0=0
me= -l-
p2r-3
6Er
3.5 TRABA.'O VIRTUAT PASA ELEME}TTOS SOMETIDOS A E'T'ERZA
rA}¡GENCIAI.
Para un elemento sometido a fuerzas tangenciales, se apliea
una fuerza tangencial virtual unitaria, en eI punto donde se
desea determinar dicha magnitud, entonces:
una
una
fuerza tangencial vj-rtua1 es: 1.4
fuerza tangencial interna v es: v. dy
análisis de fuerzas tangenciales: dy= k!v-V.ó(
,. G.A
eI principio de conservación de Ia energia fle : IIi:
1.¿ = [
k1 '''V .d,
J G.A
(3.8)
3.6 TR,ABAJO VfRTUA], PARA ELEME}flTOS SOMETIDOS A TORSION
Para un elemento sometido a torsi-ón, se aplica una momento
torsor virtual unitario, en' eI punto donde se desea
determinar dicha rnagnitud, entonces:
El trabajo de una momento vj-rtual unitario es: 1.4
E1 trabajo de un momento torsor interno t es: t,d0
Por el análisis de momentos torsores: d0 = tl .O*, además,J G.J
por el principio de conservación de Ia energía t¿,le : Ui:
lng. N. GonzálezV. @2007

Apuntes y problemas de Estructuras H¡Perestát¡cas
T1
3.7 TRABAi,ovIRruAI,PeRjA'ELEME}f,tossoMETIDosAcAI{BIoDE
TEMPERASIIRA
cuando es necesario analizar 1a variación de temperatura a
través de1 cuerpo de una barra, se puede establecer un
d.iagrama de temperaturas, un perfil de temperaturas y un
diagrama de desplazamientos de Ia siguiente manera:
(Tr > Tz)
-+------|-+-xdx
r-- T1 -------+
I'Íz
h
tm?
h
z
tm -
AT* =
T1+T2.---2-
Tt-T2
2
AL = G AT^ dx, entonces
ao =
2'o'aTm.d*
h
Aplicando una carga virtual unitaria en el punto donde
buscamos determinar eI desplazamiento, o un momento virtual
unitario donde se busca la rotación, se generarán momentos
virtuales m y ¡nO en eI Punto donde se localiza el elemento de
Iongitud dx. EI Teorema de Castigliano será para ambos
casos:
DIAGRAMA DE TEMPERATURAS
Además, la deformación lineal
de longitud dx sometida a
AL
o" =|.ee
DIAGRAMA DE DESPLAZAMIENTOS
que sufre una fibra cualquiera
cambio de temPeratura ATr es:
d0 = cr ATm dx, de donde:
1.¿= 13Jr-"-^Ir-.6"
r.e= 1?-ro
s-^Irr.6t
h
¿
(3.10)
(3.11)
+- TZ ------r ATm

3.8 TEORE!,IA DE CASTIGLIANO
Si sobre un cuerPo
elástico- actúa u:i
sistema' de "n" fuetzas,
e1las originan que el
cuerPo sufra
deicrmaci;aes traducidas
en desPlazamieotos Y
rotaciones.
Para una fuerza arbitraria Pi, la Ley de Clapeyron nos indica
que el trabajo externo originado por dicha fuerza es:
1_.
vte = -- Pi 'Ai
Para todo eI sistema de íuerzas, e1 trabajo total
Por otra parte, e1 principio de conservación de Ia energia
establece que e1 trabajo externo es igual a la enerEia
interna de deformación:
será:
+Pn^nl
r¡t^ = = Ui
u:1 f p, A, + P2 Lz + .... + P1 A, + Pn-r An-t + Pn An lu :
á,
11 a1 - E2 "2 ' -1 -t -r¡-t ¡¡-r
4,
Para materiales elásticos, Ia fuerza es proporcional a 1a é'
deformación, pudiendo escribir esta relación como' A,
D.a
A, =; é
=1 i ) ^ ] ¿ | nz 1 ii
u: i[Pr2 + Pr? + + P,2 + Pn-r2 + Pn2 ) A
2K
l¡
:É

derivando respecto de }a carga Pi:
AU
==
t 0 + 0 + .... + 2 Pi + 0
EP¡ ?:o'+ 0 l: 2q
2k
(3. 12)
3.8.1 APLICACIóN A ARMADT'RJ§,S
La energia de deformación se determina por la expresión:
.. N2t
u=-
2EA
^
=
*,*, =
# *,*'r =
$ rcr^^»
¿=rll-.r9[r.r-"EA 'AP'
La derivada pazcíal de La'energía ínterna
de ürn cuerpo. respecüo de una fuerza
cuaTqaíera, es ígual al desplazaníento
del punto de aplicacíón de dicha fue¡za,
(3-13)
3.A.2 apr,rcac¡óN A VIGAS Y
La energia de deformación se
!,ÍARCOS
determj-na por 1a expresión:
u:J*0,
^
= + f Y'='l =r-==¡a *1u2¡.ox = i$r$r o,
aP J 2.E.1 2.8.1¿
.M .AM
A - l_.Í-
J E.I 'AP
(3. 14)

Apuntes y problemas de Esbualras H¡perestáticas
o=Jfrt*ra-
Si desea determlnar rotación:
3.8.3 APLIC{CIóN A VIGAS Y MARCOS
IA}IGENCIAI.ES
(3.15)
SOMEIIDOS A II'ERZAS
(3.17)
e= f.!4-.r4r.J E.I 'EM'
La energía de deforrnación se determina por 1a expresión:
(3.16)
3.8.4 APTICACIó}¡ E BARRAS SOMETIDAS A TORSIóN
La errergia de deformación se determina por Ia expresión:
u = [k'V2 ¿'¿ 2GA
^=#i#*{r3* $rv2r o,=iS<Sr *
¡ = [
k1 'V .ráVl.a,
J G .A 'EP'
*2
u = fl.ox'2GJ
a,tZ 1
a=-t:dx =t-.3(T2).dx= [ T taTl.o,
AP'z,G,J '2.G J EP' G.J'AP'
I
'l
I
{
t
{
I
{
(
(
I
{
(
{
(
{

Ejemplo:
Tramo CB:
Tramo BA:
I"t:-x2-Mt
Apr 1
I
áMr
Ha1lar fa rotación originada por flexi-ón en el
punto C. (nl:cte).
12.O
" (ffi)",
.,TTTTTUWN,
f--/.
u1M
) ¡r, M : -6(x coscr) + 1.5 - M1
EM_ =_1
Olvl l
o2
.X
i ec:JE
0
13
a**J
0
6 (x coscr) + 1.5
dx
EI

Apuntes y problemas de Estructuras Hiperesláticas
Ejemplo: Encontrar la deformación vertical total para e1
arco de radio r contenido en el plano x-y,
sometido a carga uniformemente distribuida por unidad de
longitud de valor 6 f/..
z
^ ir e1 plann
:::::.|;,!¿
En este caso, primeramente debemos encontrar Ia posición del
centro de gravedad de 1a carga, bajo el ángulo 0. Coasiderando
queds=rdc':
Resultante: dR = gds :
R=
6.
0
f.0
r dcr
r.du = 6 r 0
Momentos axíales:
dMy: x dR = r seng. 6 r.dc¿: 6 12 senu.dcr
e
lc
M.. = 16 r- senc¿ . dq = 6 r2
YJ
dMx = y dR = r cosu,.6 r.da = 6 r
0
t"
NI = 16 12 coscr.dcr = 6 r2ÁJ
0
( 1-cos0)
2
coss. da
senO

7
M* = 6 12 coscr. dcr = 6 r2 senO
Con estas expresiones encontramos:
- 612(l-cos0) .l-cos0.x= ' '=r(-)
610 e
- 6r2sen0 -sene.
V= ore =r( , )
Analizando en planta:
-xcoso= r.(1-;oto)
^ -0-coso..
-senu : f .l-_-]
'0í
:
AM
;:=fSeDU
dY
dli aP=L
,*=r(1-cos0)at
determinan de Ia
,=ysenO
v=4-ycos0-x
Las solicitaciones serán entonées:
Momento flectors M = 6 r2(1-cos0) + p r sen0
Cortante V=6r0+p
Momento torsor: T = 6 x2(0-sen0) + p r(l-cosg)
Las deflexiones en e1 extremo libre se
siguiente manera:
Por flexión:
Por torsión:
ÍU¿
6sNr: J
0
por cortante: ouu='l2rr o't'r't'oe -
6.13.sen0'(1-cosg).r.d0 : 3.14
EI
2.4674011 . .12
GA
*_- - "(2128. (0-seno).(1-cos0).4.d0 _
-Br-¿ *
:
0.3258084468 .r4

si no se
res ul t acos
efec-rúa ',.:n anáIisis nu::réricc, ie
es clificulccsa, por e11o asunj'remos
E=2. 1'10'T/:n-
G = 8.4 ' 10' T/¡:1-
b = 0.20 ra
h = 0.30 n
r = C.00C45 !r''l
:
A = U.Ub rn
r- - i ) - -i'A
J = 0.00065 ma
coir.paraciór de
los si-guientes
E
(n)
6s en llJir.
F]"exión
(t)
Carta::t.e
(ri
Torsióir
(t)
Total
(s)
í,ñ
191.11?74
63.85
0.44C41
0.'1.1
1i1.,39177
JO,U i
31 0.73807
100.00
an
25.71425
63.69
0.1 5362
0.39
11.50027
35.9?
40.37317
100.00
1.0
0.31746
61.75 3.43
0.1 7902
34.82
0.51410
100.00
0.5
0.01s84
ÁÁ óo
0.004.í1
14.43
0.01 1 19
31.57
0.0112
100.00
0.1
0.00003
14.05
00ci 3
78',Jz
0.000c2
7.92
0.00023
100.cc
La ciefcrnacióa to-tal C:L p"rn:c anali'zado es la su¡rLa CQ 1as
ciefornaciones obt,en:-ias ¡-';ia cacia iipo Cr: esfuerzo'
üu=t5r,',+E.-+6",
De es|.a rleneía para un arco lcn ra(iio cie 3 meL]:os,
6B = 25.?1 + 0.16 + fi.50
q
E
e
E
¡
q
I
¡
T
T
I
{
q
E
(
f{
lng. ¡,¡. González V. @ 2007
-bJ-

Ejearplo: Determinar 1a flecha en el centro de 1a viga
si 1a temperaEura en 1a parte superior es
Tr = 45oF, 1a temperaEura en Ia parte inferior de 1a
viga es Í2 = 115oF Y e1 coeficiente de dilaEación de1
material es 6.8 * 10-6 17'¡r
I
a-#
T
l:l
-
0.5 0.5
,_ =
T1 +T2 _ 45+115 _ rO ,,fr__ 2
_
2 ,
1zg 2.]x.a.aT¡¡
1'Ac' - I '-
""0'*
0
integrando y sustituyendo valores
20' -
0lx
10<x
< 10:
< )o.
1
2
1
m= '110-x)
2',
- Tr-Tr 115-45"-- '- =35
120 2.1(lo-x).o.trm
I ¿ .d,
Jh
0
en 1as mismas unidades:
Acr=0.8568" =rrr;l
Ejemplo: Determinar 1as reacciones en Ia viga si eI apoyo
B sufre un asenE.ami,enEo de 5 cm hacia abajo.
Tomar como módulo de elasticidad E = 2.5'106 X/mz y momenLo
de inerci? I = 0.0045 ma.
/4. R _A_ l
-.m 77772
10.0
diagrama de deformación
8.0
T1 = 45'F
T2 = 115'F #,

:resiárces
Asuiiencic comc reiurciance 1a reacció:: en el a-§cljo
!x,9-
0
La energia <ie
Ia ex¡-,resión:
u=
Por el Primer teorena
AU
¡.- :
-e:.iz
1
I x S 1i;: I'Í,=-)r.2:<
Y
q
l):S 8: i'!^=-X.:<-9
deforr:ración i:-iEerna
a
= -x
f Iexi ór obe<lece a
,úi
:
12800..
-
t.a
243í,Í
L:':l
.
-{: -^.
dHe._:
¿'lir
Á¡ai,r^ ¡
'i'l',= ¿,* * ti'.!i ¿*
J ^,ir J i:i
<ie Castiglianc:
1q 9*, ,, a, ?rl,x2 *2 16ooc
-B= l-8'=-, ¿;a-l ür
-¿¡=:-:--¡;rad H d Er 2,!3Er
2850Cr^---Y-
- 243r.i.
El factor: EI = 11250 Tn:, sustiiLlyen3o "'alores:
288C0
ü.u5 =-.x)243.11250
I_------;l
lx. = 4.?s 'I
lng. N. Gonzále¿ V. @ 2007
J
{¡

Apuntes y problemas de Estructuras Hiperestáticás
Ejemplo: Determinar las reacciones para Ia viga sde
sección constante sometida a carga uniforme de
valor g = 3 T/¡n si e1 apoyo B sufre un asenLamienLo de 5 c¡n
hacia abajo. Tomar 1os siguientes valores como módulo de
elasLicidad E = 2.5'106 T/az e I = 0.0045 m{.
't0.0
diagrama de deformación
Ag
.-71722 "'"'.-...-....
#.m
Asumiendo como redundante 1a reacción en eI apoyo B:
3 T/m
8.0
4
21 --X¡
9'
l,a energía de def ormación
obedece a la expresión:
X2
5
2'l - -X.9'
interna debido a flexión
10
u= j
0
lulr2
d**t[ ,r'.0-
zEt d 2Er
Por eI Primer Eeorema de Castigliano: ¿A=#" dxz
10 rvrr.(+) a vz.(*l
¿n= [ o^2 dx+ [ o^2 dx
-d Er d Er

0 I x I 10:
I
0 l x I 8:
El factor EI
M.=27x-!x" ,-!*2' g- 2
u^= z7x-9x, ,-!r2-2
áMr 4J=--X
lXZ 9
8M¡ 5
:
-=--x
'oxzg
't6000.- 7000 12800.. 5t20
--Y^
X^
--
243Et - 3Et 243E1 - 3Er
3200 -. 12120
^B
=zliix2- 3Er
= 11250 Tm-, sustituyendo valores:
o.o5 = 32oo xr-g27.11250 ' 11250
xz = 39'83 r (hacia arriba)
lng. N. González V. lD 2007

CAP.4 METODO DE I,AS FUERZAS
4.1 DESCRIPCION GENERAL DEL METODO
Este método basa su enfoque en la determinación de las
fuerzas y momentos en los apoyos de Ia estructura
(redunCantes), o de 1as fuerzas internas en cualquier punto
de la estructura, de la siguiente manera:
Estructura rea].
x1
-ii, *'
6zz I
x1
6er
ESÍRUCTUMBASICA ESTRUCTUR.ABASICA
+ CARGAS + I'REDUNDANTE
x2
Estructura básica
(2t
6rz
ESTRUCTUMBASICA E§TRUCTURABASICA
+ 2'REDUNDANfE + s'REDUNDANTE
(1) +
6:z
¡zoI
6
x2
r!
--LU
lng. N. Goirzález V. @ 2007 -68-

Por compatibilidad de deformaciones en e1 apoyo A:
6¡r=o
6v:o
0=0
6ro + 6rr xr + 612 x2
6zo + 6zr xr + E2Z x2
6¡o + 6¡r xr + 632 x2
611 xl + 6n xz + 6r:
6Zr 1<r + 622 x2 + 6z:
6ar xr + 6¡z x2 + 633
en forma matricial:
(4.1)
+ 613 x3':0
LlI e¿:
+633x3-0
x:=-6ro
x¡=-6zo
x:=-6¡o
I
)
t6itl.Ix1J = t-6io]
donde:
[6ij] = maEriz de flexibilidad
.In.! 'fn.i
6i.i= I . rds 14.2)¿JJEI
[xiJ = vecE,or de fuerzas redundantes
t-6io] = vector de términos de carga
, 6io= JPo" (4.3)
tng. N. González V. @ 2007 ' oY '
:"lti: l I Il ]
6r,
6r,
6r,
I 6,',.
[3:l

Ejemplo: Encontrar 1as reacciones
vi-ga con EI constante.
para La siguiente
]__ 10, ro' t
tl
rF;T,_;+i*,IY
111
22
6zo+622x2:0
Grado de
12Wpie
hiperestaticidad = 1
12 Upie
ta ecuación de compatibilidad es:
TRAMO ORIGEN LIMITE Mo a2
AB
CB
A 0-1 0
0- 10
90x
)
-bx
30x
-rtX
-Lax
x2
6ro - Jucr2-.6s
6rz = P¿.0'JEI
Término de carga:
- 1o(e0.x-0.x2¡.(-**, r0(ao.x) (-].x) 7500
6..=t dx+Í 2 {x:---
óE'óErE.l
Término de la matriz de flexibilidad:
6". =
,?n*,r'
o**
,lr-l,r'
o* _ 5oo + 5oo _
é E, ó Et 6.E.t 6.E.t
Planteando l-a ecuación de compatibilidad:
5000 12500
E.t E'l
500
3€.1
12500 500
--+-X, = U
EI EI
= Elr.-rl

Encontrar las fuerzas en
considerando solamente fiexión'
x3
x2
Términos de carga:
los apoyos,
EjenPlo:
,rffir=
+-- ! ----------r
Grado de hiPerestaticidad - 1
.'ry.'ryN'
6ro = IM"iu.ü =
iÉ+l1.dx=
o
6zo = fte
,a.0, - 1t-*
q-fl t'l
o,= - i'-r-1¡
0
E:o = Jun.r" ¿- =
iÉ+P9
o,.= - 311¡
Términos de la matriz de flexibilidad:
6rr = 1C.o*= 9, 6rz = JrLrZ'6¡= s; 6r¡ = JrLrS-'6¡:
I
6zr: Jra
il-'¿¡: g 6zz= 1$n-= ljo,.
= *
x2

6z:: Jrnern3-.dx: iá,- = *0
f
6g, : Js3-ra.ox:
j* o- = *0
^ ,*^2 L,
d* L
ó¡¡ : JÉ' o': JE.¡ = e.r
0
6¡, = Jr3-r1-.6¡:
g
)
0xr+ 0xr+ 0 i:.:g I
324t
- L L oL I
0 x, + :¡rxz * 2., x: = - áer I
- L' L oL4 |
0 X, +
-X?
+ Xa = - :-- I
' 2Er - Er - 6Er )
^L - v
1-X" = -q-L
x3 =- #r"'
Resolver eI pórtj-co considerando solo flexión.
8r Br
Ejemplo:
4.00
ESTRUCTURA BASICA
+ CARGAS
-#
3.00 6.00
Estructura real
nInx1=1
x2=L x3=1
ESTRUCTURA BASICA ESTRUCTURA BASICA ESTRUCTURA BASICA
+ 1'REDUNDANTE + 2'REOUNDANTE + 3" REDUNDANTE
Estructura básica

Apuntes y problemas de Estruciuras H¡perestáticas
TR,A¡'IO ORIGEN T,TMITES I MO m. Itrc Itr1
BE
ED
DC
l^a
B
E
D
0-4
0-6
0-3
o-Á
1
6
6
)
0
0
-8x
-)a
x
4
4
A-v
0
6+x
q
1
1
1
1
Térainos de carga:
I
6r.o = flb-rl-'a, = lCe
ti'dx=-H
0
L
6zc = ¡l¿to'm2 .0, = j(-9:I§:-')..6, = -#J E.r d 6El E'r
I
6¡o = fUe''3-'d, = lClD'd*= -*
0
férminos <ie la matriz de flexibilidad:
6rr: is *:j*.'.i;*,-.j"=, *.is.-')'- o*=*
2 6c
ex'
6rz : Jrr-ra.ox =iH ,,.11§1" o-.1-=P o,=*
Er:: flr-r3-.0¡:já r-.i# r,.J# o-*Je_,.' o-=¿1
6zr.: flrl-'6x= ¡r, =fr
6zz =
1,21.a-:J4 *+Il9g:E.l J 6.E.1
0
tl§-rli..,,.if,
o, =#J 6.E.t
0
41
81
J2.E.
0
6z: = jra
jg-'ox:ukh o'*tJE*'o'.t h o'=#

6¡r : Jrngjrnl.dx: ar, :
*
6¡z : Irngi-m2-.dx: Sr3 = 7fr
xt*
xt*
xt*
+
+
+
xr = -1.46 r
x2 = 2.54 r
x3 = 2'33 r
-5.21
+- -1.46
6:: : F¿ 0,.:
i*.i*.j,h.i*=;i
El sistema formado es:
56
63
18
63.0 x,
202.5 x2
24.75 x,
183 x3 =
24.75 x, =
7.5 X3 =
L20
480
54
-5.21
2.54
lng. N. González V. @ 2007 -74 -

Apuntes y problemas de Estructuras Hiperestáticás
Ejeoplo: Resolver e1 arco
flexión.
gk
circular considerando solo
Por si.metria: AY:gY:4
Además:ds:5d0
I
I
,^,
iIL "///Z/¿
I
4
.nx3=1
TRLMO ORIGE¡¡ TIMITES Mo a1 tn3
AB A 0-r.l? 20 (1-cosO) 5 senO
BC B nl2-r 20 (1+coso) 5 senO 1

6ro :
nf 20.(1 - cosel.fs.sene). (s) . do + i2o.(r
1
c"se).(s.s . do
9 r/2
[--- 5ñl
[5r, I
Téroinos de carg,a:
l
I
- 6¡o : P&jrn3-.ds
tl2
oro =
'J zo ' tr -
'otel
' «sl . 0, *
,i3L$ff2.oe
[",*tI
oro :-
=., I
Términog de J.a matriz de flexi.bi1.idad:
¡ xl2
6rr = 1$ or-"[zs''*le tsl on. iru =:l'r-O.*= ,ná,iu
0 n/2
ttl2 -- . 1r
6¡:: Jrl-r3-.65 .or.,ia*#9 or=#
6:r: Jrn3jnf
.ds: ¡r, =#
6r. = P31.0, =J E,I
¡12- Í_
J
* o'*"#* o'= +#

EI sistema formado es:
196.35 xl
50.00 x1
+ 20 x3=
+ 15.?1 x3 =
- 500.00
- tt{.L6
^ --kxr = - J'bl
x3 = 4,42k-Pi"
3.67 -----+i .. . .
+ 442
4.00
Ejemplo: Resolver el pórtico con
variable, considerando
el efecto de flexión, considerando
estructura es b = 0.6 pies.
1a viga CD de inercia
para la estructura solo
que el .espesor de la
6.00
+--f--i-
2.00 8.00
Estructura !ea1

(0)
EST. BASICA
+ CARGAS
Términos de carga:
x1 =l
(1)
EST. BASICA
+ I. REDUNOANTE
t
x2='l
dx.i##*
x3=1
Q' (3)
EST, BASICA EST. BASICA
+ 2" REDUNOANTE + 3. REDUNDANTE
6,,:l!!r#*=
tj
6ro: -
¡,0 =
J&#Eo-:[;#fiffi0, -
i*#*=,,
^ 413.2381 153600 154013.2381
ürn : - ---=---¿U E E E
o,o:J&cpo-='j;ff{*q o- -
iu#i.,,
6:o =
44.4444 15360 15404.4444
- 481x - B)
o.oo0o5 -(x +10)3E
266.6667 46080 46346.6667
E
:TR;H¡.IO ORIGEN LIMITES I MO llrl B, ID.3
BE
ED
DC
.A
B
E
D
0- 6
0- I
B-10
0- 6
0.00625
0 . 00005 (x+10 )
0 . 00005 (x+10 )
0. 00 625
3
3
0
ñ
-B (x-8 )
-16
x
6
6
6-x
0
.x
x
10
1
t_
1
1
¡.0:¡ñ6"*.¿
-78 -

Apuntes y problernas de Estructuras H¡perestát¡cas
Términos de Ia maEriz de flexibilidad:
)
- 6.. = {mf-¿r=
JEI
211.1111
+
E
u',=
I-# "
.
]tt#r.n*
.
T.,-#;E
* .
]##
o,
.. 11520
Orr= ----=- +
E
2488.8890
+
E
28800 30300
+-=_EE
C,
C
C,
d,
G,
c
é,
C
c
c
c
35.1852 2880¿
-
f _.EE. 2880
o.-¡J =
E
6210...=_
E
471.4078
-------.=-
E
8
6rz= [----
6*
-.
d, +
J0.00005(x
+10)oE
§ 1 185.1850 314.8148¿_L¿EE
- 6,, _ [*, *, d*
EI
c c 30300
oz¡.= Ó:.2
= E
2
6.. = [rz-¿.x
JEI
8-t10"0
6.- = l' *' = .¿r* f *'¿¿ I a
ülo,oooos(x
+ 1o)rE ¿f
o.oooos«* + r0)3E
'dx .
J*i#
*
e 891.5389
o^^=_+
E
11520 25740
EE
u,, =
i-uu*.,.i-rfo .". jrdr* *.]**';r.,.
414.8148
+- E
v. @ 2007
:i,
!
a.
;l
L

Apuntes y problemas de Estruc{uras H¡perestáticas
.dx +
0.00005(x + l0)3E
_ 1995
E
* -
]*#*..'
b
[----]g- d,
I 0.00625E
d
+l5.15
-6zs: J%Po,.
^ 197.5308 52.4691
-¿r E E
6210
- 6¡r:6r:= E
9850
- 6¡z= 6:¡= r
10
.ox + J
I
960
E
- 6¡¡:
6:¡ :
6:: :
El sist
2
['. d*
JEI
68
[--]-. ¿' * [-----]-
jo ooozse
-" jo.oooosix + ro)3e
960 69.1358 5.8642
EEE
ema formado es:
25740 x, + 30300 x,
30300 x, + 931 62.9461 x2
6210 x, + 9850 x2
+ 62L0 ,<3
+ 9850 x3
+ 1995 x3
I
46346 .6667
154013.2381
15404.4444
X1 = 3'99 ^
xz = 5'15 k
*, : -r't.85 k-Pl"
3.99
Ing. N. González V. @ 2007

Apuntes y problemas de Estructuras Hiperestáücás
CAP. 5 METODO DEL TRABAiTO MINIMO
5.1 DESCRIPCIóN GENERAL DEL METODO
Es conocido también como Segundo Teorema de Castsigliano o
Método de Menabrea y su aplicación esEá destinada a Eodo tsipo
de estructuras hiperestáticas
EsEe mét,odo basa su enfoque en Ia determinación de Ias
fuerzas y momenEos en 1os apoyos de la estructura
(redundantes), o en cualquier punto de fa estructura, de 1a
siguiente manera:
1o) Dada Ia esErucEura, se reconocen e1 número 1as
fuerzas desconocidas como redundantes.
crado de hi.perestaticidad = 3
lr
^
ESTRUCTI'RA REJAI,
;.4Tí
x2é
INCóGNXTAS : REACCIONES
Se eligen y denominan las redundantes (x1, x2, x3)
Se determj,nan los fuerzas normales, momentos, cortantes,
etc, en función de las fuerzas redundantes, cargas
externas y geometria (Iongitudes)
N = fr(xi, P, s)
y = fr(x1 , P, S)
y = fr(x1, P, S)
X1
INCOGNIT¡S: FUERZAS INTERNAS
2o,
30)

Apuntes y problemas de Estructuras Hip€restáticás
4 o
) Por 1as conCici-ones de
Teorema de Castigliano:
borde y aplicando eI Primer
(
(
T
T
I
T
q
e
II
(
q
q
I
I
I
I
I
I
I
I
I
(
{
{
{
{
{
{
áu
=o , 6u
=o' oxz
. áU
=o' áXs
y debído a que 1a energía interna de deformación es:
áu
=0,áXr
óu
=0,oA2
u = [ N2
d.* [k1'V2¿.* f
M2d.*
f-É0,r 2EA r 2GA r 2El r 2GJ
JStfrr.. . f $tffr.. f $tffn.. Jfr tfrr. = o
I N r
áN
u.*[klvr áV
u.*f Mr dM
u.*f T ( 6T
)d"=oJ EA'AX2'. r GA'AX2' r EJ|'AXz' ¿ GJ'AX2'
#=., l*,#)o'. iS(#E'.i!}(#ro'. Jfrt4r*¡" = o
5.2 CONSIDERACIONES PR¡CTICAS
Dependiendo de1 tipo de solicitación inEerna a 1a cual esEá
sometida una esEructura, 1as expresiones obtenidas se pueden
aplicar bajo Ias siguientes consideraciones prácEicas:
- Para vigas y marcos, predomina e1 efecEo de flexi6n.
o. - Para arcos, considerando su clasificación,
predominan
los efectos de noraal y flexlón.
- Para armaduras, predomirra eI efecto de fuerza no¡:nal .

5.3 APTICACION A VIGAS
EJ emplo : Considerando eI efecEo
reacciones (EI=cte. )
de flexión, ealcular Ias
x2
M = xz.x - 2 x2
Aplicando eI principio del
someEidos a flexión:
trabajo mÍnimo
ds=dx
para elementos
EM
oxz
f^r,#, 9=o
EI
6¡(X2 .x - 2.x2).(x)'ox
x2 (72) - 648 = o
*".1*':gr it gl = o
'd E.r d E'l
Ej emplo: Considerando el efecto
de flexión, calcular 1as
t-
M = Xz.x
AM
axz- ^
q3
6L
4Tlm
t-
lng, N. González V. @ 2007
ds=dx
-84-

Apuntes y problernas de Estructuras H¡perestáticas
Aplicando el principio deI
sometidos a flexión:
L (xz .x - + ,3¡.1,.¡.d,
J--v
0 -',
x' rÉl - e
'15''
: n
Ejeoplo: Considerando e1 efecto
trabajo minimo para elementos
-,i+ *i+=.
de flexión, calcul_ar las
0<x(b,'
a<xó;
A,I
oxz
A.l
-=
h+v
ox2
P
L ------------+-
M = Xr.x
M = Xz . (b+x)-Px 3
x2
; ds:dx
; ds:cix
-,
i* ** *r.ltoyr' o,-
'i+p.x = o
*r 1$,*r, rr$r-r$»-, rr*r.t4, reo
*r=S.e.l,

Apuntes y prob¡emas de Estructuras H¡perestát¡cas
Determinar 1as reacciones para 1a siguiente
escructura, considerando ftrexión y cambio brusco
l
-fx2
M = Xz.x - 2 x2 :+
Aplicando e1 prÍncipÍo de1
someLidbs a flexión:
EJ emplo:
de inercia.
f
(.xz .* - z.12) tr) . o*
ó El
+- x
A-¡,1
&=x ; ds=dxox2
trabajo mínimo para elementos
lu.r 6M
l.
d'
= o
J 'lXz' El
* !(xz.*-2.12)
(r).0*
= o
i B E.l
*,.!r2.0, _ !*3 o" _ oL ) tr.| J E-l
0 -' 0 -'
64
-X^
- 128 +
J
Ej emplo : Determinar 1as reacciones para la siguienLe
estrucLura, considerando solo flexión y cambi-o
gradual (l-ineal) de la .altura de l-a barra.
19_ X- _ 55 = 0
3'
4f lm
4Tlm
N2

M: Xz.x - 2 xZ
ApJ-icando e1 principio
Integrando:
ad
+ :-:x , Cis=dx
Olr2
de1 traba j o minimo par.a elementos
l, «#r $=0,
En este caso, el ¡nomento de inercia no es constante y varia
con la al-tura de acuerdo a Ia siguiente expresión:
l_ b
t2x+123
12' 24
!(xz.*-z 12).(*).dx
= ol=.b- 2x+12
o n'(^l-::rt
x2 (0.085184) - 0.06833769 = 0
E je:npIo:
cuadrá t i co
Determinar
es tructura,
(parabólico)
xz = B.a2 r
Ias reacciones para la siguiente
consj-derando solo flexión y cambio
de l-a altura de Ia barra.
6.00
^2L'! = Az.X - ¿ X =)
Aplicando e1 principio del
EM
:.- =x ; cls:dxdx2
trabajo minimo para elementos
4Tlñ
[n¡.r
aM
l.
d*
= o
r '1Xz' El

En este caso. e1 momento de inercia no
con la altura de acuerdo a la siguiente
es constante y varía
expres ión:
Integrando: x2
,_ b rx+36r3
12', 72
i«xa:=f)-t-l.o- : o
0 _. t_)"
12',72
(0.000454s1) - 0.0034't222: o
Comparando los resultados medi-ante la representación gráfica
de los diagramas momentos:
10.13
6.98 23.88
4 Ílm
8.02 26.16
4 Ílm
Ul I Df/t
l
2.0 4.0 I

5.4 APTICACION A PORTICOS
Ejemplo: Considerando flexión ..r"o.rt.u.
para el siguiente marco.
1as reacciones
q
q
q
q
q
G
G
d
G
{
{
{
f;
q
q
dü
{
q
X1
Tra¡Io Orige Linites I M N/dxt ÁlAr/?¡a,
DC D 0-5 - Xrx -x
Xt'x¿
CB 0-6 1 /-5Xr-2x-+12x -5
25X1 + lQ¡12-60,«
AB A 0-5 1
- Xlx -x
Xl'x
Aplicando el principio deI trabajo minimo para elenentos
5o
2 [xL]'.¿* +
J E.I
0
250
-., X, + 150
Jratffr $=o
6¡1ru.x,
+ 10.x2 - 60.x)
J--; ¡-= ox = o
0
Xr+'120-1080=0
Xr = 1.54 ?

4llm
1.54 --+
t t-12
1.54
l2
EjempJ-o: 1as reaccionesConsiderando flexión encontrar
para ef siguiente marco.
207
1.50 6.00 X2
Tramc Orígen Límites I M
EM
a&
EM
ex2
AB
BC
A
B 0-6
1
2
- Xr.'x
-5 Xr+Xz. x-20x-30
-x 0
x
Aplicando e1 principi.o de1 trabaj o minimo para efeme;rtos
sometidos a flexiÓn:
|.¡¡.rl[1.
d*
= o
J 'aXl' El
1vrtffr*=o
z V. 6 2007

a-ri:',1
't't¿ !l :
Apuntes y problemas de Estruauás H¡p€restát¡cas
[l',t.rffil.d*=or 'áX2' El
Primera redundante:
u1xf't'-.0-
+ Jzs'xr-s'xz'-.roo .o-:0
00
350 v¿" - 45 Xz : -1350
3',
(1)
Seg'unda redundante:
(-5.Xt + Xz .x - 20 .x - 30).(x)
2.8.1
6
J
0
dx =0
Resolviendo eI sistema:
-45 Xl + 36 X2 : 990
-L.8627
25 .1724
T
T
25.1724

i
ü
=ta
4'
a
a
a
dt
ft
á
ñt
il
{
it
a
rt
Ü
=}
=ta
a
rt
a
É
r}
?
r,
i)
{'
r,
{,
il
a
e
EJ emplo : Determinar 1as reacciones
considerando flexión.
6.00
para e1 marco,
=0
Tramo Origen Límites I M
ctvl
ax1
EM
ax,
AB
bL
A
B
0-5
U-t)
l-
2
- Xr,x
-5 Xr+Xz.x-2Ox-30- 2x2 -5
Aplicando e1 principio de1 trabajo mÍnimo para el-ementos
someEicios a flexión:
2
frvr ri[l,d* =oJ 'cxt' E¡
lu.r ¡M
l.
dt
= o
|axz' El
Primera redundante z
q^
I.Xl
''' ¿'
J EI
0
6
r25.Xt -5. Xe .x +100.x -150 +10.x2t I I L dv
r 2.E.1
0
350
: x, - 45 Y.. = -1710 (1)
J
lno. N. González V. @ 2007
-

Apuntes y problemas de Estructuras Hip€restáticas
Segunda redundanle:
(-5.Xt +Xz.x-20.x-30).(x).0, : O
2.8.1
I= 19J: = 22.soo
72
1.5 x 3.6 = 5.4
Diagrama Ce momentos
6
I
0
X, '+ 72 X, = 2628
At = -!'lL¡¿
ix, = ,t.1034 r
5 .5 APLICACIóN A ESTRUCTTIRAS ESPECIAI,ES
3
Ejemplo: Una .vj.ga de madera (E = 250.000 kp,/cmz) tsiene
' longitud de 7.2 m, una sección de 10 x 30 cm y
sopcrta una carga concentrada de 3
T aplicada en eI centro.
-90 (2)
^TJ
I
v
5.40 T m
En esas condiciones,
M=
4
cm
T 0/'
' 3.60 ' 3.60 I
:-wmilffilffinruw-
e1 esfuerzo máximo por flexi.ón es:
Yqo-oo..3o = ¡oo kp/cm2
22500 2 -

La flecha debajo 1a carga es:
3000 .?2 03
= 4.15 cmYc=
48x250000.22500
E1. esfuerzo que se. presenta en .la zona máÉ sol.icitada .por
f lexión (punto medio de 'La'.viga) supera .a1 .admisible (o*á* =
240 kp/cm2) en un 508; Dé .Ia .misma.'forma se .puede:'determinar
gue la flecha.en el.punto medio.de la viga'supera a Ia-flecha
admisible (faam= L/soo = 720/4oo = 1.88 cm) en un L20.7 ?.
En consecuencia nos planEeamos 1a tarea de reducir ambas
magnitudes, para e1lo . introduciremos un puntual de,madera de
5 x 4 cm. y a1 mismo tiempo, para'lograr que e1 puntal trabaje
conjuntamente 1a viga, uLilizaremos un tensor de acero de
5,/8,', dispuesLos de 1a siguiente manera;
4.+
D77, I
I
1.50
+
Viga:
E = 250.000 kp,/cm2
b/h = 1ol30 cm
A = 300 cm2
I = 22.500 cm4
Puntal
Ep = zso.ooo kp/cm2
b/h = 5/s cm
Ap = 20 c*2
-
Cab1e,
Ec = 2. 100. o0O kp,/cm2
$ = 15 mm'
Ac=2cm2
.. Xp
^a=
-
" 2.sen«
3.60
X6 "P X6
Xp
I
"l
ol*ix'
I
Xp
xp
*t*--
I -.n
*"
"l)--:-{.:lD

-i
' ;. : - : ; ':. ¡prJ¡tes i problemas de Estructuras Hiperestát¡cas
Por e1 procedimiento de1 Trabajo Minimo, consi-derando r_os
efectos de ftexión sobre Ia viga y fuerzas axiáIes sobre eI
puntal y 1as dos porciones de cabl-e:
. M ,AM.
l-.(-).ds+ )r El 'ax' u
Deterininando, por tramosr las
fuerza .normal: 1
$«Sr,- : o
sol-lcitaciones de flexión y
Tramo Oriqien Línites M At/axp N N/Axp
AC A 0-3.6 3-Xp
2
x
2
BC B
0-3.6 s-Xp
2
x
2
DC D 0- 1.5 -Xp 1
'lrJ A 0-3.9 Xp
2 sencr
1
2 ser¡a
BD B 0-3.9
Xp
2 sena
1
2 senc
AB 0-7.2 Xp cotcr
2
cot c
2
Aplicando 1a expresión del trabajo mínimo:
6^
-:.1= *.l.orn2.- XP . 1 s.90
+ *o ..,.r0**o'"o,o.cotc.3.6-
Elá 2 2 -'. - 2.senu 2.sena EcAc ' EpAp ' ""' Z '-z EA
,7.775 13.182 13.182 13.182... 23.328
t Er
*E"fu-aoo;+
* )xP= a
(0.01.3824 + 0.003186 + 0.0003 + 0..0001382) xp = O.4t4:.2
donde: ., ^ ^^^ T
xp: ¿.Jó3 y X. = 3.098 r
nueva condición de carga que soporta Ia viga se ahora:
de

E1 nuevo esfuerzo por flexión.será
por flexión y compresión:
111000 30 2860
22500 2 300
ahora la suma deI esfuerzo
83.5 kp,/cm2
E1 momento flect.or máximo en Ia viga es:
1
M =:'.8-2.383)'7.20= 1.11 r-m
4
1.'t1
v Ia rtecha en et punto c es: ," =
(?9ol;=1t=1tl]3=o=t
= o tu cm
48.250000.22500
EI esfuerzo que soporta cada una de 1as porciones de1 tensor
de acero es:
3098
"" = -f = l-549 kP,/cm2 (tracción)
;-l!-r9!rl=oA EA'óX'
E1 esfuerzo que soporta e1 puntal de madera es:
2383
"o
:
lo
= 119' 2 kP/cm2 (comPresión)
Nota: A1 resolver esLrucLuras hiperestáticas, deben
comprobarse las Lensiones de trabajo de los materiales,
elIas no deben superar 1os valores admisibles. Cuando e11o
ocurre, deben modificarse 1as dimensiones de l-os elementos
auxiliares (puntal y t.ensores) hasta conseguir que 1os
esfuerzos de Lrabajo no superen a los admisibles.
5.5 API,ICACIóN A RETICULADOS
En e1 esLudio de retj-culados hiperestáticos se reconocen l"as
redundantes como reaccj-ones en los apoyos o fuerzas inLernas
en 1as barras.
E1 Método deI Trabajo Mínimo consist.e en
expres ión:
aplicar 1a

Apuntes y problemas de Eslructuras Hiperestát¡cas
EJemplo: Determinar las fuerzas en 1as barras de1
reticulado tomandó en cuenEa eI mismo material y
que 1os valores del área de cada barra están indicados entre
paréntesis y se expre"ar,
"a,
a*'.
El reticulado cuenta con un grado
e1Io adoptaremos como redundante ]a
esta manera efectuaremos e1 anáIisis
de hisperestaticidad, Por
fuerza en Ia barra AD, de
de la siguiente manera:
10-x
lng. N. González V. O 2007
5 - 1.333 X 5 - 1.333 X

Apuntes y problemas de Estrucluras H¡perestáticas
Tramo N
AN
:-aix
L A
AN
Nx(:-)x
dx
L
EA
AD X 1 6.00000 60 0.1000 x
DF 1.6667 X 1.6667 6.25000 45 0.3858 X
DE 1.3333 X l alaa
5.00000 Jb .0.2469 X
EF 10 0 3.75000 27 0
BF, 6.25 -'t.6667 X 1.6667 3.75000 45 -0.868'l + 0.2315 X
CF -8.0039 0 4.80234 45 0
CE 1.3333 X 1.3333 3.00000 Jb 0.1481 X
BC 6.25 0 6.00000 54 0
Sumando Ia expresión correspondiente al método:
I: -o.8681 + 1.1123 X
-0.868l +L.7123 x=0
x : 0.7804 r ( tracción)
Sustituyendo X : 0.7804
fuerzas en Las barras
todas las barras.
T en la coJ-umna correspondiente a l-as
(columna N) hallamos las fuerzas en
0.7804
9.2196
0.7804
3.959s 3.9s95

;:i:'- : ;::t_ Ilrl ,:. ' r.
Apuntes y problemas de Estrucluras Hiperestát¡cas
EJemplo: Determinar 1as reacciones
barras de1 reticulado tomando
maEerial y gue las áreas son 60 cm2.
pI
Trabajo MÍnimo
y 'fuérzás:r en las
en cuenta e1 mismo
3.0
EI reticulado es estáticamente indeterminado exteriormente
debido a que existe una reacción superabundante, adoptando
como redundanLe Ia reacción en D.
3.03.03.03.0
E1 Método deI
expresión:
consiste en apLicar 1a
tru.ráNl.L =oP 'AX'E.A
lng, N. González V. @ 2007

Tramo N
AN
Ax
L
aNLNx(-)x-
OX EA
AB 5.4000 - 0.3000 x -0.30 3.00 60 -0.081 + 0.004500 x
BC -0 60 300 bt, -0.324 + 0.018000 x
CD 10_8000 - 0.6000 x -0.60 3.00 60 -0.324 + 0.018000 x
DE 3 6t]f]f) - o ¿5no x .0.45 3.00 60 . -0.081 + 0.010125 X
EF 3.6000 - 0.4500 x -0.45 3.00 60 -0.081 + 0.010125 X
AG -9 (]0(}u + 0 5t]uo x 0.50 5.00 60 -0.375 + 0.020833 X
BG -0.40 4.00 60 -0.192 + 0.0'10667 X
BH -g 0000 + 0.5000 x 0.50 5.00 60 -0.375 + 0.020833 X
CH 0 4.00 60 0.000
DH -6 0000 - 0.5000 x -0.50 5.00 60 0.250 + 0.020833 X
DI 0 0 4.00 60 0.000
DJ 6.0000 - 0.7500 x -o 75 5.O0 60 -0.375 + 0.046875 X
EJ 0 0 4.00 60 o.000
FJ -6.0000 - 0.7500 x -0.75 5.00 60 -0.375 + 0.046875
GH -5 4000 + 0 3000 x 0.30 300 60 -0.081 + 0.004500 x
HI 7_2000 + 0.9000 x 0.s0 3.00 60 -0.324 + 0.004500 x
IJ 7.2000 + 0.9000 X 0.90 3.00 .60 -0.324 + 0.004500 x
Sumando 1a expresj-ón correspondiente aI método:
I : -3.062 + 0.313167 x
-3.062+0.313167X:0
x : 9.78 r (hacia arriba)
Sustltuyendo X:9.?B r en Ia colunna correspondiente a las
fuerzas en 1as barras (colunna N) hallamos fas fuerzas en
tocias 1as barras y por estática encontraremos Ias reacciones
restantes.
5,7 APLICACIóN A ARCOS
En eI estudio de arcos indeterminados se efectúa un recuento
de las incógnitas que se presentan y en dependencia de e11o
se determina el grado de hiperestaticidad de la estructura.
Luego se escogen l-as redundantes y se plantean fas
expresiones correspondient.es a las solicitaciones estudiadas
y qLre tienen efecto sobre el comportamiento de Ia estructura.

::.--;----,-. -.._-'.'
Apuntes y problemas de Estructurás Hiperestáticas
Ej emplo:
valor 20 x 60 cn, se .utiliza un tensor de acero de diámetro
2 cm.
jl
'i
Considerando : solamenEe e1.'- efecto de flexión e¡t
determinar la fuerza .que ,'acEúa en 'el ' tensor cuando
una carga concenErada P,= i6t .r, su cúspide'
I
I
b
Las reacciones pueden determinarse sin dificultad pero rio aÉ4
las fuerzas internas, en consecuencia eI arco es
indeterminado interiormente.
Escogiendo como redundante la fuerza en el tensor y
-aplicando
Ia &presión de1 Lraba j o rnÍnima para ef ectos de f lexión y
fuerza normal:
b
31 3r
- 101 -
Para rigidizar.un arco de acero de radio 5.00 m,
sección transversal rectangular consEanEe de
eI arco,
se aplica
5.0
x

Apuntes y problemas de Estrucluras Hiperestát¡cas
Tramo M
4,,
ax
N
A'l
=-dx
ds
AB arco 15(1-cos0)-5 xsen0 -5 senO 0 0 5de
AB tensor 0 0 1 dx
EI
j
0
-375 .sen0 .(1 - cos 0)
n 1- 10
do+125.X. p9I-$6¡¡ f !l=o
d Er dEA
750 196.3495 .. 10
-:=.¡--r-i-IJ-.X+ - .X = 0
EI EI EA
dondeE:módulode
inercia de1 arco y A
tensor:
elasticidaci de1
es el área de ]a
material, f momento de
sección transversal del
A = 3.14 .10-a cm2
I : 3.6 .10 ' cm'
luego: X: 2.4r
5.8 ANTILOS DELGADOS
Se def ine con1.o ani ll-o delgado a una estructura plana cuyas
dimensiones longj-tudinales son mucho mayores a las
dimensiones-de su sección transversal.
En estas condiciones geométricas, 1os anillos principalmente
trabajan a flexión y es suficiente considerar cono
redundantes }os momentos flectores.
GeneralmenLe Ios anil-Ios son geométricamente simétricos y si
se encuentran sometidos a cargas simétricas, en las secciones
donde coinciden l-os ejes de simetria se consideran las
fuerzas cortantes nulas y solo se consideran como redundantes
l-as fuerzas normales y los momentos fl-ectores.
lng. N. González V. @ 2007 102

i"1r.1{r:!..1':¡
EJenplo: Estudiar e1 anilLo plano delgado de La figura
considerando EI = cte "
Cortando eL anil-Lo- a 1o largo del eje x, se determina que al
no exisLir cargas horizontales, 1as cortantes en esa
dirección son nulas y las fuerzas normales en ambos exLremos
P
son iguales a ;, Ias redundant.es serán los momentos flegtores
I
x1 .
Aprovechando 1a simetrÍa trabajaremos considerando 1a cuarta
parEe de1 anillo, tomando eI extremo superior como empotrado
y eI extremo inferior libre.
EI momento flector
en un punto D de
abscisa r tx" y
ordenada ry" es:
ib
i
1
P_t-
AM
_ = _1
dxr

Apuntes y pfoblemas de Estructuras Hipereslát¡cas
Aplicando la expresión de trabajo minimo para flexión:
Ir *r*!t"-x)lds = 0
Simplificando:
En esta expresión se detectan dos
análisis de centroides de lineas:
integrales conocidas por e1
[."o
[:.-0
x1 fo. *
U
Pa
2
-: 2
Asi ]a integral
1."
- s , es Ia longitud de arco de1 anilLo.
mientras que 1a integral
estático de primer orden
representa e1 momento
i" a.
rc
de1 arco de anill-o respecto de1 eje "y"
jx.ds
Despejando f a redundante: x, :l¡-a--¿1
Jo'
La rel-ación entre eI momento estático de prj-mer orden
respecto del eje "y" y la longitud se define como coordenada
del cent::oide de ]a finea respecto del eje t'x ", fa
redunciante X1 se determina a través de 1a exp::esión:
P
Xr= [x,_-a]-2
Si eI anilIo fuese eliptico con semieje mayor a = 2 m,
semieje menor, b = 6 m. y carga P = 20Í, Ia coordenada X.:
1 . 64 4 m. , entonces :
lng. N. González V. @ 2007 104

X:. - 10(l-.644 - z) = -3.56 r-^
Si e1 anillo es circular donde r
coordenada X" : 1.9099 m., enLonces:
xl : 15(1.9099 - 3) =
3. 56
10
:3m.yP=30r,
-16. 3s r-^
1a
Si el anillo
dimensiones de
fuese un
m.yse
.P r6.ss
Y
15
cuadrado cuyas diagonales tj.enen
encuentra sometido a carga de 3T.
Para una linea rect.ar X" = 1 rn.
En consecuencia:
y : 1 q t] - ).r1 + 1t 1.50' "'
t.J
"l.
r.t
¡ 1's
Y
4
3
1.5

Con las fuerzas redundantes determinadas medi-ante e1
procedi,miento descrit,o, se pueden obtener los diagramas de
momenlos flectores, que en est.e caso.corresponde al gráfico
siguiente.
Ejemplo: Estudiar e1 anj.lIo plano delgado de fa figura
considerando EI = ite. que se encuentra someticio
a carga interior uniforme q.
Cortando e1 aniIlo a 1o largo de1 eje de simet.ría xt se
determina que las cargas horizontales se equilibran
internament.e, por e11o 1as cortantes en esa dirección son
nulas y 1as fuerzas normales en ambos extremos son iguales aI
valor qa, quedando como redundantes Los moment.os flecL.ores X1.
Aprovechando 1a simetrÍa trabajaremos consirierando 1a cuarta
parte del anil1o, tomando e} extremo súperi-or como empotrado
y e1 extremo inferior libre. Además las cargas equivalentes a
carga normal

:.¡;:,.,
":'.
1' ::g:.!: . ':¡:: 'i'r::r '.";'r.: i,r' .''': .::;.',..."
l'' :t
-
epunted"y problemas de Estruc{uras Hiperestáticas
B
o.
qffi
EI momento flector
en un punto D
de abscisa rrx'r
y ordenada try" es:
AM
i --:
i/Xr
flexión:
M: -Xr- Qa(a-x)+
Aplicando la exPresión
1o(.-x)2 + Lor'
2 '' 2 -'
de trabajo rninimo Para
,*--r-
qa(a-x)+]rru-*t' *l qy2 I (-1)ds : 0
qa ¡uo" -
'o
2ds:o
'*o')ds:o
En esta expresión se detectan también integrales conocidas
por el análisis cte centroides y momentos de inercia de
lineas:
Asi la integral
tid"
= s , es la longitud de arco del anilIo.
ü
-1
SS
xl [t" * qu' lor - qa [,,at - ]'JoJOJO¿
1 f'2. 1 i-rqJo"o.-rqJoY
Sinplificando:
sss
¡rtr 1 ,l 1 l.x, rocs +
iw' "ods - ;o 'o{*
qu' fa, *
'o

Apuntes y problemas de Estruciuras H¡perestáticas
s
mientras que la integral [{*, * yr¡¿" repr.esenta e1 momento
t -'
estático de segundo orden del arco de ani110 respecto de 10sejes "x-y", denomi-nado también moment.o polar de inercia deuna Línea.
s
!{*z *v2)
xl =g¡-e--=-¿,¡ - Ir^,
i::"'á1:'".:$:.i:-?:'i::':,'J".1,:J::.",:":::*:_r"J"i:::.deternina a L-ravés de 1a expresión:
Despejando la redund.ante:
Si e1 ani11o fuese
dimensiones de 4 m. y
de 9 T/m, eI análisis
forma:
al
un cuadrado cuyas diagonales tienen
se encuenLra sometido a carga uniforme
procedente se encamina de Ia siguiente
Y - q rrP
2's
rr-t-
En 1a solución de este problema tomamos 1a rama deI anillocomprendida en e1 primer cuadrante, adecuando 1a LeorÍadeducida y 1os result.ados del anáIisis de cenLroides ymomentos de inercia de Iíneas encontramos 1as siguientesexpresiones:
lng. N. conzáiez V. @ 2007

-1
_ : a :i
Apuntes y problemas de Estruciurás Hiperestáticas
'=
G
C
G
G
ó
G
G
j
j
c
q
t
G
Para una llnea recta, e1 momento
llnea recta respecto.de los ejes de
polar de inercia .para
referencia es:
_ 2^1, 3
P3
_ 1.6.,1,
3
Iongitud =i2 ¿!¿
En consecuencl-a ,'1
:16,5
4.5 (-+2^i2
2) = - 4gr-m
E jernp).o: Considerando solamente el- efecto de flexión
1os arcos, cieterminar 1as reacciones.
en
lng. N. González V. @ 2007 - 109 -

La cantidad de reacciones existentes els cinco; de 1as cuales
1as reacciones horizontales no pueden determinarse
directamente, en consecuencia 1a estructura es indeterminada
exteriormente.
1,
Escogiendo como redundant.e. -l-as reac.ciones. hJrizontales en 1os
apoyos, las , cualesr debido a -Ia inexistencia de cargas
externas, son iguales: i
Tramo Or¡gen Limites M
AM
ax
ds
AC A 0-n 90(1-cos0)-'180 + X 3sen0 3sene , 3ds
BC B 0-¡ -X1seno 1 senO 1 1d0
I
0
270.senO'(1 - ios 0) - 540.sen0 + X'9'sen20
2.8.1
.3.de+ *.|sen2o.de=o
d Er
810 3240 ., 27.¡r ,, 27'¡r
+,.-+^.-=U
E.t E.l 4.E.1 2.8.1
x = 35.56
r

É
5.9 APOYOS EI,ASTICOS. RESORTES
Un resorte (muelle) esta constituido por un alambre arrollado
sobre un núc1eo circular. Los resortes son di-.spositivos que
se deforman ante 1a presencia de fuerzas de tracción o
compresión, mientras el diámetro de1 alambre es mayor, mayor
es su- rigidez.
.J
I
P
La relación entre la fuerza apiicada sobre eI rescrte (p) ,
la deforroación originada (A) es:
=
Itsl
i
l=
E
e
e
e
e
e
e
e
e
E
e
E
t
5
C
C
G
C
C
é
C
é
d
é
é
G
G
ú
c
J
j
q
I^
Donc-le: P
A
1,
P = k,A
fuerza aplicada sobre eI resorte
defor¡ración longitr-rdinal ciel resorte
constante del resorte
En esL::Lrctr-rras, f os resortes se utilizan cono amortiguraCores
de fas deformaciones de Llna estructura, en este caso Los
resortes reciben 1a cienoninación cie "apoyos e7ásticos,,.
Paia e<:os casos, 1a expr:esión general del método del Trabajo
l"linimc es:
J$rffr.. J*#,#r'.' j}i,#x.. ifr rfrr,.f = o
lng. N. Gonzálaz V. @ 2007

Para el caso de estructuras con elementos rectos' en las que
solamente se considera el efecto de flexión, la expresión del
Trabajo Minimo será:
donde:
EjempJ.o.
Si en su
rigidez k
y momentos
Una viga
carga de
extremo B
= 5000 kp,/m,
de madera de
3.5 T,/m y tiene
se apoya sobre
determinar fos
Xt=
1- _
tI.r![r ¿, * 11 = o
JEI 'áXl ' k
fuerza de interacción
e1 resorte
constante deI resorte
entre la estructura y
20 x 30 cm soporta una
una longi-tud de 3.0 m.
un resorte eIástico de
diagramas de cortantes
En el extremo
deformable, €o
redundante.
3.5 T/m
B, el resorte
consecuencia 1a
funcj-ona como una apoyo
estructura presenta una
Tomando origen en el punto B:
M:Xzx* 1 ?( .,
dtvl
AM
oxz
3.5 T/m
- A.
'J
Á
112 -

Apli.cando 1a expresión del ?rabajo Minimo:
I
xz.12 _r.zs.13 ¿, * x2-=s
0t'K
Considerando que EI = 1125 T m2 y k =
l
I - 35.4375 1
1121^2--1irs +sooX2=o
Efectuando una comparación
en e1 gue eI apoyo B fuese
500 T,/m
entre eI caso estudiacio
indeformables:
y e1 caso
3.5 Tim
1rf5@
.f--
| +- x --19.10 1.40
l_e.10
| o, ------
_
, ¿.o, ----t---l
t '+o
3.5 T/m
3.s372@
ffiel+_-
6'5625 3.9J7s
t---.-6.5625
| CI=---_| -
*_,.u -__j-I75 3.9375
I 1.55
,.rrrrf
-:;z 2.21
-113-

De Ia comparación
siguiente:
En e1 segundo caso Ag = Q ,
: 0.28 mm
E jemplo.' Una viga
carga de
resorte de rigidez k:
entre ambos casos establecemos 1o
- Cuando e1 apoyo B es indaformab1e, J.a reacción
en é1 es mayor.
- S1 momento negativo en A es lra,yor cuando B
: se desplaza verticalmente
- EI. momento positiVo,eni e1. tra.Eo r"r 1r"yo= .cuando
eI ,apoyo B .no -se 'desplaza,
-.. 81.-punto de momento: máximo positivo .está más alejado
deJ- apoyo A cuando el- apoyo se desplaza.
en er primer caso ¿a=I1 =o.ooo28 m
5UUU
de madera de 30 x
5 T/m, en e] punto B
5000 T,zm. Determinar
60 cm soporta una
se apoya sobre un
las reacciones.
5 T/m
Escogiendo como redundante la fuerza en ef resorte (apoyo
e1ástico)
5 T/m
o^Lt-
B
6.0 m
Ay=25-0.4X2 Cy=25-0.6X2
Tramo AB:
2
4.0 m
2
1U x +
AM
axz
3
M = ?q. w - ñ ¿ . V^ . v
:til
M.(:r¡ = 0.16.X2 x'axz'

tf'j '"' ..' : : ; l:1;:
.
:-
. . . -Apuntes y problemas de Estruc{uras Hipeiestáticas
Tra.mo CB: M :'25.x - 0.6.X2.x - 2.5.x2
13.68 28.3.t
e1ástico, sufre
8.01
una deformación hacia
AM
, =- --0.6x. oA2
1.5x3M.(*91= 0.36.x2 *2 - ts *2 *'oxz'
Aplicando 1a expresión del Trabajo l"llnimo:
iry6r*f
o so'x, .*' js.r' *t.s.*t ox+f = o
Considerando que EI = 13500 T *2 y k = 5000 T/ur
ffit, 1.s2.x2-t2o+32a) +-J- (t.6l.xz-320+e6) *¡#*, = 0
11.52 ,, 396 7.68 .. 224 I
fus00 ^2
- 13s00 ' 13s00
nz - t s500
*
Eooo
xz = o
Co¡ilo e1 apoyo
debajo cie vaior
Bes
as = 39'31= o.oos7 m = 5.7 mm- 5000
l-----:t
I x2=2831 'I
5 T/m
N. González V. @ 2007

CAP 6 METODO DE I,A PENDIENTE - DESVTACION
6.1 INTRODUCCTON
Este método fue originar-mente presentado en er.año 1.915 por
er profesor G. A, Maney y es conocido también con el- nombre
de Método de 3-a .Defozmación..Angu],ar; su aplicación está
destinada a la obtención de
"oii.itu
ciones internas en
estructuras indeterminadas, ya sean estas vigas continuas o
pórti-cos formados por barras rectilíneas.
E] aná1isis de estas estructuras se enfoca considerando como
incógnitas 1as rotaciones angulares de ros nudos y sus
desplazamientos transversales; con estas magnitudes pueden
ser determinado,s 1os momentos flectores en cada cabeza de
barra.
Antes de obtener 1as ecuaciones fundamentares que rigen elmétodo, centraremos nuestra atención en .a.oad*. argunos
procedimientos de cá1curo para det.erminar fas rotaciones
angulares y desplazamientos transversales de 10s extremos de
barras rectilíneas prismáticas (sección constante) .
conocemos l-a existencia de varios procesos para efectuar este
trabajo, sin embargo escog:eremos aquel que resulte sencillo y
práctico en su aplicación; entonces de todos efl-os
utilizaremos ef Método de fa viga conjugada por su facir-idad
de r,ranejo. E1 método escogido utiliza fos diagramas de
momentos reales como cargas elásticas reducidas sobie Ia viga
conjugada;1a fuerza cortante en argún punto de esta vi_ga
corresponde a -r-a deformación angular en er- mismo punto de laviga real y 1os momentos flectores a los desjlazamientos
transversales respectivamente.
En consecuencia utirlzaremos r-as bases de] métocio para
cafcular ef momento que se origina en ef extremo ,,j,, y farotación angular def extremo *i,r cuando se aplica un momento
t'tij en el extremo "i" de una barra articulada - em,orradarIi- j , de Iongitud ,'L,r y sección const.ante. (f iq. 1)
r.----------.--'-_---L
i
(fis.1)

Apuntes y problemas de Estrucluras Hiperestáticas
Las condiciones de apoyo muestran que:
- En eI extremo "j', Ia rotación angular
-'Los desplazamientos transversales son
Por consiguiente, .Ia viga conjugada y
correspondientes a este,caso se muestran
+-_-.-_ L _._-_____¡
Por IMi : A1¡ = 0;
cie donde:
Aplicancio ta ecuación ae
(fis .2)
1r-.rUt 1r--1r.
2 'Et'3 2
equilibrio IFy = 6,
,H,-i r r$r
es nula (0j :
nulos lAij
1ás cargas
en l-a fíq.2
0)
Aii = 0).
e1ásticas
M¡j
EI
lEr.?u = o
El ' 3
(6.1)
obtenemos:
1
0i =:.12
clespe j ando 0i :
Reemplazando (L) en
lv1;¡ -M;;
0i =
-r---l- ¡
2.El
(2) obtenemos:
O¡=
MÜ
.L
q .trt
Iit;; = -a-E] g
1L
(6 .2)
(6.3)
(6. 4)
o tanüién:

f
Apuntes y problemas de Estructuras Hiperestátic€s
La expresión (1) permite calcular el momento en e1 extremo
It j It cuando se apl j-ca un momento Mij en e1 extremo trirr ! ]a
expresión (3) determina 1a rotación angular deI extremo rri,,
en funcj-ón del momento aplicado y 1a expresión l4) permite
calcular el momento que r se origina cuando eI extremo i sufre
una rotación angular 0i dada.
No debe. perderse de vista 7a adopción de
signos p.ara .Ios momentos y rotacíones
angwTares, En nugstro . aná-Lisis adopt.amos que
todo sentído de rotacíón horaria es positivo.
E1 anál-isis anterior puede
inverso mostrado en Ia fig
extremo "i" es Mii.
I.r-
aplicarse análogamente af problema
.3, donde e1 momento aplicado en el-
¡lij
0r=o
(fiq.3)
Ai=A;:0
i"lij 2 M¡i
jct
.. aLt ^
lvlii =
-.ui
Lr
(6.s)
(6.6)
t6.7)
Cuando ]os extremos de .la barra son perfectamente empotrados
y se origina un clesplazamiento transversal del extremo j cuya
magnitucl es A (fig.4), en anüos extremos se originan momentos
flectores reactivos, eJ-1os pueden determinarse a trawés del
método de la viga conjugada de la sigul-ente manera:
a. -
M¡l L
")- 4a

.,...'.;.-'.-,...',,..:.,.:.'.,j]jiJ:'.;.].'
:;"c. ¡ri¡!".;"a ;e !&&r-'t.*1<4di:+.¿
-i-."-*-4 ---_--l -
I Apuntes y problema§ de Eslructuras Hiperestát¡cás
tvt¡(ffii .:.:..:.
.l:.
.:::::::
::::::{l)
M¡¡
L _-{_
0i:o 0:=o
I*,
1^ Er
(fis.a)
Por »Fy = 0:
de donde:
Por >Mj =
^i
de donde:
r.tHr-} .,Tfro
r,rii = Mii =
Y^
o.l, ,Pr, ,3r L-i L rSr I L=o
l'',,,-$-tl'l
(6.8)
(5. s)
La expresión (B) m.uestra que fos momentos. originaCos ¡ror un
descenso de apoyo, son igrrales en valo¡ y signo. f.a e¡presión(9) perrnite calcul-ar el valor numérico cie dichos momentos en
función de ]as caracteristicas geométricas y mecánicas de rabar::a y de la magnitud del desplazamiento de] extrerno ,,j,,. El
signo (-) de fa ecuación (9) indica que el sentido real de
]os momentos reactivos en.r-os extremos de ra barra i-j es
contra¡io aI asumido.
si es e-L apoyo t'irr e1 que sufre un descenso de rnagnitud a,
ios momentos reactivos en los extremc.s serán tfitr. Sl r poE
aralogÍa:
^I a--
M;;
(6.10)

Apuntes y problemas de Estructuras Hiperestálicas
como aplicación de 1as ecuaciones deducidas,' analizaremos
cuatro ejemplos referidos a una viga prismática cuya longitud
es de 3.O0 m, de material con un módulo de Lfast¡_áiaaa
es E = 2OOOOO kp/oo2 y sección constante bxh =.20 x 60 crn.
EjempJ.o 1.
horario M =
Determinacj_ón de la rotación angular del extremo
izquierdo i cuando se aplica en él un momento
3. 6 T-m.
T-
rT -
De (3): 0i =
M=3.6r'm(ffi2,
.V,
?! qo' - 1 c .. ¡,4 4
1r - J,b x 10-cm'
2-los *3,6 *705 : 1,2
3,6 105 .300
-- = 0.000375
4 .-t,2 . LOt
0
1o10 kp,/cm2
rad (horar.ia)
Ejemplo 2. Determinación del
extremc izquierdo
horaria 0i = 0.0005 radianes.
momento que apl-icado en el
i que origina una rotación
De ec. (4) :
1 .'1 .2 . 7010
M = '- -- .0.000s
300
M = 480000 kp.crn = 4.8 T. m (horario)
log. N. González V. @ 2007 120 -

Apuntes y problemaS de Estructuras Hiperestáticas
Ejemp)"o 3. Determinación de los momentos en 1os apoyos
de una viga cuando eI extremo i desciencie una
magnitud de 0.45 c¡r¡.
1a'
^=0
45
t *u(A
De ec. (10):
f,,.. _ r,.. _ 6.l,z.tolo
^^.
€,
Mij = Mji : .u.45 = 2,16.10" kp
300'
l'Iij t"t1 i : 21.6 T-m (horario)
Ejemplo
de 0.25
De ec. (10) :
cm.
Determinación de
cuando e.l extre¡no
roomentoa en los apoyos
desciende una raagnitud
1os
r
wr1ffiu ¡
^=0.25I
-'-'.-" "r) j-
,,u
Mji
Mij : Mj -6:11!:.02s = -1.2. loc kp.cm
300-
Ml¡ = Mii = -72.0 T-m (antihorario)
" La ecuación del método Pendiente-Desviación (S/ope-
Deflection), es una expresión que permite calcular el
momento flector en el extremo de una barra en función
de la rotación de la tangente trazada en cada extremo a
la elástica de la barra, del giro de la cuerda que une los
extremos de la elástica (desplazamiento y de las
cargas extemas que actúan sobre ella."

Para i-nterpretar correctamente 10s resultados, adoptaremos un.
convehio de signos:
Los ríngulos de roiación de los fongentes, trozodos o lo eróstico en
cado nudo, se' consid¿rorón positivcs cuondo su sentido de rotoción
correspondo ol.gue.siguen los ogujos.del reloj y su rnognitud se
representorá por 0¡, donde i = L,2,3,4,..........,n.
Los ríngulos de rotoción de lo cuerdo gue une los extremos de ta
elóstico, respecto de lo dirección originol de lo boro, se
considenordn positivos cuondo dicho cuerda gire en senfido de los
ogujos del reloj y su mognitud se representoró por 9¡, donde i =
1.2,3.4,.......,n.
c) se considerorán momentos posifivos cuando su sentido de giro seo
tombién el gue siguen los ogujos del reloj.
En las figuras (6) y (1) se observan l-as magnitudes defj-nidas
como incógni-tas, con sus respectj-vos signos positivos.
o)
b)
Rotaciones positivas
(fis.6)
6.2 HTPOTESIS
Las hipótesis adoptadas para 1a
def método Pendiente:Desviación
siguientes:
Desplazamiento positivo
(fis 7)
obtención de las ecuaciones
(Slope - deffection) son.las
El moteriol que conforman los borros se considero
perf ectamente elástico, siendo válido el principio de
superposición. (Ley de Hooke).
Todos los nudos donde se ¿ncueniron los borros, roton
rígidomente un mismo óngulo. (Rotoción ortogonol).
tangente

': a, '.
Apunles y problemas de Estructuras Hiperestát¡cas
IE
á.J
E.§
G
G.
é
6
€
€
€
€
e
e
e
e
q
C
i{C
C
C
C
G
,G
iG
G
ie
'é
é
lé
iGt
G
G
É
e
é
á
Los borros son prismáticos (fnercia constonte).
Los borros son hornogéneos e isótropos (tiene los mismos
propiedodes en lodos los direcciones).
Se desprecia el efecto de deformoción originodo por
fuerzos cortontes.
los
5e desprecio el efecto de deformoción originodo por fuerzos
oxioles.
6. ECUACIONES DEL METODO
consideremos un pórtico constituido por elementos rectilineos
de sección constante (fig.B):
(rjg. B)
La .:iga i-jr está someticla a un sistema de cargas exterior:es
aplicacias a l-o largo de su eje 1ongitudinal. Si consideramos
que ef apoyo "A,' se asienta una magnitud Aii, todos los
nudos del pórtico que se encuentran por encima de ese apoyo
cederán ta¡¡bién 1a misma m.agnitucl (en virtud de ra hipótesi-s
referica a 1as longituCes de l-as barras), en esLas
conciiciones eI nuclo rr j r I' ocupará la posición " j " . para
alcanzar la posición final cle la viga (fig.9) , podemos
efectuar fa superposición de efectos que se muestra en fas
fi-guras 9.a - 9.d:
I
,l
I
:
rl
I
I
r

Apuntes y problemas de EstructuÍas Hiperestáticas
M¡Ü
ESTADO O
(fig.sa)
ESTADO 2
(fis.ec)
) rur';, +
ESTADO 1
(fis.sb)
" " -. -'-'-.-lz rtr)
ESTADO 3
(fis.ed)
o¡ aü I J
FI---i' 1_. _:,_. _._ _ i
"-"- --.
', i ¿il.. i
:Ar I
o¡ J rMj
ESTADO REAL
(fig.e)
c lt
M-¡tI i
i
AU
]"M"j¡
Los momentos en los extremos de la barra para su posición
final (fig.9) , pueclen ser determinados superponiendo fos
momentos en esos extremos pera l-os diferentes estados de
deformación angular y desplazamiento mostrados en .l-as figs.
9.a - 9.d.; de esta manera podemos escribir:
Mij =Mou+M1¡j +Mz¡j +M3¡j
M1¡ =Mo¡i +M1ji +M2tt +M3ji
donde:
(6.1r-)

Mo¡ y Mo¡¡= son los momentos de empotramiento
perfecto para una barra empotrada en sus
dos extremos. Estos momentos se originan
por acción de ]as cargas externas sobre
Ia barra considerada (i-j).
Los otros términos que lintervj-enen en lal ecuaciones (10),
han sido determinados en e1 aná1isis efectuado en el primer
punto de este anáIisis, sin enrbargo a rtrnnera. d.e recuerdo
podemos nuevamente incorporarlos en este resumerr:
. AtrI
M'¡¡ = -::-. g' ru1;i=f .e¡
son 1os momentos en los ext.remos de ]a barra debi-dos a fa
rotación angular de la tangente trazada a l-a elástica en ef
extremo "i".
son los momentos en f os extremos cle 1a barra debi.d.os a
rotación angular de 1a tangente trazaCa a Ia el-ástica en
extremo "j ".
¡¡2ü = .ej rvr2¡i=f.ei
,,3. 6El
¡vr r.l =- - .a¡i
c 6tr1r rJ..
¡vl lt =--.-.Aii
L'
n¡=fl o,*? n¡*E a¡¡rMo¡
2El
L
1a
e1
son fgs monentos en los extremos de la barra debidos a1
desplazarniento transversaf del extre¡no "j".
Sustituyencio estas expresiones en l-as ecuaciones 10:
,,'=?3 o,.-? r¡*E a¡tMo¡i

Factorizando eI tét^i.ro 2Er y definiendo:
L-
donde Qij es el
finalmente:
ángulor de rotación de la
(6 . L2l
cuerda, obtenemos
,U =
?' (2'0¡ + 0¡ t 3'<p¡¡) tMoi¡
,i, =
?'(0¡
+ 2'0¡ t3'<p¡¡)tMo¡i
(fig.10)
M=
2Et
e.oi+o-o)+o
I
(6.13)
Ilstas son 1as ecuaciones deI método pendiente-deswiación, en
1as que todos los ángulos de giro se miden en radianes.
6.4 RIGIDEZ
Se denomina rigidez a flexión de los extremos de una barra,
al nomento ffector que aplicado en un extremo de Ia misma
origina una rotación unitaria (un radián) en ese extremo.
Considerando la barra i-j de 1a.fig.10 1a cual se encuent.ra
sometida á un ¡nomento aplicado en su extremo tri", meciiante
las ecuaciones ( 13 ) podemos evaluar Ia magnitud de ese
monento cuando l-a tangente a 1a e1ástica trazada en dicho
nudo sea unitaria:
oj=o
¿ii =
ent-onces:

Apuntes y problemas de Estructuras Hiperesláticas
como 0i = 1, de donde se obtiene:
(6.14)
El factor Kii recibe propiamente el nombre de rigidez absoluta
de1 extremo tri't para la barra i-j. La relación entre Ia
inercia de Ia barra y su longitud, se denomina factor de
rj.gidez (kij):
[*rll-l
(6.1s)
cuancio una barra es prismática (sección constante) en toda su
longitud, tal eI caso de 1as barras estudiadas hasta atrora,
ia r:igidez es igual en ambos exlremos.
6.5 MOMENTOS DE EMPOTRAMIENTO PERFECTO
Se denominan momentos cle enpotranienLo perfecto (momentos
fijos) a l-os momentos fiectores que se presentan en los
extremos de la barra i-j, cuanclo ambos extremos se hallan
peri-ectarne.nte er.potrados en sus apcyos o cuando uno de f os
e.a:treÍnos se encuentra einpotrado y e1 0tro simp]-enente
apoyaclo, y 1a barra se encuentra sometida a cargas ev'ternas
según su eje longitudir.ral.
Las iablas No. 1 y No. 2 permiten determinar diChos r¡.or,entos
para varios tipos cle carga usuales'
lñ9. N. Gon¿ález V. (a 2007

I
i
I
ltrtOlrIENTOS DE EMPOTRAMIENTO PERIEGTO
vtr:(Hvi,
ij
+--L__---i
CARGA Mij Mji
J
t- á+ b -------+
Pab2
-----6-
t!
Pa2b_T
P
J PL
- -:-B
PL
I
q
@
L-
_
qL2
t¿
qL2
12
q
L-
_qú
30
qL2
20
-L
'
_
qL2
a^
qL2
2n
q
i,IIlrITr}._
i- a ----+-
Q'2t6-'iB-3")r
12. L L'
Q'3 (4-3')
12L' L
q
-¡-tlx
-.rflI++J.ttr-rv-*
+-- ¡12
-¡
* 5qL2
9f)
5qL2
96
,
",
ir, 11 lllll]l]lh o
"
^aa?
frti" - 2ta' + au ¡
#nt - zLa2 +a3¡
M1
--?-+-a-,-4- b-------+
-ft,-ufr frz-sir

Apuntes y problemas de Estructuras H¡perestál¡cas
6.6 APLICACI,ON A VIGAS CONTIÑUAS
Ejemplo. Analizar Ia viga de inercia constante.
4.8r tÁ
+- 4.5 -----,,--- --- 2.0 --+- 3.0 + 4.5 __f
1234
- Momentos fijos: Utilizando Ia tabla No.1:
o.,oqn2
[,7'!1-2 = --]_--1 = - 6.75 T m
12
¿..t¿.c¡r2
M2-1 = t"""' -6.75 Tm
12
8 (2.30)2
IVZ-¡- =-5.76 Tm
5¿
^ ,^ ^^'2ó.(z.uu)
M¡ z -:=-,=3.B4 Tm
c
^
o r^ rn2
M1-,,1 =-a'u
la'JU/
=-4.86 Tm
20
4 B.(4.50)2
Má ?= -3.24Tm30
Planteamiento de ecuaciones:
Las ecs. ( L3) apLi cacias a los tres Lramos c: Ia v-ga ar rojan
fas relaciones slguientes:
art¿Lt,^^
Ml-Z = *(Z)t+02-391 Z)- 6.75
+.J
tl:I
Mz-l = #QOZ+ 01 - 3p1-2)+ 6.75
4.C
f42-g - T eur+ 03 - 3p2-3)- 5.76
5

M¿-s =
fltze++o3
-3<e3-4)+3.24 d,
G
Condiciones de aPoYo: q
G
:::"'.o:;:,
-:ñ:i?:."J,"u .,io'-:il:::"i.J. ' ..#
""?:x1"'"::
1angulares 01 - 0a = 0; además ninguno de ell-os sufre J
desplazamiento transversal o asentamiento de apoyos,
-
po'
"}1'o 3
Lt -Z = LZ+ = A:-¿ - 0, con estas condiciones de
desplazamiento: Q1-2 = 9z-: : 9:-q : 0' e
G
Equilibrio de nudos' S
: : x"'r".T
t
:
^
:i" "'
o;,1
: "r'.,:'..'"":;J."l "
i i' ¿'; # T" í' "
=
fo1F4rronentos cte toáas las barras que concurren ellos'
éobtenemos,
G
M2-1 r'M2-3=0 ; 1902+4'503+11'1375/El=0 C
C
M3-z+M3-4=0 ; 4'502+1903-11'475lEl=0 C
- Soiuciones: Resolviendo el sistema formado
é
0.7726 c
o, =_: n_ C
C
0.786s G
os =--Er C
e
G
Glig. ¡'i. éonzátez V. @ 2oo7
c
,.G

Momentos fina1es:
Reeraplazando las soluciones en 1as ecuaciones individuales
para cada barra:
¡¡t-z =#vro) -o':Íu -3(o)l - 6.7s = -7.0er - m
na2-1 = ?-oE!czr#4 + o - 3(0)l + G.7s = 6 06r - m
tui2¡ - 3E1¡-3 r#q-Trr-3(0»-s 76 = -6 06r-m
Ma-z =?tr§q Y#-3(o)l+ 384=4 16r-m
Ms-¿ =
#trTq-0 - 3(0)l-4 86 = -4.16r-m
M¿_a = fl¡z1o;o9J999-3(0)l+3.24 = 3.5er-m
4.5' ., EI
Aplicando l-as ecuac.iones de fa estática se pueden calcul-ar
1as reacciones en los apoyos y dibujar diagramas de cortant.es
y momentos.
6.06 6.06
Nota. - La presentación de los cáIculos en
muesLra laboriosa, pudiendo sirnplificarse si
(11) se escríben directarnente.
e1 problema se
fas expresj-ones

Apuntes y problemas de Estructuras Hiper€stát¡cas
Ejemplo: Determinar 1os momentos para Ia viga de inercia
constante.
J
I
II
{
q
Iq
q
{
fq
t
q
10r 10r
AIll!,."
2.O . 2.0 2.4
6T 6T
3.0 3.0 3.0 3.0
4
Condiciones de borde rotacional: Los a.- i y r ;__-
empotrados y no pueden rotar, en Lv.-'ecug¡.---. 91 = A::0
Condiciones de borde traslacional: ¡io e:.:isti.endo
desplazamiento transversa] (descenso) de .l-os apoyos, sus
desplazamientos son nulos, qt-Z : QZ-¡ : g:-s : 0
Ecuaciones por tramo:
Mr-z =f rtrl-u.oo
N,t2-1=f trnr)*u.oo
Mz-s =
fffrrr+03)-7.50
l',4¡-z =
f tzos + 02) + 7.50
rvts-+ =
f trt.t-r.uo
M+-¡ =f to.lnr.uo
Equilibrio de nudos:
Nudo
Nudo
EI eguilibrio rotacional cle los
nudos 2 y 3 arroja las siguientes
ecuaciones:
1.5_-n
EI
=0
0; 402+03
0; 02 + 4
a.
3:
M2-1 + FI2-3
I'13-2 + I,13-4
-03

¡
Apuntes y problemas de Estructuras Hipere§tát¡cas
soluciones:
Momentos finales: r
Comentario:
ecuaciones,
ecuaciones
obtención y
Mt-z: -8.13 Tm
N12-1 : 7.?3 Tm
!12-3: -?.73 Tm
?.43 Tm
- 0.4
U" : --¡, I
03:
Mz-z
M:-q
MS -:
0.1
EI
A1
53
Tm
Tm
En los dos problemas, 1as rotaciones angulares están en
función de EI, si ambas caracteristicas son conocidas pueden
determínarse los valores numéricos de dichas rotaciones,' asi,
si eI móCulo de elasticidad del- material de las vi-gas es
1
E = 50.000 kp/cm'y.I mcmento de ir,ercia respecto de su eje
centroidal es I:45.000 cm4, entonces el producto Er tiene ef
)
val-or 225 Tm", Iuego, sustituyendo este valor en fas
rotaciones angulares se obtienen los siguientes re-sultados
numéricos:
0z : -0.00178 rad 0: : 0.00044 rad.
Para simplificar aún más el planteamiento de las
puede utiLizarse ef factor K = 4l de las
T,
(11) corno un número pui.o. Et procecltmiento de
utilización se describe en eI sigulente elemp1o.
111

.-'
Ejernplo: Determinar los momentos
constante,
para 1a viga de inercia
PR ,,rK t oie 12K
Condiciones de borde rotacional.: Los apoyos
empotrados y no pueden rotar, en consecuenci.a: 01
Condiciones de borde traslaci.ona]-: No
desplazamiento transversal (descenso) de 1os
desplazamientos son nu1os, et_z: gz_z = g¡_q = 0
Ecuaciones por tremo:
10.010.010.010.0
1y4son
=0q:o
existiendo
apoyos, sus
tu11-2 =
ffitnrl-.r.oo
Mz-r =
fl{rrr)*.o.oo
Mz-s =
f,eer+03)-4o.oo
f,43-2 =
f eer+02)+4o.oo
ru3-4 =
ffitrn.l-.o oo
M¿-¡ =ffitr.t+3o.oo
Equilibrio de nudcs: E1 equiribrio rotacionar de fos nudos
y 3 arroja 1as siguientes ecuaciones, asu¡niendc qu. ?E1=1,
Nudo
Nudo
02
02
,.
3:
142-1 + tr12-3=¡ , A
!13-2 + M:-q:0 ;
+ 03 - 10 = 0
+ 4 03 + 10 : 0
lng. N. González V @ 2007

So].uciones:
Momentos finales:
-26.67
Ejemplo:
Q2 : 3.3333
0: = -3.3333
Mt-z : -26.61 "rm
Mz-t = 36.67 Tm
Mz-: : -36'67 Tm
M:-z : 36.67 Tm
M:-s : -36.67 Tm
FIa-3 : 26.61 Tm
-Jb b/ -36.67
Anafizar el pórtico intrasfacional,.
9T
6T/m +--2-l
I
5.0
I
2 l=4e.ooo cm¿

Apuntes y problemas de Eslructuras Hiperestáticas
Inercias rel_ativas:
, 48000
b_a___4r 2000
. 12000
l1-5=-=--=1
I 2000'
relativas: multiplicando por !.,. io= val.._
L
absol-uta
2E(3t) 3Et ^ 1trt21) 4Et
425:
, 36000
lt_, =
-.
= ?
12000
6_+=ffi=z ;
Rigideces
de rigidez
Barra 1-2:
Barrá 2-3:
2E(4r) _ 4Er _ 8
633
'Condiciones Ce borde rotacional: Como
empotrados, no sufren rotación, entonces: 01
Condiciones de borcie traslacional_: Los
asentamientos, entonces J-os desplazanientos
implica que: e1-2 = gz-z = g2_4: e:_s : 0
l41-2 = 3(02)-8.00
it4Z-t = 3(202)+8.00
R
lvlz-s =
iQcz+03)-s.00
R
Iv13-2 =
i(z0s
+ 02) + 4.00
llr2-4 = 1,6(20a)
N14-2 =1.6(03)
Ms-s = 1(20¡)
[45-3 =
'l(63¡
]os apoyos son
:0a:0s--o
apoyos no sufren
son nulos y ello
Ing. N. Goflzález V. @ 2007

Eguilibrio de nudos:
Nudo 2: M2-t + MZ-¡
Nudo 3z M3-2 + M:-S
Soluciones:
Momentos finales:
Mz-q : 0; 43.6 02 + 8
0 ; 8A2+22
0.L012 ; 0: = -0.5845
Mt-z : -7.68 T-m
Mz-t: 8'64 T-m
Mz-: : -8.99 T-rn
M:-z = 1.17 T-m
Nlz-q : 0. 34 T-m
Ms-z: 0'17 T-nL
M:-s = -1 ' 1? T-m
Ms-: : -0 ' 58 T-m
+
I
03
0¡
0
-12
02
- lJo -

4.1'.
,:,:ri¡t:i.:ajr.1i}ii¡r]::.:' r .,'
:''
Apuntes y problemas de Eslructuras H¡perestáticas
Ejemplo: Analizar e1 pórtico
. 60k
intraslacional.
v
60"
40.0 , __=_r__ 30.0. _______r_
00.
Condiciones de borde rotacional:
0r:0a:0":0r:o
+_ 30.0,
Rigideces relativas:
Condiciones de borde
4El
Asumiendo oue '-
- 1-30
traslaciona]-:
enronces E1:o,rs
20
,Í:
'i,
ri
'ii
t'
til
;l:
ili
.il
'll
'1,
l'
,1i
iii
':t
'11
I,
:l
qr-2 = Qz-t : Qz-t' : Q:-s : 0
_ 4Et,
Ma-b=
f (en)= 0n
AtrI
Mb-.=
ñ (rOs)=2 06
l¡lb-e= 2e 06) = 1.5 05
20'
_ zEt,
Me-b=
-
( On)=0.75 0u
4Et.^
lv'lb_.=
*
(, 0b+ 0c) -225= 1.5 0¡ + 0.75 0c -225
r¡ _ 4E1,,
Mb-c=
*
( eo+20c) -225= 0.75 0b + 1.5 0c - 225
{
{
q
q
I
I
il
I
I
I
I
T

I
-....-.....,.-'....
Mc-f = *f rrr) = 1.5 oc
20'
Mr-c =
#, ," ) = 0.75 oc
Mc-d=
#,r 0")=2 o"
Md-c=
S { t")= u"
Nudo bt Mb-a * M¡-e + N15-" : Q ;
Nudo c: Mc-d * Mc-f + Mc-b : 0 ;
Soluciones: 0¡: 39.13043
Moment.os f inales:
5 05 + 0.75 ec : 225
0.75eb+50.:225
y 0.: 39.13043
Ma-b = 39.13 T-m
Mb-a = 78.26 T-m
Mb-u = 58.70 T-m
Me-b = 29.35 T-m
Mb-c = -136.96 T-m
Mc-¡ = -136.96 T-m
Mc-f = 58.70 T-m
Mf-c = 29.35 T-m
Mc-d = 78.26T-m
Md-c = 39.13 T-m
-39.1 3 7 8.26 -1 36.96 -136.96 78.26 39.1 3

6.7 TRATAMIENÍO DE APOYOS ARTICUI.ADOS
La condición de borde para un apoyo articulado consiste
";utilizar su capacidad nula de absorción de momentos, erropermite plantear una nueva ecuación, pues si bien eI momento
flector en un apoyo articulado es nu1o, Ia rotación angul-ar
de dicho nudo no €s.c€ro.: para este anárisis las ecuaciones
de1 método pendiente desviación se pueden uprl.u. si-n ni.nguna
modificación, tomando ren cuenta que e1 desplazamiento
transversal en n:-rio. sin embargo también pueden
transformarse de Ia siguiente ma;-rere:
rrl1¡ =
f 1ze¡+ 0j)t Moü
u¡i=
f {ei+ 2oj)t Moj¡
Como apoyo "j "
nulo, con esta
Despejando 0i:
es articul-ado, el momento flector en éI se
condición:
Mji =
tl (o¡ + 2*,0;)tMoi¡ = o
O,=-]0; + L
^'o"")- ,-r -ru, rv'Jl
Sustituyendo este val-or en ¡,li j :
r',r¡ =
f tz oi - 1o¡ t liuo;i) lr,roij
Transformando l-a expresión, finalmente obtenemos:
rut¡j =
f (o¡)rMo¡i t -l voj¡
En efla reconocemos que er factor de rigidez se modifica aI
vafor 3EI/L, y además que el momento de emoctramiento
perfecto también se modifica, considerando un- tipo cie barra
articulada-empotrada (Tabla 2). La aplicación de. esta última
expresión Ia realizaremos en e1 siguiente ejemplo.
lng. N. Gon¿ález V. @ 2007

E3emplo: Determinar 1os momentos
siguiente viga:
20r
4l
en los nudos para Ia
. v7m.
--j_ J
inexistencia de
que qij : 0.
Ecuaciones por tramo: Considerando e1 : 0 e
asentamiento de apoyos, 1o cual significa
(Multiplicando Las rigideces Oo. fl l,L
+_ 5.0 __-+_ 5.0
1:
.CAI A
kr-r ='-*'=1El=16lu )
Mr-z = 16(02) -
Mz-r : 76 (202) +
Mz-: : 15(02) -
ZZltttt.
-_=+--
2
z5
25
36
. 3E3l 3_
kr_r= =_El=15
124
:1602-25
:3202+25
:1502-36
Equilibrando rotacionafmente en nudo 2:
M2-r + MZ-: = 41 02 - 11 : 0
II
U?=--41
Los resultados finales son:
Mr-z = 16(= ) - 25 = -21.2553 (antihorario)
41
Mz-t= 32(+') +25 =32.4894 (horario)
41
Mz-3 : i5(#) - 36 : -32.4894 (antihorario)
En este probLema se han utilizado los momentos de
empotramiento perfecto para barras empotradas-articu-Iadas en
sus extremos,
Si aplicamos 1as ecuaciones que consideran ambos extremos
empotrados:
2Tlm
142 -

',.: ¡,: .i ' i .):t . .': :.._:::rr -,i.iri:t ,: ., ii.'. ir¡..: .-
Apuntes y problemas de Estrucluras H¡perestátic¿s
Ecuaciones por tramo: Considerando 01 = 0 e inexistencia de
asentamiento de apoyos al igual que en el problema
precedente) y multiplicando 1as rlgj_deces por (lO/Elr);
Ecuaciones por tramos:
krr=2E41 =1el =a10 5
kr^ =2E31= lEl= s
122
M1-2= 8(ez)-25= 802-25
M2-1 = 8(202)+ 25 = 16 02 + 25
M2-3 = 5(202 + 0z) - 24 = 1002 + 50g - 24
M3-2 = 5(02 + 20g) + 24 = 502 + 100s + 24
Equilibrando rotacionalmente Jos nudos 2 y 3:
Nudo
Nudo
03+1
03+24
0z+
0z+
).
-1 :
MZ-1+MZ-:=0;
M:-z : o;
26
J
J
l0
:o
:0
Res-of vi-endo e l s is tema f ormado :
0z = 0.468085106 0: : -2.634042553
Los momentos finales en fos nudos son:
M1-2 = 8(0.468085106) - 25 = -21.2553
M2-1 = 16(0.468085106) + 25 = 32.4894
lu12_3 = 10(0.468085106) + 5(-2.63 4042553) - 24 = -32.4894
M3-2 = 5(0.468085106) + 2(-2.634042553) + 24 = O

EjempJ.o: Analizar e1 pórtico intraslacional.
12f ln1 12llm
3.00
Condiciones de borde rotacionales:
0r:0s:0g:0
Mr-z: Ma-s = 0
Condiciones de borde Traslacionales:
9r-z : 9z-t: Q:-q : Qs-s : 0
Factores nr-, : 'u'L
12Tlm
3.00
2(6) ,, _ 2(6)K r ^: ' '
- < ' K^ -
^l-2- O
=", L2-3--=¿r t K-,-o:
2(6)
= 4 , Kr-.: 2(6)
=4
JJ
,, ¿lt)
^4-9: , =t4

Apuntes y problemas de Eslructuras Hip€restáticas
Mr-z:3(20r+02)-16
M2-1 :; 3 (0r + 202 ) + 16
' M24:2.a '202+0:) -,25
¡¡r-, = 2.4(02+ 2A3¡ í z-S
M3-4i: 4 (2%+0:) - 9
)
M.i-:: a (0:120:) + 9
M¿-s: 4 (20q+0s) - 9
Ms-q: 4 (04+205) + 9
Mz-t: 1 (202)
Mt-z: 1(02)
¡¿¡-e: 2 (20s)
Me-:: 2 (0:)
Ms-s: 1 (204)
Mg-q: 1(0q)
NIs-e: 1(20s+0e)
I'16-s: 1 (0s+ 200)
Mr-z : o;
M2-1 + M2-3
M3-2 + !13-a
Ma-3 + NIa-5
M5-4 + M5-6
Ms-o : o;
Resolviendo
l
+
f
Mz--t
Mz-a
Mq-s
0;
: 0,.
601+302-16:0
301+L2.BQz+2.403
2.402 + 16.803 + 40a +
403+180a+105:0
40a+1005+06+9
05+206 =0
-9:0
16 : 0
el sisterna de ecuacÍones:
0t = 2'5035
0z = 0'3263
03 : -1.1197
0q = 0. 5068
0s = -1'1601
05 : 0. 5804

Apuntes y problemas de Estructuras Hipetestáticas
Momentos fina].es:
6.8 TRATAMIENTO DE VOIiADIZOS
Un voladizo es una estructura estáticamente determinada, en
consecuencia . siempre se pueden deternr.i-nar las fuerzas
normales, cortantes y momentos flectores en el extrcemo
empotrado. Cuando se aplican las condiciones de equilibrio
rotacional de nudos, debe considerarse e1 momento reactivo en
eI extremo empotrado.
Ejemplo: Determlnar los momentos en los nudos Ce la viga.
20l
i
4l
5.0 -_--+- 5.0+-
1
3l
12.0
va/z
2
I
2.0 ---t-
Considerando 01 : 0 y multipficando Ias rigideces por (
H
, ¿Lót ¡ _.(22 =_=_t]l =5
122
25
.E
):
*',,r=ZEol=1rr=s
10 5
Ecuaciones por tramos:
t41-2 = B(20r + 0z)
Mz-t=B(01+202)
-25= B0:-
+25-160¡+
lng. N, González V. @ 2007

Mz-::5(202+0:)
M:-z=5(02+203)
Nudo 2:
Nur
4T
I
Mr +
2
. :ción de equilibrio
entonces:NI3-2-B:0;
502+1003+24
El s..teina formado se refleja en fas
2602-r 50:=
502+1003:
24:L002 + 503
24= 502+1003
+ 4. (2)
: -B T
rotacional para este nudo será
-B:0
siguientes expresicn== :
-l_
-76
+
- ¿.t
+24
m
M
M
Condiciones de eguilibrio rotacional:
Mz-r+Mz-::0; 2602+503+1:0
En este nudo concurre un volaclizo isostático,
aportando un momento flector cuyo val-or es:
v -l-as soluciones: 02: 0.2919
03 : -1.7489
l,os monrentos flnales en 1os nudos son:
§lr-z : B(0.2919) - 25 = -2?..62 T-n
Mz-r = 16(0.291 9) + 25 = 29.16 r-m
Mz-: = 10(0.2979) + 5(-l .1 4Bg) - 2q : -29.i6 r-m
Ms-z - 5(0.2979) ),2(-1.74S9) + 24:8.00 r_ni
lng. N. González V. @ 2C07 -147 -

Ejemplo: Analizar el pórtico intrasracionar- de. ra figura 15.
12f lm 12Tlm 12f lm 12Ílm . 12Tlm
.0
3.03.05.040
(fig. 1 5)
Condiciones de borde rotaci-onales:
0r:0a:0g:0
Mr-z = Ma-s:0
Condi-ciones de borde traslacionales:
9t-z= Qz-: = Q:-q: tPq-s = 0
Eactores Ki-j
?trT
nr-r='lf) =r, Kz-t:?=rn i K¡-q:?=r; Kq-s=?=4
xr-',:'f =, , g-a:29u) =z ; oo-r='tÍ) =,

Apuntes y problemas de Estructuras Hlperestáticas
Ecuaciones Por tramo:
302 -
L2.B02
16
16
oE
ac.
o
o
9
16 = 0
+ 303
601 +
301 +
2.442 +
40¡ *
40a +
t'f 1-2 : 6,
!12-1 + M2-3
I"i3_z + 143-e
!14-3 + M4-5
M5-4 + M5-6
!15-6 = 9,
Mr-z : 3 (20t +'02 )
Mz-t= 3 (0r+202)
Mz-:!: 2.41202 + 0: )
M3-2r+ 2'4(02 + 20: )
M:-q,: I (2At+0:)
¡¡s-:,: 4 (0s+ 20:)
Mq-s: 4 (20a+0s')
Ms-s: 4 (0s+20¡)
Mz-t: I (202)
Mt-z:'t (02)
M:-e: 2 (2%)
Me-:: 2 (0¡)
Ms-g: 1 (20q)
Mg-q: 1 (0q)
Ms-o: f (20s+00)
Me-s: f (0s+20s)
+
+
+
f
Considerando que eI momento flector a
debido a Ia carga uniforr¡'e es Ms-ro=-
eI siguiente sistema de ecuaciones:
Equil.ibrio de nudos:
Ia derecha de} nudo 5
Q'()2:-6 r *, obtenemos
2
+ MZ't
+ I,12 -g
+ 1"14-9
-6=
-9:0
+ 16 : 0
0
3:0
:0,
: 0; 16.80: + 40a
1B0a + 405 =
1005 + 06 +
A5 + 206
iñlll. Gon.ález V. @ 2oo7
-149-

Apuntes y problemas de EstÍucturas Hiperestáticas
Escribiendo las ecuaciones matri_cialmente:
63
a r^ ^) t¿ , ó
0 2.4
00
00
00
Momentos fi.nales:
25.43 -26.07
-26.07
0
2.4
16. B
4
0
0
16
9
-76
0
-3
0
00
00
4.0
18 4
4 10
01
0
0
0
0
t-
2
0r = 2.5078
02 : 0.31,77
0: = -1.0?92
0a : 0.3420
05- : -0. 4598
06 : 0.2299
-16 27
-2.16

6.9 PROBLEMAS CON DESPI,AZAMIENTO TRJA,NSVERSA¡
.
Frecuentemente se presentan problemas en 1os que se deben
tomar en cuenta desplazamientos transversales debidos
principalmente a1 asentamiento de apoyos u otros factores
estructurales.
Estos casos no repre.señt1ñ i:^',.r dificultad debido a que las
ecuaciones (^l---arcs del método (13) consideran este caso,
comancio en crienta que 1os desplazamientos de apoyo pueden
conocerse en forma numérica y 1os efectos que originan.
Ejemplo:
E = 1OO.0O0 kpl"*z
vertical de 1.8 óm.
1a viga prismática de inercia constante
A
45.000 c¡n' y un módulo de elasticidad
si eI apoyo 3 sufre un asentamiento
Analizar
conl=
6T 6T 1oT loT
2! J I I
. f. a=ae
2.0 2.0 2.0 3.0 3.0
(f¡9.16)
Mo¡.nentos fi-jos por descenso del- apoyo 3:
El Cescerso del apoyo 3 origina 1a aparicj-ón de nomentos cie
empctr:ar,'.iento en los tranos 2.-3 y 3-4, Ios cu¿rl-es cieben
sur¡.arse a los momentos cie empotramienLo perfecto originados
por .r-as cargas exlernas y que son igr:ales a:
r n. 6El
rvrl-l-- . A
¿
lL
3.03.0

Apuntes y problemas de Estructuras H¡p€restáticas
h
hr
ts?.
Fá
b
b
H
ta
bbF.
h.
bb
ho
b
b
ho
ho
bá
Ir
1f,
á
=l
=ü
É
=o
EÜ
-ü
-ü
Tramo 2-3: Me_¡=Ms_Z=
Tramo
Eeuaciones:
6 .(1 00000) . (45000)
6oo2
-135000 kp cm
Mz-3=Ms-z=-1.3srm
3-4: Mg-¿ = M¿-3 =
6 (1000!01:(45000)
= 1ss000 kp cm
6oo¿
Mg-¿ = M¿-s = 1.3s r m
Denominando ¡ ::El= 1
L
Ivlr -o= A. - o
Mz-t=202+B
Mz-r202+03-]..S-1.3s
Mt-z-02+203+7.5_1.35
M=-q: 2 0: - ?.5 + 1.35
!Ia-3: g, + 7.5 + 1.35
Eguilibrio de nudos: pr-anteando er- eguilibrio rotacional de1os nudos 2 y 3 (q,re son los,:.,:..o" que pueden rotar) através de l-a suma de momentos de toáas
.Ias
La..as queconcurren en e11os, obtenemos:
I'12-1 +Mz-::0;402 *0:-O.eS=0
I 02:0.2261
l.
i"I3-2 + M:-s : o; 02 + 4 0: = o ] ,, = _o.os67
Momentos finales: Reemplazando las sol-uciones 6n r - _
expresiones para cada barra:
vv4qurvrrcr srr ads
-7.77 8.45 -8.45 6.26 _6.26 8.79
,ta ,
".
, y
-7.77
lng. N. conzález V O ZOOZ

5.10 §.IATTS¡S DE PORTICOS TRASI,ACIONALE.S
un pórtico puede sufrir desplazamiénto laterar por acción de
cargas laterales (viento, empuje de tierra y otras) r por
cargas verticales no simétricas, por diferencia de rongituáes
de sus columnas y por diferencia de, geometria de 1os
elementos estructurales que i¿ _..:.iponen isecciol:,,
transversales de las barras) .
,l
En estos casos se desconoce 1a magnitud der desprazani=n-:c,
por e11o se considera una nueva ir:i.,eriita, para ei cáIcu1o
e11a se ciefine como eI ángulo de g.iro de 1a cuerda a 1a
eIástica y se representa por ap =
A
.
L
Ar introducir una nueva incógnita 1a cantidad de ecuaciones
planteadas por e1 eguilibrio rotacionar- de Ios nudos es
insuficiente; para establecer nuevas ecuaciones que pem.itaa
obtener Ios desplazamientos (nuevas i-ncógnitas) se indica el
siguiente procedimiento :
Apuntes y p.oblemas de Estructuras Hiperestát¡cas
Se es tal:-Lece
en uno o varios
de -Los grados
que tenga.
e7 equiTíbrio de fuerzas c,or-tarrtes
cortes de -La estructu-ra, dependia.fu
de TiberLad ¡ara despJ.azzaíentos
Ejenplo: Analizar e1 pórtico intraslacional_
B T/m
3.0 - ___- +_
( fiq. 17 )
Condiciones de borde:
lng. N. Gcnzález V. @ 2007
(fig.17a)

i
IApuntes y problemas de Estructuras Hiperestáticas
ñl
il
7'
=ü
='a
a
a
='
=r¡o
aúü
*
a
áa
I
ñ
ia
fr
a,
1,
rt
¡o
=ü
=e
¡t
a¡a
a
a
afü
vü
4ü
0:=04
Factores K:
Ecuaciones:
M:-:- :
Ir1-J -
Mt-z :
Mz-r:
l4Z- q =
.,9-J
Eguilibrio de
.A
= Ui 9:-t:-:54
Multiplicando los
A
Qa-z= - :4 95
reales por 10/EI
q;
valores
zEI EI
42
K1
'
:q9u :2Et= 20
.. 2E(2t) 4Et
xq-z:-;-:s=6
s ( 0t -1s<p )
s( 2 01 - 1sq )
20( 2 01 + }iz )-6
20( 0t + 2 02 )+6
8( 2 02 - 72 e I
B( 0z - t2 q )
nudos:
= 501-75
:1001-75
: 4001+20
= 20 01+40
: 1602-96
: BA2-96
I
a
oz-6
02+6
a
q
NI1-3 + Mr-z = 0; 50 01 + 20 02 - ?5 e - 6:0 (a)
M2-1 + I"f2-4 = g- 20 01 + 56 02 - 96 g + 6:0 (b)
El sistema forrnado presenta tres incógnitasr por e]1o es
necesario prantear una ecuación adi-cional, e,lra surqe ciei
equilibrio de cortantes:
Ml-¡
H4
(fig.17.b)
Por equilibrio horizontal del pórtico:
1
H3

H¡+Hq+3=0
donde:
Sus tituyendo
de donde:
i.esofviendo el
H3 = Yl:l: rlll
=
4
Ho =
M4-2 + M2-4
-5
estos valores en
1501 _ 150<o__-.-___-_l_
+
4
75 0t
15 0l - lS0 ro
4
24 0z - 192 ro
-
5
1a ecuación de equilibrio:
2402 - 192a
--+ 3=o
+ 96 0z - 15'18 9 + 60 = 0
01 = 0.231s
6z = -0.1149
tp = 0.0437
sistema formado por 1as ecs.
0.96
(c)
(a), (b) y (c):
6-03
5.11
-0.96
-2.12
-6.03
lns N GonTáEiVG?oñ7

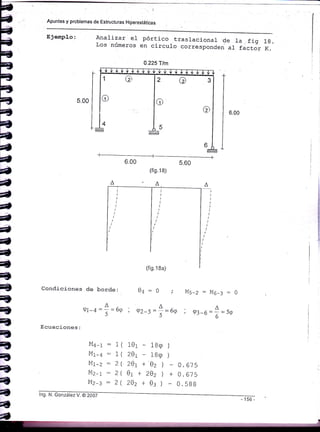
Apuntes y problemas de Estructuras Hiperestátic¿s
Analizar e1 pórtico traslacional de Ia . fig 18.Los números en círculo corresporJ".rtul factor K.
5.00
*
á
7a
ia
á
a
I
l)
¡e
=ü
É
r-
E
a
a
{t
aqü
i,
i*
Condiciones de borde:
A
qt-4=
I =otP
Ecuaciones:
0q:0
92-5 =
Ms-z = I"lo-
.A
, 93-6= -
ó
^-=6o
5
3:0
=59
M¿-r = ll
Mr-a:1(
M. ^: r/
Mr-, = )(
Mt-t = )t
- 1Bq )
-l8q)
*02 )-
2Bz ) +
+0:)
0.675
0.675
0.588
1or
20t
20t
0r+
202
0.225T|m
lng. N. González V. @ 200Z

Equilibrio cie
- Mr-s + Mr-z
60r
- Mz-r + Mz-:
'2ot
- Ni:-z + M:-e
202
- Ms-z : o;
0z+
- ¡.,1- - : n,.,ú-J
¿v3
143-2 = 2( 102 + 203 ) + 0.588
Ms-z : 1(20s + 102 - 18q )
Mz-s = l(202 t 1Bs - 18q )
Mo-¡ : 2(20a + 10: - 15q )
M¡-e = 2(20J + 106 - 15e ) ,"
: 0,
+ 2 02 - 18 v .a?5 = 0
+ M2-5 = 0;
+ 10 02 + 2 03 + 05 -18 I + 0.087:0
: 0;
+ 8 03 + 2 05 - 30 q + 0.588 : 0
2 0s - 18 tp : 0
+ 4 06 - 30 g:0
(a)
(b)
{c)
(d)
(e)
Por equilibrio
cortantes):
horizontal deI pórtico (equilibrio Ce
Ha+H5+H5 =0
M¿-l + N'lt-¿
aonoe: Há=
-
J
Mz_s + M5_2
h6=
-
t)
M¡-o + Mo-¡
u^-
-
ttH-
f)
301 - 36 rp
: c
302 + 395 - 36 ,,
5
- 03+06-10rp
Sustituyenclo estos valores en la ecuación de equilibrio:
Ing. N. González V. @ 2007 '157 '

-0.28
a
=tfr
a
=a
=t
=t-t
=tf
a
a7,
*
a
7
=,
a7,
7,
a
á
!f,
=rI.bi.
ts
a
hb
b!C
b
I.
b
301 -36<p
* 302+30s-36*
+0g+00_,109=g
55
de donde: 18 0t + 1202+200g +605+ 10306 -474<p = g (f)
Resolviendo e1 sistema fo.rmado, ,.'
. 0t = 0.1276
0e = -0'0'179
03= -A'0724
0s = 0.0363
0o = 0'0590
a = 0'0030
Resumiendo 1os momentos obtenemos:
Ho = -o.o¿gz
H5 = -o.o'109

l
?;i;:..1e11d l.l ...' :1:,,:'¡1;.:¡',' ".''; ::l:"lli:'.i;il,'','il:ji:i
,_
- . .' , -
1.20rim
E.'EMPLO. Analizar e1 pórtico de dos
la figura.
niveles mostrado en
4.00
't.00
+- 5.00 -__,__-__-¡
Condi ciones de desplazamiento:
^.(3r-" = ---l
5
Ecuaciones:
A.(D¿-q : - -l
4 9z-z:rOs-s:-fi
t41-2 : 0. 52 01 - 0. 312 A1
li2-1 = 1.04 01 - 0.312 A1
N14-5 = 05 + 0. 375 A1
Nl5-4 : 0. 5 05 - 0. 375 A1
!12-5 = 2.4 02 + t.2 0s - 3. 75
Ms-z : 7.2 Q2 + 2.40s + 3.75
Lf2-3 = 0.96 02 + 0.48 0: - 0.51 6 L2
N13-2 = 0.48 02 + 0.96 0: - 0 .576 L2
Nf5-6 : 1.44 05 + O. j2 0o - 0 .864 A2
Mo-s = 0.12 05 + 1.44 0a - 0.864 A2
M:-s = 3.2 03 + 1.60 06 - 2.50
Mo-: = 1.6 03 + 3.20 05 + 2.50
hg. N. González V. @ 2007

Nudo 2: M2-1+MZ-:+Mz_s:O
4.40 02 + 0.48 03 + 1.20 05 - 0.372Ar _ 0.516 A2= 3.75
Nudo 3:
Nudo 5:
M3-2+M¡-O=O
0.48 02 + 4.16 03 + 1.60 06 - 0.576 Lz:2.50
M5-z+Ms-a+Ms-o=0
7.20 02 + 4.34 03 + 0.72 06 - 0.375 Ar _ O .864 L2 = _3.75
Nudo 6' MO_¡ + M6_5 : 6
1.60 03 + 0.12 05 + 4.64 06 _ 0.864 Lz = _2.50
Equilibrio horizontal de 1os pisos:
Primer Piso: H1+H4+2+1=0
Hl=
.24 02 + ?.50 05 _
Segundo Piso: H2 + H5 + 1 = 0
,,, -
Mo-u+Ms-¿
I ¡4 -
-
4
6.246 A1 : -60.00
., - Mr-u+Mo-s
" 2.50
rr -
Mz-¡+M¡-z
T-1, -' 2.5A
1.44 02 + 1.44 03 .r
2.16 05 + 2.76 0o - 2.BB L2 = _2.50
Mr-z + Mz-r
lng N. Gonzátez.V @ 2007
- tou

Ordenando las ecuaciones obtenemos eI siguient.e sistema:
3.7s )
2.so I
-3.7s I
-2. so I
60. oo I
'-:.1(i .l
r 4.40
I o. ¿e
I r.zo r
I o.oo
I a.za
1.44
0.48 L.20 0.oo
4.L6 0.00 1. 60
0.00 4.34, 0.72
1.60 0.12 1.64
0.00 7. 50: ;. ¡:
1.44 2.L6: 2.16
-0.312 -0.576
0.0 -0.5?6
-0.375 -0.864
O.O .:O'.e6a
-6"2;^ 0.f
0.0 -2. b6u
Las soluciones de este sistema de cuacion¿s s,.:n:
02= 1.798949
03 = 0.844258
0s = 0.090952
0o = -0.492359
Lt = 11.51258'l
Az = 1.888604
Momentos finales:
0.59
1.05
2.00
-l.tz
a 0.67 6.10 I
)
-2.65
-4 27

1.20
4.80
1T
4.0
1
ü
ü
ü
a
t
ú
ü
t
t
t
I
t
t
I
t
,
,
t-
i
)
)
)
t
)
)
)
l
i
Ejemplo: Analizar la estructura
0.9 T/m
traslacional
0.9 T/m 0.5 T/m
J
21
t.u
1.0
5.40
lng. N. conzare- U oTooz
',1
, .{t!
!
.t
I
I
I
I
I
I
i
rl
,0
4 7.2.t
'
1.5 I :
l.ó t/m
5 9,10 I r/ 6
1.5 ¡
1.8 Tim
I
3l
l Ttm
1 9.6 I
2t
I
2 10.8 I
5t
6l
8
il

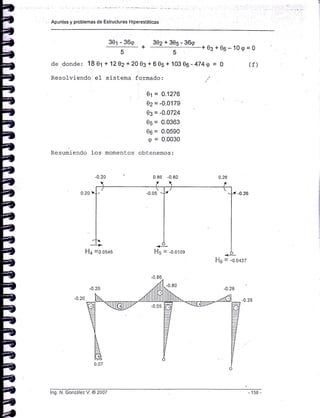
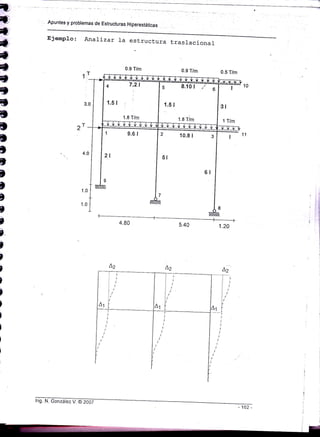
Cóndiciones de'¡árae:
og=o
Ml-Z= Mg-3=0 ; M6-1Or=-0.36 ; M3-1.1 :-0.'12
Condiciones de desplazamiento <leJ. primer piso:
,^. ^ : -a1
a] ,n- ^ : -419t-s=-; ; vz-t =-; , q3-8:-?
denominando: 4l : rs<pr
4
entcnces: q1-9 : -159r , QZ-'t = -L2(pL , 9:-8 = -10q1
Condiciones de desplazamiento deI seg,undo piso:
At L2 L2
gr_,r=-t' ; ez_s=--: ; 9:-03 3 '- - 3
Haciendo, 9: qz
3 '-
entonces: Qr-a : -qz i ¿z-t : -QZ ; 9:-e : -92
Ecuaciones:
t"l9-1 :01 - 45 <p1 ; Nlt-g = Z0r - 45 tPr
N7-2 = Afi + 202.- 12 qt ; N12-1 = 401 + 202 - 72 q7
l"ls-3:40s + 203 - 60 «pr ; II3-3:204 + a03 - 60 Q1
Nlr-z : 801 + 402 - 3.456 ; M2-t : 40r + 802 + 3.456
t42-3': 802 + 403' 1.314 ; ['13-2 : 402 + 803 + 4.374
111-4=201 +04-3<pz ; t'1,i-1 =0r+20a-3<p2
I'12-5 = 202 + 05 - 3 <pz ; i'15-2 : 0z + 205 - 3 <p2
M:-o : 403 + 206 - 6 9z ; Mo-: = 20t + 406 - 6 <p2
Mq-s : 60a + 305 - t.128 ; M5-q = 30s + 605 + 1.728
N15-6 = 605 + 306 - 2.81 ; M6-s = 30s + 605 + 2.1E7

a
ü
ü
ü
a
a
a
I
ü
ü
I
I
I
t
o
o
t
('
t
ü
e
,
a
c
a
e
ú
ü
e
t
r
a
t
7
ñ
a
EquiJ.ibrio de nudos:
Equilibrio horizontal de los pisos:
Primer Piso: H9 + H7 + H6 + 2 + 1 = O
Nudo 1:
Nudo 2:
Nudo 3:
Nudo 4:
Nudo 5:
Nudo 6:
Nudo 7:
Nudo 8:
Mt-g + Mt-2 +
MZ-1 + MZ-l +
M3-2 + M3-B +
M4-t + Ma-S:
M5-2 + M5-4 +
M6-3 + MO-s -
M:-z : 0
Ma-: : o
000
'l 02
020
300
1430
3 10 0
004
000
0 024
120
Mr-s = o
Mz-3+Mz-S=0
M:-6 -0.72 : 0
0
Ms-o : o
0.36 = 0
Piso: H1+H2+H3+1:0
Hz=
Mt-z + Mz-t
He=
Segundo
donde:
Mo-, * M, o
I¡ó-
4
Me-s + M+e
Hr=
Sustituyendo fas
siguiente sistema:
M+_r + [VIr_q
4t
J
5
Me-s + Ms-z
nr=--il Ms-o + Mas
na=---3
ecuaciones de cada barra obtenemos e1
12
4
0
1
0
0
0
0
15
1
401
))Añ
4 16 0
008
103
o20
200
020
2420 0
4aítLl
0 -45
v -t¿
2 -60
00
00
00
0 -72
4 -OU
20 -1246
00
-J . J.4CO
:
-3 io.sle
-6 :-3.654
-3 i t¡ze
-3 i O.+Sg
-6 : ¡.AZl
0i 0
0i 0
0 i-60oi-o i -l
e1 = 0.6845
0z = o.1177
0s = 0.0452
0a = 0.2087
0s = 0.0453
0o =-0.0519
0z = 1.81 10
0a = 1.5375
91 = 0.1039
q2 = 0.2544

.Apuntes y problemas de Estructuras Hiperestáticas
Resultados finales:
2.63 -2.07 -0.362.01
-0 56
-0.48 -1.46
lng. N. González V. O 2c07

Apuntes y problemas de Estructuras Hiperestátjcas
a
t
ü
a
,
a
a
a
a
a
I
tI
I
I
t
f
t
I
a
a
t
-
t
o
a
3
o
3
l
I
I
I
O
3
Ejemplo: Analizar la estructura traslacional.
T
6.00
Condiciones cie borde: 0S : 0O =O
Condiciones de desplazami-ento: er-s : gZ_O : -395
Qr-: : Q2,-4 : -3 A2
4
denominando: +:5qr y lZ:5q,
5 - - 4 -'.
q1-5 : (P2-6 :-15Q1, qt-3 : e2-4 = -75e2
Ecuaciones:
Ms-r : 7207'- 144 q1 ; M1-s
N16-2 = 7202 - 144 «p1 ; tf-z-6
Mr-z : 16001 + 8002 - 2.6661
Mz-t : 8001 + 16002 + 5.3333
Mr-¡ : 3001 + 1503 - 225 q2
M:-: = 1501 + 3003 - 225 q2
Mz-q = 3002 + 150a - 225 92
t14-2 : 1502 + 300a - 225 q2
I"l3-4 : 16003 + B00a - 3.5556
114-3 : 8003 + 1600¿ + 7.11j1
2401 - 744 q1
2402 - 144 q1
lng. N. González V

,1¡i-ii?Ji1ir.it1...,....:','r.:.r,1i:: l:r :. I . .., 1'.'.:;::,i''., ..-: . . ,'
,.:.
:Apuntes y problemas de Estructuras Hiperestáticas _ :,, , '
Fl ',..ri;;
iu I :: .
,il
.ir
!,
a
i:
i
I
I
li
I
¡
Equilibrio de'nudos:
Nudo 1, Mt-2 + Mt_3 + M1_5
Nudo 2: l"I2_1 + M2_A + 112_6
Nudo 3: M3-1 + M3_4 = Q
Nudo 4: M4_2 + iV4_3 = Q
Equilibrio horizontal de los pisos:
Pj-so 1: H5 * HO : 0
Piso 2: H1 + HZ = O
donde:
Mt-z+ Mz-t
ñ7=_.---
5
=0
:0
., -
Mq-l+Mt-+
¡¡1 - 3i
Sustituyendo -l_as
slguiente sistema:
, Mr-. + Ms-2
' r''Z = ----3_- ;
ecuaciones de
"uá"
6
Ma-o + Maa
n¡ = ---3-
barra obtenemos
Ha=
Ma-s + Ms-e
01 = 0.019-325
02 = -0.030279
03 = 0.03775{
0¿= -0.052452
<p1 = -0.000685
q2 = -0.001283
EI
214.0 80.0
80.0 214.0
'15.0 0
0 15.0
7.20 7.20
1 1 .2s 11 .25
15.0 0 -144.0
0 15. O _144.0
190.0 B0 0
80.0 190 o
0 0 -115.2
11 .25 11 .25 0
-225.0
-225.0
-225.0
-225.0
U
-225.0
i 2.6667 )
i -s.asss I
' s.sooz
I
i -7.1111
|
i0l
i6)
Resultados finales:
lng. N. González V. O ZOoz
- 167 -

.
ü
ü
a
*
a
{
a
a
a
il
t
t
I
I
t
t
o
o
a
e
a
a
-
ü
a
a
I
11
?
a
e
t
e
e
Ejemplo: Analizar la estructura como i-ntraslacional
6.00
Con las mismas condiciones rotacionales: os=
= Qz-a
= Qz-q
Ecuaciones:
Condiciones de desplazamiento:
Be =o
Qr-s
Qr -¡
M5-1:1201
M6-2 : 7202
Mt-z = 16001 +
Mz-r = 8001 +
Mr-: = 3001 +
M:-::1501 +
Mz-q : 3002 +
Ms-z -- 1502 +
M:-q : 16003 +
N14-3 : 8003 +
,' Mt-s:2401
; t42-6 = 2A0z
8002 - 2.6'661
16002 + 5.3333
1 503
3 003
1 50a
3 00a
B00a - 3.5556
1 600a 1 7.1111

Nudo 1: M1-2 + Mt-3
Nudo 2: I,l2_1 + M2_4
Nudo 3: M3-1 + M3-a
Nudo 4; M4-2; + l"la-:
Sustituyendo 1as ecuaciones
siguiente sistema:
Mr-s : o
Mz-o : o
0
0'
cada barra Pbtenemcs
01 ." 0.0205908
02 = -0.0290131
63 = 0.0387524
0¿ = -0.05'14531
e1
+
+
Ce
{214.0
I ao.o
Luo
to
80.0 15.0 0
214.0 0 15. 0
190.0 B0 0
1 5.0 B0 190
2.6667
-5.3333
3.5667
-7.1111
Resul-tados finales:
Comparando los resultados obtenidos en 1os dos últimcs
ejemplos, observam.os que Ios mcrrientos reales presentados en
1a estructura (consicielando desplazarniento cie 1os nudos) son
mayores a los momentos que se presentan cuando se estudia la
¡nisma estructura sin considerar desplazamientro Ce sus
apoyos.

Ejemplo: Análisis de un pórtico traslaciona.l sometido a
cargas horizontales.
ii /
6T
96
0.35 I l
6 T/m
10 7.2
0.3s I 0.35 I
6 T/m
56
0.80 I
6 T/m
6 z.z
0.80 I 0.8 I
6 T/m
7
7.2
0.80 I
6 T/m
vvvvvvvvgl
1
6
1.20 I
t¿
1.20 I
13
7-2
1 .20 I 1.20 I
14
3.50
4.00
4,00
2.00
ir
tl
E
F
i
4.00
Valores relativos def
6.00
ángulo de traslación
6.00
(p:
; 9z-tt:
; 9q-rs =
^^-v4-B:-- 4
A¡
Qz-rr = ----:r=
3.5
4 ro,
6qr
_Ar
6
_At
4
: -4ej
: - 6<pr
-Q2Qi-s:92-o= 9¡-z
Qs-g = Qe-ro = -Q3
=cf;l
xl
É
Además, e1 tipo de apoyos determinan que:
0n : 0r: =,01a : 015 = g

:itefi'f:j,1§fi-iji'.ri;i. ':i:: '- ':-.i::'
':
. ,.' '.r:..
:* .'' . :. I :,',npúntes y problema; de Eiiructuras Hiperestát¡cas
Ecuaciones:
M1-12 = 0.8 01 - 4.8 91
M2-13 = 0.8 02 - 4.8 91
M3-14 = 1.2fu- 10.8 rp1
M4-15 = 1 .2 0a - 10.8 q1
M1-2.=601 +f,62-3
M24 = 4.802+ 2.4fu-18
M3-4 = 4.8 03 + 2.4 0a - 18
M1-s = 0.8 01 + 0.4 0s - 1.2 <pz
M2-6 = 0.8 02 + 0.4 06 - 1.2 q2
M3-7 = 0.8 03 + 0.4 07 - 1.2 q2
M4-8 = 0.8 04 + 0.4 0g - 1.2 q2
Ms-6.=605+396-6
M6-7 = 4.8 06 + 2.4 07 - 18
Mz-a I 4.8 07 + 2.4 0s - 18
Ms-g = 0.4 05 + 0.2 09 - 0.6 93
M6-10 = 0.4 06 + 0.2 0lO - 0.6,p.
lvlt¡1 = O.4 07 + O.2 0ll - 0.6 q.
Mg-10=609+l0lO-8
l'4lO-l t = 4.8 01g + 2.4 0ll - 18
Equilibrio rotacional de nudos:
Mi2-1 = 0.4 01 - 4.8 91
M13-2 = O.4 0z- 4.8 <pt
M14-3 = 0.6 03 - 10.8 91
M15-4 = 0.6 0¿ - 10.8 q1
M2-1 =301 +602+8
M3-2 = 2.4 02 + 4.8 03 + 'lg
M4-3 = 2.4 A3 + 4.8 0¿ + 18
Ms-.1 = 0.4 01 + 0.8 05 - 1.2 92
M6-2 = O.4 02 + 0.8 06 - 1.2 92
M7-3 = 0.4 03 + O.8 07 - 1.2 q2
MB-4 = 0.4 04 + 0.8 06 - 1.2 92
['16-5=305+§96¡g
M7-6 = 2.4 06 + 4.8 0z + 1B
MB-7 = 2.4 07 + 4.8 0A + 18
Mg-s = 0.2 05 + 0.4 0g - 0.6 «ps
M10-6 = 0.2 06 + 0.4 016 - 0.6,p¡
M11-7 = 0.207 + 0.4 0lr -0.6Ea
tuI10-9=309+§0lO+8
Ml t-lO = 2.4 0rc + 4.8 0rr + 18
t4r-s
Mz-t
M:- e
1,1.1 _ a
l,ls _ 9
Mo-z
tlu_I
0
0
+M2-5 : 6
+ l,l3-7:0
+ M6-10 : 0
+1"i7-11 : g
+ M1g-11 : 0
- t,
li1-12 + l,l1-2 +
Ni2-1 + l.f2-13 +
1,13-2 + l,l3-14 *
Nia-3 + Mq-:-s +
N15-1 -1-t"15-6 +
Me-s + l'16-2 +
l"i7-6 + N{7-3 +
Me-t + Me-s:
Mg-s + Mg-ro =
1v119-9 + M16-6
Mtt-rO + Mtt-t
lng. N. González V. O 2007

Apuntes y problemas de Esfucturas Hiperestáticás
00.40oooo
000.4Oooo
2.4000.4000
6.80000.400
0 7.2 3 o 0 0.2 o
03122.4000.2
0 0 2.4 10.8 2.4 0 o
0.4002.45.600
000006.43
000.200311.2
0000.2002.4
2.25000000
1111100
0111011
/.o J
3 12.4
o 2.4
00
0.4 0
0 0.4
00
00
00.
00
00
tt
11
00
l
I
;
l
]
I
I
I
a
t
l
I
l
l
)
,
I
l
l
I
l
I
,
t-
I
a
a
l
t
t
t
I
I
t
Equilibrio de cortantes por pisos:
H12+H13+H14+H15+17 = Q
H1+H2+H3+Ha+10=0
H5+H6+Ht+3:0
E.l- sistema que se forma es:
0
2.4
1 1.6
2.4
0
0
0.4
0
0
0
0
2.25
1
0
0 -4.8 _1.2 o
0 -4.8 -1.2 o
0 -10.8 _1.2 o
0 -10.8 _1.2 o
0 0 -1.2 -0.6
0 0 -1.2 _06
0.2 0 -1.2 -0.6
00-1.20
000_0.6
2.4 0 o -0.6
5.2 0 0 _0.6
0-7000
00-80
100_6
ó
10
0
-18
8
10
0
-18
I
10
-18
-85
-33_33
-17.50
La solución del sistema de ecuaciones arroja 10s siguieiltesresultados:
0l = 2.78720
02 : 0. 93862
03 : 1.50133
0a = -0.09711
05 : 7.73115
06 : 0. 75605
0z : I .76211
0a : -2. 66533
0e : 0.'r.0329
0ro= 1.70546
0rr= -3. 91551
tPr = 1.30416
q2= 1.85614
(p3 = 3.21 491
-172-

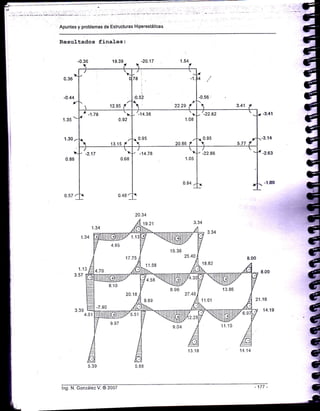
Resultados fina]-es:
1.34 20.34
il
H
I
it
E
l
I
I
3.34
I
, -1.34
-1.13 B
_ 17.75 7t
t'-l.ls
i
f -3.C4
': ')t
, f
4.70
_4.58
. -3.39 ts
,^ ro I
¡'-l l.ss -1s.s2
_4.30
, -4.78
cz"oaF
;t'".-
-f
t'4.17
I
-s.gs '*' _r1.0)
-12.28 I
-t 3.1 I
to.Jb
17.75
1 1.58
8.96
¿v. tó
o ao
tJ.ó5
27.4A
11.01

L
L
a
ü
a
a
a
a
a
a
a
ü
a
ü
I
t
il
o
o
ü
a
t
a
t
ü
a
ü
a
it
ü
ü
e
ü
a
ü
Ejemplo: Analizaremos la mi_sma
' anterior, eliminando
puntuales horizontales.
estructura de1 problema
1a aplicación de fuerza!
6 T/m
96
0.35 I
6 T/m
10 7.2
0.35 I 0_35 I
6 T/m
11
6 T/m
56
0.80 I
6 T/m
6 z.z
0.80 I o.8 I
6 T/m
7 z.z
0-80 I
6 T/m
1
6
1.20 I
12
1.20 I
IJ
7.2
1.20 I 1.20 I
14
6.00
3.50
4.00
2.00
Q1-12=-*=-4q,1 ; qr2-13=-9=-4qr
6'b
93-14=-?=-Ur, , tP,{-rs=-?=-U*,
qoj-s= g2-6 = e3-7= e4_B = -
? = -r,
Qs-s= Q6-10 = q7-11= -.11 = -*,
Además, eI tipo de apoyos determinan que:
0n:0r::6tq:grs:0

Apuntés y problemas de Estructuras H¡perestáticas
Eeuaciones:
M1-12 =
M2-'t3 =
M3-14 =
M¿-ts =
0.8 01 -4.8 q1
0.8 0z - 4.8 <pr
1.2 %- 10.8 <p1
1.2 0¿,- 10.8 91
M1-2=601*302-8
Mz-g=4.8 02*2.4 0s-18
M3-4=4.8 0¡ *2.4Aa'18
M1-5 = 0.8 01 * 0.4 0s - 1.2 q,
M2-6 = 0.8 02 * 0.4 0o - 1.2 qz
M3-7 = 0.8 0s, 0.4 h -1.2 qz
M4-B = 0.8 0¿ * 0.4 0e - 1 .2 ,p,
M5-6=605+f,Q6-6
Mo-z = 4.8 0o *2.4 07 -18
M7-8 = 4.8 A7 * 2.4 06 - 18
M5-9 = 0.4 05 * 0.2 09 - 0.6 ,ps
M6-10 = 0.4 06 * 0.2 0to-0.6,p.
Mz-rr = 0.4 ü* 0.2 0tt -0.6,ps
Ms-lo=609*30t0-B
l'¡lro-r t = 4.8 0ro *2.4 011-18
Mrz-r = 0.4 01 -4.8 91
M13-2= 0.4 02-4.8qt
M14-3=0.6 03-10.8q1
M15-4=0.6 0¿-10.8q1
Mz-l=30t*602*B
M3-2 = 2.4 0z* 4.8 03 * 1B
M4-s = 2.4 fu* 4.8 0a * 1B
Ms-1 = 0.4 01 * 0.8 0s - 1.2 qz
M6-2 = 0.4 0z + 0.8 0o - 1 .2 q,
Mz-s = 0.4 03 * 0.8 0z - 1.2 qz
Ma-¿ = 0.4 0a + 0.8 0a - 1.2 q,
M6-S=305*606*$
lVlT-6 = 2.4 8a * 4.8 07 * 18
MB-7 = 2.4 07 * 4.8 0a * 1B
Ms-s = 0.2 0s + 0.4 0e - 0.6 93
M1o-o = 0.2 06 * 0.4 01s-0.6 p3
Mtt-t =0.2 ü * 0.4 0tt -0.6 qs
[/1s-s=3 09*6 Oto*8
lvltt-to =2.4 Üo*4.8 0tt * 18
CÉ
&
§
{F
C
G
G
G
C
4q
fG
t
t
t
t
.
I
(
I
{
(
I
(
(
I
EI proceso de cálculo es similar, asi fas ecuaciones para
cada barra y el equilibrio de nudos no se modifican,
sclarnente debe corregirse el planteamiento de las ecuaciones
pará et equillbrio horizontal, así:
Hlz+HlS+Hl¿+Hl¡=0
Hl+Hz+H3+H¿=0
Hs+Ho+H7=0
Con estas condiciones, e1 sistema formado es:

ü
ü
ü
a
a
t
o
a
a
ü
o
t
ü
ü
iD
ü
t
e
?
t
o
o
a
o
a
a
1,
a
ü
ü
ü
ü
ü
e
It
0.4000000
00.400000
0 0 0.4 0 0 o o
0000.4000
7.2 3 0 0 0.2 o 0
3122.400o.20
0 2.4 10.8 2.4 0 o 0.2
0 0 2.4 5.6 o o 0
o.2 0 0 0 6.43 0
0 0.2 0 0 311.22.4
0 0 0.2 0 0 2.45.2
Q000000
1111000
1110111
7.630
3 12.4 2.4
0 2.4 1 1.6
Q02.4
0.400
00.40
000.4
000
000
000
000
1 1 2.2s
111
000
0
0
2.4
6.8
0
0
0
4.4
0
0
0
2.25
1
0
4.8 -'t.2
-4.8 -1.2
-'t0.8 -1.2
-10.8 -1.2
o -1.2
0 -1.2
o -1.2
0 -1.2
00
00
00
-70 0
0-B
00
o¡8
0 i10
0t0
o i-ra
-0.6 i I
-0.6 i 1o
-0.6 i 0
o i-la
-o.o I B
-o.o ilo
-0.6 i-18
o ioo io-6 lo
independientes
Las sol-uciones
Se observa que solamente cambian l-os términos
de fas ecuaciones de equilibri-o horizontal.
de este sistema son:
0t = 0.724305
0e = 0.496304
0e = 0.348147
%= -2.7218q1
0s = 0.831 13+
e6 = 0.408608
07 = 0.689292
0e = -3.385169
0s= 0.431742
010= 1 .682690
011= -4.269013
al = -0.058860
a2 = -0.326153
93 = -0.037591

Resul"tados fina1es:
19.39 -20.17
0.36
-0.44
1.35
1.30
12.e5 I
78
:
1
:0.52
22.2s I
-0.56
3.41
-1.78 -
L
0.92
/13.15 I
I
{

.'-14.38 !
1.08
{ 0.95 /
2086 /
,'-22.82
{ 0.95 r
r. 5.77 I
1 1?
3.57
4.58 1ililt(riil/'
lng. N. González V. @ 2007 -177 -

t_
I
ü
t
a
a
a
a
a
a
t
il
ü
?
iD
e
a
a
ü
e
a
a
a
a
a
a
a
=ti)
=t
=,e
q
<,
{t
Ejemplo:
Ios pisos.
Analizaremos la
despreciando l-os
misma estructura anterior,
desplazamientos laterales de-
6 T/m
6 T/m
96
o.35 I
6 T/m
10 7.2 11
;
0.35 1r i. 0.35 I
!:
6 T/m
1
56
o80 l
6 T/m
" 7.2
0.80 I 0_8 I
6 T/m
7
7.2
6 T/m
8
0-80 I
b
1.20 I
12
1.20 I
13
7_2
1.20 I 1.20 I
14
3.50
4.00
4.00
2.00
4.00 6.00
En este caso ]os ángulos de rotación cle las cuercias
son Qt : Qz = Q3 = 0, con ello eI sist.ena de ecuaciones se
reduce al rango 11 x 11, eliminándose Las tres úiltimas filas y
Ias tres últir¡,as colunnas de fa matri-z cie coeficientes del
problema anterior. Con esas conciiciones las soluciones del
sistema son:
01
03
05
0z
0e
oll
Q2
= 0.800928 ,
= 0.404439 ;
= 0.876752 i
= 0.709905 ;
= 0.433618 ;
= -4.265688 ;
= 0.0000 ;
0z = 0.520622
0a = -2.593727
06 = 0.426757
0B = -3.333265
010 = 1.3663
91 = 0.0000
a3 = 0.0000
lng. N, Gonzále¿ V. @ 2007

-,--f::l¡rfr!" ,-... '
' -:'' )
'. .,.' ,'"1 eórni"! y problemas de Estructuias Hiperestát¡cas
0.44
1.O2
Resultados fina].es:
f i3
-3-41
-3.11
aoa
20.1 8
9.89
iTr onzález V. @ 2007

il
a
a
fl
*
-
á
-t
-l
=t¡t
=r
a
a-t
a
a
a
a
a
a
ñ
a
a
á
a
á
=,
=,
=t
=,
=t4'
€
ri
Apuntes y problemas de Estrucluras Hiperestáticas
6.11 APLICACION A PóRTICOS ?RASLACTO¡¡ALES
=RREG{,I.ARES
se consideran pórticos traslacionares irregurares a aque]1osque en su geometria presentan dos o más gruáo" de libertad enfunción de Ia unión de vigas a corumnas u otras formasgeométricas como barras inclinadas. Estos casos se
-presentan
en naves industriales, estructuras con mezzanine, etc.
El análisj-s parte.
-
de la hipótesis asumida sobre laindeformabilidad axial de las barras componentes, además deconsiderarse que
-
los desplazamientos
"".i., medidostraüsversalmente a 1os ejes de ios elementos.
Ejemplo: Pórtico con mezzanine.
2.0
5.0
Diagrama de
6.00
desplazamj-entos :
5.40
1.5 T/m
¿ález V. @ 2007

Rigideces relativas y ángulos de desplazamientor ,
kr-s=f =0.+rr ; k1-2='4u'' =0r,, kz-o=2E521=0BEr
kc a=?El=rr; ks-+={f=ar,, k1:7='=trut =.,2.
A1 ^ :41 . A2 _. Ai+L2
e1_5 = -5; a2_6 = -? , eZ. .: - ' : qa_7 =
Sabiendo que 05 : 06 : 0r = O
Mr-s = o.a(20¡ -, ?l = 0.801 - 0,24L1
Ms-r = o.+1e1 -:4--!-¡ = 0.401 -0.24L1
Mr-z = a(201 +02)-6 = 80r +402 -6
Mz-t = 4(01 +202)+6 = 401 +802 +6
Mz-o = 0.8(2;2 -:91 = t.602- 0.48a1
)
Me
-z =0.8(02 - ¡ 9l = o.8o¡ -0.48a¡
)
Mz-: = l(202 + 03 -, ?l = 202 + 0: - 1.5a2
M:-z = I(0r + 203 -3 4-¿) = 0z + 20¡ - 1.5a2
'5
Iv13-4 = 3(203 +04)-3.645 = 603 +30.1 -3.645
M+-¡ = 3(03 +204)+3.645 = 30¡ + 604 + 3.645
M+-z = r(204 -3
";-,
= ze4 - r¡ o, -
;
o,
Mu
-+ = r(oa -3 Ofr, = o.¡ - ], ot-1 o,
Ecrraciones:
- Mt-S + M1-2 = Q-
8.801 + 402 - 0.24A1 - 6 = O (1)

Apuntes y problemas de Estructuras Híperestátícas
)
)
)
)
)
)
)
)
)
)
)
)
)
)
)
)
)
)
)
)
)
)
)
)
)
)
)
)
)
)
)
)
)
)
)
- MZ-:. + Mz-6 + M2-3 = §'
401 + 11.602 + 0: - 0l4BA1 - 1.5Au + 6 : 0 (2)
- MS-Z + M3-a : Q
02 + 803 + 30a - 1..O, -
- FIq-: * Mq-z : O;i
2703 + 560a - 3At - 3Az +
3.645: O /'
atr c1t _
^LJ.JIJ _ V (4)
(3)
Equilíbrio horizontal de fas cortantes de1 primer piso:
H5+H6+H7:6
Ml-S+MS-t
*M2-O*MO-Z * M4-7*M7-4
5B.B 01 + 117.6 02 + 105 0a - 100.56 A1 - 30 Az : 0 (s)
Equilibrio horj-zontal de las cortantes deI primer piso:
H2+Ii7=g
Mz-¡ + M¡_1
2
M¿-z + Mz-¿
+-n
7
4902 + 49 03 + 14 0a - 4 Ar - 53 A2 : 0
(6)

Resolviendo eI sistema:
0r = 1.1363
0e ='1'0845
0¡ = 0.8543
0¿ = -0.8696
Lt = -1.4117
Az = -0.3361
Ejerapl.o: Pórtico con viga inclinada
3T/m
6.0
+2
I
I
:
I
L
3.0
A
91-2 =-; =-Q
A^
g4_3 =_
. =_r,pl1
zm,
Ecuacionas:
8.0
Tomando
!lt -2
MZ -:
NIq-:
Mz-1
M:-Z
143-q
en cuenta que 01 : 0q = 0
- 02 - 0.5
^:E0z+403-16
=20t-2L
= 2 0z - 0.5 A
=q0z+803+16
=40:-24
ro

l
Apuñtes y problemas de Estructuras Hiperestáticas
(3)

]_
Ha
>
I
I
il
I
l.
t
a
a
a
a
il
il
il
I
il
t
l}
t
I
t
t
t
ü
o
t
a
a
?
i,
a
ü
a
t
e
e
e
a
a
Mz-r +Mz-:: 0 ; 1002 + 4 0¡ - 0.5^- 16: 0
M3-2 + M:-¿'= 0 ; 4 02 + 12 03 - 2.0 L+ 16 = O
Equilibrio de cortantes:
(1)
(2)
H1+Ha
Mr-z + Mz-r
6
02+403-34
M+-s + Mg-¿
3
:0
Resolviendo ef sistema:
02 : 2.57239
0z : -2.6115?
q : -2.64463
-5.16
0.07

Apuntes y problemás de Estructuras H¡perestát¡cas
*
d
ú
ú
J
#
ó
c
.f
.C
C
e
#qt
{
C
C
ó
G
G
G
G
G
G
3
J
método j
¡
¡r85-
ú
J
3.0
ecuaciones ciel
Ejemplo: Pórtico con viga inclinada.
3 T/m
6.0
Ecuaciones: Cono 01 = 05 - 0,
suedan en la forma:

(2)
D
a
a
a
il
t
il
il
t
ü
D
il
o
il
o
o
t
ü
C
o
o
ü
il
ü
o
o
t
t
o
t
o
o
ü
o
e
Mr-z:202-2L
Mz-t:402-2L
Mz-s : 02 + 0.5 0a
Mq-z = 0.5 02 + 0a
Mq-s.40a-2L ..,
Ms-¿:20a-2L
Mz-t:402+203
M:-z:202+40:
M:-q:803+40a-16
Ms-::403+804+16
Equili-brio de nudos:
Nudo 2: l4z-t + Mz-: + M2-a : 0 ;
9 02 + 2 03 + 0.5 0q - 2 L: O
Nudo 3: M:-z + N{3-a : g
(1)
202+1203+40a-16=0
Nudo 4: MS-Z + tvlS-q + l4a-5 : 0
0.5 0z + 4 03 + 13 0a - 2 L: *16 (3)
Equílibrio de cortantes: En la base del pórtico:
H1+H3:6
Mrz*Mz-r Mq-s+Ms-¿
.U
33
202+20s-2.6661
^:0
(4)

Resolviendo e1 slstema:
0z = -0.894174
0s = -2.230678
0c= 2.244946
q = -2.354340
Ejemplo: Pórtico
9 T/m
con columna inclinada
De la geornetría del triángulo de deformaciones en e} nudo 3:
I
J.U
I
%A
A1
A3tan cr
a1 2
¿3sen 0, :
--:--=:Á2 J13
2
A. -- A
oI -
^
Lr
J
t;;
A, : a''A
e
d
F
3
E
¿
a
r
ü
¡
t
t
t
t
-l

^6
nudos:
D
a
ü
I
a
a
a
rl
i,
r}
ü
!D
o
t
t
o
a
a
{l
t
lt
7'
a
á
=ta
€
=,Ee
a
a
a
la
Desplazamientos relativos :
Ecuaciones:
)
M.,_r = ZQ0, +e2 -A)-1.5
3'
1,rr.+e, +Ar-12
2'ZJ2'
á
-=(2e3 -^)
"/1
3
^Ar-z =;
M"" =
Ms-¿ =
Equilibrio de
Mr-z: o
FI2-1 '+ M2-3
M3-2 + M3-a
L2 Ar
; e:-q =
Jrt=-?
)
M2-r =
f
(er +202 A) +1.5
M" " =1(e" *2e. +A)+12
2" " 2'
A
M¿_s =
Jñ=
(e3 -
^)
11
i q24:-" q
201 +02-A- 2'25:0
Bet + 2802 + 603 - 5n - Il2 = 0
16 1 8
o2 + Q+
;5)e:
* (7 -
lElo
+ 24 : o
(1)
(2)
(3)
Ecuación de equilibrio de cortantes:
h
Por proporcionalidad de triángulos:
24- :
- = h : 6.0 m
3h
+2(3) (6+1.5)-
=0
N13-4 + NI3-4
t3
Hi
sustituyendo Ias expresiones oe fos momentos, encontramos 1a
ecuación aciicional de cortantes:

Apuntes y problemas de Estructuras HiPerestáticas
01 + 202 *
#t,
Resolviendo e1 sistema: l
«,* frro
24.15: O (4)
0t
Az
0:
A
-:-0 . 47 263
6.41789
-g.|fl1s :
-16.'1r736
Observación: La ecuación- de condición aplicada para
encontrar una nueva relación entre Ias variables' es una
variañte de las "tifi"u¿ut
anteriorrnente; si bien podriamos
efectuar e1 "q"iiiUtio
de las fuerzas horizontales en 1os
apoyos de 1a .tt;;L";' su cáIculo resultaria más laborioso
y se encontraria una ecuación que resultaria ser coidlinación
iineat de las Ya encontradas '
Ejemplo: Pórtico con vi-ga inclinaia'
-lf-
%Ít¿
1.50
Diagrarna de deformaciones :
J
307
1
ln
+
pFtg19 dg9p-FE1r9llo
Para el apoyo 2
N. Gcnzález V

Apuntes y problemas de Estrucluras H¡perestáticas
i}
ü
a
a
a
a
a
a
a
a
it
t
i,
r,
o
t
t
ft
fl
ü
t
t
a
{
*
a
f,
r'
?
?
?
ü
ü
a
a
¡l
De1 triángulo de formaciones:
A 1.50
sen ü. =
a1 2.50
,A
91-3 = -:
J
Ecuaciones:
:0.4( 0t -
: 0.4 QAt -
: 0.8 (2ü +
:0.8( 0r +
5
+ a1 =:aJ
Ar
i q1-2= -L_i Z.J
¡'
0.64) - 18.?s
0.64) + 18.75
0z - 2L)
202 - 2L)
M:-r
Mr-:
Mt-z
Mz-t
Mr-3 + Mt-z = 0; 2.4
NI2-1 : ¡,
2
:--
^3
01 + 0.8 02
01+202-
- 1.84 A + 18.75 : 0 (1)
2L:0 (2
gor goT
0t = 8.5843
0z = 19.4277
a = 23.7198
V3+V2-30:0
7s-(M1-3-NI¡-r)
u3 :---
5
Ml-r + Mr-t
- 1.5
Pero:
34.5 01 + 30 02 - 41.8 a + 112.5 = 0 (3)
2'1.69
-21 69
a
Yzvz

l.=.,.,{
, . .:,{
I
e
C
C
-C
c"(
a,
t!
t
T
It
t
a
^; 93-4=L =e
F
¡l
.¡¡.1
¡
I
I
il
I
i
il
.1
i
i
:'
t,
i
Ejemplo:
A
91-2=-;=-Q
Ecuaciones:
Mr-z :
M,,:
Ii{3-4 =
Equilibrio de
l'lz - r
M,.
2EI
-
le1
1t, I
-
(20.¡
n
/t,I
- (30¡
L_
nudos:
Mz-::
lt, I
(20r - 3o)
L
lt, I
= h @2+2fu)
2ET
=
L
(e¡+3q)
3p)
+ o:)
+ 3p)
Mz-l
N{:-z
M¿-l
Ec¡:ilibrlo cortantes:
1x,
ztf.|ro2+fo3-ir=o
] o, * ztl * ,l-le¡ * 1q, = o
lr-'LL
X1+X2+P=0
.. _ rr41-2 _ Ivr2-1 ,*tro, _ o+)"'- r- -i,
Xr = Ir'l+-:-M¡-+
={1103-04,¡,?.*--L=L."
0;
0;
(1)
(2
<ie
P
I
Í
I
a
a
a
a
e
I
e
I
a
f
f
ú
C
TL
lng. 1.,1. González V. @ 2007

ilñl
fra
*
*
-
a
=a
¡il
t¡l
iü
rl
a
a
a
a
a
t
a
t
*
a
a
=tit
il
t
a
?
=t?
a
E}
ot2
'0.2-0:-4e+á:0
Resolviendo ef sistema:
(3)
PL2h
0r---" 4El(h + 2L)
PL2h
a^ ---
4El(h + 2L)
PL2(L + zrr)
(D=-
' l2El(h + 2L)
L't1-2
M:-q
Mz-t
(L+h)
L
L
L
L
(L+h)
Mq -:
Momentos finales:
Mr-z:
Mz-r:
Mz-::
l,l:_z:
M:-q:
Mq-::
-
f inorr-l
D'
-' -(h+21)
2'
DI
.lrrr + zll
2'
- !!,n * zl,
2'
DI
l-lftr + zL)
2'
DI
' 'rh + 2L)
2'

Ejemplo:
Diagrama
. 8.00
de deformavciones:
Del triángulo de deformaciones:
Pórtico para nave
empotrados.
industrial apoyos
.+
l
'l1.50 T/m
t3.0
1
I
4.0
I
I1-.0
+
8.00
ai-az A3 A4
sen(2s) sen(90-cr) sen(90-a)
at-Az
Ar=4,
2sen(cr)
Ar-Az
-'.-"- Á

)
)
)
)
)
)
)
)
)
)
)
)
)
)
)
)
)
)
)
)
)
t
)
)
I
I
I
I
)
]
I
)
]
t
]
senü, =
t;;
a¡=a¿=1/1161-42)J
ffidonde:
Rlgideces Y ánguJ-os de desplazamiento lateral:
/
2EI EI
fi_.>=-=-=)AAiL
- 2E"lTt 2Et
f. ^= --=L0'z-) lt¡ I
/J
r. ^ -2É.-Ft =E=ro'J-+ t-^
VlJ I
. 2E2l 4El
I¿-5=---=-- =ó
1
e.-) =- 4r = -0.75a¡A
a
a?-? = * = o.s(o, -Az) = o 5a1-o'542
"173
3Ar
(p3-4 = - :* =-0.5(a1 -AZ) = -0.54¡ +0.542
tt I-1
.ot .=-'o'=-o.6oazaa-r
5 "
a -o^ n
Ecuacl-ones: -ott vL - w¿
r.f,-¡ : 5(20r + 0., - 0.7541)
Mo,-5(0r+20)-O.75At)
NIz-: : 2OQe2 + 03 + O'5A1 - 0'5Az) - B
Mt-z = 20(02 + 203 + 0'5Ar - 0'542) + B
!i3-4 = ZO(20s + 0q * 0'5A1 + 0'5Az) - B
Ntq-3 = 20(03 + 20a - 0.541 + 0'5Az) + B
Niq-s: B(20a + 0s - 0'6Az)
t'ls-q - B(0q + 20s - O'6Az)
iiilN. González v. @ 2oo7

., .! I ril 1. :.' '
: _ :-.
'1r,r..:,:-i::r.r::::,i:r-..r.1ji:.r
,"-i . ,.. '
"t:'."
Apuntes y problemas de Estruc{uras Hiperestáticas
Mz-r+MZ-::0;
50 02 + 20 03 + 6.25 L1- 10 A2 - B = 0 . (1)
M3-Z+M¡-S:0;
20 02 + B0 03 + 20 0a: 0 Q)
M4-3+Ma-S:0;
20 03 + 560a - 10 A1 + 5.2 A2+ B = 0 (3)
H1+H5 :0
tl1-2 + M2-1 M4-5 + M5-4
1501 + 1502 - 7.5 A1 24Qa + 2405 - 9-6L2
1502 + 96 0q - 37.5 A1 - 38.4 L2 : g
h3
Equilibrio traslacional: G=l ; h:6 m.
{
{
{
a
t
a
a
a
I
II
I
t
I
(
{
t
=Q
(4)
(
(
(
(
(
(
(
(
(
{
(
(
(
{
J

de
I
I
I
)
)
)
)
)
)
)
)
)
)
)
)
)
)
)
)
)
)
)
)
)
)
)
)
)
)
)
]
I
EMk : 0,
donde:
32.5 02 +
AI plantear Y resolver
que 0l = 0s : 0, Por ser
Hr(4+6) + vaQJTll - Mt-z - Ma-: - 1'5(16) (8) = 0
.. M1-2 +M2-1
¡¡ I
4
yo =
M3-4 + M4-sj 1'5 '(8) '(4)
60'0r +60 04 -20' 4 +20'
^Z
+ 48
"4=
------'--------
:
a//J
100 03 + B0 0q - 45 A1 + 30 A2 - 104:0
eI sistema de ecuaciones se
arnbos apoyos emPotrados '
(s)
cons idera
Soluciones Y momentos finales:
0z: 0-73512t
0: : -0.030755
0s : -0.6123L9
^.
= -1 .816965
Lz = -t'679950
13.4 9
-17.86
-1 2.96
ing. N. González V. @ 2007

EjempJ-o:
donde:
Pórtico para
. articulados.
nave industrial
'1.50 T/m
con apoyos
I
3.00
+
I
4.00
I
I
r loo
]-I
tlel tri-ángulo cie deformaciones :
/l a1 - A2
¿t,,/l¡,
/ I ! sen(2o)
1t
Ar-A¡
sen(90-e) sen(90-a)
senü, =
A::
J
ar-Az
^ --ol -' 2sen(cr)
i;,
a3=a+=f(ar-az)
I
I
(
{
lng. N. González V. @ 2007 - 197 -
-_--.-

t
t
ü
a
a
a
a
a
a
a
a
=l
?
t
t
?
t
a
a
ü
a
a
a
a
a
a
a
a
ü
i,
a
e
ü
a
o
a
Rigideces y ángulos de desplazamiento lateral:
f,_., =E =
El
= s
42
, zl^[tt 2Et
rr_r = =-=20"ltt I
- 2E^lt-731 2Et
t1_¿= = =20
^!ll I
. 2E2l 4Et
l4_S=-:-=-'_ =8
))
3Ar
t_2=____r=_0.7541
ez- 3 =$ = o.t1o1-Az)= 0.541-o.5ar
e3-4 = -+ = -0.5(a1 -^z) = -0.5a1 + 0.5a2
' Jz¡
3L'>
q4-5 ='--: = -0.6042
Ecuaciones:
Mr-z : 5(201 + 0z . 0.75Ar)
Mz-r : 5(0r + 202 - 0.7541)
Mz-: : 20(202 + 03 + 0.5A1 - 0.sA2) - B
i,l3-2 : 20(02 + 203 + 0.5At - 0.5A2) + B
I'13-4 = 20(203 + 0a - 0.541 + 0.5A2) - B
M4-3 : 20(03 + 20a - 0.541 + 0.5A2) + B
Mq-s=B(20q+05-0.642)
Ms-s=B(0q+20s-0.642)
N11-2 : ¡, 10 01 + 5 0z - 3.75 A1 : 0 (1)
MZ-t + MZ-::0
5 0i + 50 02 + 20 03 + 6.25 L1 - 10 A2 - B = 0 (2)
N13-2 't- M3-4 : 0; 20 02 + B0 03 + 20 0a = 0 (3)
lng. N. González V. @ 2007 "198 -

M¿-3+M¿-S=0
2003+560a+805
Ms-e:o; 80¿
Eguilibrio de cortantes:
Eguilibrio traslacional :
- 10 A1 + 5.2 A2 + 8.= 0
+1605-4.842=O
(4)
(5)
H1 +fl5 =g
M¡-2 + N12-1 M4-5 + M5-4
45
--J->
H5
25 01 + 50 02 + 64 0a + 32 05 - 18.?5 79.2L2=g (6)A1 -
;
k
I}IK : O,
lr1(4+6) + vaeJTl)
AI
I
_L
H1 =$
h _3
16 8
h:6
T
4l
I
- M¿-: - 1. s (16) (B) = 0
M1-Z +M2-1
4
lQg. N. González V. @ 2007
Hr=

t
I
i r. _ M3-4 + M4-3 + 1.5 '(8) '(4)
v4-
4
,r. _ 60 03 + 60 .04 -20.A1 +20.L2 + 48
-- .173
de donde:
12.501 + 25 02+ 10003 + B0 0a - 3041 + 3042 - 113.3?5 = 0
Solueiones y momentos finales:
(1
e1 = -2.34038
A2 = 1.56274
03 = -0.04066
e4 = -1.40011
05 = 1.64920
q1 = -4.15736
q2 = 3.16383
-15.52
19.52 -24.39
-24.39

:. "':. ti- . ., .t:; .i:-.., ...i::i:.._:.:i ",.1:.,"-i:: ::r.. :
.
1.5 T1m
:
3..U t/m
Ejemplo: Análisis de pórtico traslacional'
la columna 4-8 se conecta con el
una articulación por debajo de 1as vigas 1-2
considerando que
nudo 2 mediante
v 2-3.
4.0
5.0
4.0
Diagrama de desPlazamientos :

Ecuaciones:
Mt-r= 0.8 0t - 0.48 A1
Mr-z = 1.6 01 - 0.48 A1
Mr-z= 2.4 + 1.2 02 - 4:
Mz¡= 1:2 01 + 2.4 A2 + 4
Mr-s=:0r + 0.5 9. - 0.375 A2
Ms-r = 0.5 01 + 0s - 0.375 A2
Me-q : 1.2 Aa - 0.12 Ay
Mq-a : 2.4 0q - 0.72 L1
Mz-::202+0:-9
M:-z= 02 + 2 03 + 9
M2-6= e2 + 0.5 0o - 0.315 L2
Me-z= 0.5 0z + 0o - 0.375 A2
l"ls-o= 2 05 + 0a - 2
Mo-s= 0s + 2 06 + 2
l"le-3= 0.8 03 - O.48 A1
M:-s= 1.6 0: - 0.48 A1
Equilibrio de rotacional y de cortantes:
I"l1-7 1l'11-2 + Mr-s = 0
N12-1 +M2-3+NI2-6=6
M:-2 + l'13-9:6
!15-1 + MS-O : 0
NI6-5+t'{6-2=6
N14-s = 6
H7+Hg+H9:6
H1+H2=Q
El sistema que se forma es:

':.i;::l:,1":
5 1.2 0
t.2 5.4 l-
0 1 3.6
00.0
0.s 0 0
0 0.5 0
2,c v ¿.;
110
0 0.5
00
00
2.4 0
03
01
3.5 0
01
0
0.5
0
0
1
3
0
1
-0. 48 -0. 3?5 : 4
0 -0.37s i s
-0.48 0 i -9
-0.72 o , 0
0 -0.375 : 2
o -0.375',,-2
-3.36 0 i 0
0 -1 ' 0
0z = 1.80769
0< = -'1.08906
0o = -1.15031
92 = 1.98708
0r = 0.03746
0s = -3.48616
0s= 1.29225
91 = -3.63021
lng. ll. González V. @ 2007

Ejempl.o: Pórtico para graderia de campo deportivo
6.20
5.20
3.00
5.00
12.00
7.00
4.00
9.00
EI diagrama de desplazamientos
l-ateral de las barras de la
siguiente gráfico:
de f os nuclos
estructura se
y 1a traslación
muestran en el
119.44 r
4.2 Í.
4.4 r
1.5 T/m
6. 125 r
3.0 T/m

, : i.r¡l,:. :¡1:1:;,;','1,,-,r :-1:,, t':'. t;li ;
".ir:
: ':ri- :,i' r-'.
i :i::':i: ll
Rpuntes'í proHémas de Estiu¿turas H¡perestáiicas
A4
i':
42.é3
Siendo los apoyos de la estructura ernpotrados:
0s: oro:6ri = o
Las ecuaciones correspondientes para 1as barras son:
IVs-1 = 0.80t -0.4BAl -0.4842
lVll-9 = 1.601 - 0.4BAt - 0.48A2
M1-4 = 40t + 20¿ - 108
M¿-1 =20t+40¿+108
M1o-2=202-1.SLt
M2-'10 = 4oz-1.5L1
M1 1-3 = 3.2503 - 2.4375L1
M3-11=6.50¡-2.4375Lt
M2-3 = 202 + 93 -20.25
M3-2 = 0Z + 201+ 20.25

M2-4 = 302 + 1.50a-1.125L2
M4-2 = 1.502 + 30¿- 1 .125L2
M4-5 = 404+19g-26,
MS-4 = 204 + 405 -2L3
Ms-o ,= 3.50g + 1.7500 -0.75Á2.¡ 0.75a3
M6-3 = 1.7503 + 3.500 - 0.75Lá- 0.75as
M5-6 = 1.605 + 0.800 - 10.125
M6-5 =0.895 + 1.606 + 10.125
M5-7 = 805 + 49, -5.4545L¿
M7-s =405+807-5.4545&
M6-B = 206 +'lgU - 0.3571&
MB-6 ='106 + 2gu - 0.35714¿
M7-B = 3.55090t + 1.77550a- 67.50
MB-7 = 1.7755V + 3.55090s + 67.50
Eguilibrio rotacional de nudos:
Nudo 1:
5.6 01 + 20¿'-0.48 A1 - 0.48
^2
= 108
Nudo 2:
9 02 + $3 + '1'5 0¿ - 1.5 At - 1.125 L2 = 20-25
Nudo 3:
0z+ 12 03 + 1.75 0a-2.4375 A1 - 0.75 Lz-0.75 Ls= -20.25
Nudo 4:
Nudo 5:
201+ 1.5 02 + 1'l 04 + 205-1.125 Lz- 2A3 = -1gg
2 0a + ll.60s + 0.8 0o + 4 0z -2 M-5.4545 La,= 10.125
Nudo 6:
1.75 0s + 0.8 0s + 7.1 0o + 0a- 0.75 L2-0.7543-0.3571 Aa = -10.125
Nudo 7:
4 05 + l) 0z + 2 0e - 4.4545 A4 = 67.50
Nudo B:
0O + 2 0Z + 6 0g - 0.3571 L¿,= -67.50
lng. l.l. González V. @ 2007

Corte 1-1
Corte 2-2
C480j+i
üorte 3-3
0.8(tv'lr-g. lVls-r) * M2-10* M10-2 * M3-ll * M¡-g= 0
0.48 01 + 1.5 0z + 2.4315 03 - 2.1608 A1 - 0.1920 L2= O
Hg+Hz+Fls=0
28(Na'i-s* fvlg-l) + 35(l/lz-+ * Mq-z) + 20(Ms_o + trl6-3) = 0
1?5 e2 + 0.75 03 + 1.1250¿ + 0.75 06 - 0.192 A1 - 0.S638 A2 _0.2143:3= e
H4+fl3=g
7(M¿-s + Ms-a,) + 3(fvl3-6 + tv,l6-e) = 0
0.75 03 t'20¿ + 2 0s + 0.ZS 06 - 0.2143 A2- 1.5476 A3 = 0

Corte 4-4
Hs+H6=0
8.4(Ms-z + Mz-s) + 2.2(Mo-a + Me-o) = 0
5.4545 es + 0.3571 06 + 5.4545 e7 + 0.3571 0s - 5.0437 A4 = Q
Resclviendo ef sistema que se forma, 1as soluciones
momentos finales son:
e1 = 27.42281
oz= 7.35826
03 = -1.76809
04 = -20.72737
0s = 4.'15894
o6 = -o.ogo¿o
07 = 16.3701 1
eB = -15.33788
A1 = 9.26751
r2 = -6.Untr.
^3
= -22.51006
A4 = 21.06304
32.70
-4.03
IZ,JJ
-ro 6A
_ññ ?A
-7.30 24.07
lnq. N. González V. @ 2007

Analisis estructural

Más contenido relacionado

La actualidad más candente

Similar a Analisis estructural

Más de Masael Sanchez

Último

Analisis estructural