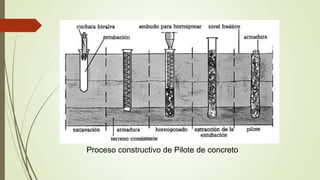
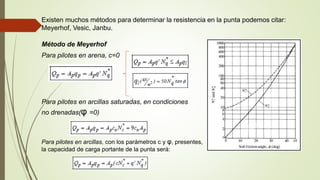
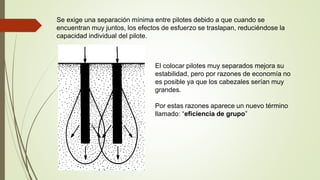
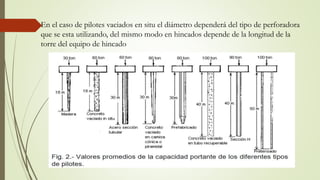
Este documento describe los tipos, clasificaciones, análisis y diseño de pilotes de fundación. Explica que los pilotes transmiten cargas estructurales a través de capas superficiales de suelo de baja capacidad de carga hacia estratos más profundos. Clasifica los pilotes según su material, mecanismo de transferencia de carga y método de instalación. Describe métodos para estimar la capacidad de carga última de pilotes incluyendo fórmulas, ensayos de carga y parámetros de suelo. Explica cómo calcular la capac

1. CAPACIDAD DE CARGA, ASENTAMIENTO, ANÁLISIS Y
DISEÑO ESTRUCTURAL DE PILOTES DE FUNDACION
 1. INTRODUCCION
Los pilotes son piezas relativamente largas y delgadas, construidas o insertadas dentro del terreno
para transmitir las cargas de la estructura a través del estrato de suelo de poca capacidad de carga
hacia estratos de suelo o roca más profundos y con una mayor capacidad de carga. Aunque este
no es el único factor, ya que la carencia de buenas condiciones de cimentación superficial puede
ser:
 Baja capacidad portante del subsuelo natural.
 Nivel alto de la capa freática que producirían elevados costos de agotamiento.
 Existencia de estratos de subsuelo de alta compresibilidad, como turbas y materiales de relleno
de reciente colocación que todavía no se han consolidado suficientemente.
 Subsuelos susceptibles de sufrir movimientos debidos a humedad o ruptura plástica.

2. Proceso constructivo de Pilote de concreto

3. 2. DESIGNACIONES
Con el objeto de uniformizar la notación para este capítulo se pone a consideración el
siguiente esquema con las designaciones de cada elemento que se manejará dentro del
capítulo.

4. 3. CLASIFICACIÓN DE PILOTES
La clasificación de los pilotes es diversa y varía según los parámetros con los que se
esté trabajando a considerar se dan algunas de estas clasificaciones.
3.1 SEGÚN EL MATERIAL DEL QUE ESTÁN CONSTITUIDOS.
Podrán ser divididos en:
a) pilotes de madera , usados en Europa con datos de hace no menos de 12000 años
b) pilotes de concreto
Fabricados “IN SITU”
Una gran parte de los pilotes de Hormigón que se constituyeron actualmente lo son “in
situ”, efectuando una perforación en el terreno y se rellena con HO fresco, que fragua
ya en su interior.

5.  b1) Pilotes Pretensados
Los Pilotes Pretensados se desarrollan a partir de los Pilotes de Hormigón Armado
elegidos principalmente por las grandes longitudes que pueden alcanzar.
c) pilotes de metálicos
El Pilote metálico utilizado en Europa por las características de trabajo, es de forma tubular,
acondicionamiento para soportar el ataque del agua de mar; caracterizado por alcanzar
grandes profundidades mediante la soldadura de partes.
d) pilotes compuestos.
Comparación de pilotes fabricados con diferentes materiales. En la tabla 4.1 se presenta un
resumen de los aspectos más importantes para diferentes tipos de pilotes tales como:
dimensiones usuales, valores recomendados de cargas permisibles, ventajas y desventajas
sobre el campo de su aplicación.

6.  3.2 SEGÚN EL MECANISMO DE TRANSFERENCIA DE CARGA AL
SUELO
Si el estrato de carga para los pilotes de la cimentación es de un material duro y relativamente
impenetrable, como roca o arena y grava muy densas, los pilotes derivan la mayor parte de su
capacidad de soporte de la resistencia del estrato a la punta de los pilotes. En estas condiciones,
se llaman pilotes de carga final o de punta. Por otro lado, si los pilotes no alcanzan un estrato
impenetrable, pero son llevados por alguna distancia hacia suelo impenetrable, su capacidad de
soporte se deriva en parte de la carga final y en parte de la fricción superficial entre la superficie
empotrada del pilote y del suelo adyacente. Los pilotes que obtiene su capacidad de soporte por
medio de fricción superficial o adhesión son llamados pilotes de fricción

7. 3.3. SEGÚN LA FORMA DE INSTALACIÓN DEL PILOTE EN EL SITIO
Los principales tipos de pilotes de uso general son los siguientes:
Pilote hincado. Unidades preformadas, usualmente de madera, concreto o acero, hincado
hacia el suelo mediante martillo.
Pilotes hincados y colados en sitio. Formados hincando un tubo, con una orilla cerrada hacia
el suelo y llenando el tubo con concreto. El tubo puede ser removido.
Pilotes de gato. Unidades de acero o concreto hincados en el suelo mediante gato hidráulico.
Pilotes perforados y colados en sitio. Pilotes formados perforando un orificio en el suelo y
llenándolo con concreto.
Pilotes mixtos. Combinaciones de dos o más de los tipos anteriores, o combinaciones de
diferentes materiales en el mismo pilote.

9. 4. ESTIMACION DE LA CAPACIDAD ULTIMA DE
CARGA EN PILOTES
Seleccionar el tipo de pilote a ser usado y estimar la longitud necesaria, es claramente
un trabajo nada fácil; Sin embargo a trabes de numerosas investigaciones, tanto teóricas
como experimentales, destinadas a predecir el comportamiento y la capacidad de carga
de los pilotes en suelos granulares y suelos cohesivos, y aunque el mecanismo no es
aun enteramente entendido y puede que nunca lo sea, estos estudios proveen un
valioso aporte a la resolución del problema de la determinación, de la capacidad ultima
del pilote.
La capacidad de carga portante ultima de un pilote esta dado por una simple ecuación

10. 4.1 PILOTES BAJO LA ACCIÓN DE UNA CARGA
En las primeras etapas, de la carga, el asentamiento es muy pequeño y se debe casi por
completo al movimiento elástico en el pilote y en el suelo adyacente.
Cuando la carga se elimina en un punto tal como “A” en la figura 4.9a, la cabeza del pilote
recobrara casi el nivel original
Al incrementarse la carga, la curva carga-asentamiento se escalona, y la liberación de
carga desde un punto B mostrará otra vez algún “rebote” elástico, pero la cabeza del
pilote no regresará a su nivel original indicando que ha tenido lugar una “deformación
permanente”
Cuando la carga llega al punto de falla C, el asentamiento se incrementa rápidamente
con muy poco aumento ulterior de la carga

11. En todos los casos en que los pilotes son soportados por completo por el suelo los pasos
para calcular las cargas permisibles del pilote son los siguientes:
Determinar el nivel de la base de los pilotes requerido para evitar un asentamiento excesivo del
grupo de pilotes.
Calcular el diámetro requerido de los pilotes
Examinar la economía en la variación del número y diámetros de los pilotes en el grupo para
sostener la carga total de la estructura.

12. 4.2. CAPACIDAD VERTICAL ÚLTIMA DEL SUELO.
La determinación de la carga vertical última del suelo puede ser resuelto por cuatro métodos distintos:
4.2.1. Formulas estáticas.
Se basan en teorías que determinan la capacidad de carga del suelo o roca a partir de
parámetros de resistencia e índice como Cohesión, Angulo de fricción, peso especifico, qu

13. 4.2.2. Ensayos de carga.
Método en principio bueno, resulta muy costoso y lento. Por estas razones, el número de
pilotes que se pueden ensayar suele ser pequeño, con lo cual su valor estadístico, cuando
el terreno no es homogéneo, es escaso.
4.2.3. Ensayos in Situ .
Su mayor inconveniente es su costo y el tiempo que necesitan para su realización.
4.2.4 Fórmulas de hinca (dinámicas).
Se basan en la energía transmitida al pilote por el impacto del martillo de hincado.

14. 4.3 CAPACIDAD DE CARGA PORTANTE EN LA PUNTA DEL PILOTE
El termino puede ser
despreciado ya que D es
relativamente pequeño.

15. Existen muchos métodos para determinar la resistencia en la punta podemos citar:
Meyerhof, Vesic, Janbu.
Método de Meyerhof
Para pilotes en arena, c=0
Para pilotes en arcillas saturadas, en condiciones
no drenadas(φ =0)
Para pilotes en arcillas, con los parámetros c y φ, presentes,
la capacidad de carga portante de la punta será:

16. Método de Vesic
' '1 2
( )
3
o
o
K
q


donde:
σo’ = esfuerzo efectivo normal medio del terreno al nivel de la punta
Ko = coeficiente de presión de tierra en reposo = 1 – senφ
Irr = índice de rigidez reducida para el suelo
Ir = índice de rigidez
Es = módulo de elasticidad del suelo
μs = relación de Poisson del suelo
Δ = deformación unitaria promedio en la zona plástica debajo la punta
* *
( 1)cotc qN N  
*
( )rrN f I 
1
r
rr
r
I
I
I

 
'
2(1 )( tan )
s
r
s
E
I
c q 

 

17. En arena densa o arcilla saturada (no existe cambio de volumen) :
0 rr rI I   
Para φ = 0 (condición no drenada) :
* 4
(ln 1) 1
3 2
c rrN I

   
Los valores de Ir se pueden estimar de acuerdo a la siguiente tabla:

18. Método de Janbu
Janbu (1976) propuso calcular Qp como sigue
Los factores de capacidad portante son calculados
asumiendo una superficie de falla en el suelo, en la
punta del pilote similar a la asumida en el dibujo del
gráfico
* ' *
( )p p p p c qQ A q A cN qN  
'
* 2 2 2 tan
(tan 1 tan ) ( )qN e  
   
* *
( 1)cotc qN N  
El ángulo η′ puede variar desde 70º en arcillas sueltas a
105º en suelos de arenas densas.

19. Método de J. Brinch Hansen
'
( )p p p p u c q c cQ A q A c N qN S d  
tan 2
6
4
( 1)cot
tan (45 )
2
1 (0.2 tan )
0.35
1
0.6
(1 7tan )
c q
q
c
c
b
N N
N e
D
S
l
d
D
L
 




 
 
  
 


donde:
Sc = factor de forma
dc = factor de profundidad
Tiene valores limite para:
20bL
D
bL  

20. 4.4 CAPACIDAD DE CARGA PORTANTE DEBIDA A LA RESISTENCIA
POR FRICCIÓN ENTRE EL SUELO Y EL PILOTE
Qf =ΣpΔLf
p = Perímetro de la sección del pilote
ΔL = Incremento de la longitud del pilote sobre la cual p y f se
mantienen constante
f = resistencia unitaria de fricción a una profundidad Z

21. Resistencia de fricción en arenas
f = K σ′vtanδ
K = coeficiente de presión de tierra
σv ′ = esfuerzo efectivo vertical a la profundidad bajo
consideración.
δ = ángulo de fricción entre el suelo y el pilote.
Dr = densidad relativa %
Ktanδ = 0.18 + 0.0065Dr
K = 0.5 + 0.008Dr
δ=de 0.5 φ a o.8 φ

22. Resistencia de fricción en arcillas
Método λ Qf = pLfav
Cu será igual
esfuerzo efectivo con la profundidad.

23. Método α

24. Método β
σv ′ = Esfuerzo efectivo vertical
β = K tan φ R
φ R = ángulo de fricción interna drenado, de la arcilla
remoldeada
K = coeficiente de presión de tierra
K senR= 1− φ (para arcillas normalmente consolidadas)
K = (1− senφ R ) OCR (para arcillas sobreconsolidadas)
para arcillas normalmente consolidadas
para arcillas sobreconsolidadas.

25. CONSIDERACIONES ESPECIALES PARA ESTIMAR LA CAPACIDAD
DE CARGA PORTANTE EN LA PUNTA DEL PILOTE
Capacidad de apoyo en suelos no cohesivos
Estimar la capacidad de carga sobre pilotes
SPT
PRUEBA DE CARGA
Esfuerzo efectivo al nivel de la punta del pilote
LC = 10D ; Para arenas sueltas.
LC = 15D ; Para arenas de densidad media.
LC = 20D ; Para arenas densas.

26. Método basado en la prueba de penetración standard (SPT).
Qp = Apqp = Apq'Nq
AP= Área de la punta del pilote
qP =Resistencia unitaria de la punta del pilote
q’ = Esfuerzo vertical efectivo al nivel de la punta del
pilote

27. Capacidad de apoyo en suelos cohesivos
NC: El factor de capacidad de carga, se puede considerar igual a 9, siempre y cuando el pilote
sea hundido al menos cinco diámetros dentro del estrato decarga.
cb : Esfuerzo de corte no drenado, en la base del pilote.
Ap: Área de la punta del pilote.
Para secciones Tubulares y Perfiles H, Ap debe ser considerada como la mitad del área bruta,
esto con el objeto de poder representar el aflojamiento posible, del tapón de arcilla sujeta a una
alta presión de carga.

28. 4.5. CAPACIDAD DE CARGA ADMISIBLE (PERMISIBLE)
EN PILOTES
Luego de obtener la capacidad de carga portante ultima del pilote, determinado por la suma
de la capacidad de carga portante de la punta del pilote más la capacidad de carga portante,
debida a la resistencia por fricción entre el pilote y el suelo, un razonable factor de seguridad
debe ser usado para obtener la capacidad de carga admisible para cada pilote, es decir:
𝑄 𝑎𝑑𝑚 =
𝑄 𝑢
𝐹𝑠
Donde:
𝑄 𝑎𝑑𝑚= capacidad de carga admisible del pilote.
𝑄 𝑢= capacidad de carga portante ultima del pilote
Fs = factor de seguridad
El factor de seguridad generalmente usado, esta entre 2.5 y 4 dependiendo del grado de
incertidumbre en el cálculo de la carga ultima

29. 4.6. COYLE Y CASTELLO (DISEÑO DE
CORRELACIÓN)
Coyle y Castelo (1981) analizaron 24 grandes extensiones de pruebas de carga en campo
de pilotes hincados en arena.
Para las arenas , la carga última puede ser expresada como:
𝑄 𝑢 = 𝑄 𝑝 + 𝑄 𝑓 = q’ 𝑁𝑞
∗ 𝐴 𝑝 + 𝑓𝑎𝑏 p L
Donde: 𝑞′= esfuerzo vertical efectivo en la punta del pilote
𝑓𝑎𝑏= resistencia de fricción promedio para el total del fuste , y puede ser expresado
como 𝑓𝑎𝑏= 𝑘 𝜎𝑣 𝑡𝑎𝑛𝛿
K = coeficiente de presión lateral del suelo
σ v ′= presión efectiva de sobrecarga, promedio
δ= ángulo de fricción entre el suelo y el pilote.

30. Basados en los estudios, el cálculo del valor e, del factor de capacidad portante (𝑁𝑞
∗) esta
correlacionado con la relación de. El gráfico 4.6. muestra los valores de 𝑁𝑞
∗ para varios
valores de la relación de empotramiento y ángulos de fricción del suelo. Note que 𝑁𝑞
∗
incrementa con L/D hasta un máximo valor y después decrece.

31. Llegamos a tener la fórmula:
𝑄 𝑈 = 𝑞′ 𝛮 𝑞
∗ 𝐴 𝑝 + 𝑝𝐿𝐾 𝜎𝑣 tan 0.8𝛷 Ec. 4.60
Usando el resultado de 24 pruebas de carga de pilotes, Coyle y Castelo mostraron que la
ecuación 4.60 puede predecir la carga ultima con una banda de error de.

32. 4.7. PILOTES SOBRE ROCA CON RESISTENCIA DE
PUNTA.
Algunas veces los pilotes alcanzan estratos de roca, en tales casos se debe
evaluar la capacidad de carga de la roca. El punto de resistencia unitaria última
en roca es aproximadamente:
𝑞 𝑝 = 𝑞 𝑢(𝑁 𝜙 + 1)
Donde:
𝑁 𝜙 = 𝑡𝑎𝑛2(45 +
𝜙
2
)
𝑞 𝑢 =esfuerzo de compresión no confinado de la roca
𝛷 = Angulo de fricción drenado

33. El esfuerzo de compresión no confinado de la roca puede determinarse con pruebas de
laboratorio de muestras recogidas durante la investigación de campo. Sin embargo se debe
tener mucho cuidado en la obtención del valor de porque las muestras son de pequeño
diámetro, y se ve que si el diámetro de la muestra se incrementa el valor de disminuye, para
muestra de diámetro más grande de 1 metro el valor de se mantiene mas o menos constante.
Este efecto de escala es causado principalmente por la distribución al azar de grietas y
rupturas progresivas a la largo de planos de deslizamiento. Por consiguiente siempre se
recomienda que:
𝑞 𝑢(𝑑𝑖𝑠𝑒ñ𝑜) =
𝑞 𝑢(𝑙𝑎𝑏𝑜𝑟𝑎𝑡𝑜𝑟𝑖𝑜)
5
Un factor de seguridad de al menos de 3 debe usarse para determinar la capacidad de carga
de estos pilotes entonces:
𝑄 𝑝(𝑎𝑑𝑚𝑖𝑠𝑖𝑏𝑙𝑒) =
(𝑞 𝑢 (𝑁 𝛷+1))𝐴 𝑃
𝐹𝑠

34. 4.8. CALCULO DE ASENTAMIENTOS.
* La verificación de los asentamientos para los estados de servicio en una estructura es
importante. Es así, que se deben verificar asentamientos totales y parciales para evitar
grandes deformaciones en las estructuras.
Cuando una estructura actúa sobre un suelo se producen los asentamientos inmediatos y de
consolidación.
* Los asentamientos son función de varios factores, tales como el tipo de suelo (granulares
o cohesivos), tipo de cimentación (rígida o flexible), estratificación del suelo, tipos de cargas
impuestas, etc.
* Los ensayos de laboratorio juegan un papel importante para la determinación de
parámetros de comportamiento del suelo, como los de consolidación, resistencia, elásticos,
etc. Entre los más utilizados para la estimación de los asentamientos están el ensayo de
penetración estándar (SPT) y el ensayo de penetración de cono (CPT).

35. 4.8.1. ASENTAMIENTO DE PILOTE AISLADO
El asentamiento de un pilote bajo una carga de trabajo vertical se debe a tres
factores:
𝒔 = 𝒔 𝟏 + 𝒔 𝟐 + 𝒔 𝟑
Donde:
S: Asentamiento total del pilote.
𝑠1: Asentamiento producido por la deformación axial del pilote.
𝑠2: Asentamiento causado por la carga en la punta del pilote.
𝑠3: Asentamiento causado por la carga transmitida a través del fuste del pilote.

36. 4.8.1.1 Determinación de 𝒔 𝟏 , asentamiento por la deformación axial del
pilote.
Si el material del pilote de asume como elástico, la deformación de pilote puede evaluarse
utilizando los principios fundamentales de la mecánica de materiales:
𝑠1 =
𝑄 𝑤𝑝 + 𝜉𝑄 𝑤𝑠 𝐿
𝐴 𝑃 𝐸 𝑝
donde:
𝑄 𝑤𝑡 = carga soportada en la punta del pilote bajo carga de trabajo
𝑄 𝑤𝑠 = carga soportada por friccion superficial bajo carga de trabajo
𝐴 𝑝= Area de la sección del pilote
L= longitud del pilote
𝐸 𝑝 = módulo de elasticidad del material
La magnitud de ξ dependerá de la naturaleza de la resistencia unitaria de fricción
(superficial) a lo largo del pilote. Si la distribución de es uniforme o parabólica, como se
muestra en la figura 4.18 ξ = 0.5, sin embargo, para una distribución triangular de ξ la
magnitud de ξ = 0.67.

37. Tipos de distribución de resistencia friccional a través del fuste
del pilote
(Braja M.Das, pag. 615, 1999)

38. 4.8.1.2 Determinación de 𝒔 𝟐, asentamiento causado por la carga en la punta del
pilote.
El asentamiento de un pilote ocasionado por la carga soportada en la punta del pilote puede
ser expresada en forma similar a la de una fundación superficial.
𝑠2 =
𝑞 𝑤𝑝 𝐷
𝐸𝑠
1 − 𝑢 𝑠
2
𝐼 𝑤𝑝
Donde:
D= ancho o diámetro del pilote
𝑞 𝑤𝑝 = Carga puntual por unidad del área de la punta del pilote =
𝑄 𝑤𝑝
𝐴 𝑝
𝑢 𝑠= Coeficiente de poisson del suelo
𝐼 𝑤𝑝 = Factor de influencia

39. Para propósitos prácticos 𝐼 𝑤𝑝 es igual a 𝛼 𝑟 y calcularse del gráfico 6.9

40. En ausencia de otros resultados experimentales los valores del coeficiente de poisson
pueden ser obtenidos de la tabla 4.4
Vessic propuso un método semi-empírico para obtener la magnitud de 𝑠2
𝑠2 =
𝑄 𝑤𝑝 𝐶 𝑝
𝐷𝑞 𝑝
donde: 𝑞 𝑝 = Resistencia ultima del pilote
𝐶 𝑝= Coeficiente empírico

41. valores representativos de 𝐶 𝑝 para varios suelos se da en la tabla 4.5

42.  4.8.1.3 Determinación de s3 , asentamiento debido a la carga
transmitida a lo largo del fuste del pilote .
 El asentamiento de un pilote debido la carga soportada por el mismo esta dado por una
ecuación similar
𝑠3 =
𝑄 𝑤𝑠
𝑝𝐿
𝐷
𝐸𝑠
(1 − 𝑢 𝑠
2)𝐼 𝑤𝑠
Donde:
p= perímetro del pilote
L= longitud embebida del pilote
𝐼 𝑤𝑠= Factor de influencia
Observe que el término de
𝑄 𝑤𝑠
𝑃𝐿
es el valor promedio de la fricción a lo largo del pilote. El valor de
𝐼 𝑤𝑠 es una relación empírica dada por:
𝐼 𝑤𝑠 = 2 + 0.35
𝐿
𝐷

43. El asentamiento por consolidación de un grupo de pilotes en arcilla se
estima aproximadamente usando método de la distribución de esfuerzo 2:1
El procedimiento para estimar el asentamiento consta de los siguientes
pasos:
4.8.2. ASENTAMIENTO POR CONSOLIDACIÓN DE UN GRUPO DE
PILOTES
1. Se debe calcular la presión ejercida
sobre el grupo de pilotes, Qg.
2. Se asume que la carga, Qg, es
transmitida al suelo a una
profundidad de 2L/3 de la parte
superior del pilote, como se muestra
en la figura
La carga se expande a lo largo de
líneas con una proporción de 2
verticalmente : 1 horizontalmente
desde esta profundidad.

44. 3. Calculamos el incremento de
esfuerzos causados a la mitad de cada
estrato de suelo por la carga Qg.

45. 4. Se calcula el asentamiento de cada capa causada por el incremento de
esfuerzo, como:





 

0
)1(0
log*
P
PP
Ce c
5. El asentamiento total de consolidación del grupo de pilotes se
calcula como:

46. *Cuando se conoce la curva de presión-índice de vacíos de un ensayo de odómetro, índice
de compresión, índice de expansión e índice de vacíos puede calcularse el asentamiento
unidimensional de consolidación.
)log(
1 c
o
o
cc
p
Pp
e
HC
S




*Para arcilla sobreconsolidada :po+Δpprom<pc
*Para arcilla normalmente consolidada:
)log(
1 c
promo
o
cs
c
p
Pp
e
HC
S




*Para arcilla sobreconsolidada :po<pc<po+Δpprom
)log(
1
log
1 c
promo
o
cc
o
c
o
cs
c
p
Pp
e
HC
p
p
e
HC
S






po=presión efectiva promedio en la capa de arcilla antes de la construcción de la fundación
Δpprom=incremento promedio de la presión en la capa de arcilla debido a la construcción de la fundación
pc=presión de preconsolidación
eo=índice de vacíos de inicial de la capa de arcilla
Cc= indice de compresión
Cs=índice de expansión
Hc=espesor de la capa de arcilla
4.8.3. ASENTAMIENTO DE CONSOLIDACIÓN

47. *Δp sobre la capa de arcilla no es constante con la profundidad,
decrece según la profundidad va incrementándose.
*El incremento promedio de presión se obtiene como: )4(
6
1
bmt PPPS 
Donde:
Δpt=Incremento e presión en la parte superior de la capa de arcilla
Δpm=Incremento e presión en la parte media de la capa de arcilla
Δpt=Incremento e presión en la base de la capa de arcilla
Sskempton y Bjerrum proponen la siguiente fórmula: oedgc  
Donde:
μg=coeficiente depende del tipo de arcilla
ρoed=Asentamiento calculado basado en las pruebas de odómetro

48. μg puede calcularse experimentalmente pero para fines prácticos se establece la
siguiente tabla:
El asentamiento por odómetro de una capa de suelo se establece como:
Hm zvoed  Donde:
mv: Coeficiente promedio de compresibilidad por volumen obtenido para el
incremento efectivo de la presión en la capa considerada.
σz=Esfuerzo vertical efectivo promedio impuesto en la capa particular resultante
de la presión neta de la cimentación qn.
H: Espesor de la capa
***El asentamiento de consolidación= ρoed+ρc

49. *Se pueden obtener valores para mz de la siguiente tabla:
*Se debe corregir los asentamientos de consolidación para tomar
en cuenta la profundidad de la cimentación.

50. *Se debe aplicar un factor de corrección a ρc mediante las curvas de corrección
establecidas por Fox, aplicable solo en asentamientos inmediatos
ASENTAMIENTO FINAL
Se establece como la suma de los asentamientos corregidos tanto inmediato como de
consolidación:
cif  

51. 4.9. GRUPO DE PILOTES
Generalmente los pilotes se colocan en grupos, y los mecanismo de falla son
diferentes a los de un pilote, el trabajo del grupo depende del tipo de suelo,
de la separación entre los pilotes y la forma de ejecución de los mismos.

52. Se exige una separación mínima entre pilotes debido a que cuando se
encuentran muy juntos, los efectos de esfuerzo se traslapan, reduciéndose la
capacidad individual del pilote.
El colocar pilotes muy separados mejora su
estabilidad, pero por razones de economía no
es posible ya que los cabezales serían muy
grandes.
Por estas razones aparece un nuevo término
llamado: “eficiencia de grupo”

53. CARGA ULTIMA DE APOYO PARA GRUPO DE PILOTES
Todas las formulas propuestas para el calculo de la eficiencia están basadas en intuición y
se tienen pocos datos para solventarlas (Coduto 2000). No obstante en la práctica se suele
usar la Fórmula de Converse – Labarre, propuesta por Bolín(1941), presentada en la sgte
figura:
 ziQunziQgu ,*,
Donde: Qgu = carga ultima de apoyo del grupo de
pilotes a una profundidad zi
Qu = carga ultima de apoyo del pilote sin
efecto de grupo a una profundidad zi

54. Dcde *02.0*5,2  Dc = Longitud enterrada del
pilote
Por razones de economía y construcción se recomienda “e” entre 2,5
a 3,5 veces el diámetro de los pilotes aislados.
CARGA MÁXIMA SEGURA DE APOYO
FS
ziQgu
ziQs
,
, 
De Rutier y Beringen plantean un factor de seguridad global para cargas
estáticas y condiciones óptimas de ejecución igual a 2,0
El espaciamiento entre pilotes no debe ser menor a la distancia calculada en la
siguiente ecuación:

55. 4.9.1. EFICIENCIA DEL GRUPO
Donde:
n= eficiencia de grupo
Qg(u)= capacidad última de carga del grupo de pilotes
Qu= capacidad ultima de carga de cada pilote sin el efecto de grupo.

56. Método simplificado para obtener la eficiencia del grupo de pilotes de
fricción, en arena.
Partimos de la gráfica:

57. Dependiendo del espacio dentro del grupo pueden actuar de 2 maneras:
 Como un bloque donde la capacidad por fricción es:
Donde: f prom.=resistencia por fricción unitaria promedio
Pg = perímetro de la sección del bloque
 Como pilotes individuales: donde la capacidad por fricción es:

58. Donde: f prom = Resistencia por fricción unitaria.
P = perímetro de la sección transversal de cada pilote.
Remplazando en la ecuación de la eficiencia tenemos:
Simplificando:

59. En caso de que la eficiencia sea mayor o igual a la unidad los
pilotes se comportan como pilotes individuales.
Para el caso en que sea menor que la unidad tenemos:
Existen varias otras ecuaciones propuestas por diferentes autores para la
eficiencia de grupos de pilotes:

60. 4.9.2. GRUPO DE PILOTES EN ARENAS
Basados en observaciones experimentales de un grupo de pilotes
se puede decir:
• Para pilotes hincados con d > 3D, Qg(u) puede tomarse como
ΣQu que incluye la resistencia por fricción y por punta para los
pilotes individuales.
• Para pilotes taladrados en arena con espacios convencionales
(d ≈ 3D), Qg(u) puede tomarse como 2/3 a 3/4 veces ΣQu
(resistencias de punta y fricción de cada pilote)

61. 4.9.3. GRUPO DE PILOTES EN
ARCILLASLa capacidad última de carga de un grupo de pilotes en arcilla se puede
estimar determinando:

62. Donde: Cu(p)= cohesión no drenada de la arcilla en la punta del pilote.
Remplazando tenemos:
Donde α= factor empírico de adhesión en arcillas normalmente consolidadas
p= perímetro del pilote.

63. Determinamos la capacidad última asumiendo que los pilotes del grupo actúan
como un bloque de dimensiones Lg x Bg x L la resistencia superficial del
bloque es:
Se calcula la capacidad de carga en la punta:
Se obtiene el valor del el factor Nc de las siguiente gráfica:
Nc = factor de capacidad de carga.
qp =resistencia unitaria en la punta del pilote
Cu = resistencia ultima al corte
Donde:

64. entonces la carga última es:
• Comparar los valores obtenidos en los pasos
anteriores y elegimos el menor valor de Q g (u).
Ecuación 2

65. 4.9.4. PILOTES EN ROCA
Para pilotes de punta descasando sobre roca la mayoría de los
códigos especifican que:
Siempre tomando en cuenta que la distancia mínima centro a centro
de los pilotes sea D+30 cm.

66. En el caso de pilotes vaciados en situ el diámetro dependerá del tipo de perforadora
que se esta utilizando, del mismo modo en hincados depende de la longitud de la
torre del equipo de hincado

67. EJERCICIO PILOTE AISLADO
Un pilote de concreto hincado en arcilla tiene un diámetro de 400mm.
a) Calcular la capacidad ultima de carga en la punta del pilote
b) Calcular la resistencia por fricción para todos los estratos de arcilla, por distintos
métodos para los estratos de arcilla φr=30, los 10 primeros metros están
normalmente consolidados, el estrato inferior tiene un OCR de 2:
c) Determine el asentamiento del pilote para Ep=210 Mpa
d) Estimar la capacidad admisible neta del pilote para un FS=4
e) determinar la eficiencia y la capacidad ultima de carga para un grupo de pilotes
f) determinar el asentamiento del grupo de pilotes
g) Calcular el refuerzo longitudinal y transversal de acero

68. Se cuenta con los siguientes datos del suelo.
H= 5 mts.
Ps= 18 KN/m3
C= 30 KN/m2
φ= 0 °
Pa= 0 KN/m3
H= 5 mts.
Ps= 18 KN/m3
C= 30 KN/m2
φ= 0 °
Pa= 9,81 KN/m3
H= 20 mts.
Ps= 19,6 KN/m3
C= 100 KN/m2
φ= 0 °
Pa= 9,81 KN/m3
Estrato 1(Arcilla)
Estrato 2(Arcilla)
Estrato 3(Arcilla)

69. 1. CALCULO DE LOS ESFUERZOS EFECTIVOS DEL SUELO.
N° H(mts) Esf.Suelo Es.Efectivo
1 0 0 0 0
2 5 90 0 90
3 5 180 49,05 130,95
4 20 572 245,25 326,75
𝐴𝑝 =
𝜋
4
∗ 𝐷2
= 0,126 𝑚2
𝑃 = 𝜋 ∗ 𝐷 = 1,257 𝑚𝑡𝑠
2. CALCULO DEL AREA Y PERIMETRO.

70. 3. CALCULO DE LA CAPACIDAD ULTIMA DE CARGA EN LA PUNTA
DEL PILOTE.
a) METODO DE MEYERHOF
Para arcillas saturadas en condiciones no drenadas donde angulo de friccion φ=0
𝑄 𝑝 = 𝑁𝑐
∗ ∗ 𝐶 𝑢 ∗ 𝐴 𝑝 Del grafico encontramos el valor de Nc
𝑄 𝑝 = 9 ∗ 𝐶 𝑢 ∗ 𝐴 𝑝
Cu= cohesión en condición no drenada del suelo debajo
la punta
Ap= Área transversal del pilote.
Cu= 100 KN/m2
Ap= 0,126 m2. 𝑄 𝑝 = 9 ∗ 𝐶 𝑢 ∗ 𝐴 𝑝 = 113,08 𝐾𝑁

71. b) METODO DE J. BRINCH HANSEN
𝑄 𝑝 = 𝐴 𝑝 ∗ 𝑞 𝑝 = 𝐴 𝑝 ∗ 𝐶 𝑢 ∗ 𝑁𝑐 + 𝑞′ ∗ 𝑁𝑞 ∗ 𝑆𝑐 ∗ 𝑑 𝑐 =
factor de capacidad de carga
factor de capacidad de carga
Factor de forma
𝑁𝑞 = 𝑒 𝜋 tan 𝜃 tan 45 +
𝜃
2
2
= 1
𝑁𝑐 = 𝑁𝑞 − 1 ∗ cot 𝜃 = 0
𝑆𝑐 = 1 + 0,2 + tan 𝜃6
𝐷
𝑙
= 1,2
Factor de profundidad 𝑑 𝑐 = 1 +
0,35
𝐷
𝐿 𝑏
+
0,6
1 + 7 tan 𝜃4
= 1,22
para pilotes :
𝐷
𝑙
= 1
𝑄 𝑝 = 𝐴 𝑝 ∗ 𝑞 𝑝 = 𝐴 𝑝 ∗ 𝐶 𝑢 ∗ 𝑁𝑐 + 𝑞′ ∗ 𝑁𝑞 ∗ 𝑆𝑐 ∗ 𝑑 𝑐 = 60,05 𝐾𝑁
Esfuerzo efectivo vertical en a punta q’=326,75 Cohesión Cu=100

72. c) METODO DE VESIC
Vesic en 1977 propuso un método para estimar la capacidad de carga de punta en pilote con base en
la teoría de expansión de cavidades. Basada en parámetros de esfuerzos efectivos.
𝑄 𝑝 = 𝐴 𝑝 ∗ 𝑞 𝑝 = 𝐴 𝑝 ∗ 𝑐 ∗ 𝑁𝑐 + 𝜎′ ∗ 𝑁 𝜎
Esfuerzo efectivo normal medio del terreno a nivel de la
punta
𝜎′ =
1 + 2𝑘 𝑜
3
𝑞′ = 326,75
Coeficiente de presión de tierra en reposo 𝑘 𝑜 = 1 − sin 𝜃 = 1
Para los valores de factores de carga se utilizara el Abaco
De acuerdo con la teoría de Vesic tenemos
𝐼𝑟𝑟 =
𝐼𝑟
1 + 𝐼𝑟∆
Ir =Indice de rigidez
Irr =Indice de rigidez reducida para el suelo
∆= deformacion unitaria promedio en la zona plastica debajo la punta

73. en arenas densas o arcillas saturada no existe cambio de volumen.
∆= 0 𝐼𝑟𝑟 =
𝐼𝑟
1 + 𝐼𝑟∆ 𝐼𝑟𝑟 = 𝐼𝑟
Los valores de Ir se pueden estimar de acuerdo a la siguiente tabla:
Tabla extraida texto Bowles
De la tabla tenemos los valores de:
𝑁𝑐 =10,04 𝑁 𝜎 =1
𝑄 𝑝 = 𝐴 𝑝 ∗ 𝑞 𝑝 = 𝐴 𝑝 ∗ 𝑐 ∗ 𝑁𝑐 + 𝜎′ ∗ 𝑁 𝜎
𝑄 𝑝 = 167,23 𝐾𝑁

74. Calculamos el promedio de lo métodos utilizados
𝑄 𝑝=113,458 KN
Método de Meyerhof 𝑄 𝑝 = 113,08 𝐾𝑁
Método de J.Brinch Hansen 𝑄 𝑝 = 60,05 𝐾𝑁
Método de Vesic 𝑄 𝑝 = 167,23 𝐾𝑁
4. CALCULO DE LA RESISTENCIA AL FUSTE.
a) METODO ALFA (α)
𝑄𝑠 = 𝛼 ∗ 𝐶 𝑢∗ 𝑃 ∗ ∆𝐿
Qs=Resistencia al fuste
Cu=Cohesion
P=Perímetro del pilote
L=Variación profundidad
Coheficiente experimental de adhesión

75. Del abaco :
𝑄𝑠 = (1 ∗ 30 ∗ 1,275 ∗ 5)+(1*30*1,275*5)+(0,5*100*1,275*20)=1633,632 KN
para arcillas normalmente consolidadas
con C<50 kN/m2 alfa=1
Cu=30
Cu=30
Cu=100
α1= 1
α2= 1
α3= 0,5

76. b) METODO β
para estratos normalmente consolidados:
Para estratos sobre consolidados:
K= coeficiente de presión de la tierra
ØR=Angulo de fricción drenada de la arcilla
esfuerzo vertical efectivo (a la mitad del estrato)
P= perímetro
Los primeros dos estratos se encuentran normalmente consolidados:
𝑓1 = 1 − sin 30 ∗ tan 30 ∗
0+90
2
= 12,99 KN/m2
𝑓2 = 1 − sin 30 ∗ tan 30 ∗
90+130,95
2
=31,89 KN/m2
estrato 1
estrato 2

77. el tercer estrato es sobre consolidados:
𝑓3 = 1 − sin 30 ∗ tan 30 ∗ 2 ∗
130,95+326,75
2
=93,43 KN/m2
La resistencia al fuste:
Qs=2630,099 KN
C) METODO λ VIJAEYVERGIYA Y FOCHT 1972
𝑄𝑠 = 𝑝𝐿𝑓𝑝𝑟𝑜𝑚 𝑓𝑝𝑟𝑜𝑚 = 𝜆 𝜎𝑣
′ + 2𝐶 𝑢
Para un pilote de L= 30 Mts λ=0,14
Del Abaco tenemos un valor aproximado de λ

78. Calculamos el valor promedio de Cu 𝐶 𝑢 =
1
𝐿
𝐶 𝑢𝑖 𝐿𝑖 = 76,67
Calculamos el área formada por los esfuerzos efectivos
A1=225
A2=552,38
A3=4577
Calculamos el valor promedio del esfuerzo efectivo
𝜎𝑣
′ =
𝐴𝑖
𝐿
= 178,48 𝐾𝑁/𝑚2
Reemplazando valores : 𝑓𝑝𝑟𝑜𝑚 = 𝜆 𝜎𝑣
′ + 2𝐶 𝑢 =46,45 KN/m2
𝑄𝑠 = 𝑝𝐿𝑓𝑝𝑟𝑜𝑚 = 1751,27 𝐾𝑁
Los valores de resistencia al fuste por el metodo alfa y metodo λ son similares y se
puede obtener un promedio:
𝑄𝑠 =
𝑄𝑠−𝛼 + 𝑄𝑠−𝜆
2
= 1692,45 𝐾𝑁

79. 5. Determine el asentamiento del pilote para Ep210Mpa.
El asentamiento de un pilote bajo carga de trabajo vertical es causado por
3 factores.
𝑆𝑡 = 𝑆1 + 𝑆2 + 𝑆3
S1= asentamiento elastico delpilote
S2= Asentamiento delpilotecausado por la carga en la punta
S3= Asentamiento causado por la carga transmitada a lo largo delfustedelpilote
Si el material se considera elastico la deformacion del fuste se evalua usando los pprincipios
fundamentales de la mecanica de materiales:
S1=14,18 mm
Qwp= 113,4585 Carga en la punta del pilote bajo condicon de carga de trabajo KN
Qws= 1692,451 Carga por resistencia de friccion superficial bajo condicion de carga de trabajo KN
Ap= 0,126 area de la seccion transversal del pilote M2
L= 30 Longitud del pilote Mts
Ep= 21000000 Modulo de elasticidad del material del pilote. KN/m2
ε= 0,67 Depende de la resistencia por friccion unitaria a la largo del fuste. Vesic.

80. Asentamiento de un pilote causado por la carga en la punta, similar a la de cimentacion
superficial.
𝑆2 =
𝑞 𝑤𝑝 𝐷
𝐸𝑠
1 − 𝜇 𝑠
2 𝐼 𝑤𝑝 = 10,74 𝑚𝑚.
qwp= 902,874 Carga puntal por area unitaria en la punta del pilote Qwp/Ap
D= 0,4 Diametro del pilote
Es= 24000 Modulo de elasticidad del suelo KN/m2
u= 0,4 Relacion de poisson del suelo arcilloso entre 0,4-0,5
Iwp 0,85 Factor de influencia

81. Vesic desarrolla una formula mas simple donde interviene un coeficiente Cp.
S2=9,42 mm.

82. Asentamiento de un pilote causado por la carga llevada en el fuste :
𝑆3 =
𝑄 𝑤𝑠
𝑝𝐿
𝐷
𝐸𝑠
1 − 𝜇 𝑠
2
𝐼 𝑤𝑠 = 3,16 𝑚𝑚.
Qws= 1692,451 Carga por resistencia de friccion superficial bajo condicion de carga de trabajo KN
D= 0,4 Diametro del pilote
p 1,257 Perimetro del pilote
L= 30 Longitud empotrada del pilote
u= 0,4 Relacion de poisson del suelo arcilloso entre 0,4-0,5
Iws 5,031089 Factor de influencia
Es= 24000 Modulo de elasticidad del suelo KN/m2
𝐼 𝑤𝑠 = 2 + 0,35
𝐿
𝐷
= 5,03
Asentamiento total:
𝑆𝑡 = 𝑆1 + 𝑆2 + 𝑆3 =28,08 mm

83. Verificamos estos asentamientos de acuerdo a la tablas de Bowles.

84. EJERCICIO GRUPO DE PILOTES.
1.DETERMINACION DEL NUMERO DE PILOTES
#𝑝𝑖𝑙𝑜𝑡𝑒𝑠 =
𝐶𝑀+𝐶𝑉 ∗𝐾
𝑃 𝑢
=5,5 usaremos 6 pilotes
CM,CV= Cargas permanentes
K= Coheficiente que reemplaza al peso propio de la zapata K=1,1
Pu=Carga de trabajo del pilote (tabla)
CM= 300
CV= 50
K= 1,1
Pu= 70

85. 2. DETERMINACION DE LA SEPARACION ENTRE PILOTES.
CONFIGURACION GEOMETRICA DE LA CIMENTACION:
La disposición geométrica de una cimentación por pilotes se realizara tanteando diferentes
disposiciones de pilotes hasta alcanzar una situación optima.
Los datos geométricos de mayor interés para analizar el comportamiento de un pilote aislado
son la longitud dentro el terreno y su diámetro, o la ley de variación de su diámetro si es que este
no fuera constante.
En los grupos de pilotes será necesario tener en cuenta además su distribución geométrica en
particular su separación.
Disposición de los pilotes según varios autores para suelos arcillosos.
La separación entre pilotes será de acuerdo a la siguiente figura
de Liu y otros 1985:
Separacion 1: S1 = 3*D = 1,2 Mts
Separacion 2: S2 = 1,5*D= 0,6 Mts

86. La eficiencia puede estimarse por diversas formulas empiricas entra las que tenemos:
𝜂 =
𝑄 𝑔(𝑢)
𝑄 𝑢
Qg(u) = Capacidad ultima de carga del grupo de pilotes.
Qu = Capacidad ultima de carga de cada pilote sin efecto del
grupo.
Ecuacion Converse-Labarre:
𝜂 = 1 −
𝑛−1 𝑚+ 𝑚−1 𝑛
90𝑚𝑛
tan−1 𝐷
𝑑
= 0,76
D= 0,4 Diametro del pilote Mts.
d= 1,2 separacion entre pilotes Mts
m= 3 numero de pilotes por fila
n= 2 numero de pilotes por columna

87. Ecuacion Los angeles Group Action:
𝜂 = 1 −
𝐷
𝜋𝑑
𝑛−1 𝑚+ 𝑚−1 𝑛+ 2(𝑚−1)(𝑛−1)
𝑚𝑛
=0,83
D= 0,4 Diametro del pilote Mts.
d= 1,2 separacion entre pilotes Mts
m= 3 numero de pilotes por fila
n= 2 numero de pilotes por columna

88. 4. CALCULO DE LA CAPACIDAD ULTIMA DE CARGA DE UN GRUPO
DE PILOTES EN ARCILLA SATURADA
La capacidad ultima de carga de un grupo de pilotes se estima de la siguiente
manera
𝑄 𝑢 = 𝑛𝑚 𝑄 𝑝 + 𝑄𝑠 =
Resistencia en la punta por metodo de Meyerhoof
𝑄 𝑝 = 𝑁𝑐
∗ ∗ 𝐶 𝑢 ∗ 𝐴 𝑝 = 1133,10 𝐾𝑁
Cu= 100 KN/m2
Ap= 0,13 m2.
Resistencia en el fuste por metodo de Alfa
𝑄𝑠 = 𝛼 ∗ 𝐶 𝑢∗ 𝑃 ∗ ∆𝐿
Qs = (1 ∗ 30 ∗ 1,275 ∗ 5)+(1*30*1,275*5)+(0,5*100*1,275*20)=1633,632 KN
Reemplazando en la formula: 𝑄 𝑢 = 10480,4𝐾𝑁

89. 2. Suponiendo que los pilotes del grupo actuan como un bloque con dimensiones
Lg*Bg*L
Lg= 2,8 Mts
Bg= 1,6 Mts
L= 30 Mts
𝐿 𝑔
𝐵𝑔
= 1,75
𝐿
𝐵𝑔
= 18,75
Con esos valores ingreasamos al abaco para encontrar el valor de Nc
Nc= 8,5
Cu= 30
Cu= 30
Cu= 100
FS= 4

90. 𝑄 𝑢 = 𝐿 𝑔 𝐵𝑔 𝑐 𝑢𝑝 𝑁𝑐
∗ + 2 𝐿 𝑔 + 𝐵𝑔 𝑐 𝑢 𝐿 = 24048,00 𝐾𝑁
Elegimos el menor valor:
𝑄 𝑢 = 10480,4𝐾𝑁 𝑄 𝑢 = 24048,00 𝐾𝑁
A partir de este valor y con el factor de seguridad podemos determinar e capacidad
admisible.
𝑄 𝑎𝑑𝑚 =
𝑄 𝑢
𝐹𝑆
= 2620,094 𝐾𝑁

91. 4. CALCULO DEL ASENTAMIENTO POR CONSOLIDACION DEL
GRUPO DE PILOTES.
El procedimiento de calculo implica los siguientes pasos:
1. Los pilotes se encuentran a una profundidad L y sometido a una carga total que representa
la carga total de la superestructura sobre los pilotes.
2. Suponemos que la Carga Qg es transmitida al suelo comenzando a una profundidad de 2L/3
desde la parte superior del pilote.
L= 30 Mts.
L1= 20 Mts
Qg= 10480,4 KN
L2= 10 Mts
Lg= 2,8 Mts
Bg= 1,6 Mts
Z1= 20 Mts

92. 3. Calculamos el incremento del esfuerzo causado a la mitad de cada estrato de suelo
por la carga Qg.
∆𝜎1
′
=
𝑄 𝑔
(𝐿 𝑔 + 𝑍1)(𝐵𝑔 + 𝑍1)
= 21,28 𝐾𝑁/𝑚2
4. Calculamos el asentamiento de cada estrato causado por el esfuerzo incrementado:
∆𝑆1
′
=
𝐶𝑐 𝐻
1 + 𝑒0
∗ 𝑙𝑜𝑔
𝑝 𝑜 + ∆𝜎
𝑝 𝑜
= 0,035 𝑀𝑡𝑠
e= 0,82 Indice de vacios
Cc= 0,2 Indice de compresion del suelo
Po= 424,65 Esfuerzo efectivo en la mitad del estrato
H= 20 Espesor del estrato
21,28
5. El asentamiento total por consolidacion del grupo de pilotes es entonces.
∆𝑆1
′
= 35 𝑚𝑚.