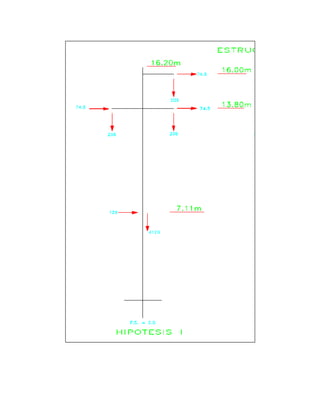
Este documento presenta cálculos para determinar las fuerzas en los soportes de una línea de transmisión de 60 kV. Calcula distancias mínimas, fuerzas del viento, pesos y ángulos de oscilación. Luego determina los momentos flectores y fuerzas equivalentes bajo tres hipótesis de carga para concluir que se requiere un poste de concreto armado de 18m de longitud y una capacidad de carga de 600kg.

1. EJEMPLO DE CALCULO DE FUERZAS EN SOPORTES
Sea una Línea de Transmisión en 60 kV, cuyos elementos tienen las características siguientes:
Conductor : Cobre duro. Peso Unitario : 620 kg/km
Diámetro total : 10.75 mm Tiro de Rotura : 2753 kg
Sección : 70 mm
2
.
Por otra parte del cálculo mecánico del conductor se obtienen los datos siguientes:
Flecha máxima : 3.8 m Tiro Máximo del Conductor : 645 kg
Presión del Viento : 24 kg/m
2
Longitud Cadena : 1.10m
Peso de la cadena : 50 kg Fuerza del viento sobre cadena : 10 kg
Por otra parte, con fines de cálculo tomaremos los datos:
Vano viento = vano Peso = 250m
Se requiere realizar los cálculos de los soportes, los mismos que serán de concreto armado y
centrigudado (CAC). La fotografía muestra un típico p
oste de concreto de 18.0m y su cimentación
pre fabricada, los mismos que fueron instalados en la Línea de Transmisión en 60 kV Subestación
Huacho Nueva (ETECEN) – Andahuasi (ADINELSA)

2. i
SOLUCION:
Distancias Mínimas:
Conductor a tierra:
)
0
.
6
(
150
3
.
5
min m
mínimo
U
d N
=
+
=
siendo UN es la Tensión Nominal en kV
m
d
d 0
.
6
7
.
5
150
60
3
.
5 min
min =
→
=
+
=
Conductor a Soporte:
)
5
.
0
(
150
1
.
0
min m
mínimo
U
d N
=
+
=
m
d 5
.
0
150
60
1
.
0
min =
+
=
Distancia Vertical entre conductores:
c
f
k
d λ
+
= max
el valor de k puede ser obtenido de la tabla adjunta.
Si consideramos que la cadena de aisladores no deberá
oscilar mas de 40°, y en razón que la Tensión Nominal
del cálculo es de 60 kV, obtenemos el valor k = 0.6
l
lc = 1.10, es la longitud de la cadena.
En consecuencia:
m
f
k
d c 329
.
1
1
.
1
8
.
3
6
.
0
max =
+
=
+
= λ
Cálculo del ángulo de oscilación de la cadena, con fines de cálculo de la longitud mínima de la
cruceta que suspende la cadena:
( )
a
c
va
vc
w
w
F
F
i
tg
5
.
0
5
.
0
+
+
=
Fuerza unitaria que provoca el viento sobre el conductor:
m
kg
p
w c
v
v /
258
.
0
1000
75
.
10
24
1000
=






=






=
φ

3. Entonces la Fuerza del viento sobre el conductor es:
kg
x
a
w
F v
v
vc 5
.
64
250
258
.
0 =
=
=
Peso (kg) del conductor que soporta la cadena:
( )( ) ( )( ) kg
m
m
kg
a
m
kg
w p
c 155
250
/
620
.
0
/
620
.
0 =
=
=
Por tanto el ángulo de oscilación d e la cadena es:
( ) °
=
→
+
+
=
+
+
= 1
.
21
50
5
.
0
155
10
5
.
0
5
.
64
5
.
0
5
.
0
i
x
x
w
w
F
F
i
tg
a
c
va
vc
Longitud mínima de la cruceta:
( ) ( ) m
sen
i
sen
D
L c
c 9
.
0
1
.
21
1
.
1
5
.
0
min =
+
=
+
= λ
La fotografía muestra las crucetas típicas que serán
instaladas.

4. 5
5
5
5
a
a
SOPORTE TIPO SC
Características:
La sigla tiene que ver con: S de suspensión y C porque es de concreto.
Soporte de alineamiento (no acepta ángulo bajo ninguna circunstancia).
Las cadenas son verticales.
Si:
A = Tramo de poste libre en la punta
(usualmente entre 0.20 y 0.30 m).
B = Distancia igual a dos veces la longitud
de la cadena, en ella deberá verificarse
que la distancia mínima entre el conductor
y masa del soporte deberá ser d
min = 0.5
m (calculado antes), así como la distancia
vertical mínima entre conductores deberá
ser d =1.329m también calculado, lo que
se cumple ampliamente.
C = 1.1m es la longitud de la cadena.
D = fmax es la flecha (m) máxima.
E =6.0 m (mínimo), es la distancia mínima
del conductor al terreno.
F = 10%L es la parte que se entierra el
poste, siendo L la longitud del mismo.
Siendo el claro entre el conductor y el
terreno E (m):
Por tanto;
( )
F
D
C
B
A
L
E +
+
+
+
−
=
( )
L
L
E 1
.
0
8
.
3
1
.
1
20
.
2
20
.
0 +
+
+
+
−
=
m
L
E 0
.
6
3
.
7
9
.
0 >
−
=
Si L =18m
Entonces:
( ) m
m
E 0
.
6
9
.
8
3
.
7
18
9
.
0 >
=
−
=
En consecuencia, tomaremos este poste
para el cálculo.

5. El diámetro del poste en el punto de empotramiento al terreno es:
( ) 






 −
−
+
=
t
t
p
u
p
e
H
e
H
D
D
D
D
siendo Dp (m) el diámetro en la punta del poste.
Du (m) el diámetro en la parte inferior del poste.
e (m) es la altura de empotramiento normado al valor 10%Ht, tal que L =Ht es la longitud del
poste.
( ) m
De 453
.
0
18
8
.
1
18
21
.
0
48
.
0
21
.
0 =





 −
−
+
=
La altura de aplicación de la Fuerza del Viento sobre el poste es:
( )
( )
e
p
e
p
D
D
D
D
e
H
+
+
=
3
2
( )
( )
m
x
H 11
.
7
453
.
0
21
.
0
3
453
.
0
21
.
0
2
8
.
1
=
+
+
=
La fuerza del Viento sobre el poste es:
( )
e
H
D
D
p
F t
e
p
v
vp −







 +
=
2
( ) kg
m
kg
Fvp 129
8
.
1
18
2
453
.
0
21
.
0
/
24 2
=
−





 +
=

6. wc+wa
Fvp
wp
wc+wa
Fvc+Fva
Fvc+Fva
Fvc+Fva
5
5
5
5
a
a
SOPORTE SC: HIPÓTESIS I TRACCIONES NORMALES
La figura muestra las fuerzas
externas que son aplicadas al poste
instalado y sus respectivos puntos de
aplicación. Se puede mostrar que:
5
.
64
=
vc
F (kg) es la fuerza del
viento sobre el conductor.
10
=
va
F (kg) es la fuerza del viento
sobre la cadena de aisladores.
129
=
vp
F (kg) es la fuerza del
viento sobre el poste.
155
=
c
w (kg) es el peso total del
conductor a que es sometida la
cadena de aisladores y es el
producto de el peso unitario del
conductor (kg/m) por el vano peso.
50
=
a
w (kg) es el peso total de la
cadena y sus accesorios.
4170
=
p
w (kg) es el peso total del
soporte, incluido las crucetas.
La figura muestra como
complemento, el bloque de
cimentación, la puesta a tierra del
soporte que es través de una varilla,
así como el dispositivo anti
escalamiento.
La fuerzas transversales
corresponden al ejercido por el viento
y son siempre perpendiculares a la
dirección de la línea, que es el supuesto extremo. Por otra parte el enterramiento del poste es
como mínimo el 10% de la longitud del poste.

8. La figura muestra los valores de fuerzas obtenidas y sus puntos de aplicación, es decir las
distancias desde el suelo.
De este ARBOL DE CARGAS, podemos deducir que el Momento que tiende a voltear la estructura
que lo llamaremos momento Flector es:
11
.
7
129
8
.
13
5
.
74
2
16
5
.
74 x
x
x
x
M f +
+
=
m
kg
M f −
= 39
.
4165
La fuerza equivalente que provocaría este Momento flector y ubicado en la punta es:
)
(
12
.
257
20
.
16
39
.
4165
9
.
0
punta
la
en
aplicado
kg
L
Meq
Feq =
=
=
La fuerza Nominal, definida como la fuerza de diseño incluído el coeficiente de seguridad es:
( ) ( ) kg
cs
F
F eq
N 24
.
514
0
.
2
12
.
257 =
=
=
Podemos adelantar que un poste de concreto de 18m que “resista” 600kg es suficiente.
La Fuerza Vertical total es:
kg
x
FV 4785
4170
205
3 =
+
=
dato que será empleado para el diseño de la cimentación de concreto del poste.
COMENTARIOS:

9. ESTRUCTURA SC: HIPÓTESIS II DESEQUILIBRIOS (8%) UNILATERALES DE
TRACCIONES
wp
wc+wa
wc+wa
5
5
5
5
a
a
0.08Tc
0.08Tc
0.08Tc wc+wa

10. Tc = 645 kg es el Tiro Máximo del conductor, en consecuencia el Momento flector, que hace que el
poste deba caer en forma transversal es:
El Momento flector (transversal) que tiende a
voltear la estructura es:
kgm
x
M f 325
.
341
665
.
1
205 =
=
El momento flector (longitudinal) que tiende a
voltear la estructura en dirección a la línea es:
08
.
2260
8
.
13
6
.
51
2
20
.
16
6
.
51 =
+
= x
x
x
Ml
Entonces el Momento flector equivalente
(resultante) será:
2
2
l
f
feq M
M
M +
=
2
2
08
.
2260
325
.
341 +
=
feq
M
m
kg
M feq −
= 708
.
2285
Por otra parte el Momento Torsor es:
m
kg
x
Mt −
=
= 91
.
85
665
.
1
6
.
51
El Momento equivalente tomaremos como el
promedio entre el momento flector y la resultante
del Momento flector y el Torsor:
[ ]
2
2
2
1
t
f
f
eq M
M
M
M +
+
=
[ ]
2
2
91
.
85
708
.
2285
708
.
2285
2
1
+
+
=
eq
M
m
kg
M eq −
= 51
.
2286
En consecuencia, la fuerza equivalente (cuyo punto de aplicación es la punta del poste) será:
kg
L
M
F
eq
eq 14
.
141
20
.
16
51
.
2286
9
.
0
=
=
=
Finalmente, la f uerza nominal de diseño será:
kg
x
cs
F
F eq
N 7
.
211
5
.
1
14
.
141
)
( =
=
=
Las Fuerzas Verticales serán:
kg
x
FV 4785
4170
205
3 =
+
=

11. wp
wc+wa
wc+wa
0.5Tc
ESTRUCTURA SC: HIPÓTESIS III ROTURA DEL CONDUCTOR
El Momento flector es:
m
kg
x
M f −
=
= 325
.
341
665
.
1
205
El Momento Torsor:
m
kg
x
Mt −
=
= 96
.
536
665
.
1
5
.
322
El momento equivalente:
[ ]
2
2
2
1
t
f
f
eq M
M
M
M +
+
=
[ ]
2
2
96
.
536
325
.
341
325
.
341
2
1
+
+
=
eq
M
m
kg
M eq −
= 94
.
586
La fuerza equivalente que origina este
momento sería:
kg
L
M
F
eq
eq 23
.
36
20
.
16
94
.
586
9
.
0
=
=
=
La Fuerza Nominal:
kg
Feq
cs
F
F eq
N 345
.
54
)
5
.
1
(
)
( =
=
=
Fuerza Vertical total:
kg
x
FV 4785
4170
205
3 =
+
=
CONCLUSION:
Con lo cálculos en las tres hipótesis hemos
obtenido:
Por tanto se requiere un poste de Concreto armado y centrifugado de características:
CAC 1x600/18/210/480

12. COMENTARIOS:

14. SOPORTE TIPO S1C
VERIFICACIÓN DE DIMENSIONES
CARACTERÍSTICAS:
• Estructura de alineamiento (0° de ángulo
de línea).
• Disposición de fases vertical.
• No lleva retenidas o vientos.
La distancia del conductor al terreno deberá
ser:
( )
F
D
C
B
A
L
E +
+
+
+
−
=
( )
L
F
C
B
A
L
E 1
.
0
max +
+
+
+
−
=
( )
D
C
B
A
L
E +
+
+
−
= 9
.
0
( )
8
.
3
1
.
1
4
.
4
2
.
0
9
.
0 +
+
+
−
= L
E
5
.
9
9
.
0 −
= L
E
Si L=18.00m
( ) )
(
0
.
6
7
.
6
5
.
9
0
.
18
9
.
0 mínimo
m
E >
=
−
=

15. SOPORTE TIPO S1C : HIPÓTESIS I FUERZAS NORMALES
El Momento flector es:
)
11
.
7
(
129
)
665
.
1
(
205
3
)
60
.
11
8
.
13
16
(
5
.
74 +
+
+
+
= x
M f
realizando operaciones:
m
kg
M f −
= 465
.
5025
Fuerza equivalente en la punta:
m
kg
L
M
F
f
eq −
=
=
= 21
.
310
20
.
16
465
.
5025
9
.
0
La fuerza nominal:
( ) kg
x
fs
F
F eq
N 42
.
620
0
.
2
21
.
310 =
=
=
La Fuerza Vertical total:
kg
x
FV 4785
4170
205
3 =
+
=

16. SOPORTE TIPO S1C : HIPÓTESIS II DESEQUILIBRIO (8%) DE TRACCIONES
UNILATERALES

17. El Momento flector es:
m
kg
x
M f −
=
= 975
.
1023
)
665
.
1
(
205
3
El momento torsor:
m
kg
x
x
Mt −
=
= 742
.
257
665
.
1
6
.
51
3
Momento Equivalente:
2
2
2
1
t
f
eq M
M
M +
=
2
2
742
.
257
975
.
1023
2
1
+
=
eq
M
m
kg
M eq −
= 945
.
1039
La fuerza equivalente:
kg
L
M
F
eq
eq 19
.
64
20
.
16
945
.
1039
9
.
0
=
=
=
La fuerza nominal:
kg
fs
F
F eq
N 285
.
96
)
5
.
1
(
19
.
64
)
( =
=
=
La fuerza vertical total:
kg
x
FV 4785
4170
205
3 =
+
=

18. SOPORTE TIPO S1C : HIPÓTESIS III ROTURA DE CONDUCTOR EN EL PUNTO
MAS DESFAVORABLE

19. El momento flector es:
m
-
1023.975kg
5
3x205x1.66
Mf =
=
El momento torsor:
m
kg
x
Mt −
=
= 9625
.
536
665
.
1
5
.
322
Momento Equivalente:
[ ] m
kg
M
M
M
M t
f
f
eq −
=
+
+
= 1
.
1090
2
1 2
2
La fuerza equivalente:
kg
L
M
F
eq
eq 30
.
67
20
.
16
1
.
1090
9
.
0
=
=
=
La fuerza nominal:
kg
fs
F
F eq
N 9
.
100
)
5
.
1
(
30
.
67
)
( =
=
=
La fuerza vertical total:
kg
x
FV 4785
4170
205
3 =
+
=

20. SOPORTE TIPO RC
VERIFICACIÓN DE DIMENSIONES
CARACTERÍSTICAS:
• Estructura de anclaje - alineamiento (0° de ángulo de línea).
• Disposición de fases triangular.
• Lleva dos retenidas o vientos.
La distancia del conductor al terreno deberá ser:
( )
E
C
B
A
L
D +
+
+
−
=
( )
L
F
B
A
L
D 1
.
0
max +
+
+
−
=
( )
8
.
3
2
.
2
20
.
0
9
.
0 +
+
−
= L
D
2
.
6
9
.
0 −
= L
E
Si L=18.00m
( ) 0
.
6
10
2
.
6
0
.
18
9
.
0 >
=
−
= m
E
PLANTA
LADO
R E T E N I D A
R E T E N I D A
37°
37°

21. SOPORTE TIPO RC : HIPÓTESIS I FUERZAS NORMALES
RETENIDA
RETENIDA

22. Recordemos que:
kg
w
kg
w a
c 50
155 =
=
kg
F
kg
F va
vc 10
5
.
64 =
=
El Momento flector es:

23. 665
.
1
50
)
11
.
7
(
129
)
8
.
13
(
5
.
84
2
)
16
(
5
.
94 x
x
M f +
+
+
=
realizando operaciones:
m
kg
M f −
= 64
.
4844
Fuerza equivalente en la punta:
m
kg
L
M
F
f
eq −
=
=
= 0
.
300
20
.
16
64
.
4844
9
.
0
La fuerza nominal:
( ) kg
x
fs
F
F eq
N 0
.
600
0
.
2
21
.
310 =
=
=
La Fuerza Vertical total:
kg
x
FV 4835
50
4170
255
3 =
+
+
=
En esta hipótesis las retenidas no trabajan, en razón que no existen tiros longitudinales.

24. SOPORTE TIPO RC : HIPÓTESIS II DESEQUILIBRIO (50%) DE TRACCIONES
UNILATERALES
RETENIDA
RETENIDA

25. El Momento flector es:
m
kg
M f −
=
= 25
.
83
)
665
.
1
(
50
El momento que tiende a voltear la estructura en sentido longitudinal es:
m
kg
x
Mlong −
=
+
= 24
.
14061
)
8
.
13
2
16
(
5
.
322
Momento Equivalente:
2
2
long
f
eq M
M
M +
=
2
2
14061
25
.
83 +
=
eq
M
m
kg
M eq −
= 24
.
14061
La fuerza equivalente:
kg
L
M
F
eq
eq 98
.
867
20
.
16
24
.
14061
9
.
0
=
=
=
La fuerza nominal:
kg
fs
F
F eq
N 1302
)
5
.
1
(
98
.
867
)
( =
=
=
La fuerza vertical total:
kg
x
FV 4835
50
4170
255
3 =
+
+
=

26. F
F
TR
TR
CALCULO DE LA RETENIDA:
Las retenidas deberán soportar el
Tiro longitudinal, ya que estas se
instalarán en ese sentido. En
consecuencia el tiro longitudinal
calculado es:
m
kg
Mlong −
= 24
.
14061
Calcularemos las dos fuerzas
(iguales) en los puntos donde se
ubicarán las retenidas. Ambas
fuerzas equilibrarán el momento
Longitudinal.
long
M
Fx
Fx =
+ 5
.
13
30
.
15
En consecuencia:
kg
F 23
.
488
=
Cada retenida deberá equilibrar
esta Fuerza, de tal manera que:
θ
θ
sen
F
T
F
sen
T R
R =
→
=
kg
sen
TR 26
.
811
37
23
.
488
=
°
=
Si utilizamos el cable para retenida de ½”f de acero galvanizado del tipo Siemens Martín cuyo Tiro
de rotura es 5489kg, entonces el coeficiente de seguridad de trabajo de la retenida será:
77
.
6
26
.
811
5489
=
=
=
R
T
TR
cs

27. SOPORTE TIPO RC : HIPÓTESIS III ROTURA DE CONDUCTOR EN EL PUNTO MAS
DESFAVORABLE
RETENIDA
RETENIDA

28. Se observa que si se rompe el
conductor superior, se producirá un
momento que tratará de voltear la
estructura en el sentido longitudinal a
la línea, dicho momento longitudinal
es:
m
-
kg
10320
x16.0
645
Mlong =
=
La fuerza equivalente:
kg
L
M
F
long
eq 037
.
637
20
.
16
10320
9
.
0
=
=
=
por simple inspección si comparamos
esta fuerza con la obtenida en la
Hipótesis II, vemos que:
II
eq
III
eq F
F <
En consecuencia, prevalecen los
cálculos de la Hipótesis II.
La fuerza vertical total:
kg
x
FV 4835
50
4170
255
3 =
+
+
=
CONCLUSIÓN: Se requiere tres
postes con la especificación.
CAC 3X1500/18/210/480

30. SOPORTE TIPO A2-60°
Características:
• Estructura de Angulo y anclaje.
• Soporta ángulo hasta 60°.
• Tiene seis retenidas en las dos direcciones opuestas a la línea.
• El puente del conductor se hace con tres cadenas auxiliares de suspensión.
FRENTE
LADO
37°
37°
RETENIDA
RETENIDA
RETENIDA
2
RETENIDAS
PLANTA
PLANTA
RETENIDAS

31. DIMENSIONES
Se deduce que:
( )
F
D
C
B
A
L
E +
+
+
+
−
=
( ) m
L
f
C
B
A
L
E 00
.
6
1
.
0
max >
+
+
+
+
−
=
( ) m
L
L
E 00
.
6
1
.
0
8
.
3
2
.
2
2
.
2
6
.
0 >
+
+
+
+
−
=
de donde se deduce que:
m
L
L 4
.
16
0
.
6
8
.
8
9
.
0 >
→
>
−
En consecuencia, un poste de L= 18.0 m es suficiente.
FRENTE
RETENIDA
37°
RETENIDA
37°
RETENIDA
16.00m
15.80m
13.40m
11.20m

32. SOPORTE TIPO A2-60° HIPÓTESIS I FUERZAS NORMALES.
FRENTE
RETENIDA
37°
RETENIDA
RETENIDA
37°
Fva R
Fva R
Fva R
Fvc+2Fva
Fvc+2Fva
Fvc+2Fva
wc+2wa
wc+2wa
wc+2wa
wa
wa
wa
Fvp
wp
HIPOTESIS NORMAL

34. La resultante por efecto del ángulo topográfico es:






=
2
2
β
sen
T
R C
( ) kg
sen
R 645
2
60
645
2 =






=
Recordemos que:
5
.
64
=
vc
F (kg) es la fuerza del viento sobre el conductor.
10
=
va
F (kg) es la fuerza del viento sobre la cadena de aisladores.
129
=
vp
F (kg) es la fuerza del viento sobre el poste.
129
=
c
w (kg) es el peso total del conductor a que es sometida la cadena de aisladores y es el
producto de el peso unitario del conductor (kg/m) por el vano peso.
50
=
a
w (kg) es el peso total de la cadena y sus accesorios.
4170
=
p
w (kg) es el peso total del soporte, incluido las crucetas.
Del ARBOL DE CARGAS, podemos deducir que el Momento que tiende a voltear la estructura es:
11
.
7
129
)
20
.
11
40
.
13
80
.
15
)(
645
10
5
.
84
(
665
.
1
50
3 x
x
x
M f +
+
+
+
+
+
=
m
kg
M f −
= 31043
La fuerza equivalente que provocaría este Momento flector y ubicado en la punta es:
)
(
1916
20
.
16
31043
9
.
0
punta
la
en
aplicado
kg
L
Meq
Feq =
=
=
La fuerza Nominal, definida como la fuerza de diseño incluído el coeficiente de seguridad es:
( ) ( ) kg
cs
F
F eq
N 3832
0
.
2
1916 =
=
=
La Fuerza Vertical total es:
kg
x
x
FV 5085
4170
50
3
255
3 =
+
+
=
dato que será empleado para el diseño de la cimentación de concreto del poste.

35. RETENIDA
RETENIDA
37°
RETENIDA
37°
16.20m
15.80m
15.8-0.6=15.2m
13.40m
13.40-0.6=12.80m
11.20m
11.20-0.6=10.60m
TR
TR
TR
TR
F1
F1
F1
PLANTA
RETENIDAS
Feq
F
F
b
CALCULO DE RETENIDAS
Calculemos las fuerzas F (ambas en dirección a los conductores y en la punta) que equilibran Feq.






=





 −
=
2
2
180
cos
β
β
sen
F
F
F eq
eq
kg
sen
F 958
2
60
1916 =






=
Esta fuerza deberá ser equilibrada por un juego de 3
retenidas, cada una de ellas deberá soportar la misma fuerza
F1, tal como se muestra en la figura.
Por tanto, igualando momentos:
( ) 20
.
16
958
6
.
10
8
.
12
2
.
15
1 x
F =
+
+
kg
F 8
.
421
1 =
Cada retenida deberá soportar la Fuerza F1 =421.8kg
En consecuencia la componente horizontal de la fuerza en la
retenida, deberá tener precisamente este valor:
8
.
421
=
θ
sen
TR
kg
sen
sen
TR 667
37
8
.
421
8
.
421
=
=
=
θ
Si la retenida es de ½”f, con Tiro de Rotura = 5489kg, entonces
el coeficiente de seguridad de la retenida es:
23
.
8
667
5489
Re
=
=
=
tenida
T
Trotura
cs

36. ESTRUCTURA A2EC: HIPÓTESIS II DESEQUILIBRIOS (50%) UNILATERALES DE
TRACCIONES
FRENTE
wp
wc+2wa
RETENIDA
wa
wc+2wa
37°
RETENIDA
wa
wc+2wa
RETENIDA
37°
wa
1.5Tc
1.5Tc
1.5Tc
Tc
Tc
Tc
HIPOTESIS II

38. b
Como tenemos 50% de tracciones unilaterales, entonces la resultante es:
β
cos
2
1
2
k
k
T
R C
−
+
=
Si la resultante R hace un ángulo a con la Fuerza Tc;
entonces:








−
+
=
−
β
β
α
cos
2
1
2
1
k
k
ksen
sen
En nuestro ejemplo: Tc = 645; k=1.5; b=60°
Por tanto:
R = 853.25 kg y a = 79.1°
El Momento flector es:
( ) ( )
665
1
50
3
20
11
40
13
80
15
25
853 .
.
.
.
. x
M f +
+
+
=
m
kg
M f −
= 05
34721.
La fuerza equivalente en la punta es:
kg
M
F
f
eq 27
2143
20
16
.
.
=
=
La fuerza vertical total es:
kg
x
x
FV 5085
4170
255
3
50
3 =
+
+
=
COMENTARIOS

39. CALCULO DE RETENIDAS
Vemos que:
I
eq
II
eq F
F >
En consecuencia, calculamos las retenidas en razón que la HIPÓTESIS II, prevalece, pero el
cálculo es análogo a la Hipótesis I.
Calculemos las fuerzas F (ambas en dirección a los conductores y en la punta) que equilibran Feq.






=
2
β
sen
F
F eq
kg
sen
F 6
1071
2
60
27
2143 .
. =






=
Esta fuerza deberá ser equilibrada por el juego de 3 retenidas, cada una de ellas deberá soportar
la misma fuerza F1, tal como se muestra en la figura.
Por tanto, igualando momentos:
( ) 20
16
6
1071
6
10
8
12
2
15
1 .
.
.
.
. x
F =
+
+
kg
F 74
449
1 .
=
Cada retenida deberá soportar la Fuerza F1 =449.74kg
En consecuencia la componente horizontal de la fuerza en la retenida, deberá tener precisamente
este valor:
74
449.
=
θ
sen
TR
kg
sen
sen
TR 3
747
37
74
449
74
449
.
.
.
=
=
=
θ
Si la retenida es de ½”f, con Tiro de Rotura = 5489kg, entonces el coeficiente de seguridad de la
retenida es:
34
7
3
747
5489
.
.
Re
=
=
=
tenida
T
Trotura
cs

40. ESTRUCTURA A2EC: HIPÓTESIS III ROTURA DEL CONDUCTOR
wc+2wa
wc+2wa
RETENIDA
RETENIDA
FRENTE
wp
wa
wa
37°
wc+2wa
RETENIDA
37°
wa
HIPOTESIS III

42. El Momento flector debido al peso de las cadenas es:
m
kg
x
x
M f −
=
= 75
249
665
1
50
3 .
.
El Momento que tiende a voltear la estructura en sentido longitudinal es:
m
kg
x
Mlong −
=
= 10191
80
15
645 .
El momento equivalente:
2
2
long
f
eq M
M
M +
=
m
kg
M eq −
= 06
10194.
La fuerza equivalente que origina este momento sería:
kg
L
M
F
eq
eq 629
20
16
06
10194
9
0
=
=
=
.
.
.
si se compara obtenemos:
II
eq
I
eq
III
eq F
F
F <
<
En consecuencia, prevalecen los cálculos efectuados para la Hipótesis II, incluyendo las
conclusiones para las retenidas.
Fuerza Vertical total:
kg
x
x
FV 5085
4170
50
3
255
3 =
+
+
=
CONCLUSION:
Con lo cálculos en las tres hipótesis hemos obtenido:
Por tanto se requieren tres postes de Concreto armado y centrifugado de características:
CAC 1x2200/18