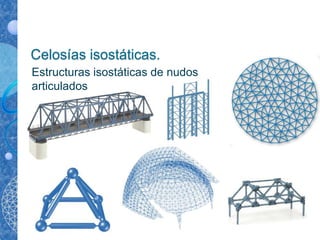
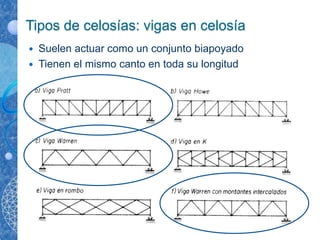
El documento describe las celosías isostáticas, que son estructuras planas formadas por barras articuladas. Estas estructuras cumplen cuatro hipótesis: articulaciones sin rozamiento, cargas sólo en los nudos, barras de directriz recta y estructura y cargas en un plano. El documento también presenta los métodos para analizar las celosías isostáticas, como el método de los nudos y el método de Ritter.

1. Celosías isostáticas.
Estructuras isostáticas de nudos
articulados

2. Estructuras articuladas planas o celosías
planas
 Estructuras formadas por barras articuladas en sus
extremos
 Hipótesis:
◦ Articulaciones sin rozamiento
◦ Cargas sólo en los nudos
◦ Barras de directriz recta
◦ Estructura y cargas en un plano
 Si se cumplen estas hipótesis, las barras sólo pueden
estar sometidas a esfuerzos normales.

3. En la práctica: articulaciones
Nudos próximos a una articulación real:
Nudos no articulados pero asimilables
La condición que,
teóricamente, deben cumplir
los nudos es que los ejes de
las barras concurran en un
punto o casi.

4. En la práctica: cargas en los nudos
Se sustituyen las cargas sobre barra por las reacciones que se generan en
los nudos de una barra biarticulada cambiadas de signo.

5. En la práctica: estructura y cargas en un
plano
 Pueden aislarse partes de una estructura 3D para ser
estudiadas en 2D.
 Esto implica:
◦ Que las cargas situadas fuera del plano deben trasladarse al
plano y, en concreto, a los nudos.
◦ La estructura debe estar suficientemente arriostrada en la
dirección perpendicular al plano considerado.
2 celosías
planas
paralelas
Arriostramientos
superiores

6. En la práctica: ejemplo de traspaso de
cargas
Ejemplo de puente
• Las vigas sobre las que
descansará la losa
transmiten su carga a los
nudos inferiores.
• Carga superficial qs
kN/m2,
• Ancho B
• Distancia entre nudos
inferiores L
 Carga lineal que se llevaría
cada una de las dos
celosías:
q = qsxB/2 [kN/m]
 Carga en cada nudo:
PP P P P
P/2P/2

7. Uso de las celosías
 Todo tipo de usos
 Grandes vanos o grandes
cargas
 Frente a vigas de alma llena:
◦ Ahorro de material
◦ Mayor mano de obra

8. Tipos de celosías: vigas en celosía
 Suelen actuar como un conjunto biapoyado
 Tienen el mismo canto en toda su longitud

9. Tipos de celosías: cerchas
 Actúan
como
vigas
biapoyada
s de canto
variable
 Se ajustan
mejor a
cargas
verticales
centradas
o
repartidas
PL/4
P/2
P/2
PL/8
P/2
P/2

10. Barras de una celosía: cordones y relleno
 Cordones:
◦ Barras alineadas en borde superior e inferior
◦ Generalmente de una pieza aunque cada tramo se considere una
barra biarticulada
◦ Soportan los momentos flectores del conjunto
 Barras de relleno:
◦ Barras entre los cordones
◦ Diagonales o montantes (perpendiculares a cordón)
◦ Soportan los cortantes del conjunto

11. Formas de generación de celosías: simples
 Simples de generación externa isostáticas:
◦ Parte de 2 apoyos fijos y se añaden sucesivamente 2 barras y 1
nudo
 Simples de generación interna isostáticas:
◦ Se parte de 1 triángulo básico y se añaden sucesivamente 2 B y 1 N
◦ Se añaden finalmente apoyos isostáticos (3 reacciones no
concurrentes)

12. Formas de generación de celosías:
compuestas
 Celosías compuestas isostáticas:
◦ Unión de conjuntos triangulados simples y barras
◦ Los conjuntos triangulados funcionan como barras
◦ Formas de generación igual que en las simples
◦ También pueden unirse dos conjuntos triangulados mediante 3
barras no concurrentes
Generación internaGeneración externa Unión por tres barras
 Celosías complejas:
◦ Cuando la forma de generación no se corresponde con las simples ni
con las compuestas

13. Caracterización estática y cinemática
 C. Estática=Grado de Hiperestaticidad GH=B+R-2N
◦ Hipoestática (GH<0 es mecanismo), Isostática (GH=0), Hiperestática
(GH>0)
 C. Cinemática
◦ Íntimamente ligado a lo anterior
◦ Caracterización del funcionamiento o no como mecanismo
◦ Variante: mecanismo o conjunto hipoestático
◦ Invariante: estructura isostática o hiperestática en equilibrio
◦ De variación instantánea: no puede obtener el equilibrio si no se
produce un mínimo desplazamiento.
 Si a un nudo sólo llegan 2 barras alineadas
 Si todas las reacciones posibles concurren en un punto (Eq. de momentos
imposible)
F
F
F
Variante Invariante Variación instantánea

14. Caracterización cinemática: variación
instantánea
 Ejemplos:
◦ 2 barras alineadas en 1
nudo
◦ Reacciones concurrentes

15. Esfuerzos en celosías isostáticas: barras de
esf. 0
 Existen barras de celosía que a priori podemos
identificar como elementos sin esfuerzo: barras de
esfuerzo 0
a) 2 barras no alineadas que concurren en un nudo sin carga
b) 3 barras concurren en un nudo sin carga, estando dos de ellas
alineadas. La barra no alineada será una barra de esfuerzo 0 y puede
eliminarse el nudo.
(a)
F
a
F
a
(b)
0
a
0
a
0
a
F
a
F
a

16. Esfuerzos en celosías isostáticas: método
nudos
 Se basa en las ideas básicas siguientes:
1. Las barras de las celosías sólo transmiten esfuerzos axiles o
normales.
2. Las fuerzas que llegan a los nudos deben estar en equilibrio.
Equilibrio de fuerzas verticales: ∑FV=0
Equilibrio de fuerzas horizontales: ∑FH=0
NI
NII
R
FF
NI
R
NII
F
Fuerzas sobre el nudo Equilibrio de vectores de fuerza
planteado vectorial-
gráficamente
I
II
3. Las compresiones son fuerzas que llegan al nudo y las
tracciones salen
4. Si existen barras de esfuerzo 0 que se detecten a priori, estas se
pueden excluir del cálculo

17. Método de los nudos: ejemplo
Se tiene una viga en celosía tipo Warren de canto L con dos tramos de
longitud 2L y una carga P en cada uno de los nudos centrales superiores.
Obténganse los esfuerzos en las barras.
P
a
P
a
2L
a
4L
a
L
a
1. Obtener las reacciones
P
a
P
a
3L
a
4L
a
L
RV1
a
RV3
a
RH1
a L
a
1
a
2
a
3
a
4
a 5
a
6
a
7
a
∑Fv=0 RV1+RV3-P-P=0
∑FH=0 RH1 =0
∑M1=0 RV3·4L-P·3L-P·L=0
RV1=P ; RV3=P
Estas reacciones son evidentes.
Una estructura simétrica debe tener
reacciones simétricas.
2. Eliminar barras de
esfuerzo 0
PP
P P
0
0
0
0
1 2 3
4
5 6
7

18. Método de los nudos: ejemplo (continuación)
3. Planteamos equilibrio en nudos
Nudo 1
Usando los resultados de 1: Nudo
5
P
a
Nudo 1
a
N15
a
N12
a
45º
a
-P
a
-P √2
aP
a
Solución nudo 1
a
P
a
Nudo 5
a N56
a45º
a
Solución nudo 5
a
45º
a
N52
a
-P √2
a
P
a
P
a
-P √2
a
0
a0
a
0
a
0
a-P
a+P
a
+P
a
-P √2
a
-P √2
a
0
a
0
a
0
a0
a
0
a
0
a-P
a+P
a
+P
-P √2
a
-P √2
a
De modo simplificado:
a
0
a
0
a
3. Dibujamos el resultado final de los esfuerzos normales
• En este caso tenemos en cuenta que los esfuerzos normales en una estructura
simétrica deben ser simétricos

19. Esfuerzos en celosías isostáticas: método
Ritter
 Método de las secciones o de Ritter:
◦ Se corta la estructura por 1 sección y se plantea equilibrio en el
trozo aislado
 Obtener las reacciones y eliminar barras de esfuerzo 0
 Aislar un trozo de celosía cortando un máximo de 3 barras (3 incógnitas
de axiles). Las 3 barras no pueden concurrir en un mismo punto. Hay casos donde se
pueden cortar más de 3 barras y llegar a la solución igualmente (si hay varias concurrentes).
 Plantear 3 ecuaciones de equilibrio en el trozo aislado. Plantear varios
equilibrios de momentos con respecto a puntos por los que pasen 1 o 2 incógnitas de
esfuerzo
P
a
0
a
0
a
P
a
V
a
R
a
H
a V
a
H
a
N1
aN2
a N3
a
A
a
B
a
∑MA=0 → N3
∑MB=0 → N1
∑FV=0 → N2
Considerar barras de
esfuerzo 0 y obtener
reacciones
Método de las
secciones

20. Métodos para vigas en celosía
 Se asimila la viga en celosía con una barra sometida a
flexión
 Hipótesis:
◦ Los cordones soportan el momento flector
◦ Las barras de relleno soportan el cortante
S
MS
VS
MS
VS
NcordS
NcordI
Ndiag
α
h
Cordón sup compr. e inf.
tracc.

21. Vigas en ceosía: N de los cordones
 Ncord=MS/h
 Pero si sabemos que el esfuerzo debe ser constante entre cada dos
nudos ¿Qué momento tomamos si la sección que consideramos
está entre 2 nudos?
◦ Para esto debemos fijarnos en el punto que usaríamos en Ritter.
NcordS
a
MA
a
A
a
B
a
NcordI
a
Ndiag
a
Para obtener NcordS por Ritter plantearíamos
equilibrio de momentos respecto a B, por tanto:
NcordS= MB/h
MB
a
Para obtener NcordI por Ritter plantearíamos
equilibrio de momentos respecto a A, por tanto:
NcordI= MA/h
Obsérvese que en este ejemplo NcordS es mayor que NcordI, lo que contrarresta la componente horizontal hacia la derecha de Ndiag.

22. Vigas en celosía: N de las diagonales
 La única fuerza con componente en la dirección del cortante
es el esfuerzo en la diagonal.
 Ndiag=Vs/senα
Compresión
Tracción
Tracción
Compresión
Signo del cortante: depende de dirección de la diagonal

23. Vigas en celosía: cálculo de
desplazamientos
Cálculo aproximado de
desplazamientos asimilando
a vigas de alma llena.
Aproximar el momento de
inercia total I al 75% del de
los cordones
I=0,75·Icordones
Aplicando Steiner y
despreciando el momento de
inercia respecto a su eje:
Icordones=2·[I0+A(h/2)2]≈2A(h/2)2
Así, pueden usarse tablas,
p. ej.

24. Consideraciones sobre diseño de celosías
 Las cargas sobre barra deben trasladarse a nudos
◦ Después de resolver téngase en cuenta el diagrama de M y V
 Barras comprimidas esbeltas: PANDEO
◦ Las barras comprimidas deben ser lo más cortas posible
VIGA PRATT: diagonales traccionadas.
BIEN
VIGA HOWE: diagonales comprimidas.
MAL
V

25. Estructuras articuladas espaciales
 Simples de generación
externa
◦ Se parte de 3 apoyos fijos
◦ Se añaden 3B+1N
 Simples de generación
interna
◦ Se parte de tetraedro básico
◦ Se añaden 3B+1N
◦ Se añaden apoyos (6
reacciones)
 Hiperestaticidad: GH=B+R-
3N
Ry
a
Rx
a
Rz
a