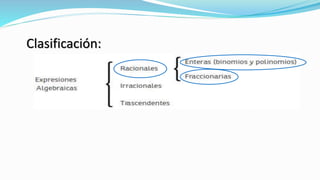
Este documento describe las expresiones algebraicas y los polinomios. Define un monomio como una expresión algebraica con un solo término y sin operaciones de suma o resta. Un polinomio se define como la suma algebraica de monomios. Explica cómo clasificar polinomios según su grado, ordenarlos, y realizar operaciones como suma, multiplicación y división con ellos.

1. Atribución – No Comercial (by-nc): Se permite la generación de obras derivadas siempre que no se haga con fines comerciales.
Tampoco se puede utilizar la obra original con fines comerciales. Esta licencia no es una licencia libre.

3. Expresiones Algebraicas. Polinomios

4. ¿Qué dice el material de estudio al respecto?
Página 30
Son ejemplos de expresiones algebraicas:
xy
yx
2
22
 3322
33 babbaa 

5. Clasificación:

6.  Expresiones Algebraicas Racionales Enteras:
son expresiones en las cuales las variables pueden estar afectadas por las
operaciones de adición, sustracción, multiplicación y potenciación con
exponentes enteros no negativos.
𝑐𝑥 + 𝑑𝑎𝑥2 + 𝑏𝑥 + 𝑐 𝑥2 – 2𝑥𝑦 + 𝑦2
A continuación desarrollaremos como se clasifican según sus
términos.

7.  Monomio: Es toda expresión entera en la que no intervienen las
operaciones de adición ni de sustracción. El factor numérico que lo
compone se llama coeficiente.
ba2
3zxy3
3
1

;
Se dice que dos monomios son semejantes si sólo difieren en su coeficiente.
Por ejemplo: yx2
4 yx2
5
6

;
En caso que sean exactamente coincidentes en cada uno de sus factores los
monomios son iguales.
 Grado de un monomio: Se llama grado de un monomio a la suma de los
exponentes de las variables intervinientes.
El monomio es de 7mo. grado.
232
9 zyx

8.  Polinomio: Es la suma algebraica de monomios, también
llamados términos del polinomio. Cuando el polinomio tiene
sólo dos términos se llama binomio, cuando tiene sólo tres
términos se llama trinomio, etc.
 Grado de un polinomio: Es el mayor de los grados de los
monomios que componen el polinomio. se simboliza con: gr
[p(x)].
Por ejemplo
𝑃 𝑥 = 2𝑥4
− 3𝑥3
+ 2𝑥 + 5 entonces 𝑔𝑟 𝑃 𝑥 = 4
𝑔𝑟 3𝑥𝑦3
− 7𝑥2
𝑦3
= 5

9. Polinomio en una variable
Con:
𝑎 𝑛, … , 𝑎1, 𝑎0 Coeficientes reales
𝑎 𝑛≠ 0 coeficiente principal
𝑎0 Término independiente

10.  Polinomio de una variable ordenado: Se dice que un polinomio
se encuentra ordenado si se expresa de modo que el grado de
cada término vaya aumentando o disminuyendo sucesivamente
desde el primer término hasta el último.
 La ordenación será creciente si los exponentes de la variable
van del menor al mayor o decreciente en el caso contrario.
El polinomio 𝑃 𝑥 = −2𝑥3
+ 5𝑥2
− 2 está ordenado
decrecientemente. Mientras que el polinomio 𝑄 𝑥 = 6 −
𝜋𝑥2
+ 𝑥6
se encuentra ordenado en forma creciente.

11. Un polinomio se dice completo cuando en la expresión aparecen
explícitamente todos los términos correspondientes a las potencias
de la variable.
Por ejemplo el polinomio 𝑃 𝑥 = 𝑥5
− 1
Se completa sumando términos nulos de los grados entre 5 y 0 que
faltan: 𝑃 𝑥 = 𝑥5
+ 0𝑥4
+ 0𝑥3
+ 0𝑥2
+ 0𝑥 − 1

13. Operaciones con Polinomios de una variable.
 Adición de polinomios: Para encontrar la suma entre dos polinomios se
agrupan los términos o monomios de igual grado y se suman sus coeficientes.

17. Multiplicación de Polinomios: Para multiplicar dos polinomios se utiliza la propiedad
distributiva, la propiedad de las potencias de igual base, efectuando luego la suma de
monomios de igual grado.
−2𝑥2
+ 𝑥 − 1 ∙ 3𝑥3
+ 2𝑥 =
= −2𝑥2
+ 𝑥 − 1 ∙ 3𝑥3
+ −2𝑥2
+ 𝑥 − 1 ∙ 2𝑥 =
= −6𝑥5 + 3𝑥4 − 3𝑥3 + −4𝑥3 + 2𝑥2 − 2𝑥 =
= −6𝑥5 + 3𝑥4 − 7𝑥3 + 2𝑥2 − 2𝑥

18.  Nota: La ordenación de los polinomios facilita el cálculo del producto. Se
tiene, por ejemplo, la siguiente disposición práctica:
2371076
2246
23
2246
22
123
2345
23
234
2345
2
23






xxxxx
xxx
xxxx
xxxx
xx
xxx

20.  División
Para poder dividir polinomios el grado del dividendo debe ser
mayor o igual al grado del divisor.
 División de un polinomio por un monomio:
Se utiliza la propiedad distributiva y las propiedades de las potencias de igual
base.
4𝑥2
− 16𝑥5
+ 36𝑥3
: −2𝑥2
=
4𝑥2
− 16𝑥5
+ 36𝑥3
−2𝑥2
=
4𝑥2
−2𝑥2
−
16𝑥5
−2𝑥2
+
36𝑥3
−2𝑥2
= −2 + 8𝑥3 − 18𝑥

21.  Cociente entre dos polinomio:
El algoritmo de división para polinomios:
Sean 𝐹(𝑥) y 𝐺(𝑥) polinomios con G(𝑥) ≠ 0 , entonces existen polinomios únicos 𝑞(𝑥)
y 𝑟(𝑥) tales que: 𝐹(𝑥) = 𝐺(𝑥) . 𝑞(𝑥) + 𝑟(𝑥)
O en forma equivalente
Siendo 𝑟(𝑥) el polinomio resto y q(𝑥) el polinomio cociente
𝐹(𝑥) 𝐺(𝑥)
𝑟(𝑥) 𝑞(𝑥)

22. Ejemplo: Consideremos la división:
Cociente: 𝟐𝒙 𝟐
− 𝟒𝒙 − 𝟏
Resto: −9