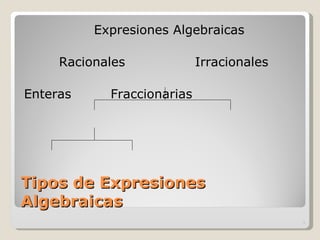
El documento habla sobre expresiones algebraicas. Define una expresión algebraica como una expresión que relaciona valores indeterminados con constantes a través de operaciones como suma, resta, multiplicación, división, potencias y raíces. Explica que las expresiones algebraicas pueden ser racionales, irracionales, enteras o fraccionarias dependiendo de los tipos de operaciones involucradas. También define polinomios como expresiones algebraicas especiales y explica conceptos como términos, monomios, binomios y trinomios.

1. EXPRESIONES ALGEBRAICAS Prof. Marcial Parisuaña

2. Expresiones Algebraicas Una expresión algebraica es una expresión en la que se relacionan valores indeterminados con constantes y cifras, todas ellas ligadas por un número finito de operaciones de suma, resta, producto, cociente, potencia y raíz. Ejemplos

3. Tipos de Expresiones Algebraicas Expresiones Algebraicas Racionales Irracionales Enteras Fraccionarias

4. Expresión Algebraica Racional Es racional cuando las variables no están afectadas por la radicación Ejemplo

5. Expresión Algebraica Irracional Es irracional cuando las variables están afectadas por la radicación Ejemplo

6. Expr.Algebraica Racional Entera Una expresión algebraicas es racional entera cuando la indeterminada está afectada sólo por operaciones de suma, resta, multiplicación y potencia natural. Ejemplo

7. Expresión Algebraica Racional Fraccionaria Una expresión algebraicas racional es fraccionaria cuando la indeterminada aparece en algún denominador. Ejemplo

8. Polinomios Son las expresiones algebraicas más usadas. Sean a 0 , a 1 , a 2 , …, a n números reales y n un número natural, llamaremos polinomio en indeterminada x a toda expresión algebraica entera de la forma: a 0 + a 1 x + a 2 x 2 + … + a n x n

9. Ejemplos de polinomios A los polinomios en indeterminada x los simbolizaremos con letras mayúsculas indicando la indeterminada entre paréntesis: P(x) ; Q(x) ; T(x).

10. Términos Monomio : polinomio con un solo término. Binomio : polinomio con dos términos. Trinomio : polinomio con tres términos. Cada monomio a i x i se llama término . El polinomio será de grado n si el término de mayor grado es a n x n con a n  0. A a 0 se lo llama término independiente . A a n se lo llama término principal .

11. Ejemplos El polinomio 0 + 0x + 0x 2 + … +0x n se llama polinomio nulo . Lo simbolizaremos por O p (x) . No se le asigna grado.

12. Algunos productos importantes (x+a) 2 =(x+a)(x+a)= x 2 + 2ax + a 2 (x-a) 2 =(x-a)(x-a)= x 2 - 2ax + a 2 (x+a) 3 = x 3 + 3ax 2 + 3a 2 x + a 3 (x-a) 3 = x 3 - 3ax 2 + 3a 2 x - a 3 (x+a)(x-a)= x 2 –ax +ax-a 2 = x 2 -a 2