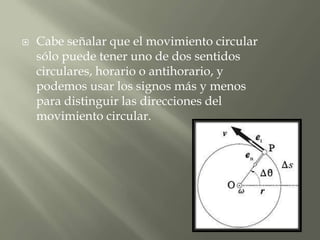
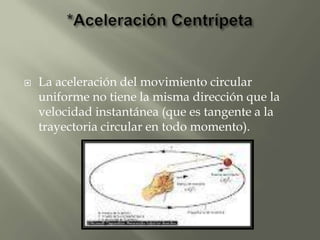
Este documento trata sobre el tema del movimiento circular y gravitacional. Explica conceptos como el movimiento circular uniforme, la relación entre la velocidad tangencial y la velocidad angular, y las leyes de Kepler sobre el movimiento de los planetas. También cubre conceptos como el periodo y la aceleración en el movimiento circular.

1. UNIVERSIDAD AUTONOMA DEL CARMEN
ESCUELA PREPARATORIA DIURNA
UNIDAD ACADEMICA CAMPUS II
MAESTRO
MARDOQUEO MORENO HERNANDEZ
ALUMNA
CHAO MEY ESTIFALIS BALAN LANDERO
TEMA
MOVIMIENTO CIRCULAR Y GRAVITACIONAL

3.  Decimos que un objeto gira cuando el eje de
rotación está dentro del cuerpo, y que da vuelta
cuando el eje está afuera del cuerpo.
 El movimiento circular es movimiento en dos
dimensiones.

4. 

5. 

7. 

8.  Cabe señalar que el movimiento circular
sólo puede tener uno de dos sentidos
circulares, horario o antihorario, y
podemos usar los signos más y menos
para distinguir las direcciones del
movimiento circular.

9. 

10.  Si combinamos las dos ecuaciones para s
obtenemos la relación entre rapidez
tangencial (ʋ) y rapidez angular (ω)
 ʋ = rω
(relación entre rapidez tangencial y rapidez
angular para movimiento circular)
 Donde ω está en radianes por segundo.

11.  El tiempo que tarda un objeto en movimiento
circular en efectuar una revolución completa (
un ciclo) se denomina periodo (T).
 La unidad estándar de periodo es el segundo
(s).

12. 

14.  El movimiento circular uniforme se da cuando
un objeto se mueve con rapidez constante por
una trayectoria circular.

15.  La aceleración del movimiento circular
uniforme no tiene la misma dirección que la
velocidad instantánea (que es tangente a la
trayectoria circular en todo momento).

16. 

18. 

20. 

22.  *La primera ley de Kepler (ley de órbitas)
señala:
 Los planetas se mueven en órbitas elípticas, con
el Sol en uno de los puntos focales.

23.  *La segunda ley de Kepler (ley de áreas) señala:
 Una línea del Sol a un planeta barre áreas
iguales en lapsos de tiempo iguales.

24. 

25.  Se requiere una rapidez tangencial menor que
la rapidez de escape para que un satélite entre
en órbita. Puesto que la fuerza centrípeta que
actúa sobre él proviene de la atracción
gravitacional entre el satélite y la Tierra, de
nueva cuenta escribimos