El documento presenta un resumen de 3 oraciones de un accidente de tránsito ocurrido en El Salvador. Explica que durante un accidente, la energía cinética de los vehículos involucrados se distribuye en la deformación de los vehículos, ruido y lesiones a los pasajeros. Además, presenta información sobre el Ministerio de Educación de El Salvador y los objetivos del material educativo de Física que se está desarrollando.


















![MAGNITUDES FÍSICAS Física
rectangular, al igual que la razón matemática de la
longitud con el tiempo, resulta en la rapidez de un
cuerpo en movimiento.
( ) ( ) ( ) (Ec. 1)
[ ] [ ] [ ]
Figura 5. Una caja es una figura rectangular cuyo volumen se
obtiene al medir lo ancho, largo y alto, al multiplicar esas tres
mediciones de longitud.
En conclusión las magnitudes físicas son todas
aquellas cantidades que se pueden medir directa o
indirectamente.
Tabla 2. Unidades de magnitudes físicas compuestas en (Sl).
Instrumentos de Medición
El uso de los instrumentos es una de las grandes
adaptaciones que el ser humano ha adquirido en su
evolución; estos instrumentos se han construido
para ejecutar tanto medidas directas como
indirectas.
Para familiarizar al estudiante con los diferentes
instrumentos de medición coloque imágenes o
muéstreles los instrumentos que miden las
diferentes magnitudes. Debe pedirles que llenen una
tabla semejante a la tabla 3, identificando la
magnitud que mide, las diferentes unidades en que
se expresa y el sistema de unidades a que
pertenece; nombrar otros instrumentos de medición
diferentes y semejantes a los mostrados
En nuestro país se utilizan diversos sistemas de
medición sin utilizar instrumentos adecuados que
garanticen la venta equitativa de los productos.
Por ejemplo las ventas de frijoles, de cebollas,
zanahorias y plátanos entre otros ¿Cómo se
cuantifican?
Figura 6. Ventas de zanahorias, cebollas, y jocotes.
Al comprar jugo en un supermercado se observa que
en algunos productos el volumen se expresa en
litros, otros en onzas, y en mililitros, lo que confunde
a la población al no expresarse en una medida
estándar.
Los doctores utilizan instrumentos de medición para
la toma datos generales como el peso, el pulso
cardíaco, la estatura y otros más especializados, para
obtener la cantidad suficiente de información para
Magnitud Unidad (u) Abreviación Dimensiones
Fuerza (F) Newtons N [ ]
Presión (P) Pascal Pa
[ ]
Energía (E) Joules J [ ]
Frecuencia (f) Hertz Hz
[ ]
Potencial
Eléctrico (V)
Voltios V
[ ]
Campo
Magnético
(B)
Teslas T
[ ]
5](https://image.slidesharecdn.com/c08-170424214125/75/CIENCIAS-8-21-2048.jpg)















![MAGNITUDES FÍSICAS Física
Magnitud Física: Son las propiedades que pueden
medirse de la materia, expresadas con un numero y
unidad.
Medición: Es la comparación de magnitudes con
una misma unidad de medida.
Unidad de Medida: Es una cantidad establecida por
un patrón.
Exactitud: Es la proximidad de medida de una
magnitud con respecto a un valor establecido como
verdadero utilizando un instrumento.
Precisión: Es la dispersión de los diferentes valores
resultado de medidas hechas.
Cifras Significativas: Son los dígitos de un numero
son tomados en cuenta según la exactitud y
precisión del instrumento utilizado.
Notación Científica: es la representación de
números enteros o decimales en términos de base
10.
Escalar: Una magnitud física.
Vector: Una magnitud física que posee dirección y
sentido.
Si desea enriquecer más su conocimiento, consulte:
1. Franco, A. (2010) “Unidades de Medidas”, [página web]. Física con Ordenador. Recuperado en
septiembre 2011, http://goo.gl/xO6TL
2. Fendt, W. (2010). “Composición de Fuerzas (Suma de Vectores)”, [página web]. Recuperado en
septiembre 2011, http://goo.gl/9qhfK
3. Henderson,T. (2011) “Vectores: Operaciones Fundamentales”, [página web]. The Physics Classroom.
Recuperado en octubre 2011, http://goo.gl/07C7a
4. Serway, R. Faughn, J./Holt (2005) “Physics” 1er edición, New York, E.E.U.U: Holt, Rhinehart and
Winston.
21](https://image.slidesharecdn.com/c08-170424214125/75/CIENCIAS-8-37-2048.jpg)
















![DINÁMICA NEWTONIANA Física
Impulso y cantidad de Movimiento
Los cuerpos poseen ciertas propiedades físicas como
la densidad, geometría y masa; cuando estos
cuerpos están en movimiento también se les puede
asociar una velocidad, la cual en algunos instantes es
constante y en otros cambia constantemente. La
cantidad de movimiento ⃑⃑ que posee un cuerpo se
establece de la siguiente manera:
⃑⃑ ⃑ (Ec. 2)
Esta ecuación describe la relación entre la masa y la
velocidad de los cuerpos de forma vectorial. Sus
unidades son [ ], lo que permite relacionar por
qué se aplica una menor fuerza al mover una silla
que al mover un escritorio hecho del mismo
material. Como el escritorio posee una mayor
cantidad de masa, se resiste más a ponerse en
movimiento; la resistencia que posee un cuerpo a
moverse es lo que se denomina inercia.
Cuando la cantidad de movimiento no es constante
es necesario calcular el impulso . El impulso
aplicado a un cuerpo es igual a la variación o cambio
de la cantidad de movimiento ⃑⃑ , es decir que es
equivalente al producto de la masa con el cambio de
velocidad que experimenta un cuerpo ⃑⃑ y se
expresa de la siguiente manera:
⃑⃑ ⃑⃑ ⃑⃑
El cambio de la cantidad de movimiento dependerá
de la cantidad de movimiento final menos el inicial.
⃑⃑ ⃑⃑ ⃑⃑
Como la masa de la silla no cambia:
⃑⃑ ⃑⃑ ⃑⃑
⃑⃑ ⃑⃑ (Ec. 3)
Por ejemplo si la silla que viaja a cambia su
velocidad a en un lapso de tiempo de cinco
segundos, el impulso recibido para cambiar su
velocidad será:
⃑⃑ ⃑⃑ ⃑⃑
⃑⃑ ( )
⃑⃑
⃑⃑
La silla experimenta un impulso de , esto
es lo necesario para que la silla cambie su velocidad
a partir de a .
Para que la silla experimente un impulso como el
calculado anteriormente, este debe de obtenerlo de
una fuerza externa, por lo que el impulso también
puede considerarse como el producto entre una
fuerza y el tiempo durante el cual es aplicada.
⃑⃑⃑⃑⃗ ⃑⃑⃑⃑⃗
⃑⃑⃑⃑⃑⃗ ⃑⃑⃑⃑⃗ ⃑⃑⃑⃑⃑⃗ ⃑⃑⃑⃑⃗
⃑⃑⃑⃑⃑⃗ ( )
⃑⃑⃑⃑⃑⃗ ( )
⃑⃑⃑⃑⃑⃑⃗ ⃑⃑⃑⃑⃑⃗
Ejemplo 1. Si un escritorio tiene una masa de
y una silla una masa de y los dos
se trasladan a una velocidad de ¿Cuál
tendrá mayor cantidad de movimiento o inercia?
Lo que permite interpretar que el escritorio
posee una mayor inercia o mayor cantidad de
movimiento que la silla.
40](https://image.slidesharecdn.com/c08-170424214125/75/CIENCIAS-8-56-2048.jpg)



![DINÁMICA NEWTONIANA Física
Retomando el impulso (Ec. 3) sobre un cuerpo, se
sabe que para generar un cambio en la cantidad de
movimiento se necesita implementar una fuerza
externa (Ec. 5), lo cual expresa que la fuerza es igual
al cambio de la cantidad de movimiento en un lapso
de tiempo.
⃑⃑
⃑⃑
Sustituyendo el cambio de la cantidad de
movimiento
⃑⃑
⃑⃑
Debido al principio de conservación de la masa
asumimos que la masa del cuerpo es constante por
lo que un cambio de masa en un lapso de tiempo no
es posible y solamente es posible el cambio de
velocidad en un intervalo de tiempo:
⃑⃑
⃑⃑
El cambio de velocidad en un intervalo de tiempo es
la definición de aceleración (⃑⃑
⃑⃑
) , obteniendo
así la ecuación que describe la segunda ley de
Newton:
⃑⃑ ⃑⃑ (Ec. 6)
Sus unidades de medición en el sistema
internacional se reconocen como Newton,
[ ]. Otras unidades conocidas son los
Dinas en el sistema cgs y Libras fuerza en el sistema
inglés.
⃑⃑
⃑⃑
El cambio de velocidad en un intervalo de tiempo es
la definición de aceleración (⃑⃑
⃑⃑
) , obteniendo
así la ecuación que describe la segunda ley de
Newton:
⃑⃑ ⃑⃑
Sus unidades de medición en el sistema
internacional se reconocen como Newton,
[ ]. Otras unidades conocidas son los
Dinas en el sistema cgs y Libras fuerza en el sistema
inglés.
ACTIVIDAD INTEGRADORA CON… MATEMÁTICAS
RELACIONES ALGEBRÁICAS Y PROPORCIONES
Al interpretar la ecuación 5, podemos establecer diferentes
relaciones, tal como la segunda ley de Newton establece:
1. La aceleración es directamente proporcional a la fuerza
neta que se ejerce sobre un cuerpo.
Reordenando la (Ec.5) en términos de la aceleración
obtendremos:
⃗
⃑⃑⃑⃑⃗
(Ec. 7)
Esto comprueba que la aceleración tiene una relación
directa con la fuerza; si consideramos un cuerpo con una
masa constante, a medida aumenta la fuerza neta
ejercida sobre él también la aceleración del cuerpo
aumenta ¿En qué proporción aumenta?
2. La aceleración es inversamente proporcional a la masa
del cuerpo.
Según la ecuación 7, la variable de la masa se encuentra
en el denominador de la fracción, entonces la proporción
de la relación entre la fuerza neta y la aceleración
dependerá también de la masa del cuerpo.
3. Es importante recalcar que la dirección de la aceleración y
fuerza neta son la misma.
Ahora utilizando las relaciones de las ecuaciones 5 y 6,
resolver y analizar las proporciones y hallar los resultados de
cada variable de la tabla 1.
Tabla 1. Valores de fuerza, masa y aceleración
Fuerza (N) Masa (kg) Aceleración
(m/s
2
)
1) 10 2
2) 20 10
3) 20 4
4) 2 5
5) 10 10
⃑⃑ ⃑⃑
Calculando las variables ausentes podemos observar
entre la primera fila y la segunda que al doblar la cantidad
de fuerza ejercida sobre un cuerpo con una masa de 2 kg,
también se dobla la magnitud de aceleración.
Comparando la segunda fila con la cuarta, notamos que al
reducir la fuerza a la mitad también la aceleración se
reduce en una misma proporción.
44](https://image.slidesharecdn.com/c08-170424214125/75/CIENCIAS-8-60-2048.jpg)















![TRABAJO Y ENERGÍA Física
El sistema de referencia desde donde midamos afectará considerablemente la cantidad de energía potencial
gravitatoria que se encuentre almacenada. Analicemos la situación presentada en la figura 7. Suponga que deja
caer una pelota desde el segundo piso hacia el primer piso (del punto A al punto B); si tomamos como sistema
de referencia el techo del primer piso la altura que se utiliza para calcular el potencial es . Pero si la misma
pelota esta vez cae desde el segundo piso hasta el suelo (del punto A al punto C), al tomar el suelo como
sistema referencia la altura a utilizar para nuestro cálculo es . Se puede concluir entonces que el mismo
objeto puede tener diferentes valores de energía potencial dependiendo del sistema de referencia del cual se
mida su altura.
Figura 7. Objeto cayendo desde el segundo piso.
Energía potencial elástica
Imagine que tiene un resorte en posición horizontal
sobre una mesa. Al presionar un objeto con el
resorte y liberarlo, el objeto se desplaza a lo largo de
la mesa. La energía cinética que el objeto adquirió
provino de la energía almacenada en el resorte
comprimido.
Esta energía potencial se le llama energía potencia
elástica. Esta es almacenada en cualquier objeto que
se estira o se comprime, tales como resortes o en
cuerdas estiradas.
La longitud del resorte, cuando no actúa ninguna
fuerza externa, es llamada longitud de relajación del
resorte. Cuando una fuerza externa comprime o
estira el resorte, la energía potencial elástica es
almacenada en el resorte. La cantidad de energía
almacenada dependerá de la distancia que el resorte
es comprimido o estirado desde su longitud de
relajación, como se muestra en la figura 8. La energía
potencial elástica puede ser determinada usando la
siguiente ecuación:
(Ec. 6)
Figura 8. Representación esquemática de un resorte siendo
comprimido con un objeto.
El símbolo es llamado constante de elasticidad.
Físicamente, la constante de elasticidad nos indica el
grado de dificultad que un resorte ofrece ante una
deformación. Un resorte con baja constante de
elasticidad fácilmente se puede comprimir o estirar,
mientras que un resorte con alta constante de
elasticidad requerirá más fuerza para comprimirlo o
estirarlo.
Las unidades en el SI para la constante de elasticidad
son [N/m]. Si por ejemplo un resorte posee una
constante de elasticidad de 5 N/m, esto significa que
para poder estirar o comprimir el resorte una
𝐸 𝑝𝑔 𝑚𝑔
𝐸 𝑝𝑔 𝑘𝑔 𝑚 𝑠⁄ 2 𝑚
𝑬 𝒑𝒈 𝟏𝟗𝟔𝟎 𝑱
Ejemplo 2. ¿Cuál es la energía potencial
gravitatoria de un objeto de masa 𝑘𝑔 a
una altura en referencia al suelo de 2 𝑚?
Solución
Utilizando y sustituyendo en la ecuación 5
60](https://image.slidesharecdn.com/c08-170424214125/75/CIENCIAS-8-76-2048.jpg)



![TRABAJO Y ENERGÍA Física
Despejando la velocidad tenemos que:
√
2
⁄
La velocidad en el punto final es de ⁄ ,
tomando en cuenta que esto es válido despreciando
la perdida de energía por fricción. En la vida real no
se puede eliminar la fricción, por lo cual es dato de la
velocidad real debe de ser menor que el calculado.
8. POTENCIA
La potencia es la razón (o velocidad) a la cual la
energía es transferida. La mayoría de equipos
electrónicos especifican la potencia a la cual
trabajan, los motores también detallan la potencia
que son capaces de suministrar.
Pero, ¿en qué nos beneficia conocer la potencia de
estos equipos?, en la vida cotidiana conocer la
potencia de los equipos es muy importante ya que a
partir de su uso depende el consumo de energía
reflejado en nuestras facturas de electricidad. La
potencia puede ser expresada por medio de la
ecuación:
(Ec. 9)
Donde es la energía transferida en cualquiera de
sus formas (aplica para energía química, calorífica,
etc.) y es el tiempo que le toma realizar esa
transferencia o gasto de energía. De la ecuación
podemos ver que las unidades del sistema
internacional para la potencia es Joule/segundo, lo
que se conoce como Watts [W].
Por ejemplo, si tenemos un bombillo de y uno
de , quiere decir que por cada segundo que
estos bombillos estén encendido consumirán una
energía de y respectivamente.
El recibo de electricidad que mensualmente
recibimos, las unidades vienen en kilowatt-hora
(kw.h), con el fin de utilizar valores pequeños puesto
que el valor en joules es demasiado alto. Para
convertirlo en unidades de energía del Sistema
Internacional, multiplicamos por (ya que
1 kilowatt-hora equivale a ) el resultado
será en joules. Si por ejemplo, nuestro recibo
expresa un consumo de , realizamos la
multiplicación y el resultado es: 2 .
El siguiente ejemplo le servirá de guía, para realizar
la actividad 3 con el estudiantado:
Ejemplo 4. Si un foco de 100 W se mantiene
encendido cinco horas diarias durante los 30 días del
mes, a) ¿cuánta será la energía consumida en joules
por el foco durante los 30 días? b) ¿A cuánto
equivale en kw.h? c) Si el recibo de electricidad del
mes muestra un consumo de 120 kw.h ¿cuánto es el
porcentaje que le corresponde solamente al consumo
de ese foco?
Solución
a) Los de potencia que consume el foco son
100 joules por cada segundo, en una hora
tenemos:
Este resultado nos indica que, por cada hora que el
foco de 100 W pasa encendido consume
joules de energía. Si lo multiplicamos por cinco horas
tendremos el consumo diario de energía:
Para terminar multiplicamos por 30 el resultado
anterior, de esta manera podemos obtener el
consumo mensual.
64](https://image.slidesharecdn.com/c08-170424214125/75/CIENCIAS-8-80-2048.jpg)












![TERMODINÁMICA I Física
energía cinética (transferencia de calor) a las moléculas del hielo (partículas azules), pasando a estado líquido.
Algunos materiales tienen mayores capacidades para
conducir calor que otros, debido a sus estructuras
atómicas, por ejemplo los metales, que son buenos
conductores de calor y la electricidad debido a que
tienen en su última capa electrones libres que se
mueven con mayor facilidad; estructuras como el
plástico no conducen calor ni electricidad, por sus
estructuras compactas que se vuelven más difícil de
movilizar, sin embargo, eso no significa que no
conducen, ya que lo hacen de manera más lenta que
los conductores.
Si colocamos un recipiente de aluminio y una caja de
cartón en la refrigeradora y luego de un tiempo las
extraemos de la refrigeradora ¿cuál estará más fría?
El aluminio ya que es un mejor conductor, transmite
de manera más rápida la energía de vibración y
cinética de traslación.
La transmisión de calor por medio de la conducción
se cuantifica como la cantidad de calor transmitido
por unidad de tiempo. Si consideramos la
distribución de calor en una pared y que solo fluye
en una dirección podemos establecer la siguiente
ecuación del flujo de calor:
(Ec. 4)
Figura 11. Esquema de una pared por la cual fluye calor (T1>T2).
Donde k es la constante de conductividad térmica
que posee el material, en este caso el concreto de la
pared, y se expresa en unidades de [ ], L es la
longitud que recorre el calor con dirección
perpendicular al área de transmisión (A), y ΔT es la
diferencia de temperatura establecida entre el
medio y el material. Resultando el flujo con unidades
de ⌊ ⌋ [ ].
La convección consiste en el movimiento de masas
de líquidos y gases debido a la diferencia de
temperaturas; la convección conlleva en su proceso
una combinación de fenómenos físicos como la
conducción, fuerza de empuje y diferencias de
presión. Este fenómeno de transmisión de calor
ocurre solamente en los fluidos: líquidos y gases.
Tomemos el caso de una vela y el aire que lo rodea
(Fig. 12); el movimiento de las masas de aire por
convección conlleva varios pasos, que constituyen
una celda de convección:
1) La llama tiene contacto con la masa de aire,
debido a la diferencia de temperaturas entre ambos
permite que el calor se transmita por conducción,
agitando los átomos que constituyen el aire.
2) Luego las partículas del aire chocan entre sí de
manera aleatoria expandiéndose (difusión) y
separándose entre sí disminuyendo la densidad
promedio de esa masa permitiendo que la fuerza de
empuje actúe moviendo la masa menos densa y con
mayor temperatura (energía cinética de traslación
promedio) hacia arriba.
3) El desplazamiento de la masa de aire con menor
densidad y mayor temperatura genera una
diferencia de presión permitiendo el movimiento de
masa de aire de mayor densidad y menor
temperatura hacia la fuente de calor (la llama).
Figura 12. Imagen que muestra las diferencias de densidades
provocados por la combustión que se genera en la llama de la
vela con el oxígeno del aire.
77](https://image.slidesharecdn.com/c08-170424214125/75/CIENCIAS-8-93-2048.jpg)

![TERMODINÁMICA I Física
El núcleo interior y el núcleo exterior que se
encuentran a grandes temperaturas mueven masas
de material hacia la superficie terrestre por medio
de celdas de convección, los materiales más fríos
que ingresan por medio de placas de subducción
alimentan los mantos inferiores que desplazan
material a altas temperaturas hacia la superficie
terrestre, excretándolos a través de las placas
tectónicas divergentes y volcanes submarinos y
terrestres.
Figura 13. Playa El Espino, en el amanecer (arriba) y en el
atardecer (abajo). Por la mañana las brisas van del mar hacia la
tierra. Por la tarde la brisa va de la tierra hacia el mar.
Figura 14. Modelo de las celdas de convección que ocurre en los
mantos subterráneos de la Tierra.
La convección también incluye procesos donde
existen cambios de fases, tales como la ebullición y
la condensación. El primero se observa al calentar
agua en una olla; en este caso se forman burbujas de
vapor de aire en el fondo de la olla que se encuentra
a mayor temperatura, ocurriendo luego el cambio de
fase de líquido a gaseoso.
El segundo caso ocurre cuando se forman gotas de
agua en las afueras de una botella de agua fría
expuesta a la temperatura ambiente (Fig. 15); aquí el
vapor de agua en el ambiente se convierte en líquido
al tener contacto con la botella.
Figura 15. Condensación sobre la superficie de una botella de
agua helada.
La ecuación que nos determina la cantidad de calor
que se transfiere en un proceso de convección es:
( ) (Ec. 5)
Donde es el coeficiente de transferencia de calor
en forma de convección, posee unidades de [ ],
que son la potencia (watts) entre área de contacto
por temperatura (Kelvin). Las diferencias de
temperaturas son establecidas en la diferencia de
temperatura entre la superficie y el fluido. La
transferencia de calor por convección depende de
las condiciones geométricas y propiedades del
material de superficie así como de las propiedades
del fluido en movimiento.
Radiación Térmica
Cuando se sale a caminar en un día soleado se
percibe un aumento de temperatura en nuestra piel,
debido a que las terminaciones nerviosas de nuestra
A
79](https://image.slidesharecdn.com/c08-170424214125/75/CIENCIAS-8-95-2048.jpg)

![TERMODINÁMICA I Física
Los átomos emiten radiación cuando uno de sus
electrones pierde energía y pasa a un orbital de
menor energía (Fig. 17B), la diferencia energética
entre los orbitales es la energía de radiación; un
átomo absorbe radiación cuando uno de sus
electrones gana energía (Fig. 17A) y pasa a un orbital
de mayor energía (Lección 1 de Química).
Figura 17. A) Absorción energética de los electrones. B) emisión
energética de los electrones.
Cuando un cuerpo emite energía en forma de
radiación, esta depende de la capacidad de radiación
que posee una superficie comparado con la
capacidad de radiación de un cuerpo negro ( ), la
constante de Stephen Boltzman ( ) y la temperatura
de la superficie:
(Ec. 6)
Sus unidades son expresadas en watts sobre área
[ ]. En el caso de un cuerpo que absorbe energía
en forma de radiación, la energía depende de la
constante de absorción (G) y de la capacidad de
absorción de los materiales ( ); depende entonces
tanto de la naturaleza de la radiación absorbida
como del material y se expresa:
(Ec. 7)
Una manera práctica para relacionar la intensidad de
emisión y absorción de la radiación se explica por
medio de la figura 18.
Figura 18. Esquema representativo de la intensidad de la
radiación de la luz de un foco y un rayo láser.
En el caso del foco de luz, la radiación que es emitida
a una potencia de es absorbida a la distancia de
un metro por el ojo con una intensidad de
, debido a la manera de distribución de la
fuente que expande el área de contacto; ocurre el
caso contrario con el rayo láser el cual, debido a su
naturaleza no expansiva, mantiene y concentra la
radiación en un área de contacto constante, dicho de
otro modo, mantiene la intensidad de radiación.
La medida estándar de la radiación solar incidente es
de en un día despejado a nivel del mar; la
exposición a altas intensidades de radiación o
intensidades bajas en tiempos prolongados tienen
consecuencias en los seres vivos. En el caso humano
con vestimenta común su límite soportable de
radiación en un lapso breve temporal es y el
límite soportable en el caso de un bombero con traje
estructural es del orden de en un lapso
prolongado de tiempo.
Estos límites de absorción y emisión de los
materiales pueden ser comparados con la capacidad
de reflejar y absorber la luz, como en el caso de un
papel aluminio que refleja la radiación y los
materiales metálicos que absorben radiación.
81](https://image.slidesharecdn.com/c08-170424214125/75/CIENCIAS-8-97-2048.jpg)







![TERMODINÁMICA II Física
temperatura. A la cantidad de energía necesaria para
elevar un kilogramo de su masa en un grado
centígrado de temperatura, se le conoce como calor
especifico.
En conclusión el agua posee mayor calor específico
que la arena, dado que el agua necesita una mayor
cantidad de energía para elevar su temperatura
promedio. Por el contrario, la arena seca eleva su
temperatura rápidamente, por lo que posee un calor
especifico bajo.
Figura 6. Jugadores practicando sobre arena húmeda sin tener la
sensación de un gran aumento de temperatura en la planta de
los pies.
El calor específico puede cuantificarse estableciendo
las siguientes relaciones: se sabe que el flujo de calor
aumenta de manera directa la temperatura de un
cuerpo, ; si duplicamos la cantidad de masa
del cuerpo y suministramos la misma cantidad de
calor entonces es lógico que el cambio de
temperatura será menor, por lo que el calor es
directamente proporcional a la temperatura y la
masa, ; la cantidad de calor también
depende de las propiedades del material del cuerpo
como mencionamos anteriormente, lo que nos
permite definir la siguiente ecuación:
(Ec. 7)
Por lo que el calor específico se puede definir
matemáticamente como:
(Ec. 8)
Sus unidades son [ ]. La capacidad calorífica es
propia para cada material, algunos valores se
reflejan en la tabla 2.
Tabla 2. Valores de calor especifico para diversos materiales a
presión constante.
Sustancia
[ ]
Plomo (Pb) 128
Oro (Au) 129
Mercurio (Hg) 138
Cobre (Cu) 387
Hierro (Fe) 448
Arena 830
Vidrio 837
Aluminio (Al) 899
Aire 1 007
Vapor 2 001
Hielo 2 009
Agua 4 186
Para entender mejor este concepto analizaremos el
siguiente fenómeno: si se tienen dos globos inflados
uno con aire y otro con agua ¿qué sucederá si se
coloca cada globo sobre una llama? (Fig. 7); el globo
con aire explota de manera casi instantánea
mientras que el globo con agua se puede dejar por
más tiempo sin reventarse, ¿por qué?
Figura 7. Un globo con agua puesto sobre las llamas.
89](https://image.slidesharecdn.com/c08-170424214125/75/CIENCIAS-8-105-2048.jpg)













![ESTÁTICA DE FLUIDOS Física
1. DENSIDAD, TENSIÓN SUPERFICIAL, CAPILARIDAD
l llenar un globo con un mismo volumen de
aire y otro con agua podemos observar que
el globo toma la forma cuasi esférica en
ambos casos (Fig. 1); al presionar con un dedo los
globos y luego liberar la presión, éstos recuperan su
forma original ¿Por qué? Observamos también, que
es más difícil penetrar el globo con agua que el de
aire; esto no sucedería si el globo estuviese relleno
de concreto o madera ¿por qué el globo que
contiene agua es más pesado que el globo con aire?
Figura 1. El globo verde contiene aire, el rosado, agua.
Esto es debido a que tanto el agua, que se encuentra
en fase líquida, y el aire en fase gaseosa, poseen
estructuras moleculares que son menos compactas
que los materiales en fase sólida; por eso la materia
en cada una de las fases (líquida, sólida y gaseosa)
posee propiedades características.
En la figura 2 vemos que las estructuras más
compactas (A) simulan un sólido, las más dispersas
un gas (C) y las intermedias los líquidos (B). Si
lanzamos una canica dentro de cada una de las cajas
observaremos que las estructuras más compactas
chocan e interaccionan más entre sí; dispersarlas
requiere una mayor cantidad de energía que
dispersar a las de compactación intermedia. Las
menos dispersas apenas poseen interacción
molecular alguna.
Figura 2. Modelos de estructuras moleculares de un A) sólido, B)
líquido y C) gas.
Al comparar la cantidad de partículas en cada uno de
los cuadros de la figura 2, se puede definir cuál tiene
mayor concentración de materia (A), y cuál menor
concentración (C). Lo anterior nos ayuda a definir la
propiedad intensiva de la densidad, la cual poseen
todos los cuerpos; esta propiedad depende de la
cantidad de masa o materia que se concentra en un
espacio o volumen dado, lo que nos permite
establecer lo siguiente:
(Ec. 1)
Donde representa la densidad, la masa de la
materia y el volumen que ocupa, sus unidades en
el Sistema Internacional son [ ].
¡Cuidado con el concepto de peso y densidad!
muchas veces se confunde peso con densidad; en el
caso de la figura 2, “A” posee mayor concentración
de materia, y pesa más que “C”, suponiendo que
ambas poseen las mismas dimensiones o volumen;
por otro lado, ¿ocuparían un mismo volumen 1 kg de
madera y 1 kg de cobre?
En este ejemplo, observamos que la masa de la
madera y el cobre son iguales, pero el espacio que
ocupan son diferentes; la madera aproximadamente
ocuparía el tamaño de un cubo con aristas de 12 cm
(1.66 x 10-3
m3
) y un cubo de cobre ocuparía el
espacio de un cubo con aristas de 5 cm (1.12 x 10-4
m3
), esto confirma que la densidad del cobre es
mayor que la de la madera, porque concentra más
cantidad de materia en un mismo volumen.
Por lo tanto:
A
104](https://image.slidesharecdn.com/c08-170424214125/75/CIENCIAS-8-120-2048.jpg)
![ESTÁTICA DE FLUIDOS Física
Figura. 3. Proporción del tamaño de dos cubos de igual masa, el
de la izquierda hecho de madera y de cobre el de la derecha.
Tabla 1. Valores de densidad a temperatura ambiente (25 °C) y
a 1 atmósfera.
Materia Densidad [ ] Fase
Iridio 22 650 Sólida
Osmio 22 610 Sólida
Oro 19 300 Sólida
Mercurio 13 600 Líquida
Cobre 8 920 Sólida
Aluminio 2 700 Sólida
Concreto 2 300 Sólida
Glicerina 1 260 Líquida
Agua de mar 1 025 Líquida
Agua 1 000 Líquida
Hielo 919 Sólido
Alcohol Etílico 785 Líquida
Gasolina 680 Líquida
Dióxido de
Carbono
198 Gaseosa
Oxigeno 143 Gaseosa
Aire 129 Gaseosa
Vapor de agua 59.8 Gaseosa
Helio 17.9 Gaseosa
Hidrogeno 8.99 Gaseosa
En la tabla 1, observamos que los valores más altos
de densidad los poseen materiales sólidos, dado el
mayor grado de compactación entre sus moléculas
(con excepción del mercurio que es un metal
líquido). Los materiales en fase gaseosa son los de
menor densidad, debido a la separación existente
entre las moléculas que los constituyen.
Retomando al caso de los globos al inicio de la
lección, aunque estos poseen volúmenes similares
(aproximadamente un litro, equivalente a 0.001m3
),
el globo con agua contiene más masa que el globo
con aire ¿por qué? Retomando la fórmula de la
densidad en términos de la masa:
, entonces
El valor de la densidad del agua líquida, explica que
esta concentra mayor cantidad de materia que un
mismo volumen de aire, por lo que es predecible que
la masa de agua es mayor:
( ) ( )
( )( )
Por lo que comprobamos que , en
los globos.
Como se mencionó, el estado líquido es la fase
intermedia entre los sólidos y los gases, en términos
de las distancias intermoleculares entre sus
partículas. Una de sus propiedades es que los
líquidos toman la forma del recipiente que los
contiene; se podría pensar por eso que no tienen
forma propia, pero sí la poseen (ver actividad 1).
Al observar los clavadistas olímpicos surge la
pregunta ¿por qué un clavadista no puede lanzarse al
agua con los brazos extendidos o de espalda? Esto se
explica por otra propiedad que poseen los líquidos
¿Cuál es el objeto más denso?
Los objetos más densos en nuestro universo son las estrellas
de neutrones. Estas estrellas se forman cuando explota una
estrella tipo supernova. Tienen al inicio aproximadamente dos
veces el tamaño del Sol, luego de explotar, acumulan materia
en un volumen con diámetro de 19.31 Km. Una cucharada de
ese material supernova tendría una masa de
aproximadamente, mil millones de toneladas, por lo que este
material es aproximadamente 8 billones de veces más denso
que el Iridio.
105](https://image.slidesharecdn.com/c08-170424214125/75/CIENCIAS-8-121-2048.jpg)







![ESTÁTICA DE FLUIDOS Física
contacto, distribuyéndose la fuerza de manera más
amplia (Fig. 15). En el caso del ladrillo colocado de
forma vertical, posee menor área de contacto, por
ende concentra más la misma cantidad de fuerza.
La presión se define como la fuerza aplicada de
manera perpendicular a una superficie o área de un
objeto.
⃑
(Ec. 2)
Cuyas unidades son [ ] [ ]
Las unidades de medición son los pascales (Pa). La
presión es inversamente proporcional al área, es
decir una mayor área implica una menor presión y
una menor área implica una mayor presión.
Regresando a la figura 15:
Las fuerzas 𝐹⃑ 𝐹⃑2 y, como 2 ↔ 2
Cuando se inserta una aguja sobre un objeto o
material, se pueden alcanzar presiones de
aproximadamente Pa debido al área
extremadamente pequeña de la punta de la aguja
que no supera los 1x10-10
m2
.
Figura 16. La relación entre el área de contacto y la presión: un
mosquito perfora la piel fácilmente por la gran presión ejercida
debido a la diminuta área de la probóscide.
Para surfear se necesitan tablas con áreas de
contacto grandes para poder distribuir el peso de la
persona de la mejor manera, disminuyendo la
presión sobre el agua, evitando así que se hunda.
Figura 17. Un surfeador utiliza una tabla con área grande para
poder deslizarse sobre las olas en la playa El Sunzal.
La fuerza y la presión son directamente
proporcionales; por ejemplo, retomando el caso de
una aguja, si se aplica una fuerza de 𝑁 sobre esta,
la presión será mayor que al aplicar 𝑁, dado que
el área de la aguja es la misma.
2 y 𝐹⃑ 𝐹⃑2 𝑠 2
Los ejemplos anteriores mencionan objetos sólidos,
pero ¿cómo funciona la presión en un cuerpo líquido
o gaseoso? En el caso de los líquidos estos no se
comprimen de manera significativa al ser sometidos
a una presión determinada, es decir que mantienen
prácticamente su volumen inicial. Los gases son
comprensibles dado que su volumen cambia según la
presión a la cual se encuentra sometido (Fig. 18).
Figura 18. Un líquido y un gas comprimidos dentro de una
jeringa. El líquido no cambia su volumen significativamente al
efectuar una presión sobre él; los gases sí.
A pesar de que los líquidos son poco comprensibles
poseen características comunes con los gases, pues
113](https://image.slidesharecdn.com/c08-170424214125/75/CIENCIAS-8-129-2048.jpg)




![ESTÁTICA DE FLUIDOS Física
Fluidos: Es la materia en fase líquida o gaseosa, poseen densidades menores respecto a los materiales en fase
sólida y existe una mayor movilidad entre sus partículas.
Tensión Superficial: Se debe a la fuerza intermolecular entre las moléculas de un líquido. Se define como la
resistencia al aumento de superficie en éstos.
Presión: Es la cantidad de fuerza aplicada de manera perpendicular sobre un área de contacto de un cuerpo.
Fuerza de Empuje: Es la fuerza equivalente al peso de la masa de fluido desplazado por el cuerpo sumergido en
este.
Principio de Pascal: Un cambio de presión aplicado a un fluido en reposo dentro de un recipiente se transmite
sin alteración a través de todo el fluido.
Si desea enriquecer más su conocimiento, consulte:
1. La Web de Física (2010) Fluidos y Medios Continuos. Recuperado en noviembre de 2011, de
http://goo.gl/mHDJ5
2. Planeta Sedna (2003, septiembre) Principio de Pascal. Argentina, Pellini Claudio, recuperado en diciembre
2011 http://goo.gl/8jhsx
3. Física con Ordenador (2010, diciembre) Curso Interactivo de Física en Internet, [en línea], Universidad País
Vasco, España: Franco, A. recuperado noviembre de 2011, http://goo.gl/uh06u.
4. Serway, R, Faughn, J. (2005). Physics (1era Ed.) E.E.UU. Holt Rinehart and Winston.
118](https://image.slidesharecdn.com/c08-170424214125/75/CIENCIAS-8-134-2048.jpg)





















![ONDAS MECÁNICAS Física
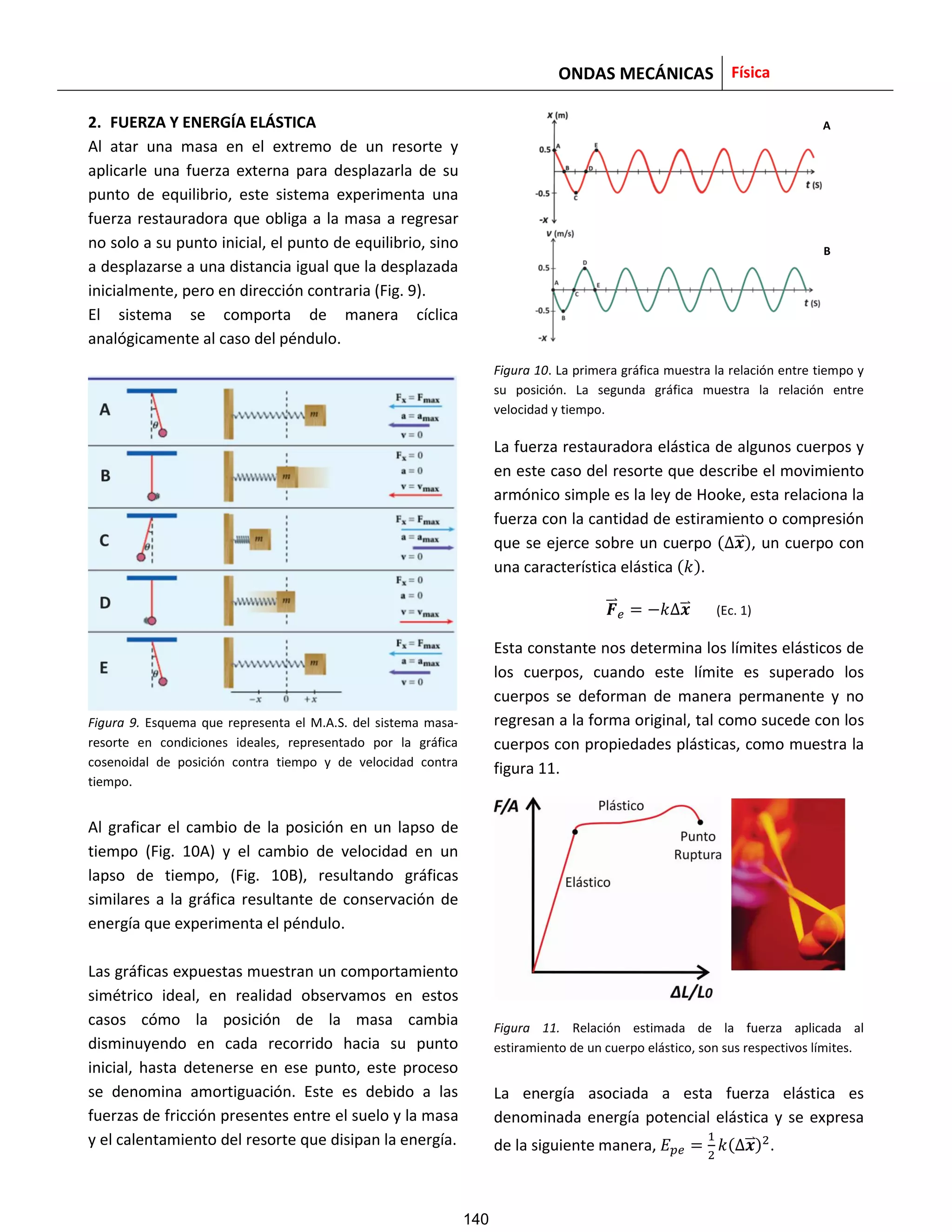
Figura 12. Esquema de cómo las estructuras moleculares de los
sólidos amorfos se adecuan según la fuerza aplicada. La
plastilina, el plástico, el hule y el policloropreno que constituye
los globos, son sólidos que poseen estructuras con arreglos
compactos pero sin un orden específico denominándose como
amorfos. Las estructuras sólidas amorfas generan espacios entre
sí, permitiendo partículas de aire insertarse y proporcionándole
la flexibilidad conocida.
3. PROPIEDADES DE LAS ONDAS
La perturbación de la materia genera vibraciones
periódicas que liberan energía y esta se transporta
en forma de ondas, tal como se observa cuando una
gota de agua cae en un líquido (Fig. 13). La fuerza
gravitatoria obliga a la gota caer y perturbar el agua,
generando ondas transversales que transportan la
energía; para comprender la forma que las ondas
transportan energía es necesario conocer sus
respectivas características y las propiedades
ondulatorias.
Figura 13. Ondas generadas debido a la caída de la gota sobre el
agua en reposo.
Al observar la aguja segundera sobre el número 12
en el reloj en la pared, se sabe que esta aguja vuelve
a marcar ese número después de transcurrir un
minuto, cumpliendo un ciclo, tal como el recorrido
cíclico del sistema masa resorte (Fig. 9). El tiempo
que tarda la aguja para llegar a la posición en el cual
se inició el conteo del tiempo, es lo que se denomina
periodo (T), es decir el tiempo que tarda para
cumplirse un ciclo.
La frecuencia (f) se relaciona de manera inversa al
periodo; este se define como la cantidad de ciclos
que ocurren en un lapso de tiempo.
(Ec. 2)
Sus unidades son [ 𝑠
] que llevan por nombre Hertz.
La frecuencia es muy importante para conocer la
velocidad que posee una onda de la siguiente
manera:
𝜆 y también como:
𝜆
Donde el símbolo λ es la distancia en el ciclo
mostrado (Fig. 14) entre cresta y cresta; esto se
denomina longitud de onda (λ) y posee unidades de
metros por lo que el producto entre la longitud de
onda con frecuencia resulta en velocidad.
El periodo también se puede definir a partir de las
crestas de la onda, como el tiempo que le toma
viajar a la onda de la posición de la cresta 1 a la
cresta 2.
Por ejemplo, si asumimos que tenemos una longitud
de onda equivalente a dos metros y que el tiempo en
que viajó de cresta a cresta fue de cuatro segundos,
la velocidad con que la onda esta viajando es:
2.0 (
1
4.0
) 0.5
O también, expresado en función de la frecuencia
como:
2.0 0.25 −
0.5
141](https://image.slidesharecdn.com/c08-170424214125/75/CIENCIAS-8-157-2048.jpg)















![ONDAS MECÁNICAS Física
RESUMEN
Vibración: Es el movimiento oscilatorio generado
por las fuerzas restauradoras que experimenta un
cuerpo.
Movimiento Armónico Simple: Es el movimiento de
desplazamiento alrededor de un punto de equilibrio
y que presenta un patrón periódico.
Periodo: Es el tiempo que tarda un objeto para
completar un ciclo.
Frecuencia: Es la cantidad de ciclos que cumple el
movimiento de un cuerpo en un segundo.
Longitud de onda: es la distancia existente entre
crestas o valles sucesivos en una onda.
Ondas estacionarias: Ondas que se interfieren a
determinadas frecuencias y muestran una simetría
donde estas interferencias son nulas y otras poseen
un desplazamiento máximo.
Sonido: Es una onda mecánica longitudinal producto
de la vibración de los cuerpos.
Resonancia: Es el aumento de la amplitud de las
ondas generadas por un objeto, debido a la
vibración, a la frecuencia natural de este.
Si desea enriquecer más su conocimiento, consulte:
Serway, (2005) Physics: Mechanical and Sound Waves. New York: Holt Rhinehart.
Berg, R. (2005) Physics of Sound. New York Addison Wesley.
Física con Ordenador (2008) Medida de la constante del muelle [en línea], País Vasco, España: Franco, A.
Recuperado en enero de 2012, de http://goo.gl/SGfwq.
Hyper physics (2011) Propagación del Sonido [en línea], Georgia State University: Departament of Physics and
Astronomy. Recuperado enero 2012 de http://goo.gl/nsBB7
The Physics Classroom (2011) Waves, [en linea], Glenbrook High School, Illinois: Henderson, T., Recuperado
diciembre 2011 de http://goo.gl/3QzVZ
158](https://image.slidesharecdn.com/c08-170424214125/75/CIENCIAS-8-174-2048.jpg)








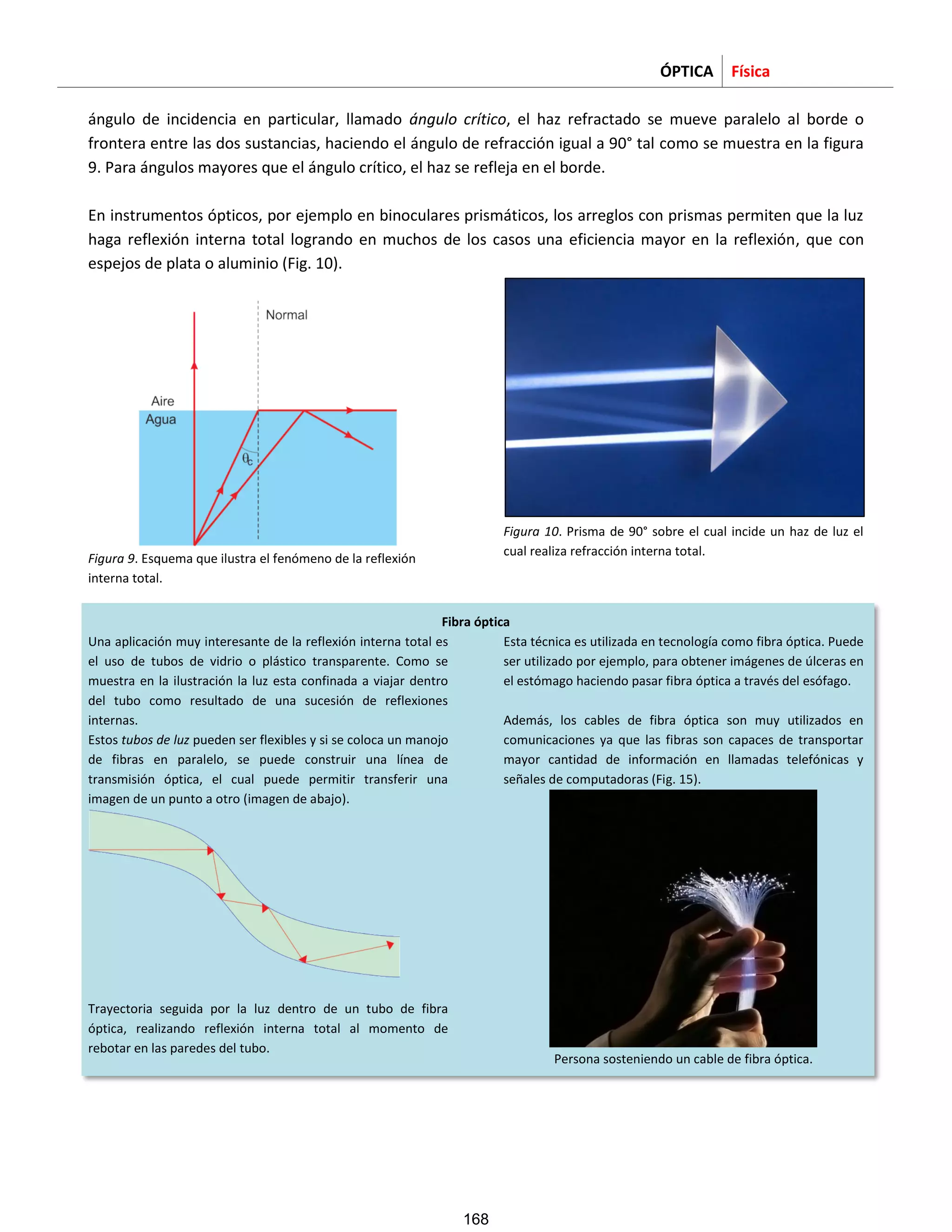













![ELECTRICIDAD Física
Campo Eléctrico
Al igual que cuando una fruta cae por encontrarse
inmersa en un campo gravitatorio, también las
partículas cargadas se encuentran sometidas a un
campo eléctrico debido a su naturaleza eléctrica.
Estas acciones a distancias poseen sin embargo
diferencias; el campo y fuerza eléctrica son mucho
más intensas que las gravitatorias pero poseen
menor alcance.
Un ejemplo que ayuda a concebir la idea de un
campo, es cuando el camión recolector de basura
llega a tu colonia; este espacio es alterado dado que
a medida se acerca a tu hogar se percibe con mayor
intensidad el olfato y sonido, y disminuye medida se
aleja dicho camión.
El campo eléctrico describe como los objetos
cargados afectan el espacio que los rodea y existen
independientemente de si lo percibimos o no, la
manera de cómo afecta el espacio depende de la
intensidad del campo y es cuantificado de una
manera vectorial como en los siguientes términos.
⃑⃑
⃑
(Ec. 2)
Donde la fuerza eléctrica ejercida sobre dos cargas
puntuales es dividido entre una carga de prueba (q0)
(Fig. 13).
Figura 13. Esquema de dos partículas de cargas opuestas;
generan una fuerza eléctrica y un campo eléctrico en la misma
dirección de la fuerza eléctrica sobre una carga de prueba
positiva.
Desarrollando la ecuación de la fuerza eléctrica, se
observa que el campo depende directamente de la
carga puntual que se analiza e inversamente a la
distancia entre las cargas u objetos de interacción:
⃑⃑ (Ec. 3)
Esta razón define la intensidad de un campo
eléctrico que ejerce una carga sobre una carga de
prueba, sus dimensiones son [⃑⃑] [ ].
Ejemplo 3. Si el campo eléctrico de un electrón que
pertenece a un átomo de hidrogeno es de
. Calcula la distancia del electrón hacia
el núcleo del átomo.
⃑⃑
Conocemos y
Trabajando la ecuación en términos de la distancia
entre el núcleo y el electrón, obtenemos:
⃑⃑
√
⃑⃑ √( )
( )
Este es la distancia promedio existente entre las
partículas del átomo de hidrógeno.
Los campos eléctricos varían según el caso; por
ejemplo, el campo eléctrico es mucho más intenso
en medio de una tormenta eléctrica ( ) que
el campo debajo de la luz de una lámpara eléctrica
( ).
El campo del primero es 1000 veces más intenso que
el segundo, esto es debido a la diferencia de carga
que poseen; el campo de una tormenta eléctrica
puede igualarse al campo generado debajo de la
lámpara, al alejarnos de la tormenta eléctrica varios
kilómetros.
Entonces al igual que la fuerza eléctrica, el campo
eléctrico aumenta su intensidad a medida que
184](https://image.slidesharecdn.com/c08-170424214125/75/CIENCIAS-8-200-2048.jpg)



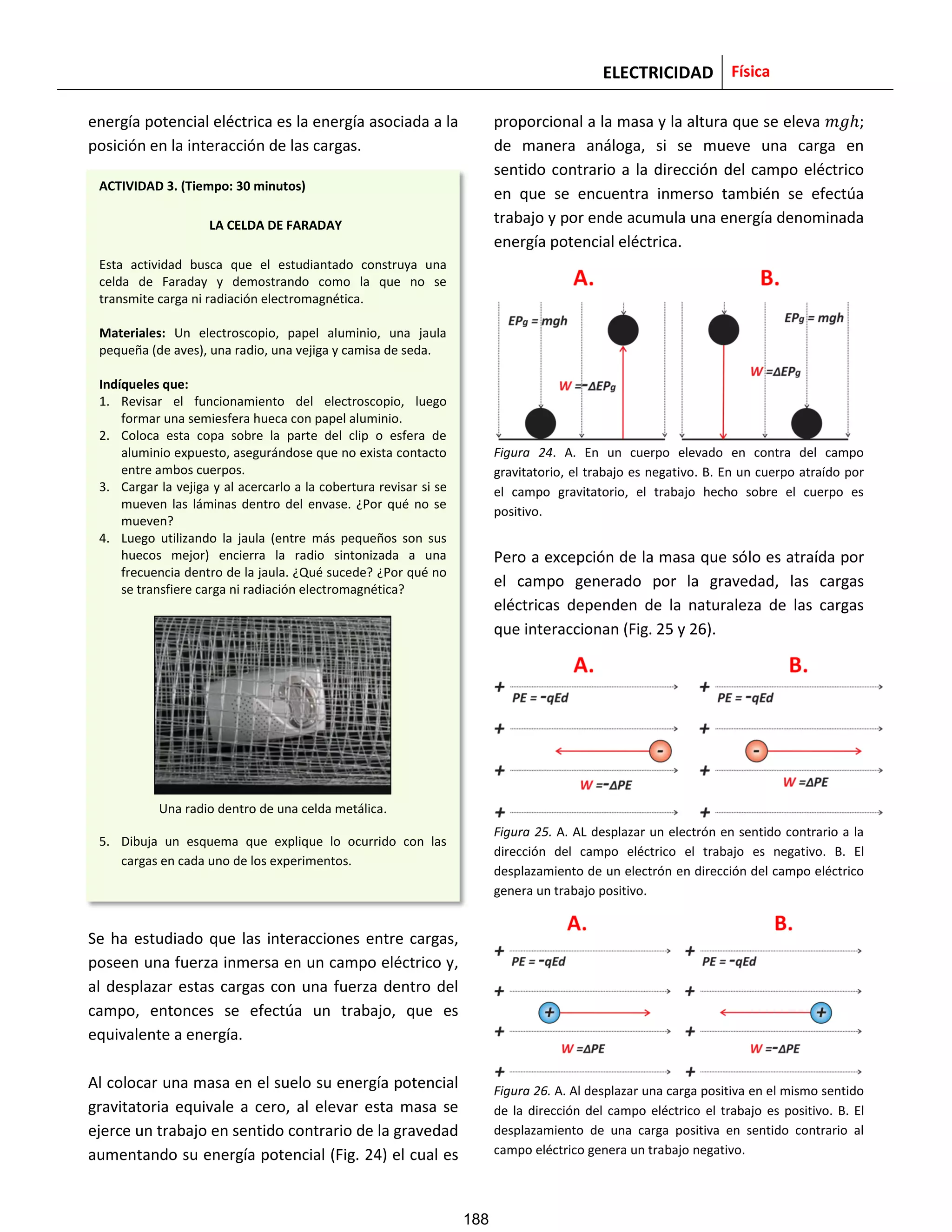
![ELECTRICIDAD Física
En los casos donde el trabajo es positivo significa que
se gana energía potencial eléctrica y el trabajo
negativo pierde energía potencial eléctrica, siempre
y cuando el desplazamiento no sea perpendicular al
campo eléctrico. Retomando el concepto de trabajo
y energía donde éste equivale a la fuerza que
desplaza un cuerpo a una distancia.
| ⃑| | ⃑| (Ec. 4)
En términos eléctricos el trabajo realizado se expresa
en términos de energía potencial eléctrica y se
expresa en:
| ⃑ | | ⃑|
Relacionando la fuerza eléctrica con el campo
eléctrico, sustituimos en la ecuación de energía
potencial eléctrico.
( ) (Ec. 5)
Las unidades correspondientes en el SI son en Joules.
[ ] [ ] [ ] [ ]
En la vida cotidiana se conoce que una batería posee
energía eléctrica almacenada; cuando se adquiere
una batería AA, la información dice que posee la
capacidad de suministrar 1.5 Voltios ¿qué significa
esto? ¿Por qué esta energía no se expresa en Joule?
Los 1.5 Voltios, son la cantidad de energía eléctrica
que se le proporciona a los electrones
desplazándolos para luego disipar la energía en
forma de calor alimentando los dispositivos para su
funcionamiento.
Las unidades de Voltios involucran las unidades de
Joule; al igual que a un punto del campo gravitatorio
se le puede asociar un potencial gravitatorio
independientemente si existe una masa en esa
ubicación, también existe un potencial eléctrico en
los campos eléctricos independientemente exista
una carga en esa posición (Fig. 27).
Figura 27. Un punto independientemente de que exista carga en
él, también posee un potencial eléctrico.
El potencial eléctrico sobre una carga se define
como:
( )
(Ec. 6)
Sus unidades son expresadas en [ ] y equivalen a
unidades de voltios [ ].
El potencial eléctrico nos informa sobre la energía
asociada a un punto específico del espacio del
campo eléctrico; esta definición es muy útil para
cargas en estados estáticos, pero para cargas en
movimiento es necesario asociar la cantidad de
energía que representa para que una carga se
desplace en un espacio del campo eléctrico; para eso
se utiliza el diferencial de potencial eléctrico ( ).
La diferencia de potencial energético es el cambio
energético que necesitaría o adquirirá una carga
eléctrica para trasladarse en ese diferencial espacial,
independientemente exista una carga o no, en esos
puntos.
(Ec. 7)
En el caso de la batería con el foco, el dato de 1.5
Voltios especifica que una carga al desplazarse en
este diferencial energético acumula 1.5 J de energía,
al recorrer el circuito la carga cede esta energía al
foco cayendo a su punto original (Fig. 28).
189](https://image.slidesharecdn.com/c08-170424214125/75/CIENCIAS-8-205-2048.jpg)
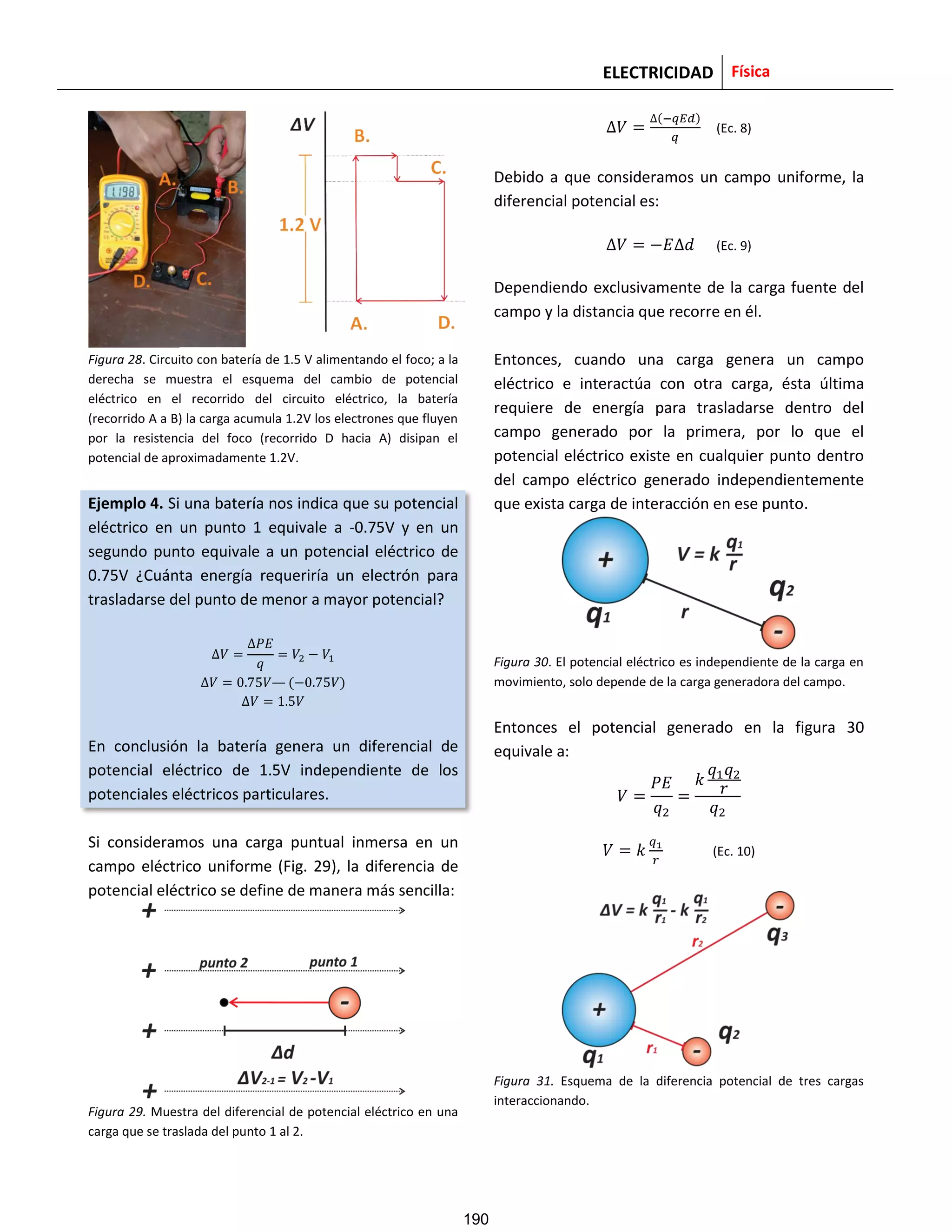
![ELECTRICIDAD Física
Un diferencial potencial eléctrico, como el de la
figura 31, equivale a:
( ) (Ec. 11)
Si la distancia de uno de los puntos es sumamente
grande, entre mayor sea la distancia el valor
resultante se hace despreciable. Por ejemplo, al
dividir:
( )
( )
( )
Entonces una carga que se encuentre en el infinito
no tiene ningún efecto sobre el sistema estudiado y
basta con la siguiente definición de diferencia de
potencial eléctrico:
(Ec. 12)
Corriente eléctrica
La corriente de agua en un rio (Fig. 32) fluye debido a
diferencias de potenciales gravitatorias que se
transforman en energía cinética hasta llegar en
algunos casos, a la costa oceánica.
Figura 32. Corriente de agua del río Sapo Morazán.
De manera similar funciona la corriente eléctrica;
ésta trata sobre el flujo de carga a través de
diferentes medios, por lo que podemos definirla
como:
(Ec. 13)
Donde es la cantidad de carga que atraviesa en
una sección transversal de un material conductor en
un lapso de tiempo determinado. Sus unidades son
[ ] y equivalen a la unidad de Amperios, [ ].
Figura 33. Flujo de electrones similar a un flujo de agua.
Como se mencionó sobre el comportamiento de las
cargas en los diferentes tipos de materiales, el flujo
de carga es óptimo en los materiales conductores,
verificado a través de un circuito que cuando es
interrumpido con un material aislante las cargas no
fluyen (Fig. 34).
Figura 34. Fotos de circuitos interrumpidos por material A.
aislante (tapón de lapicero) y B. material conductor (llave de
metal).
Al pensar como fluyen los electrones dentro del
material conductor existen convenios para
determinar la dirección del flujo de electrones (Fig.
35).
Figura 35. La corriente eléctrica se define en sentido contrario
del movimiento de los electrones.
191](https://image.slidesharecdn.com/c08-170424214125/75/CIENCIAS-8-207-2048.jpg)


![ELECTRICIDAD Física
Ejemplo 5. La velocidad de arrastre con una
corriente aplicada de 10 amperios sobre un alambre
eléctrico de cobre es aproximadamente de
.
Si la cantidad de alambre eléctrico existente entre el
interruptor y un foco es de 5.0 metros, calculen el
tiempo que tardarían los electrones para trasladarse
esa distancia.
Retomando la ecuación de velocidad y dado que
conocemos la distancia podemos conocer el tiempo.
Eso equivale aproximadamente 339 minutos lo que
implica que tardaría más de cinco horas para
trasladarse esos cinco metros.
La corriente y el ATP
Actualmente la biología estudia la aplicación de micro corrientes
en los vasos sanguíneos de los seres vivos para ayudar el proceso
de producción de ATP.
Transporte activo de nutrientes desde el exterior hacia el
interior de la célula.
Esta electro estimulación débil con micro corrientes son del
orden aproximado de provocando una mayor eficiencia en
la síntesis de proteínas, la descomposición de la histamina, acido
láctico, bradiquinina entre otros, y mejora el transporte activo
de los aminoácidos, favoreciendo la recuperación de ligamentos
dañados acelerando la cura de heridas, úlceras y alivio de dolor.
Figura 39. Modelo de un circuito interrumpido por un clip.
La resistencia eléctrica se define como la razón de la
diferencia de potencial eléctrico que causa el
movimiento de la carga dividido entre la corriente.
(Ec. 15)
Este posee la unidad de Ohm [ ] y es constante en
ciertos materiales como en los metales, debido a que
su razón es lineal (Fig. 40). Existen materiales que no
obedecen esta ley debido a que su resistencia no es
constante, como en el caso de los diodos o ciertos
filamentos usados en los focos.
Figura 40. La gráfica lineal representa un material óhmico y la
grafica exponencial representa un material no óhmico.
Una manera de comprobar un material no óhmico es
dibujando una gráfica de voltaje versus corriente y
utilizando una fuente de voltaje variable conectado a
194](https://image.slidesharecdn.com/c08-170424214125/75/CIENCIAS-8-210-2048.jpg)
![ELECTRICIDAD Física
un foco de lámpara, midiendo la corriente del foco
utilizando un multímetro a diferentes voltajes (desde
1 V hasta 12 V, para no quemar el foco), resultando
en una grafica similar a la derecha de la figura 40.
Al no poseer una fuente variable se puede utilizar
varias baterías de 1.5 V, agregar baterías para
aumentar la diferencia de potencial del circuito
(hasta llegar a 12 V), midiendo la variación de
corriente del foco de lámpara y construyendo la
gráfica resultante.
Actividad 4. (Tiempo: 15 minutos)
LEY DE OHM
Calcular las variables faltantes de la siguiente tabla con sus
respectivos esquemas y analizar el comportamiento de la
resistencia.
Tabla I. Tabular los datos faltantes y dibujar el esquema del
circuito.
Al mantener una resistencia constante y al aumentar el
voltaje la corriente también aumenta.
Manteniendo el voltaje constante y disminuyendo la
corriente la resistencia aumenta.
Manteniendo la corriente constante y aumentando la
resistencia el voltaje aumenta el voltaje del circuito.
Al pensar en la carretera en que viajan los
electrones, viajar en una calle hecha de asfalto no es
igual a viajar en una hecha de cemento; agregando
factores como lo ancho y largo de esta carretera,
pueden relacionarse las variables que afectan la
resistencia (Fig. 41).
Cada material posee una estructura atómica o
molecular específica lo que les confiere una
característica denominada coeficiente de resistividad
( ); por ejemplo, si una estructura es más compacta
entonces el flujo de electrones es más difícil.
Lo largo del material ( ) es directamente
proporcional a la resistencia, dado que entre más
larga sea la carretera, los electrones tendrán una
mayor distancia y obstáculos que recorrer; entre
más largo el material mayor la resistencia. Lo ancho
se relaciona con el área ( ) que posee el material
conductor; a mayor área mayor cantidad de
electrones que pueden fluir y por ende se genera
una menor resistencia. Esto permite reformular la
ecuación de resistencia de la siguiente manera:
(Ec. 16)
Existe otro factor influyente que es la temperatura; a
mayor temperatura los átomos aumentan su energía
de vibración y traslación aumentando a la vez la
cantidad de choques de los electrones en
movimiento, por lo que un material conductor a
mayor temperatura aumenta su resistencia.
( )[ ( )]
(Ec. 17)
Figura 41. Factores que afectan el flujo de electrones en un
material conductor.
Voltaje ( ) Corriente
( )
Resistencia
total ( )
1.5 V 0.5 A
3 V 3 Ω
1.5 A 3 Ω
1.5 V 0.25 A
3 V 6 Ω
0.75 A
4.5 V 9 Ω
195](https://image.slidesharecdn.com/c08-170424214125/75/CIENCIAS-8-211-2048.jpg)







![ELECTRICIDAD Física
La potencia eléctrica se pude definir de la siguiente
manera:
(Ec. 20)
El potencial eléctrico en términos del diferencial de
potencia eléctrica se relaciona así:
( )( )
Y sustituyendo en la ecuación de potencia eléctrica:
( )( )
Se conoce que la carga en un lapso de tiempo define
a la corriente eléctrica; la ecuación puede ser
replanteada de la siguiente manera:
(Ec. 21)
Sus unidades son definidas como Watt (vatios)
[ ] dado que se deduce como [ ]. La potencia para
un material que cumpla la ley de Ohm puede
rescribirse en la ecuación de potencia eléctrica
como,
( )
También, en términos del diferencial de potencial
eléctrico:
( )
(Ec. 22)
Las tres ecuaciones expresan las mismas unidades de
energía disipada por segundo.
Ejemplo 9. Tomasa decide, para ahorrar energía
eléctrica remplazar el foco de su cuarto que posee
una potencia de por uno de ; ella lo
utiliza un promedio de 4 horas por día. ¿Cuánto
dinero ahorra en el mes si la compañía eléctrica
cobra un estimado de $0.22 /kW·h?
Tomasa utiliza el foco a aproximadamente 4 horas
en un día y en un mes posee 30 días lo que significa
el consumo de 120 horas en el mes.
El foco consume cada hora y al
multiplicarlo por la cantidad de horas en el mes y por
la tarifa estimada obtenemos el consumo por ese
foco.
El consumo por parte del foco de es:
Al restar los montos consumidos con los diferentes
tipos de foco Tomasa ahorra $0.66 cada mes,
¿cuánto ahorraría si equipara toda su casa con focos
de esa potencia?
Actividad 7. (Tiempo: 90 minutos)
CALCULANDO LA CANTIDAD DE KILO WATTS
Materiales: Aparatos electrodomésticos: televisión, radio,
tostadoras, refrigeradoras, recibo de energía eléctrica, lápiz
calculadoras.
1. Buscar los datos de la cantidad de potencia eléctrica que
ejerce cada uno de los dispositivos eléctricos de tu casa.
El costo de la energía eléctrica se cuantifica con las unidades
de kilowatt por hora ( ).
2. Calcula el costo kilowatt hora utilizando tu recibo de energía
eléctrica.
3. Calcula la cantidad de potencia eléctrica por hora que
consume cada uno de los electrodomésticos usados.
¿Cuántas horas son utilizadas cada electrodoméstico en un
día?
4. Calcula el costo mensual de energía eléctrica consumida y
luego compara con el recibo de energía eléctrica.
5. Discute con la clase las maneras de ahorrar energía ya que
no solo es necesario por los costos económicos sino también
por los desgastes ambientales.
6. Investigar sobre las diferentes fuentes de energías
renovables y discutir en clase.
203](https://image.slidesharecdn.com/c08-170424214125/75/CIENCIAS-8-219-2048.jpg)
![ELECTRICIDAD Física
RESUMEN
Electrones de Valencia: Son los electrones que se encuentran en los orbitales más externos de los átomos,
algunos poseen la facilidad de generar enlaces que conforman moléculas, o compuestos. Según la estructura
en que se encuentren hacen un cuerpo conductor o aislante.
Conductor eléctrico: Son materiales que debido a sus estructuras atómicas permiten el flujo de electrones.
Aislante eléctrico: Son materiales que debido a sus estructuras atómicas no permiten el flujo d electrones
libres.
Fuerza Eléctrica: es el resultado de las interacciones entre las cargas negativas (electrones) y las cargas
positivas (protones), donde las cargas opuestas (negativas-positivas) generan una fuerza de atracción y la
interacción de cargas iguales generan una fuerza de repulsión.
Campo Eléctrico: es una región del espacio donde la una carga de prueba experimenta una fuerza eléctrica.
Potencial Eléctrico: es la cantidad de trabajo que se debe ejecutar contra una fuerza eléctrica para desplazar
una carga de un punto de referencia hacia otro punto, acumulando energía potencial eléctrica.
Voltaje: es la diferencia de energía de potencial eléctrica que posee una fuente de energía eléctrica o fuerza
electromotriz que ejercen sobre los electrones en un circuito eléctrico cerrado.
Corriente Eléctrica: es la razón de la cantidad de cargas eléctricas que fluyen por un área transversal
determinada.
Resistencia Eléctrica: es la oposición hacia el flujo de corriente eléctrica que presenta los materiales.
Si desea enriquecer más su conocimiento, consulte:
1. Física con Ordenador (2008) La Ley de Coulomb, [en línea], País Vasco, España: Franco, A. Recuperado en
febrero de 2012, de http://goo.gl/5Jy1k.
2. Las Maravillas de la Física (2005) Electricidad, [en línea], Universidad de Wisconsin, California, Estados
Unidos. Prof. Clint Sprott. Consultado febrero 2012 de: http://goo.gl/nrABU
3. Fundación de Tiburones/Hai-Stiftung (1997) Los Sentidos del Tiburón, [en línea], Canadá. Consultado
febrero 2012 de: http://www.shark.ch/Information/Senses/index.html
4. Proyecto Virtual Feria de Ciencia (2011) La Invención de la Celda de Faraday, [en línea], Julian Rubin.
Consultado enero 2012 de: http://goo.gl/OHGRw
5. Fun Projects (2010) Circuitos con Plastilina, [en línea], Universidad St. Thomas, Estados Unidos, AnnMarie
Thomas. Consultado marzo 2012 de: http://goo.gl/tQlCX
204](https://image.slidesharecdn.com/c08-170424214125/75/CIENCIAS-8-220-2048.jpg)























![ASTRONOMÍA Física
perihelio) el área que barrió es exactamente la
misma que la anteriormente descrita.
Lo que podemos concluir a partir de la segunda ley
de Kepler, es que los planetas viajan a mayor
velocidad cuando están en el perihelio porque tienen
que desplazarse una mayor longitud para barrer la
misma área; en cambio en el afelio, el movimiento
del planeta es a menor velocidad puesto que con
solo recorrer una distancia pequeña lograr barrer un
área grande.
Figura 7. Ilustración de la segunda ley de Kepler.
La tercera ley de Kepler es la que se utiliza para
poder determinar el período que le toma a un
planeta dar una vuelta completa sobre su órbita; el
período de la órbita depende de la distancia del semi
eje mayor. Entre más grande es la distancia que
tiene el semi-eje mayor de la órbita mayor será el
tiempo que le toma el poder realizarla (Fig. 8). El
tiempo suele ser expresado en años aunque en
muchos textos también puede ser encontrado en
días. La distancia del semi-eje mayor, según el
sistema internacional, por tratarse de una longitud,
debe ser expresada en metros. Debido a que en
astronomía las distancias son muy grandes se suelen
expresar en unidades astronómicas (UA), Años Luz
(Yl) y Parsec (Pc).
Una unidad astronómica es la distancia media Sol-
Tierra la cual es de ; las unidades
astronómicas son muy utilizadas para expresar
distancias de objetos dentro del Sistema Solar. Los
valores de distancia media y período del planeta se
encuentran expresados en la Tabla 2.
4. LEY DE GRAVITACION UNIVERSAL
Isaac Newton en su estudio del movimiento de la
Luna, logró determinar lo que se conoce hoy en día
como Ley de Gravitación Universal, en la que
establece la fuerza de atracción qué experimentan
dos objetos (Fig. 9), siendo directamente
proporcional a sus masas e inversamente
proporcional al cuadrado de la distancia que los
separa. Más adelante se encontró el valor esa
proporcionalidad dando como resultado la expresión
matemática:
Donde, y son las masas de los 2 objetos a
analizar, es la constante de gravitación universal
cuyo valor es ⁄ y es la
distancia de separación entre los objetos.
Figura 8. Ilustración de la tercera le de Kepler.
Tabla 2. Valores de Distancia desde el Sol y periodo orbital para
los planetas del Sistema Solar
Planeta Distancia desde el Sol
[UA]
Periodo
[años]
Mercurio 0.387 0.24
Venus 0.723 0.62
Tierra 1.000 1.00
Marte 1.524 1.88
Júpiter 5.203 11.86
Saturno 9.539 29.46
Urano 19.182 84.01
Neptuno 30.058 164.8
¿Cómo construyen una elipse los jardineros?
Para poder lograr una forma elíptica en la decoración de los
jardines, los jardineros colocan 2 estacas a la distancia que
consideran mas apropiada (cada estaca es un foco de la elipse,
entre mas grande es la distancia entre las estacas mas achatada
queda la elipse), luego de colocar las estacas colocan un lazo
que abarque las 2 estacas fijas y una varilla móvil, manteniendo
siempre tensa la cuerda desplazan la varilla alrededor de las
estacas hasta que se forma la elipse.
(Ec. 1)
228](https://image.slidesharecdn.com/c08-170424214125/75/CIENCIAS-8-244-2048.jpg)














![ASTRONOMÍA Física
ACTIVIDAD EVALUADORA
1. El año luz es una unidad de:
a. Tiempo
b. Distancia
c. Velocidad
d. Peso
2. La velocidad de escape es la velocidad mínima necesaria para liberarse de la atracción de la fuerza
gravedad. La velocidad de escape es √ donde es la aceleración de la gravedad a romper, y el
radio del planeta. Completa la siguiente tabla:
Planeta Gravedad [ ⁄ ] Radio [m] *Velocidad de escape [ ⁄ ]
Mercurio 3.78
Venus 8.60
Tierra 9.81
Marte 3.72
Júpiter 22.9
Saturo 9.05
Urano 7.7
Neptuno 11.0
* note que las unidades en que deben ser colocadas las velocidades es ⁄ y no en ⁄ .
3. Si la distancia entre dos objetos se cuadruplica, la fuerza gravitacional entre ellos:
a. Incrementa en un factor de 4
b. Reduce en un factor de 4
c. Reduce en un factor de 8
d. Reduce en un factor de 16
4. ¿Cuales son las diferencias y semejanzas entre un planeta y un planeta enano?
5. ¿Por qué la Luna no es considerada un planeta?
6. ¿Por qué Urano y Neptuno se ven azules?
7. La baja densidad de los planetas Júpiter y Saturno comparada con la Tierra sugiere que:
a. Son huecos.
b. Su atracción gravitatoria ha comprimido su núcleo en una rara forma de hierro.
c. Contienen grandes cantidades de elementos ligeros tales como hidrogeno y helio.
d. Son bien calientes.
243](https://image.slidesharecdn.com/c08-170424214125/75/CIENCIAS-8-259-2048.jpg)

