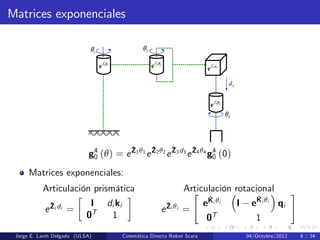
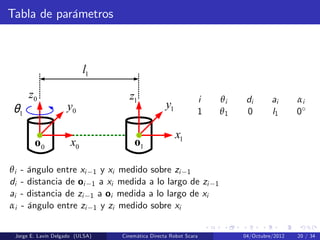
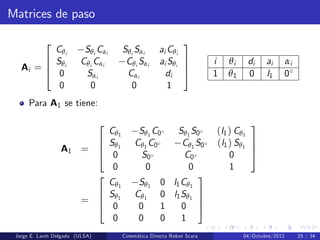
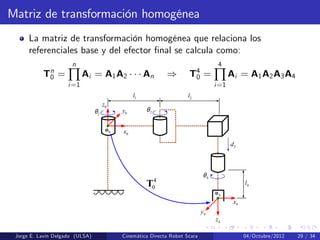
Este documento presenta la cinemática directa de un robot Scara. Explica la teoría de tornillos para modelar la cinemática del robot. Define las configuraciones inicial y final del robot, así como los ejes de rotación y traslación de cada articulación. Deriva las matrices exponenciales para cada articulación y utiliza estas matrices para calcular la pose final del efector usando la ecuación de cinemática directa.

1. Robótica I
Cinemática Directa Robot Scara
Jorge Enrique Lavín Delgado
Universidad La Salle
Jueves 04 de Octubre de 2012
Jorge E. Lavín Delgado (ULSA) Cinemática Directa Robot Scara 04/Octubre/2012 1 / 34

2. Teoría de Tornillos
0z
0x
0y
0o
4z
4x
4y
4o
4l
4θ
3d
2θ
2l
1θ
1l
La pose del efector …nal está dada por:
gn
0 (θ) = e
^Z1θ1
e
^Z2θ2
e
^Znθn
gn
0 (0)
g4
0 (θ) = e
^Z1θ1
e
^Z2θ2
e
^Z3d3
e
^Z4θ4
g4
0 (0) (1)
Jorge E. Lavín Delgado (ULSA) Cinemática Directa Robot Scara 04/Octubre/2012 2 / 34

3. Con…guración inicial
0z
0x
0y
0o
4z
4x
4y
4o
4l
4θ
3d
2θ
2l
1θ
1l
Con…guración (pose) inicial:
g4
0 (0) =
R4
0 (0) d4
0 (0)
0T 1
=
2
6
6
4
1 0 0 l1 + l2
0 1 0 0
0 0 1 l4
0 0 0 1
3
7
7
5
Jorge E. Lavín Delgado (ULSA) Cinemática Directa Robot Scara 04/Octubre/2012 3 / 34

4. Ejes de rotación y traslación
0z
0x
0y
0o
4θ
3d
2θ1θ
1k 2k
3k
4k
Ejes de rotación y/o traslación (ki ) de las articulaciones:
k1 = 0 0 1
T
k3 = 0 0 1
T
k2 = 0 0 1
T
k4 = 0 0 1
T
Jorge E. Lavín Delgado (ULSA) Cinemática Directa Robot Scara 04/Octubre/2012 4 / 34

5. Puntos sobre los ejes de rotación
0z
0x
0y
0o
4θ
3d
2θ
2l
1θ
1l
1k 2k
4k
1q
2q 4q
Puntos “arbitrarios” (qi ) sobre los ejes de rotación:
q1 = 0 0 0
T
q2 = l1 0 0
T
q4 = l1 + l2 0 0
T
Jorge E. Lavín Delgado (ULSA) Cinemática Directa Robot Scara 04/Octubre/2012 5 / 34

6. Matrices exponenciales
4θ
3d
2θ1θ
1 1
ˆZ θ
e 2 2
ˆZ θ
e
4 4
ˆZ θ
e
3 3
ˆZ d
e
g4
0 (θ) = e
^Z1θ1
e
^Z2θ2
e
^Z3d3
e
^Z4θ4
g4
0 (0)
Matrices exponenciales:
Articulación prismática Articulación rotacional
e
^Zi di =
I di ki
0T 1
e
^Zi θi =
"
e
^Ki θi I e
^Ki θi
qi
0T 1
#
Jorge E. Lavín Delgado (ULSA) Cinemática Directa Robot Scara 04/Octubre/2012 6 / 34

7. Matrices exponenciales
k1 = 0 0 1
T
k2 = 0 0 1
T
k4 = 0 0 1
T
Matrices de rotación:
e
^Ki θi
=
2
4
k2
x vθi
+ Cθi
kx ky vθi
kz Sθi
kx kz vθi
+ ky Sθi
kx ky vθi
+ kz Sθi
k2
y vθi
+ Cθi
ky kz vθi
kx Sθi
kx kz vθi
ky Sθi
ky kz vθi
+ kx Sθi
k2
z vθi
+ Cθi
3
5
vθi
= 1 Cθi
e
^K1θ1
=
2
4
Cθ1
Sθ1
0
Sθ1
Cθ1
0
0 0 1
3
5 e
^K2θ2
=
2
4
Cθ2
Sθ2
0
Sθ2
Cθ2
0
0 0 1
3
5
e
^K4θ4
=
2
4
Cθ4
Sθ4
0
Sθ4
Cθ4
0
0 0 1
3
5
Jorge E. Lavín Delgado (ULSA) Cinemática Directa Robot Scara 04/Octubre/2012 7 / 34

8. Matrices exponenciales
Articulación 1 (Rotacional):
e
^Zi θi
=
"
e
^Ki θi I e
^Ki θi
qi
0T 1
#
e
^K1θ1
=
2
4
Cθ1
Sθ1
0
Sθ1
Cθ1
0
0 0 1
3
5 q1 = 0 0 0
T
I e
^K1θ1
q1 =
2
4
1 Cθ1
Sθ1
0
Sθ1
1 Cθ1
0
0 0 0
3
5
2
4
0
0
0
3
5 =
2
4
0
0
0
3
5
) e
^Z1θ1
=
2
6
6
4
Cθ1
Sθ1
0 0
Sθ1
Cθ1
0 0
0 0 1 0
0 0 0 1
3
7
7
5
Jorge E. Lavín Delgado (ULSA) Cinemática Directa Robot Scara 04/Octubre/2012 8 / 34

9. Matrices exponenciales
Articulación 2 (Rotacional):
e
^Zi θi
=
"
e
^Ki θi I e
^Ki θi
qi
0T 1
#
e
^K2θ2
=
2
4
Cθ2
Sθ2
0
Sθ2
Cθ2
0
0 0 1
3
5 q2 = l1 0 0
T
I e
^K2θ2
q2 =
2
4
1 Cθ2
Sθ2
0
Sθ2
1 Cθ2
0
0 0 0
3
5
2
4
l1
0
0
3
5 =
2
4
l1 (1 Cθ2
)
l1Sθ2
0
3
5
) e
^Z2θ2
=
2
6
6
4
Cθ2
Sθ2
0 l1 (1 Cθ2
)
Sθ2
Cθ2
0 l1Sθ2
0 0 1 0
0 0 0 1
3
7
7
5
Jorge E. Lavín Delgado (ULSA) Cinemática Directa Robot Scara 04/Octubre/2012 9 / 34

10. Matrices exponenciales
Articulación 3 (Prismática):
e
^Zi di
=
I di ki
0T 1
k3 = 0 0 1
T
d3k3 = d3
2
4
0
0
1
3
5 =
2
4
0
0
d3
3
5
) e
^Z3d3
=
2
6
6
4
1 0 0 0
0 1 0 0
0 0 1 d3
0 0 0 1
3
7
7
5
Jorge E. Lavín Delgado (ULSA) Cinemática Directa Robot Scara 04/Octubre/2012 10 / 34

11. Matrices exponenciales
Articulación 4 (Rotacional):
e
^Zi θi
=
"
e
^Ki θi I e
^Ki θi
qi
0T 1
#
e
^K4θ4
=
2
4
Cθ4
Sθ4
0
Sθ4
Cθ4
0
0 0 1
3
5 q4 = l1 + l2 0 0
T
I e
^K4θ4
q4 =
2
4
(l1 + l2) (1 Cθ4
)
(l1 + l2) Sθ4
0
3
5
) e
^Z4θ4
=
2
6
6
4
Cθ4
Sθ4
0 (l1 + l2) (1 Cθ4
)
Sθ4
Cθ4
0 (l1 + l2) Sθ4
0 0 1 0
0 0 0 1
3
7
7
5
Jorge E. Lavín Delgado (ULSA) Cinemática Directa Robot Scara 04/Octubre/2012 11 / 34

12. Pose del efector …nal
La pose del efector …nal se obtiene con la ecuación (1):
g4
0 (θ) = e
^Z1θ1
e
^Z2θ2
e
^Z3d3
e
^Z4θ4
g4
0 (0)
=
2
6
6
4
Cθ1
Sθ1
0 0
Sθ1
Cθ1
0 0
0 0 1 0
0 0 0 1
3
7
7
5
2
6
6
4
Cθ2
Sθ2
0 l1 (1 Cθ2
)
Sθ2
Cθ2
0 l1Sθ2
0 0 1 0
0 0 0 1
3
7
7
5
2
6
6
4
1 0 0 0
0 1 0 0
0 0 1 d3
0 0 0 1
3
7
7
5
2
6
6
4
Cθ4
Sθ4
0 (l1 + l2) (1 Cθ4
)
Sθ4
Cθ4
0 (l1 + l2) Sθ4
0 0 1 0
0 0 0 1
3
7
7
5
2
6
6
4
1 0 0 l1 + l2
0 1 0 0
0 0 1 l4
0 0 0 1
3
7
7
5
Jorge E. Lavín Delgado (ULSA) Cinemática Directa Robot Scara 04/Octubre/2012 12 / 34

13. Pose del efector …nal
La pose del efector …nal se obtiene con la ecuación (1):
g4
0 (θ) = e
^Z1θ1
e
^Z2θ2
e
^Z3d3
e
^Z4θ4
g4
0 (0)
e
^Z1θ1
e
^Z2θ2
=
2
6
6
4
Cθ1
Sθ1
0 0
Sθ1
Cθ1
0 0
0 0 1 0
0 0 0 1
3
7
7
5
2
6
6
4
Cθ2
Sθ2
0 l1 (1 Cθ2
)
Sθ2
Cθ2
0 l1Sθ2
0 0 1 0
0 0 0 1
3
7
7
5
=
2
6
6
4
Cθ1+θ2
Sθ1+θ2
0 l1 (Cθ1
Cθ1+θ2
)
Sθ1+θ2
Cθ1+θ2
0 l1 (Sθ1
Sθ1+θ2
)
0 0 1 0
0 0 0 1
3
7
7
5
sen (x y) = sen x cos y cos x sen y
cos (x y) = cos x cos y sen x sen y
Jorge E. Lavín Delgado (ULSA) Cinemática Directa Robot Scara 04/Octubre/2012 13 / 34

14. Pose del efector …nal
La pose del efector …nal se obtiene con la ecuación (1):
g4
0 (θ) = e
^Z1θ1
e
^Z2θ2
e
^Z3d3
e
^Z4θ4
g4
0 (0)
e
^Z3d3
e
^Z4θ4
=
2
6
6
4
1 0 0 0
0 1 0 0
0 0 1 d3
0 0 0 1
3
7
7
5
2
6
6
4
Cθ4
Sθ4
0 (l1 + l2) (1 Cθ4
)
Sθ4
Cθ4
0 (l1 + l2) Sθ4
0 0 1 0
0 0 0 1
3
7
7
5
=
2
6
6
4
Cθ4
Sθ4
0 (l1 + l2) (1 Cθ4
)
Sθ4
Cθ4
0 (l1 + l2) Sθ4
0 0 1 d3
0 0 0 1
3
7
7
5
Jorge E. Lavín Delgado (ULSA) Cinemática Directa Robot Scara 04/Octubre/2012 14 / 34

15. Pose del efector …nal
La pose del efector …nal se obtiene con la ecuación (1):
g4
0 (θ) = e
^Z1θ1
e
^Z2θ2
e
^Z3d3
e
^Z4θ4
g4
0 (0)
e
^Z3d3
e
^Z4θ4
g4
0 (0)
=
2
6
6
4
Cθ4
Sθ4
0 (l1 + l2) (1 Cθ4
)
Sθ4
Cθ4
0 (l1 + l2) Sθ4
0 0 1 d3
0 0 0 1
3
7
7
5
2
6
6
4
1 0 0 l1 + l2
0 1 0 0
0 0 1 l4
0 0 0 1
3
7
7
5
=
2
6
6
4
Cθ4
Sθ4
0 l1 + l2
Sθ4
Cθ4
0 0
0 0 1 (d3 + l4)
0 0 0 1
3
7
7
5
Jorge E. Lavín Delgado (ULSA) Cinemática Directa Robot Scara 04/Octubre/2012 15 / 34

16. Pose del efector …nal
La pose del efector …nal se obtiene con la ecuación (1):
g4
0 (θ) = e
^Z1θ1
e
^Z2θ2
e
^Z3d3
e
^Z4θ4
g4
0 (0)
=
2
6
6
4
Cθ1+θ2
Sθ1+θ2
0 l1 (Cθ1
Cθ1+θ2
)
Sθ1+θ2
Cθ1+θ2
0 l1 (Sθ1
Sθ1+θ2
)
0 0 1 0
0 0 0 1
3
7
7
5
2
6
6
4
Cθ4
Sθ4
0 l1 + l2
Sθ4
Cθ4
0 0
0 0 1 (d3 + l4)
0 0 0 1
3
7
7
5
=
2
6
6
4
r11 r12 r13 dx
r21 r22 r23 dy
r31 r32 r33 dz
0 0 0 1
3
7
7
5
Jorge E. Lavín Delgado (ULSA) Cinemática Directa Robot Scara 04/Octubre/2012 16 / 34

17. Pose del efector …nal
Finalmente, la pose del efector …nal está dada por:
g4
0 (θ) =
2
6
6
4
r11 r12 r13 dx
r21 r22 r23 dy
r31 r32 r33 dz
0 0 0 1
3
7
7
5
donde
r11 = Cθ1+θ2
Cθ4
+ Sθ1+θ2
Sθ4
r13 = 0
r21 = Sθ1+θ2
Cθ4
Cθ1+θ2
Sθ4
r23 = 0
r31 = 0 r33 = 1
r12 = Cθ1+θ2
Sθ4
+ Sθ1+θ2
Cθ4
dx = l1Cθ1
+ l2Cθ1+θ2
r22 = Sθ1+θ2
Sθ4
Cθ1+θ2
Cθ4
dy = l1Sθ1
+ l2Sθ1+θ2
r32 = 0 dz = (d3 + l4)
Jorge E. Lavín Delgado (ULSA) Cinemática Directa Robot Scara 04/Octubre/2012 17 / 34

18. Denavit Hartenberg
Diagrama cinemático
4l
4θ
3d
2θ
2l
1θ
1l
Jorge E. Lavín Delgado (ULSA) Cinemática Directa Robot Scara 04/Octubre/2012 18 / 34

19. Asignación de referenciales
4l
4θ
3d
2θ
2l1l
0z
0x
0y
0o
1θ
1x
1y1z
1o 2x
2y
2z
2o
3x
3y
3z
3o
4x
4y
4z
4o
Jorge E. Lavín Delgado (ULSA) Cinemática Directa Robot Scara 04/Octubre/2012 19 / 34

20. Tabla de parámetros
1l
0z
0x
0y
0o
1θ
1x
1y1z
1o
i θi di ai αi
1 θ1 0 l1 0
θi - ángulo entre xi 1 y xi medido sobre zi 1
di - distancia de oi 1 a xi medida a lo largo de zi 1
ai - distancia de zi 1 a oi medida a lo largo de xi
αi - ángulo entre zi 1 y zi medido sobre xi
Jorge E. Lavín Delgado (ULSA) Cinemática Directa Robot Scara 04/Octubre/2012 20 / 34

21. Tabla de parámetros
2θ
2l
1x
1y1z
1o 2x
2y
2z
2o
i θi di ai αi
2 θ2 0 l2 180
θi - ángulo entre xi 1 y xi medido sobre zi 1
di - distancia de oi 1 a xi medida a lo largo de zi 1
ai - distancia de zi 1 a oi medida a lo largo de xi
αi - ángulo entre zi 1 y zi medido sobre xi
Jorge E. Lavín Delgado (ULSA) Cinemática Directa Robot Scara 04/Octubre/2012 21 / 34

22. Tabla de parámetros
3d
2x
2y
2z
2o
3x
3y
3z
3o
i θi di ai αi
3 0 d3 0 0
θi - ángulo entre xi 1 y xi medido sobre zi 1
di - distancia de oi 1 a xi medida a lo largo de zi 1
ai - distancia de zi 1 a oi medida a lo largo de xi
αi - ángulo entre zi 1 y zi medido sobre xi
Jorge E. Lavín Delgado (ULSA) Cinemática Directa Robot Scara 04/Octubre/2012 22 / 34

23. Tabla de parámetros
4l
4θ
3x
3y
3z
3o
4x
4y
4z
4o
i θi di ai αi
4 θ4 l4 0 0
θi - ángulo entre xi 1 y xi medido sobre zi 1
di - distancia de oi 1 a xi medida a lo largo de zi 1
ai - distancia de zi 1 a oi medida a lo largo de xi
αi - ángulo entre zi 1 y zi medido sobre xi
Jorge E. Lavín Delgado (ULSA) Cinemática Directa Robot Scara 04/Octubre/2012 23 / 34

24. Matrices de paso
Para obtener las matrices de paso Ai , sólo hay que sustituir los
parámetros θi , di , ai y αi en (2):
Ai =
2
6
6
4
Cθi
Sθi
Cαi Sθi
Sαi ai Cθi
Sθi
Cθi
Cαi Cθi
Sαi ai Sθi
0 Sαi Cαi di
0 0 0 1
3
7
7
5 (2)
Tabla de parámetros:
i θi di ai αi
1 θ1 0 l1 0
2 θ2 0 l2 180
3 0 d3 0 0
4 θ4 l4 0 0
Jorge E. Lavín Delgado (ULSA) Cinemática Directa Robot Scara 04/Octubre/2012 24 / 34

25. Matrices de paso
Ai =
2
6
6
4
Cθi
Sθi
Cαi Sθi
Sαi ai Cθi
Sθi
Cθi
Cαi Cθi
Sαi ai Sθi
0 Sαi Cαi di
0 0 0 1
3
7
7
5
i θi di ai αi
1 θ1 0 l1 0
Para A1 se tiene:
A1 =
2
6
6
4
Cθ1
Sθ1
C0 Sθ1
S0 (l1) Cθ1
Sθ1
Cθ1
C0 Cθ1
S0 (l1) Sθ1
0 S0 C0 0
0 0 0 1
3
7
7
5
=
2
6
6
4
Cθ1
Sθ1
0 l1Cθ1
Sθ1
Cθ1
0 l1Sθ1
0 0 1 0
0 0 0 1
3
7
7
5
Jorge E. Lavín Delgado (ULSA) Cinemática Directa Robot Scara 04/Octubre/2012 25 / 34

26. Matrices de paso
Ai =
2
6
6
4
Cθi
Sθi
Cαi Sθi
Sαi ai Cθi
Sθi
Cθi
Cαi Cθi
Sαi ai Sθi
0 Sαi Cαi di
0 0 0 1
3
7
7
5
i θi di ai αi
2 θ2 0 l2 180
Para A2 se tiene:
A2 =
2
6
6
4
Cθ2
Sθ2
C180 Sθ2
S180 (l2) Cθ2
Sθ2
Cθ2
C180 Cθ2
S180 (l2) Sθ2
0 S180 C180 0
0 0 0 1
3
7
7
5
=
2
6
6
4
Cθ2
Sθ2
0 l2Cθ2
Sθ2
Cθ2
0 l2Sθ2
0 0 1 0
0 0 0 1
3
7
7
5
Jorge E. Lavín Delgado (ULSA) Cinemática Directa Robot Scara 04/Octubre/2012 26 / 34

27. Matrices de paso
Ai =
2
6
6
4
Cθi
Sθi
Cαi Sθi
Sαi ai Cθi
Sθi
Cθi
Cαi Cθi
Sαi ai Sθi
0 Sαi Cαi di
0 0 0 1
3
7
7
5
i θi di ai αi
3 0 d3 0 0
Para A3 se tiene:
A3 =
2
6
6
4
C0 S0 C0 S0 S0 (0) C0
S0 C0 C0 C0 S0 (0) S0
0 S0 C0 d3
0 0 0 1
3
7
7
5
=
2
6
6
4
1 0 0 0
0 1 0 0
0 0 1 d3
0 0 0 1
3
7
7
5
Jorge E. Lavín Delgado (ULSA) Cinemática Directa Robot Scara 04/Octubre/2012 27 / 34

28. Matrices de paso
Ai =
2
6
6
4
Cθi
Sθi
Cαi Sθi
Sαi ai Cθi
Sθi
Cθi
Cαi Cθi
Sαi ai Sθi
0 Sαi Cαi di
0 0 0 1
3
7
7
5
i θi di ai αi
4 θ4 l4 0 0
Para A4 se tiene:
A4 =
2
6
6
4
Cθ4
Sθ4
C0 Sθ4
S0 (0) Cθ4
Sθ4
Cθ4
C0 Cθ4
S0 (0) Sθ4
0 S0 C0 l4
0 0 0 1
3
7
7
5
=
2
6
6
4
Cθ4
Sθ4
0 0
Sθ4
Cθ4
0 0
0 0 1 l4
0 0 0 1
3
7
7
5
Jorge E. Lavín Delgado (ULSA) Cinemática Directa Robot Scara 04/Octubre/2012 28 / 34

29. Matriz de transformación homogénea
La matriz de transformación homogénea que relaciona los
referenciales base y del efector …nal se calcula como:
Tn
0 =
n
∏
i=1
Ai = A1A2 An ) T4
0 =
4
∏
i=1
Ai = A1A2A3A4
0z
0x
0y
0o
4z
4x
4y
4o
4l
4θ
3d
2θ
2l
1θ
1l
4
0T
Jorge E. Lavín Delgado (ULSA) Cinemática Directa Robot Scara 04/Octubre/2012 29 / 34

30. Matriz de transformación homogénea
T4
0 =
4
∏
i=1
Ai = A1A2A3A4
=
2
6
6
4
Cθ1
Sθ1
0 l1Cθ1
Sθ1
Cθ1
0 l1Sθ1
0 0 1 0
0 0 0 1
3
7
7
5
2
6
6
4
Cθ2
Sθ2
0 l2Cθ2
Sθ2
Cθ2
0 l2Sθ2
0 0 1 0
0 0 0 1
3
7
7
5
2
6
6
4
1 0 0 0
0 1 0 0
0 0 1 d3
0 0 0 1
3
7
7
5
2
6
6
4
Cθ4
Sθ4
0 0
Sθ4
Cθ4
0 0
0 0 1 l4
0 0 0 1
3
7
7
5
Tenga en cuenta que en general el producto de matrices no es
conmutativo, es decir, AB 6= BA.
Por otro lado, una buena asociación de matrices simpli…ca de manera
notoria los cálculos.
Jorge E. Lavín Delgado (ULSA) Cinemática Directa Robot Scara 04/Octubre/2012 30 / 34

31. Matriz de transformación homogénea
La matriz de transformación homogénea está dada por:
T4
0 =
4
∏
i=1
Ai = A1A2A3A4
A1A2 =
2
6
6
4
Cθ1
Sθ1
0 l1Cθ1
Sθ1
Cθ1
0 l1Sθ1
0 0 1 0
0 0 0 1
3
7
7
5
2
6
6
4
Cθ2
Sθ2
0 l2Cθ2
Sθ2
Cθ2
0 l2Sθ2
0 0 1 0
0 0 0 1
3
7
7
5
=
2
6
6
4
Cθ1+θ2
Sθ1+θ2
0 l1Cθ1
+ l2Cθ1+θ2
Sθ1+θ2
Cθ1+θ2
0 l1Sθ1
+ l2Sθ1+θ2
0 0 1 0
0 0 0 1
3
7
7
5
sen (x y) = sen x cos y cos x sen y
cos (x y) = cos x cos y sen x sen y
Jorge E. Lavín Delgado (ULSA) Cinemática Directa Robot Scara 04/Octubre/2012 31 / 34

32. Matriz de transformación homogénea
La matriz de transformación homogénea está dada por:
T4
0 = A1A2A3A4
A3A4 =
2
6
6
4
1 0 0 0
0 1 0 0
0 0 1 d3
0 0 0 1
3
7
7
5
2
6
6
4
Cθ4
Sθ4
0 0
Sθ4
Cθ4
0 0
0 0 1 l4
0 0 0 1
3
7
7
5
=
2
6
6
4
Cθ4
Sθ4
0 0
Sθ4
Cθ4
0 0
0 0 1 d3 + l4
0 0 0 1
3
7
7
5
Jorge E. Lavín Delgado (ULSA) Cinemática Directa Robot Scara 04/Octubre/2012 32 / 34

33. Matriz de transformación homogénea
Se sigue que la matriz de transformación homogénea T4
0 es:
T4
0 = A1A2A3A4
=
2
6
6
4
Cθ1+θ2
Sθ1+θ2
0 l1Cθ1
+ l2Cθ1+θ2
Sθ1+θ2
Cθ1+θ2
0 l1Sθ1
+ l2Sθ1+θ2
0 0 1 0
0 0 0 1
3
7
7
5
2
6
6
4
Cθ4
Sθ4
0 0
Sθ4
Cθ4
0 0
0 0 1 d3 + l4
0 0 0 1
3
7
7
5
=
2
6
6
4
r11 r12 r13 dx
r21 r22 r23 dy
r31 r32 r33 dz
0 0 0 1
3
7
7
5
Jorge E. Lavín Delgado (ULSA) Cinemática Directa Robot Scara 04/Octubre/2012 33 / 34

34. Matriz de transformación homogénea
Se sigue que la matriz de transformación homogénea T4
0 es:
T4
0 =
2
6
6
4
r11 r12 r13 dx
r21 r22 r23 dy
r31 r32 r33 dz
0 0 0 1
3
7
7
5
donde
r11 = Cθ1+θ2
Cθ4
+ Sθ1+θ2
Sθ4
r13 = 0
r21 = Sθ1+θ2
Cθ4
Cθ1+θ2
Sθ4
r23 = 0
r31 = 0 r33 = 1
r12 = Cθ1+θ2
Sθ4
+ Sθ1+θ2
Cθ4
dx = l1Cθ1
+ l2Cθ1+θ2
r22 = Sθ1+θ2
Sθ4
Cθ1+θ2
Cθ4
dy = l1Sθ1
+ l2Sθ1+θ2
r32 = 0 dz = (d3 + l4)
Jorge E. Lavín Delgado (ULSA) Cinemática Directa Robot Scara 04/Octubre/2012 34 / 34