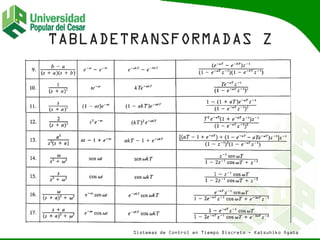
La transformada Z es una herramienta análoga a la transformada de Laplace para sistemas de tiempo discreto. Se define la transformada Z de una secuencia discreta x(k) y de una función muestreada x(kT). El documento presenta ejemplos de cálculo de transformadas Z para diferentes funciones y desarrolla propiedades como linealidad y traslación. También explica métodos para calcular la transformada Z inversa como división directa, uso de la función delta de Kronecker y expansión en fracciones parciales.

1. UNIDAD II

2. • La transformada Zeta es una
herramienta útil en teoría de
control en tiempo discreto y su
papel es análogo al que juega la
transformada de Laplace en tiempo
continuo
• Dada una secuencia discreta x(k) se
define su transformada Z como:

3. • La transformada Z para una función
en el tiempo x(t) o de la
secuencia x(kT), donde t es un
número positivo, k adopta valores
enteros positivos desde 0, y T es
el periodo de muestreo
• Estas dos ecuaciones se conocen
como la transformada unilateral de
Z

4. EJEMPLOS:
• La transformada Z de la secuencia impulso que
viene definida por x(0) = 1, x( 1) = 0, x( 2) =
0, ... será:
NOTA: Es importante resaltar que, cuando se trata
con una secuencia de tiempo x(kT) obtenida
mediante muestreo, la transformada Z, X(z),
involucra al periodo de muestreo T. Por otro lado,
para una secuencia de tiempo x(k) , la
transformada no incluye explícitamente a T.

5. 1. EJEMPLO: La transformada Z para el
escalón unitario definida como
es:

6. 2. EJEMPLO: Para la rampa Unitaria definida
como
• Al muestrearla se obtiene
• Cuya figura es:
Sistemas de Control en Tiempo Discreto - Katsuhiko Ogata

7. • Su transformada es

8. 3. EJEMPLO: obtener la transformada Z
de:
• SOLUCIÓN

9. 4. EJEMPLO: Considere la función
senoidal
• SOLUCIÓN: Observemos
Recordando que

10. Se tiene que:

11. 5. EJEMPLO: Considere la función
cosenoidal
SOLUCIÓN

13. 6. EJEMPLO: Obtenga la transformada Z de
SOLUCIÓN: se observa que la
expresión está dada en s, una
manera de obtener la transformada
Z es convertir X(s) al tiempo
x(t) y luego obtener la
transformada Z de x(t)

14. De allí que la transformada Inversa de X(s)
es:
Por consiguiente:

15. Sistemas de Control en Tiempo Discreto - Katsuhiko Ogata

16. Sistemas de Control en Tiempo Discreto - Katsuhiko Ogata

17. Sistemas de Control en Tiempo Discreto - Katsuhiko Ogata

18. • Linealidad de la transformada z: Si f(kT)
y g(kT) tienen transformada z, y α y β
son escalares, siendo T el periodo de
muestreo, entonces
• Suma y Resta: Si f(k) y g(k) tienen
transformadas F(z) y G(z), entonces:
Z(f(k)+g(k))=F(z)+G(z)
Z(f(k)-g(k)) = F(z)-G(z)

19. • Multiplicación por una constante:
Z(rf(k)) = rF(z)
• Traslación real
Z(f(kT-nT) = (z-n)F(z) y también
• Multiplicación por akT: Si X(z) es la
transformada Z de x(kT) entonces
  





 



1
0
)()(
n
k
kn
zkTxznTkTfZ

20. • Teorema de traslación compleja: Si x(t)
tiene la transformada Z, X(z) , entonces
la transformada Z de viene dada por
• Teorema del valor inicial: Si x(t) tiene
por transformada Z, X(z) , y si el
existe, entonces el valor inicial x(0)
de x(t) ó x(k) está dado por:
)(lim zX
z 
)( aT
ezX 
)(txe aT

)(lim)0()(lim
0
zXxkTx
zk 


21. • Teorema del Valor Final: Suponemos que x(kT) ,
siendo T el periodo de muestreo, tiene la
transformada Z, X(z) , con x(kT) = 0 para
valores negativos de k, y que todos los polos
de X(z) están dentro del círculo unitario,
con la posible excepción de un sólo polo en z
= 1. Esta es la condición para la estabilidad
de X(z) , es decir, la condición para que x(kT)
con (k = 0, 1, 2...) permanezca finita. Entonces
el valor final de x(kT) , que es su valor
conforme el tiempo tiende a infinito, puede
obtenerse mediante:
)()1(lim)(lim 1
1
zXzkTx
zk
 


22. Sistemas de Control en Tiempo Discreto - Katsuhiko Ogata

23. Sistemas de Control en Tiempo Discreto - Katsuhiko Ogata

24. 1. Encuentre la Transformada Z de una
función escalón Unitario que está
retrasada dos y cuatro periodos de
muestreo respectivamente, como se muestra
Para dos periodos de muestreo Para cuatro periodos de muestreo
1(t-2T) 1(t-4T)

25. • SOLUCIÓN :
Para la señal escalón unitario
desplazada dos periodos de muestreo
se obtiene
Para la señal escalón unitario
desplazada cuatro periodos de
muestreo se obtiene
1
2
1
22
11
1
)](1[)]2(1[ 







z
z
z
ztZzTtZ
1
4
1
44
11
1
)](1[)]4(1[ 







z
z
z
ztZzTtZ

26. 2. Obtenga la transformada Z de e-atsen(wt)
utilizando el teorema de traslación
compleja.
SOLUCIÓN:
Sabiendo
Entonces según el teorema, en la transformada Z de
la función solo se reemplaza z por zeaT obtenemos:

27. • La transformada Z inversa de X(z) da como
resultado la correspondiente secuencia de tiempo
x(kT).
Se debe observar que a partir de la transformada
inversa sólo se obtiene la secuencia de tiempo en
los instantes de muestreo. Por lo tanto, la
transformada z inversa de X(z) da como resultado
una única x (kT) , pero no una única x(t) , ya
que no dice nada de los valores de x(t) en los
instantes de tiempo no muestreados. Esto
significa que puede haber distintas funciones de
tiempo xi(t) con la misma x(kT).

28. Existen diferentes métodos para
calcular la transformada Z inversa.
Un método obvio es referirse a una
tabla de transformadas Z, pero es
laborioso (si se utiliza una tabla de
transformadas Z no muy extensa, es
necesario expresar una transformada Z
complicada como una suma de
transformadas Z más sencillas).
Existen cuatro métodos para obtener
la transformada z inversa:

29. I. Método de la división directa. En
este método la transformada z
inversa se obtiene mediante la
expansión de X(z) en una serie
infinita de potencias de z-1.
Este método es útil cuando es
difícil obtener una expresión en
forma cerrada para la
transformada Z inversa, o se
desea encontrar sólo algunos de
los primeros términos de x(k).

30. EJEMPLO: encuentre x(k) para k= 0, 1,
2 , 3, 4 cuando X(z) esta dado por:
SOLUCIÓN: X(z) se escribe como un
cociente de potencias de z-1

31. 21
2.02.11 
 zz
...68.184.181710 4321
 
zzzz
...68.184.181710)( 4321
 
zzzzzX
Al comparar esta expresión con
en una serie infinita
se obtiene




0
)(
k
k
zkx
Luego se divide la expresión

32. II.Método computacional. En este
método, la transformada Z
inversa se obtiene utilizando
la función delta de Kronecker,
donde

33. EJEMPLO: considere una sistema G(z)
definido por:
SOLUCIÓN: Suponiendo que u(k), la
entrada al sistema G(z) es la
entrada Delta de Kronecker, la
transformada Z de la entrada delta
de Kronecker es U(z)=1.

34. Con el enfoque de la ecuación en
diferencias, se puede obtener,
despejando
Solo resta hallar los valores de la
ecuación en diferencias:

35. Tomando los valores de k=-2, -1,
0,1,2 … se obtienen los valores:
• Para k=-2
• Para k=-1
• Para k=0
00000)0(
)2(3393,0)1(4673,0)2(6607,0)1(5327,1)0(


x
uuxxx
4673,00)1(4673,000)1(
)1(3393,0)0(4673,0)1(6607,0)0(5327,1)1(


x
uuxxx
37693,0)1(3393,000)4673,0(5327,1)2(
)0(3393,0)1(4673,0)0(6607,0)1(5327,1)2(


x
uuxxx

36. Método computacional: enfoque en
Matlab:
Delta de Kronecker: dk=[1 zeros(1,N)]
%donde N es el número de términos
mas uno, que se necesitan.
num=[0 0.4673 -0.3393]; %numerador
den=[1 -1.5327 0.6607]; %denominador
dk=[1 zeros(1,50)]; %delta para 51
valores
X=filter(num,den,dk) % entrega la
secuencia de 51 valores

37. III.Método de expansión en fracciones
parciales: Es idéntico al que se utiliza
en la transformada de Laplace, y requiere
que todos los términos de la expansión en
fracciones parciales se puedan reconocer
fácilmente en la tabla de pares de
transformadas Z. Si X( z ) tiene uno o
más ceros en el origen (z = 0), entonces
X(z)/z ó X(z) se expande en la suma de
términos sencillos de primer o segundo
orden mediante la expansión en fracciones
parciales, y se emplea una tabla de
transformadas Z para encontrar la función
del tiempo correspondiente para cada uno
de los términos expandidos.

38. Teniendo en cuenta la fracción
𝐹 𝑧 =
𝑁(𝑧)
𝐷(𝑧)
=
𝑁(𝑧)
𝑧 + 𝑝1 𝑧 + 𝑝2 𝑧 + 𝑝3 … (𝑧 + 𝑝𝑖)
Donde p1, p2, p3…pi son las raíces del
polinomio
Estas raíces podrán ser: reales
simples, reales múltiples, complejas
simples, complejas múltiples.

39. A. RAICES REALES SIMPLES:
- La función F(z) se podrá
descomponer en la siguiente forma:
𝐹 𝑧 =
𝑁(𝑧)
𝐷(𝑧)
=
𝐴1
𝑧 + 𝑝1
+
𝐴2
𝑧 + 𝑝2
+
𝐴3
𝑧 + 𝑝3
…
𝐴𝑖
𝑧 + 𝑝𝑖
𝐴𝑖 = (𝑧 + 𝑝𝑖)𝐹(𝑧) |(𝑧=−𝑝𝑖)

40. B. RAICES REALES MÚLTIPLES:
para raíces reales múltiples
tenemos le siguiente fracción:
𝐹 𝑧 =
𝑁(𝑧)
𝐷(𝑧)
=
𝑁(𝑧)
𝑧 + 𝑝1 𝑧 + 𝑝2 𝑧 + 𝑝3 … 𝑧 + 𝑝𝑖 𝑟
=
𝐴1
𝑧 + 𝑝1
…
𝐴 𝑛
𝑧 + 𝑝𝑛
+
𝑎1
𝑧 + 𝑝𝑖
+
𝑎2
𝑧 + 𝑝𝑖
2
…
𝑎 𝑟
𝑧 + 𝑝𝑖 𝑟

41. Los coeficientes A1...An se calculan
según lo visto anteriormente y para
los coeficientes a1 …ar se calculan
de la siguiente manera:
𝑎 𝑟 =
𝑁 𝑧
𝐷 𝑧
𝑧 + 𝑝𝑖 𝑟
𝑧=−𝑝𝑖
𝑎 𝑟−1 =
𝑑
𝑑𝑧
𝑁 𝑧
𝐷 𝑧
𝑧 + 𝑝𝑖 𝑟
𝑧=−𝑝𝑖
𝑎1 =
1
𝑟 − 1 !
𝑑 𝑟−1
𝑑𝑧 𝑟−1
𝑁 𝑧
𝐷 𝑧
𝑧 + 𝑝𝑖 𝑟
𝑧=−𝑝𝑖

42. C. RAICES COMPLEJAS CONJUGADAS: Supongamos el
denominador de 2º orden cuyas raíces son: α +jwd
- Los pasos a dar son los siguientes:
a) Obtener fracciones con un denominador de segundo
grado (cuyas raíces son complejas conjugadas) y
un numerador de primer grado
b) Obtener los valores de A y B
c) Descomponer y trasformar la fracción en
transformadas Z cuya antitransformada esté en
las tablas.
01
2
2 azaza
BAz



43. NOTA: Un procedimiento de uso muy común para los casos
donde todos los polos sean diferentes y hay por lo
menos un cero en el origen, es dividir ambos miembros
de X(z) entre ‘z’ y entonces expandir X(z)/z en
fracciones parciales en lugar de X(z). Si X(z)/z
involucra un polo múltiple y no tiene mas polos,
también se puede expandir X(z)/z en fracciones
parciales.
POLO SIMPLE
POLO MÚLTIPLE

44. 1. Obtener la transformada Z inversa de:
SOLUCIÓN: Para la expansión en fracciones
parciales de X(z)/z
Cuya transformada
inversa es:

45. 2. Obtener la transformada Z inversa
de:
SOLUCIÓN:

46. Continuando
De allí que
y
Se tiene que:

47. IV.Método de la integral de inversión: está
basado en la teoría de variable
compleja, siendo necesario también
revisar el teorema de los residuos. La
ecuación que da la transformada Z
inversa en términos de los residuos se
puede obtener como sigue:

48. Si el denominador de X(z)zk-1 contiene
polo simple en z=zi entonces el
residuo es:
Si el denominador de X(z)zk-1 contiene
polos múltiples de orden q en z=zi
entonces el residuo es:

49. NOTA: Si X(z) tiene un cero de orden r en el
origen, entonces X(z)zk-1 en la ecuación de x(kT)
involucrará un cero de orden r+k-1 en el origen.
Si r≥1 entonces r+k-1≥0 para k≥0 y no hay polo
z=0 en X(z)zk-1. Sin embargo si r≤0 entonces
habrá un polo z=0 para uno o mas valores de
positivos de k. En tal caso la inversión se hace
por separado. Por consiguiente, este método es
sencillo cuando X(z)zk-1 no tiene polos en el
origen (z=0). Si los tiene el cálculo puede
tornarse tedioso y la técnica de fracciones
parciales podría ser la mas indicada.

50. 1. Obtenga x(kT)empleando el método de
integral de inversión cuando X(z) esta
dada por
))(1(
)1(
)( aT
aT
ezz
ez
zX 




))(1(
)1(
)( 1
aT
kat
k
ezz
ze
zzX 





SOLUCIÓN:
Observe que
Para k=0, 1, 2 …, X(z)zk-1 tiene dos polos
simples en z=z1=1 y z=z2=e-aT. Por lo
tanto la ecuación de los residuos queda
 
  
21
2
1
Kx(k)
poloelen
1
1
residuo)(
K
zz
ezz
ze
kx
i
iaT
kaT










 



51. Continuando
Por lo tanto
para k=0, 1, 2, …
ekT
eKKkTx 
 1)( 21

52. 2. Obtenga la transformada inversa
de:
)()1(
)( 2
2
aT
ezz
z
zX 


)()1(
)( 2
1
1
aT
k
k
ezz
z
zzX 




SOLUCIÓN: empleando el método de la
integral de inversión se obtiene.
Para k=0, 1, 2 …, X(z)zk-1 tiene un polo
simple en z=z1=e-aT y un polo doble en
z=z2=1. Por lo tanto la ecuación de los
residuos queda
   
21
2
1
2
1
Kx(k)
poloelen
1
residuo)(
K
zz
ezz
z
kx
i
iaT
k









 



53. Continuando
Por lo tanto

54. 3. Con el método de la integral de
inversión o de residuos obtenga la
transformada inversa de:
)2)(1(
10
)(


zz
zX
)2)(1(
10
)2)(1(
10
)(
1
1






zzz
z
zz
z
zzX
kk
k
SOLUCIÓN: aplicando el concepto de
integral de inversión se obtiene,
Observe que X(z)zk-1 tiene u polo en
el origen (z=0), entonces dicho
ejercicio se desarrolla de la
siguiente manera

55. Continuando:
Para k=0 ,X(z)zk-1 tiene 3 polos simples z1=1,
z2=2 y z3=0
Para k=1,2,3…, X(z)zk-1 tiene 2 polos simples
z1=1 y z2=2
Se resuelve por separado.
Para k=0 los residuos son x(0)=K1+K2+K3
Residuo K1 para el polo simple z1=1
Residuo K2 para el polo simple z2=2
Residuo K1 para el polo simple z3=0
  
poloelen
21
10
residuo)0(
3
1










i
izz
zzz
x

56. Por lo tanto
Para k≥1 se desarrolla
Donde:
  
21
2
1
1
Kx(k)
poloelen
21
10
residuo)(
K
zz
zz
z
kx
i
i
k









 


57. Por lo tanto
La solución total se halla sumando todos
los residuos y escribiéndola como una
única respuesta, de esta manera la
transformada inversa de X(z) es
Una forma alterna de escribir esta
respuesta es

58. Considere un sistema en el tiempo discreto,
lineal e invariante en el tiempo
caracterizado por la siguiente ecuación en
diferencias
Donde u(k) y x(k) son la entrada y salida
respectivamente al sistema, de la k-ésima
iteración. Definiendo la transformada como
Z[x(k)]=X(z) entonces x(k+1), x(k+2),
x(k+3),… y x(k-1), x(k-2), x(k-3),… se puede
expresar en términos de X(z) y de las
condiciones iniciales.

59. La transformada z se obtienen de la
siguiente tabla.
Sistemas de Control en Tiempo Discreto - Katsuhiko Ogata

60. 1. Resuelva la siguiente ecuación en diferencias
empleando el método de la transformada Z
SOLUCIÓN: utilizando la tabla se obtiene
Al tomar la Transformada z de ambos miembros de la
ecuación de diferencias se obtiene
0)(2)(3)(2
 zXzzXzzXz

61. Al sustituir la condiciones
iniciales, simplificando y
despejando se obtiene
Si se observa que
Con lo cual:
para k≥0
kk
kx )2()1()( 

62. 2. Obtenga la solución de la siguiente ecuación en
diferencias con condiciones iniciales de x(0)=1
y x(1)=0, donde a y b son constantes

63. SOLUCIÓN: la transformada z de la ecuación en
diferencias está dada por
despejando

64. Resolviendo esta ecuación, nos queda
A partir de esta ecuación se pueden
obtener dos casos para su solución,
cuando a ≠ b y a =b
Para el caso en donde a ≠ b se obtiene
De allí que
abzbaz
zbaz



)(
)(
2
2
abzbaz
baz
z
zX



)(
)()(
2
bz
B
az
A
bzaz
baz
z
zX







))((
)()(

65. Continuando con los valores de A y B
Remplazando
A partir de esta ecuación se puede obtener la
transformada inversa de las tablas y sus
propiedades.
para k≥0 y a≠b
ab
b
ba
baa
bzaz
baz
azB
ba
a
ab
bab
bzaz
baz
bzA
az
bz


















)(
))((
)(
)(
)(
))((
)(
)(
11
1
1
1
1
)(
11)(













azab
b
bzba
a
az
z
ab
b
bz
z
ba
a
zX
azab
b
bzba
a
z
zX
kk
b
ba
a
a
ab
b
kx )()()( 





66. Para el caso en donde a = b se obtiene
De allí que
Continuando con los valores de A1 y A2
22
)2(
)2()(
azaz
az
z
zX



2
21
2
)()(
)2()(
az
A
az
A
az
az
z
zX







12
)(
)2(
)(
2
)(
)2(
)(
2
2
1
2
2
2












az
az
az
az
az
dz
d
az
az
bz
dz
d
A
aaz
az
az
bzA

67. reemplazando
Cuya solución
para k≥0 y a=b
1
)()()( 
 kk
aakakx
21
1
12
2
)1(1
1
)(
)(
)(
1)(















az
az
azaz
az
az
z
zX
az
a
azz
zX

68. • OGATA, Katsuhiko. Sistemas De Control En Tiempo
Discreto. Segunda Edición.
• DORSEY, John. Sistemas de Control Continuo y
Discreto
• BIBLIOGRAFÍA WEB
• ASTRÖM, Kral J- Computer Controlled Systems.
Tercera Edición
• PARASKEVOPOLUS,P. Modern Contol Ingineering.
Primera Edición.
• CHEN, Chi-Tsong. Analog And Digital Control System
Design. Tercera Edición
• SMITH C., CORRIPIO A., Control Automático de
Procesos. Primera Edición
• DORF R., BISHOP R., Sistemas de Control Moderno.
Décima Edición.