La cinética estudia la velocidad de los procesos químicos. La velocidad de reacción depende de factores como la concentración de los reactivos, la temperatura y la presencia de catalizadores. La cinética puede determinar el orden de una reacción y expresar matemáticamente cómo afectan estos factores a la velocidad a través de leyes de velocidad y la constante de velocidad.

2. Cinética
La cinética estudia la velocidad a la que
suceden los procesos químicos.
Además de la información acerca de la
velocidad a la que suceden las reacciones, la
cinética también puede dar idea del
mecanismo de reacción (cómo sucede
exactamente la reacción).

3. Cinética química
La velocidad de reacción es el cambio de la concentración
de un reactante o un producto por unidad de tiempo (M/s).
A B
∆[A] ∆[A] = Cambio de concentración en A
V=- respecto a un periodo de tiempo ∆t.
∆t
∆[B] ∆[B] = Cambio de concentración en B
V=
∆t respecto a un periodo de tiempo ∆t.
Porque [A] decrece con el tiempo, ∆[A] es negativo.
13.1

4. A B
Tiempo
∆[A]
V=-
∆t
∆[B]
V=
∆t
13.1

5. Br2 (ac) + HCOOH (ac) 2Br- (ac) + 2H+ (ac) + CO2 (g)
Tiempo
13.1

6. Br2 (ac) + HCOOH (ac) 2Br- (ac) + 2H+ (ac) + CO2 (g)
Pendiente de
la tangente
Pendiente
de Pendiente de
la tangente la tangente
∆[Br2] [Br2]final – [Br2]inicial
Velocidad promedio= - =-
∆t tfinal - tinicial
Velocidad instantánea =Velocidad en un tiempo específico
13.1.

7. Velocidad α [Br2]
Velocidad = k [Br2]
V
k= =Velocidad cte.
[Br2]
= 3.50 x 10-3 s-1
13.1

8. Velocidades de reacción y
estequiometría
¿Qué pasa si la relación no es 1:1?
2 HI(g) → H2(g) + I2(g)
•En tal caso,
1 ∆[HI] ∆[I2]
Velocidad = − =
2 ∆t ∆t

9. Velocidad de reacción y
Estequiometría
Generalizando para cualquier ecuación
aA + bB → cC + dD (1)
Velocidad = - -

10. Ejercicio
¿Cuál es la relación entre la velocidad de desaparición
del ozono y la velocidad de aparición del oxígeno en
la ecuación?
 2 O3 (g) → 3 O2
Si la velocidad de aparición de O2 ∆[O2]/∆t es de 6 x
10-5 M/s en un instante determinado ¿cuál es el valor
de la velocidad de aparición de O3, -∆[O3]/∆t en ese
momento?

11. Ejercicio
La descomposión del N2O5 se lleva a cabo conforme a
la siguiente reacción
2N2O5 → 4NO2 + O2
Si la descomposición del N2O5 en un instante
determinado en un recipiente de reacción es de 4,2 x
10-7 M/s ¿Cuál es la velocidad de aparición de
a) NO2 b) O2

12. Concentración y velocidad
Puede obtenerse información acerca de la
velocidad de una reacción observando cómo
cambia la reacción cuando cambia la
concentración.

13. Concentración y velocidad
NH4+(ac) + NO2−(ac) N2(g) + 2 H2O(l)
Si se comparan los experimentos 1 y 2, se
observa que cuando se duplica [NH4+], la
velocidad inicial se duplica.

14. Concentración y velocidad
NH4+(ac) + NO2−(ac) N2(g) + 2 H2O(l)
Asimismo, cuando se comparan los
experimentos 5 y 6, se observa que cuando se
duplica [NO2−], la velocidad inicial se duplica.

15. Concentración y velocidad
 Esto significa que:
Velocidad ∝ [NH4+]
Velocidad ∝ [NO2−]
Por lo tanto, Velocidad ∝ [NH+] [NO2−]
• Lo cual, cuando se escribe como una ecuación
se vuelve:
Velocidad = k [NH4+] [NO2−]
 A esta ecuación se le llama ley de velocidad,
y k es la constante de velocidad.

16. Leyes de velocidad
Una ley de velocidad muestra la relación entre la
velocidad de la reacción y las concentraciones de los
reactivos.
Los exponentes indican el orden de la reacción con
respecto de cada reactivo.
Dado que la ley de velocidad es:
Velocidad = k [NH4+] [NO2−]
La reacción es:
de primer orden en [NH4+] y
de primer orden en [NO2−].

17. Leyes de velocidad
Velocidad = k [NH4+] [NO2−]
El orden general de la reacción puede
encontrarse adicionando los exponentes de
los reactivos en la ley de velocidad.
Esta reacción es de segundo orden general.

18. Exponentes de la ecuación de
Velocidad
Los exponentes determinan el orden de reacción con respecto a los
reactivos y la suma de ellos establece el orden general de reacción.
Si la concentración varía y no se ve afectada la velocidad, la
reacción es de orden 0
Si la concentración varía y la velocidad varía en la misma
proporción, la reacción es de orden 1
Si la concentración se duplica y la velocidad varía en una
proporción de 22, la reacción es de orden 2
Si la concentración se triplica y la velocidad varía en una proporción
de 32 es de orden 3
Para V =
El orden general de reacción es 2

19. Ejercicio
Se midió la velocidad inicial de la reacción A + B → C con
diversas concentraciones iniciales de A y B siendo los resultados
los siguientes
Experimento [A] (M) [B] (M) Velocidad inicial (M/s)
1 0,1 0,1 4 x 10 -5
2 0,1 0,2 4 x 10-5
3 0,2 0,1 16 x 10-5
Con base en estos datos determine
A) ecuación de velocidad de la reacción
B) la magnitud de la constante de velocidad
C) la velocidad de reacción cuando [A] = 0,05M y [B] = 0,1M

20. Ejercicio
Se midieron los datos siguientes de la reacción del óxido nítrico
con hidrógeno:
2NO(g) + 2H2(g) → N2(g) + 2H2O(g)
Experimento [NO] (M) [H2] (M) Velocidad
inicial (M/s)
1 0,1 0,1 1,23 x 10-3
2 0,1 0,2 2,46 x 10-3
3 0,2 0,1 4,92 x 10-3
a) Determine la ecuación de velocidad de esta reacción
b) Calcule la constante de velocidad
c) Calcule la velocidad cuando [NO]=0,05M y [H2]=0,150M

21. Factores que afectan la velocidad
de reacción
Naturaleza de los reactivos
Cambios de concentración
Cambios de temperatura
Presencia de un catalizador

22. Efecto de la Naturaleza de los
reactivos combinan se hallan en estado sólido, la
Cuando una o todas las sustancias que se
velocidad de reacción depende de la
superficie expuesta en la reacción. Cuando
los sólidos están molidos o en granos,
aumenta la superficie de contacto y por
consiguiente, aumenta la posibilidad de
choque y la reacción es más veloz.
Lo mismo ocurre cuando las sustancias
reaccionantes no son miscibles entre sí,
como por ejemplo, en la hidrólisis neutra de
un aceite, se hace reaccionar éste con agua,
para lograrlo, el agua de la parte inferior
(recordemos que el aceite es más liviano que
el agua) se recircula hacia la parte superior
rociándola sobre la superficie del aceite.
Otro ejemplo sería el de un kilo de viruta de
madera, que se quema más rápido que un
tronco de un kilo de masa.

23. Efecto del Cambio de la
Concentración
Una forma de estudiar el efecto de la
concentración en la velocidad de reacción
consiste en establecer cómo depende la
velocidad al comienzo de la reacción
(velocidad inicial) de las concentraciones de
partida
La dependencia de la concentración se
expresa:
V = k [R]
Para la reacción (1)
[ ] [ ] m n
V =
k A B (2)
Donde:
K es la constante de velocidad
m y n determinan el orden de reacción (son números enteros
pequeños 0, 1, 2….)

24. La constante de velocidad y sus
unidades
De lo expuesto anteriormente (2) se deduce que k
depende del orden de reacción
Si Velocidad se expresa en M/s y Concentración en M
Para una reacción de primer orden: k= V/[A] s-1
Para una reacción de segundo orden: k = V/[A] 2 M-1s-1
Para una reacción de tercer orden: k = V/[A]2[B] M-2s-1

25. Reacción de Primer Orden
∆[ A]
[ A]
∆t
ln[ A] t − ln[ A] 0 = −kt ln
[ A] t = −kt
[ A] 0
ln[ A] t = − kt + ln[ A] 0

26. Ejercicio
La constante de velocidad de primer orden de la
descomposición de cierto insecticida en agua a 12°C es
de 1,45 año-1 . Cierta cantidad de este insecticida es
arrastrada a un lago el 1 de junio y alcanza una
concentración de 5 x 10-7 g/cc de agua. Suponga que la
temperatura media del lago es 12°C . Calcular
a) Cuál es la concentración del insecticida el 1 de
junio del año siguiente
b) Cuánto tiempo tardará la concentración del
insecticida en descender a 3,0 x 10-7 g/cc

27. Considere el proceso en el
que el isonitrilo de metilo
se convierte en
acetonitrilo
CH3NC CH3CN

28. CH3NC CH3CN
Se obtuvieron estos
datos para esta
reacción a 198.9 °C.

29. Cuando ln P se grafica como una función del
tiempo, resulta una línea recta.
Por lo tanto,
El proceso es de primer orden.
k es el negativo de la pendiente: 5.1 × 10−5 s−1.

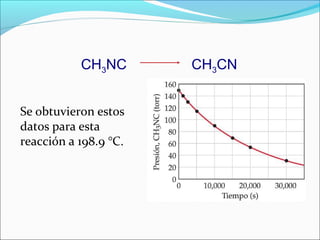
30. Reacciones de Segundo Orden
Es aquella cuya velocidad depende de la concentración de un
reactivo elevada a la segunda potencia o de las concentraciones
de dos reactivos diferentes, cada una elevada a la primera
potencia.
∆[ A]
= k [ A]
2
Velocidad = −
∆t
Si relacionamos la concentración de A al comienzo de la
reacción [A]0 con su concentración en cualquier otro tiempo t,
[A]t 1 1
= kt +
[ A] t [ A] 0
↓ ↓ ↓
Dónde Y = mx + b

31. Ejercicio
Se obtuvieron los siguientes datos de la descomposición
en fase gaseosa de dióxido de nitrógeno a 300°C,
NO2(g) → NO(g) + ½ O2(g)
Tiempo (s) [NO2] (M)
0 0,01000
50 0,00787
100 0,00649
200 0,00481
300 0,00380
Determinar el orden de la reacción con respecto a NO2

32. Vida media
Vida media se define
como el tiempo
requerido para que
reaccione la mitad de
un reactivo.
Debido a que t1/2 en
[A] es la mitad de [A]
original
[A]t = 0.5 [A]0.

33. Vida media
Para un proceso de primer orden, esto es:
0.5 [A]0
ln = −kt1/2
[A]0
ln 0.5 = −kt1/2
−0.693 = −kt1/2
0.693
= t1/2
k
NOTA: Por tanto, para un proceso de primer orden la vida
media no depende de [A]0.

34. Vida media
Para un proceso de segundo orden:
1 1
= kt1/2 +
0.5 [A]0 [A]0
2 1
= kt1/2 +
[A]0 [A]0
2 − 1 = 1 = kt
[A]0 [A]0 1/2
1
= t1/2
k[A]0

35. Resumen de la cinética de las reacciones de orden
cero, orden uno y orden dos
Tiempo de
Orden Ley de velocidad concentración Vida media
[A]0
0 V=k [A] = [A]0 - kt t½ =
2k
ln2
1 V = k [A] ln[A] = ln[A]0 - kt t½ =
k
1 1 1
2 V = k [A] 2 = + kt t½ =
[A] [A]0 k[A]0
13.3

36. Efecto de la Temperatura
La velocidad de casi todas las reacciones cambia por efecto
de la temperatura.
Cuando dos moléculas interaccionan, parte de la energía
cinética se convierte en energía vibracional. Si la energía es
muy grande, las moléculas comenzarán a vibrar fuertemente,
con lo cual algunos enlaces se romperán. El rompimiento de
los enlaces es el primer paso para que se produzca una
reacción. ¿Pero que pasa si la energía es pequeña? ¿o muy
grande?

37. Esto depende de las
moléculas que deben
reaccionar, pero siempre
será necesaria una
cantidad mínima de
energía para que la
reacción se produzca; a
esa energía se la llama
Energía de activación

38. A+B AB+ + C+D
Reacción exotérmica Reacción endotérmica
La energía de activación (Ea ) es la energía mínima requerida para iniciar una
reacción.
13.4

39. El modelo de colisiones hace fácil entender el efecto de la
temperatura en la velocidad de reacción, porque al aumentar la
temperatura aumenta la energía cinética de las moléculas y con
ello se aumenta la posibilidad de que se supere la energía de
activación durante la colisión.
El concepto de energía de activación fue concebido a finales del
siglo XIX por el químico sueco Svante Arrhenius, quien demostró
que la constante de velocidad para una reacción varía con la
temperatura de acuerdo a la siguiente expresión conocida como la
Ecuación de Arrhenius
− Ea
k = Ae RT
Donde: Ea es la energía de activación
R es la constante de los gases
T es la temperatura absoluta
e es la base de los logaritmos naturales
A es el número de choques entre las partículas reaccionantes

40. Si obtenemos el logaritmo para cada lado de la igualdad, nos
queda:
ln k = − Ea + ln A
RT
Ecuación que puede identificarse con la ecuación de una recta

41. Ejercicio
La tabla siguiente muestra las constantes de
velocidad del reacomodo del metil isonitrilo a
diversas temperaturas
Temperatura (°C) k (s-1)
189,7 2,52 x 10-5
198,9 5,25 x 10-5
230,3 6,30 x 10-4
251,2 3,16 x 10-3
En base a estos datos, calcule la energía de activación
de la reacción
Cuál es el valor de la constante de velocidad a 430°C

42. Efecto de los catalizadores
Un catalizador es una sustancia
que modifica la velocidad de
una reacción, sin que sufra un
cambio químico permanente y
sin consumirse durante la
misma
Su presencia en muchos casos
disminuye la necesidad de altas
temperaturas y altas presiones
en procesos industriales, razón
por lo que actualmente se
hacen grandes inversiones de
dinero en estudios, buscando
más y mejores catalizadores.

43. Catálisis
Una forma en la
que un catalizador
puede acelerar
una reacción es
juntar los
reactivos y ayudar
a que se rompan
los enlaces.

44. Existen dos tipos de catálisis: homogénea y
heterogénea.
En la catálisis homogénea todas las sustancias
(reactivos, productos y catalizadores) están en el
mismo estado físico. En la heterogénea en cambio el
catalizador es una sustancia sólida y las demás
sustancias están en otros estados físicos.

46. Temperatura y velocidad
Por lo general, a medida
que aumenta la
temperatura, aumenta la
velocidad de la reacción.
Esto se debe a que k
depende de la
temperatura.

47. Modelo de colisiones
En una reacción química, se rompen enlaces y se
forman nuevos enlaces.
Las moléculas sólo pueden reaccionar si colisionan
entre sí.

48. Modelo de colisiones
Las moléculas deben colisionar con la
orientación correcta y con la energía suficiente
para ocasionar la ruptura y formación de
enlaces.

49. Energía de activación
En otras palabras, se requiere una cantidad mínima de
energía para la reacción: energía de activación, Ea.
Al igual que la pelota no puede subir la colina si no rueda
hacia arriba con la suficiente energía, una reacción no puede
ocurrir a menos que las moléculas posean suficiente energía
para superar la barrera de la energía de activación.

50. Diagramas coordinados
Cinética
de la reacción
química
Es de ayuda
visualizar los
cambios de energía
durante un proceso
en un diagrama
coordinado de la
reacción como éste
para el reacomodo
del isonitrilo de
metilo.

51. Diagramas coordinados
Cinética
de la reacción
química
El diagrama muestra la
energía de los reactivos y
productos (y, por lo
tanto, ∆E).
El punto alto en el
diagrama es el estado de
transición.
• A la especie presente en el estado de transición se le
llama complejo activado.
• El espacio de energía entre los reactivos y el complejo
activado es la barrera de la energía de activación.

52. Distribuciones de
Cinética
Maxwell–Boltzmann
química
La temperatura se
define como una
medida de la energía
cinética promedio de
las moléculas en una
muestra.
• A cualquier temperatura existe una distribución
amplia de las energías cinéticas.

53. Distribuciones de
Cinética
Maxwell–Boltzmann
química
A medida que
aumenta la
temperatura, la curva
se aplana y amplía.
Por tanto, a
temperaturas más
altas, una gran
población de
moléculas tiene mayor
energía.

54. Distribuciones de
Cinética
Maxwell–Boltzmann
química
Si la línea punteada representa la energía de
activación, entonces a medida que la temperatura
aumente, aumentará la fracción de moléculas que
puedan superar la barrera de la energía de
activación.
• Como resultado, la
velocidad de la
reacción aumenta.

55. Distribuciones de
Cinética
Maxwell–Boltzmann
química
Esta fracción de moléculas puede determinarse a través de
la expresión: -Ea
f = e RT
donde R es la constante del gas y T es la temperatura
Kelvin.

56. La ecuación de Arrhenius
Svante Arrhenius desarrolló una relación matemática
entre k y Ea:
-E a
k = A e RT
donde A es el factor de frecuencia; un número que
representa la probabilidad de que las colisiones
sucedan con la orientación apropiada para la reacción.

57. La ecuación de Arrhenius
Al sacar el logaritmo
natural de ambos lados,
la ecuación se convierte
en:
Ea
ln k = - ( 1 ) + ln A
R T
y = m x + b
Por lo tanto, si se determina k de forma experimental
a varias temperaturas, Ea puede calcularse a partir de
1
la pendiente de la gráfica de ln k frente a T .

58. Mecanismos de reacción
A la secuencia de eventos que describen el
proceso real por el cual los reactivos se
convierten en productos se le llama
mecanismo de reacción.

59. Mecanismos de reacción
Las reacciones pueden suceder a través de
una o de varias etapas.
A cada uno de estos procesos se le llama
reacción elemental o proceso elemental.

60. Mecanismos de reacción
La molecularidad de un proceso indica cuántas
moléculas están involucradas en el proceso.

61. Mecanismos multietapas
En un proceso multietapas una de las etapas
será más lenta que las otras.
La reacción general no puede suceder más
rápidamente que su etapa determinante de la
velocidad más lenta.

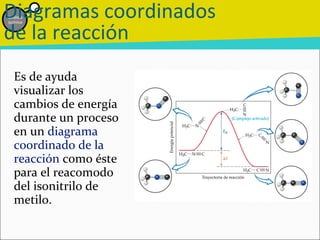
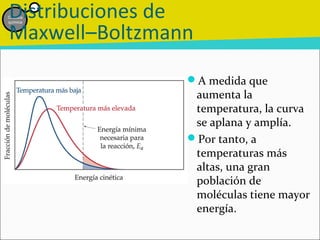
62. Etapa inicial lenta
NO2 (g) + CO (g) → NO (g) + CO2 (g)
La ley de velocidad para esta reacción se encontró de
forma experimental como:
Velocidad = k [NO2]2
El CO es necesario para que suceda esta reacción, pero
la velocidad de la reacción no depende de su
concentración.
Esto sugiere que la reacción sucede en dos etapas.

63. Etapa inicial lenta
Un mecanismo propuesto para esta reacción es:
Etapa 1: NO2 + NO2 → NO3 + NO (lenta)
Etapa 2: NO3 + CO → NO2 + CO2 (rápida)
El NO3 intermediario se consume en la segunda etapa.
Ya que el CO no está involucrado en la etapa determinante
de la velocidad lenta, no aparece en la ley de velocidad.

64. Etapa inicial rápida
2 NO (g) + Br2 (g) → 2 NOBr (g)
La ley de velocidad para esta reacción se
encontró como:
Velocidad = k [NO]2 [Br2]
Debido a que los procesos termomoleculares
son raros, esta ley de velocidad sugiere un
mecanismo de dos etapas.

65. Etapa inicial rápida
Un mecanismo propuesto es:
Etapa 1: NO + Br2 NOBr2 (rápida)
Etapa 2: NOBr2 + NO → 2 NOBr (lenta)
La etapa 1 incluye las reacciones directa
e inversa.

66. Etapa inicial rápida
La velocidad de la reacción general depende de
la velocidad de la etapa lenta.
La ley de velocidad para esa etapa sería:
Velocidad = k2 [NOBr2] [NO]
¿Pero cómo determinamos [NOBr2]?

67. Etapa inicial rápida
El NOBr2 reacciona de dos formas:
Con NO para formar NOBr.
Por descomposición para volver a formar NO y Br2.
Los reactivos y los productos de la primera
etapa están en equilibrio entre sí.
Por lo tanto:
Velocidadf = Velocidadr

68. Etapa inicial rápida
Debido a que Velocidadf = Velocidadr ,
k1 [NO] [Br2] = k−1 [NOBr2]
Despejando [NOBr2] tenemos:
k1
[NO] [Br2] = [NOBr2]
k−1

69. Etapa inicial rápida
La sustitución de esta expresión para [NOBr2] en la
ley de velocidad para la etapa determinante de la
velocidad da:
k2k1
Promedio = [NO] [Br2] [NO]
k−1
= k [NO]2 [Br2]

70. Catálisis
La catálisis aumenta la velocidad de una reacción
al disminuir la energía de activación de la reacción.
La catálisis cambia el mecanismo por el cual
sucede el proceso.

71. Catálisis
Una forma en la
que un catalizador
puede acelerar
una reacción es
juntar los
reactivos y ayudar
a que se rompan
los enlaces.

72. Enzimas
Las enzimas son los
catalizadores en los
sistemas biológicos.
El sustrato se ajusta
dentro del sitio activo
de la enzima de forma
muy similar a como
una llave encaja en
una cerradura.