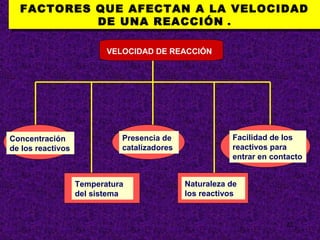
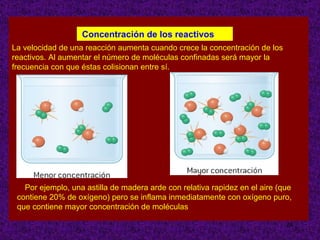
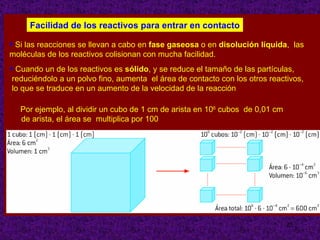
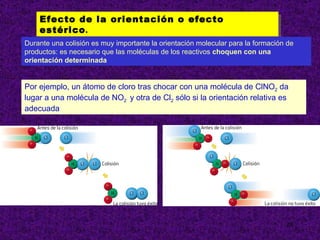
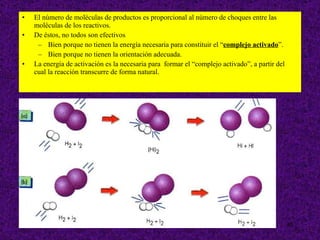
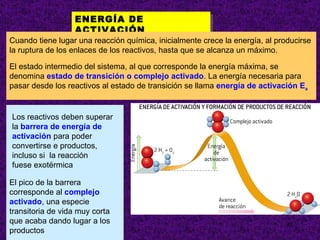
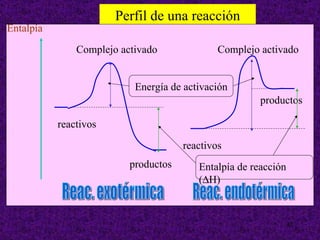
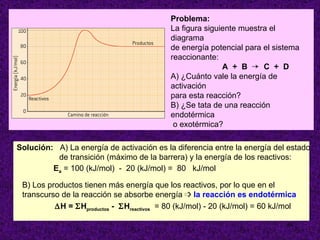
El documento explica conceptos clave sobre la cinética química, incluyendo la velocidad de reacción, el orden de reacción y cómo determinar experimentalmente la ecuación de velocidad. La velocidad de reacción depende de cómo cambian las concentraciones de los reactivos y productos con el tiempo. El orden de reacción describe cómo afecta la concentración de cada reactivo a la velocidad. Se puede determinar el orden mediante experimentos que mantienen constante la concentración de todos menos uno de los reactivos.

1. CINÉTICA QUÍMICA 2º Bachillerato Carmen Peña IES.Altaír Getafe

2. Cuando se produce una reacción química, las concentraciones de cada reactivo y producto va variando con el tiempo, hasta que se produce el equilibrio químico, en el cual las concentraciones de todas las sustancias permanecen constantes. Es la derivada de la concentración de un reactivo o producto con respecto al tiempo tomada siempre como valor positivo. Es decir el cociente de la variación de la concentra-ción de algún reactivo o producto por unidad de tiempo cuando los intervalos de tiempo tienden a 0. VELOCIDAD DE UNA REACCIÓN QUÍMICA .

3. La velocidad de una reacción es una magnitud positiva que expresa el cambio de la concentración de un reactivo o un producto con el tiempo Algunas reacciones son casi instantáneas, como la explosión del TNT; otras son muy lentas, como la transformación de diamante en grafito Ejemplo I 2 (g) + H 2 (g)  2 HI (g) La velocidad de la reacción puede expresarse en término del aumento de la concentración de producto ocurrida en un intervalo de tiempo  t : También puede expresarse como la disminución de la concentración de los reactivos ocurrida en un intervalo de tiempo  t :

4. Problema : En la reacción 2 CO 2  2 CO + O 2 se han formado 0,3 moles de O 2 en10 segundos. Calcula la velocidad de reacción en ese intervalo de tiempo, referida al reactivo y a los productos Solución : De acuerdo con la estequiometría de la reacción, se formarán 0,6 moles de CO mientras que desaparecerán 0,6 moles de CO 2 Velocidad de desaparición de CO 2 en el intervalo de 10 s: Velocidad de aparición de CO en el intervalo de 10 s: Velocidad de aparición de O 2 en el intervalo de 10 s:

5. Para la reacción I 2 (g) + H 2 (g)  2 HI (g) la velocidad instantánea de aparición de reactivo, en el momento t, será : La pendiente de la recta tangente a la curva (es decir, la velocidad de reacción) disminuye con el tiempo, a medida que los reactivos se consumen. La velocidad de una reacción en un instante dado ( velocidad instantánea ) es igual a la pendiente de la recta tangente a la curva concentración-tiempo, relativa a reactivos o productos, en el punto correspondiente a ese instante. El cociente coincide con la pendiente de la recta tangente a la curva que representa [HI] frente al tiempo.

6. Ejemplo de velocidad de reacción Br 2 (ac) + HCOOH (ac)  2 HBr (ac) + CO 2 (g) Tiempo (s) [Br 2  (mol/l) vel. media 0 0’0120 3’8 · 10 –5 50 0’0101 3’4 · 10 –5 100 0’0084 2’6 · 10 –5 150 0’0071 2’4 · 10 –5 200 0’0059

7. Br 2 (ac) + HCOOH (ac)  2 HBr (ac) + CO 2 (g) La velocidad puede expresarse como: d[Br 2 ] d[HCOOH ] d[CO 2 ] d[HBr] v = – ——— = – ————— = ——— = ——— dt dt dt 2 · dt Parece claro que la velocidad de aparición de HBr será el doble que la de aparición de CO 2 por lo que en este caso la velocidad habrá que definirla como la mitad de la derivada de [HBr] con respecto al tiempo.

8. Ejemplo: Expresar la velocidad de la siguiente reacción química en función de la concentración de cada una de las especies implicadas en la reacción: 4 NH 3 (g) + 3 O 2 (g)  2 N 2 (g) + 6 H 2 O (g) d[NH 3 ] d[O 2 ] d[ N 2 ] d[H 2 O] v = – ——— = – ——— = ——— = ——— 4 · dt 3 · dt 2 · dt 6 · dt

9. ORDEN DE UNA REACCIÓN . Cuando todos los reactivos se hallan formando una misma fase física (reacciones homogéneas), la velocidad es proporcional a las concentraciones de los reactivos elevada cada una de ellas a una determinada potencia. Sea la reacción: a A + b B  productos La velocidad de reacción se expresa como: v = K [ A ] m [ B ] n Esta ecuación se denomina ecuación de la velocidad o ley de la velocidad de la reacción y debe determinarse experimentalmente K = constante de velocidad o velocidad específica El valor del exponente al que está elevada la concentración de un reactivo en la ecuación de velocidad se denomina orden de la reacción con respecto a dicho reactivo. La suma de todos los exponentes se llama orden total o simplemente orden de la reacción

10. En la expresión: v = k · [A  n · [B  m se denomina orden de reacción ... ...al valor suma de los exponentes “n + m”. Se llama orden de reacción parcial a cada uno de los exponentes. Es decir, la reacción anterior es de orden “n” con respecto a A y de orden “m” con respecto a B.

11. Problema : La ley de velocidad para la reacción A  B es de la forma v = K [A] 2 ¿Cuál es el orden de la reacción con respecto a A y el orden total? Solución : La reacción es de orden 2 con respecto a A El orden total también es 2 , ya que en la reacción de velocidad sólo aparece la concentración de A Problema : La velocidad de la reacción del proceso no espontáneo aA + bB  productos está dada por la expresión v = K [A] [B] ¿Cuál es el orden total de la reacción? Solución : La reacción es de primer orden respecto al reactivo A La reacción es de primer orden respecto al reactivo B El orden total de la reacción es 1 + 1 = 2

12. Ejemplo: Determina los órdenes de reacción total y parciales de las reacciones anteriores: H 2 (g) + I 2 (g)  2 HI (g) v = k · [H 2  · [I 2  H 2 (g) + Br 2 (g)  2 HBr (g) v = k · [H 2  · [Br 2  1/2 H 2 (g) + I 2 (g)  2 HI (g) v = k · [H 2  · [I 2  Reacción de segundo orden (1 + 1) De primer orden respecto al H 2 y de primer orden respecto al I 2 . H 2 (g) + Br 2 (g)  2 HBr (g) v = k · [H 2  · [Br 2  ½ Reacción de orden 3 / 2 (1 + ½ ) De primer orden respecto al H 2 y de orden ½ respecto al Br 2 .

13. Determinación de la ecuación de velocidad Consiste en medir la velocidad inicial manteniendo las concentraciones de todos los reactivos constantes excepto la de uno y ver cómo afecta la variación de éste al valor de la velocidad. Si por ejemplo, al doblar la concentración de un reactivo la velocidad se multiplica por cuatro, podemos deducir que el orden parcial respecto a ese reactivo es “2”.

14. Determinación experimental de la ecuación de velocidad Ejemplo: Determinar el orden de reacción : CH 3 -Cl (g) + H 2 O (g)  CH 3 -OH (g) + HCl (g) usando los datos de la tabla. 11,35 0,5 0,25 3 5,67 0,25 0,50 2 1 2,83 0,25 0,25 Experiencia v (mol·l –1 ·s –1 ) [H 2 O] (mol/l) [CH 3 -Cl] (mol/l)

15. v = k · [CH 3 -Cl  n · [H 2 O  m En las experiencias 1 y 2 vemos que no cambia [H 2 O  luego el cambio de “v” se debe al cambio de [CH 3 -Cl  . Como al doblar [CH 3 -Cl  se dobla la velocidad podemos deducir que el orden de reacción respecto del CH 3 -Cl es “1”. En las experiencias 1 y 3 vemos que no cambia [CH 3 -Cl  luego el cambio de “v” se debe al cambio de [H 2 O  . Como al doblar [H 2 O  se cuadruplica la velocidad podemos deducir que el orden de reacción respecto del H 2 O es “2”. v = k · [CH 3 -Cl  · [H 2 O  2 Y el orden total de la reacción es “3”. El valor de “k” se calcula a partir de cualquier experiencia y resulta 181’4 mol –2 l 2 s –1 .

16. También puede calcularse usando logaritmos: log v = log k + n · log [CH 3 -Cl  + m · log [H 2 O  Aplicamos dicha expresión a cada experimento: (1) log 2,83 = log k + n · log 0,25 M + m · log 0,25 M (2) log 5,67 = log k + n · log 0,50 M + m · log 0,25 M (3) log 11,35 = log k + n · log 0,25 M + m · log 0,50 M Si restamos dos ecuaciones en las que se mantenga constante uno de los reactivos, podremos obtener el orden de reacción parcial del otro. Así, al restar (1) – (2) eliminamos “k” y [H 2 O  : log (2,83/5,67) = n · log (0,25/0,50) Análogamente restando (1) – (3) eliminamos “k” y [CH 3 -Cl  log (2,83/11,35) = m · log (0,25/0,50) log (2,83/5,67) log (2,83/11,35) n = —————— = 1 ; m = ——————— = 2 log (0,25/0,50) log (0,25/0,50)

17. Ejercicio A: En la obtención del ácido nítrico, una de las etapas principales es la oxidación del óxido nítrico a dióxido de nitrógeno: 2 NO(g) + O 2 (g)  2 NO 2 (g). Para esta reacción, se ha determinado experimentalmente que su ecuación de velocidad es: v = k [NO] 2 · [O 2 ] y que la constante de velocidad, a 250 ºC, vale: k = 6,5 . 10 -3 mol -2 L 2 s -1 . Calcular la velocidad de oxidación del NO, a dicha temperatura, cuando las concentraciones iniciales (mol L -1 ) de los reactivos son: a) [NO] = 0,100 M ; [O 2 ] = 0,210 M b) [NO] = 0,200 M; [O 2 ] = 0,420 M Sustituyendo los datos resulta: a) v = 6,5 . 10 -3 M -2 s -1. (0,100 M) 2 . 0,210 M = 1,37·10 -5 mol L -1 s -1 b) v = 6,5 . 10 -3 M -2 s -1. (0,200 M) 2 . 0,420 M = 1,09·10 -4 mol L -1 s -1 Como puede comprobarse, en el caso b), en el que ambas concentraciones se han duplicado, la velocidad es 8 veces mayor (2 2 . 2).

18. Ejercicio B: El oxido nítrico, NO, reacciona con hidrógeno formando óxido nitroso, N 2 O: 2NO(g) + H 2 (g)  N 2 O (g) + H 2 O (g). En una serie de experimentos se han obtenidos los siguientes resultados: Determinar la ecuación de la velocidad y calcular el valor de la constante de velocidad. Por la simple inspección de los datos se puede ver que, cuando se duplica [H 2 ], manteniendo constante [NO] (experimento 1ª y 2ª), la velocidad se hace también doble, es decir, que “v” es proporcional a [H 2 ] 1 . En cambio, cuando se mantiene constante [H 2 ] y se duplica [NO] (experimento 1ª y 3ª), la velocidad se multiplica por 4 (=2 2 ), es decir, que la “v” es proporcional a [NO] 2 . Por tanto, la ecuación de velocidad será:

19. 2NO(g) + H 2 (g)  N 2 O (g) + H 2 O (g). v = k [NO] 2 [H 2 ] Se trata, pues, de una reacción de primer orden respecto al H 2 , de segundo orden respecto al NO y de orden total igual a tres. Para calcular el valor de k, basta despejar de la ecuación anterior y sustituir los datos de cualquiera de las experiencias. Por ejemplo, sustituyendo las datos de la primera experiencia, resulta: v 2,6 . 10 -2 mol L -1 s -1 k —————— = —————————————— = [NO] 2 [H 2 ] (0,064 mol L -1 ) 2 . (0,022 mol L -1 ) k = 2,9 . 10 2 mol -2 L 2 s -1

20. Molecularidad La reacción: H 2 (g) + I 2 (g)  2 HI (g) es una reacción elemental (que sucede en una sola etapa) y para que suceda es necesario el choque de dos moléculas (una de H 2 y otra de I 2 ). Se dice que es una reacción “bimolecular” Se llama molecularidad al número de moléculas de reactivos que colisionan simultáneamente para formar el complejo activado en una reacción elemental. Se trata de un número entero y positivo. Así hablamos de reacciones unimoleculares, bimoleculares, trimoleculares, etc… Generalmente, en reacciones elementales, coincide con el orden de reacción. Sin embargo, existen casos en los que no coinciden, como las reacciones de hidrólisis en los que interviene una molécula de agua ya que al ser [H 2 O] prácticamente constante la velocidad es independiente de ésta. Es raro que una reacción intervengan más de tres moléculas pues es muy poco probable que chocan entre sí simultáneamente con la energía y orientación adecuadas.

21. MECANISMOS DE REACCIÓN En la reacción elemental: H 2 (g) + I 2 (g)  2 HI (g) vista anteriormente, v = k · [H 2  · [I 2  Sin embargo, la mayoría de las reacciones suceden en etapas. El conjunto de estas etapas se conoce como “ mecanismo de la reacción ”. Las sustancias que van apareciendo y que no son los productos finales se conocen como “ intermedios de reacción ”. La velocidad de la reacción dependerá de las sustancias que reaccionen en la etapa más lenta. La reacción NO 2 (g) + CO (g)  NO (g) + CO 2 (g) sucede en dos etapas: 1ª etapa (lenta): 2 NO 2  NO + NO 3 2ª etapa (rápida): NO 3 + CO  NO 2 + CO 2 La reacción global es la suma de las dos. NO 3 es un intermedio de reacción. En la etapa lenta intervienen dos moléculas de NO 2, , luego v = k · [NO 2  2

22. FACTORES QUE AFECTAN A LA VELOCIDAD DE UNA REACCIÓN . VELOCIDAD DE REACCIÓN Concentración de los reactivos Temperatura del sistema Presencia de catalizadores Naturaleza de los reactivos Facilidad de los reactivos para entrar en contacto

23. Naturaleza de los reactivos: La velocidad de reacción varía mucho según la naturaleza de los reactivos. Por ejemplo, un trozo de sodio pierde inmediatamente su brillo debido a su reacción con el oxígeno y el agua atmosféricos. El hierro también reacciona con el oxígeno y la humedad del aire, formando herrumbre, pero de forma más lenta Oxidación del hierro Oxidación del sodio

24. Concentración de los reactivos La velocidad de una reacción aumenta cuando crece la concentración de los reactivos. Al aumentar el número de moléculas confinadas será mayor la frecuencia con que éstas colisionan entre sí. Por ejemplo, una astilla de madera arde con relativa rapidez en el aire (que contiene 20% de oxígeno) pero se inflama inmediatamente con oxígeno puro, que contiene mayor concentración de moléculas

25. Facilidad de los reactivos para entrar en contacto Si las reacciones se llevan a cabo en fase gaseosa o en disolución líquida , las moléculas de los reactivos colisionan con mucha facilidad. Cuando un de los reactivos es sólido , y se reduce el tamaño de las partículas, reduciéndolo a un polvo fino, aumenta el área de contacto con los otros reactivos, lo que se traduce en un aumento de la velocidad de la reacción Por ejemplo, al dividir un cubo de 1 cm de arista en 10 6 cubos de 0,01 cm de arista, el área se multiplica por 100

26. Temperatura del sistema La velocidad de casi todas las reacciones aumenta al elevar la temperatura. Un aumento de 10 ºC hace que se duplique la velocidad de la reacción. Cuanto más alta sea la temperatura, mayor será la energía cinéticas de las moléculas, lo que supone un aumento del número de colisiones moleculares y por consiguiente, un aumento de la velocidad de la reacción. La temperatura de los insectos sigue las oscilaciones del ambiente. Por ello, la actividad de una abeja es inferior en invierno, porque las reacciones bioquímicas de su organismo son más lentas. El carbón y la gasolina no arden a temperatura ambiente, pero cuando se calientan se produce una rápida combustión.

27. Al final de la reacción, los catalizadores aparecen íntegros , aunque a veces, en distinto estado de agregación. Por ejemplo, la reacción entre H 2 y O 2 ocurre a velocidad despreciable a temperatura ambiente, pero en presencia de platino finamente dividido la reacción es bastante rápida. La naturaleza del catalizador puede determinar los productos de la reacción . Presencia de un catalizador Si se utiliza óxido de cinc, se forma metanol Ejemplo: cuando se utiliza níquel como catalizador, la reacción entre el CO y el H 2 produce metano Los catalizadores son sustancias que, añadidas a los reactivos, aumentan la velocidad de la reacción.

28. LA TEORÍA DE COLISIONES. No toda colisión entre las moléculas reaccionantes da lugar a la formación de productos.Si fuera así, las reacciones en fase líquida o gaseosa serían todas rapidísimas, casi instantáneas, ya que en tales medios el número de colisiones por segundo es extraordinariamente grande Deben tener una orientación adecuada Deben poseer energía suficiente Para que una reacción pueda tener lugar, las moléculas de las sustancias reaccionantes deben chocar entre sí. Cualquier factor que aumente la frecuencia con que ocurren tales colisiones deberá aumentar la velocidad de reacción.Por tanto, es de esperar que se cumpla el siguiente postulado: La velocidad de una reacción es proporcional al número de colisiones producidas por unidad de tiempo, entre las moléculas de los reactivos. (teoría de colisiones) Para que un choque resulte efectivo y dé lugar a una reacción se requiere que las moléculas implicadas cumplan las siguientes condiciones:

29. Efecto de la orientación o efecto estérico . Por ejemplo, un átomo de cloro tras chocar con una molécula de ClNO 2 da lugar a una molécula de NO 2 y otra de Cl 2 sólo si la orientación relativa es adecuada Durante una colisión es muy importante la orientación molecular para la formación de productos: es necesario que las moléculas de los reactivos choquen con una orientación determinada

30. El número de moléculas de productos es proporcional al número de choques entre las moléculas de los reactivos. De éstos, no todos son efectivos Bien porque no tienen la energía necesaria para constituir el “ complejo activado ”. Bien porque no tienen la orientación adecuada. La energía de activación es la necesaria para formar el “complejo activado”, a partir del cual la reacción transcurre de forma natural.

31. ENERGÍA DE ACTIVACIÓN Cuando tiene lugar una reacción química, inicialmente crece la energía, al producirse la ruptura de los enlaces de los reactivos, hasta que se alcanza un máximo. El estado intermedio del sistema, al que corresponde la energía máxima, se denomina estado de transición o complejo activado . La energía necesaria para pasar desde los reactivos al estado de transición se llama energía de activación E a Los reactivos deben superar la barrera de energía de activación para poder convertirse e productos, incluso si la reacción fuese exotérmica El pico de la barrera corresponde al complejo activado , una especie transitoria de vida muy corta que acaba dando lugar a los productos

32. Perfil de una reacción reactivos reactivos productos productos Energía de activación Entalpía de reacción (  H) Reac. exotérmica Reac. endotérmica Entalpía Complejo activado Complejo activado

33. Normalmente, la energía cinética de las moléculas reaccionantes suministra la energía de activación . Sólo los choques entre moléculas de energía cinética igual o superior a la energía de activación E a son eficaces La velocidad de una reacción aumenta al diminuir su E a La constante de velocidad K , está relacionada con la E a mediante la ecuación de Arrhenius La constante de proporcionalidad A , es una característica de la reacción; R es la constante de los gases ideales y T es la temperatura absoluta

34. Problema: La figura siguiente muestra el diagrama de energía potencial para el sistema reaccionante: A + B  C + D A) ¿Cuánto vale la energía de activación para esta reacción? B) ¿Se tata de una reacción endotérmica o exotérmica? Solución: A) La energía de activación es la diferencia entre la energía del estado de transición (máximo de la barrera) y la energía de los reactivos: E a = 100 (kJ/mol) - 20 (kJ/mol) = 80 kJ/mol B) Los productos tienen más energía que los reactivos, por lo que en el transcurso de la reacción se absorbe energía  la reacción es endotérmica  H =  H productos -  H reactivos = 80 (kJ/mol) - 20 (kJ/mol) = 60 kJ/mol

35. Problema: La energía de activación de la reacción A + B  Productos es de 108 kJ/mol.Sabiendo que la constante de velocidad de dicha reacción vale k = 6,2 • 10 -5 s -1 a 35 ºC, calcula cuánto valdrá dicha constante cuando la temperatura sea de 50 ºC Dato: R = 8,31 J/mol K Solución: De acuerdo con la ecuación de Arrhenius : Despejando A y sustituyendo los valores dados tenemos: El valor de A es constante y no depende de la temperatura. Por tanto, a 50 ºC, la constante de velocidad, k, valdrá:

36. Catálisis. Se reserva el término catalizador a las sustancias que aceleran la velocidad de reacción; si la sustancia disminuye la velocidad de reacción se denomina inhibidor o catalizador negativo . La acción del catalizador se llama catálisis El catalizador no aparece en la ecuación neta de la reacción , ya que se regenera en el transcurso de la misma Los catalizadores aumentan la velocidad de reacción debido a que disminuyen la energía de activación. El catalizador cambia el mecanismo de la reacción: proporciona un camino de reacción alternativo, cuya E a sea menor Los valores de  H r ,  S r y  G r no se ven afectados por la presencia del catalizador La presencia del catalizador no afecta en nada al calor de reacción ni a la espontaneidad del proceso

37. Catalizadores Intervienen en alguna etapa de la reacción pero no se modifican pues se recuperan al final y no aparece en la ecuación global ajustada. Modifican el mecanismo y por tanto E a . No modifican las constantes de los equilibrios . Pueden ser: Positivos: hacen que “v”  pues consiguen que E a  . Negativos : hacen que “v”  pues consiguen que E a  . Los catalizadores también pueden clasificarse en: Homogéneos: en la misma fase que los reactivos. Heterogéneos: se encuentra en distinta fase.

38. TIPOS DE CATÁLISIS Catálisis homogénea : el catalizador se encuentra en la misma fase que los reactivos. Catálisis heterogénea : el catalizador se encuentra en una fase diferente de la de los reactivos. Su mecanismo se basa en la adsorción de las moléculas reaccionantes (gases) en la superficie del catalizador (sólido), sobre la que ocurre la reacción. Ejemplo : fabricación de H 2 SO 4 por el método de las cámaras de plomo: 2 SO 2 (g) + O 2 (g)  2SO 3 (g) se cataliza con una mezcla gaseosa de NO 2 + NO Ejemplo : O 2 + 2H 2  2 H 2 O sobre platino

39. El reactivo o sustrato encaja perfectamente en un punto específico de la superficie de la enzima, manteniéndose en esta posición por fuerzas intermoleculares Después de esta adsorción , la configuración de la enzima puede variar, debilitándose el enlace clave del sustrato y aumentando la velocidad de reacción Catálisis enzimática : las sustancias que catalizan las reacciones bioquímicas se llaman enzimas (proteinas de elevada masa molecular) Ejemplo : las reacciones que tienen lugar en el cuerpo humano pueden realizarse a la temperatura del organismo (37ºC) gracias a la acción de las enzimas