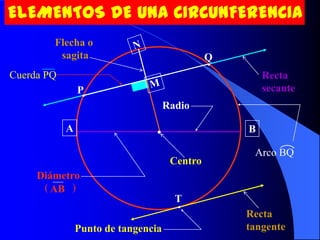
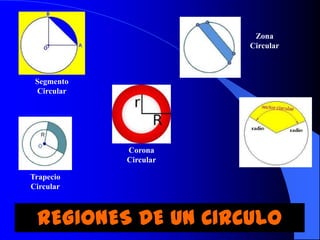
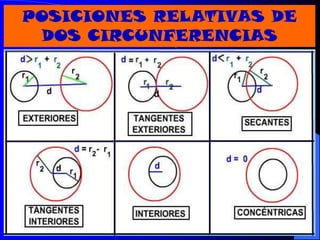
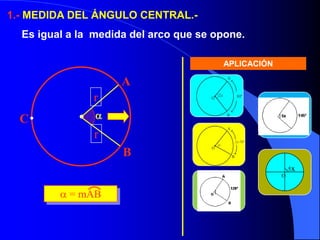
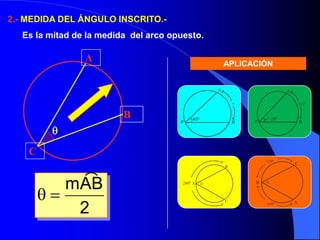
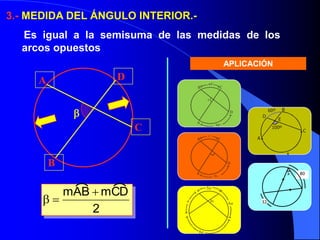
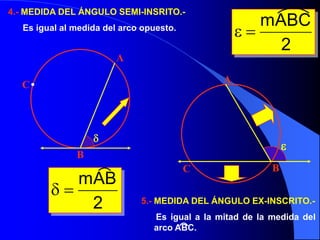
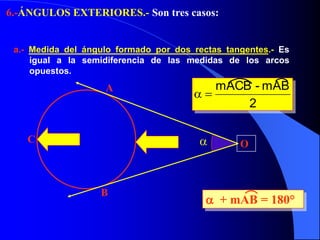
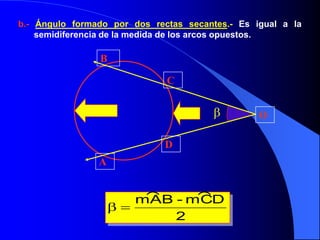
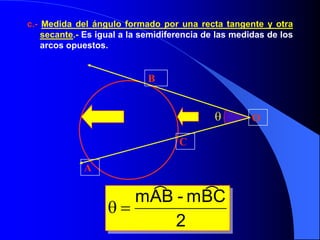
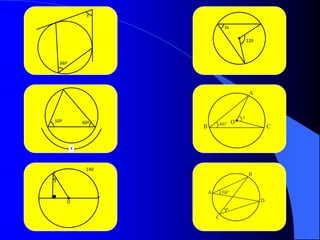
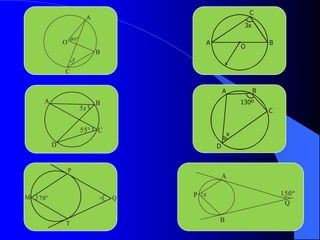
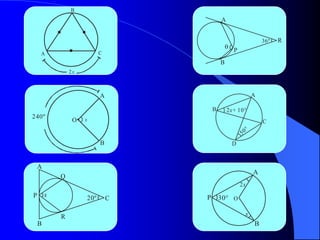
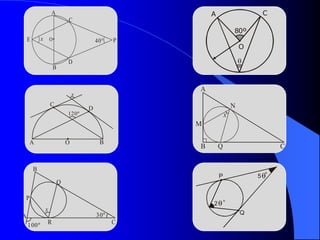
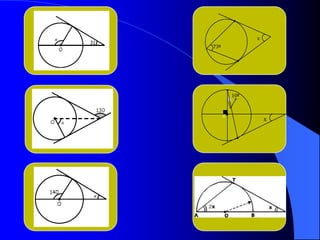
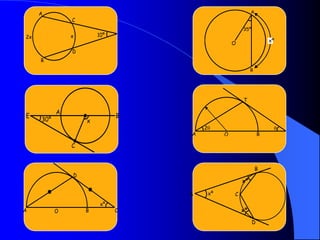
El documento describe la circunferencia y el círculo. La circunferencia es el conjunto de puntos equidistantes de un punto central. El círculo es la porción de plano que incluye la circunferencia y su interior. El documento también define elementos como el radio, diámetro y arco, y describe las relaciones entre ángulos y arcos en un círculo, incluyendo ángulos centrales, inscritos y exteriores. Finalmente, presenta problemas variados sobre estas propiedades.

1. CIRCUNFERENCIA
Y
CÍRCULO
Profesor :
Carlos E. Hernández Hernández
Grado:
2do de Secundaria
2011

2. CIRCUNFERENCIA
Es un lugar geométrico de un conjunto de infinitos
puntos que equidistan de un punto situado en el
centro.

3. CÍRCULO
Es la porción de plano que comprende la circunferencia
y su interior.
El perimetro del círculo es igual a la longitud de la
circunferencia, entonces se cumple:
Lo= 2πr

4. ELEMENTOS DE UNA CIRCUNFERENCIA
Flecha o
sagita Q

Cuerda PQ Recta
P secante

Radio
A  B
Arco BQ
Centro
Diámetro
( AB )
T

Recta
Punto de tangencia tangente

5. Zona
Circular
Segmento
Circular
Corona
Circular
Trapecio
Circular
REGIONES DE UN CIRCULO

6. POSICIONES RELATIVAS DE
DOS CIRCUNFERENCIAS

8. 1.- MEDIDA DEL ÁNGULO CENTRAL.-
Es igual a la medida del arco que se opone.
APLICACIÓN
A
A
r O
2x 80º
C  B
A
r 2 x -70º
x
O
B B
5x
O
 = mAB

9. 2.- MEDIDA DEL ÁNGULO INSCRITO.-
Es la mitad de la medida del arco opuesto.
A APLICACIÓN
A A
x 13 2º
B 40º P
x+ 28º
B
P B

C
12 0º
C
B
mAB 260º A x B x
 C A
2 14 0º

10. 3.- MEDIDA DEL ÁNGULO INTERIOR.-
Es igual a la semisuma de las medidas de los
arcos opuestos
APLICACIÓN
A D 44 º
B C
x
 D
D
60º
E
B
A
C 98 º
100º
C
x
B C A
x
B D
A
4x
x 80
mAB  mCD
5a
 a 
6a 32
2
8a

11. 4.- MEDIDA DEL ÁNGULO SEMI-INSRITO.-
mABC
Es igual al medida del arco opuesto.

2
A
C A


B
C B
mAB

2 5.- MEDIDA DEL ÁNGULO EX-INSCRITO.-
Es igual a la mitad de la medida del
arco ABC.

12. 6.-ÁNGULOS EXTERIORES.- Son tres casos:
a.- Medida del ángulo formado por dos rectas tangentes.- Es
igual a la semidiferencia de las medidas de los arcos
opuestos.
A mACB - mAB

2
C  O
B
 + mAB = 180°

13. b.- Ángulo formado por dos rectas secantes.- Es igual a la
semidiferencia de la medida de los arcos opuestos.
B
C
 O
D
A
mAB - mCD

2

14. c.- Medida del ángulo formado por una recta tangente y otra
secante.- Es igual a la semidiferencia de las medidas de los
arcos opuestos.
B
 O
C
A
mAB - mBC

2

15. PROBLEMAS
VARIADOS

16. x
3x
120
66º
A
x
50º 60º 40 º O
B C
x
140
B
x
A 50º
O D

C

17. C
A
3x
80°
O A B
O
B
x
C
A B
A B 130º
5x C
55° C
x
D D
P
A
P x 150º
M 70º x Q
Q
T
B

18. B
A
36º R

C P
A
B
2x
A A
B 2 x + 10°
240º x
O C
°
50
B D
A
A
Q
2x
P x 20º C P 30° O
R x
B B

19. A A C
C
80º
E x O . 40° P
O
D 
B
A
x
C N
D
120º x
M
A O B
B Q C
B
P 5 °
Q
P
2°
x
30º Q
A
100º R C

20. x
73º
10º
O
x