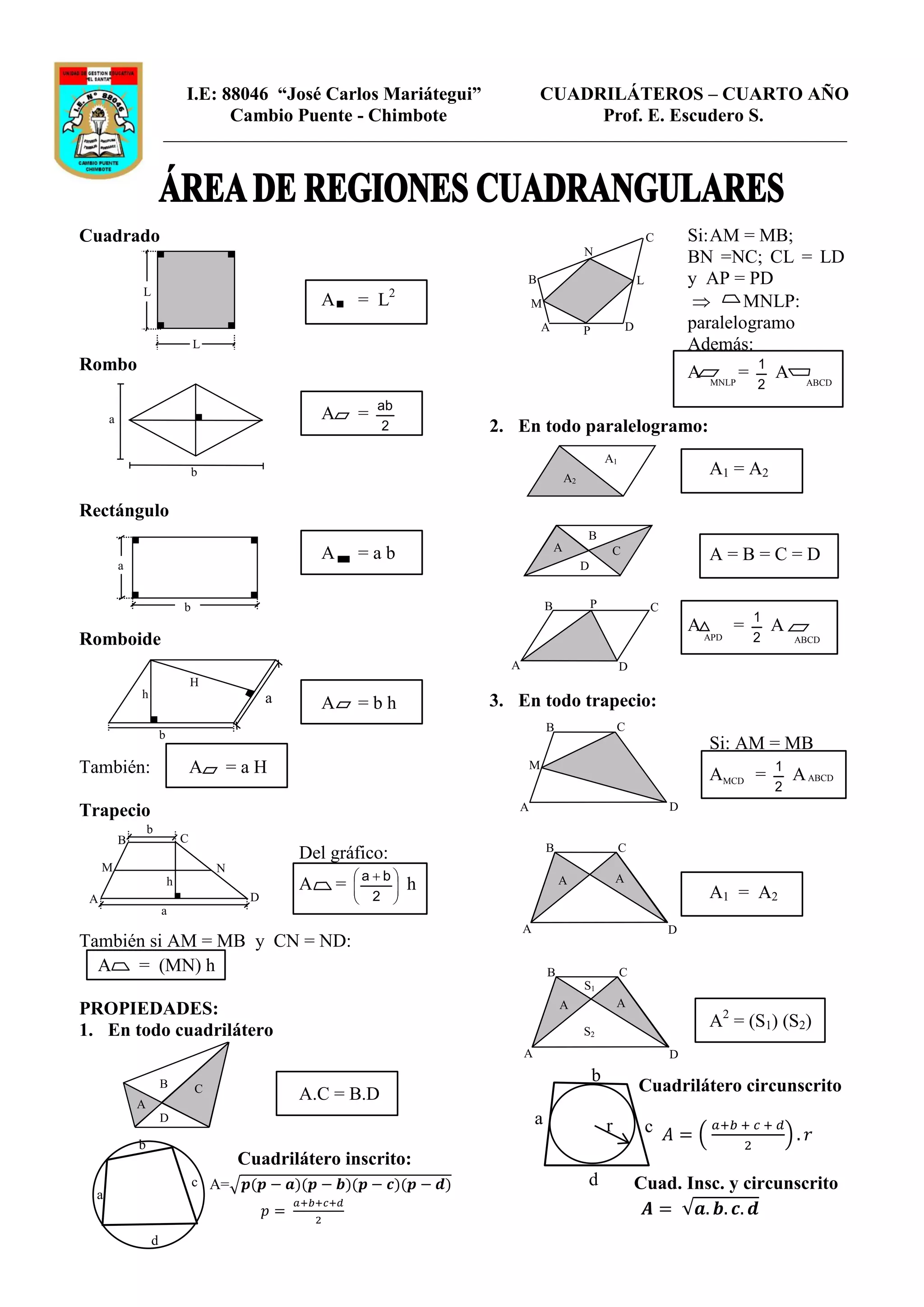
Este documento presenta fórmulas y propiedades de cuadriláteros como cuadrados, rectángulos, rombos, romboides, trapecios y paralelogramos. Explica que en todo paralelogramo los lados opuestos son iguales y los ángulos opuestos son suplementarios. También detalla que en todo trapecio la suma de las distancias entre los lados no paralelos es igual al doble del área. Por último, indica que en un cuadrilátero inscrito y circunscrito, el área del cuad

1. I.E: 88046 “José Carlos Mariátegui” CUADRILÁTEROS – CUARTO AÑO
Cambio Puente - Chimbote Prof. E. Escudero S.
Cuadrado C Si: AM = MB;
N
BN =NC; CL = LD
B L y AP = PD
L

2
A = L M MNLP:
A P D paralelogramo
L Además:
Rombo A MNLP = 1 A ABCD
2
ab
a A =
2 2. En todo paralelogramo:
A1
b A2
A1 = A2
Rectángulo
B
A
A =ab C A=B=C=D
a D
b B P C
1
A = A
Romboide APD 2 ABCD
A D
H
h a A =bh 3. En todo trapecio:
B C
b
Si: AM = MB
También: A =aH M
AMCD = 1
A ABCD
2
Trapecio A D
b
B C
B C
Del gráfico:
M N
ab A
h A = 
 2 
 h A
A D   A1 = A2
a
A D
También si AM = MB y CN = ND:
A = (MN) h B C
S1
A A
PROPIEDADES:
1. En todo cuadrilátero S2
A2 = (S1) (S2)
A D
b
B C
A.C = B.D Cuadrilátero circunscrito
A
D a r c
b
( )
Cuadrilátero inscrito:
c A=√ d Cuad. Insc. y circunscrito
a
√
d

2. TAREA DOMICILIARIA
1. Dos lados de un romboide miden 6 y 10 cm 10. Un rectángulo tiene un área de 96 m2. Hallar
respectivamente, y una altura mide 9 cm. sus dimensiones, sabiendo que su base excede
Hallar su área. a su altura en 4 m.
A) 30 cm2 C) 48 cm2 E) 72 cm2 A) 6 y 8 m C) 8 y 12 m E) 8 y 14 m
B) 36 cm2 D) 54 cm2 B) 4 y 12 m D) 4 y 16 m
2. Un cuadrado ABCD, tiene 10 m de lado. 11. Hallar el área de un cuadrado inscrito en un
Calcular el área del cuadrado formado al unir semicírculo de 3 5 m de radio.
sucesivamente los puntos medios de los lados. A) 24 m2 C) 45 m2 E) 25 m2
A) 15 m2 C) 50 m2 E) 80 m2 B) 36 m 2
D) 15 m 2
2 2
B) 25 m D) 75 m
12. Al unir los puntos medios de tres lados de un
3. La base de un rectángulo es 20 m. Calcular su cuadrilátero se forma un triángulo, cuyos
área si la recta que une el punto medio de su lados miden 5 m, 7 m y 8 m. Hallar el área del
base con un vértice superior es 2 61 m. cuadrilátero.
A) 60 m2 C) 100 m2 E) 240 m2 A) 20 3 m2 C) 10 3 m2 E) 40 3 m2
2 2 2 2
B) 80 m D) 120 m B) 40 m D) 20 m
4. El área de un cuadrado es 18 m2 y está inscrito 13. Se da un romboide ABCD, en donde AB = 10
en una circunferencia. Hallar el radio de la m y la altura respecto a este lado es 4 m. Se
circunferencia. toma en el interior del romboide un punto “E”
A) 3m B) 4m C) 6m D) 8m E) 9m cualquiera. Hallar la suma de las áreas de los
triángulo ABE y DEC.
5. Las bases de un trapecio son 8 m y 3 m; la A) 5 m2 C) 15 m2 E) 25 m2
altura es 4 m. Calcular su área. B) 10 m2 D) 20 m2
A) 11 m2 C) 18 m2 E) 22 m2
2 2
B) 15 m D) 20 m 14. Una de las diagonales de un trapezoide
simétrico es igual a la altura de un trapecio
6. Las bases de un trapecio son 12 m y 5 m y su cuyas bases suman 14m. Sabiendo que los dos
altura es 4 m. Calcular el área del triángulo cuadriláteros tienen la misma área, hallar la
formado al unir el punto medio de uno de los otra diagonal del trapezoide.
lados no paralelos con los extremos del otro A) 7 m C) 21 m E) N.A.
no paralelo. B) 14 m D) 28 m
A) 11 m2 C) 17 m2 E) 34 m2
B) 15 m2 D) 28 m2 15. Si se disminuyera el largo de cierto rectángulo
en 4 cm y se incrementara el ancho en 3 cm,
7. El semiperímetro de un rombo es 26 m, y la resultaría un cuadrado con la misma área que
diagonal menor mide 10 m. Hallar su área. el rectángulo original. Hallar el perímetro, en
A) 120 m2 C) 90 m2 E) 60 m2 cm, del rectángulo original.
B) 100 m2 D) 80 m2 A) 20 B) 30 C) 40 D) 50 E) 60
8. Calcular el área de un rombo cuyo perímetro 16. Hallar el área de un rectángulo cuyos lados se
es 32 m y su inradio mide 3 m. diferencian en 2 cm; sabiendo además, que el
A) 48 m2 C) 36 m2 E) 96 m2 perímetro de este rectángulo es igual al de un
2 2
B) 24 m D) 32 m triángulo equilátero de área 16 3 cm2.
A) 21 cm2 C) 40 cm2 E) N.A.
9. Al unir los puntos medios de los lados del B) 35 cm 2
D) 45 cm2
cuadrilátero ABCD, se forma el
paralelogramo EFGH, cuya base mayor es 14 17. Hallar el perímetro de un cuadrado que tiene
m y su altura 6 m. Calcular el área del igual área que un rombo de lado 4 108 cm y
cuadrilátero.
uno de cuyos ángulos mide 60°.
A) 324 m2 C) 192 m2 E) 124 m2
A)10cm B)15cm C)18cm D)12cm E)16cm
B) 242 m2 D) 168 m2