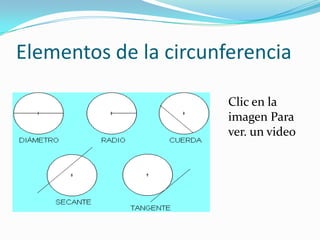
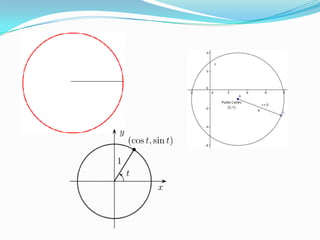
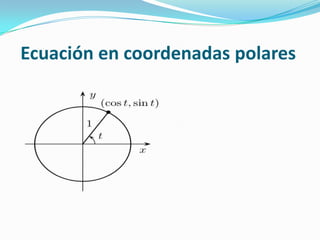
Este documento describe los elementos básicos de una circunferencia. Define una circunferencia como una línea curva cerrada cuyos puntos están equidistantes de un punto central llamado centro. Explica conceptos como radio, diámetro, ángulos centrales e inscritos, ecuaciones cartesiana y polar de una circunferencia, y cómo calcular el área y longitud de una circunferencia.

1. TEMA A TRATAR:

2. ESCUELA: CETIs 162 ALVARO BREGON

• NL
 José Rodrigo Limón de Anda 32
 Heriberto Nuño Tapia 40
 Arnold Emmanuel Pérez Pulido 44
 Lunes, 05 de Diciembre de 2011

3. Elementos de la circunferencia
Clic en la
imagen Para
ver. un video

4. ELEMETOS DE LA CIRCUNFERENCIA
Clic para iniciar el video

5. ¿Qué es la circunferencia?
 La circunferencia es una línea curva, plana y
cerrada, cuya definición más usual es:
 Una circunferencia es el conjunto de todos los puntos
de un plano que equidistan de otro punto fijo y
coplanario llamado centro.

7. La circunferencia y un punto
Un punto en el plano puede ser:
 Exterior a la circunferencia, si la distancia del centro al
punto es mayor que la longitud del radio.
 Perteneciente a la circunferencia, si la distancia del
centro al punto es igual a la longitud del radio.
 Interior a la circunferencia, si la distancia del centro al
punto es menor a la longitud del radio

8. La circunferencia y un punto
Al hacer clic en la
imagen Para ver. un
video

9. Relación entre la circunferencia y
diámetro Clic Para iniciar ver. video

10. Ángulos en un circunferencia
 Ángulos en una circunferencia
 Ángulos en la circunferencia.
 Arco capaz: los cuatro ángulos inscritos determinan el mismo
arco y por tanto son iguales.
 Un ángulo, respecto de una circunferencia, pueden ser:
 Ángulo central, si tiene su vértice en el centro de esta. Sus
lados contienen a dos radios.
 La amplitud de un ángulo central es igual a la del arco que
abarca. Ángulo inscrito, si su vértice es un punto de la
circunferencia y sus lados contienen dos cuerdas.

11. Ángulos en un circunferencia
 Ángulo semi-inscrito, si su vértice es un punto de la
circunferencia y sus lados contienen una cuerda y una recta
tangente a la circunferencia. El vértice es el punto de
tangencia.
 La amplitud de un ángulo semi-inscrito es la mitad de la
del arco que abarca. Ángulo interior, si su vértice está en el
interior de la circunferencia.
 La amplitud de un ángulo interior es la mitad de la suma de
dos medidas: la del arco que abarcan sus lados más la del
arco que abarcan sus prolongaciones. Ángulo exterior, si
tiene su vértice en el exterior de la circunferencia

12. Longitud de la circunferencia
 Longitud de la circunferencia
 La longitud de una circunferencia es:
 donde es la longitud del radio.
 Pues (número pi), por definición, es el cociente entre
la longitud de la circunferencia y el diámetro:

13. Ecuaciones de la circunferencia
 Ecuación en coordenadas cartesianas
 En un sistema de coordenadas cartesianas-y, la
circunferencia con centro en el punto (a, b) y radio r consta
de todos los puntos (x, y) que satisfacen la ecuación
 . Cuando el centro está en el origen (0, 0), la ecuación
anterior se simplifica al
 . La circunferencia con centro en el origen y de radio la
unidad, es llamada circunferencia gonio métrica
circunferencia unidad o circunferencia unitria.

14. Ecuaciones de la circunferencia
 De la ecuación general de una circunferencia,
 se deduce:
 resultando:
 Si conocemos los puntos extremos de un diámetro: ,
 la ecuación de la circunferencia es:

15. Ecuación en coordenadas polares
 Cuando la circunferencia tiene centro en el origen y el
radio es c, se describe en coordenadas polares como
 Cuando el centro no está en el origen, sino en el punto
y el radio es , la ecuación se transforma en:

16. Ecuación en coordenadas polares

17. Area de una circunferencia
 Área del círculo = π × área del cuadrado sombreado.
 El área del círculo delimitado por la circunferencia es:
 Esta última fórmula se deduce sabiendo que el área de
cualquier polígono regular es igual al semiproducto
entre el apotemay el perímetro del polígono, es decir:

18. Area de una circunferecia
 Considerando la circunferencia como el caso límite de
un polígono regular de infinitos lados, entonces, el
apotema coincide con el radio, y el perímetro con la
longitud de la circunferencia, por tanto:

19. Ecuación vectorial de la
circunferencia
 La circunferencia con centro en el origen y radio
R, tiene por ecuación vectorial
 . Se puede deducir fácilmente desde la ecuación
cartesiana, ya que la componente X y la componente
Y, al cuadrado y sumadas deben dar por resultado el
radio de la circunferencia al cuadrado. En el espacio
esta misma ecuación da como resultado un
cilindro, dejando el parámetro Z libre.

20. BIBLIOGRAFIA:
 http://www.youtube.com/watch?v=kSDes72Vy3A
 http://es.wikipedia.org/wiki/Circunferencia
 http://es.wikipedia.org/wiki/archivo