Incrustar presentación
Descargar para leer sin conexión




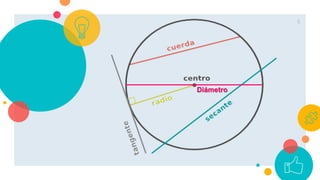
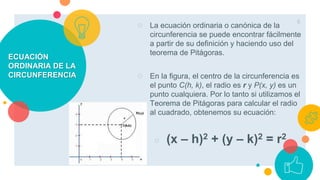

La circunferencia es un lugar geométrico de puntos que equidistan de un punto central llamado centro. El diámetro une dos puntos de la circunferencia pasando por su centro, mientras que el radio une el centro con cualquier punto. La ecuación ordinaria de una circunferencia se puede encontrar usando el teorema de Pitágoras para igualar la distancia entre un punto cualquiera y el centro al radio al cuadrado.






