Uu

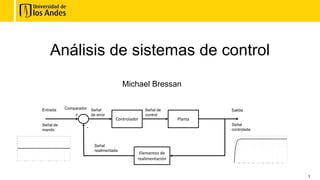
1. 1
Análisis de sistemas de control
Michael Bressan
Comparador
Controlador Planta
+
-
Elementos de
realimentación
Señal
de error
Señal
realimentada
Señal de
control
Señal
controlada
Salida
Entrada
Señal de
mando

2. 2 Recordatorio Algebra lineal
𝐴 =
𝑎11 𝑎12 ⋯ 𝑎1𝑛
𝑎21 𝑎22 ⋯ 𝑎2𝑛
⋮ ⋮ … ⋮
𝑎𝑛1 𝑎𝑛2 … 𝑎𝑛𝑛
𝐼 =
1 0 … 0
0 1 … 0
⋮ ⋮ … ⋮
0 0 … 1
• Matriz cuadrada de orden n, 𝐴 ∈
ℝ𝑛𝑥𝑛
• Matriz identidad de orden n,
• Característica polinómica de A:
• Valores propios de A:
det 𝐴 − λ𝑖I = 0
i=1,2,…,n
• Vectores propios de A:
𝐴𝑣𝑖 = λ𝑖𝑣𝑖
i=1,2,…,n
P λ = det λI − A = λ𝑛
+ 𝑎1λ𝑛−1
+ ⋯ + 𝑎𝑛−1λ + 𝑎𝑛

3. Solución Ecuación de Estado
Asumimos que se tiene la representación en el espacio de estado:
𝑥 𝑡 = 𝐴𝑥(𝑡)
Se puede escribir como:
𝑥1 𝑡 = 𝑎11𝑥1 𝑡 + ⋯ + 𝑎1𝑛𝑥𝑛 𝑡
𝑥2 𝑡 = 𝑎21𝑥1 𝑡 + ⋯ + 𝑎2𝑛𝑥𝑛 𝑡
𝑥𝑛 𝑡 = 𝑎𝑛1𝑥1 𝑡 + ⋯ + 𝑎𝑛𝑛𝑥𝑛 𝑡
⋮
Se asume que se conocen las condiciones iniciales del sistema x(0), por lo cual se podría integrar a ambos lados de la ecuación
para así obtener
𝑥1 𝑡 − 𝑥1 0 =
0
𝑡
𝑎11𝑥1 𝜏 + ⋯ + 𝑎1𝑛𝑥𝑛 𝜏 𝑑𝜏
𝑥2 𝑡 − 𝑥2 0 =
0
𝑡
𝑎21𝑥1 𝜏 + ⋯ + 𝑎2𝑛𝑥𝑛 𝜏 𝑑𝜏
𝑥𝑛 𝑡 − 𝑥𝑛 0 =
0
𝑡
𝑎𝑛1𝑥1 𝜏 + ⋯ + 𝑎𝑛𝑛𝑥𝑛 𝜏 𝑑𝜏
3

4. Solución Ecuación de Estado
De forma matricial, se convierte en :
𝑥 𝑡 =
0
𝑡
𝐴𝑥 𝜏 𝑑𝜏 + 𝑥(0)
Cuyo 𝑥 𝜏 solución de la ecuación cuando 𝑥 𝑡 𝑡=𝜏
𝑥 𝜏 =
0
𝑡
𝐴𝑥 𝜏′ 𝑑𝜏′ + 𝑥(0)
Reemplazamos 𝑥 𝜏 en la ecuación 𝑥 𝑡 :
𝑥 𝑡 =
0
𝑡
𝐴
0
𝑡
𝐴𝑥 𝜏′ 𝑑𝜏′ + 𝑥(0) 𝑑𝜏 + 𝑥(0)
Si repetimos el proceso, se obtiene
𝑥 𝑡 = 𝐼 +
0
𝑡
𝐴𝑑𝜏 +
0
𝑡
0
𝜏
𝐴2
𝑑𝜏′
𝑑𝜏 +
0
𝑡
0
𝜏
0
𝜏′
𝐴3
𝑑𝜏′′
𝑑𝜏′
𝑑𝜏 + ⋯ + 𝑥(0)
4

5. Solución Ecuación de Estado
El sistema es lineal e invariante en el tiempo, la matriz A es constante. Por lo tanto:
Lo que tenemos entre paréntesis, es la aproximación en series de Taylor de una exponencial. Por lo tanto:
Este término Φ 𝑡 se conoce como matriz de transición de estado
𝑥 𝑡 = 𝐼 + 𝐴𝑡 +
𝐴2𝑡2
2!
+
𝐴3𝑡3
3!
+ ⋯ 𝑥(0)
𝑥 𝑡 = 𝑒𝐴𝑡
𝑥 0 = Φ 𝑡 𝑥(0)
5

6. Matriz de transición
El sistema es lineal e invariante en el tiempo, la matriz A es constante. Por lo tanto:
Lo que tenemos entre paréntesis, es la aproximación en series de Taylor de una exponencial. Por lo tanto:
Este término Φ 𝑡 se conoce como matriz de transición de estado
𝑥 𝑡 = 𝐼 + 𝐴𝑡 +
𝐴2𝑡2
2!
+
𝐴3𝑡3
3!
+ ⋯ 𝑥(0)
𝑥 𝑡 = 𝑒𝐴𝑡
𝑥 0 = Φ 𝑡 𝑥(0)
6
Φ 𝑡 = 𝑒𝐴𝑡
= ℒ−1
𝑠𝐼 − 𝐴 −1
Φ−1
𝑡 = 𝑒−𝐴𝑡
= Φ −𝑡

7. Propiedades de la Matriz de
Transición de Estado
7
Propiedades de la matriz de transición de estado :
Φ 0 = 𝐼
Φ−1
𝑡 = Φ −𝑡
Φ𝑘 𝑡 = Φ 𝑘𝑡
Φ 𝑡1 + 𝑡2 = Φ 𝑡1 Φ 𝑡2
Φ 𝑡1 − 𝑡2 Φ 𝑡1 − 𝑡0 = 𝑒𝐴(𝑡2−𝑡0)

8. Sistema con Respuesta Forzada
• Para un sistema lineal de tiempo continuo 𝑥 = 𝐴𝑥 + 𝐵𝑢 con una condición inicial 𝑥(0) = 𝑥0 ∈ ℝ𝑛
, existe una única solución
x(t):
𝑥 𝑡 = 𝑒𝐴𝑡
𝑥0 +
0
𝑡
𝑒𝐴 𝑡−𝜏
𝐵𝑢 𝜏 𝑑𝜏
Respuesta natural Respuesta forzada
8

9. Método de diagonalización de la
matriz A
• Si la matriz de estado A ∈ ℝ𝑛𝑥𝑛
es diagonal, mostramos fácilmente:
𝐴 =
λ1 0 ⋯ 0
0 λ2 ⋯ 0
⋮ ⋮ ⋱ ⋮
0 0 … λ𝑛 Φ 𝑡 = 𝑒𝐴𝑡
=
𝑒λ1𝑡 0 ⋯ 0
0 𝑒λ2𝑡
⋯ 0
⋮ ⋮ ⋱ ⋮
0 0 … 𝑒λ𝑛𝑡
• Supongamos una matriz P, una matriz es diagonalizable :
1. Una propiedad de los valores y vectores propios es que los autovectores de autovalores diferentes son linealmente
independientes. Por lo tanto, si todos los autovalores de la matriz son únicos la matriz es diagonalizable.
2. La multiplicidad algebraica es el número de veces que se repite un valor propio (o autovalor), y la multiplicidad
geométrica es la dimensión del núcleo (o kernel) de la matriz restándole el autovalor en su diagonal principal.
Entonces, si por cada valor propio la multiplicidad algebraica es igual a la multiplicidad geométrica, la matriz es
diagonalizable.
𝛼𝜆 = 𝑚𝑢𝑙𝑡𝑖𝑝𝑙𝑖𝑐𝑖𝑑𝑎𝑑 𝑎𝑙𝑔𝑒𝑏𝑟𝑎𝑖𝑐𝑎 = 𝑚𝑢𝑙𝑡𝑖𝑝𝑙𝑖𝑐𝑖𝑑𝑎𝑑 𝑑𝑒𝑙 𝑣𝑎𝑙𝑜𝑟 𝑝𝑟𝑜𝑝𝑖𝑜
𝑚𝜆 = 𝑚𝑢𝑙𝑡𝑖𝑝𝑙𝑖𝑐𝑖𝑑𝑎𝑑 𝑔𝑒𝑜𝑚é𝑡𝑟𝑖𝑐𝑎 = dim 𝐾𝑒𝑟 𝐴 − 𝜆𝐼 = 𝑛 − 𝑟𝑔(𝐴 − 𝜆𝐼)
𝑠𝑖𝛼𝜆 = 𝑚𝜆 ∀𝜆 𝑒𝑛𝑡𝑜𝑛𝑐𝑒𝑠 𝑙𝑎 𝑚𝑎𝑡𝑟𝑖𝑧 𝑒𝑠 𝑑𝑖𝑎𝑔𝑜𝑛𝑎𝑙𝑖𝑧𝑎𝑏𝑙𝑒
9
𝜆𝐼 − 𝐴 = 0

10. Método de diagonalización de la
matriz A
• Si A ∈ ℝ𝑛𝑥𝑛 es diagonalizable, A = 𝑇𝐽𝑇−1 y :
𝐽 = 𝑇−1𝐴𝑇 =
λ1 0 ⋯ 0
0 λ2 ⋯ 0
⋮ ⋮ ⋱ ⋮
0 0 … λ𝑛
𝑒𝐴𝑡
= 𝑇
𝑒λ1𝑡
0 ⋯ 0
0 𝑒λ2𝑡 ⋯ 0
⋮ ⋮ ⋱ ⋮
0 0 … 𝑒λ𝑛𝑡
𝑇−1
• Supongamos u(t)=0 y asumimos que A es diagonalizable
𝑥 𝑡 = 𝑒𝐴𝑡
𝑥 0 = 𝑇𝑒𝐽𝑡
𝑇−1
𝑥0 = 𝑣1 … 𝑣𝑛
𝑒𝜆1𝑡 … 0
⋱
0 … 𝑒𝜆𝑛𝑡
𝛼
𝑥(𝑡) = 𝑣1𝑒𝜆1𝑡 … 𝑣𝑛𝑒𝜆𝑛𝑡
𝛼1
⋮
𝛼1
= 𝑖=0
𝑛
𝛼1𝑒𝜆𝑖𝑡𝑣𝑖
• La trayectoria es la respuesta natural
• 𝑣𝑖 es el vector propio de A, 𝜆𝑖 es el valor propio de A, 𝛼 = 𝑇−1
𝑥(0) ∈ ℝ𝑛
• La evolución del sistema depende de los valores propios 𝜆𝑖 llamado modo del sistema de A valor propio de A,
𝛼 = 𝑆−1𝑥(0) ∈ ℝ𝑛
• El model 𝜆𝑖 está “excitado” si 𝛼𝑖 ≠ 0
10

11. Métodos de realización de espacio
de estado
𝐻 𝑠 =
1
𝑠3 + 𝑎1𝑠2 + 𝑎2𝑠2 + 𝑎3
=
𝑌(𝑠)
𝑈(𝑠)
Forma canónica de controlabilidad:
𝑦 𝑡 + 𝑎1𝑦 𝑡 + 𝑎2 𝑦 𝑡 + 𝑎3𝑦 𝑡 = 𝑢(𝑡)
𝑥 𝑡 =
𝑦 𝑡
𝑦 𝑡
𝑦 𝑡
=
−𝑎1 −𝑎2 −𝑎3
1 0 0
0 1 0
𝑦 𝑡
𝑦 𝑡
𝑦 𝑡
+
1
0
0
𝑢(𝑡)
𝑦 𝑡 = 0 0 1 𝑥 𝑡 + 0 𝑢(𝑡)
11

12. Métodos de realización de espacio
de estado
𝐻 𝑠 =
𝑏1𝑠2 + 𝑏2𝑠2 + 𝑏3
𝑠3 + 𝑎1𝑠2 + 𝑎2𝑠2 + 𝑎3
=
𝑌(𝑠)
𝑈(𝑠)
Forma canónica de controlabilidad (función propria)
𝑥 𝑡 =
−𝑎1 −𝑎2 −𝑎3
1 0 0
0 1 0
𝑥(𝑡) +
1
0
0
𝑢(𝑡)
𝑦 𝑡 = 𝑏1 𝑏2 𝑏3 𝑥 𝑡 + 0 𝑢(𝑡)
12

13. Métodos de realización de espacio
de estado
𝐻 𝑠 =
𝑏0𝑠3 + 𝑏1𝑠2 + 𝑏2𝑠 + 𝑏1
𝑠3 + 𝑎1𝑠2 + 𝑎1𝑠2 + 𝑎3
=
𝑌(𝑠)
𝑈(𝑠)
Forma canónica de controlabilidad (función impropia)
𝐻 𝑠 =
𝛽1𝑠2 + 𝛽2𝑠 + 𝛽3
𝑠3 + 𝑎1𝑠2 + 𝑎1𝑠2 + 𝑎3
+ 𝐷 𝛽𝑖 se configura via la división de polinomio
Ejemplo: 𝐻 𝑠 =
3𝑠4
+ 5𝑠3
+ 24𝑠2
+ 23𝑠 − 5
2𝑠4 + 6𝑠3 + 15𝑠2 + 12𝑠 + 5
13