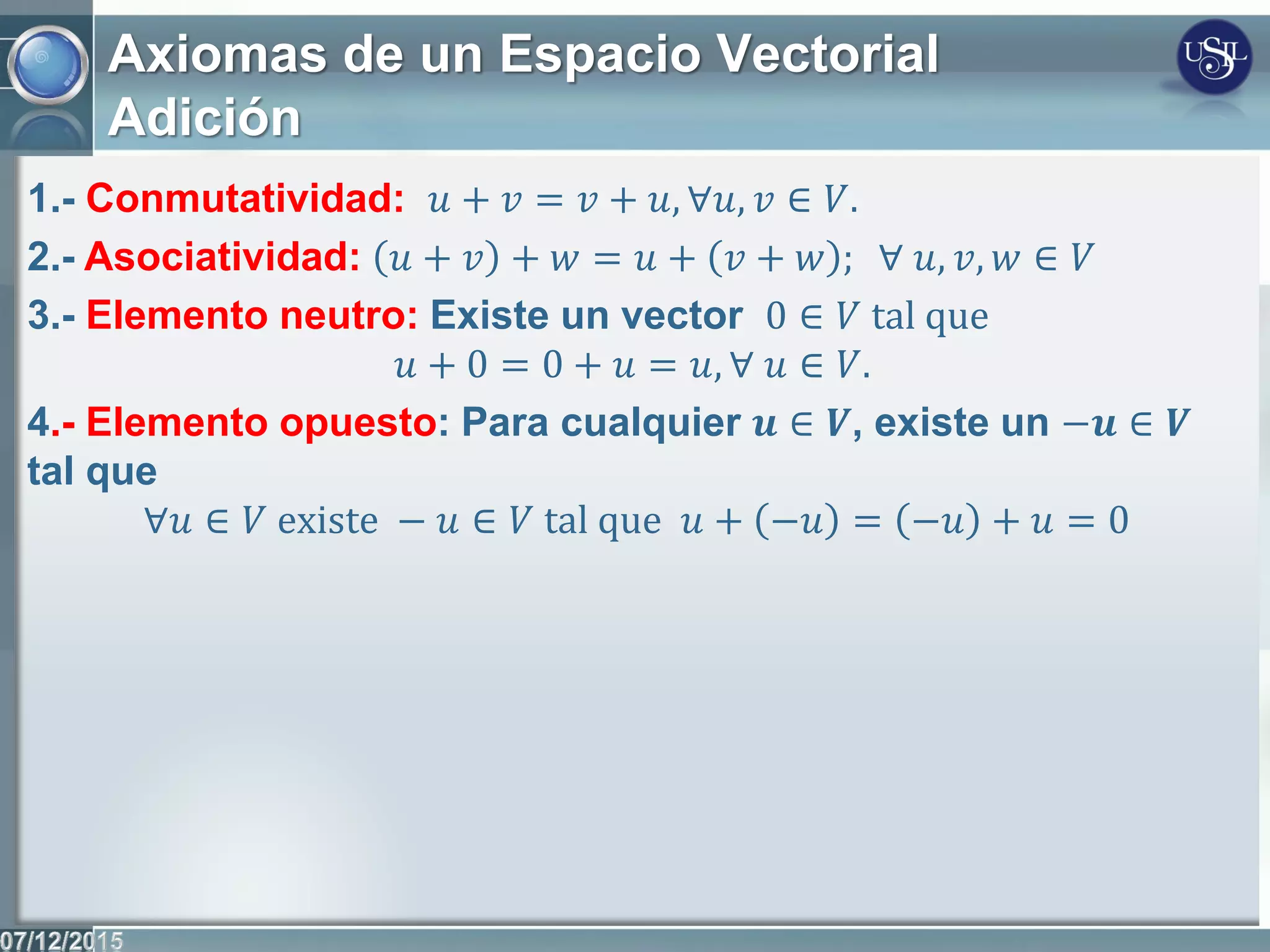
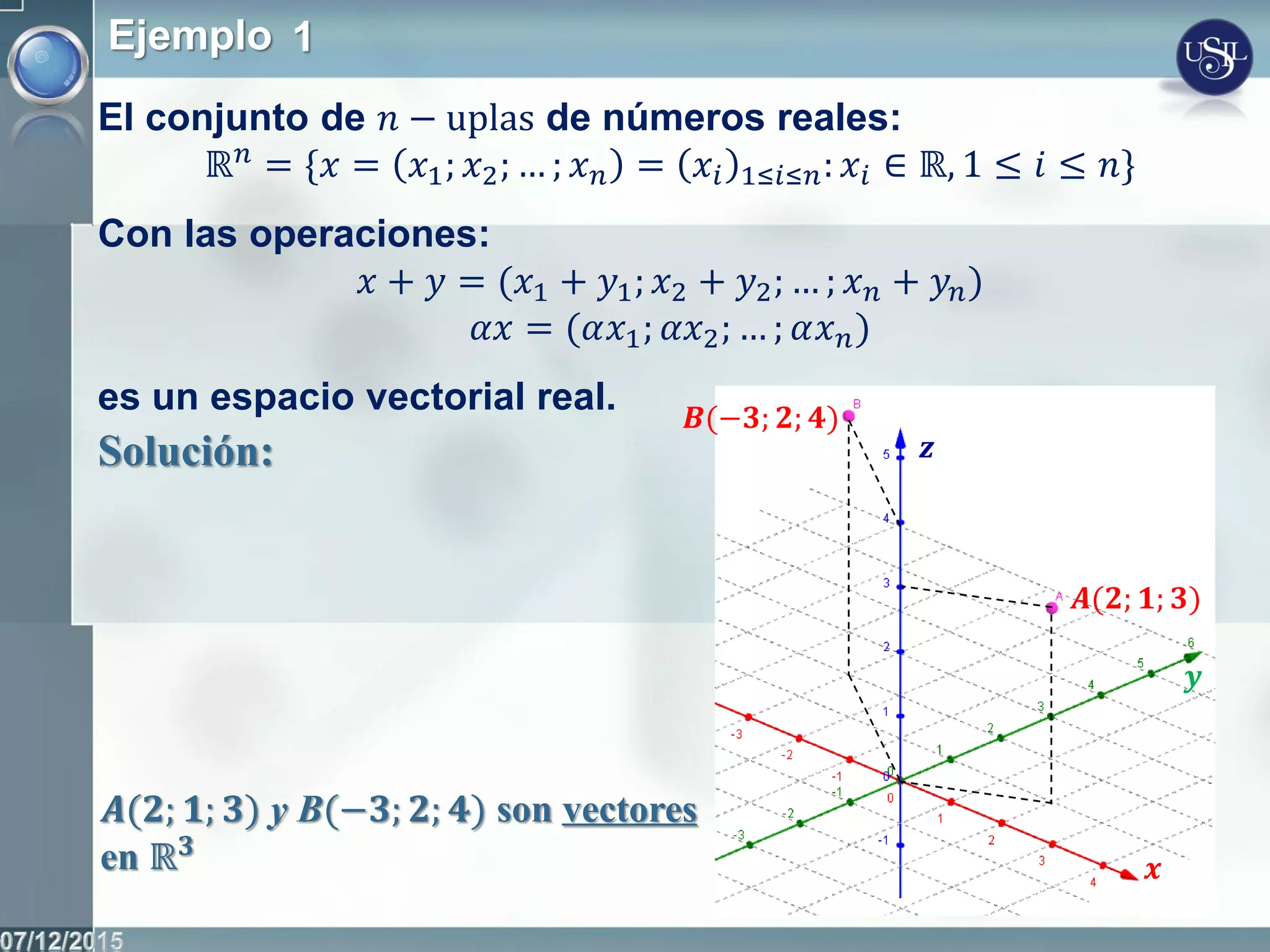
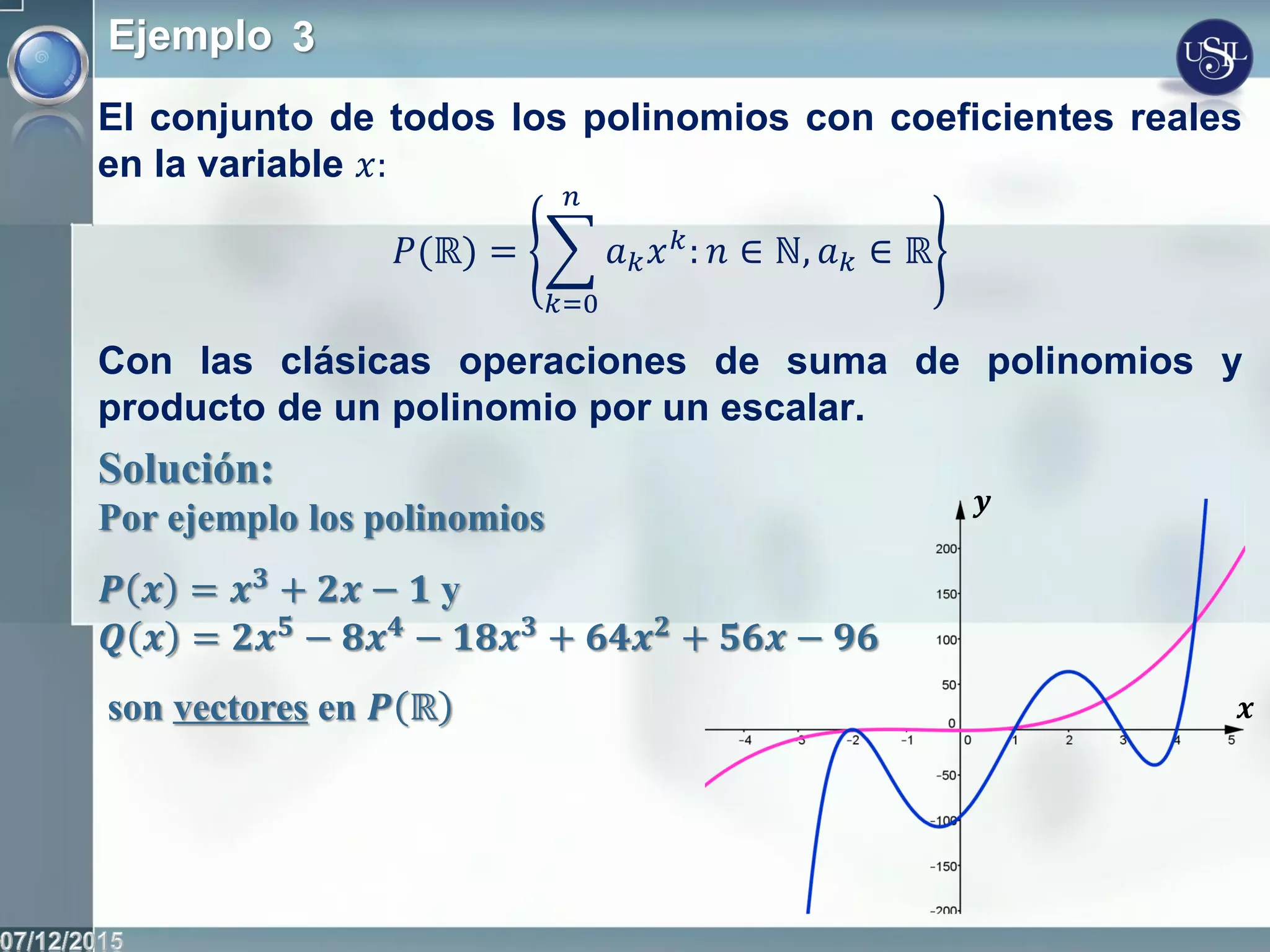
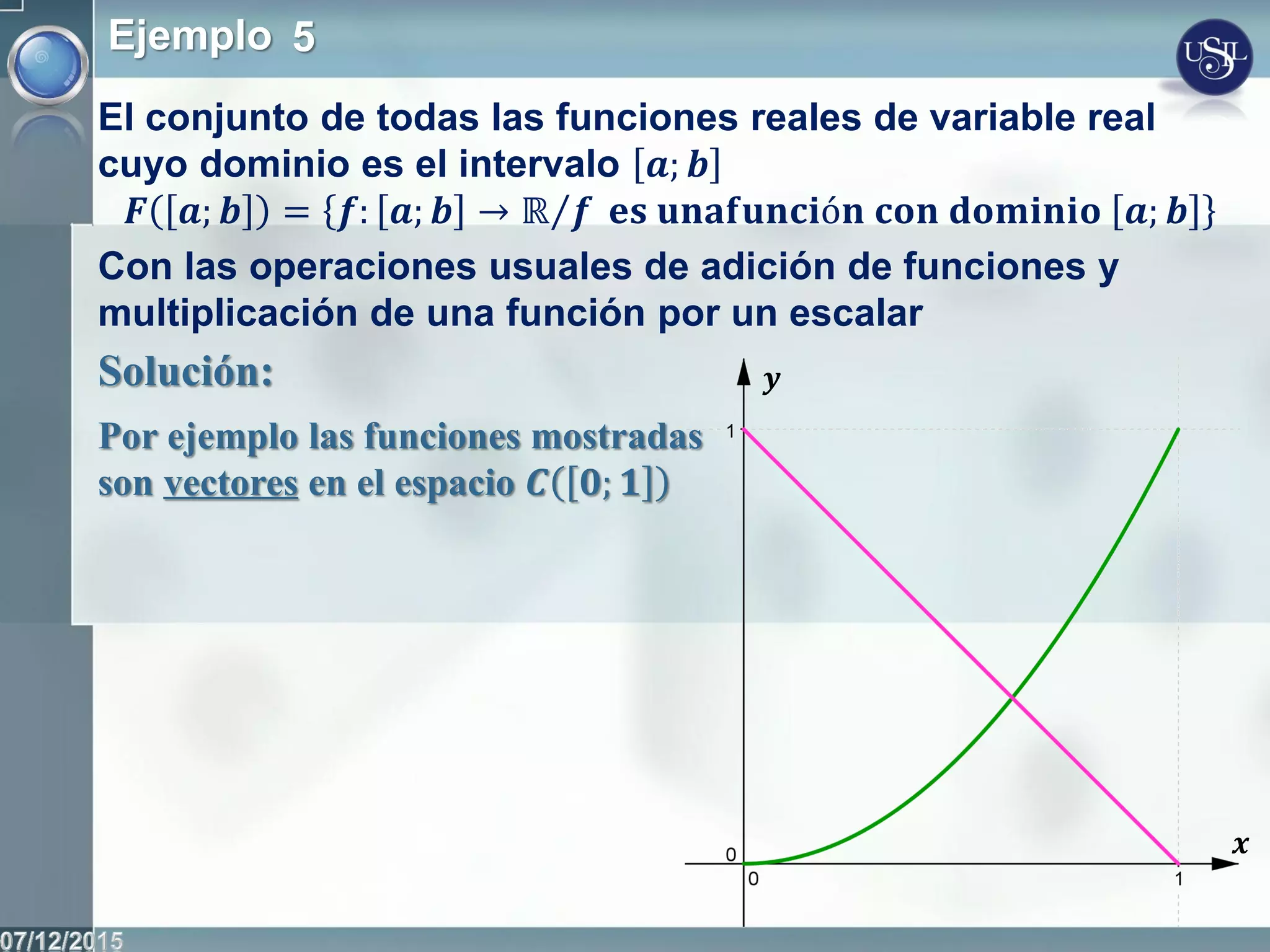
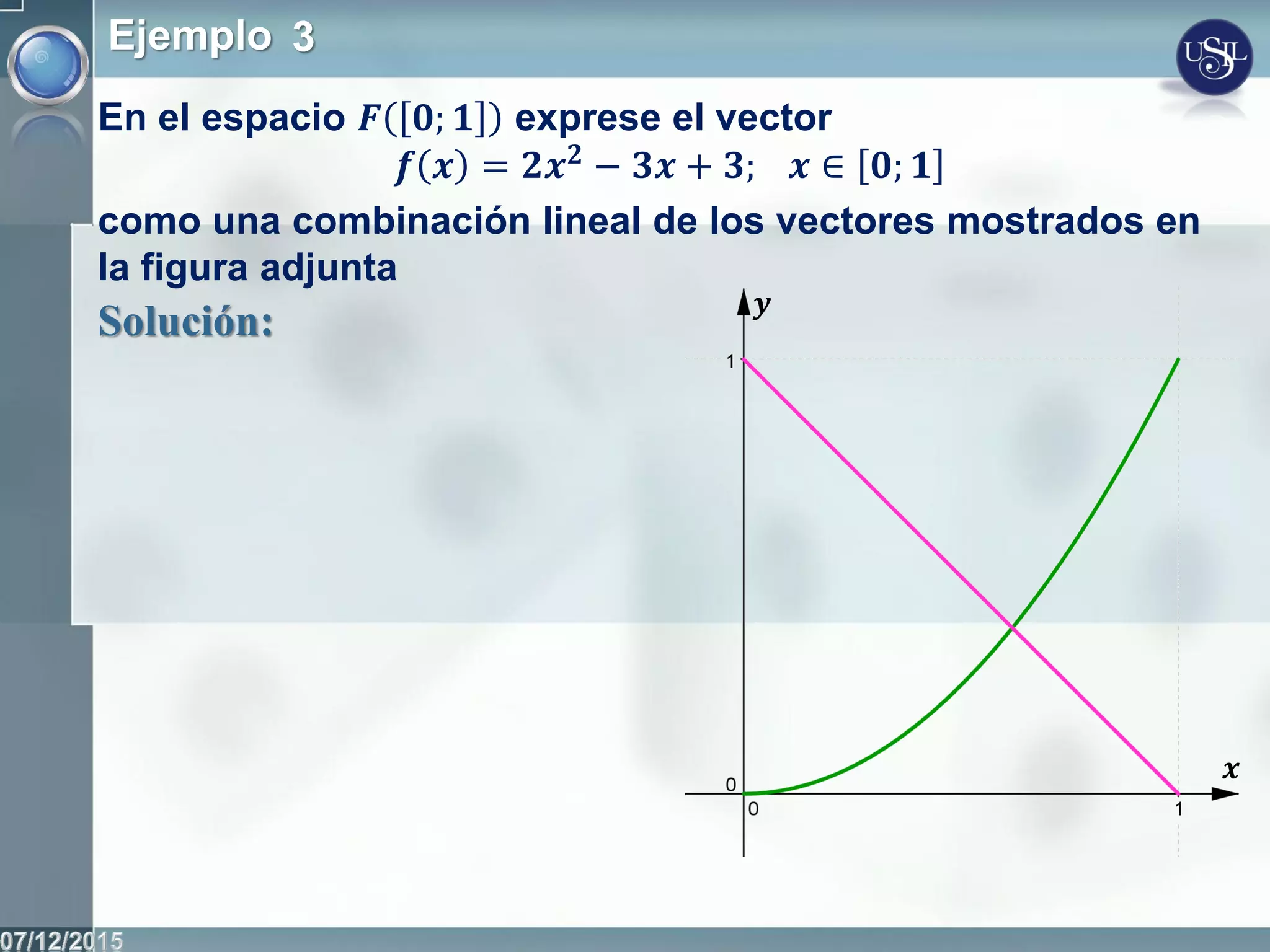
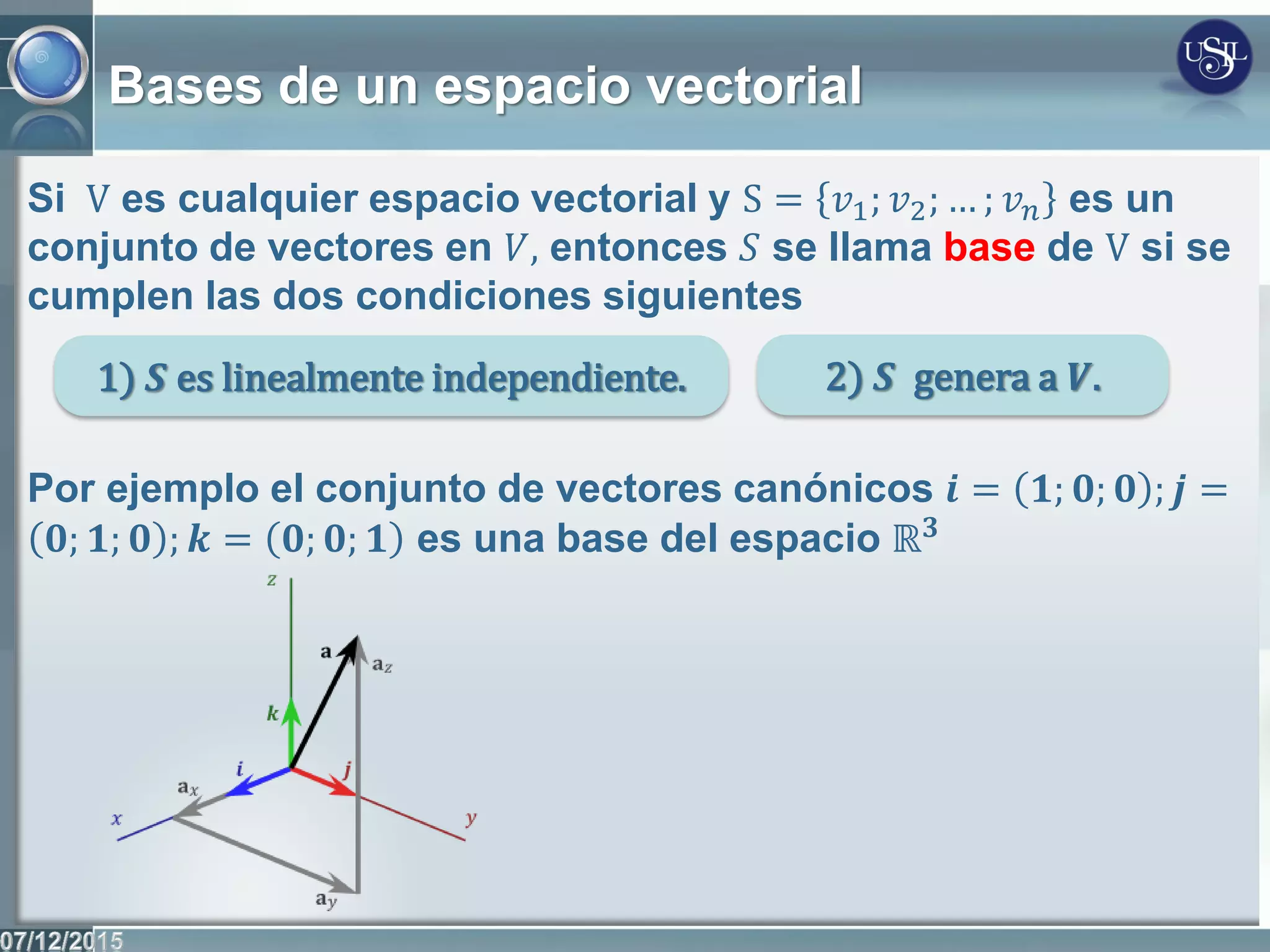
Este documento introduce los conceptos fundamentales de los espacios vectoriales y las transformaciones lineales. Define un espacio vectorial como un conjunto no vacío con dos operaciones definidas (adición y multiplicación por escalares) que cumplen ciertos axiomas. Presenta ejemplos de espacios vectoriales como Rn, las matrices y los polinomios. Explica las nociones de combinación lineal, dependencia e independencia lineal de vectores, y define un conjunto generador y una base de un espacio vectorial.

1. ÁLGEBRA LINEAL Y ECUACIONES
DIFERENCIALES
FORMACIÓN POR COMPETENCIAS
Espacios Vectoriales y
Transformaciones
lineales

2. OBJETIVOS
 Definir espacios vectoriales
 Reconocer los axiomas de un Espacio Vectorial
 Reconocer cuando un conjunto es la base de un
Espacio Vectorial
 Definir una Transformación Lineal
 Identificar a las Transformaciones Lineales
 Aplicar los métodos estudiados a diferentes
problemas de contexto real

4. Espacios Vectoriales
Un Espacio Vectorial es un conjunto no vacío 𝑉 de objetos,
llamados vectores, en el que están definidas dos operaciones,
llamadas adición y multiplicación por un escalar (números
reales), sujeta a diez axiomas (o reglas)
Adición: +: 𝑽 × 𝑽 → 𝑽
A cada par 𝒖; 𝒗 ∈ 𝑽 × 𝑽 se le
asocia otro vector 𝒖 + 𝒗 ∈ 𝑽
Multiplicación por un escalar:
⋅∶ ℝ × 𝑽 → 𝑽
A cada par 𝜶; 𝒗 ∈ ℝ × 𝑽 se le
asocia otro vector 𝜶 𝒗 ∈ 𝑽

5. Axiomas de un Espacio Vectorial
Adición
1.- Conmutatividad: 𝑢 + 𝑣 = 𝑣 + 𝑢, ∀𝑢, 𝑣 ∈ 𝑉.
2.- Asociatividad: 𝑢 + 𝑣 + 𝑤 = 𝑢 + 𝑣 + 𝑤 ; ∀ 𝑢, 𝑣, 𝑤 ∈ 𝑉
3.- Elemento neutro: Existe un vector 0 ∈ 𝑉 tal que
𝑢 + 0 = 0 + 𝑢 = 𝑢, ∀ 𝑢 ∈ 𝑉.
4.- Elemento opuesto: Para cualquier 𝒖 ∈ 𝑽, existe un −𝒖 ∈ 𝑽
tal que
∀𝑢 ∈ 𝑉 existe − 𝑢 ∈ 𝑉 tal que 𝑢 + −𝑢 = −𝑢 + 𝑢 = 0

6. Axiomas de un Espacio Vectorial:
Producto por un escalar
5.- Ley asociativa de la multiplicación por escalares: Para 𝒖 ∈ 𝑽
y 𝜶, 𝜷 ∈ ℝ se cumple: 𝜶 𝜷𝒖 = 𝜶𝜷 𝒖
6.- Primera ley distributiva: Para 𝒖, 𝒗 ∈ 𝑽 y 𝜶 ∈ ℝ se cumple:
𝜶 𝒖 + 𝒗 = 𝜶𝒖 + 𝜶𝒗
7.- Segunda ley distributiva: Para 𝒖 ∈ 𝑽 y 𝜶, 𝜷 ∈ ℝ se cumple:
𝜶 + 𝜷 𝒖 = 𝜶𝒖 + 𝜷𝒖.
8.- Para cada vector 𝒖 ∈ 𝑽 se cumple
1. 𝑢 = 𝑢

7. Ejemplo 1
El conjunto de 𝑛 − uplas de números reales:
ℝ 𝑛 = *𝑥 = 𝑥1; 𝑥2; … ; 𝑥 𝑛 = 𝑥𝑖 1≤𝑖≤𝑛: 𝑥𝑖 ∈ ℝ, 1 ≤ 𝑖 ≤ 𝑛+
Con las operaciones:
𝑥 + 𝑦 = (𝑥1 + 𝑦1; 𝑥2 + 𝑦2; … ; 𝑥 𝑛 + 𝑦𝑛)
𝛼𝑥 = (𝛼𝑥1; 𝛼𝑥2; … ; 𝛼𝑥 𝑛)
es un espacio vectorial real.
Solución:
𝑩(−𝟑; 𝟐; 𝟒)
𝑨(𝟐; 𝟏; 𝟑)
𝒚
𝒙
𝒛
𝑨(𝟐; 𝟏; 𝟑) y B(−𝟑; 𝟐; 𝟒) son vectores
en ℝ 𝟑

8. Ejemplo 2
El conjunto de matrices reales de orden 𝑛 × 𝑚:
ℳ𝑛×𝑚(ℝ) = *𝐴 = 𝑎𝑖𝑗 1≤𝑖≤𝑛
1≤𝑗≤𝑚
, 𝑎𝑖𝑗 ∈ 𝑅, 1 ≤ 𝑖 ≤ 𝑛, 1 ≤ 𝑗 ≤ 𝑚+
con las operaciones: suma de matrices y producto por
números reales, es un espacio vectorial real
Solución:
Por ejemplo las matrices
𝑨 =
−𝟏 𝟐 𝟎
𝟎 𝟑 𝟐
y 𝑩 = 𝟎 𝟏
𝟏
𝟐
𝟎 𝟎 𝟏
son vectores en ℳ𝟐×𝟑 ℝ

9. Ejemplo 3
El conjunto de todos los polinomios con coeficientes reales
en la variable 𝑥:
𝑃(ℝ) = 𝑎 𝑘 𝑥 𝑘
:
𝑛
𝑘=0
𝑛 ∈ ℕ, 𝑎 𝑘 ∈ ℝ
Con las clásicas operaciones de suma de polinomios y
producto de un polinomio por un escalar.
Solución:
Por ejemplo los polinomios
𝑷 𝒙 = 𝒙 𝟑 + 𝟐𝒙 − 𝟏 y
𝑸 𝒙 = 𝟐𝒙 𝟓 − 𝟖𝒙 𝟒 − 𝟏𝟖𝒙 𝟑 + 𝟔𝟒𝒙 𝟐 + 𝟓𝟔𝒙 − 𝟗𝟔
son vectores en 𝑷 ℝ 𝒙
𝒚

10. Ejemplo 4
El conjunto de todos los polinomios con coeficientes reales
en la variable 𝑥 de grado menor o igual a 𝒓 ∈ ℕ
𝑃𝒓 ℝ = 𝑷 𝒙 = 𝒂 𝒌 𝒙 𝒌
𝒏
𝒌=𝟏
𝒏 ∈ ℕ ∪ 𝟎 ; 𝒏 ≤ 𝒓; 𝒂 𝒌 ∈ ℝ
Con las clásicas operaciones de suma de polinomios y
producto de un polinomio por un escalar.
Solución:

11. Ejemplo 5
El conjunto de todas las funciones reales de variable real
cuyo dominio es el intervalo 𝒂; 𝒃
𝑭 𝒂; 𝒃 = 𝒇: 𝒂; 𝒃 → ℝ 𝒇 𝐞𝐬 𝐮𝐧𝐚𝐟𝐮𝐧𝐜𝐢ó𝐧 𝐜𝐨𝐧 𝐝𝐨𝐦𝐢𝐧𝐢𝐨 𝒂; 𝒃
Con las operaciones usuales de adición de funciones y
multiplicación de una función por un escalar
Solución:
Por ejemplo las funciones mostradas
son vectores en el espacio 𝑪 𝟎; 𝟏
𝒙
𝒚

12. Ejercicio 1
Considere los vectores 𝒖 = 𝟏; 𝟐; −𝟏 y 𝒗 = 𝟐; 𝟎; 𝟑 .
Demuestre que el conjunto
𝑨 = 𝒕𝒖 + 𝒔𝒗 𝒕, 𝒔 ∈ ℝ ⊂ ℝ 𝟑
Es un espacio vectorial con las operaciones usuales de ℝ 𝟑
Solución:

13. Combinación lineal
Sea 𝑉 un espacio vectorial. Se dice que 𝑣 ∈ 𝑉 es combinación
lineal de los vectores 𝑣1; 𝑣2; … ; 𝑣 𝑛 ⊂ 𝑉, si existen escalares
𝛼1; 𝛼2; … ; 𝛼 𝑛, tal que
𝑣 = 𝛼𝑖 𝑣𝑖
𝑛
𝑖=1
Por ejemplo en ℝ 𝟑 el vector 𝒗 = 𝟏; 𝟐; −𝟑 es una combinación
lineal de los vectores 𝒊 = 𝟏; 𝟎; 𝟎 ; 𝐣 = (𝟎; 𝟏; 𝟎) y 𝒌 = (𝟎; 𝟎; 𝟏)
pues
𝒗 = 𝟏 𝒊 + 𝟐 𝒋 + −𝟑 𝒌

14. Ejemplo 1
Exprese el vector 𝒗 = 𝟏; 𝟐; 𝟑 como una combinación lineal
de los vectores 𝒗 𝟏 = 𝟏; 𝟏; 𝟏 ; 𝒗 𝟐 = 𝟐; 𝟒; 𝟎 y 𝒗 𝟑 = 𝟎; 𝟎; 𝟏
Solución:

15. Ejemplo 2
Exprese la matriz 𝑨 =
−𝟏 𝟎
𝟐 𝟒
como una combinación lineal
de las matrices 𝑨 𝟏 =
𝟏 𝟏
𝟐 𝟐
y 𝑨 𝟐 =
𝟑 𝟐
𝟑 𝟓
Solución:

16. Ejemplo 3
En el espacio 𝑭 𝟎; 𝟏 exprese el vector
𝒇 𝒙 = 𝟐𝒙 𝟐 − 𝟑𝒙 + 𝟑; 𝒙 ∈ 𝟎; 𝟏
como una combinación lineal de los vectores mostrados en
la figura adjunta
𝒙
𝒚
Solución:

17. Dependencia e independencia lineal de
vectores
Sea 𝑉 un espacio vectorial. Se dice que el conjunto de
vectores 𝑣1; 𝑣2; … ; 𝑣 𝑛 ⊂ 𝑉, es linealmente dependiente (L.D) si
y sólo si existen escalares 𝛼1; 𝛼2; … ; 𝛼 𝑛, con algún 𝛼𝑖 ≠ 0, tales
que:
𝛼𝑖 𝑣𝑖 = 0
𝑛
𝑖=1
En caso contrario, se dice que el conjunto 𝑣1; 𝑣2; … ; 𝑣 𝑛 es
linealmente independiente (L.I)

18. Observación
Para estudiar si un conjunto de vectores 𝑣1; 𝑣2; … ; 𝑣 𝑛 , es
linealmente dependiente o independiente, se plantea la
ecuación:
𝛼𝑖 𝑣𝑖 = 0
𝑛
𝑖=1
y se estudian sus soluciones.
𝑪𝒂𝒔𝒐 𝟏
Si admite alguna solución no nula ( 𝛼𝑖 ≠ 0 para algún 𝑖 ),
entonces el conjunto de vectores es linealmente dependiente.
Si admite sólo solución nula (𝛼𝑖 = 0 para todo 𝑖), entonces el
conjunto de vectores es linealmente independiente.
𝑪𝒂𝒔𝒐 𝟐

19. Ejemplo 1
Analice si los vectores 𝑣1 = 1; 0; −1; 2 , 𝑣2 = 1; 1; 0; 1 y
𝑣3 = 2; 1; −1; 1 son linealmente independientes en el espacio
ℝ 𝟒.
Solución:

20. Ejemplo 2
Solución:
Analice si los vectores 𝑣1 = 3; 3; 4 , 𝑣2 = 4; 1; −2 y 𝑣3 =
−3; 1; 5 son linealmente independientes en el espacio ℝ 𝟑.

21. Ejercicio 1
Determine si el siguiente conjunto de funciones en 𝑃2 es
linealmente independiente o dependiente.
𝑆 = 1 + 𝑥 − 2𝑥2
, 2 + 5𝑥 − 𝑥2
, 𝑥 + 𝑥2
Solución:

22. Ejercicio 2
Determine si el siguiente conjunto:
𝑆 = 𝑒2𝑥
; 𝑠𝑒𝑛 5𝑥 ; 𝑥2
es linealmente independiente o dependiente en el espacio de
funciones 𝑭 −𝝅; 𝝅
Solución:

23. Conjunto generador de un espacio
vectorial
Sea 𝑽 un espacio vectorial y S = 𝑣1; 𝑣2; … ; 𝑣 𝑛 ⊂ 𝑽. El
conjunto 𝑆 se denomina conjunto generador de 𝑉 si todo
vector en 𝑉 puede expresarse como una combinación lineal de
vectores en 𝑆. En estos casos se dice que 𝑆 genera a 𝑉.

24. Ejemplo 1
Demuestre que los vectores generan el espacio vectorial
dado.
a. 𝟏; 𝟎; 𝟎 , 𝟎; 𝟏; 𝟎 ; 𝟎; 𝟎; 𝟏 ; 𝑽 = ℝ 𝟑
b. 𝟏; 𝒙; 𝒙 𝟐
; 𝑽 = 𝑷 𝟐 ℝ
c. 𝟏; 𝟐; 𝟑 ; 𝟎; 𝟏; 𝟐 ; −𝟏; 𝟎; 𝟏 ; 𝑽 = ℝ 𝟑
Solución:

25. Ejemplo 2
Sea 𝑽 el espacio vectorial de ecuación
𝒙 + 𝒛 = 𝟎
con las operaciones usuales de ℝ 𝟑. Demuestre que los
vectores 𝒖 = 𝟏; 𝟏; 𝟏 y 𝒗 = 𝟎; 𝟏; 𝟎 generan el espacio
vectorial 𝑽, pero que no generan el espacio ℝ 𝟑
.
Solución:

26. Bases de un espacio vectorial
Si V es cualquier espacio vectorial y S = 𝑣1; 𝑣2; … ; 𝑣 𝑛 es un
conjunto de vectores en 𝑉, entonces 𝑆 se llama base de V si se
cumplen las dos condiciones siguientes
1) 𝑺 es linealmente independiente. 2) 𝑺 genera a 𝑽.
Por ejemplo el conjunto de vectores canónicos 𝒊 = 𝟏; 𝟎; 𝟎 ; 𝒋 =
𝟎; 𝟏; 𝟎 ; 𝒌 = 𝟎; 𝟎; 𝟏 es una base del espacio ℝ 𝟑

27. Teorema
Si S = 𝑣1; 𝑣2; … ; 𝑣 𝑛 es una base del espacio vectorial 𝑉,
entonces todo vector 𝑣 ∈ 𝑉 se puede expresar en forma única
como una combinación lineal de los vectores de la base, es
decir
𝒗 = 𝑐1 𝑣1 + 𝑐2 𝑣2 + ⋯ + 𝑐 𝑛 𝑣 𝑛
donde 𝑐𝑖 son escalares

28. Ejemplo 1
Demuestre que cada uno de los siguientes conjuntos forman
una base de 𝑅3.
a.- (1; 0; 0); (0; 1; 0); (0; 0; 1)
b.- (1; 2; 3); (0; 1; 2); (−2; 0; 1)
Solución:

29. Ejemplo 2
Verifique que el siguiente conjunto es una base de 𝑃3.
S = 1; 1 + 𝑥; 1 − 𝑥; 1 + 𝑥 + 𝑥2; 1 − 𝑥 + 𝑥2
Solución:

31. Transformaciónes
Una transformación (función o mapeo) 𝑇 de 𝑅 𝑛 a 𝑅 𝑚 es una
regla que asigna a cada vector 𝑥 de 𝑅 𝑛 un vector 𝑇(𝑥) en 𝑅 𝑚.
𝒙
𝒚
(𝟐; 𝟐)
𝑻 𝟐; 𝟐 = (𝟒; 𝟐)
(𝟒; 𝟒)
𝑻 𝟒; 𝟒 = (𝟐; 𝟒)
Para cada punto 𝑷,
se le asocia el vector
𝑻(𝑷)
Transformación 𝑻: ℝ 𝟐 → ℝ 𝟐

32. Transformación lineal
Una transformación lineal 𝑇 de 𝑅 𝑛 a 𝑅 𝑚 es una
transformación que cumple los siguientes axiomas
T1.- 𝑻 𝒖 + 𝒗 = 𝑻 𝒖 + 𝑻 𝒗 ∀ 𝒖; 𝒗 ∈ ℝ 𝒏
.
T2.- 𝑻 𝜶𝒖 = 𝜶𝑻 𝒖 ∀ 𝒖 ∈ ℝ 𝒏 , ∀ 𝜶 ∈ ℝ

33. Ejemplo 1
Sea la función 𝑻 ∶ ℝ 𝟐 → ℝ 𝟐 definida por
𝑻 𝒙; 𝒚 = 𝒙 − 𝒚; 𝒙
a.- Demuestre que 𝑻 es una transformación lineal.
b.- Halle la imagen del punto 𝟏; 𝟐
c.- Esboce la gráfica de la imagen del segmento mostrado en
la gráfica
Solución:
𝒙
𝒚

34. TEOREMA
Sea 𝑻: ℝ 𝒏 → ℝ 𝒎 entonces se cumple:
1.- 𝑻 es lineal si y solo si para cualquier 𝒖, 𝒗 ∈ ℝ 𝒏 y 𝜶, 𝜷 ∈ ℝ se
cumple
𝑻 𝜶𝒖 + 𝜷𝒗 = 𝜶𝑻 𝒖 + 𝜷𝑻 𝒗
2.- Si 𝑻 es una transformación lineal, entonces se cumple
𝑻 𝟎 = 𝟎
Por ejemplo, usando la propiedad 2 podemos deducir
inmediatamente que las siguientes transformaciones NO SON
lineales.
𝑻 𝒙; 𝒚 = 𝒙 + 𝟐𝒚; 𝒙 − 𝟑𝒚; 𝟏
𝑻 𝒙; 𝒚; 𝒛 = 𝒙 + 𝒚; 𝒙 − 𝟏
𝑻 𝒙 = 𝟐𝒙 + 𝟏

35. Ejercicio 1
Dado un vector 𝑣 = (𝑣1; 𝑣2) y una transformación lineal
T: 𝑅2
→ 𝑅2
definida por: T 𝑣1; 𝑣2 = (𝑣1 − 𝑣2; 𝑣1 + 2𝑣2) determine
a.- La imagen de 𝑣 = −1; 2 , generada por la transformación
𝑇.
b.- La preimagen que a través de la transformación 𝑇 genera
𝑤 = (−1; 11)
Solución:

36. Ejercicio 2
Sea T: 𝑅2
→ 𝑅2
una transformación lineal para la cual se
cumple
𝑇 1; 2 = (2; 3) y 𝑇 0; 1 = 1; 4 .
Determine la regla de correspondencia de 𝑇
Solución:

37. Ejercicio 3
Sea T: 𝑅3
→ 𝑅3
una transformación lineal para la cual
𝑇 𝒊 = 2; −1; 4 , 𝑇 𝒋 = 1; 5; −2 y 𝑇 𝒊 + 𝒌 = 0; 3; 1 . Calcule
𝑇(2; 3; −2)
Solución:

38. Ejercicio 4
Dada la transformación lineal 𝑇,
definida por
𝑇 𝑥; 𝑦 = 𝑥 − 3𝑦; −3𝑥 + 9𝑦
si D es la región triangular que
se muestra en la figura, grafique
la imagen 𝑇(𝐷)
Solución:
𝒙
𝒚

39. Ejercicio 5
Considere la transformación: 𝑇: ℝ2
→ ℝ2
definida por:
𝑇 𝑥; 𝑦 =
𝑦−𝑥
2
;
𝑦+𝑥
2
y la región 𝐷 ⊂ ℝ2
limitada por dos rectas
de ecuaciones 𝑦 = 𝑥; 𝑦 = −𝑥 y la gráfica de la curva de
ecuación: 𝑥2
+ 𝑦2
= 2𝑦 con 𝑦 ≥ 1
a.- Demuestre que 𝑇 es una transformación lineal.
b.- Grafique la región 𝐷.
c.- Usando la transformación lineal, grafique 𝑇(𝐷).
Solución:

40. Bibliografía
4. Calculus – Larson Edwards
3. Introducción al Álgebra Lineal – Howard Anton
1. Algebra lineal y sus aplicaciones –David C. Lay.
2. Introducción al Álgebra Lineal – Larson Edwards.
5. Álgebra Lineal – Bernard Kolman; David R. Hill