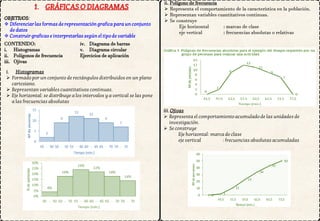
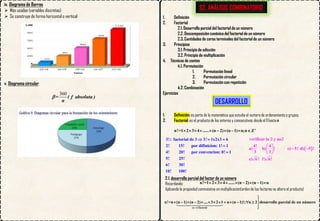
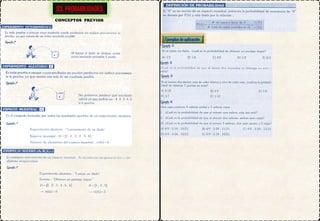
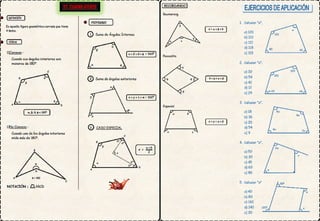
1. El documento presenta diferentes formas de representación gráfica para conjuntos de datos, incluyendo histogramas, polígonos de frecuencia, ojivas y diagramas de barras y circulares. Explica cómo construir e interpretar cada gráfico según el tipo de variable. 2. Incluye ejemplos y ejercicios prácticos sobre cómo construir e interpretar histogramas, polígonos de frecuencia y ojivas. 3. El objetivo es diferenciar las formas de representación gráfica y saber construir e interpretar gráficos según si la variable

2. 1. GRÁFICAS O DIAGRAMAS
OBJETIVOS:
❖ Diferenciar las formas de representación grafica para un conjunto
de datos
❖ Construir graficas e interpretarlas según el tipo de variable
CONTENIDO:
i. Histogramas
ii. Polígonos de frecuencia
iii. Ojivas
iv. Diagrama de barras
v. Diagrama circular
Ejercicios de aplicación
i. Histogramas
➢ Formado por un conjunto de rectángulos distribuidos en un plano
cartesiano.
➢ Representan variables cuantitativos continuas.
➢ Eje horizontal: se distribuye a los intervalos y a vertical se las pone
a las frecuencias absolutas
ii. Polígono de frecuencia
➢ Representa el comportamiento de la característica en la población.
➢ Representan variables cuantitativos continuas.
➢ Se construye
Eje horizontal : marcas de clase
eje vertical : frecuencias absolutas o relativas
iii. Ojivas
➢ Representa el comportamiento acumulado de las unidades de
investigación.
➢ Se construye
Eje horizontal: marca de clase
eje vertical : frecuencias absolutas acumuladas

3. iv. Diagrama de Barras
➢ Más usadas (variables discretas)
➢ Se construye de forma horizontal o vertical
v. Diagrama circular
360
= ( f absoluta )
n

S2. ANÁLISIS COMBINATORIO
1. Definición
2. Factorial
2.1. Desarrollo parcial del factorial de un número
2.2. Descomposición canónica del factorial de un número
2.3. Cantidades de ceros terminales del factorial de un número
3. Principios
3.1. Principio de adicción
3.2. Principio de multiplicación
4. Técnicas de conteo
4.1. Permutación
1. Permutación lineal
2. Permutación circular
3. Permutación con repetición
4.2. Combinación
Ejercicios
1. Definición: es parte de la matemática que estudia el numero de ordenamiento o grupos.
2. Factorial: es el producto de los enteros y consecutivos desde el 1 hasta n
3!: factorial de 3 3! 1x2x3 6
2! 15! por difinicion: 1! 1
4! 20! por convencion: 0! 1
5! 25!
6! 30!
10! 100!
 = =
=
=
( )
verificar la y no
4! 4
a) b) ! c) 5! d) 5 !
3 3
e) 6! f) 6!
 
 
− −
 
 
2.1. desarrollo parcial del factor de un número
Recordando:
Aplicando la propiedad conmutativa en multiplicación(orden de los factores no altera el producto)
n!=1 2 3 4 ...... (n 2) (n 1) n;n Z+
     −  −  
(n 1)!factorial
n!=n (n 1) (n 2) .... 3 2 1 n (n 1)!; n 2 desarrollo parcial de un número
−


 −  −     =  −   


n!=1 2 3 4 ...... (n 2) (n 1) n
     −  − 

4. Además n! se puede desarrollar explícitamente según lo requiera el ejercicio especificado, es decir:
Ejemplos de aplicación
Observación: para determinar los
exponentes de los factores primos de n!
es por divisiones sucesivas.
Teniendo como divisor del fator
primo al cual se desea hallar su
exponente, para 2 y 3
n!=n×(n-1)×(n-2)!
n!=n×(n-1)×(n-2)×(n-3)!
Simplificar la siguinte expresión
45! 296!+297!+298!
A= B=
43! 298!+297!
12! 11!+10!+9!
C D=
9!*4! 121 8!
=

2.2. Descomposición canónica del factorial de un número
Quiere decir que: todo numero entero mayor a 1 se puede expresar en términos de sus factores primos.
3
1 2 4 n
a
a a a a
1 2 3
n!=2 ×3 ×5 ×7 ×.....×p ; donde: a ,a ,a ... Z y p n
+
 
Ejemplos de aplicación
4!= 6!
8!= 10!=
=
a)40! b)6!
c)100! d)16!
a b
Hallar el valor de: E=
c d
−
−
Nota: cuando se aplica las divisiones
sucesivas no se toman en cuenta los
residuos
2.3. Cantidades de ceros terminales del factorial de un número
Calcular los ceros terminales del factorial “n” (n>5), depende directamente del exponente menor
de 2 ó de 5
α
β
2 3
3 2
2 si, < # de ceros es:
si
si, < # de ceros es:
5
1500=2 .3.5 #de ceros =2
1400=2 .5 .7 #de ceros =2
     

 
   
 



a)67! b)50! c)100!
d)10! e)16! f)15!
Calcular el número de ceros
3. PRINCIPIOS FUNDAMENTALES DEL ANÁLISIS COMBINATORIO
3.1. Principio de adicción
( )
- si el evento A ocurre de maneras
ocurren de formas distintas
"m"
A B m+n
"n" m
- B ocurre de aneras diferentes

 


❖ En el principio de adición, o bien ocurre un caso o bien ocurre el otro caso, pero nunca pueden ocurrir
simultáneamente.
Ejemplos de aplicación
1. Gildder desea viajar de Huánuco a Iquitos y tiene a su disposición 5 líneas terrestres y 2 líneas áreas
¿de cuántas maneras distintas puede realizar su viaje?
Solución:
realizara de (2+5)=7 maneras diferentes

El evento A tiene m maneras distintas de ocurrir, seguido del evento B en n maneras distintas de ocurrir,
entonces el numero de maneras distintas en que puede ocurrir el evento A seguido del evento B es: mxn.
Este principio también es valido si los acontecimientos son simultáneos.
2. Un repuesto de automóvil se vende en 8 tiendas del distrito de Wanchaq, en 7 tiendas de San Sebastián o
en 6 tiendas de San Jerónimo. ¿de cuántas formas diferentes una persona puede comprar el repuesto?
3. Raúl puede comprar un libro de aritmética que es vendido en tres lugares distintos: frente a la unsaac
en 2 puestos de venta; en av la cultura en 3 librerías y en la feria de libros en 4 puestos diferentes. ¿de
cuantas maneras puede obtener el libro de aritmética?
4. Alfonso desea cruzar un rio, para ello puede utilizar dos botes, tres lanchas pequeñas o un deslizador.
¿de cuantas formas podrá cruzarel rio utilizando uno de los medios de transporte señalados?
5. ¿de cuántas formas se podrá ir de M a N sin retroceder? Cada línea representa un camino
3.2. Principio de la multiplicación (y)
1. Rommel desea vestirse para ir a una reunión y para ello dispone de 3 pantalones y de 2 caminas, todas
sus prendas son de diferente color. ¿de cuántas maneras distintas podrá vestirse, si se pone un pantalón y
una camisa?
Ejemplos de aplicación

5. 2. Un medico general clasifica a sus pacientes de acuerdo a: su sexo (M y F), tipo de sangre (A, B, AB u O) y
en cuanto a la presión sanguínea (normal, alta o baja). ¿en cuantas clasificaciones distintas pueden estar
los pacientes de este medico?
4. TÉCNICAS DEL CONTEO
4.1. permutación(p. general o caótica)
➢ La característica principal es el orden de sus elementos; y debido a eso a esto una permutación es
diferente de otra cuando el orden de sus elementos es distinto.
➢ Un problema será una permutación cuando al variar uno o más elementos los resultados que se
obtienen son diferentes.
n
k
n!
P = ; 0<k n
(n-k)!

donde:
n: # total de elementos
k : # de grupos que se forman o se toman
−
−
n
k
P se lee: Permutacion de "n" elementos tomados de "k" en "k"

Ejemplos de aplicación
7
3
7! 7! 7 6 5 4!
P =
(7 3)! 4!
  
= =
− 4!
210
Se pueden formar 210 números diferentes
=

2. Se tiene 9 colores diferentes para pintar los mapas de los países de: Argentina, Brasil, Colombia,
Ecuador, Perú y Uruguay. Si se sabe que el mapa del Perú será pintado de color rojo, ¿de cuantas formas
diferentes se podrán pintar si solamente se usa un color en cada mapa? Rpta: 6720
1. Con las cifras: 2, 3, 4, 5, 7 y 8, ¿Cuántos números de tres cifras diferentes se pueden formar?
4.1.1. permutación lineal (simple): es aquella en donde participan todos los elementos y éstos se
arreglan u ordenan en líneas recta
n
n n
P =P =n!; n 1
 
(n)
P se lee: permutación lineal de "n" elementos

4.1.2. permutación circular (cíclica): es un ordenamiento de elementos diferentes alrededor de un
objeto.
En estas condiciones no hay primer ni último elemento, por hallarse todos en una línea imaginaria cerrada.
1. ¿de cuantas maneras distintas 4 atletas pueden llegar a la meta en una carrera de 100 metros planos si
no hay empate en ningún puesto?
(n)
PC (n 1)!; n 2
= −  
1. ¿Cuántos anagramas diferentes se pueden obtener con todas las letras de la palabra PAPA?
4.1.3. permutación con repetición: se da cuando los elementos a ordenar no son todos ellos distintos, es
decir, hay un elemento o más de uno que se están repitiendo.
1 2 3 p
k ,k ,k ..
2
.
1
k
p
n
2 3 p
1 3 .
n
P
k ! k
: k .
..
dond
!
! k ! !
k k ..
R
k
n
k
e
 
+ + +
=
 
+ 
Una anagrama es una palabra o palabras formadas por la reordenación de las letras que constituyen otra
u otras palabras, tengan o no sentido lingüístico.
4
2;2 y se lee: "Permutacion de 4 elementos con repeticion de dos letras P y dos letras A".
PR
Luego: 4
2;2
4! 24
PC = 6
2! 2! 2 2
= =
 
Se pueden formar 6 anagramas diferen
PAPA
PAAP
PPAA
A
P
tes
PAP
A PA
AAPP




 





6. 4.2. Combinación (simple)
❖ Es una selección o grupo de elementos que se pueden formar con parte o con todos los elementos
disponibles de un conjunto.
❖ No interesa el ordende sus elementos.
❖ Será combinación cuando al variar uno o más elementos los resultados que se obtienen son iguales.
La fórmula general es:
n n
k k
n!
;0 k n
k!(
C ( )
n k)!
= 
= 
−
Donde:
❖ n: # total de elementos
❖ k: # de grupos que se seleccionan
n
k
C se lee: Combinaciones de "n" elementos tomados de "k" en "k"

Ejemplos de aplicación
1. Si se disponen de 9 frutas diferentes. ¿Cuántos jugos surtidos de 4 cifras distintas se podrá
preparar? R: 126
2. ¿Cuántos equipos de 2 varones y 3 mujeres pueden formarse con 10 varones y 6 mujeres? R: 900
3. ¿Cuántos comités diferentes de 3 miembros se pueden formar a partir de un grupo de 10 personas?
R:120
4. Un juego consiste en seleccionar 5 números de un total de 28 números. Para ganar basta con acertar
a los 5 números sin importar el orden en que aparezcan. ¿Cuál es la probabilidad de gnar al acertar a
los 5 números en una sola oportunidad? R c: 98,280, P(G)=1/98,280=0.0000101750
5. En una clase hay 35 alumnos y se quieren formar equipos de 3 personas. ¿Cuántos equipos se pueden
formar? R:6,545
TÚ PUEDES
1. hallar el valor de "r" en:
r!(r!-3)
=18;
r!+4
2. calcule "a+b", si se sabe que
1!+3!+5!+7!+.........+89!=..........ab
3. la expresion "E" adjunta a continuacion, ¿en cuantos ceros ter
R4
;r a4 y b7 a+b=11
= 
7
s
mina?
183!
E= ,
72!
4. determine en cuantos ceros acaba la siguiente expresion
L=(349!+
s
r 28cero
4
26 5
5!) r c
; 5 ero
=
=
R=30
R=75
R=240
7
R=120
R=1260
R=43200
R=120

7. S3. PROBABILIDADES
Ejemplos de aplicación

10. S4. POLÍGONOS
En todo polígono con “n” lados
Racso
Rubiños
Uniciencias

12. S5. CUADRILATEROS

13. S7. CUADRILATEROS

14. S6 y S7. PERIMETROS Y ÁREAS DE REGIONES GEOMETRICAS

15. S7. AREAS DE REGIONES PLANAS

16. S8. POLIEDROS REGULARES

17. S9. SOLIDOS GEOEMTRICOS