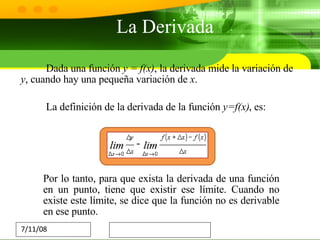
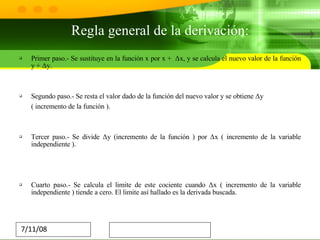
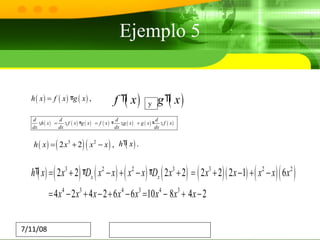
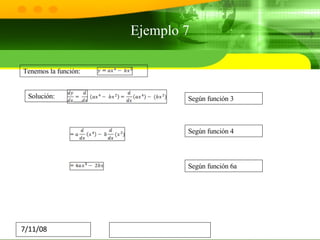
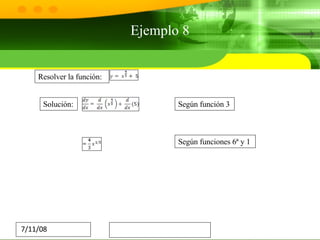
El documento trata sobre el cálculo diferencial. Explica que estudia los incrementos en variables continuas y la derivada mide la variación de la función cuando hay pequeñas variaciones en la variable independiente. También describe algunas aplicaciones importantes como maximizar/minimizar cosas, calcular velocidad y pendiente, y crear modelos en áreas como ingeniería, física y crecimiento poblacional. Finalmente, concluye que el cálculo diferencial ha sido fundamental para los avances de la humanidad y ha permitido logros como la fabricación de chips y la computación.

1. Universidad Veracruzana Matemáticas Aplicadas Equipo Nº2 Cálculo Diferencial

2. Calculo Diferencial Cálculo: Rama de las matemáticas que se ocupa del estudio de los incrementos en las variables, pendientes de curvas, valores máximo y mínimo de funciones y de la determinación de longitudes, áreas y volúmenes. Su uso es muy extenso, sobre todo en ciencias e ingeniería, siempre que haya cantidades que varíen de forma continua. El cálculo diferencial estudia los incrementos en las variables

3. Dada una función y = f(x) , la derivada mide la variación de y , cuando hay una pequeña variación de x . La definición de la derivada de la función y=f(x) , es: Por lo tanto, para que exista la derivada de una función en un punto, tiene que existir ese límite. Cuando no existe este límite, se dice que la función no es derivable en ese punto. La Derivada Funcion General

4. Importancia y Aplicación 2.- Para maximizar o minimizar cosas. Por ejemplo si se quiere reducir costos en una empresa que se dedica a empacar productos X, pero se descubre que se puede seguir empacando la misma cantidad de X con cajas más pequeñas. Administración 3.-En temas como la velocidad (razón entre la distancia recorrida y el tiempo empleado en recorrerla) de una partícula en un momento determinado, la pendiente (razón entre la diferencia de las ordenadas y las abscisas de dos puntos en el plano cartesiano) de la recta tangente a una gráfica en un punto dado de ésta, etc. 5.- Sirve para procesos estrocásticos (modelos financieros muy avanzados). 6.- Se puede crear un modelo de ecuaciones diferenciales para proponer un modelo de crecimiento poblacional, crecimiento de activos de empresas, comportamiento de partes mecánicas de un automóvil , ya muchas aplicaciones mas en ingeniería y física.

5. Aplicación del Calculo Diferencial al área de Computación o Informática El calculo diferencial tiene un importante campo de aplicación en esta área: Fabricación de chips (obleas de microprocesadores ) Miniaturización de componentes internos Administración de las compuertas de los circuitos integrados Compresión y digitalización de imágenes, sonidos y videos. Han coadyuvado a aumentar la inteligencia artificial en los sistemas de computo

6. Regla general de la derivación: Primer paso.- Se sustituye en la función x por x + Δx, y se calcula el nuevo valor de la función y + Δy. Segundo paso.- Se resta el valor dado de la función del nuevo valor y se obtiene Δy ( incremento de la función ). Tercer paso.- Se divide Δy (incremento de la función ) por Δx ( incremento de la variable independiente ). Cuarto paso.- Se calcula el limite de este cociente cuando Δx ( incremento de la variable independiente ) tiende a cero. El limite así hallado es la derivada buscada.

7. Formulas o Teoremas

8. Ejemplo 1 Tenemos la función:

9. Ejemplo 2 Para este caso Tenemos la función:

10. Ejemplo 3 Tenemos la función:

11. Ejemplo 4 Determine si

12. Ejemplo 5 y

13. Ejemplo 6

14. Ejemplo 7 Tenemos la función: Solución: Según función 3 Según función 4 Según función 6a

15. Ejemplo 8 Resolver la función: Solución: Según función 3 Según funciones 6ª y 1

16. Ejemplo 9 Tenemos la función: Solución: Según función 7 (multiplicando numerador y denominador por )

17. Conclusiones A todo lo visto anteriormente se llego a la conclusión de que el calculo diferencial, es algo elemental para el ser humano ya que es el responsable de la mayoría de los avances que tiene la humanidad logrando prácticamente que existamos. Ya que de lo contrario no podríamos tener lo que ahora existe.

18. ¡Gracias por su atención!