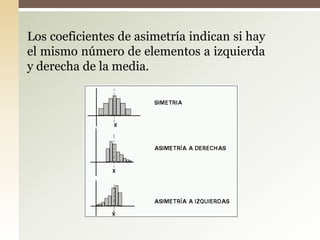
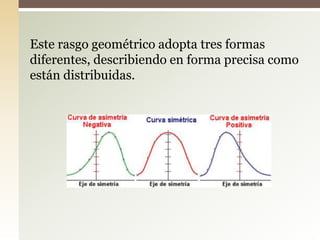
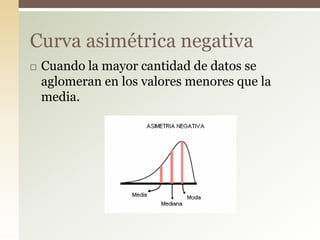
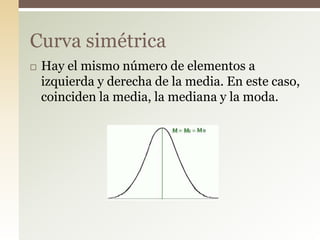
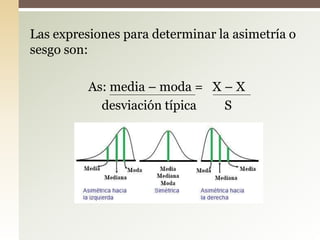
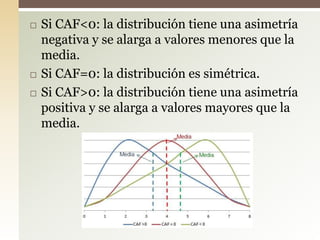
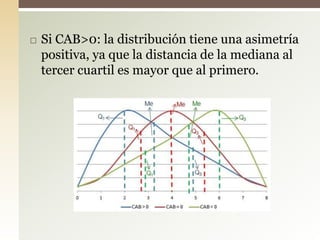
Este documento explica el concepto de sesgo o asimetría, que mide la simetría de una distribución de datos respecto a la media. Existen tres tipos de sesgo: negativo cuando la mayoría de datos están por debajo de la media, positivo cuando están por encima, y simétrico cuando hay la misma cantidad a ambos lados. Se pueden calcular coeficientes de asimetría como el de Fisher, Pearson o Bowley para cuantificar el grado de sesgo.

1. Sesgo
Probabilidad & Estadística grupo:631

2. Tambien conocida como asimetria es la medida
que indica la simetría de la distribución de una
variable respecto a la media aritmética, sin
necesidad de hacer la representación gráfica.
¿Que es un sesgo?

3. Los coeficientes de asimetría indican si hay
el mismo número de elementos a izquierda
y derecha de la media.

4.  Esta medida nos permite identificar si los
datos se distribuyen de forma uniforme
alrededor del punto central (Media
aritmética).
Nos ayuda para…

5. Este rasgo geométrico adopta tres formas
diferentes, describiendo en forma precisa como
están distribuidas.

6.  Cuando la mayor cantidad de datos se
aglomeran en los valores menores que la
media.
Curva asimétrica negativa

7.  Hay el mismo número de elementos a
izquierda y derecha de la media. En este caso,
coinciden la media, la mediana y la moda.
Curva simétrica

8.  Cuando la mayoría de los datos se encuentran
por encima del valor de la media aritmética.
Curva asimétrica positiva

9.  Se representa mediante la ecuación
matemática:
 Donde (g1) representa el coeficiente de
asimetría de Fisher, (Xi) cada uno de los
valores, () la media de la muestra y (ni) la
frecuencia de cada valor.
El coeficiente de asimetría

10.  (g1 = 0): Se acepta que la distribución es
Simétrica, es decir, existe aproximadamente
la misma cantidad de valores a los dos lados
de la media.
 (g1 > 0): La curva es asimétricamente positiva
por lo que los valores se tienden a reunir más
en la parte izquierda que en la derecha de la
media.
Los resultados de esta ecuación se
interpretan:

11.  (g1 < 0): La curva es asimétricamente
negativa por lo que los valores se tienden a
reunir más en la parte derecha de la media.
 Desde luego entre mayor sea el número
(Positivo o Negativo), mayor será la distancia
que separa la aglomeración de los valores con
respecto a la media.

12. Las expresiones para determinar la asimetría o
sesgo son:
As: media – moda = X – X
desviación típica S

13. Un conjunto de datos , tiene por media
aritmética 2.3 , moda 2 y desviación estándar
1.2, ¿ Que tipo de sesgo tienen sus datos?
Formula:
As= 2.3 – 2 = 0.25
1.2
Ejemplo:

14.  Coeficiente de asimetría de Fisher
 Coeficiente de asimetría de Pearson
 Coeficiente de asimetría de Bowley
Existen tres coeficientes de
asimetría:

15.  CAF evalúa la proximidad de los datos a su
media x. Cuanto mayor sea la suma ∑(xi–x)3,
mayor será la asimetría.
Coeficiente de asimetría de Fisher

16.  Si CAF<0: la distribución tiene una asimetría
negativa y se alarga a valores menores que la
media.
 Si CAF=0: la distribución es simétrica.
 Si CAF>0: la distribución tiene una asimetría
positiva y se alarga a valores mayores que la
media.

17.  CAB toma como referencia los cuartiles para
determinar si la distribución es simétrica o
no. Para aplicar este coeficiente, se supone
que el comportamiento de la distribución en
los extremos es similar.
Coeficiente de asimetría de Bowley

18.  Si CAB<0: la distribución tiene una asimetría
negativa, puesto que la distancia de la
mediana al primer cuartil es menor que al
tercero.
 Si CAB=0: la distribución es simétrica, ya que
el primer y tercer cuartil están a la misma
distancia de la mediana.

19.  Si CAB>0: la distribución tiene una asimetría
positiva, ya que la distancia de la mediana al
tercer cuartil es mayor que al primero.