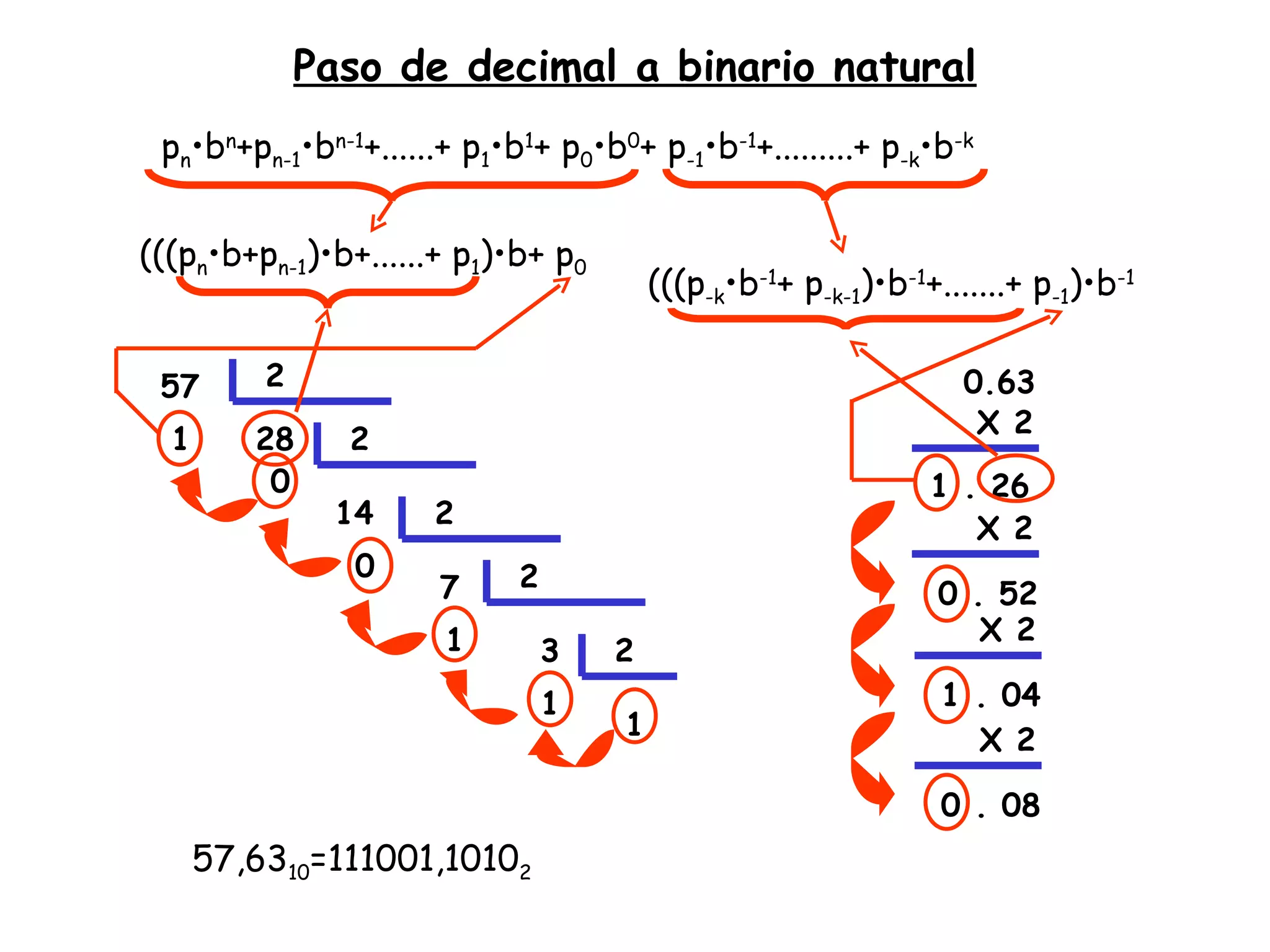
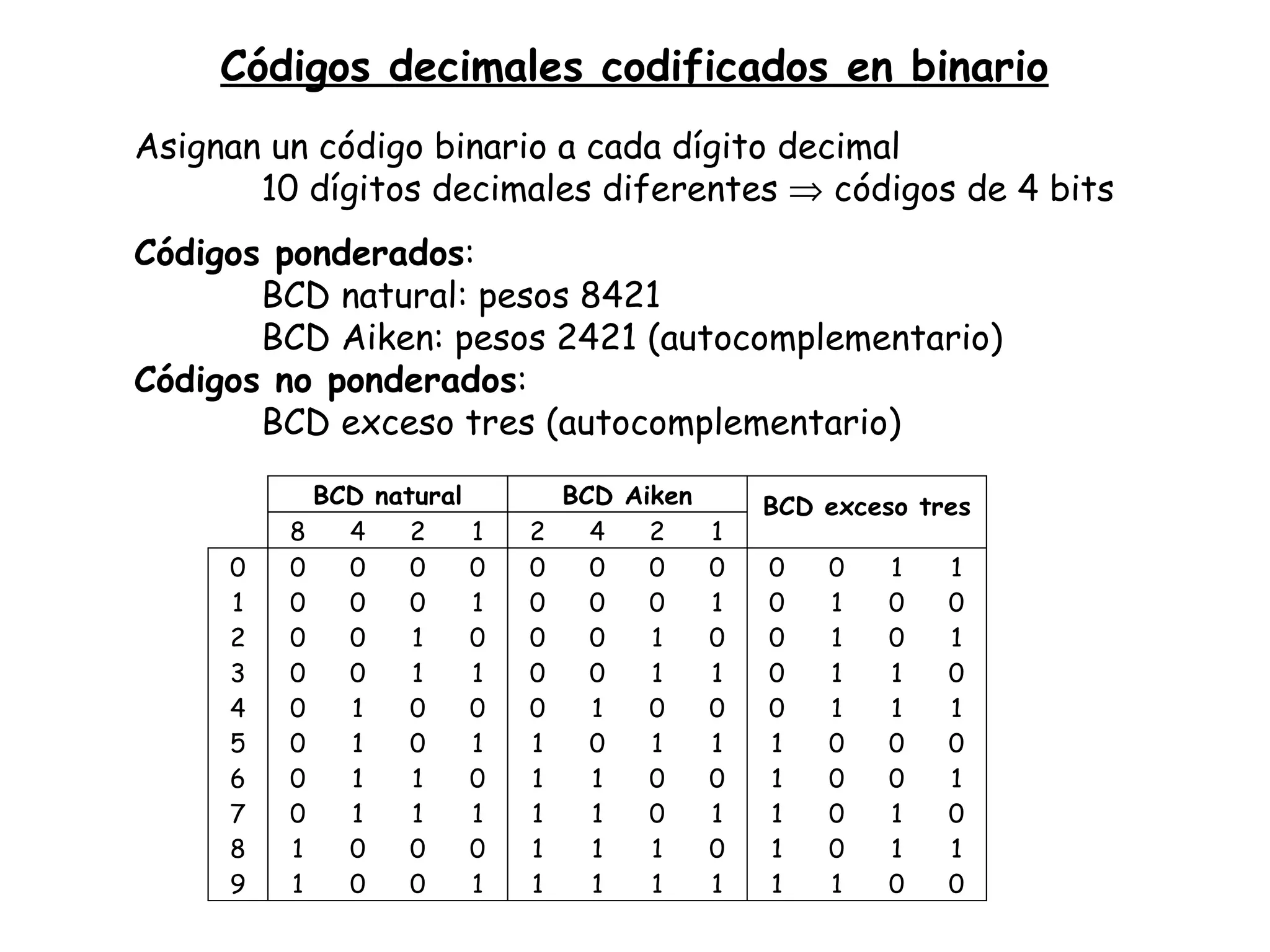
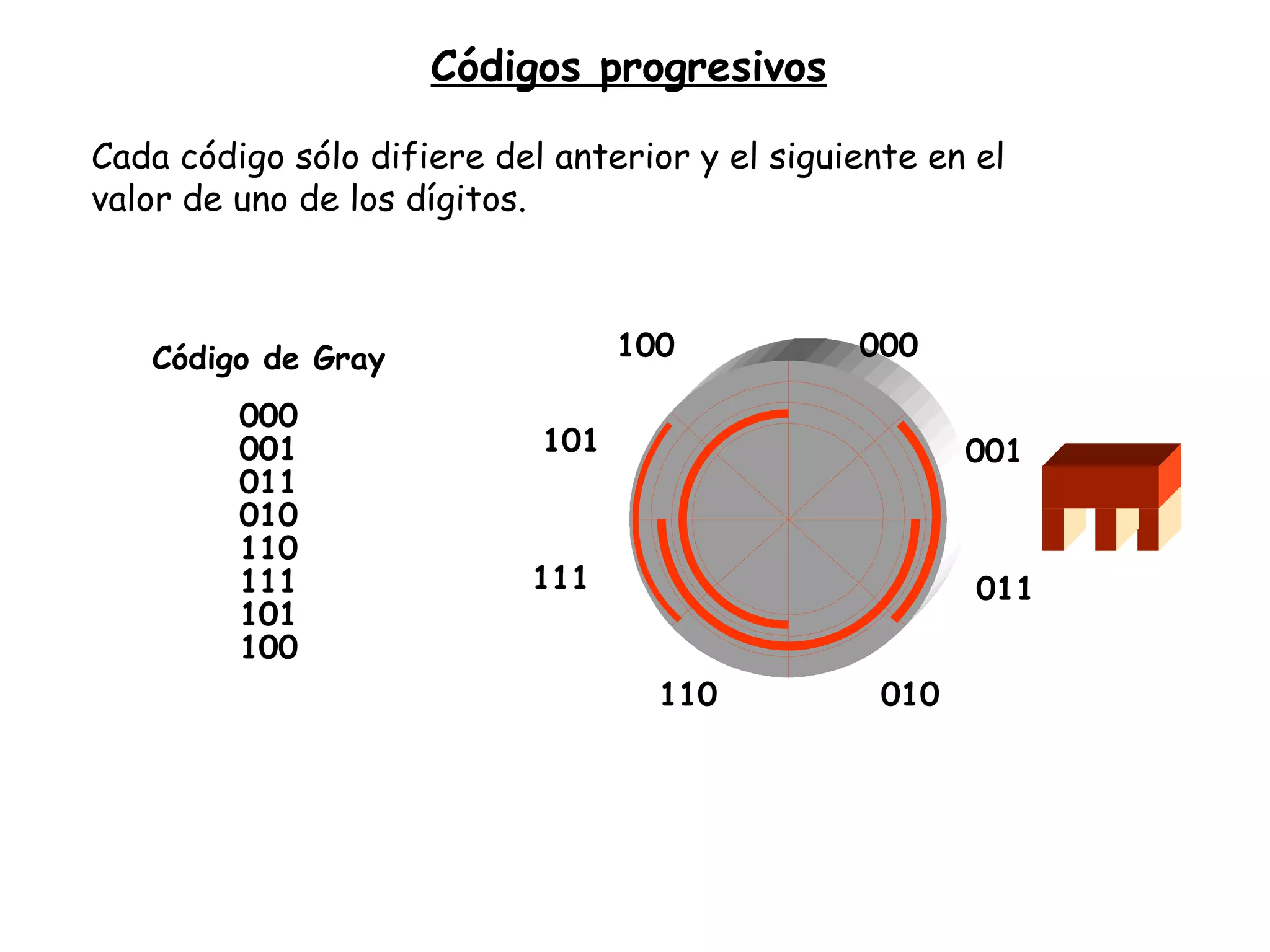
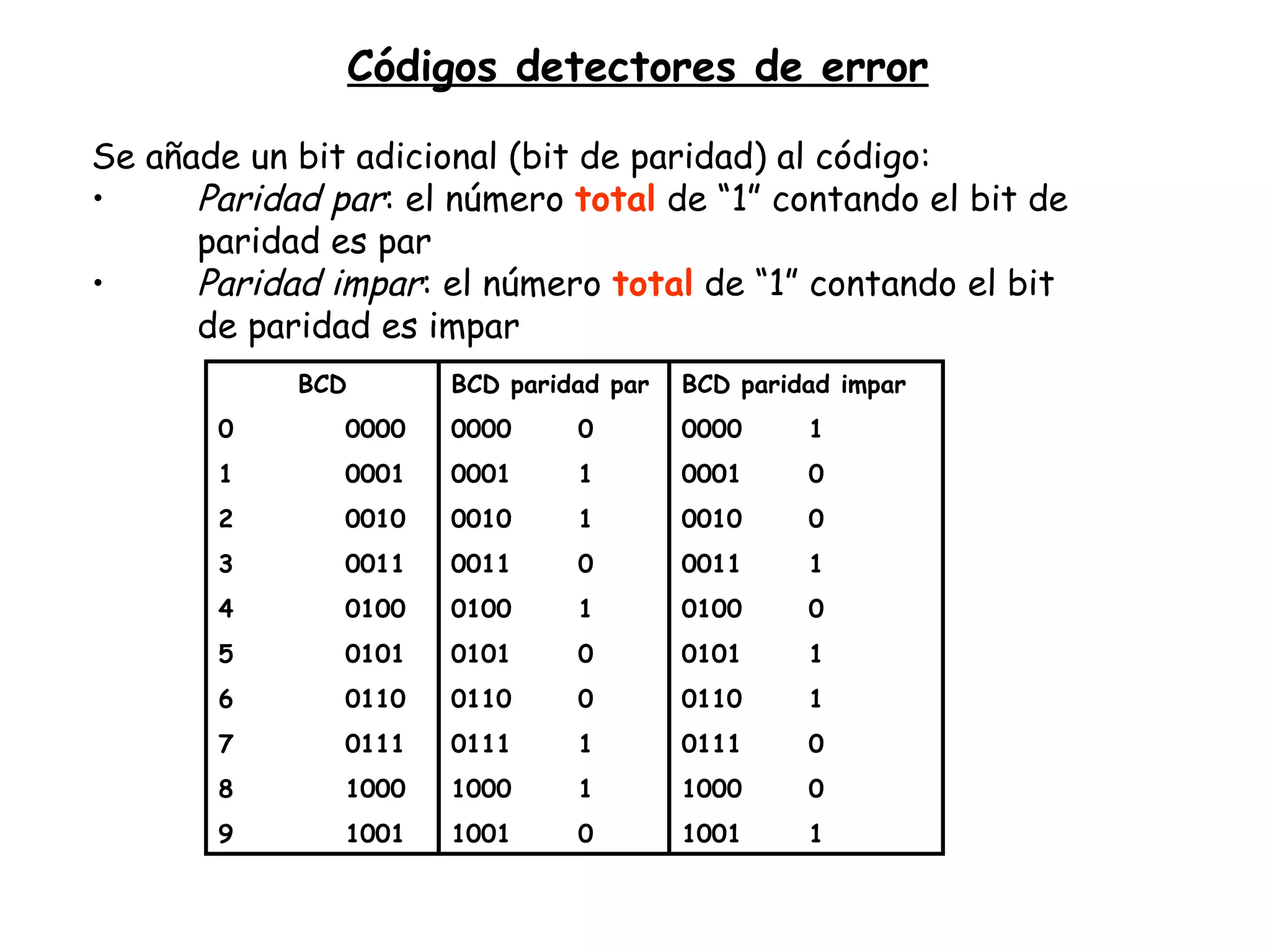
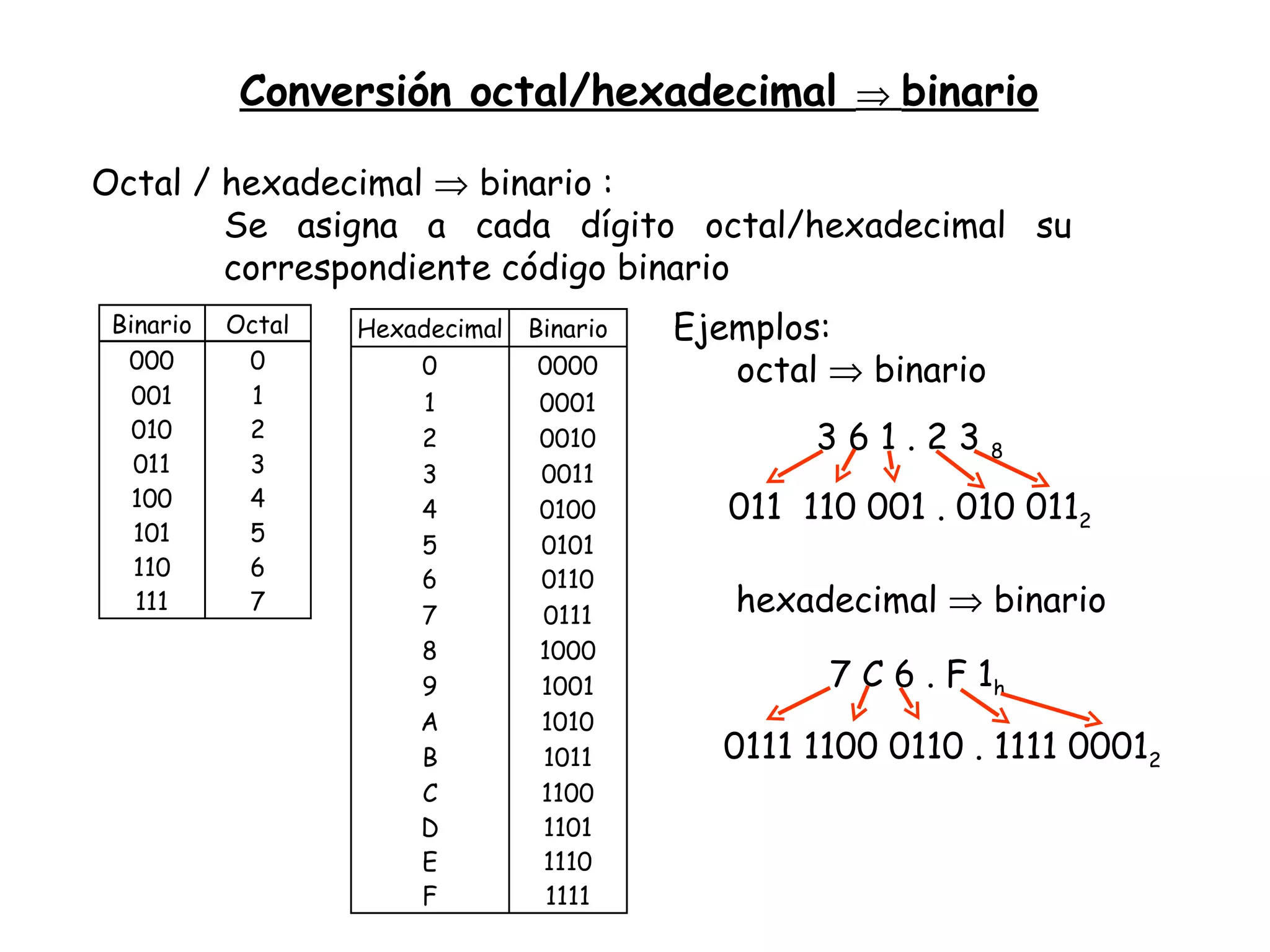
Este documento presenta información sobre el curso de Electrónica Digital. Incluye detalles sobre la profesora, horarios de tutoría, bibliografía recomendada, grupos de prácticas, fechas de exámenes y contenido del programa. También introduce conceptos básicos sobre códigos binarios, conversiones entre sistemas numéricos y representación digital de la información.

1. ELECTRÓNICA DIGITAL Marta Hernando Despacho 3.1.16 [email_address] 985 182 073 Tutorías: Lunes 9.30-11.30 Martes 11.30-13.30, 18.00-19.00 Jueves 19.00-20.00 AULANET: Presentaciones, problemas, exámenes, guías de prácticas

2. Bibliografía: “ Fundamentos de Sistemas Digitales”, Thomas L. Floyd, Ed. Prentice Hall “ Problemas resueltos de Electrónica Digital”, Javier García Zubía, Ed. Thomson Paraninfo “ Sistemas Digitales y Tecnología de Computadores”, José Mª Angulo y Javier García Zubía, Ed. Thomson Paraninfo “ Diseño Digital. Principios y prácticas”, John F. Wakerly, Ed. Prentice Hall “ Fundamentos de lógica digital con diseño VHDL”, Stephen Brown y Zvonko Vranesic, Ed. McGraw-Hill

3. Prácticas: 7 prácticas de 2h (1.4 créditos) Primera práctica: 26 de octubre Repetidores que hayan hecho las prácticas pueden hacer un trabajo Grupos: PL1: PI-Z Jueves 9.30-11.30 PL2: D-MA Martes 9.30-11.30 PL3: A-C Viernes 9.30-11.30 PL4: Lunes 11.30-13.30 PL5: ME-PE Jueves 11.30-13.30

4. Prácticas 20%. Asistencia obligatoria + memoria Evaluación: Examen 80% (mínimo 4.0)

5. Programa: I. Introducción: Codificación y operaciones con códigos. Álgebra de Boole. Puertas lógicas. Funciones lógicas y su simplificación. II. Circuitos combinacionales: Bloques SSI y MSI. Diseño de circuitos secuenciales. III. Circuitos secuenciales: Bloques MSI secuenciales asíncronos y síncronos. Aplicaciones. IV. Introducción a la lógica programada: Memorias y dispositivos lógicos programables.

6. Lección 1 ELECTRÓNICA DIGITAL 1 er curso I.T. Telemática E.U.I.T. Informática de Gijón CÓDIGOS BINARIOS

7. Magnitud analógica: toma valores continuos Magnitud digital: toma valores discretos Ejemplo de magnitud analógica: Ejemplo de magnitud analógica discretizada: Cada valor discreto se puede representar por un código digital Magnitudes analógicas/digitales

8. Sistema binario Es aquel sistema que sólo tiene dos estados distintos: VERDADERO/FALSO ABIERTO/CERRADO 0/1 ENCENDIDO/APAGADO ALTO/BAJO 0V/5V Los dos estados se suelen representar por los símbolos 0 y 1 A los dos símbolos se les llama BITS ( bi nary dig it ) A los grupos de bits (combinaciones de 0s y 1s) se les llama CÓDIGOS: 0011 00101 111100000 011100

9. Códigos binarios CÓDIGO : Representación unívoca de la información, de tal manera que a cada dato se le asigna una combinación de símbolos determinados y viceversa. Código binario natural Código decimal codificado en binario Códigos progresivos Códigos detectores de error Códigos correctores de error

10. Un número se representa por una sucesión ordenada de dígitos situados a izquierda y derecha de un punto de referencia (punto o coma decimal). En un código posicional de base b, cada uno de los posibles dígitos tiene un valor dado por la expresión p i •b i , siendo p el dígito e i su posición respecto al punto de referencia (dígitos a la izquierda: posiciones positivas, dígitos a la derecha: posiciones negativas, 0: primera posición a la izquierda): Para un número N en base b con n+1 dígitos enteros y k dígitos decimales, su valor será: p n •b n +p n-1 •b n-1 +......+ p 1 •b 1 + p 0 •b 0 + p -1 •b -1 +.........+ p -k •b -k En base 2, b=2 y p puede tomar valores 0 o 1. Por ejemplo: 1 0 1 0 2 = 1 • 2 3 + 0 • 2 2 + 1 • 2 1 + 0 • 2 0 = 8 + 0 + 2 + 0 = 10 10 Paso de binario a decimal: resolver el polinomio Código binario natural

11. Parte entera : Se divide el número decimal por dos, siendo el resto el dígito binario menos significativo (p 0 ); el cociente de esta división se vuelve a dividir por dos indicando el nuevo resto el dígito siguiente (p 1 ); se continúa el proceso hasta que el cociente sea menor que dos. Paso de decimal a binario natural p n •b n +p n-1 •b n-1 +......+ p 1 •b 1 + p 0 •b 0 + p -1 •b -1 +.........+ p -k •b -k Parte decimal : Se multiplica por dos; la parte decimal se vuelve a multiplicar por dos y así sucesivamente hasta que el resultado decimal sea cero o se alcance la precisión necesaria. El número binario equivalente es la sucesión de valores enteros generada

12. Paso de decimal a binario natural (((p n •b+p n-1 )•b+......+ p 1 )•b+ p 0 57 28 1 2 14 0 2 7 0 2 3 1 2 1 1 (((p -k •b -1 + p -k-1 )•b -1 +.......+ p -1 )•b -1 p n •b n +p n-1 •b n-1 +......+ p 1 •b 1 + p 0 •b 0 + p -1 •b -1 +.........+ p -k •b -k 0.63 X 2 2 1 . 26 X 2 0 . 52 X 2 1 . 04 X 2 0 . 08 57,63 10 =111001,1010 2

13. Códigos decimales codificados en binario Asignan un código binario a cada dígito decimal 10 dígitos decimales diferentes  códigos de 4 bits Códigos ponderados : BCD natural: pesos 8421 BCD Aiken: pesos 2421 (autocomplementario) Códigos no ponderados : BCD exceso tres (autocomplementario)

14. Códigos progresivos Cada código sólo difiere del anterior y el siguiente en el valor de uno de los dígitos. 000 001 011 010 110 111 101 100 Código de Gray 000 001 011 010 110 111 101 100

15. Códigos detectores de error Se añade un bit adicional (bit de paridad) al código: Paridad par : el número total de “1” contando el bit de paridad es par Paridad impar : el número total de “1” contando el bit de paridad es impar BCD 0 0000 1 0001 2 0010 3 0011 4 0100 5 0101 6 0110 7 0111 8 1000 9 1001 BCD paridad par 0000 0 0001 1 0010 1 0011 0 0100 1 0101 0 0110 0 0111 1 1000 1 1001 0 BCD paridad impar 0000 1 0001 0 0010 0 0011 1 0100 0 0101 1 0110 1 0111 0 1000 0 1001 1

16. Códigos correctores de error La paridad simple detecta pero no corrige; se hace preciso acudir a la Paridad entrelazada: 000001 1 000011 0 010101 1 111011 1 101100 1 Datos enviados, con paridad horizontal par Palabra de paridad vertical par 000101 1 000011 0 010101 1 111011 1 101100 1 ¡ Se puede corregir en la recepción!

17. Códigos de carácter Código ASCII: Una secuencia de bits se utiliza para representar caracteres : J=1001010 ( A merican S tandard C ode I nformation I nterchange) También se utiliza para mandar comandos: Retorno de carro a una impresora ...

18. Códigos octal y hexadecimal Código octal : Código en base 8 Cada dígito toma valores entre 0 y 7 5470 8 = 5*8 3 + 4*8 2 + 7*8 1 + 0*8 0 = 2560 + 256 + 56 + 0 = 2872 10 Código hexadecimal : Código en base 16 Cada dígito toma valores entre 0 y 15; se hace preciso distinguir de alguna forma los dígitos que tienen dos cifras Ejemplo: 1 5 7 6 ¿ Es “uno” y “cinco” o es “quince”? Los dígitos a partir del 10 (inclusive) se denominan con letras: A, B, C, D, E y F 5B70 h = 5*16 3 +11*16 2 +7*16 1 +0*16 0 = 20480+2816+112+0=23408 10

19. Conversión binario  octal/hexadecimal Binario  octal: Se agrupan los bits de tres en tres a partir del punto decimal, asignando el código octal a cada grupo 10110.1001 2 = 0 1 0 1 1 0 . 1 0 0 1 0 0 =26.44 8 Binario  hexadecimal: Se agrupan los bits de cuatro en cuatro a partir del punto decimal, asignando el código hexadecimal a cada grupo 10110.1001 2 = 0 0 0 1 0 1 1 0 . 1 0 0 1 =16.9 h

20. Conversión octal/hexadecimal  binario Octal / hexadecimal  binario : Se asigna a cada dígito octal/hexadecimal su correspondiente código binario 3 6 1 . 2 3 8 011 110 001 . 010 011 2 7 C 6 . F 1 h 0111 1100 0110 . 1111 0001 2 Ejemplos: octal  binario hexadecimal  binario